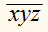Как найти двузначное число формулы

Найдем сколько всего двузначных чисел. Двузначные числа — состоят из двух цифр и находятся в диапазоне от 10 до 99. Наименьшее двузначное число — 10, а наибольшее — 99. Чтобы найти общее количество таких чисел, мы можем просто вычесть наименьшее из наибольшего и добавить 1 к результату. Следовательно, 99 — 10 + 1 = 90. Это значение необходимо знать в 5 классе по математике.

Оно довольно часто используется как в элементарной, так и в высшей математике. Действительно, данное знание понадобится вам и при решении задач из ОГЭ и ЕГЭ по математике. Заметьте, что мы используем только элементы натурального ряда. Определить количество можно и другими способами. Их и рассмотрим в данной статье и решим несколько задач, а еще совершим небольшой экскурс в историю математики.

Описание

Любая запись числа содержит разряды, в случае записи 2х значного числа разрядов тоже два: разряд десятков и разряд единиц. Для записи мы пользуемся символами — цифрами. Для записи разряда десятков нам понадобятся 9 цифр (0 не подойдет — если мы поставим в разряде десятков ноль, то получим только разряд единиц). А в разряде единиц нам понадобятся все 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Запись такого числа:

stackrel{десятки}{a} , stackrel{единицы}{b}

Например, возьмём случайное число 89 (восемьдесят девять) — у него в записи 8 — количество десятков, 9 — количество единиц.

Вычисление

Как еще можно определить сколько всего двузначных натуральных чисел. Существует 10 возможных цифр для разряда единиц и 9 возможных цифр для разряда десятков. Так как мы не можем обозначить через 0 количество десятков — так как таких чисел двузначных не бывает.

Для каждого значения в разряде десятков есть десять вариантов записи числа единиц, например, если разряд десятков 1:

• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19

А всего у нас может быть 9 вариантов записи разряда десятков.

Значит общее количество можно получить, умножив количество вариантов записи десятков на количество вариантов записи единиц:

9·10=90.

Другими словами, существует 90 различных натуральных двузначных чисел, которые можно составить, используя цифры от 0 до 9. Самым маленьким будет 10, а самым большим — 99.

Приведем все из них (вы можете в дальнейшем возвращаться к этой записи при решении задач на похожую тему, когда нужно «найти все делящиеся на 2», «найти все кратные 8», например):

• 10, 11, 12, 13, 14, 15, 16, 17, 18, 19,
• 20, 21, 22, 23, 24, 25, 26, 27, 28, 29
• 30, 31, 32, 33, 34, 35, 36, 37, 38, 39
• 40, 41, 42, 43, 44, 45, 46, 47, 48, 49
• 50, 51, 52, 53, 54, 55, 56, 57, 58, 59
• 60, 61, 62, 63, 64, 65, 66, 67, 68, 69
• 70, 71, 72, 73, 74, 75, 76, 77, 78, 79
• 80, 81, 82, 83, 84, 85, 86, 87, 88, 89
• 90, 91, 92, 93, 94, 95, 96, 97, 98, 99.

Подсчитаем количество четных и нечетных из них. В каждом ряду будет 5 четных (например, в первом ряду это будут 10, 12, 14, 16, 18) и 5 нечетных (в первом ряду 11, 13, 15, 17, 19), так как рядов всего 9, то получаем 45 четных двузначных чисел и 45 нечетных.

Простые двузначные числа: 11, 13, 17, 19, 23, 29, 31, 37, 43, 47, 53, 59, 67, 73, 79, 83, 89, 97.

Примеры

Задача 1. Найдите количество всех двузначных чисел, делящихся на 3 без остатка.

Решение:

Чтобы определить количество 2-х значных натуральных чисел, делящихся на 3, нам сначала нужно вспомнить признак делимости на 3.

Правило. Число делится на 3, если сумма его цифр также делится на 3. Например, 21 делится на 3, потому что 2 + 1 = 3, а 66 делится на 3 потому что 6+6=12, а 12 делится на 3.

Мы можем начать с перечисления всех вариантов и проверки того, какие из них делятся на 3.

Вот они: 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99. Пересчитаем и увидим, что их всего 30. Но есть и более простой способ решения этой задачи — альтернативный.

В качестве альтернативы мы можем использовать более математический подход, чем простое подсчитывание. Мы знаем, что двузначные натуральные числа находятся в диапазоне от 10 до 99 и их всего 90. Мы можем найти количество тех из них, которые делятся на 3, путем деления 90 на количество возможных исходов для каждых трех.

Каждое третье, начиная с 12, будет делиться на 3: 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42…93, 96, 99. То есть, повторимся для лучшего понимания, из 90 каждое третье будет делиться на 3.

Тогда если мы разделим 90 на 3, мы получим 30 без остатка.

Ответ: 30

Задача 2. Определите количество двузначных чисел, делящихся на 5 без остатка.

Решение:

Число делится на 5, если оно оканчивается на 0 или 5. Следовательно, чтобы найти количество двузначных натуральных чисел, которые делятся на 5, нам нужно найти те из них, которые оканчиваются на 0 или 5.

Сначала мы рассмотрим оканчивающиеся на 0. Это числа от 10 до 99, которые кратны 10. Мы знаем, что между 10 и 99 есть 9 чисел кратных 10, то есть 10, 20, 30, 40, 50, 60, 70, 80 и 90.

Теперь мы рассмотрим те, что оканчиваются на 5. Мы знаем, что между 15 и 95 существует 9 чисел кратных 5, то есть 15, 25, 35, 45, 55, 65, 75, 85, 95.

Чтобы получить общее количество, складываем оканчивающиеся на 0 и оканчивающиеся на 5:

9 (оканчивающиеся на 0) + 9 (оканчивающиеся на 5) = 18

Следовательно, существует 18 двузначных натуральных чисел, делящихся на 5. Это числа: 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90.

Ответ: 18.

Задача 3. В ящике находятся шары, на них нанесены только двузначные числа. Маша вынимает шар, определите вероятность того, что число на шаре будет делиться на 5.

Ответ: Всего чисел, кратных пяти — восемнадцать (смотрите предыдущую задачу). Маша может достать любой шар. Благоприятных исходов 18. А всего исходов — 90.

Таким образом, рассчитываем вероятность, как отношение количества благоприятных исходов к общему количеству исходов.

P=18/90= 0,2.

Ответ: 0,2.

Задача 3. Сколько всего двузначных чисел, в записи которых есть цифра 1?

Решение: опираясь на список, можно просто выписать все его элементы, удовлетворяющие условию задачи:

10, 11, 12, 13, 14, 15, 16, 17, 18, 19,

20, 21, 22, 23, 24, 25, 26, 27, 28, 29

30, 31, 32, 33, 34, 35, 36, 37, 38, 39

40, 41, 42, 43, 44, 45, 46, 47, 48, 49

50, 51, 52, 53, 54, 55, 56, 57, 58, 59

60, 61, 62, 63, 64, 65, 66, 67, 68, 69

70, 71, 72, 73, 74, 75, 76, 77, 78, 79

80, 81, 82, 83, 84, 85, 86, 87, 88, 89

90, 91, 92, 93, 94, 95, 96, 97, 98, 99.

Это будут: все элементы первого ряда 10, 11, 12, 13, 14, 15, 16, 17, 18, 19 — здесь цифра 1 стоит в разряде десятков. И по одному элементу из каждого из следующих рядов: 21, 31, 41, 51, 61, 71, 81, 91. Итого: 18.

Ответ: 18.

Немного истории математики

Понятие двузначных чисел, то есть состоящих из двух цифр, берет свое начало в развитии ранних систем счета. В ранних цивилизациях счет в основном производился с помощью пальцев, и это был первый способ счета. Люди считали на пальцах рук и ног, чтобы представлять сколько у них предметов, продуктов, добычи.

По мере того как общества становились более сложными и возникала потребность в более сложных способах счета, люди начали использовать другие объекты для представления количества. Они начали использовать камешки, палочки или другие мелкие предметы, а затем помещали их в группы, чтобы представить большие числа. Такое представление называется «система подсчета».

По мере развития системы подсчета люди начали использовать символы, и именно здесь мы видим начало происхождения системы счисления. В первых системах счисления использовались простые метки или символы, например, линия для обозначения единицы, две линии для обозначения двух и так далее.

Со временем эти символы стали более сложными и изощренными, и, в конце концов, была разработана концепция позиционной записи. Разрядность — это концепция представления чисел с помощью цифр, где каждая цифра представляет разную степень числа 10. Например, в записи 42 — 4 представляет четыре десятка, а 2 — две единицы.

Эта система позволяла представлять гораздо большие числа с использованием меньшего количества символов, а также делала арифметические операции, такие как сложение и вычитание, намного более эффективными. Это та система, которую мы используем до сих пор.

Похожая статья — сколько всего трехзначных чисел.

Обозначение
десятеричной записи числа.

у – цифра указывающая количество
десятков в числе
z – цифра указывающая
количество единиц в числе.


ПРИМЕР:


Четырёхзначное число с цифрами  a, b, c 
и  d  можно обозначить

Эта запись означает


1000a + 100b + 10c + d.


ПРИМЕР:


378
= 100 × 3 + 10 × 7 + 8.


ЗАДАЧА:


В двузначном числе цифра десятков на  4  больше цифры единиц. Когда это число
разделили на цифру единиц, то в частном получилось  24, а в остатке число, которое
на  2  меньше делителя. Найти задуманное число.

РЕШЕНИЕ:


Решая эту
задачу, можно использовать обозначение десятеричной записи числа. Заданное
число можно обозначить

В
соответствии с этим обозначением можно записать:

а по условию задачи имеем:

= 24
и ост (х – 4) – 2

=
24(х – 4) + х – 6.

10х + х
– 4 = 24(х – 4) + х – 6,
10х – 4 = 24х – 96 – 6,
 14х
= 98,  х = 7, тогда  10 × 7 + 7 – 4 = 73.
Задуманное число  73.


Алгоритм
решения задач, в которых используется формула двузначного числа.


Вводится
обозначение:


х – цифра десятков
у – цифра единиц


Искомое
двузначное число


10х + у


Составляется
система уравнений.


ЗАДАЧА:


Двузначное число в четыре раза больше суммы
его цифр. Если к этому числу прибавить произведение его цифр, то получится  32. Найдите это
двузначное число.


РЕШЕНИЕ:


х – цифра
десятков,  у – цифра
единиц.
10х + у – искомое число, тогда по условию задачи:

2х² + 12х – 32 = 0,
х² + 6х
– 16 = 0.
х₁ = –8 (посторонний корень)
х₁ = 2, тогда  у =
4.


ОТВЕТ:  24


Задания к уроку 37

Думаю, что для решения данной задачи достаточно второй части условия.

Мы имеем некое пока неизвестное двузначное число. Обозначим первую его цифру буквой a, а вторую цифру — буквой b. Всё число в целом я обозначу здесь как <ab>.

Мы знаем, что обратное число, то есть <ba>, составляет 208 % от числа <ab>.

Можем написать уравнение:

<ba> = <ab> * 2,8

В то же время что такое <ab> и <ba>? Это соответственно 10b + a и 10a + b.

Имеем:

10b + a = 2,08(10a + b)

a + 10 b = 20,8a + 2,08b

20,8a + 2,08b = a + 10b

20,8a – a = 10b – 2,08b

19,8a = 7,92b |:7,92

2,5a = b.

Мы получили простейшее соотношение цифр искомого числа: вторая его цифра в два с половиной раз больше первой.

Каково же может быть значение a? Очевидно, что b<=9, отсюда 2,5a<=9, a<=3,6. Но, очевидно, a должно быть натуральным числом (a не может равняться нулю, так как в начале числа ноль, как правило, не пишется, и у тогда у нас будет однозначное число, а ведь по условию необходимо двузначное). Кроме того, a непременно должно быть чётным, так как при умножении его на 2,5 получается целое число (b). Единственное чётное натуральное число, меньшее, чем 3,6 — число 2.

Итак, a = 2. Отсюда легко находим b: b = 2,5 * 2 = 5.

Искомое число равно 25.

Разумеется, теперь можно проверить выполнение первого условия задачи:

[(2^2 + 5^2) – 1] : (2 + 5) = (29 – 1) : 7 = 28 : 7 = 4. Вроде всё сходится.

Я пробовал составлять уравнение и по первому условию задачи.

Получается такое вот уравненьице:

a^2 + b^2 = 4a + 4b + 1

или, что равносильно:

b^2 – 4b + a^2 – 4a – 1 = 0

Уж не знаю, можно ли решить его, не применяя метод перебора. Но я честно перебрал все значения для a от 1 до 9. Натуральные решения для b получаются только при a = 2 и при a = 5: 1) a = 2, b = 5; 2) a = 5, b = 2. Итак, мы получили два числа: 25 и 52. Поскольку уравнение для первого условия задачи симметрично, то первому условию удовлетворяет как 25, так и 52. Однако же число 52 не подходит по второму условию (для числа 52 обращённое число меньше исходного). Так что остаётся только одно-единственное число — это 25.

Содержание:

1. Правила и формулы комбинаторики
2. Примеры решения
3. Пример 1.
4. Пример 2.
5. Пример 3.
6. Пример 4.
7. Пример 5.
8. Пример 6.
9. Пример 7.

Правила и формулы комбинаторики

При решении задач теории вероятностей используются правила и формулы комбинаторики.

Правило суммы. Пусть дана некоторая совокупность объектов (произвольной природы). Если некоторый объект может быть выбран из этой совокупности способами, а другой объект может быть выбран способами, то выбор либо объекта либо объекта можно осуществить способами.

Правило произведения. Если объект может быть выбран способами и после каждого такого выбора объект можно выбрать способами, то выбор упорядоченной пары объектов можно осуществить способами.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Примеры решения

Пример 1.

Сколько имеется двузначных чисел, составленных из разных цифр?

Решение:

Первой цифрой числа может быть одна из цифр 1, 2, …, 9, а второй — одна из оставшихся после выбора первой цифры, а также 0 (одна из девяти цифр). Искомое количество, согласно правилу произведения, равно

Размещениями из (различных) элементов по элементов называются комбинации, состоящие из элементов, взятых из элементов которые отличаются друг от друга либо составом взятых элементов, либо их порядком. Число размещений равно

Пример 2.

Сколько трехзначных чисел можно составить из шести цифр 0, 1, 2, 3, 4, 5?

Решение:

Из данных шести цифр отобрать три (в определенном порядке) можно способами. Из этого количества нужно вычесть те тройки чисел, которые начинаются с нуля (т.е. количество двузначных чисел); оно равно числу размещений из цифр 1, 2, 3, 4, 5 по две, т.е. Искомое число трехзначных чисел равно

Перестановками элементов называются комбинации, состоящие из этих элементов, отличающиеся друг от друга только порядком расположения элементов. Число перестановок равно

Эту формулу можно получить из выражения для при

Возможно вам будут полезны данные страницы:

Пример 3.

Сколькими способами можно рассадить за столом 4 человека?

Решение:

Искомое число способов равно числу перестановок четырех элементов, т.е.

Сочетаниями из (различных) элементов по называются комбинации, состоящие из элементов, взятых из данных элементов которые отличаются друг от друга хотя бы одним элементом. Число сочетаний равно

Число сочетаний удовлетворяет соотношению

Пример 4.

Сколькими способами можно отобрать три шара из ящика,

содержащего шесть пронумерованных шаров?

Решение:

Искомое число способов равно числу сочетаний из шести элементов по три, т.е.

Пусть задано конечное множество элементов некоторой природы. Из них можно составлять определенные комбинации, количество которых изучает комбинаторика. Некоторые ее формулы используются в теории вероятностей; приведем их.

Комбинации, состоящие из одной и той же совокупности разных элементов и отличающиеся только порядком их расположения, называются перестановками. Число всех возможных перестановок определяется произведением чисел

от единицы до

Пример 5.

Сколько четырехзначных чисел можно составить из цифр 1, 2, 3 и 4 с использованием всех указанных цифр в каждом числе?

Решение:

Искомое число

Комбинации по элементов, составленные из разных элементов отличающиеся друг от друга либо элементами, либо их порядком, называются размещениями. Число всевозможных размещений

Пример 6.

Сколько трехзначных чисел можно составить из семи разных цифр при отсутствии среди них нуля?

Решение:

Искомое количество цифр

Комбинации, содержащие по элементов каждая, составленные из разных элементов и различающиеся хотя бы одним элементом, называются сочетаниями. Число сочетаний определяется по формуле

Соответственно справедливы следующие формулы:

Первую из формул (1.4) удобно использовать, в частности, в расчетах, когда

Напомним формулу бинома Ньютона, в которой участвуют коэффициенты

(1.3):

Пример 7.

Сколькими способами можно выбрать:

а) по две карты;

б) по 32 карты,

из колоды, содержащей 36 игральных карт?

Решение:

Искомое число способов: