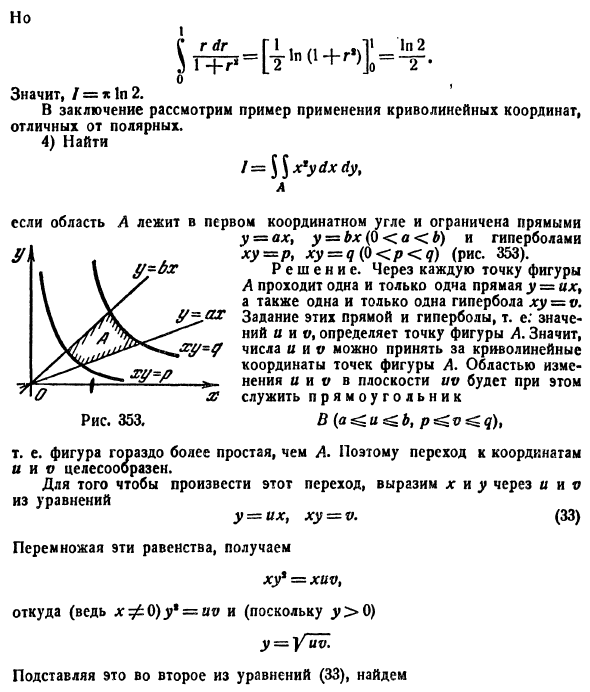
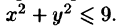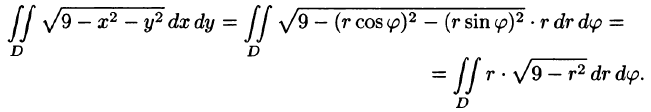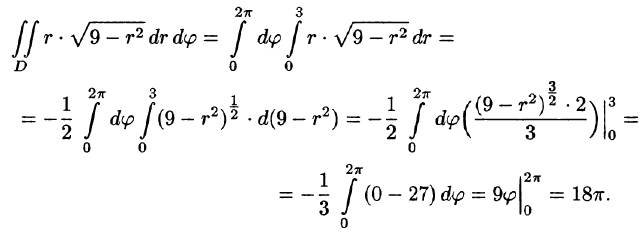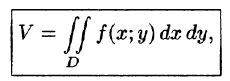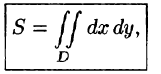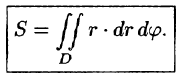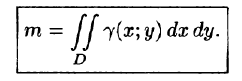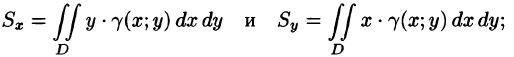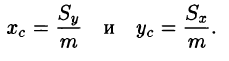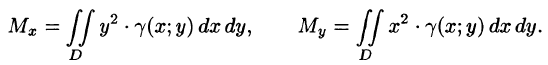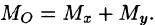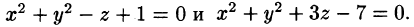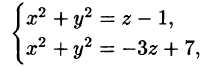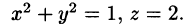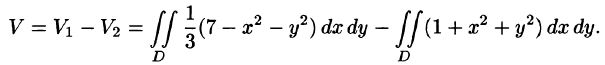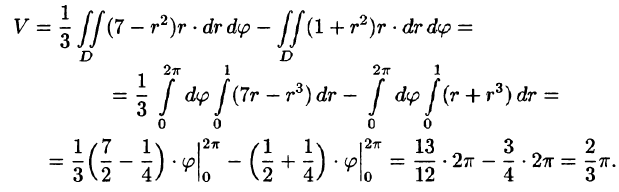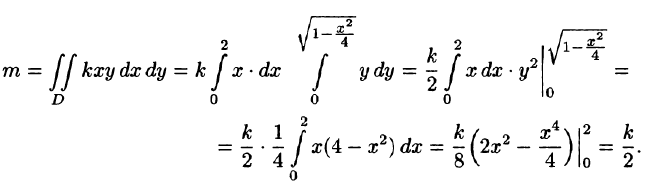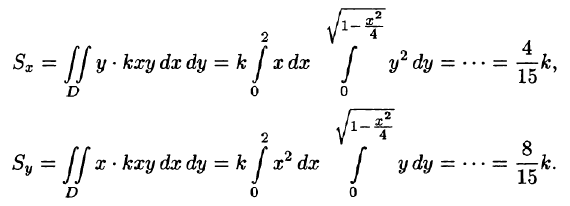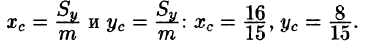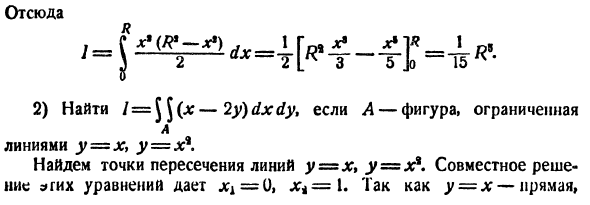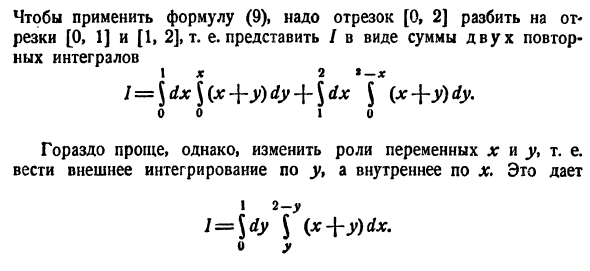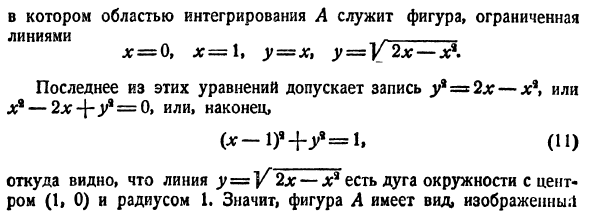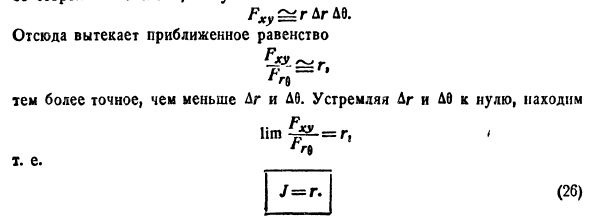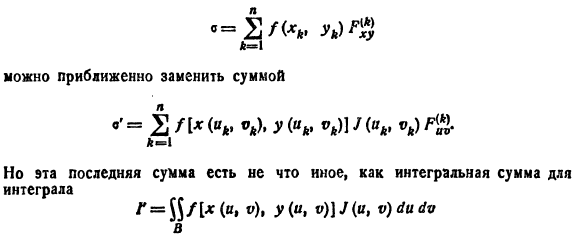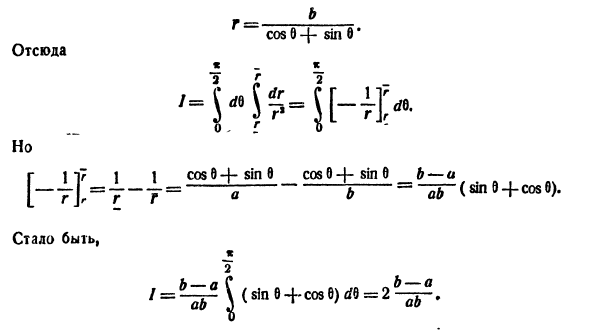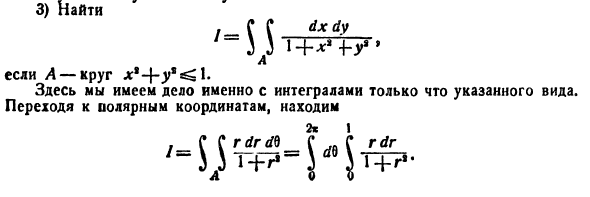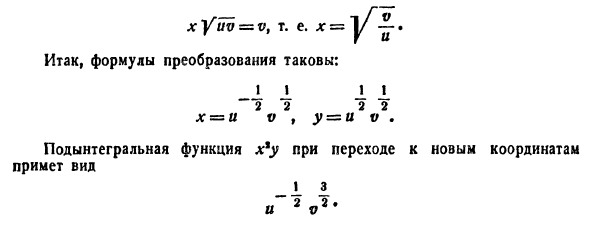(схема 40)
Для функции двух переменных имеет место обобщение определенного интеграла — двойной интеграл, относящийся к кратным интегралам.
Рассмотрим в плоскости x0y замкнутую
область D с границей L. Пусть непрерывная функция f(x,y) определена в области D. Произвольными линиями разобьем область D на конечное число n частей
– площадок: 

соответствующих площадок, но и их площади.
В каждой из ∆Si (внутри или на границе) возьмем точку Pi;
получим n точек: 

сумму произведений вида 

Эта
сумма называется интегральной суммой для функции f(x,y) в
области D. Если f ≥ 0 в области D, то каждое
слагаемое 
Рассмотрим произвольную
последовательность интегральных сумм, составленных с помощью функции f(x,y) для данной области D:

при
различных способах разбиения
области D на
части ∆Si. Очевидно, при n→∞ максимальный диаметр
площадок ∆Si стремится к нулю.
Теорема
6.1.
Если функция f(x,y) непрерывна в замкнутой области D, то
существует предел последовательности (6.2) интегральных сумм (6.1) при условии, что максимальный диаметр площадок ∆Si стремится к нулю, а n→∞. Этот предел один и тот же
для любой последовательности вида (6.2), то есть он не зависит ни от способов разбиения
области D на площадки ∆Si, ни от
выбора точек Pi внутри площадок ∆Si
Этот предел 

Область D при этом называется
областью интегрирования.
1. Вычисление двойного интеграла в декартовой система
координат
Рассмотрим область D, лежащую в плоскости x0y и являющуюся правильной в направлении оси 0y. Это означает, что всякая прямая, параллельная оси 0y и проходящая через
внутреннюю точку области, пересекает границу области в двух точках N1 и N2.
Мы
предположим, что в рассматриваемом случае область D
ограничена линиями: 

на отрезке [a;b]. Аналогично определяется
область D, правильная
в направлении оси 0x.
Если область D является правильной как в направлении оси 0x, так и в направлении оси 0y, то
она называется просто правильной областью.
Пусть функция f(x,y) непрерывна в области D. Рассмотрим
выражение

которое назовем двукратным
интегралом от функции f(x,y) по
области D. В этом
выражении сначала вычисляется внутренний интеграл, стоящий в скобках, причем
интегрирование производится по y, а x
считается постоянной величиной. В
результате интегрирования получится непрерывная функция от x:

Эту функцию мы интегрируем по x
в пределах от a
до b:

В результате получается некоторое постоянное число.
Теорема
6.2. Двойной интеграл от непрерывной функции f(x,y) по
правильной области D равен двукратному
интегралу от этой функции по области, то
есть

Пусть правильная в направлении оси 0x область D
ограничена линиями 

Очевидно, что в этом случае

Таким образом, для вычисления двойного
интеграла его надо представить в виде двукратного, в зависимости от вида
области D или
подынтегральной функции, либо с помощью формулы (6.5), либо (6.6) .
Пример
6.1. Вычислить 
определяемый неравенствами и

Решение. Применим
формулу (6.5), считая внутренний интеграл по переменной y:
Если область D является правильной в направлении обеих осей
координат, то применимы обе формулы (6.5) и (6.6), следовательно,

Таким образом, повторное интегрирование не
зависит от порядка интегрирования. Поэтому при вычислении двойного
интеграла следует пользоваться той из двух формул, которая приводит к менее трудоемким
выкладкам. Полезно для упражнения в вычислении повторного интегрирования рассматривать задачу о замене порядка
интегрирования в двойном интеграле 
последовательность действий:
1) чертят область интегрирования D, которая
находится в полосе между прямыми x=a и x=b, при этом ограничена снизу линией y=φ1(x), а сверху
– линией y=φ2(x);
2) область D проектируют на ось 0y и находят уравнения
прямых y=c и y=d, ограничивающих снизу и
сверху полосу, в которой расположена область
D;
3) находят
левую x=ψ1(y) и правую x=ψ2(y) границу области D.
Аналогичные выкладки производят при
необходимости замены порядка интегрирования в двойном интеграле :
1) чертят область интегрирования D, которая находится в полосе между прямыми y=c и y=d, при этом ограничена слева линией x=ψ1(y), а справа
– линией x=ψ2(y);
2) область D проектируют на ось 0x и находят уравнения
прямых x=a и x=b, ограничивающих слева и
справа полосу, в которой расположена область
D;
3) находят нижнюю y=φ1(x) и
верхнюю y=φ2(x) границу области D.
Примечание. В случае, когда какая-либо из этих границ состоит из
двух или большего числа линий, записанных разными уравнениями, то область D разбивается на части, а интеграл – на сумму
интегралов по этим частям
Пример 6.2. Изменить
порядок интегрирования 
Решение. Область D расположена в плоскости x0y между прямыми x=0 и x=1 (рис. 6.1). Ее нижняя граница y=x,
верхняя –

области является прямая x=0, правой на участке
участке

2. Вычисление двойного интеграла в полярной системе
координат
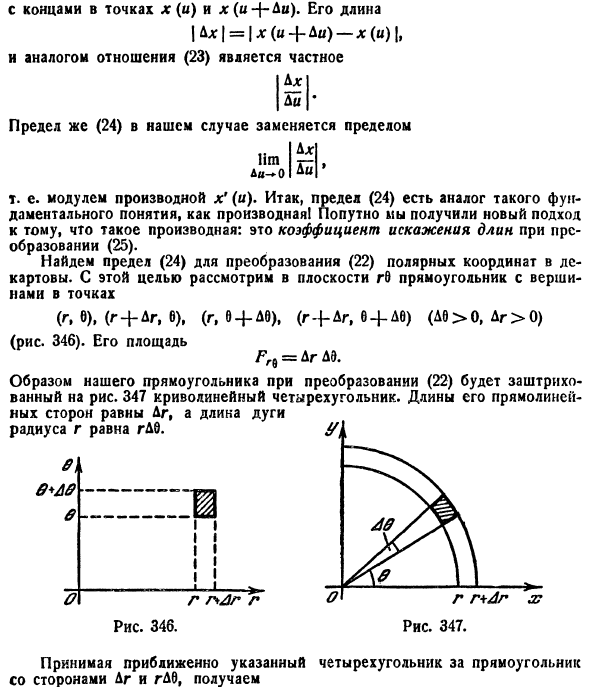
Пусть область D задана в полярной системе координат (рис. 6.2). Если ее полюс O совпадает с началом
координат декартовой системы, а полярная ось совпадает с осью 0x, то формулы перехода имеют
вид:

полярной системе. Тогда

Для вычисления
такого двойного интеграла применяют то же правило сведения его к двукратному
интегралу. Так, если область D имеет
вид, изображенный на рисунке 6.2 (ограничена лучами φ=α и φ=β,
где α < β, и кривыми 
луч, выходящий из полюса, пересекает ее границу L не более чем в двух точках), то правую часть формулы
(6.7) можно записать в виде:

Внутренний интеграл берется при
постоянном φ и переменной r, при
вычислении внешнего интеграла φ
становится переменной.
Если полюс O лежит внутри области D, то каждый полярный радиус
пересекает контур L в одной точке. При этом следует рассматривать 
Пример 6.3. Вычислить двойной интеграл 
полукруг с центром в точке (3;0) и с радиусом, равным 3 (рис. 6.3).
Решение. Перейдём к полярной
системе координат. Пусть полюс совпадает
с началом координат, а полярная ось совпадает с положительным направлением оси 0x. Чтобы найти
уравнение полуокружности АМО в полярной системе координат, выберем на ней
произвольную точку M(r;φ) и определим
зависимость между полярными координатами r и φ. Как видно, при любом выборе точки M угол АМО будет прямым. Следовательно, r=OA∙cos φ или r=6∙cos φ (так как AO=6). Таким образом, в
заданной области D полярный радиус r меняется от 0 до 6∙cos φ, а полярный угол φ
– от 0 до
Переходя к полярной системе координат с помощью (6.8),
получаем:
Примечание. Переход к полярным координатам полезен, когда подынтегральная
функция имеет вид 
линий, ограничивающих область D, также преобразуются к полярным координатам
Двойные интегралы используют в математике, механике, физике. С его помощью можно решить огромное количество непростых задач. Ниже приведено 10 примеров на двойные и тройные интегралы, которые в значительной степени облегчат подготовку к контрольной работе или экзамену. Примеры взяты из индивидуальной работы по высшей математики.
ВАРИАНТ — 12
Двойной интеграл
ЗАДАНИЕ 1.18 Изменить порядок интегрирования в двойном интеграле:
Решение: Сначала записываем область интегрирования, которая ограничена границами
где y=2/x — гипербола.
y=-x2-4x-3 — парабола с вершиной в точке S (-2;1), ветками вниз.
Чтобы знать, как расставить пределы интегрирования при изменении порядка интегрирования изобразим область интегрирования на плоскости
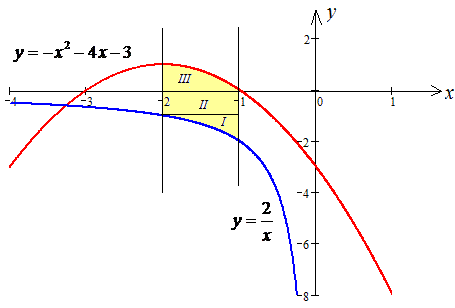
y=2/x, отсюда x=2/y; y=-x2-4x-3, отсюда 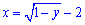
Из рисунка видим, что при изменении порядка интегрирования область необходимо разделить на три части: D=D1+D2+D3.
Расставим пределы интегрирования в каждой области:
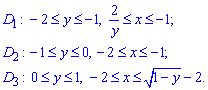
Изменяем порядок интегрирования функции
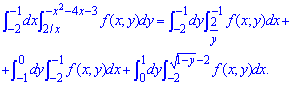
ЗАДАНИЕ 2.19 Найти площадь плоской фигуры, заданной следующими условиями, : y=2x, y=5, 2x-2y+3=0.
Решение: Прежде всего выполняем построение всех кривых, чтобы видеть как будут изменяться пределы интегрирования
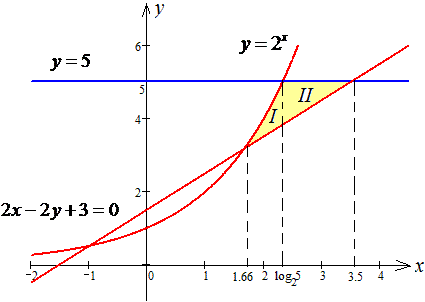
1 и 2
отсюда
Дальше точки пересечения 2 и 3 функций
отсюда
Напоследок пересечение 1 и 3 ф-й
отсюда
Заданную область будем разбивать на две области: D=D1+D2.
Расставим пределы для каждой из областей:
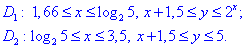
Через двойной интеграл находим площадь фигуры которая ограничена заданными кривыми, :
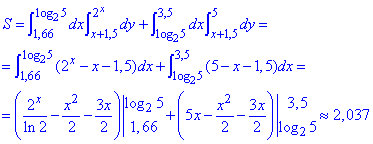
При округлении площадь криволинейной трапеции равна 2,037 единиц квадратных.
ЗАДАНИЕ 3.20 Найти двойной интеграл 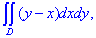
Решение: Найдем точки пересечения графиков заданных функций: y=x2-1 и y=3:
3=x2-1, x2-4=0, (x-2)(x+2)=0, x=-2; x=2.
Параболу и прямую изобразим графически
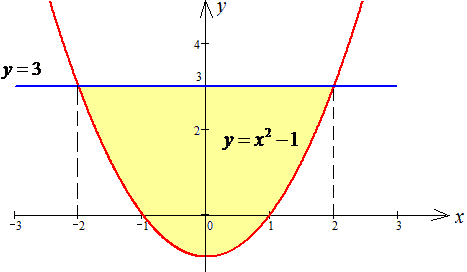
Вычислим двойной интеграл по области которая ограничена параболой и прямой:
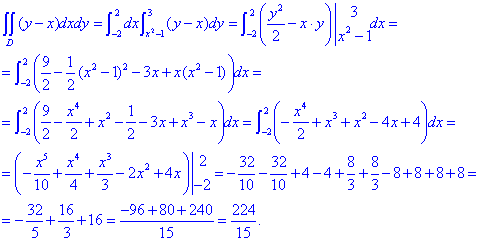
ЗАДАНИЕ 4.21 Найти двойной интеграл, используя полярные координаты:
Решение: Построим область интегрирования, которая ограничена кривыми
где 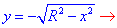
Получили круг с центром в точке O (0;0) и радиусом R (нижняя половина).
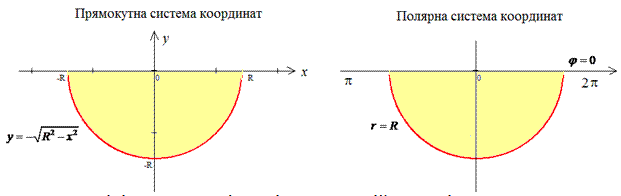
перейдем к полярной системе координат (СК).
При этом подынтегральную функцию следует умножить на якобиан перехода, который находим через определитель из производных:
Перепишем подинтегральную функцию в полярной СК :
Пределы интегрирования при переходе к полярной системе координат изменятся на следующие:
Вычислим двойной интеграл:
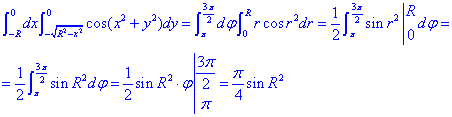
ЗАДАНИЕ 5.22 Вычислить площадь области D, ограниченной указанными линиями: D: x3=3y, y2=3x.
Решение: Найдем точку пересечения двух графиков 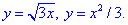
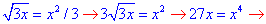
Графики кривой в декартовой системе координат имеет вид
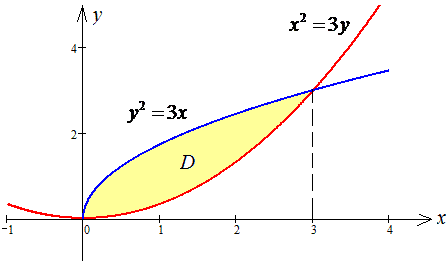
Найдем площадь криволинейной трапеции которая ограничена указанными линиями:
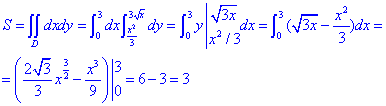
ЗАДАНИЕ 6.23 Используя двойной интеграл, вычислить, перейдя к полярным координатам, площадь плоской фигуры : (x2+y2)3=4a2xy (x2-y2).
Решение: Сначала построим чотирёх лепесток
Перейдем к полярной системе координат:
Якобиан перехода из предыдущих примеров равен I=r.
Найдем пределы интегрирования в новой системе координат
Переменные приобретают значение:
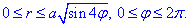
Расставляем пределы интегрирования в двойном интеграле, таким образом найдем четверть площади плоской фигуры.
Дальше результат умножим на 4:
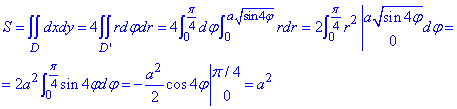
Внимательно проанализируйте как определять пределы интегрирования. Это тяжелее всего, что может быть в подобных задачах.
Как вычислить определенный интеграл, как правило, должны знать все студенты. Здесь лишь расширяется его приложение.
Тройной интеграл
ЗАДАНИЕ 8.25 Расставить пределы интегрирования в тройном интеграле 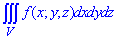
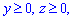
Нарисовать область интегрирования.
Решение: Уравнение поверхности в пространстве z=4 (x2+y2) — эллиптический параболоид.
График параболоида и проекция в декартовую плоскость тела имеют вид
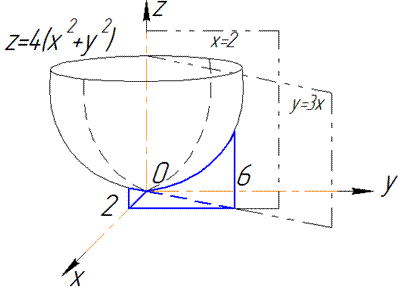
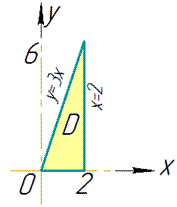
V:
Расставляем пределы интегрирования в соответствии с областью
ЗАДАНИЕ 9.6 Вычислить тройные интегралы:
где V:
Решение: Выполним построение области интегрирования
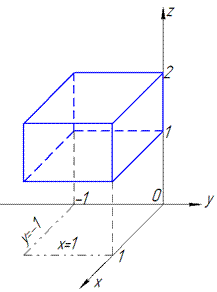
Вычисления не сложны, поэтому превращение в формуле проанализируйте самостоятельно.
Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.
Пусть в замкнутой облас
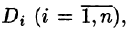

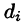
В каждой области 
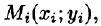
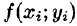

Эта сумма называется интегральной суммой функции f(x; у) в области D.
Рассмотрим предел интегральной суммы (53.1), когда п стремится к бесконечности таким образом, что 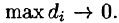
Таким образом, двойной интеграл определяется равенством
В этом случае функция f(x;y) называется интегрируемой в области D; D — область интегрирования; х и у — переменные интегрирования; dx dy (или dS) — элемент площади.
Для всякой ли функции f(x; у) существует двойной интеграл? На этот вопрос отвечает следующая теорема, которую мы приведем здесь без доказательства.
Теорема:
Достаточное условие интегрируемости функции. Если функция z = f(x;y) непрерывна в замкнутой области D, то она интегрируема в этой области.
Замечания:
- Далее будем рассматривать только функции, непрерывные в области интегрирования, хотя двойной интеграл может существовать не только для непрерывных функций.
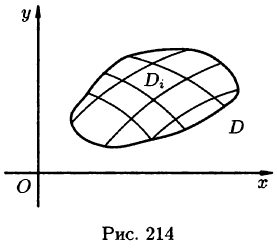
- Из определения двойного интеграла следует, что для интегрируемой в области D функции предел интегральных сумм существует и не зависит от способа разбиения области. Таким образом, мы можем разбивать область D на площадки прямыми, параллельными координатным осям (см. рис. 215). При этом
равенство (53.2) можно записать в виде
Геометрический и физический смысл двойного интеграла
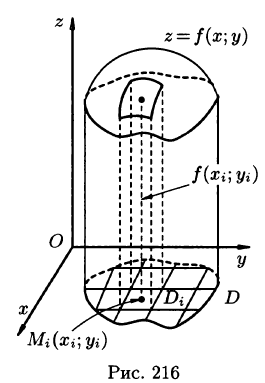
Рассмотрим две задачи, приводящие к двойному интегралу. Объем цилиндрического тела
Рассмотрим тело, ограниченное сверху поверхностью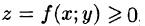

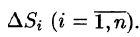

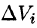
Возьмем на каждой площадке Di произвольную точку 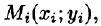

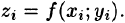
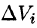
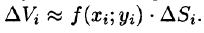
Это равенство тем точнее, чем больше число п и чем меньше размеры «элементарных областей» 

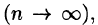
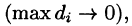
или, согласно равенству (53.2),
Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.
Масса плоской пластинки
Требуется найти массу m плоской пластинки D. зная, что ее поверхностная плотность 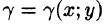
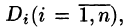


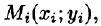
Если области D, достаточно малы, то плотность в каждой точке 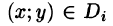
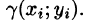

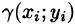
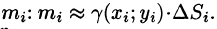
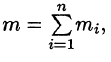
Точное значение массы получим как предел суммы (53.5) при условии
или, согласно равенству (53.2),
Итак, двойной интеграл от функции 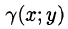
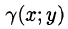
Основные свойства двойного интеграла
Можно заметить, что процесс построения интеграла в области D дословно повторяет уже знакомую нам процедуру определения интеграла функции одной переменной на отрезке (см. § 35). Аналогичны и свойства этих интегралов и их доказательства (см. § 38). Поэтому перечислим основные свойства двойного интеграла, считая подынтегральные функции интегрируемыми.
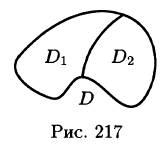
3.Если область D разбить линией на две области 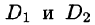
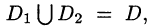
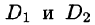
4.Если в области D имеет место неравенство 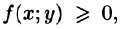
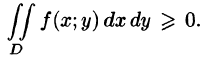
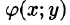
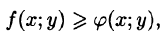
6.Если функция f(x;y) непрерывна в замкнутой области D, площадь которой 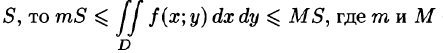
7.Если функция f(x;y) непрерывна в замкнутой области D, площадь которой S, то в этой области существует такая точка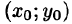
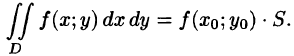
называют средним значением функции f(x; у) в области D.
Вычисление двойного интеграла в декартовых координатах
Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.
Пусть требуется вычислить двойной интеграл 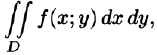
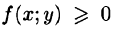
где S(x) — площадь сечения плоскостью, перпендикулярной оси Ох, а х = а, х = b — уравнения плоскостей, ограничивающих данное тело.
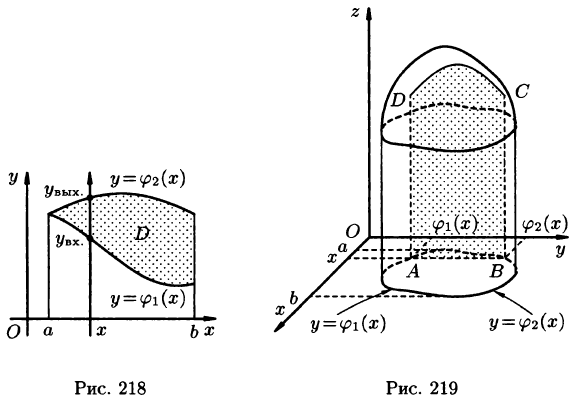
Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямыми x = a и x = b и кривыми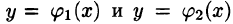
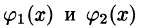
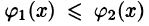
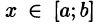
Построим сечение цилиндрического тела плоскостью, перпендикулярной оси
В сечении получим криволинейную трапецию ABCD, ограниченную линиями
(см. рис. 219).
Площадь S(x) этой трапеции находим с помощью определенного интеграла
Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:
С другой стороны, в п. 53.2 было доказано, что объем цилиндрического тела определяется как двойной интеграл от функции 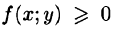
Это равенство обычно записывается в виде
Формула (53.7) представляет собой способ вычисления двойного интеграла в декартовых координатах. Правую часть формулы (53.7) называют двукратным (или повторным) интегралом от функции f(x;y) по области D. При этом 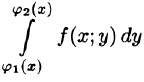
Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая х постоянным, затем берем внешний интеграл, т. е. результат первого интегрирования интегрируем по х в пределах от а до b.
Если же область D ограничена прямыми 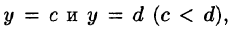
для всех 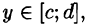
Здесь, при вычислении внутреннего интеграла, считаем у постоянным.
Замечания:
- Формулы (53.7) и (53.8) справедливы и в случае, когда
- Если область D правильная в обоих направлениях, то двойной интеграл можно вычислять как по формуле (53.7), так и по формуле (53.8).
- Если область D не является правильной ни «по x», ни «по у», то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении оси Ох или оси Оу.
- Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные.
Пример:
Вычислить 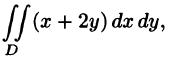
Решение:
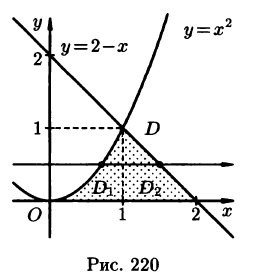
На рисунке 220 изображена область интегрирования D. Она правильная в направлении оси Ох. Для вычисления данного двойного интеграла воспользуемся формулой (53.8):
Отметим, что для вычисления данного двойного интеграла можно воспользоваться формулой (53.7). Но для этого область D следует разбить на две области: 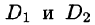
Ответ, разумеется, один и тот же.
Вычисление двойного интеграла в полярных координатах
Для упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делалось и при вычислении определенного интеграла), т. е. вводят новые переменные под знаком двойного интеграла.
Определим преобразование независимых переменных х и у (замену переменных) как
Если функции (53.9) имеют в некоторой области D* плоскости Ouv непрерывные частные производные первого порядка и отличный от нуля определитель
а функция f(х; у) непрерывна в области D, то справедлива формула замены переменных в двойном интеграле:
Функциональный определитель (53.10) называется определителем Якоби или якобианом (Г. Якоби — немецкий математик). Доказательство формулы (53.11) не приводим.
Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат х и у полярными координатами
В качестве инь возьмем полярные координаты 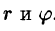
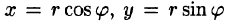
Правые части в этих равенствах — непрерывно дифференцируемые функции. Якобиан преобразования определяется из (53.10) как
Формула замены переменных (53.11) принимает вид:
где D* — область в полярной системе координат, соответствующая области D в декартовой системе координат.
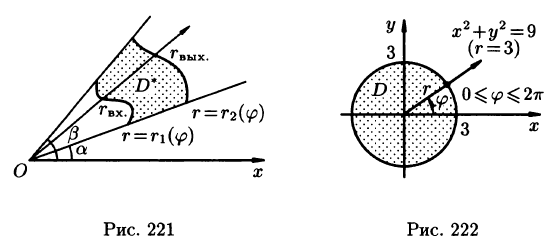
Для вычисления двойного интеграла в полярных координатах применяют то же правило сведения его к двукратному интегралу. Так, если
область D* имеет вид, изображенный на рисунке 221 (ограничена лучами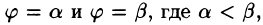
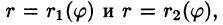
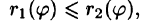
Внутренний интеграл берется при постоянном
Замечания:
- Переход к полярным координатам полезен, когда подынтегральная функция имеет вид
область D есть круг, кольцо или часть таковых.
- На практике переход к полярным координатам осуществляется путем замены
уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по
(исследуя закон изменения
точки
при ее отождествлении с точкой (х; у) области D).
Пример:
Вычислить 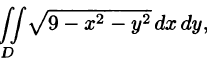
Решение: Применив формулу (53.12), перейдем к полярным координатам:
Область D в полярной системе координат определяется неравенствами (см. рис. 222) 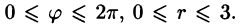
Приложения двойного интеграла
Приведем некоторые примеры применения двойного интеграла.
Объем тела
Как уже показано (п. 53.2), объем цилиндрического тела находится по формуле
где z = f(x;y) — уравнение поверхности, ограничивающей тело сверху.
Площадь плоской фигуры
Если положить в формуле (53.4) f(x;y) = 1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой Н = 1. Объем такого цилиндра, как известно, численно равен площади S основания D. Получаем формулу для вычисления площади S области D:
или, в полярных координатах,
Масса плоской фигуры
Как уже показано (п. 53.2), масса плоской пластинки D с переменной плотностью 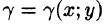
Статические моменты и координаты центра тяжести плоской фигуры
Статические моменты фигуры D относительно осей Ох и Оу (см. п. 41.6) могут быть вычислены по формулам
а координаты центра масс фигуры по формулам
Моменты инерции плоской фигуры
Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на квадрат расстояния d точки до оси, т. е. 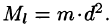
Момент инерции фигуры относительно начала координат — по формуле
Замечание:
Приведенными примерами не исчерпывается применение двойного интеграла. Далее мы встретим приложение двойного интеграла к вычислению площадей поверхностей фигур (п. 57.3).
Пример:
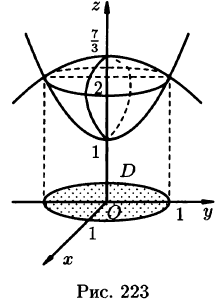
Найти объем тела, ограниченного поверхностями
Решение: Данное тело ограничено двумя параболоидами (см. рис. 223). Решая систему
находим уравнение линии их пересечения:
Искомый объем равен разности объемов двух цилиндрических тел с одним основанием (круг 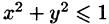
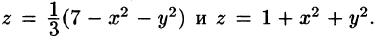
Переходя к полярным координатам, находим:
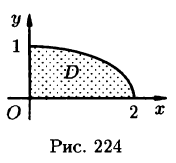
Пример:
Найти массу, статические моменты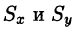
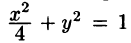
Решение: По формуле (53.6) находим массу пластинки. По условию, 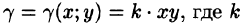
Находим статические моменты пластинки:
Находим координаты центра тяжести пластинки, используя формулы
Двойной интеграл
Смотрите также:
Предмет высшая математика
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат










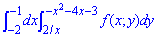
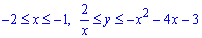
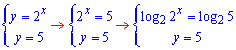
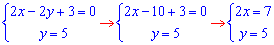
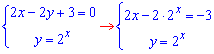
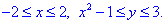
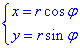
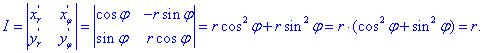
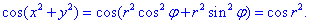
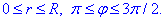
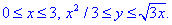
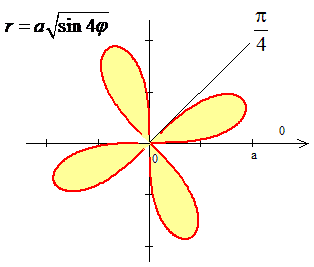
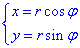
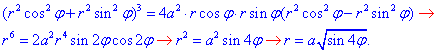
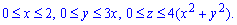
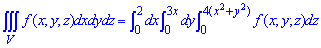
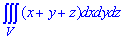
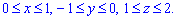
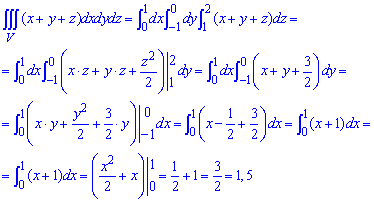
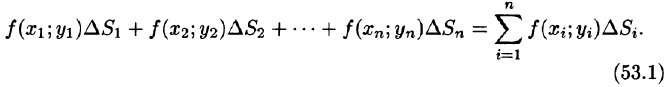
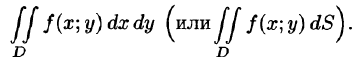
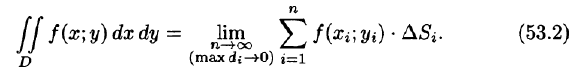
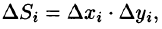 равенство (53.2) можно записать в виде
равенство (53.2) можно записать в виде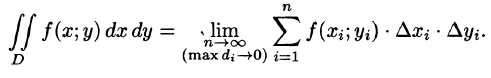
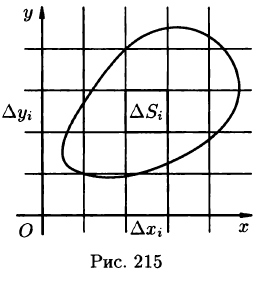

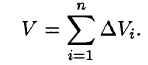
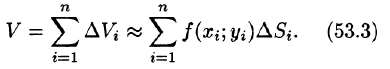
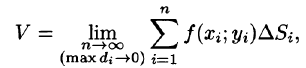
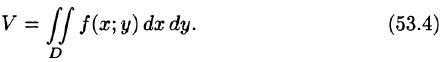
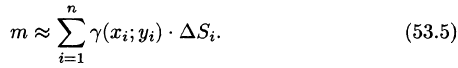
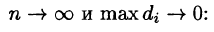
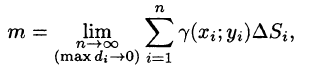
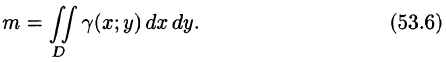
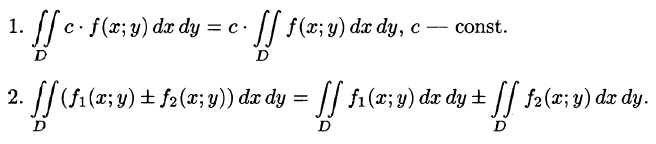
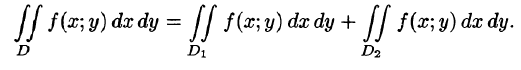
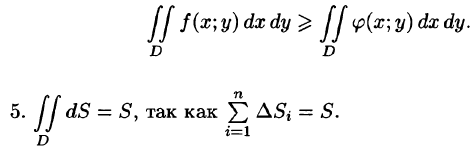
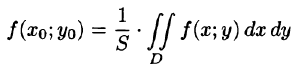
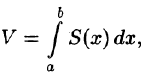
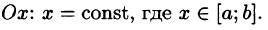
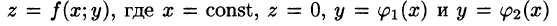
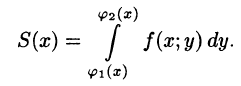
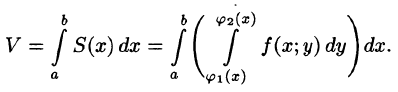
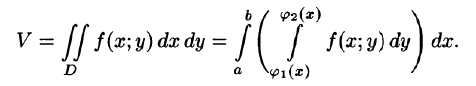
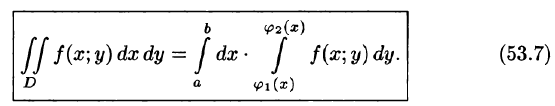
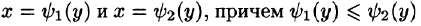
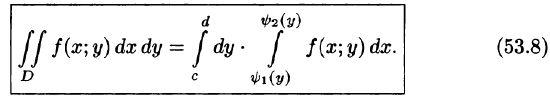
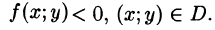
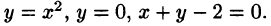
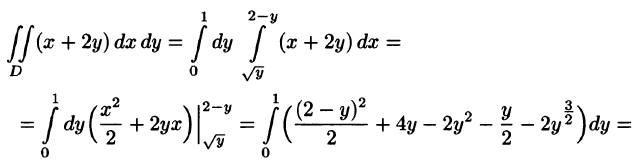
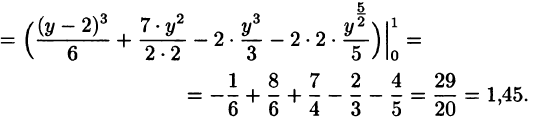
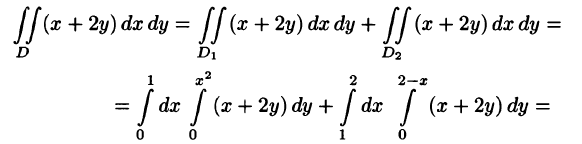
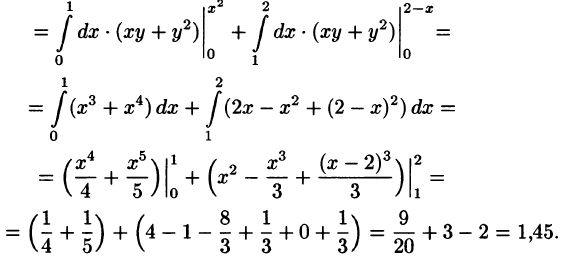
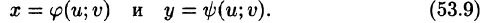

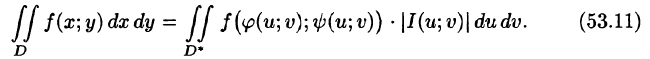
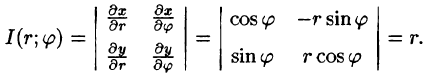
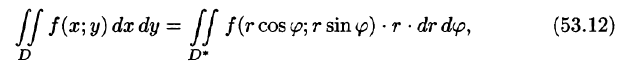
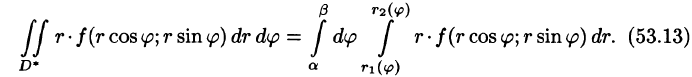
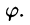
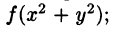 область D есть круг, кольцо или часть таковых.
область D есть круг, кольцо или часть таковых.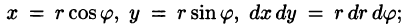 уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по
уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по 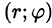 при ее отождествлении с точкой (х; у) области D).
при ее отождествлении с точкой (х; у) области D).