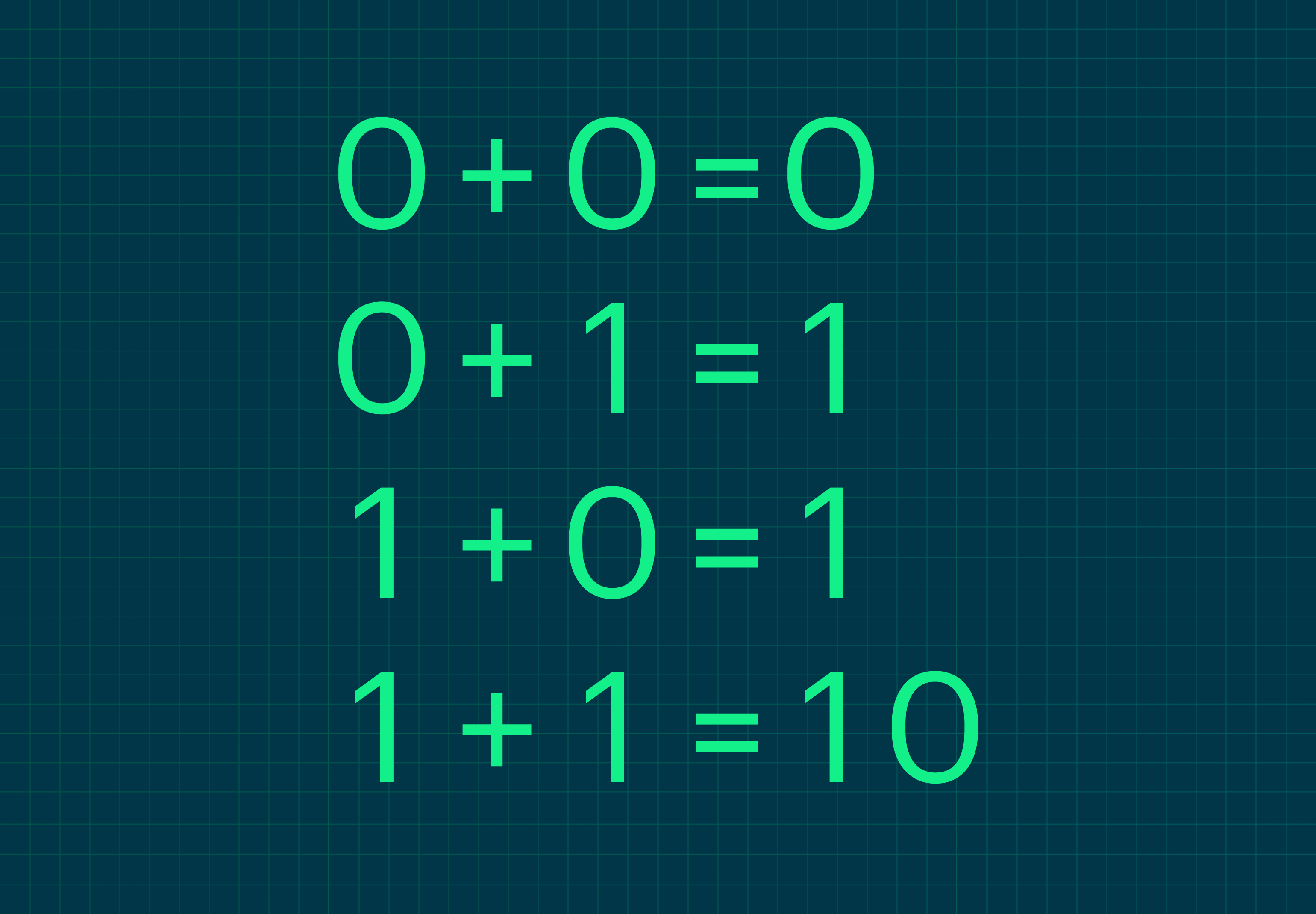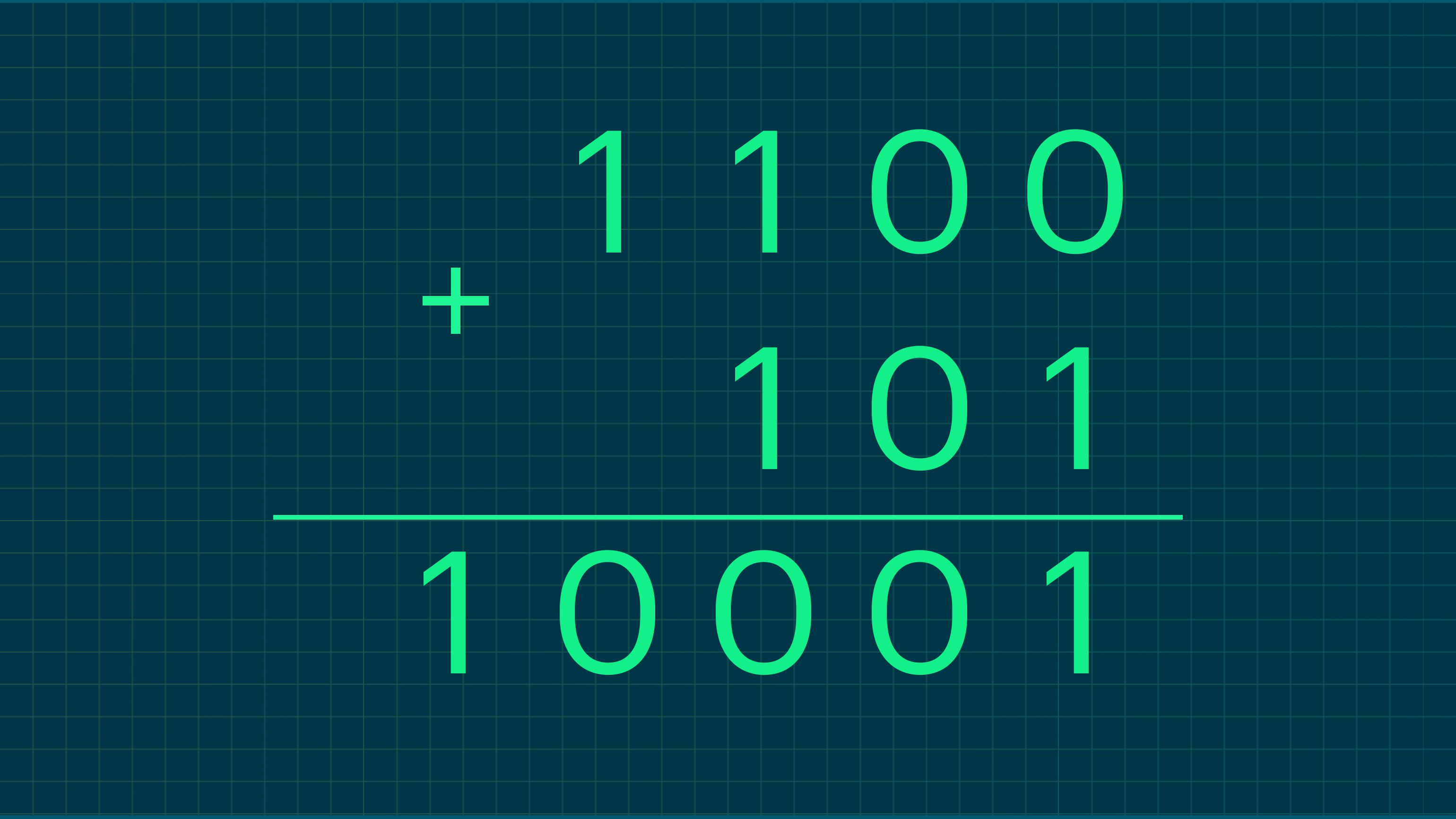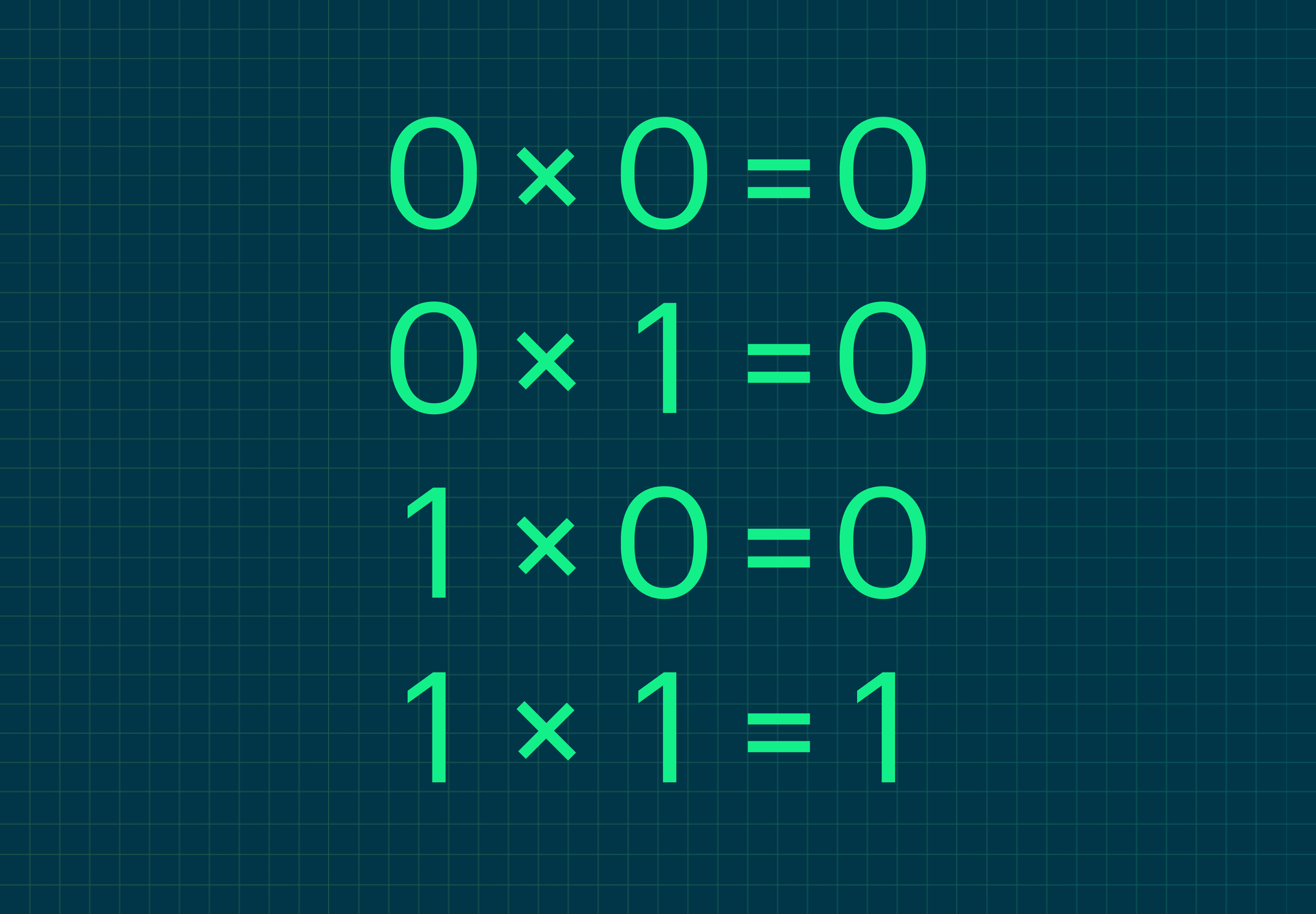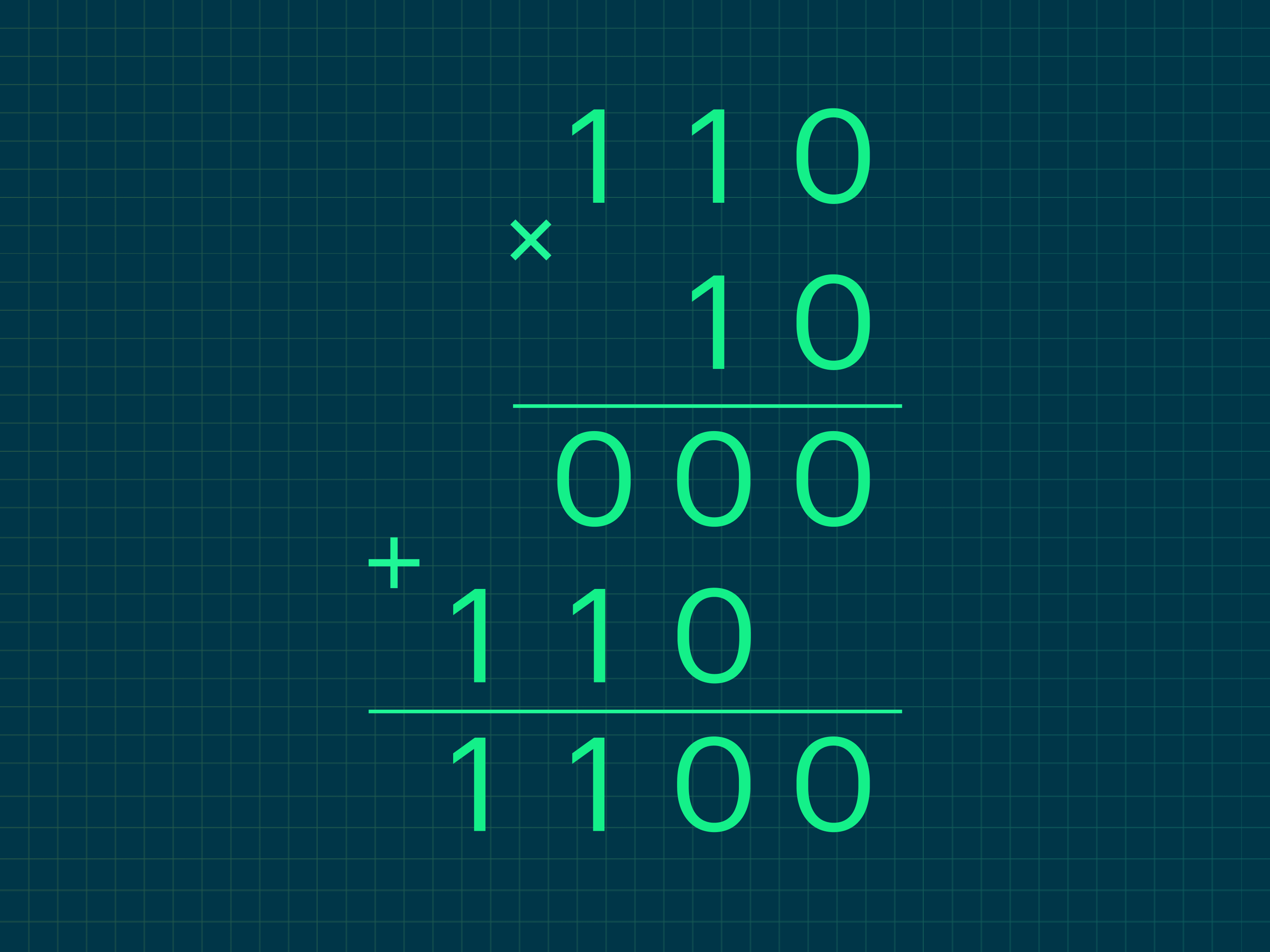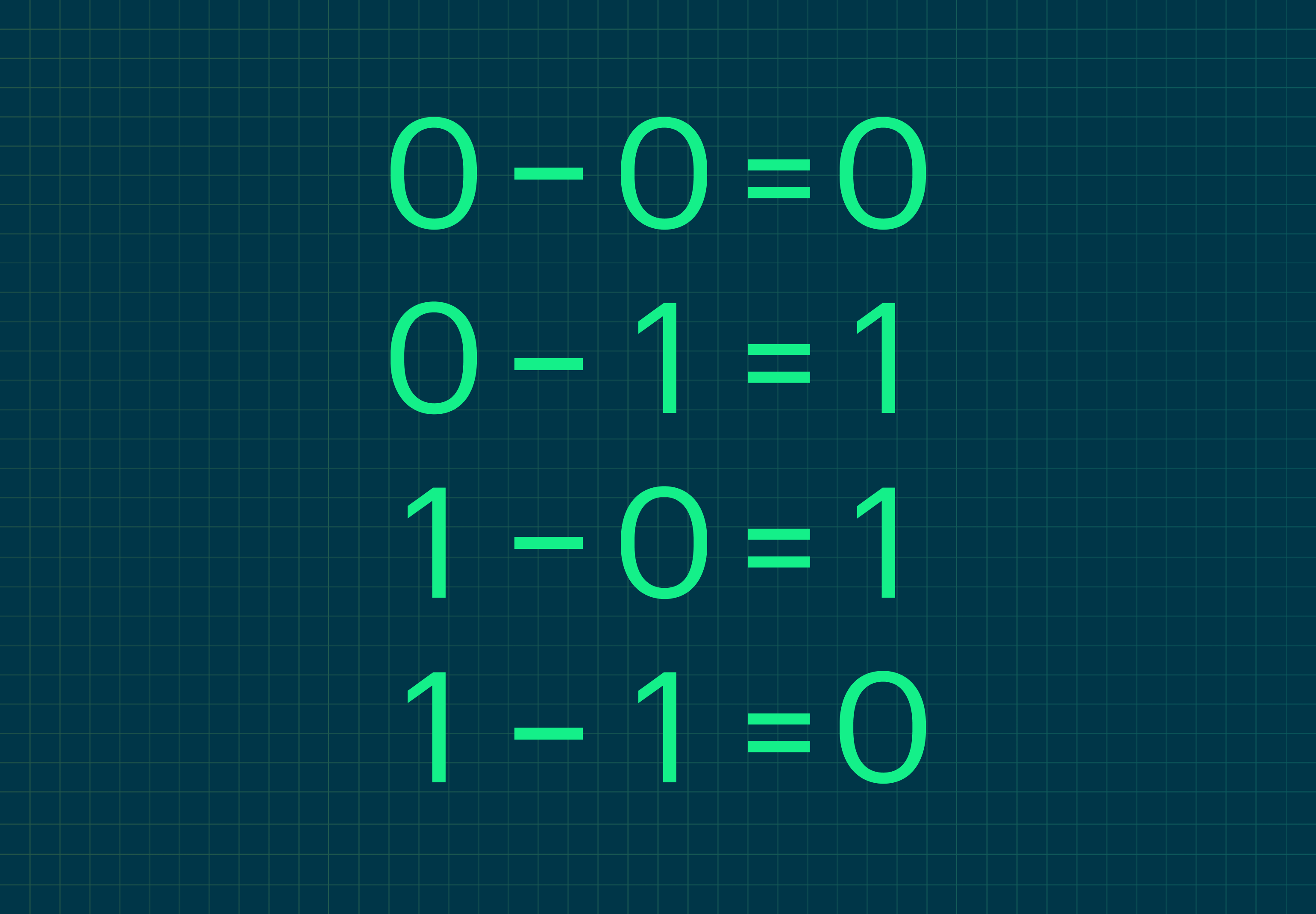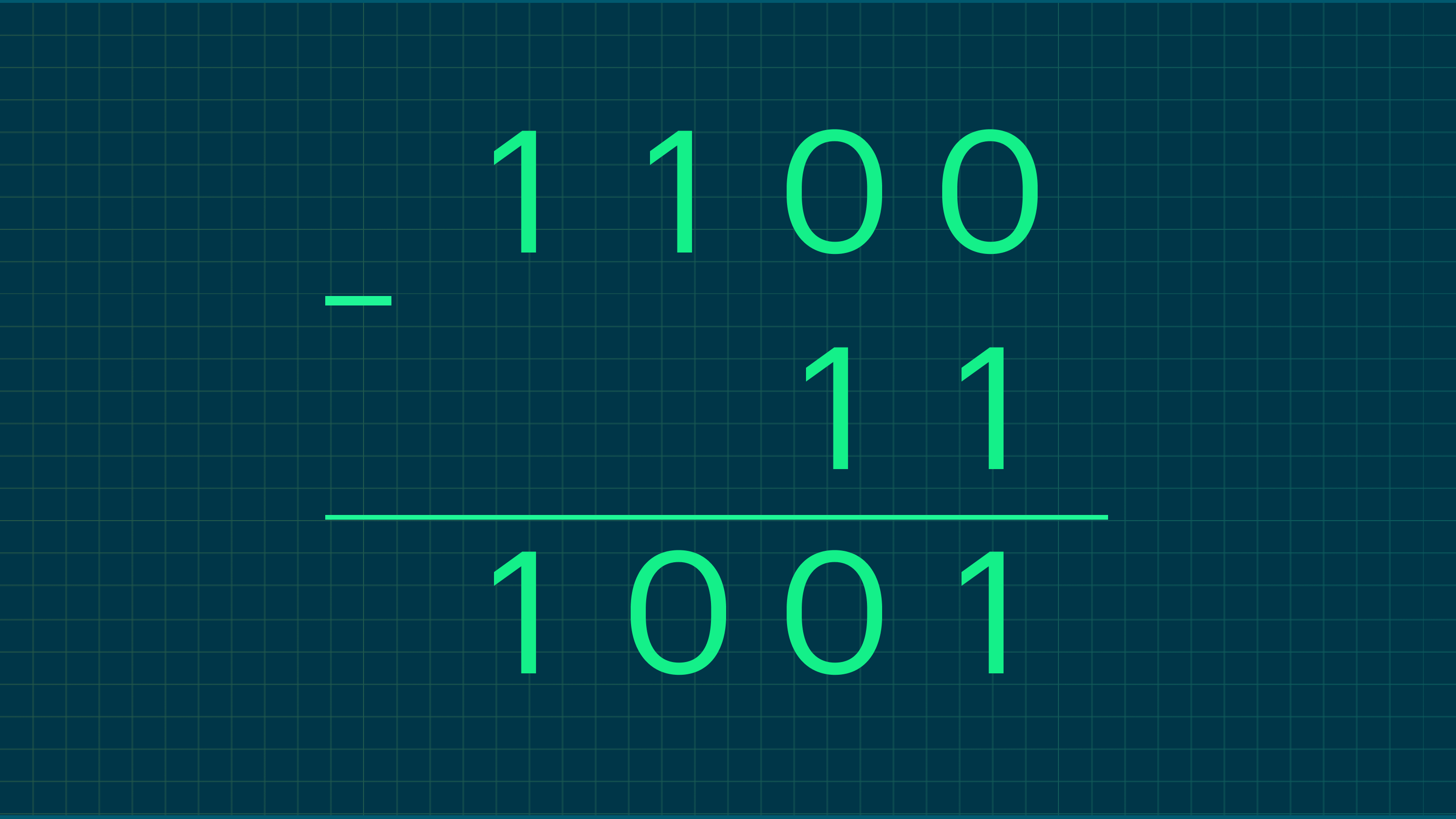Загрузить PDF
Загрузить PDF
Из этой статьи вы узнаете, как считать в двоичной системе счисления, которая используется во всех компьютерах. Поначалу это покажется необычным, но если знать всего несколько правил и немного попрактиковаться, можно научиться быстро считать в двоичной системе.
Справочная таблица
|
Десятичная система |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
Двоичная система |
0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 |
-
1
Ознакомьтесь с основами двоичной системы. Система счисления, которой мы ежедневно пользуемся, называется десятичной, потому что она включает десять цифр (от 0 до 9). В двоичной системе счисления используются всего две цифры — 0 и 1.
-
2
Прибавьте единицу, изменив последний 0 на 1. Если двоичное число заканчивается на 0, измените этот 0 на 1, чтобы прибавить к данному числу единицу. Это аналогично сложению первых двух чисел:
- 0 = ноль
- 1 = один
- Если двоичное число состоит из нескольких цифр, учитывайте только последний 0: 1010 + 1 = 1011.
-
3
Припишите к двоичному числу еще одну цифру, если оно состоит только из единиц. Итак, мы получили 1 для единицы, но цифр больше нет. Чтобы посчитать до двух, напишите еще одну цифру. Припишите 1 слева от двоичного числа, а все остальные цифры этого числа сделайте нолями.
- 0 = ноль
- 1 = один
- 10 = два
- Аналогичное правило используется в десятичной системе счисления, когда больше нет цифр, например, 9 + 1 = 10. В двоичной системе такое случается гораздо чаще, потому что в ней используются всего две цифры.
-
4
Воспользуйтесь описанными правилами, чтобы посчитать до пяти. Попробуйте сделать это самостоятельно, а потом проверьте результат:
- 0 = ноль
- 1 = один
- 10 = два
- 11 = три
- 100 = четыре
- 101 = пять
-
5
Посчитайте до шести. Теперь необходимо найти результат сложения 5+1 в двоичной системе, а именно сложить двоичные числа 101 + 1. Правило заключается в том, что нужно проигнорировать первую цифру. Таким образом, сложите 1 + 1, чтобы получить 10 (это цифра 2 в двоичной системе). Теперь восстановите первую цифру и получите:
- 110 = шесть
-
6
Сосчитайте до десяти. Все правила уже описаны; других правил нет. Попробуйте сосчитать до десяти, а потом проверьте результат:
- 110 = шесть
- 111 = семь
- 1000 = восемь
- 1001 = девять
- 1010 = десять
-
7
Научитесь добавлять новые цифры. Обратите внимание, что десять (1010) не является каким-то особенным числом в двоичной системе. Сейчас нас больше интересует число восемь. Восемь (1000) равно 2 x 2 x 2 (10 х 10 х 10). Умножайте числа на два (10), чтобы находить другие числа, например, шестнадцать (10000) и тридцать два (100000).
-
8
Попрактикуйтесь в нахождении больших чисел. Теперь вы знаете все правила, необходимые для счета в двоичной системе. Если вы запутались, вспомните, что нужно делать с последними цифрами. Вот несколько примеров:
- Двенадцать плюс один = 1100 + 1 = 1101 = тринадцать (0 + 1 = 1, а остальные цифры не меняются).
- Пятнадцать плюс один = 1111 + 1 = 10000 = шестнадцать (цифр больше нет, поэтому слева от 1111 мы приписываем 1, а все остальные цифры превращаем в ноли).
- Сорок пять плюс один = 101101 + 1 = 101110 = сорок шесть (1 + 1 = 10, а остальные цифры не меняются).
Реклама
-
1
Запишите разряд каждой цифры двоичного числа. Вспомните, что каждая цифра десятичного числа стоит в определенном разряде: разряде единиц, разряде десяток и так далее. Так как в двоичной системе всего две цифры, каждый разряд умножается на два (если перемещаться по цифрам числа слева направо):
- 1 — это разряд единиц;
- 1 0 — это разряд двоек;
- 1 00 — это разряд четверок;
- 1 000 — это разряд восьмерок.
-
2
Умножьте каждую цифру двоичного числа на соответствующий разряд. Начните с крайней правой цифры — она стоит в разряде единиц, поэтому ее нужно умножить на 1; на следующей строке умножьте вторую справа цифру на 2; на следующей строке умножьте третью справа цифру на 4 и так далее. Например:
- Преобразуйте двоичное число 10011 в десятичное.
- Первая справа цифра 1. Она находится в разряде единиц. Поэтому умножьте ее на единицу: 1 x 1 = 1.
- Вторая справа цифра тоже 1. Она находится в разряде двоек. Поэтому умножьте ее на два: 1 x 2 = 2.
- Следующая цифра 0. Умножьте ее на четыре: 0 x 4 = 0.
- Следующая цифра тоже 0. Умножьте ее на восемь: 0 x 8 = 0.
- Последняя (справа) цифра 1. Умножьте ее на шестнадцать: 1 x 16 = 16.
-
3
Сложите полученные результаты. Вы преобразовали каждую цифру двоичного числа в цифру десятичной системы. Чтобы найти десятичное число, сложите все полученные значения. В нашем примере:
- 1 + 2 + 16 = 19.
- Таким образом 10011 (в двоичной системе) = 19 (в десятичной системе).
Реклама
Советы
- Также можно научиться считать в двоичной системе на пальцах. Каждый вытянутый палец будет цифрой 1, а каждый согнутый — 0.[1]
Реклама
Об этой статье
Эту страницу просматривали 44 982 раза.
Была ли эта статья полезной?
Если у вас в школе была информатика, не исключено, что там было упражнение на перевод обычных чисел в двоичную систему и обратно. Маловероятно, что кто-то вам объяснял практический смысл этой процедуры и откуда вообще берётся двоичное счисление. Давайте закроем этот разрыв.
Эта статья не имеет практической ценности — читайте её просто ради интереса к окружающему миру. Если нужны практические статьи, заходите в наш раздел «Где-то баг», там каждая статья — это практически применимый проект.
Отличный план
Чтобы объяснить всё это, нам понадобится несколько тезисов:
- Система записи числа — это шифр.
- Мы привыкли шифровать десятью знаками.
- Но система записи чисел может быть любой. Это условность.
- Двоичная система — это тоже нормальная система.
- Всё тлен и суета.
Система записи — это шифр
Если у нас есть девять коров, мы можем записать их как 🐄🐄🐄🐄🐄🐄🐄🐄🐄 или как 9 × 🐄.
Почему 9 означает «девять»? И почему вообще есть такое слово? Почему такое количество мы называем этим словом? Вопрос философский, и короткий ответ — нам нужно одинаково называть числа, чтобы друг друга понимать. Слово «девять», цифра 9, а также остальные слова — это шифр, который мы выучили в школе, чтобы друг с другом общаться.
Допустим, к нашему стаду прибиваются еще 🐄🐄🐄. Теперь у нас 🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄 — двенадцать коров, 12. Почему мы знаем, что 12 — это «двенадцать»? Потому что мы договорились так шифровать числа.
Нам очень легко расшифровывать записи типа 12, 1920, 100 500 и т. д. — мы к ним привыкли, мы учили это в школе. Но это шифр. 12 × 🐄 — это не то же самое, что 🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄. Это некая абстракция, которой мы пользуемся, чтобы упростить себе счёт.
Мы привыкли шифровать десятью знаками
У нас есть знаки 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 — всего десять знаков. Этим числом знаков мы шифруем количество единиц, десятков, сотен, тысяч и так далее.
Мы договорились, что нам важен порядок записи числа. Мы знаем, что самый правый знак в записи означает число единиц, следующий знак (влево) означает число десятков, потом сотен и далее.
Например, перед нами число 19 547. Мы знаем, что в нём есть:
1 × 10 000
9 × 1000
5 × 100
4 × 10
7 × 1
Если приглядеться, то каждый следующий разряд числа показывает следующую степень десятки:
1 × 104
9 × 103
5 × 102
4 × 101
7 × 100
Нам удобно считать степенями десятки, потому что у нас по десять пальцев и мы с раннего детства научились считать до десяти.
Система записи — это условность
Представим бредовую ситуацию: у нас не 10 пальцев, а 6. И в школе нас учили считать не десятками, а шестёрками. И вместо привычных цифр мы бы использовали знаки ØABCDE. Ø — это по-нашему ноль, A — 1, B — 2, E — 5.
Вот как выглядели бы привычные нам цифры в этой бредовой системе счисления:
| 0 — Ø 1 — A 2 — B 3 — C 4 — D 5 — E |
6 — AØ 7 — AA 8 — AB 9 — AC 10 — AD 11 — AE |
12 — BØ 13 — BA 14 — BB 15 — BC 16 — BD 17 — BE |
18 — CØ 19 — CA 20 — CB 21 — CC 22 — CD 23 — CE |
24 — DØ 25 — DA 26 — DB 27 — DC 28 — DD 29 — DE |
30 — EØ 31 — EA 32 — EB 33 — EC 34 — ED 35 — EE |
36 — AØØ 37 — AØA 38 — AØB 39 — AØC 40 — AØD 41 — AØE |
В этой системе мы считаем степенями шестёрки. Число ABADØ можно было бы перевести в привычную нам десятичную запись вот так:
A × 64 = 1 × 1296 = 1296
B × 63 = 2 × 216 = 432
A × 62 = 1 × 36 = 36
D × 61 = 4 × 6 = 24
Ø × 60 = 0 × 1 = 0
1296 + 432 + 36 + 24 + 0 = 1788. В нашей десятичной системе это 1788, а у людей из параллельной вселенной это ABADØ, и это равноценно.
Выглядит бредово, но попробуйте вообразить, что у нас в сумме всего шесть пальцев. Каждый столбик — как раз шесть чисел. Очень легко считать в уме. Если бы нас с детства учили считать шестёрками, мы бы спокойно выучили этот способ и без проблем всё считали. А счёт десятками вызывал бы у нас искреннее недоумение: «Что за бред, считать числом AD? Гораздо удобнее считать от Ø до E!»
То, как мы шифруем и записываем числа, — это следствие многовековой традиции и физиологии. Вселенной, космосу, природе и стадам коров глубоко безразлично, что мы считаем степенями десятки. Природа не укладывается в эту нашу систему счёта.
Например, свет распространяется в вакууме со скоростью 299 792 458 метров в секунду. Ему плевать, что нам для ровного счёта хотелось бы, чтобы он летел со скоростью 300 тысяч километров в секунду. А ускорение свободного падения тела возле поверхности Земли — 9,81 м/с2. Так и хочется спросить: «Тело, а ты не могло бы иметь ускорение 10 м/с2?» — но телу плевать на наши системы счисления.
Двоичная система (тоже нормальная)
Внутри компьютера работают транзисторы. У них нет знаков 0, 1, 2, 3… 9. Транзисторы могут быть только включёнными и выключенными — обозначим их 💡 и ⚫.
Мы можем научить компьютер шифровать наши числа этими транзисторами так же, как шестипалые люди шифровали наши числа буквами. Только у нас будет не 6 букв, а всего две: 💡 и ⚫. И выходит, что в каждом разряде будет стоять не число десяток в разной степени, не число шестёрок в разной степени, а число… двоек в разной степени. И так как у нас всего два знака, то получается, что мы можем обозначить либо наличие двойки в какой-то степени, либо отсутствие:
| 0 — ⚫ 1 — 💡 2 — 💡⚫ 4 — 💡⚫⚫ |
8 — 💡⚫⚫⚫ 9 — 💡⚫⚫💡 10 — 💡⚫💡⚫ 11 — 💡⚫💡💡 12 — 💡💡⚫⚫ 13 — 💡💡⚫💡 14 — 💡💡💡⚫ 15 — 💡💡💡💡 |
16 — 💡⚫⚫⚫⚫ 17 — 💡⚫⚫⚫💡 18 — 💡⚫⚫💡⚫ 19 — 💡⚫⚫💡💡 20 — 💡⚫💡⚫⚫ 21 — 💡⚫💡⚫💡 21 — 💡⚫💡💡⚫ 23 — 💡⚫💡💡💡 24 — 💡💡⚫⚫⚫ 25 — 💡💡⚫⚫💡 26 — 💡💡⚫💡⚫ 27 — 💡💡⚫💡💡 28 — 💡💡💡⚫⚫ 29 — 💡💡💡⚫💡 30 — 💡💡💡💡⚫ 31 — 💡💡💡💡💡 |
32 — 💡⚫⚫⚫⚫⚫ 33 — 💡⚫⚫⚫⚫💡 34 — 💡⚫⚫⚫💡⚫ 35 — 💡⚫⚫⚫💡💡 36 — 💡⚫⚫💡⚫⚫ 37 — 💡⚫⚫💡⚫💡 38 — 💡⚫⚫💡💡⚫ 39 — 💡⚫⚫💡💡💡 40 — 💡⚫💡⚫⚫⚫ 41 — 💡⚫💡⚫⚫💡 42 — 💡⚫💡⚫💡⚫ 43 — 💡⚫💡⚫💡💡 44 — 💡⚫💡💡⚫⚫ 45 — 💡⚫💡💡⚫💡 46 — 💡⚫💡💡💡⚫ 47 — 💡⚫💡💡💡💡 48 — 💡💡⚫⚫⚫⚫ 49 — 💡💡⚫⚫⚫💡 50 — 💡💡⚫⚫💡⚫ 51 — 💡💡⚫⚫💡💡 52 — 💡💡⚫💡⚫⚫ 53 — 💡💡⚫💡⚫💡 54 — 💡💡⚫💡💡⚫ 55 — 💡💡⚫💡💡💡 56 — 💡💡💡⚫⚫⚫ 57 — 💡💡💡⚫⚫💡 58 — 💡💡💡⚫💡⚫ 59 — 💡💡💡⚫💡💡 60 — 💡💡💡💡⚫⚫ 61 — 💡💡💡💡⚫💡 62 — 💡💡💡💡💡⚫ 63 — 💡💡💡💡💡💡 |
Если перед нами число 💡 ⚫💡⚫⚫ 💡💡⚫⚫, мы можем разложить его на разряды, как в предыдущих примерах:
💡 = 1 × 28 = 256
⚫ = 0 × 27 = 0
💡 = 1 × 26 = 64
⚫ = 0 × 25 = 0
⚫ = 0 × 24 = 0
💡 = 1 × 23 = 8
💡 = 1 × 22 = 4
⚫ = 0 × 21 = 0
⚫ = 0 × 20 = 0
256 + 0 + 64 + 0 + 0 + 8 + 4 + 0 + 0 = 332
Получается, что десятипалые люди могут записать это число с помощью цифр 332, а компьютер с транзисторами — последовательностью транзисторов 💡⚫💡⚫⚫ 💡💡⚫⚫.
Если теперь заменить включённые транзисторы на единицы, а выключенные на нули, получится запись 1 0100 1100. Это и есть наша двоичная запись того же самого числа.
Почему говорят, что компьютер состоит из единиц и нулей (и всё тлен)
Инженеры научились шифровать привычные для нас числа в последовательность включённых и выключенных транзисторов.
Дальше эти транзисторы научились соединять таким образом, чтобы они умели складывать зашифрованные числа. Например, если сложить 💡⚫⚫ и ⚫⚫💡, получится 💡⚫💡. Мы писали об этом подробнее в статье о сложении через транзисторы.
Дальше эти суммы научились получать супербыстро. Потом научились получать разницу. Потом умножать. Потом делить. Потом всё это тоже научились делать супербыстро. Потом научились шифровать не только числа, но и буквы. Научились их хранить и считывать. Научились шифровать цвета и координаты. Научились хранить картинки. Последовательности картинок. Видео. Инструкции для компьютера. Программы. Операционные системы. Игры. Нейросети. Дипфейки.
И всё это основано на том, что компьютер умеет быстро-быстро складывать числа, зашифрованные как последовательности включённых и выключенных транзисторов.
При этом компьютер не понимает, что он делает. Он просто гоняет ток по транзисторам. Транзисторы не понимают, что они делают. По ним просто бежит ток. Лишь люди придают всему этому смысл.
Когда человека не станет, скорость света будет по-прежнему 299 792 458 метров в секунду. Но уже не будет тех, кто примется считать метры и секунды. Такие дела.
-
Двоичная система счисления. Правила двоичной арифметики.
В двоичнойсистеме счисления для
записи чисел используется две цифры 0
и 1. Основание системы q=2 записывается
как 102= [1*21+0*20]10.
В данной СС любое число может быть
представлено последовательностью
двоичных цифр. Эта запись соответствует
сумме степеней цифры 2, взятых с указанными
в ней коэффициентами:
X=am×2m+am-1×2m-1+…+a1×21+a0×20+…
. Например, двоичное число
(10101101)2=1×27+0×26+1×25+0×24+1×23+1×22+0×21+1×20=17310.
Арифметические операции над двоичными
числами отличаются простотой и легкостью
технического выполнения.
Правила двоичной арифметики:
Сложение:0+0=0 1+0=1
0+1=1 1+1=10
— перенос единицы в старший разряд.
Вычитание:0-0=0 1-1=0
1-0=1 10-1=1
— заем единицы в старшем разряде.
Умножение:0х0=0 1х0=0
0х1=0 1х1=1
Двоичная система счисления является
основной для использования в ЭВМ,
удобной из-за простоты выполнения
арифметических операций над двоичными
числами. С точки зрения затрат оборудования
на создание ЭВМ эта система уступает
только троичной системе счисления.
В двоично-кодированных системах
счисления, имеющих основанияq,
отличные от 2 (q>2), каждая
цифра числа представляется в двоичной
системе счисления. Наибольшее применение
в ЭВМ получили шестнадцатеричная
система счисления и десятичная
двоично-кодированная система
счисления.
-
Восьмеричная и шестнадцатеричная системы счисления.
Восьмеричная и шестнадцатеричная
системы счисления являются
вспомогательными системами при подготовке
задачи к решению. Удобство их использования
состоит в том, что числа соответственно
в 3 и 4 раза короче двоичной системы, а
перевод в двоичную систему счисления
и наоборот несложен и выполняется
простым механическим способом.
Пример 2.1.
Число 137,458
перевести в двоичную систему счисления.
Перевод осуществляется заменой каждой
восьмеричной цифры трехзначным
двоичным числом (триадой):
|
1 |
3 |
7, |
4 |
5 |
|
001 |
011 |
111, |
100 |
101 |
т,е 137,458
= 001011111,1001012.
И наоборот, заменой каждой триады слева
и справа от запятой эквивалентным
значением восьмеричной цифры образуется
восьмеричное число.
Если в крайней
слева или справа триаде окажется меньше
трех двоичных чисел, то эти тройки
дополняют нулями.
Пример 2.2.
Число 5F,9416
перевести в двоичную систему счисления.
Перевод осуществляется заменой каждой
шестнадцатеричной цифры четырехзначным
двоичным числом (тетрадой):
|
5 |
F, |
9 |
4 |
|
0101 |
1111 |
1001 |
0100 |
т.e.
5F,9416=01011111,100101002.
Число
5F,9416
в восьмеричной системе счисления
имеет вид 137,458.
В десятичной двоично-кодированной
системе счисления, часто называемой
двоично-десятичной системой, используются
десятичные числа. В ней каждую цифру
десятичного числа (от 0 до 9) заменяют
тетрадой.
Пример 2.3.
Число 273,5910
перевести в двоично-десятичную систему
счисления. Перевод осуществим следующим
образом:
|
2 |
7 |
3, |
5 |
9 |
|
0010 |
0111 |
0011 |
0101 |
1001 |
т.е. 273,5910
= 001001110011,010110012-10
Двоично-десятичную запись числа
используют непосредственно или как
промежуточную форму записи между обычной
десятичной его записью и машинной
двоичной. Вычислительная машина сама
по специальной программе переводит
двоично-десятичные числа в двоичные и
обратно.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
#статьи
- 27 фев 2023
-
0
Двоичная арифметика: сложение, умножение, вычитание, деление бинарных чисел
Учимся складывать, вычитать, умножать и делить двоичные числа — работаем с фундаментальными законами современной цифровой электроники.
Иллюстрация: Катя Павловская для Skillbox Media
Любитель научной фантастики и технологического прогресса. Хорошо сочетает в себе заумного технаря и утончённого гуманитария. Пишет про IT и радуется этому.
Мы привыкли считать всё в десятичной системе, потому что у нас 10 пальцев — и это удобно. Но если бы у нас было больше пальцев, например 12, то система могла бы быть двенадцатиричной и мы бы воспринимали её как обычную.
Когда дело доходит до двоичной системы счисления, сложно вот так сразу переключиться на её арифметику — хотя, казалось бы, принципы такие же, как для десятичной. Ведь там есть все привычные операции: сложение, вычитание, умножение, деление. Единственное отличие: в двоичных числах используются всего две цифры — ноль и единица.
Давайте избавимся от страха и наконец узнаем, как проводить знакомые нам математические операции в двоичной системе.
Правила сложения двоичных чисел похожи на привычные нам: сложение происходит поразрядно справа налево, при этом важно помнить о переносе чисел в новый разряд.
В десятичной системе у нас всего 10 цифр: от 0 до 9. Когда мы складываем 1 и 9, у нас получается переполнение, так как больше 9 в одном разряде нельзя записать. Поэтому мы переносим единицу в следующий, получаем 10.
Двоичная система работает аналогично: чтобы понять, как складывать числа, нужно помнить об этом переполнении. Всего в двоичной системе две цифры — 0 и 1. Если сложить 1 и 1, мы получим переполнение, а значит, единица пойдёт в следующий разряд, результатом станет 10 (только не «десять», а «один-ноль»).
Если представить правила сложения двоичных чисел в общем виде, получим такую таблицу:
Но лучше разобраться на примерах.
Пример 1. Давайте сложим 1100 и 101.
Рассмотрим пример подробнее. Как мы уже упоминали ранее, сложение происходит справа налево. Разряды считаются тоже справа налево:
- Первый: 0 + 1 = 1.
- Второй: 0 + 0 = 0.
- Третий: 1 + 1 = 10 — переполнение, единица переходит в следующий разряд.
- Четвёртый: 1 + 0 + 1 = 10 — добавляем единицу из прошлого разряда, получаем переполнение, единица переходит в следующий разряд.
- Пятый: 0 + 0 + 1 = 1 — единица пришла из предыдущего разряда.
Пример 2. Сложим 1111 и 111.
Теперь поразрядно:
- Первый: 1 + 1 = 0 — единица переходит в следующий разряд.
- Второй: 1 + 1 + 1 = 1 — единица переходит в следующий разряд.
- Третий: 1 + 1 + 1 = 1 — единица переходит в следующий разряд.
- Четвёртый: 1 + 0 + 1 = 0 — единица переходит в следующий разряд.
- Пятый: 0 + 0 + 1 = 1.
Вроде бы пока несложно. Так что попробуйте сами сложить 1101 и 1011, чтобы закрепить знания.
Ответ
1101 + 1011 = 11000.
Умножение в двоичной системе, как в десятичной, основано на сложении — и умении считать в столбик.
Сведём в таблицу правила умножения двоичных чисел:
Давайте теперь посмотрим на реальных примерах, как правильно умножать двоичные числа.
Пример 1. Умножим 110 на 10.
Здесь мы воспользуемся привычным школьным «столбиком»: сначала умножаем верхнее число, 110, на 0, затем на 1, а потом складываем полученные два и получаем результат.
По сути, если мы умножаем число на ноль, то оно превращается в ноль, а если на единицу — остаётся неизменным, но сдвигается на число разрядов, равное номеру разряда этой единицы, как в обычном умножении:
- 110 × 0 = 000;
- 110 × 1 = 110.
Сдвигаем 110 на один разряд влево и складываем результаты промежуточных умножений:
- 000 + 1100 = 1100.
Мы получили 1100, потому что сместили результат умножения 110 × 1 на один разряд влево, а затем добавили один 0 справа — как в обычном умножении.
Пример 2. Давайте теперь умножим 101 на 101.
Не пугайтесь, что у нас получилось три числа, которые нужно сложить: правила остаются теми же. Ещё можно приписывать дополнительные нули туда, где находится пустое пространство — это поможет не запутаться.
Разберём пошагово:
- 101 × 1 = 101;
- 101 × 0 = 000;
- 101 × 1 = 101.
Снова сдвигаем влево промежуточные результаты и складываем:
- 101 + 0000 + 10100 = 11001.
Попробуйте сами умножить 1101 на 111.
Ответ
1011011.
Правила двоичного вычитания тоже ничем не отличаются от десятичного. Мы также вычитаем поразрядно и, если нужно, занимаем единицу из старшего разряда.
Таблица вычитания выглядит так:
Заметьте, что 0 − 1 = 1. Это всё потому, что мы занимаем единицу из старшего разряда и получаем 10, или 2 в десятичной системе, а если вычесть из 10 число 1, получим 1 (ведь 2 − 1 = 1).
Перейдём к примерам, чтобы понять, как вычитать одно число из другого.
Пример 1. Вычтем из 1100 число 11.
Разберём подробнее поразрядно:
- Первый: 0 − 1 = 1 — занимаем единицу из старшего разряда.
- Второй: 1 − 1 = 0 — так как отсюда заняли единицу, но у нас её не было, мы взяли её из следующего разряда и вычли единицу из этого.
- Третий: 0 − 0 = 0 — из этого разряда единица ушла в первый.
- Четвёртый: 1 − 0 = 1 — здесь всё нормально.
Всё то же знакомое нам вычитание.
Пример 2. Вычтем из 1011 число 101.
Тот же алгоритм по разрядам:
- Первый: 1 − 1 = 0.
- Второй: 1 − 0 = 1.
- Третий: 0 − 1 = 1 — заняли единицу из следующего разряда.
- Четвёртый: 0 − 0 = 0 — отдали единицу в предыдущий разряд.
Кажется, что всё несложно. Попробуйте теперь сами вычесть из 11010 число 1111.
Ответ
1011.
Вы удивитесь, но правила деления двоичных чисел похожи на деление десятичных. Рисуем привычный «столбик», умножаем, вычитаем, получаем результат.
Таблицы тут нет, потому что она бессмысленна — давайте сразу на примерах разбирать, как делить двоичные числа.
Пример 1. Поделить 1100 на 10.
У нас есть только два варианта: умножить делитель на 1 или на 0. Поэтому алгоритм будет таким:
- Смотрим на делимое, видим, что первые две его цифры — 11. Умножаем делитель на 1 и вычитаем из 11 число 10.
- Получили 1, дописываем справа следующую по порядку цифру — 0. Теперь 10 равно делителю, значит, тоже умножаем его на 1 и вычитаем.
- Получаем 0. Но у нас ещё остался один 0 у делимого — дописываем его справа от полученного 0.
- Число 0 меньше, чем 10, поэтому умножаем делитель на 0. Получаем конечный ответ — 110.
Пример 2. Поделить 10010 на 110.
Пошаговый алгоритм:
- Первые три числа делимого меньше, чем делитель — значит, умножаем делитель на 0 и вычитаем. Получаем 100.
- Дописываем 1 справа от 100, видим, что 1001 больше, чем 110, поэтому умножаем делитель на 1 и вычитаем его из 1001. Получаем 11.
- Дописываем 0 справа. Полученное 110 равно делителю, поэтому тоже умножаем его на 1, получаем конечный результат.
Попробуйте сами теперь поделить 10100 на 100.
Ответ
101.
Двоичная арифметика во многом похожа на десятичную: мы так же можем складывать, вычитать, делить и умножать числа столбиком. Правда, в двоичной системе всего две цифры: 0 и 1 — поэтому привычные математические операции в ней могут показаться немного странными. К счастью, в основе двоичной арифметики лежат простые принципы, которые нужно запомнить.
Научитесь: Профессия Python-разработчик
Узнать больше
О чем речь? Можно с уверенностью назвать двоичную систему счисления одной из основных, которые используются в вычислительной технике. А значит, привычные нам компьютер и смартфон применяют 0 и 1 для расчетов.
На что обратить внимание? Стоит отметить, что такая «популярность» – это дань традиции, заложенной праотцом вычислительных машин Блезом Паскалем. И все же, порой, нужно переводить показатели двоичной системы в 10-ю или 16-ю. Как же это сделать?
В статье рассказывается:
- Общепринятые системы счисления
- Числа, используемые в двоичной системе счисления
- Сложение, вычитание и умножение в двоичной системе счисления
- Как переводить числа в двоичной системе счисления в десятичную
- Алгоритм перевода из двоичной системы счисления в шестнадцатеричную
-
Пройди тест и узнай, какая сфера тебе подходит:
айти, дизайн или маркетинг.Бесплатно от Geekbrains
Общепринятые системы счисления
Человечество в ходе своего развития со временем стало нуждаться в способах подсчета. Нужно было считать, например, количество добычи или убитых врагов из других племен. И эта нужда у древних людей только возрастала. Поначалу пользовались абстрактными понятиями типа «нисколько», «один», «много». Затем в употребление вошла «пара», означающая два каких-то предмета. Уже одно это нововведение существенно упростило жизнь древнему человеку.
В дальнейшем люди стали считать единицами, используя в качестве таковых пальцы на руках и ногах, зарубки на деревьях, кости зверей, узелки на веревках. Благодаря изобретению таких примитивных счетных машин человечество спустя тысячелетия смогло понять, что в древности люди умели не только считать, но также фиксировать результаты счета.
С течением времени возникла необходимость в символьном обозначении любого количества больше единицы. В итоге древними египтянами были впервые придуманы знаки, обозначающие 1, 5 и 10.
Система чисел, состоящая из определенных знаков (цифр), фактически и является системой счисления. Другими словами, это способ численного выражения с помощью принятых правил и специальных знаков, называемых цифрами.
Скачать
файл
Любая система счисления принадлежит к одной из двух категорий:
Позиционные СС
Конкретное значение числа определяется не только цифрами, но и их позицией. Сюда относят арабскую систему, где первый разряд справа отведен для единиц, второй разряд справа — для десятков, третий разряд справа — для сотен и т. д. Таким образом, для записи числа 475 необходимо в крайней правой позиции расположить пятерку (пять единиц), после нее — семерку (семь десятков) и затем — четверку (четыре сотни). Позиционными считаются также системы счисления с основаниями (2, 8, 16).
Непозиционные СС
Значение числа определяется только знаком (цифрой). Для обозначения единиц, десятков, сотен и тысяч используются отдельные символы. Наиболее показательным представителем данной группы является римская система счисления. Здесь имеется еще одна отличительная особенность. Для записи очень больших чисел необязательно использовать весь набор знаков — на такие случаи существуют функции сложения и вычитания.
К примеру, число 475 римскими цифрами может выглядеть как CCCCXXXXXXXIIIII либо, в сокращенном виде, как CDLXXV. В последнем варианте используются именно вычитание и прибавление. Значение цифры, стоящей слева от большего числа, отнимается соответственно от этого числа. Если эта цифра стоит справа, то значение прибавляется.
Впервые позиционная система счисления была введена в Вавилоне. Примечательно, что она была шестнадцатеричная. К 19 веку распространение получила двенадцатеричная система.
Прежде чем разбирать, как записывается двоичная система счисления, определимся с терминами. Алфавит любой СС состоит из знаков, обозначающих отдельные цифры. Основанием называют значение, равное количеству знаков для кодирования чисел и представляющее собой целое число от 2 и выше.
Когда рассматривается несколько разных СС, тип каждой из них обычно обозначается подстрочным знаком. По умолчанию, если не указано основание, число является десятичным. Позиция цифры в числе называется разрядом.
Числа, используемые в двоичной системе счисления
Состав двоичной системы счисления — цифры 0 и 1. Основание равно 2. В крайней правой позиции числа указывается количество единиц, левее — количество двоек, затем количество четверок и т. д.
Таким образом, любое натуральное число кодируется в последовательный ряд из нулей и единиц — это и будет являться двоичной системой счисления. Решение такой задачи покажем на примере ниже.
10112 = 1*23 + 0*2*2+1*21+1*20 =1*8 + 1*2+1=1110
Как известно, двоичная система счисления используется вычислительной техникой для хранения информации, а также для преобразования данных в графические изображения. В свою очередь обработка двоичного кода требует предварительного размещения каждой цифры внутри особой электронной схемы (триггера). Эта схема может пребывать в одном из двух состояний — «ноль» или «единица».
Отдельное число, состоящее из нескольких цифр, сохраняется группой триггеров — регистром. Оперативная память компьютера фактически является совокупностью таких регистров.
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда
Подборка 50+ ресурсов об IT-сфере
Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT
ТОП 50+ сервисов и приложений от Geekbrains
Безопасные и надежные программы для работы в наши дни
Уже скачали 20982 
С точки зрения вычислительной техники любое сохраняемое число представляет собой машинное слово, арифметические и логические операции над которым выполняет арифметико-логическое устройство (АЛУ). Чтобы компьютеру было проще работать с регистрами, они нумеруются (или наделяются адресами).
Так, для сложения двух чисел используются адреса регистров, где они расположены, а не сами эти числа. Данные записываются в восьмеричной и шестнадцатеричной системах для более быстрого и простого перевода чисел в двоичный формат.
Тем не менее, конечный пользователь видит всю числовую информацию в привычном ему десятичном виде. Почему так происходит? Изначально, нажимая на клавишу, пользователь передает компьютеру соответствующую последовательность электрических сигналов (нулей и единиц). Для каждого символа определен конкретный набор этих импульсов.
Специальные программы (драйверы клавиатуры и экрана) преобразуют эти сигналы в читаемый вид путем обращения к кодовой таблице. Например, стандарт Unicode позволяет закодировать таким образом 65536 символов. Именно так используется двоичная система счисления в информатике — нули и единицы преобразуются программным способом в текст и изображения на экране.
Далее приведем очевидные достоинства использования двоичного способа представления информации.
- От технических устройств требуется лишь два устойчивых состояния (например, наличие тока и отсутствие тока и т. д.).
- Вычислительной технике значительно проще выполнять операции с двоичными данными, чем с десятичными.
- Таблицы сложения и умножения в двоичной системе имеют гораздо меньший размер по сравнению с такими же таблицами для десятичной системы.
Недостатки:
- возможное превращение конечных десятичных дробей в бесконечные двоичные;
- большее количество занимаемых разрядов по сравнению с десятичной записью;
- сложность с восприятием записи чисел, поскольку двоичная система счисления — этопредставление только в виде нулей и единиц.
Сложение, вычитание и умножение в двоичной системе счисления
Для того, чтобы складывать числа, пользуются следующей таблицей:
| + | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 10 (переход в старший разряд) |
Таблица вычитания в двоичной системе счисления выглядит так:
| — | 0 | 1 |
| 0 | 0 | 1 |
| 1 | (взятие из старшего разряда) 1 | 0 |
Только до 29.05
Скачай подборку тестов, чтобы определить свои самые конкурентные скиллы
Список документов:
Тест на определение компетенций
Чек-лист «Как избежать обмана при трудоустройстве»
Инструкция по выходу из выгорания
Чтобы получить файл, укажите e-mail:
Подтвердите, что вы не робот,
указав номер телефона:
Уже скачали 7503
Умножение выполняется по следующей таблице:
Как переводить числа в двоичной системе счисления в десятичную
Сперва приведем алфавиты трех используемых систем — двоичной, десятичной и шестнадцатеричной.
| Основание | Наименование системы | Алфавит |
| 2 | Двоичная | 0, 1 |
| 10 | Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| 16 | Шестнадцатеричная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Как уже упоминалось, двоичная система счисления имеет основание 2. Чтобы перевести число в десятичный формат, можно воспользоваться такой таблицей степеней данного основания:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Здесь ряд начинается с единицы, а каждая последующая цифра является результатом умножения предыдущей на двойку. После 1 ставится так называемая двоичная точка.
В качестве примера переведем число 1011011 двоичной системы счисления в 10-ный формат (число 91):
0*2+1=1>>1*2+0=2>>2*2+1=5>>5*2+1=11>>11*2+0=22>>22*2+1=45>> 45*2+1=91.
А конвертация 101111 в десятичную систему даст число 47:
0*2+1=1>>1*2+0=2>>2*2+1=5>>5*2+1=11>> 11*2+1=23 >> 23*2+1=47
НУЖНА КАРТИНКА
Таким же образом можно переводить и дробные числа. Для примера возьмем 1011010, 101 в двоичной системе счисления. Перевод чисел в десятичную можно осуществлять в таком виде:
1*26 + 0*25 + 1*24 + 1*2 + 0 *22 + 1 * 21 + 0 * 20 + 1 * 2-1 + 0 * 2-2 + 1 * 2-3 = 90,625
Иначе говоря, расчет будет следующим:
1*64+0*32+1*16+1*8+0*4+1*2+0*1+1*0,5+0*0,25+1*0,125 = 90,625
Полученное значение в десятичной системе также высчитывается по таблице:
| 64 | 32 | 16 | 8 | 4 | 2 | 1 | 0,5 | 0,25 | 0,125 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0. | .1 | 0 | 1 |
| +64 | +0 | +16 | +8 | +0 | +2 | +0 | +0.5 | +0 | +1.125 |
Алгоритм перевода из двоичной системы счисления в шестнадцатеричную
Здесь необходимо выполнить 2 шага:
- Перевод числа из двоичной системы в десятичную
- Преобразование полученного значения в шестнадцатеричный формат
К примеру, имеется число 1011101 в двоичной системе счисления. Запись чисел для выполнения первого шага осуществляется по формуле:
A2 = an-1 ∙ 2n-1 + an-2 ∙ 2n-2 + ∙∙∙ + a0 ∙ 20
Подставляем значения:
10111012=1 ∙ 26 + 0 ∙ 25 + 1 ∙ 24 + 1 ∙ 23 + 1 ∙ 22 + 0 ∙ 21 + 1 ∙ 20 = 1 ∙ 64 + 0 ∙ 32 + 1 ∙ 16 + 1 ∙ 8 + 1 ∙ 4 + 0 ∙ 2 + 1 ∙ 1 = 64 + 0 + 16 + 8 + 4 + 0 + 1 = 9310
Теперь полученное десятичное число необходимо преобразовать в шестнадцатеричное. Для этого 93 многократно последовательно делим на 16 до тех пор, пока остаток не станет меньше 16.
В процессе деления остатки нужно записывать в обратном порядке. Результатом всех операций будет число 9310=5D16.
НУЖНА КАРТИНКА
Перевод дробных чисел в шестнадцатеричный формат выполняется аналогичным образом — через промежуточный этап перевода в десятичную систему.
Вновь покажем это на примере. Преобразуем двоичное число 10001100.110 сначала в десятичную систему по формуле:
An = an-1 ∙ qn-1 + an-2 ∙ qn-2 + ∙∙∙ + a0 ∙ q0 + a-1 ∙ q-1 + ∙∙∙ + a-m ∙ q-m
Подставляем наши значения:
10001100.1102=1 ∙ 27 + 0 ∙ 26 + 0 ∙ 25 + 0 ∙ 24 + 1 ∙ 23 + 1 ∙ 22 + 0 ∙ 21 + 0 ∙ 20 + 1 ∙ 2-1 + 1 ∙ 2-2 + 0 ∙ 2-3 = 1 ∙ 128 + 0 ∙ 64 + 0 ∙ 32 + 0 ∙ 16 + 1 ∙ 8 + 1 ∙ 4 + 0 ∙ 2 + 0 ∙ 1 + 1 ∙ 0.5 + 1 ∙ 0.25 + 0 ∙ 0.125 = 128 + 0 + 0 + 0 + 8 + 4 + 0 + 0 + 0.5 + 0.25 + 0 = 140.7510
Следует отметить сильное сходство формул расчетов дробного и целого десятичных чисел. Тем не менее, отличия также имеются.
Вторым этапом переводим число 140,75 в шестнадцатеричный формат. Это делается в два подэтапа:
- Перевод отдельно целой части числа.
- Перевод отдельно дробной части числа.
Итак, нам необходимо сначала преобразовать 140 в шестнадцатеричную систему счисления, последовательно деля это число на 16, пока остаток не станет меньше делителя.
После записи остатков в обратном порядке получаем результат: 14010=8C16
Операции с дробной частью отличаются тем, что мы многократно и последовательно умножаем ее, пока она не станет равной нулю (или значению в соответствии с заданной точностью).
В нашем случае это будет выглядеть так: 0.75 * 16 = 12.0 (C).
Поскольку после первого же умножения дробная часть обнулилась, дальнейшие итерации прекращаем. Итоговый результат: 0.12 (0.С) или, иначе, 0.75 ∙ 16 = 12.0 (C)
Читайте также
Остался последний этап — соединение преобразованных целой и дробной частей: 140.7510=8C.C16. Это и будет общим решением всей задачи.
Сперва может показаться, что изложенный здесь материал слишком сложен и запутан для простого обывателя. На самом деле двоичная арифметика предельно логична и понятна. Пользование таблицами сложения и умножения не представляет сложности, если в них разобраться.