Дробная степень
Какими свойствами обладает степень с дробным показателем (дробная степень)? Как выполнить возведение числа в дробную степень?
Определение.
1) Степенью числа a (a>0) с рациональным показателем r
где m — целое число, n — натуральное число (n>1), называется число
2) При a=0 и r>0
В частности,
При a<0 степень с дробным показателем не определяется.
Все свойства степеней из курса алгебры 7 класса выполняются и для степеней с рациональными показателями.
Для упрощения вычислений при возведении числа в дробную степень удобно использовать таблицу степеней и следующее свойство корня:
Примеры.
Выполнить возведение в дробную степень:
Если показатель степени — десятичная дробь, нужно предварительно перевести ее в обыкновенную.
Смешанное число нужно предварительно перевести в неправильную дробь:
А как вычисляется отрицательная дробная степень?
Степень с отрицательным рациональным показателем также определена только для a>0:
При возведении обыкновенной дроби в степень с отрицательным показателем удобно использовать формулу:
Примеры.
Выполнить возведение в степень с отрицательным рациональным показателем:
Дробное число в дробную степень
Возведение дробного числа в дробную степень, не так сложна, если понимать что мы хотим сделать. Хотя у многих подобный вопрос вызывает панику.
Данную тему мы уже поднимали в материале Корни и степени комплексных чисел онлайн но вернемся еще раз к написанному.
Для того, что бы нам решать подобные задачи нам необходимо знать связь натурального логарифма )
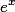
Связь очень проста })
Из последней формулы следует вывод что
Подумав, теперь легко решить нашу поставленную задачу
Что бы возвести дробное число в дробную степень
вычислим значение натурального логарифма
и результат возведем в экспоненту
Это и будет являтся результатом возведения дробного числа в дробную степень.
Примеры
Удачных расчетов!
Определение
Возведение целого числа в дробную степень — это арифметический процесс, при котором находится значение степени числа, выраженной дробью.
Преимущества дробной степени над записью выражения с помощью корней
Использовать дробную степень проще, чем записывать выражения с помощью корней. Это связано с тем, что вычислить значение числа в определенной степени легче, чем применять свойства корней. Если возведение в степень займет один шаг, то вычисление корня производится в несколько шагов.
Правило возведения
Возведение числа в дробную степень осуществляется согласно правилу: пусть (frac pq) — обыкновенная дробь, причём (p) и (q) больше нуля и (q≠1). Тогда для возведения числа a в дробную степень нужно извлечь из него корень q-ой степени и возвести в степень числителя, которая равна (p).
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В математической форме это правило выглядит так:
(a^frac qp=;sqrt[p]{a^q},;ageq0,;p>0,;q>1)
Правило, когда показатель степени является дробью
Если показателем степени является десятичная дробь, то нужно перевести ее в обыкновенную:
(625^{0,75} = 625^frac3{4;} = sqrt[4]{625^3} = 53 = 125)
В случае, если число смешанное, необходимо перевести его в неправильную дробь:
(left(15frac58right)^frac23;=;left(frac{125}8right)^frac23;=;sqrt[3]{left(frac{125}8right)^2};=;left(sqrt[3]{frac{125}8}right)^2;=;left(frac52right)^2;=;frac{25}4;=;6frac14)
При возведении дроби в отрицательную степень следует использовать формулу:
(left(frac abright)^{-n};=;left(frac baright)^n)
К примеру:
(625^{-frac34};=;frac1{625^{frac34}};=;frac1{sqrt[4]{625^3}};=;frac1{5^3};=;frac1{125})
Решение в виде задачи, примеры
Пример 1
Найти: (81^frac14)
Решение
(81^frac14=sqrt[4]{81^1}=3)
Ответ: 3.
Пример 2
Вычислить: (135^frac9{10})
Решение
(135^frac9{10}=;sqrt[10]{135^9})
Ответ: (;sqrt[10]{135^9}).
Пример 3
Найти: (left(1frac35right)^frac13)
Решение
(left(1frac35right)^frac13=left(frac85right)^frac13=sqrt[3]{left(frac85right)^1}=sqrt[3]{frac85}=sqrt[3]{frac{2^3}5}=frac2{sqrt[3]5})
Ответ: (frac2{sqrt[3]5}).
|
Как возвести число в дробную степень?Alexsandr82 6 лет назад
Как возвести число в дробную степень? То есть как например, возвести число 2 в степень 2/3? Alexsandr82 5 лет назад Для того чтобы возвести число в дробную степень нужно выполнить две операции: во-первых, возвести число в степень числителя дробной степени (числитель — это то что у дроби находится сверху), во-вторых, из того что получилось после возведения в степень нужно извлеч корень той степени чему равен знаменатель дробной степени (знаменатель — это то что стоит внизу дроби). Например, нам нужно возвести 3 в степень 3/7, сначало мы возводим 3 в степень числителя т.е. в куб, получаем 27, а затем извлекаме корень седьмой степени. Если дробная степень представленна с целой частью, то есть например нужно 2 возвести в степень 1 целая 1/3 то степень нужно представить в виде обычной дроби т.е. в данном случае это будет 4/3, а затем производить вычисления, 2 возводим в 4 степень получаем 16 и затем берем кубический корень из 16. Таким же образом в случае если нужно возвести число в степень 1,5, степень можно представить в виде обычной дроби 15/10 или 3/2 и произвести вычисления. комментировать
в избранное
ссылка
отблагодарить Валентина МД 5 лет назад Чтобы возвести число в дробную степень, надо возвести его в ту степень, которая показана в числителе и извлечь корень той степени, которая указана в знаменателе. Например: 2 в степени 2/1, это 2 во второй степени или другое название 2 в квадрате, равно 2*2. 2 в степени 1/2, это корень квадратный из 2. 2 в степени 2/3, это 2, возведена во вторую степень (квадрат), и потом из полученного результата извлечён корень 3 степени (куб) комментировать
в избранное
ссылка
отблагодарить vdtest 6 лет назад Чтобы возвести число в дробную степень надо возвести число в степень числителя дробной степени и вычислить из этого значения корень степени знаменателя дробной степени то есть результатом возведения в степень будет корень степени знаменателя дробной степени из числа в степени числителя дробной степени Пример комментировать
в избранное
ссылка
отблагодарить Знаете ответ? |
Дробная степень числа
- Дробный показатель степени
- Действия над степенями с дробными показателями
Дробный показатель
Число с дробным показателем степени равно корню с показателем, равным знаменателю, и подкоренным числом в степени, равной числителю.
Чтобы разобраться, почему число в дробной степени равно корню, надо вспомнить правило извлечения корня из степени:
Чтобы извлечь корень из степени, надо показатель степени разделить на показатель корня:
Следовательно, если показатель степени не делится на показатель корня, то получается дробная степень:
Поэтому извлечение корня всегда может быть заменено возведением в степень.
Действия над степенями с дробными показателями
Действия над степенями с дробными показателями совершаются по тем же правилам, которые установлены для степеней с целым показателем.
При доказательстве этого положения, будем сначала предполагать, что члены дробей: 

В частном случае n или q могут равняться единице.
При умножении дробных степеней с одинаковыми основаниями их показатели складываются:
При делении дробных степеней с одинаковыми основаниями из показателя делимого вычитается показатель делителя:
Чтобы возвести степень в другую степень, в случае дробных показателей, достаточно перемножить показатели степеней:
Чтобы извлечь корень из дробной степени, достаточно показатель степени разделить на показатель корня:
Правила действий применимы не только к положительным дробным показателям, но и к отрицательным.

=xln(e))
=1)
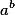
=bln(a))
})
=%3E7.69028=%3Ee^{7.690286}=2187)
=%3E-0.613914=%3Ee^{-0.613914}=0.5412279)







