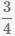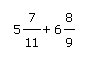Калькулятор «Конвертер десятичных дробей в обыкновенные»
Как записать 3.9 в виде дроби?
Ответ: Десятичная дробь 3.9 в обыкновенном виде это 3 9/10
3.9==3
Число 3.9 в виде обыкновенной дроби это 3 9/10
Объяснение конвертации дроби 3.9 в десятичную
Для того, чтобы найти простейшую дробную форму числа 3.9 необходимо сперва записать нашу десятичную дробь 3.9 как обыкновенную. Любое число можно легко записать в виде дроби, для этого нужно всего лишь разделить его на 1 (единицу):
Далее, нам необходимо избавиться от дробной части в числителе (3.9), т.е. сделать числитель целым числом. Для этого мы умножим числитель и знаменатель на 10 (т.к. в дробном числе 3.9 после запятой находится 1 знака)
Теперь необходимо сократить получившуюся дробь до самой простой формы. Для этого нужно найти Наибольший Общий Делитель (НОД) для чисел 39 и 10. Для того чтобы найти НОД для двух чисел, вы можете воспользоваться нашим Калькулятором НОД . НОД для чисел 10 и 39 равен 1. Следовательно, для того, чтобы упростить нашу дробь, необходимо разделить числитель и знаменатель на 1:
Вот и все! 3.9 как обыкновенная правильная дробь в самой простой форме это 3 9/10.
Похожие расчеты
Поделитесь текущим расчетом
https://calculat.io/ru/number/decimal-as-a-fraction/3.9
<a href=»https://calculat.io/ru/number/decimal-as-a-fraction/3.9″>3.9 в виде обыкновенной дроби — Calculatio</a>
О калькуляторе «Конвертер десятичных дробей в обыкновенные»
Данный онлайн-конвертер десятичных дробей в обыкновенные дроби — это инструмент, который поможет вам быстро и легко конвертировать любое десятичное число в обыкновенную дробь. Например, он может помочь узнать как записать 3.9 в виде дроби? Конвертер будет особенно полезен тем, кто ежедневно работает с дробями или использует их в учебных или профессиональных целях.
Чтобы использовать данный конвертер, все, что вам нужно сделать, это ввести десятичное число, которое вы хотите конвертировать, в соответствующее поле, например, ‘3.9’. После того как вы ввели десятичное число, нажмите кнопку ‘Конвертировать’, чтобы начать процесс конвертации.
Конвертер выведет результат и покажет обыкновенную дробь, которая эквивалентна введенному вами десятичному числу, а также предоставит пошаговое объяснение процесса конвертации. Кроме того, конечная дробь будет упрощена до простейшей формы, используя наибольший общий делитель (НОД).
Например, если вы введете ‘3.9’ в конвертер, он покажет вам, что данное десятичное число эквивалентно дроби ‘3 9/10’. Он также объяснит, как был получен данный ответ, показав шаги, выполненные в процессе конвертации.
В целом, онлайн-конвертер десятичных дробей в обыкновенные дроби — это необходимый инструмент для всех, кто работает с дробями в повседневной жизни, в учебной или профессиональной сфере. Он быстрый, простой в использовании и предоставляет точные результаты, что делает его ценным инструментом для всех, кто нуждается в конвертации десятичных дробей в обыкновенные.
Калькулятор «Конвертер десятичных дробей в обыкновенные»
Таблица конвертации десятичных дробей в обыкновенные
Калькулятор дробей
- Главная
- /
- Математика
- /
- Арифметика
- /
- Калькулятор дробей
Если вам необходимо произвести математические операции с дробями воспользуйтесь нашим онлайн калькулятором:
Просто заполните необходимые поля и получите ответ и подробное решение.
Данный калькулятор может работать как с положительными, так и с отрицательными дробями.
При этом нужно помнить, что:
− ac = a− c = − ac
Всегда нужно использовать только последний вариант.
Сложение дробей
С одинаковыми знаменателями
При сложении дробей с одинаковыми знаменателями складываются только числители, а знаменатель остаётся прежним.
Формула
ac + bc = a + bc
Пример
Для примера сложим следующие дроби с равными знаменателями:
27 + 47 = 2 + 47 = 67
С разными знаменателями
При сложении дробей с разными знаменателями для начала необходимо привести дроби к общему знаменателю. А затем сложить числители.
Формула (универсальная)
ac + bd = a⋅d + b⋅cc⋅d
Пример №1
Для примера сложим следующие дроби с разными знаменателями:
12+13=1⋅32⋅3+1⋅23⋅2=36+26=3+26=56
Пример №2
Существуют также частные случаи, когда знаменатель одной дроби можно привести к знаменателю второй. Например:
12+14=1⋅22⋅2+14=24+14=2+14=34
Этот же пример можно решить и применяя вышеуказанную универсальную формулу:
12+14=1⋅42⋅4+1⋅24⋅2=48+28=4+28=68=34
Обратите внимание, что мы сократили дробь:
68=3 ⋅ 24 ⋅ 2=34
Сложение смешанных чисел
Смешанные числа — это такие числа, у которых есть как дробная часть, так и целая.
Преобразуя в неправильную дробь
Для начала смешанное число (дробь) нужно преобразовать в неправильную дробь, а потом можно складывать как в предыдущих примерах.
Формула
a bc + d ef = b + a ⋅ cc + e + d ⋅ ff
Пример
Для примера сложим два смешанных числа:
312+123=1+3⋅22+2+1⋅33=72+53=7⋅32⋅3+5⋅23⋅2=216+106=21+106=316=5⋅6+16=5⋅66 + 16=516
Обратите внимание, что из полученной неправильной дроби мы выделили целую часть:
316=5⋅6+16=5⋅66 + 16=516
Складывая целую и дробную части отдельно
Целую и дробную части смешанных чисел можно складывать по отдельности.
Формула
a bc + d ef = (a + d) + (bc + ef)
Пример
Решим предыдущий пример этим способом:
3 12 + 1 23 = (3+1)+(12+23) = 4+1⋅32⋅3+2⋅23⋅2=4+36+46=4+3+46=4+76=4+116 = 516
Вычитание дробей
Вычитание дробей происходит по тем же принципам, что и сложение.
С одинаковыми знаменателями
Формула
ac − bc = a − bc
Пример
Для примера вычтем одну дробь из другой с равными знаменателями:
35−25=3−25=15
С разными знаменателями
Тут также, как и при сложении, дроби нужно подвести под общий знаменатель, а затем вычитать.
Формула
ac − bd = a⋅d − b⋅cc⋅d
Пример
Для примера вычтем одну дробь из другой, с разными знаменателями:
34−13=3⋅34⋅3−1⋅43⋅4=912−412=9−412=512
Вычитание смешанных чисел
Для начала смешанные числа преобразуем в неправильные дроби, потом приводим полученные дроби к общему знаменателю, а затем вычтем одну из другой. Далее выделяем целую часть если она есть.
Формула
a bc − d ef = b + a ⋅ cc − e + d ⋅ ff
Пример
312−123=1+3⋅22−2+1⋅33=72−53=7⋅32⋅3−5⋅23⋅2=216−106=21−106=116=1⋅6+56=1⋅66 + 56=156
Умножение дробей
При умножении дробей неважно одинаковые или разные у них знаменатели. Числитель одной дроби умножается на числитель другой, а знаменатели тоже перемножаются между собой.
Формула
ac ⋅ be = a ⋅ bc ⋅ e
Давайте рассмотрим несколько примеров:
Пример №1
Умножим дроби с одинаковыми знаменателями:
13⋅23=1⋅23⋅3=29
Пример №2
Умножим дроби с разными знаменателями:
13⋅24=1⋅23⋅4=212=1⋅26⋅2=16
Пример №3
Умножим смешанные числа:
112⋅223=1+1⋅22⋅2+2⋅33=32⋅83=3⋅82⋅3=246=4
Деление дробей
При делении одной дроби на другую также неважно одинаковые или разные у них знаменатели. Чтобы разделить одну дробь на другую нужно перемножить числитель первой дроби и знаменатель второй, а знаменатель первой умножить на числитель второй.
Формула
ac : be = a ⋅ ec ⋅ b
Давайте рассмотрим несколько примеров:
Пример №1
Разделим одну дробь на другую с таким же знаменателем:
23:13=23⋅31=2⋅33⋅1=63=2
Пример №2
Делим дроби с разными знаменателями:
12:23=12⋅32=1⋅32⋅2=34
Пример №3
Деление смешанных чисел:
412:223=1+4⋅22:2+2⋅33=92:83=92⋅38=9⋅32⋅8=2716=1⋅16+1116=1⋅1616 + 1116=11116
См. также
Калькулятор дробей
Онлайн калькулятор дробей позволяет производить простейшие арифметические операции с дробями: сложение дробей, вычитание дробей, умножение дробей, деление дробей. Чтобы произвести вычисления, заполните поля соответствующие числителям и знаменателям двух дробей. Если дробь имеет вид «смешанной дроби», то также заполните поле, соответствующее целой части дроби. Если у дроби нет целой части, т.е. дробь имеет вид «простой дроби», то оставьте данное поле пустым. Затем нажмите кнопку «Вычислить».
Вид дроби:
простые дроби
смешанные дроби
| Дробь 1 | Дробь 2 | Результат | ||||||||
| = | ||||||||||
| +/− | +/− |
Вычислить
Дробью в математике называется число, представляющее часть единицы или несколько её частей. Обыкновенная дробь записывается в виде двух чисел, разделенных обычно горизонтальной чертой, обозначающей знак деления. Число, располагающееся над чертой, называется числителем. Число, располагающееся под чертой, называется знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби — количество взятых этих частей целого.
Дроби бывают правильными и неправильными. Правильной называется дробь, у которой числитель меньше знаменателя. Если у дроби числитель больше знаменателя, то такая дробь называется неправильной. Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть,называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь (см. пример ниже).
Калькулятор дробей выполнит основные арифметические действия с дробями и смешанными числами.
Если целая часть заполнена, калькулятор приведет смешанное число в неправильную дробь и выполнит операцию.
Заполните поля калькулятора чтобы найти сумму, разность, произведение и отношение дробей.
Основные операции с дробями
Сложение и вычитание
Чтобы сложить дроби с разными знаменателями необходимо: привести дробные части к наименьшему общему знаменателю;
затем сложить их числители. Рассмотрим на примере как сложить две дроби с разными знаменателями.
Пример Сложить дроби  и
и 
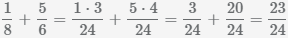
Наименьшее общее кратное знаменателей (8 и 6) равно 24.
Для нахождения разности дробей необходимо: привести дробные части к наименьшему общему знаменателю; затем выполнить вычитание числителей.
Пример Найти разность дробей  и
и 
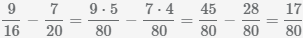
Общее кратное знаменателей НОК(16, 20)=80. Для вычисления наименьшего общего кратного можно воспользоваться калькулятором. Калькулятор вычислит НОК автоматически.
Умножение и деление
Для умножения двух дробей нужно: перемножить их числители и знаменатели 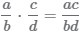
Чтобы разделить дробь на другую нужно: умножить первую дробь на дробь, обратную второй: 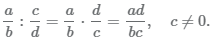
Приведение к общему знаменателю
Чтобы совершать операции с дробями часто требуется привести дроби к общему знаменателю.
Рассмотрим процесс приведения двух дробей 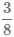
к наименьшему общему знаменателю :
Пример Сравнить дроби  и
и 
Для сравнения дробей приведем их к общему знаменателю и сравним их числители. Воспользуемся шагами описанными выше и найдем наименьшее общее кратное знаменателей дробей и далее преобразуем:
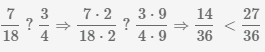
НОК(18, 4)=36, дополнительный множитель первой дроби 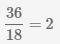
доп. множитель второй дроби 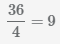
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Теория
- Дроби. Оглавление
- Сложение дробей
- Умножение дробей
- Деление дробей
Copyright calcs.su © 2021
Калькулятор дробей предназначен для быстрого расчета операций с дробями, поможет легко дроби сложить, умножить, поделить или вычесть.
Современные школьники начинают изучение дробей уже в 5 классе, с каждым годом упражнения с ними усложняются. Математические термины и величины, которые мы узнаем в школе, редко могут пригодиться нам во взрослой жизни. Однако дроби, в отличие от логарифмов и степеней, встречаются в повседневности достаточно часто (измерение расстояния, взвешивание товара и т.д.). Наш калькулятор предназначен для быстрого проведения операций с дробями.
Для начала определим, что такое дроби и какие они бывают. Дробями называют отношение одного числа к другому, это число, состоящее из целого количества долей единицы.
Разновидности дробей:
- Обыкновенные
- Десятичные
- Смешанные
Пример обыкновенных дробей:
Верхнее значение является числителем, нижнее знаменателем. Черточка показывает нам, что верхнее число делится на нижнее. Вместо подобного формата написания, когда черточка находится горизонтально, можно писать по-другому. Можно ставить наклонную линию, например:
1/2, 3/7, 19/5, 32/8, 10/100, 4/1
Десятичные дроби являются самой популярной разновидностью дробей. Они состоят из целой части и дробной, отделенные запятой.
Пример десятичных дробей:
0,2, или 6,71 или 0,125
Смешанные дроби состоят из целого числа и дробной части. Чтобы узнать значение этой дроби, нужно сложить целое число и дробь.
Пример смешанных дробей:
Калькулятор дробей на нашем сайте способен быстро в онлайн-режиме выполнить любые математические операции с дробями:
- Сложение
- Вычитание
- Умножение
- Деление
Для осуществления расчета нужно ввести цифры в поля и выбрать действие. У дробей нужно заполнить числитель и знаменатель, целое число может не писаться (если дробь обыкновенная). Не забудьте нажать на кнопку «равно».
Удобно, что калькулятор сразу предоставляет процесс решения примера с дробями, а не только готовый ответ. Именно благодаря развернутому решению вы можете использовать данный материал при решении школьных задач и для лучшего освоения пройденного материала.
Пример:
Вам нужно осуществить расчет примера:
После введения показателей в поля формы получаем:
Чтобы сделать самостоятельный расчет, введите данные в форму.
Калькулятор дробей
Введите две дроби:
|
= |
|||||||
Сопутствующие разделы:
Математический калькулятор онлайн


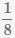 и
и 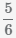
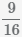 и
и 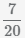
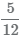
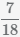 и
и