При
выборке малого объема точечная оценка
может значительно отличаться от
оцениваемого параметра, и часто для
исследований более эффективны интервальные
оценки.
О. 1.
Интервальной называют оценку, которая
определяется некоторым промежутком
(интервалом). Такие оценки позволяют
установить точность и надежность
выборочных оценок.
Очевидно,
статистическая оценка
тем точнее, чем меньше абсолютная
величина разности
,
т. е.
(*), где
есть погрешность.
О. 2.
Вероятность γ, с которой можно
утверждать, что выполняется неравенство
(*), называется надежностью или
доверительной вероятностью.
На
практике надежность обычно задают
близкой к единице, т. е. берут γ = 0,95,
γ = 0,99, γ = 0,999.
Итак,
или
есть вероятность того, что интервал
заключает в себе неизвестный параметр
.
О. 3.
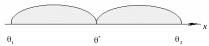
Интервал
,
который содержит неизвестный параметр
с заданной надежностью
γ, называется доверительным интервалом
(рис. 14).
О. 4.
Числа
называются доверительными границами.
δ
δ
Рис. 14.
Доверительный интервал
Чем
меньше δ, тем выше точность оценки.
О. 5.
называется уровнем значимости.
При
увеличении объема выборки длина
доверительного интервала уменьшается,
а с приближением
длина его увеличивается.
4.3. Доверительные интервалы для параметров нормального распределения Доверительный интервал для математического ожидания при известном σ
Пусть
для некоторой случайной величины,
распределенной по нормальному закону,
известно среднее квадратическое
отклонение, а сами значения этой с.в.
получены в эксперименте (имеется
выборка). Требуется определить среднее
значение данной с.в., учитывая известное
σ. Задача оценки истинного значения
измеряемой величины формулируется как
задача оценки математического ожидания
или центра нормального распределения.
Выбрав надежность γ, строим доверительный
интервал для математического ожидания:
.
Здесь
значение параметра t
находим из условия
,
где Ф(t) есть
затабулированная интегральная функция
Лапласа
(см. табл. П. 1).
О. 1.
Оценка
называется классической.
Погрешность
определяет точность классической
оценки.
Доверительный интервал для оценки математического ожидания нормального распределения при неизвестном σ
Пусть
с.в. Х генеральной совокупности
распределена нормально, но теперь
среднее квадратическое отклонение
(СКО) σ
неизвестно.
Тогда доверительный интервал для
математического ожидания
,
где
– выборочная средняя;
– исправленное среднее квадратическое
отклонение; n
– объем выборки;
находим по таблице квантилей
распределения Стьюдента (см. табл. П.
2).
Доверительный интервал для ско нормального распределения
Пусть
с.в. Х распределена нормально.
Требуется оценить СКО σ генеральной
совокупности по исправленному выборочному
СКО.
Тогда
доверительный интервал для СКО
,
при q < 1;
,
при q > 1,
где
определяется по табл. П. 3.
4.4. Решение типовых задач
Пример
1. Из ГС извлечена выборка объема n
= 50.
-
хi
2
5
7
10
ni
16
12
8
14
Найти
несмещенную оценку генеральной средней,
оценку
генеральной дисперсии и
исправленную оценку генеральной
дисперсии.
Решение.
Несмещенной оценкой генеральной
средней является выборочная средняя,
т. е.
.
Оценкой генеральной
дисперсии является выборочная дисперсия
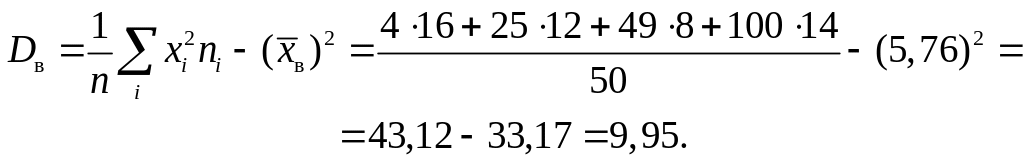
Соответственно,
исправленной оценкой генеральной
дисперсии является величина
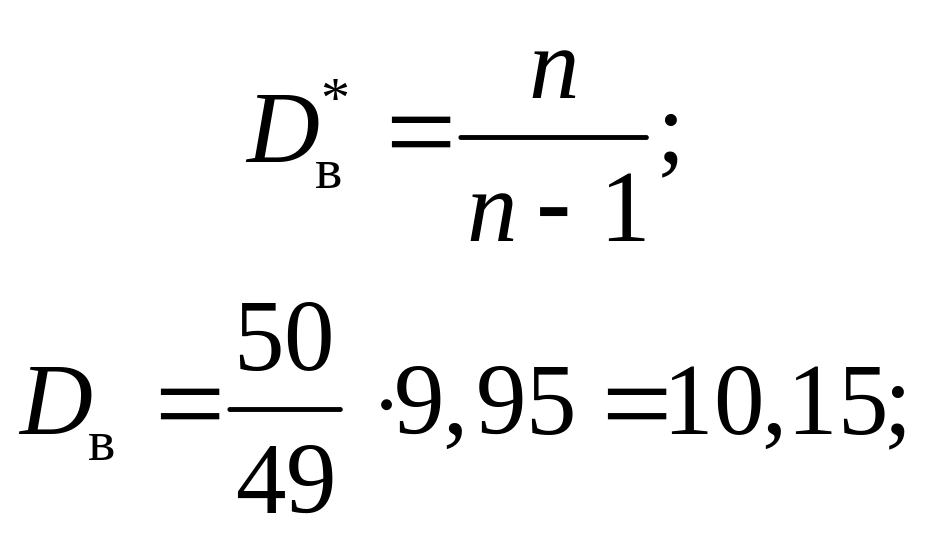
.
Пример
2. Найти точечные оценки для выборки
-
хi
186
192
194
ni
2
5
3
Решение.
Перейдем к новым переменным. Пусть c
= 192 – «ложный нуль».
-
ui
– 6
0
2
ni
2
5
3
Вычислим выборочное среднее:
.

Пример 3. Автомат
режет проволоку, проектная длина которой
5 см, а среднее квадратическое отклонение
0,3 см. Контролер производил выборочные
измерения и получил следующие результаты:
51, 47, 48, 46, 54, 49, 47, 50, 53, 46, 46, 47, 48, 49, 52, 51, 48,
47, 49, 51, 45 (в мм). Учитывая, что длина отрезка
– величина, распределенная по нормальному
закону, найдите с надежностью 0,95
доверительный интервал для математического
ожидания генеральной совокупности
(нарезанной проволоки) и примите решение
о необходимости доналадки автомата.
Решение. Построим сгруппированный
вариационный ряд.
|
хi |
45 |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
|
ni |
1 |
3 |
4 |
3 |
3 |
1 |
3 |
2 |
1 |
Объем
выборки n = 21. Найдем
выборочное среднее хв = 48,76.
Среднее квадратическое отклонение
известно: = 3 мм. Из
условия 2Ф(t) = 0,95
по таблице найдем t =
1,96. Тогда точность
вычислим по формуле
.
Получаем = 1,28.
Строим
доверительный интервал для математического
ожидания с известным
= 3 мм:
48,76 – 1,28 < a < 48,76 +
1,28,
47,48 < а < 50,04.
Вообще
говоря, в допустимые размеры от 47 мм до
53 мм данные выборки попадают, но, очевидно,
следует отрегулировать автомат для
большей точности.
Пример
4. Фирма «Бублик» заявляет, что вес их
изделий равен 100 г. Петя решил проверить
правдивость фирмы. Сколько бубликов
ему нужно купить, чтобы с вероятностью
0,99 убедиться
в том, что истинный вес
отклоняется от рекламируемого не более
чем на 3 г? Учтите, что у Пети есть весы,
систематическая ошибка взвешивания на
которых равна нулю, а случайные ошибки
подчинены нормальному закону со средним
квадратическим отклонением 5 г.
Решение. Исследуемое
отклонение истинного веса от рекламируемого
3 г – это точность .
Значение t находим по
таблице из условия 2Ф(t)
= 0,99. Получаем t = 2,54.
Из формулы
находим
,
то есть Пете нужно купить не менее 18
бубликов, чтобы определить истинный
вес бубликов этой фирмы.
Пример
5. В пруду выращивается рыба. Когда
рыба достигнет своего промышленного
веса 750 г, можно объявлять массовый лов.
Технолог рыбозавода произвел контрольное
взвешивание и получил следующие
результаты: 680, 695, 780, 657, 723, 745, 790, 715, 735,
689, 693, 727, 685, 758, 762, 742, 794, 652, 673, 763, 683, 789, 770,
670, 648, 784, 791, 621, 753, 698, 768, 675, 729, 762, 772, 657, 683,
758, 795, 760. Построив доверительный интервал,
с надежностью 0,95 определите, следует
ли разрешать массовый лов.
Решение.
Так как величины достаточно плотно
расположены на числовой шкале, построим
интервальный ряд из 5 интервалов. Объем
выборки – 40. Наименьшее значение – 621,
наибольшее – 795. Размах выборки – 174.
Длина интервала 174 : 4 = 43,5,
левая граница интервального ряда –
599,25.
|
хi; |
599,25; 642,75 |
642,75; 686,25 |
686,25; 729,75 |
729,75; 773,25 |
773,25; 816,75 |
|
ni |
1 |
11 |
9 |
13 |
6 |
|
621 |
664,5 |
708 |
751,5 |
795 |
Используя
данные интервального ряда, находим
выборочное среднее хв = 721,05
и исправленное среднее квадратическое
отклонение S = 49,1.
Учитывая
надежность = 0,95 и
объем выборки n = 40,
находим t
по таблице квантилей распределения
Стьюдента: t
= 2,023.
Строим
доверительный интервал для математического
ожидания нормально распределенной
генеральной совокупности при неизвестном
:
или 705,33 < а < 736,77.
Пока
лов рыбы начинать рано.
Пример
6. Произведено: а) 12; б) 6 измерений
расстояния новым дальномером. Исправленное
СКО S случайных ошибок
измерения оказалось равным 0,6 м. Найти
точность прибора с надежностью 0,99.
Решение.
Точность прибора характеризуется
средним квадратическим отклонением
случайных ошибок измерения. А случайные
ошибки любого измерения – нормально
распределенная случайная величина.
Поэтому необходимо найти доверительный
интервал для СКО генеральной совокупности.
а) γ =
0,99, n = 12, по табл. П. 3
находим q(0,99; 12) = 0,9 <
1.
Тогда
доверительный интервал находим по
формуле
0,6(1 –
0,9) < σ < 0,6(1 + 0,9).
Окончательно
получаем 0,06 м < σ < 1,14
м. Это и есть точность испытываемого
дальномера.
б) γ =
0,99, n = 6, по табл. П. 3
находим q(0,99; 6) = 2,01 >
1.
Тогда
доверительный интервал находим по
формуле
0 < σ
< 0,6(1 + 2,01).
Окончательно
получаем 0 < σ < 1,806 м.
Это и есть точность испытываемого
дальномера.
На этом
примере можно убедиться, что большее
количество испытаний дает более точную
оценку.
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Для начала напомним следующее определение:
Пусть нам дано исправленное среднее квадратическое отклонение $S$. Оценим неизвестное генеральное среднее квадратическое отклонение, то есть найдем доверительный интервал, который покрывает величину $sigma $.
Для этого нам необходимо, чтобы выполнялось равенство
неравенство
Отметим, что так как среднее квадратическое отклонение больше нуля, то при $q>1$ доверительный интервал будет иметь вид:
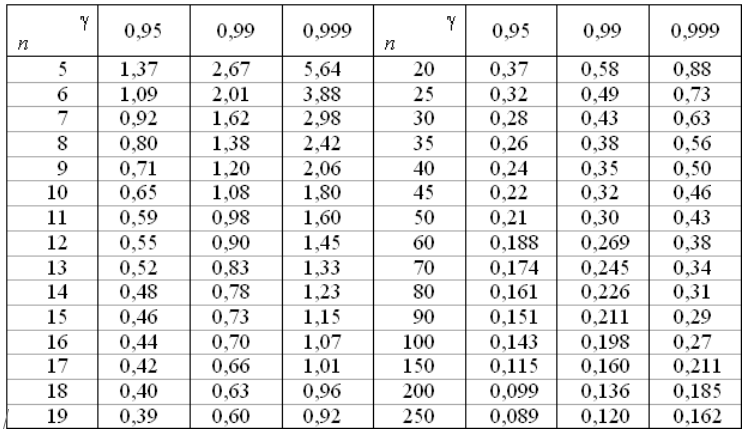
Величина $q$ имеет табличные значения:
Рисунок 1. Таблица значений величины $q$.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Доверительный интеграл для оценки дисперсии
С понятием среднего квадратического отклонения тесно связано понятие дисперсии.
Пусть нам дано исправленная дисперсия. Оценим неизвестное генеральную дисперсию, то есть найдем доверительный интервал, который покрывает величину $D$.
Так как среднее квадратическое отклонение равно квадратному корню от дисперсии, то исправленная дисперсия равна квадрату исправленного среднего квадратического отклонения $S^2.$
Таким образом, получим, что доверительный интервал имеет вид:
Отметим, что так как среднее квадратическое отклонение больше нуля, то при $q>1$ доверительный интервал будет иметь вид:
Пример задач на нахождение доверительного интервала
Пример 1
Пусть выборка имеет исправленное среднее квадратическое отклонение $S=0,4$. Пусть объем выборки $n=60$, а надежности равна $gamma =0,95$. Найти доверительный интервал для оценки среднего квадратического отклонения данного распределения.
Решение:
Для начала найдем величину $q$ из таблицы 1. Так как, по условию задачи, $n=60$ и $gamma =0,95$, то получим, что $q=0,188$.
Видим, что $q
[left(Sleft(1-qright),Sleft(1+qright)right)] [left(0,4cdot 0,812;0,4cdot 1,188right)=(0,3248;0,4752)]
Ответ: $(0,3248;0,4752)$.
«Доверительные интервалы для оценки среднего квадратического отклонения» 👇
Пример 2
Пусть выборка имеет исправленное среднее квадратическое отклонение $S=0,9$. Пусть объем выборки $n=10$, а надежности равна $gamma =0,999$. Найти доверительный интервал для оценки среднего квадратического отклонения данного распределения.
Решение:
Для начала найдем величину $q$ из таблицы 1. Так как, по условию задачи, $n=10$ и $gamma =0,999$, то получим, что $q=1,8$.
Видим, что $q
[left(0;Sleft(1+qright)right)] [left(0;0,9cdot 2,8right)=(0;;2,52)]
Ответ: $(0;2,52)$.
Пример 3
Пусть выборка имеет исправленное среднее квадратическое отклонение $S=0,3$. Пусть объем выборки $n=30$, а надежности равна $gamma =0,99$. Найти доверительный интервал для дисперсии данного распределения.
Решение:
Для начала найдем величину $q$ из таблицы 1. Так как, по условию задачи, $n=30$ и $gamma =0,99$, то получим, что $q=0,43$.
Видим, что $q
[left(S^2left(1-qright),S^2left(1+qright)right)] [left(0,09cdot 0,57;0,09cdot 1,43right)=(0,0513;0,1287)]
Ответ: $(0,0513;0,1287)$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Доверительный интервал для математического ожидания нормальной случайной
величины при неизвестной дисперсии
Пусть
, причем
и
неизвестны. Необходимо построить доверительный интервал,
накрывающий с надежностью
истинное значение параметра
.
Для этого из генеральной
совокупности СВ
извлекается
выборка объема
:
.
1) В качестве точечной
оценки математического ожидания
используется
выборочное среднее
, а в
качестве оценки дисперсии
–
исправленная выборочная дисперсия
которой соответствует стандартное отклонение
.
2) Для нахождения
доверительного интервала строится статистика
имеющая в этом случае распределение Стьюдента с
числом степеней свободы
независимо
от значений параметров
и
.
3) Задается требуемый
уровень значимости
.
4) Применяется следующая
формула расчета вероятности:
где
–
критическая точка распределения Стьюдента, которая находится по таблице критических точек распределения Стьюдента (односторонняя критическая область).
Тогда:
Это означает, что
интервал:
накрывает неизвестный
параметр
с
надежностью
Доверительный интервал для математического ожидания
нормальной случайной величины при известной дисперсии
Пусть количественный
признак
генеральной
совокупности имеет нормальное распределение
с
заданной дисперсией
и
неизвестным математическим ожиданием
. Построим
доверительный интервал для
.
1) Пусть для оценки
извлечена
выборка
объема
. Тогда
2) Составим случайную
величину:
Нетрудно показать, что случайная величина
имеет стандартизированное нормальное распределение, то есть:
3) Зададим уровень
значимости
.
4) Применяя формулу нахождения
вероятности отклонения нормальной величины от математического ожидания, имеем:
Это означает, что
доверительный интервал
накрывает неизвестный
параметр
с надежностью
. Точность оценки определяется величиной:
Число
определяется
по таблице значений функции Лапласа из равенства
Окончательно получаем:
Доверительный интервал для
дисперсии нормальной случайной величины при неизвестном математическом ожидании
Пусть
, причем
и
–
неизвестны. Пусть для оценки
извлечена выборка объема
:
.
1) В качестве точечной оценки дисперсии
используется
исправленная выборочная дисперсия
:
которой соответствует стандартное отклонение
.
2) При нахождении
доверительного интервала для дисперсии в этом случае вводится статистика
имеющая
–
распределение с числом степеней свободы
независимо
от значения параметра
.
3) Задается требуемый
уровень значимости
.
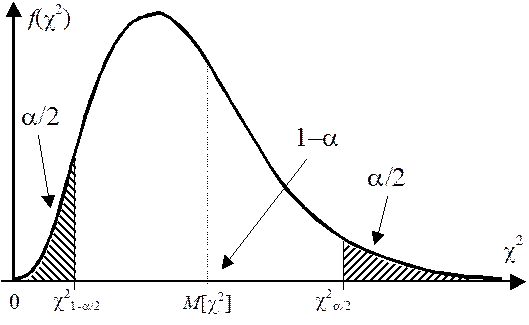
4) Тогда, используя таблицу критических точек хи-квадрат распределения, нетрудно указать критические
точки
, для которых будет выполняться следующее
равенство:
Подставив вместо
соответствующее значение, получим:
Получаем доверительный
интервал для неизвестной дисперсии:
Доверительный интервал для
дисперсии нормальной случайной величины при известном математическом ожидании
Пусть
, причем
–
известна, а
–
неизвестна. Пусть для оценки
извлечена выборка объема
:
.
1) В качестве точечной оценки дисперсии
используется выборочная дисперсия:
2) При нахождении
доверительного интервала для дисперсии в этом случае вводится статистика
имеющая
–
распределение с числом степеней свободы
независимо
от значения параметра
.
3) Задается требуемый
уровень значимости
.
4) Тогда, используя таблицу критических точек хи-квадрат распределения,
нетрудно указать критические точки
, для которых будет выполняться следующее
равенство:
Подставив вместо
соответствующее значение, получим:
Получаем доверительный
интервал для неизвестной дисперсии:
Доверительный интервал для
среднего квадратического отклонения
Извлекая квадратный корень:
Положив:
Получим следующий
доверительный интервал для среднего квадратического
отклонения:
Для отыскания
по заданным
и
пользуются специальными таблицами.
Для проверки на нормальность заданного распределения случайной величины можно использовать
правило трех сигм.
Задача
Имеется
три независимых реализации нормальной случайной величины: 0.8, 3.2, 2.0.
Построить
доверительные интервалы для среднего и дисперсии с надежностью
Указание:
воспользоваться таблицами Стьюдента и хи-квадрат.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Вычисление средней и дисперсии
Вычислим среднее и
исправленную дисперсию
:
Нахождение доверительных интервалов для средней и дисперсии
Найдем доверительный интервал для оценки
неизвестного среднего. Он считается по формуле:
По таблице критических точек t-критерия Стьюдента, для уровня значимости
(односторонняя критическая область):
Искомый
доверительный интервал для среднего:
Найдем доверительный интервал для оценки дисперсии.
Он считается по формуле:
Для уровня значимости
и
получаем по таблице значений хи-квадрат:
Искомый доверительный интервал для дисперсии:
Ответ
Кроме этой задачи на другой странице сайта есть
пример расчета доверительного интервала математического ожидания и среднего квадратического отклонения для интервального вариационного ряда
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Для помощи во время экзамена/зачета в онлайн режиме необходимо договариваться заранее.
Способы расчета доверительного интервала

21 апреля 2016
Часто оценщику приходится анализировать рынок недвижимости того сегмента, в котором располагается объект оценки. Если рынок развит, проанализировать всю совокупность представленных объектов бывает сложно, поэтому для анализа используется выборка объектов. Не всегда эта выборка получается однородной, иногда требуется очистить ее от экстремумов – слишком высоких или слишком низких предложений рынка. Для этой цели применяется доверительный интервал. Цель данного исследования – провести сравнительный анализ двух способов расчета доверительного интервала и выбрать оптимальный вариант расчета при работе с разными выборками в системе estimatica.pro.
Способы расчета доверительного интервала
Доверительный интервал – вычисленный на основе выборки интервал значений признака, который с известной вероятностью содержит оцениваемый параметр генеральной совокупности.
Смысл вычисления доверительного интервала заключается в построении по данным выборки такого интервала, чтобы можно было утверждать с заданной вероятностью, что значение оцениваемого параметра находится в этом интервале. Другими словами, доверительный интервал с определенной вероятностью содержит неизвестное значение оцениваемой величины. Чем шире интервал, тем выше неточность.
Существуют разные методы определения доверительного интервала. В этой статье рассмотрим 2 способа:
- через медиану и среднеквадратическое отклонение;
- через критическое значение t-статистики (коэффициент Стьюдента).
Этапы сравнительного анализа разных способов расчета ДИ:
1. формируем выборку данных;
2. обрабатываем ее статистическими методами: рассчитываем среднее значение, медиану, дисперсию и т.д.;
3. рассчитываем доверительный интервал двумя способами;
4. анализируем очищенные выборки и полученные доверительные интервалы.
Этап 1. Выборка данных
Выборка сформирована с помощью системы estimatica.pro. В выборку вошло 91 предложение о продаже 1 комнатных квартир в 3-ем ценовом поясе с типом планировки «Хрущевка».
Таблица 1. Исходная выборка
|
№ |
Цена 1 кв.м., д.е. |
|
1 |
50943 |
|
2 |
35000 |
|
3 |
51613 |
|
4 |
50645 |
|
5 |
49841 |
|
… |
… |
|
86 |
58772 |
|
87 |
70714 |
|
88 |
53393 |
|
89 |
54876 |
|
90 |
52542 |
|
91 |
56140 |
Рис.1. Исходная выборка

Этап 2. Обработка исходной выборки
Обработка выборки методами статистики требует вычисления следующих значений:
1. Среднее арифметическое значение
2. Медиана – число, характеризующее выборку: ровно половина элементов выборки больше медианы, другая половина меньше медианы
(для выборки, имеющей нечетное число значений)
3. Размах – разница между максимальным и минимальным значениями в выборке
4. Дисперсия – используется для более точного оценивания вариации данных
5. Среднеквадратическое отклонение по выборке (далее – СКО) – наиболее распространённый показатель рассеивания значений корректировок вокруг среднего арифметического значения.
6. Коэффициент вариации – отражает степень разбросанности значений корректировок
7. коэффициент осцилляции – отражает относительное колебание крайних значений цен в выборке вокруг средней
Таблица 2. Статистические показатели исходной выборки
|
Показатель |
Значение |
|
Ср. значение |
54970 |
|
Медиана |
53934 |
|
Размах |
39194 |
|
Дисперсия |
45126821 |
|
СКО |
6755 |
|
Коэф. вариации |
12,29% |
|
Коэф. осциляции |
71,30% |
Коэффициент вариации, который характеризует однородность данных, составляет 12,29%, однако коэффициент осцилляции слишком велик. Таким образом, мы можем утверждать, что исходная выборка не является однородной, поэтому перейдем к расчету доверительного интервала.
Этап 3. Расчёт доверительного интервала
Способ 1. Расчёт через медиану и среднеквадратическое отклонение.
Доверительный интервал определяется следующим образом: минимальное значение — из медианы вычитается СКО; максимальное значение – к медиане прибавляется СКО.
Формула доверительного интервала:
Таким образом, доверительный интервал (47179 д.е.; 60689 д.е.)
Значения, содержащиеся в исходной выборке и не попадающие в доверительный интервал, удаляем. Удалено 20 объектов, что составило 22% выборки.
Рис. 2. Значения, попавшие в доверительный интервал 1.

Способ 2. Построение доверительного интервала через критическое значение t-статистики (коэффициент Стьюдента)
С.В. Грибовский в книге «Математические методы оценки стоимости имущества» описывает способ вычисления доверительного интервала через коэффициент Стьюдента. При расчете этим методом оценщик должен сам задать уровень значимости ∝, определяющий вероятность, с которой будет построен доверительный интервал. Обычно используются уровни значимости 0,1; 0,05 и 0,01. Им соответствуют доверительные вероятности 0,9; 0,95 и 0,99. При таком методе полагают истинные значения математического ожидания и дисперсии практически неизвестными (что почти всегда верно при решении практических задач оценки).
Формула доверительного интервала:
n — объем выборки;
— критическое значение t- статистики (распределения Стьюдента) с уровнем значимости ∝,числом степеней свободы n-1,которое определяется по специальным статистическим таблицам либо с помощью MS Excel (
→»Статистические»→ СТЬЮДРАСПОБР);
∝ — уровень значимости, принимаем ∝=0,01.
Значения, содержащиеся в исходной выборке и не попадающие в доверительный интервал, удаляем. Удалено 62 объекта, что составило 68% выборки.
Рис. 2. Значения, попавшие в доверительный интервал 2.
Этап 4. Анализ разных способов расчета доверительного интервала
Два способа расчета доверительного интервала – через медиану и коэффициент Стьюдента – привели к разным значениям интервалов. Соответственно, получилось две различные очищенные выборки.
Таблица 3. Статистические показатели по трем выборкам.
|
Показатель |
Исходная выборка |
1 вариант |
2 вариант |
|
Среднее значение |
54970 |
53593 |
54750 |
|
Медиана |
53934 |
53425 |
54688 |
|
Размах |
39194 |
12888 |
3677 |
|
Дисперсия |
45126821 |
8919645 |
1228707 |
|
СКО |
6755 |
3008 |
1128 |
|
Коэф. вариации |
12,29% |
5,61% |
2,06% |
|
Коэф. осциляции |
71,30% |
24,05% |
6,72% |
|
Количество выбывших объектов, шт. |
20 |
62 |
На основании выполненных расчетов можно сказать, что полученные разными методами значения доверительных интервалов пересекаются, поэтому можно использовать любой из способов расчета на усмотрение оценщика.
Однако мы считаем, что при работе в системе estimatica.pro целесообразно выбирать метод расчета доверительного интервала в зависимости от степени развитости рынка:
- если рынок неразвит, применять метод расчета через медиану и среднеквадратическое отклонение, так как количество выбывших объектов в этом случае невелико;
- если рынок развит, применять расчет через критическое значение t-статистики (коэффициент Стьюдента), так как есть возможность сформировать большую исходную выборку.
При подготовке статьи были использованы:
1. Грибовский С.В., Сивец С.А., Левыкина И.А. Математические методы оценки стоимости имущества. Москва, 2014 г.
2. Данные системы estimatica.pro
Читайте также:
Расчет корректировок методом парных продаж
Статью подготовили: Наталья Ничкова и Михаил Филимонов
Построение доверительного интервала
для МО СВ, имеющей нормальное распределение с известным СКО
Пусть x~N(M[x],
s[x]),
причём s[x] – известно, а M[x]=?.
1. Определяется точечная оценка МО по выборке объема n

Поскольку 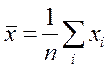
– значения одной и той же СВ x, то в силу центральной предельной
теоремы, ~N(M[
],s[
]).
Поскольку точечная оценка является
несмещенной, то . СКО оценки
МО СВ x равно
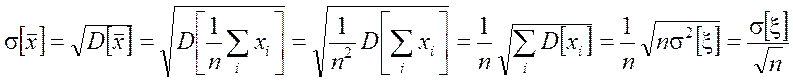
2. Рассмотрим вспомогательную случайную величину:
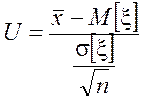
которая, как и величина имеет нормальное распределение с МО:
и дисперсией:
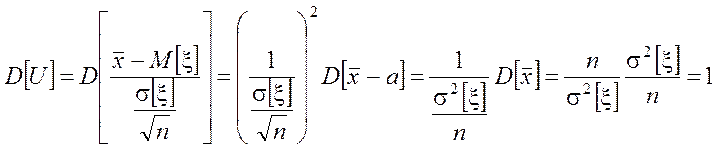
Таким образом, x~N(M[x],s[x])
, ~N (M[x],
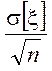
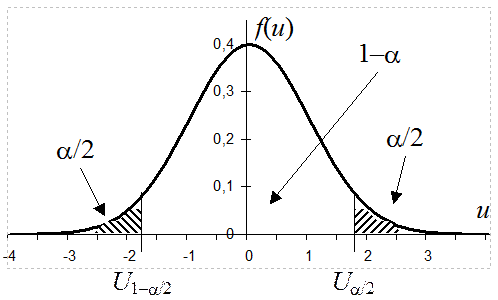
3. Для заданной Pдов=1–a
определяется интервал (,
) из
условий:
P{U<}=a/2; P{U>
}=a/2.
На основании симметрии функции плотности нормального
распределения Ua/2=–U1-a/2. Квантили U уровня (1–a/2)
и (a/2) определяются по таблицам квантилей стандартного
нормального распределения.
4. Определив интервал (,
), который с доверительной
вероятностью накрывает значение U, определяется доверительный интервал
для M[x] обратным преобразованием:
Þ
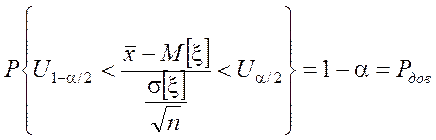
Þ
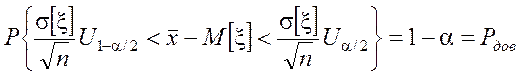
Þ
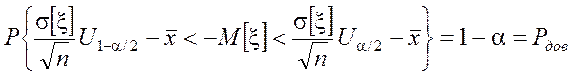
Учитывая,
что Ua/2=–U1-a/2
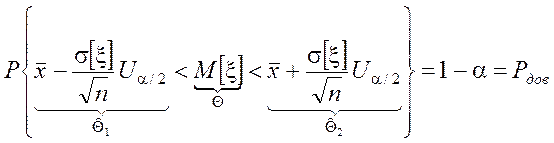
Доверительный интервал найден. Абсолютная погрешность
интервальной оценки МО равна: 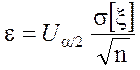
Построение доверительного интервала
для МО СВ, имеющей нормальное распределение с неизвестным СКО
Пусть x~N(M[x],
s[x]),
причём M[x]=?, s[x]=?.
1. Определяется точечная оценка МО и СКО по выборке
объёма n:
,
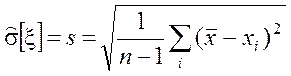
2. Составляется вспомогательная СВ
(выборочная статистика):
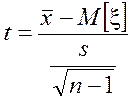
которая имеет распределение
Стьюдента с n=n–1 степенями свободы.
Таким образом, если x~N(M[x],
s[x]),
то t~t(n–1).
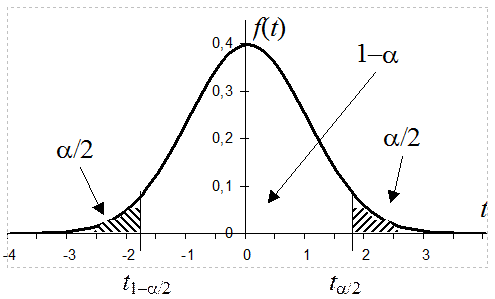
3. Для заданной доверительной
вероятности Pдов=1–a определяется интервал (t1–a/2,
n–1, ta/2,
n–1) из условий:
P{t < t1–a/2, n–1}=a/2;
P{t>ta/2,
n–1}=a/2.
Квантили распределения Стьюдента уровня (1-a/2)
и (a/2) для различного числа степеней свободы (n–1)
определяются по таблицам. На основании симметрии функции плотности
распределения Стьюдента t1–a/2,
n–1 = – ta/2,
n–1 .
4. Определив интервал (t1–a/2,
n–1, ta/2,
n–1), который с
доверительной вероятностью накрывает значение t, определяется
доверительный интервал для M[x] следующим обратным
преобразованием:
Þ
Þ
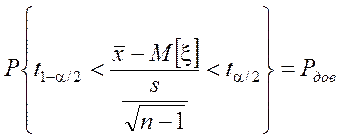
Þ
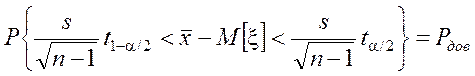
Þ
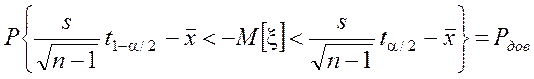
Учитывая,
что ta/2=–t1–a/2
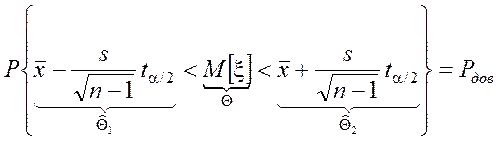
Т.о. доверительный интервал для МО СВ, имеющей
нормальное распределение с неизвестным СКО найден. Абсолютная погрешность
оценки МО равна 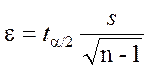
Построение доверительного интервала
для СКО СВ, имеющей нормальное распределение
Пусть x~N(M[x],
s[x]),
причём M[x]=?, s[x]=?.
1. Определяется точечная оценка МО и СКО по выборке
объёма n:
,
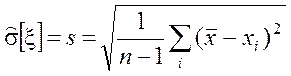
2. Составляется вспомогательная СВ
(выборочная статистика):
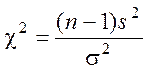
которая имеет распределение c2
с n=n–1
степенями свободы.
Т.о., если x~N(M[x],
s[x]),
то c2 ~c2 (n–1).
3. Для заданной доверительной
вероятности Pдов=1–a, определяется интервал (c2 1–a/2,
n–1, c2 a/2,
n–1) из условий:
P{c2 < c2 1–a/2,
n–1}=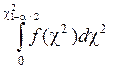
P{c2 > c2 a/2, n–1}=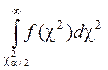
Квантили распределения c2 уровня (1–a/2)
и (a/2) для различного числа степеней свободы (n–1)
можно найти в специальных таблицах.
4. Определив интервал (c2 1–a/2, n–1, c2 a/2, n–1), который с доверительной
вероятностью накрывает значение c2 , можно найти доверительный интервал
для СКО s[x] следующим обратным
преобразованием:
Þ
Þ
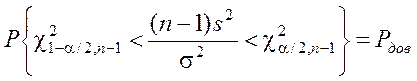
Þ
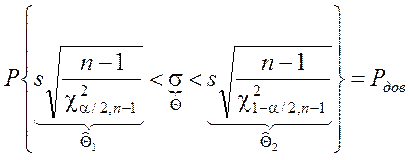
Следовательно доверительный интервал для СКО СВ,
имеющей нормальное распределение, найден.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.