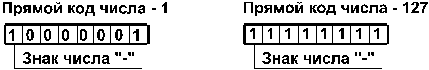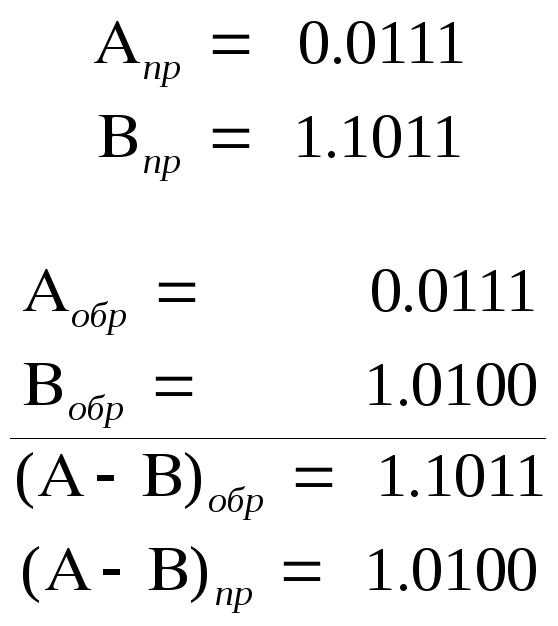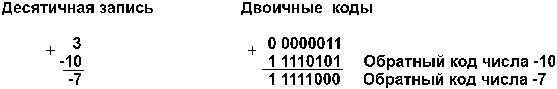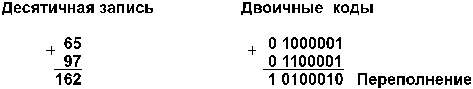Двоичное число: прямой, обратный и дополнительный коды
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа
Прямой, обратный и дополнительный коды двоичного числа — способы представления двоичных чисел с фиксированной запятой в компьютерной (микроконтроллерной) арифметике, предназначенные для записи отрицательных и неотрицательных чисел
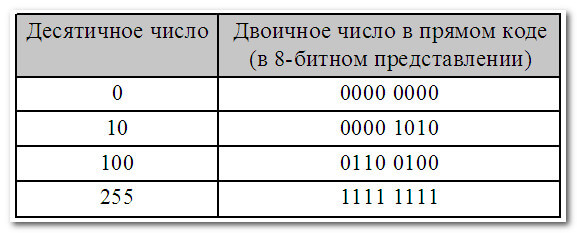
Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Прямой код — способ представления двоичных чисел с фиксированной запятой. Главным образом используется для записи неотрицательных чисел
Прямой код используется в двух вариантах.
В первом (основной) — для записи только неотрицательных чисел:
Второй вариант — для записи как положительных, так и отрицательных чисел.
В этом случае старший бит (в нашем случае — восьмой) объявляется знаковым разрядом (знаковым битом).
При этом, если:
— знаковый разряд равен 0, то число положительное
— знаковый разряд равен 1, то число отрицательное
В этом случае диапазон десятичных чисел, которые можно записать в прямом коде составляет от — 127 до +127:
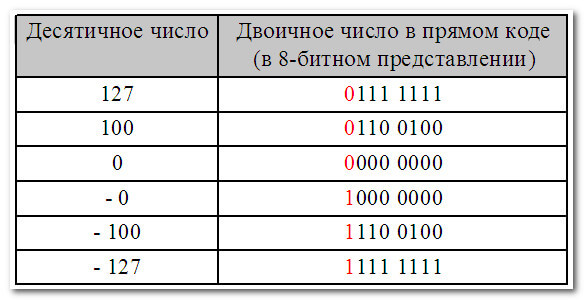
Прямой код используется главным образом для представления неотрицательных чисел.
Использование прямого кода для представления отрицательных чисел является неэффективным — очень сложно реализовать арифметические операции и, кроме того, в прямом коде два представления нуля — положительный ноль и отрицательный ноль (чего не бывает):
Обратный код
Обратный код — метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения.
Обратный двоичный код положительного числа состоит из одноразрядного кода знака (битового знака) — двоичной цифры 0, за которым следует значение числа.
Обратный двоичный код отрицательного числа состоит из одноразрядного кода знака (битового знака) — двоичной цифры 1, за которым следует инвертированное значение положительного числа.
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
При 8-битном двоичном числе — знаковый бит (как и в прямом коде) старший (8-й)
Диапазон десятичных чисел, который можно записать в обратном коде от -127 до + 127
Арифметические операции с отрицательными числами в обратном коде:
(Арифметические операции с двоичными числами)
1-й пример (для положительного результата)
Дано два числа:
100 = 0110 0100
-25 = — 0001 1001
Необходимо их сложить:
100 + (-25) = 100 — 25 = 75
1-й этап
Переводим число -25 в двоичное число в обратном коде:
25 = 0001 1001
-25= 1110 0110
и складываем два числа:
0110 0100 (100) + 1110 0110 (-25) = 1 0100 1010, отбрасываем старшую 1 (у нас получился лишний 9-й разряд — переполнение), = 0100 1010
2-й этап
Отброшенную в результате старшую единицу прибавляем к результату:
0100 1010 + 1 = 0100 1011 (знаковый бит =0, значит число положительное), что равно 75 в десятичной системе
2-й пример (для отрицательного результата)
Дано два числа:
5 = 0000 0101
-10 = — 0000 1010
Необходимо их сложить:
5 + (-10) = 5 — 10 = -5
1-й этап
Переводим число -10 в двоичное число в обратном коде:
10 = 0000 1010
-10= 1111 0101
и складываем два числа:
0000 0101 (5) + 1111 0101 (-10) = 1111 1010 (знаковый бит =1, значит число отрицательное)
2-й этап
Раз результат получился отрицательный, значит число представлено в обратном коде.
Переводим результат в прямой код (путем инвертирования значения, знаковый бит не трогаем):
1111 1010 —-> 1000 0101
Проверяем:
1000 0101 = — 0000 0101 = -5
Обратный код решает проблему сложения и вычитания чисел с различными знаками, но и имеет свои недостатки:
— арифметические операции проводятся в два этапа
— как и в прямом коде два представления нуля — положительный и отрицательный
Дополнительный код
Дополнительный код — наиболее распространенный способ представления отрицательных чисел. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел.
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Диапазон десятичных чисел которые можно записать в дополнительном коде от -128 до +127. Запись положительных двоичных чисел в дополнительном коде та-же, что и в прямом и обратном кодах.
Дополнительный код отрицательного числа можно получить двумя способами
1-й способ:
— инвертируем значение отрицательного числа, записанного в прямом коде (знаковый бит не трогаем)
— к полученной инверсии прибавляем 1
Пример:
Дано десятичное число -10
Переводим в прямой код:
10 = 0000 1010 —-> -10 = 1000 1010
Инвертируем значение (получаем обратный код):
1000 1010 —-> 1111 0101
К полученной инверсии прибавляем 1:
1111 0101 + 1 = 1111 0110 — десятичное число -10 в дополнительном коде
2-й способ:
Вычитание числа из нуля
Дано десятичное число 10, необходимо получить отрицательное число (-10) в дополнительном двоичном коде
Переводим 10 в двоичное число:
10 = 0000 1010
Вычитаем из нуля:
0 — 0000 1010 = 1111 0110 — десятичное число -10 в дополнительном коде
Арифметические операции с отрицательными числами в дополнительном коде
Дано: необходимо сложить два числа -10 и 5
-10 + 5 = -5
Решение:
5 = 0000 0101
-10 = 1111 0110 (в дополнительном коде)
Складываем:
1111 0110 + 0000 0101 = 1111 1011, что соответствует числу -5 в дополнительном коде
Как мы видим на этом примере — дополнительный код отрицательного двоичного числа наиболее подходит для выполнения арифметических операций сложения и вычитания отрицательных чисел.
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода
Предыдущие статьи:
1. Микроконтроллеры — первый шаг
2. Системы счисления: десятичная, двоичная и шестнадцатиричная
3. Логические операции, логические выражения, логические элементы
4. Битовые операции

Загрузка…
Машинные коды[править]
Все операции в ЭВМ выполняются над числами, представленными специальными машинными кодами. Их использование позволяет обрабатывать знаковые разряды чисел так же, как и значащие разряды, а также заменять операцию вычитания операцией сложения.
Различают следующие коды двоичных чисел:
- прямой код (П),
- обратный код (ОК),
- дополнительный код (ДК).
Прямой код[править]
Прямой код двоичного числа образуется из абсолютного значения этого числа и кода знака (0 или 1) перед его старшим числовым разрядом.
Пример.
А10 = +10; А2 = +1010; [А2]п = 0|1010
В10 = –15; В2 = –1111; [В2]п = 1|1111
Обратный код[править]
Обратный код двоичного числа образуется по следующему правилу. Обратный код положительных чисел совпадает с их прямым кодом. Обратный код отрицательного числа содержит единицу в знаковом разряде числа, а значащие разряды числа заменяются на инверсные, т.е. нули заменяются единицами, а единицы нулями.
Пример.
А10 = +10; А2 = +1010; [А2]ок = [А2]п = 0|1010
В10 = –15; В2 = –1111; [В2]ок = 1|0000
Свое название обратный код получил потому, что коды цифр отрицательного числа заменены на инверсные. Наиболее важные свойства обратного кода чисел:
- сложение положительного числа С с его отрицательным значением в обратном коде дает т.н. машинную единицу МЕок=1|11…11, состоящую из единиц в знаковом и в значащих разрядах числа;
- нуль в обратном коде имеет двоякое значение. Он может быть как положительным числом – 0|00…00, так и отрицательным 1|11…11. Значение отрицательного числа совпадает с МЕок. Двойственное представление 0 явилось причиной того, что в современных ЭВМ все числа представляются не обратным, а дополнительным кодом.
Дополнительный код[править]
Дополнительный код положительных чисел совпадает с их прямым кодом. Дополнительный код отрицательного числа представляет собой результат суммирования обратного кода числа с единицей младшего разряда (20 – для целых чисел, 2-л – для дробных)
Пример.
А10 = +10; А2 = +1010; [А2]дк = [А2]ок = [А2]п = 0|1010
В10 = –15; В2 = –1111; [В2]дк = [В2]ок + 20 = 1|0000+1 = 1|0001
Основные свойства дополнительного кода:
• сложение дополнительных кодов положительного числа С с его отрицательным значением дает т.н. машинную единицу дополнительного кода:
МЕдк=МЕок + 20 = 10|00…00,
т.е. число 10 (два) в знаковых разрядах числа;
• дополнительный код называется так потому, что представление отрицательных чисел является дополнением прямого кода чисел до машинной единицы
МЕдк.
Модифицированные обратные и дополнительные коды[править]
Модифицированные обратные и дополнительные коды двоичных чисел отличаются соответственно от обратных и дополнительных кодов удвоением значений знаковых разрядов. Знак «+» в этих кодах кодируется двумя нулевыми знаковыми разрядами, а знак «–» – двумя единичными разрядами.
Пример.
А10 = +10; А2 = +1010; [А2]дк = [А2]ок = [А2]п = 0|1010
[А2]мок = [А2]мдк = 00|1010
В10 = –15; В2 = –1111; [В2]дк= [В2]ок+20 = 1|0000+1 = 1|0001
[В2]мок= [В2]мдк= 11|0001
Целью введения модифицированных кодов являются фиксация и обнаружение случаев получения неправильного результата, когда значение результата превышает максимально возможный результат в отведенной разрядной сетке машины. В этом случае перенос из значащего разряда может исказить значение младшего знакового разряда. Значение знаковых разрядов «01» свидетельствует о положительном переполнении разрядной сетки, а «10» — об отрицательном переполнении. В настоящее время практически во всех компьютерах роль сдвоенных разрядов для фиксации переполнения разрядной сетки играют переносы, идущие в знаковый и из знакового разряда.
Арифметические действия в машинных кодах.[править]
Сложение (вычитание). Операция вычитания приводится к операции сложения путем преобразования чисел в обратный или дополнительный код согласно таблице.
| Требуемая операция | Необходимое преобразование |
|---|---|
| А+В | А+В |
| А-В | А+(-В) |
| -А+В | (-А)+В |
| -А-В | (-А)+(-В) |
Здесь А и В неотрицательные числа.
Скобки в представленных выражениях указывают на замену операции вычитания операцией сложения с обратным или дополнительным кодом соответствующего числа. Сложение двоичных чисел осуществляется последовательно, поразрядно в соответствии с таблицей. При выполнении сложения цифр необходимо соблюдать следующие правила:
- Слагаемые должны иметь одинаковое число разрядов. Для выравнивания разрядной сетки слагаемых можно дописывать незначащие нули слева к целой части числа и незначащие нули справа к дробной части числа.
- Знаковые разряды участвуют в сложении так же, как и значащие.
- Необходимые преобразования кодов производятся с изменением знаков чисел. Приписанные незначащие нули изменяют свое значение при преобразованиях по общему правилу.
- При преобразовании единицы переноса из старшего знакового разряда, в случае использования ОК, эта единица складывается с младшим числовым разрядом. При использовании ДК единица переноса теряется. Знак результата формируется автоматически, результат представляется в том коде, в котором представлены исходные слагаемые.
Пример 1. Сложить два числа: А10 = 7, В10 = 16.
А2 = +111 = +0111; В2 = +10000.
Исходные числа имеют различную разрядность, необходимо провести выравнивание разрядной сетки:
[A2]п = [A2]ок = [A2]дк = 0|00111; [В2]п = [В2]ок = [В2]дк = 0|10000.
Сложение в обратном или дополнительном коде дает один и тот же результат:
0|00111
+0|10000
———-
С2 = 0|10111
С10 = +23
Пример 2. Сложить два числа: А10 = +16, В10 = -7 в ОК и ДК.
По таблице необходимо преобразование А+(-В), в которой второй член преобразуется с учетом знака
[A2]п = [A2]ок = [A2]дк = 0|10000;
[В2]п = 1|111 = 1|00111; [В2]ок = 1|11000; [В2]дк = 1|11001
При сложении чисел в ОК и ДК были получены переносы в знаковый разряд и из знакового разряда. В случае ОК перенос из знакового разряда требует дополнительного прибавления единицы младшего разряда (п.4 правил). В случае ДК этот перенос игнорируется.
Практическая часть.[править]
Задание:
- Взять две пары десятичных двузначных целых числа: А, В, С, D. (Варианты по списку)
- Вычислить (А-В)ок, (В-А)дк, (С-D)ок, (D-C)дк.
Варианты
- Вариант — 78, 56, 11, 35;
- Вариант — 67, 36, 45, 22;
- Вариант — 21, 87, 38, 44;
- Вариант — 99, 26, -73, 26,
- Вариант — 28, 33, 42, 54;
- Вариант — 61, 43, 65, 41;
- Вариант — 11, 84, 49, 53;
- Вариант — 85,- 47, 43, 66;
- Вариант — 48, 52, 65, 88;
- Вариант — 26, 58, 63, 77;
- Вариант — 91, 22, 46, -14;
- Вариант — 57, 14, 69, 55;
- Вариант — 77, 98, 25, -88;
- Вариант — 46, 66, 35, 36;
- Вариант — 44, 37, 92, 28;
- Вариант — 63, 46, 83, 71;
- Вариант — 35, -51, 63, 24;
- Вариант — 25, 95, -38, 33;
- Вариант — 32, 29, 86, 27;
- Вариант — 49, 55, -73, 22
- Вариант — 33, -77, 53, 71;
- Вариант — 48, 86, 62, 42;
- Вариант — 69, -48, 11, 20;
- Вариант — 10; 82, 80, 45;
- Вариант — 70, 93, -27, 30;
- Вариант — 88, -40, 16, 83;
- Вариант — 64, 80, -17, 77;
- Вариант — 40, 46, -73, 19;
- Вариант — 14, -60, 11, 27;
- Вариант — 90, 73, -10, 20.
to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more
Для определения
знака числа в двоичном коде используются
0 и 1. Нулем кодируется знак «+»,
Единицей кодируется знак «-«.
Для представления
положительных и отрицательных чисел в
вычислительной технике используются
ПРЯМОЙ, ОБРАТНЫЙ и ДОПОЛНИТЕЛЬНЫЙ коды.
Положительные
числа в
прямом, обратном и дополнительном кодах
изображаются одинаково — двоичными
кодами с цифрой 0 в знаковом разряде.
Например:
Отрицательные
числа в
прямом, обратном и дополнительном кодах
имеют разное изображение.
1.
Прямой код.
В знаковый разряд помещается цифра 1, а
в разряды цифровой части числа — двоичный
код его абсолютной величины. Например:
2.
Обратный
код. Получается
инвертированием всех цифр двоичного
кода абсолютной величины числа, включая
разряд знака: нули заменяются единицами,
а единицы — нулями. Например:
3.
Дополнительный
код. Получается
образованием обратного кода с последующим
прибавлением единицы к его младшему
разряду. Например:
Обычно
отрицательные
десятичные числа при вводе в машину
автоматически преобразуются в обратный
или дополнительный двоичный код
и в таком виде хранятся, перемещаются
и участвуют в операциях. При выводе
таких чисел из машины происходит обратное
преобразование в отрицательные десятичные
числа.
Пример:
Представить число +7, -12, -15, -16 в прямом,
обратном и дополнительном кодах.
-
Число
Прямой
кодОбратный
кодДополнительный
код-12
1
00011001
11100111
1110100-15
1
00011111
11100001
1110001-16
1
00100001
11011111
1110000
При
переводе из
обратного
в прямой
код происходит инверсия
цифр числа.
При
переводе из
дополнительного в прямой код
происходит 1)
инверсия цифр числа,
2)добавляется
+1 в младший
разряд инвертированного числа.
Арифметические
действия над числами со знаком
В
большинстве компьютеров операция
вычитания не используется. Вместо нее
производится сложение обратных или
дополнительных кодов уменьшаемого и
вычитаемого.
Это позволяет существенно упростить
конструкцию АЛУ.
Сложение
обратных кодов.
Здесь при сложении чисел А и В имеют
место четыре основных и два особых
случая:
Алгебраическое сложение
|
|A|<|B| |
|A|>|B| |
|
|
Обратный код |
|
|
|
Дополнительный |
|
|
Если
результат получен со знаком минус (с
«1»), то результат необходимо
преобразовать в прямой код!!!
1.
А и В положительные.
При суммировании складываются все
разряды, включая разряд знака. Так как
знаковые разряды положительных слагаемых
равны нулю, разряд знака суммы тоже
равен нулю. Например:
Получен правильный
результат.
2.
А положительное, B отрицательное и по
абсолютной величине больше, чем А.
|A|
< |B|
Например:
Если результат
получен со знаком минус с «1», то
результат необходимо преобразовать в
прямой код!!!
Получен
правильный результат в обратном коде.
При переводе в прямой код биты цифровой
части результата инвертируются: 1 0000111
= -710.
3.
А положительное, B отрицательное и по
абсолютной величине меньше, чем А.
|A|
> |B|
Например:
Компьютер
исправляет полученный первоначально
неправильный результат (6 вместо 7)
переносом
единицы из
знакового разряда в младший разряд
суммы.
4.
А и В отрицательные.
Например:
Полученный
первоначально неправильный результат
(обратный код числа -1110
вместо обратного кода числа -1010)
компьютер исправляет переносом единицы
из знакового разряда в младший разряд
суммы. При переводе результата в прямой
код биты цифровой части числа инвертируются:
1 0001010 = -1010.
При
сложении может возникнуть ситуация,
когда старшие разряды результата
операции не помещаются в отведенной
для него области памяти. Такая ситуация
называется переполнением
разрядной сетки формата числа.
Для обнаружения переполнения и оповещения
о возникшей ошибке в компьютере
используются специальные средства.
Ниже приведены два возможных случая
переполнения.
5.
А и В положительные, сумма А+В больше,
либо равна 2n-1,
где n — количество разрядов формата
чисел (для однобайтового формата n=8,
2n-1
= 27 = 128). Вариант
переполнения.
Например:
Семи
разрядов цифровой части числового
формата недостаточно
для размещения восьмиразрядной суммы
(16210
= 101000102),
поэтому старший
разряд суммы оказывается в знаковом
разряде. Это
вызывает несовпадение
знака суммы и знаков слагаемых,
что является
свидетельством переполнения разрядной
сетки.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
19 апреля автор курса «Алгоритмы для разработчиков» в Яндекс.Практикуме и разработчик в компании Joom Александра Воронцова провела открытый вебинар «Оптимизация на простых типах данных». У Аси за спиной 11 лет разработки, опыт олимпиадного программирования, а также работа в Яндексе с высоконагруженными проектами.
Мы подготовили расшифровку вебинара в двух частях. Первая часть — про строки и работу с ними, вторая — про числа.
Статья будет полезна разработчикам на Python и C/C++, которые хотят научиться трюкам для ускорения кода, а также программистам на других языках, которым интересны фишки, связанные с типами данных.

Числа
Что же происходит с числами? Числа как тип данных тоже кодируются битами ноликов и единичек. Вот пример.
Итак, мы умеем хранить положительные числа. А если нам надо каким-то образом зафиксировать ещё и знак числа? Числа же могут быть как положительными, так и отрицательными.
Из-за того, что нам удобно выделять память не отдельными битами, а байтовыми блоками, оказывается, что мы не можем добавить к нашему числу дополнительный 9-й бит и использовать его для хранения знака числа.
Так что нам надо отрезать 1 бит от 8-битного числа (на нашем маленьком примере).
Посмотрим на левую часть. У нас есть положительные числа. В этом случае на самой левой позиции всегда будет записан нолик, а дальше — то число, которое мы хотим увидеть.
А теперь смотрите на нижнюю часть слайда — там есть отрицательные числа. Что делать? Просто записать единичку и следом записать такое же число, как и в случае с положительным — рабочий вариант. Это называется прямой код: мы сравниваем в первой строке, как выглядит чёрная часть массивчика, сравниваем во второй строке и видим, что они равны. Удобно.
Но оказывается, что если мы хотим сложить 75 и –75, то в прямом коде это делать неудобно, потому что у нас не получится 0. Попробуйте сами.
Дополнительный и обратный коды
Поэтому эволюционно в computer science было решено, что удобнее использовать обратный код. Это когда мы берём и все символы (если на первом месте единичка) переворачиваем. В целом вариант удобный, и тут уже при сложении 75 и –75 получается –0. Вроде бы уже сильно ближе, но что это вообще за –0 такой?
Вместо этого есть возможность использовать дополнительный код. Обратный код от дополнительного отличается тем, что вместо простой инверсии мы в конце добавляем ещё единичку. То есть у нас в самой правой ячейке был нолик, а теперь там единичка.
При этом если бы у нас уже была единичка в самой правой ячейке, то в дополнительном коде у нас стал бы нолик, а единичка перенеслась бы в следующий разряд.
В таком случае сложение двух чисел в дополнительном коде будет давать нам просто +0. Что мы имеем благодаря такому хранению целых чисел — мы можем сохранить в 8 битах (в 1 байте) числа от 27-1 до 27. В отрицательных числах просто на одно значение больше.
Зачем всё это знать
Давайте посмотрим пример, на который я сама натыкалась в Java несколько раз, скопипастила его с одного сайта.
public class OverflowUnderflow {
public static void main(String args[]){
//roll over effect to lower limit in overflow
int overflowExample = 2147483647;
System.out.println("Overflow: "+ (overflowExample + 1));
//roll over effect to upper limit in underflow
int underflowExample = -2147483648;
System.out.println("Underflow: "+ (underflowExample - 1));
}
}
26
Overflow: -2147483648
Underflow: 2147483647
В чём суть. Java, несмотря на то, какой это большой и полезный язык с количеством разных функций, имеет такую особенность: если взять максимальное целое число, которое влезает в 4 байта, в положительном у нас получится overflowExample, а в отрицательном underflowExample. В коде видно, что underflowExample на единичку по модулю больше, то есть у нас в отрицательном поле есть на 1 резервное число больше.
ОК, добавим к максимальному числу единичку, из минимального числа вычтем единичку и выведем это на экран. И оказывается, что у нас уменьшенное минимальное число больше, чем увеличенное максимальное.
И вот такое перескакивание через границу может вам встретиться в реальном коде. Я сама такое встречала, когда мне важно было посчитать количество фотографий у пользователя. Это был фотограф, который фотографировал всё, до чего дотягивался, и было довольно неприятно, когда ты пытаешься посчитать количество фотографий, а у тебя на выходе внезапно отрицательное число. На это всегда надо обращать внимание. Зная, как оно устроено внутри, вы будете понимать предпосылки и корни возможных проблем.
Длинная арифметика
Далеко не всегда числа у нас такие, как в примерах. Давайте попробуем посчитать зарплату какого-то бизнесмена. Чтобы не так грустно было считать, представим, что это за год.
В зависимости от языков программирования у нас есть разные варианты. Тот же Python умеет считать длинную арифметику из коробки. В Java, насколько я помню, она тоже есть в дополнительной библиотеке. А вот во времена моего детства нас такие штуки заставляли писать руками, чтобы понимать, что происходит в библиотеках, когда мы переключаемся на вычисления длинных чисел.
Итак, варианты.
Давайте хранить наши десятичные числа в массиве, под каждую цифру — своя ячейка. Поэтому, когда захотим складывать, мы будем делать это по цифре. Временами у нас будут ситуации, когда нам будет необходим перенос через разряд. Для этого заведём ещё одну дополнительную переменную и будем её периодически прибавлять, вовремя обнулять — ничего сложного, но надо это реализовать аккуратно.
Какие у такого сложения могут быть подводные камни? Будет оно работать быстро или медленно? Когда именно оно будет работать медленно?
У нас линейная сложность, много девяток, мы можем выделить под результат массив неправильного размера, и он у нас не влезет. Чем больше у нас цифр, тем дольше работает наша программа. Причём чем больше цифр в самом длинном из чисел.
ОК, с суммированием всё неплохо, с вычитанием тоже.
А что, если в длинной арифметике нам нужно сделать перемножение? В школе всё было просто: в столбик, сдвигаем цифры, всё здорово. А в случае с длинной арифметикой с ходу непонятно, что делать.
Есть простой вариант: мы можем в цикле прибавлять меньшее из чисел, например 321, и в цикле 321 раз складываем 876 435.
В принципе, работать будет. Сложность тут равна длине первого числа, перемноженной на значение второго числа. Может, и многовато, особенно потому, что значение существенно больше, чем длина числа.
Но есть вариант удобнее, если понимать, что происходит внутри.
Давайте посмотрим на простые (не такие длинные) числа и запишем их двоичной системе счисления.
Вот у нас семёрка. Она будет выглядеть как три единички подряд в двоичной системе.
А вот 14, тоже несложно — 21+22+23. Или расписать иначе, как 2*(20+21+22), а это мы уже видели у семёрки.
Тут полезно заметить, что оба этих числа выглядят друг на друга подозрительно похожими с точностью до нолика справа. Это как раз связано с тем, что одно является другим, умноженным на 2. Поэтому степень двойки в сумме повышается. И выходит, что мы, зная битовую форму числа, быстро можем умножать на 2.
Для небольшой проверки рассчитайте в двоичной форме число 28.
Как это поможет в исходной задаче?
Мы же хотели умножать одно длинное число на другое длинное, помните? Давайте представим число 321 в двоичном виде, а точнее, тут нам удобнее его представить в форме сумм степеней двойки.
Соответственно, каждую из этих трёх строчек мы можем получить в двоичной форме довольно быстро, просто просчитав одно исходное число 876 435. У нас есть специальный побитовый оператор, который позволяет подобное.
Вот так это число выглядит в двоичной форме.
У первого числа справа 8 ноликов, у второго справа 6 ноликов, у последнего справа нулей нет.
Вопрос: если мы говорим, что длинная арифметика — это долго, что у нас десятичные числа долго складываются, что это линейное время, почему число, записанное в двоичной форме (которая всегда длиннее десятичной), работает быстро?
Тут бы хорошо рассказать, как оно вообще бывает, но сократим: процессор устроен так, что в нём есть специальный кусочек под названием сумматор. Этот двоичный сумматор как раз и предназначен для очень быстрого суммирования двоичных чисел. Восхитительная штука. Перекодировка тоже происходит почти моментально.
Результат такого вычисления позволяет нам сначала узнать, чему будет равно 26. Какие тут варианты — исходное число не помещается, но мы можем сложить нужное количество раз число с самим собой. Сложив один раз, мы получим 2 в первой степени, сложив два раза — 2 во второй и так далее.
Итого мы сначала рассчитаем 26 и прибавим к нему 28. На вычисление 26 у нас потребуется шесть операций сложения, каждая за линейное время, на 28 мы просто сделаем ещё два сложения числа с самим собой. И получится результат.
Для процессора все числа двоичные, но когда мы используем длинную арифметику, как мы сделали в примере на массивах, у нас в одной ячейке хранится не одна цифра и не один бит информации, а в лучшем случае однобайтное число. А как вы помните, один даже беззнаковый байт — это 27.
И вместо того, чтобы просто складывать два числа, на самом деле под капотом происходит сложение одних 8 битов с другими 8 битами. Вот и получается ещё дольше, чем в нашем примере.
Что ещё важно. Понимание алгоритмов — это здорово, но существует следующий уровень — понимание не только алгоритмов, но и устройства процессоров, потому что там внезапно много интересного. Оттуда же можно почерпнуть, что хоть двоичная система кажется базисом, но математически она не самая оптимальная, и во всём этом реально интересно разбираться.
Вот что ещё можно делать для того, чтобы избегать самостоятельной реализации длинной арифметики и не мучиться со сложными умножениями (заметьте, мы ещё не обсуждали с вами деление и возведение в степень).
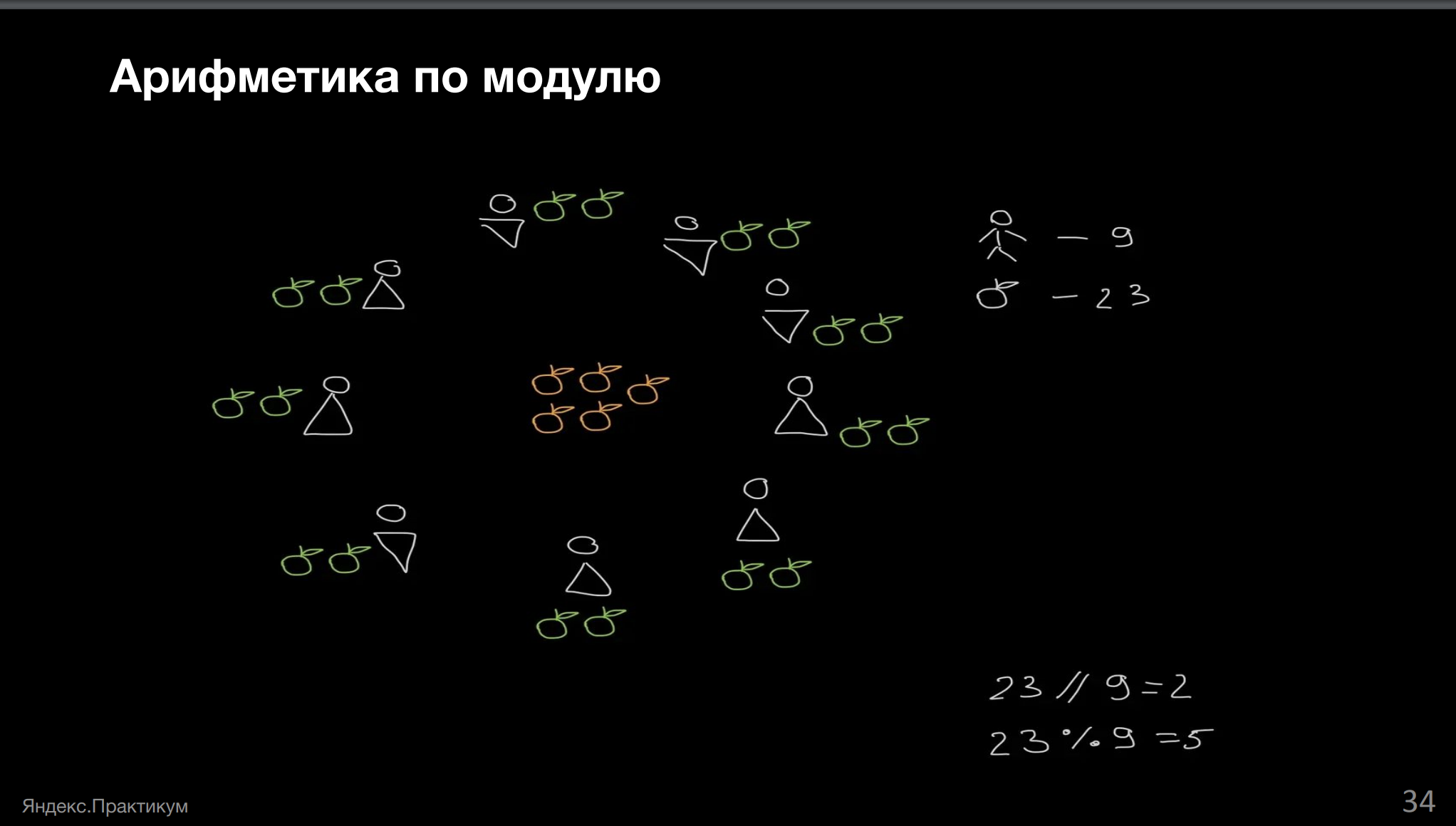
Зачастую для решения задачи нам достаточно не получить точный ответ, а узнать какой-то признак. Например, у нас есть задачка.
Собрали урожай яблок на 23 килограмма, собирали урожай вдевятером. Делить надо всё поровну. Оставшиеся яблоки отвезут бабушке.
Сколько яблок надо отвезти бабушке?
Пока у нас 23 кг, всё не так уже плохо: бабушка получает остаток от деления 23 на 9, то есть 5 кг.
А если количество кг яблок не влезает в целочисленную переменную?
То есть у нас есть десятки тысяч рабочих на комбайнах. Чтобы просуммировать такое значение и поделить его на количество рабочих, нам не обязательно собирать все яблоки в единую кучу. Мы можем просто результат каждого рабочего взять по модулю и суммировать дальше их, всякий раз оставляя только этот самый признак.
Условно вот что мы вычисляем в этот момент времени: если бы работы выполнял только один рабочий и мы бы все его яблоки распределили по остальным рабочим поровну и взяли бы остаток, мы бы получили вклад этого рабочего в остаток яблок для бабушки.
Но затем оказывается, что работал ещё и второй рабочий, вот он докидывает в кучу свои яблоки, из докинутых яблок мы понимаем, что можно опять поровну всем раздать, поэтому обновляется процент.
То есть не надо вычислять какую-то гигантскую сумму, а можно просто всякий раз брать остаток от деления по модулю. Во многих языках программирования это обозначается как процент, но не имеет отношения к привычным процентам, имейте в виду.
Удобно. Работает. Но не идеально и оставляет простор для ошибок.
Где всё это применять
Во многих местах, например, в кибербезопасности — тайна вашей переписки.
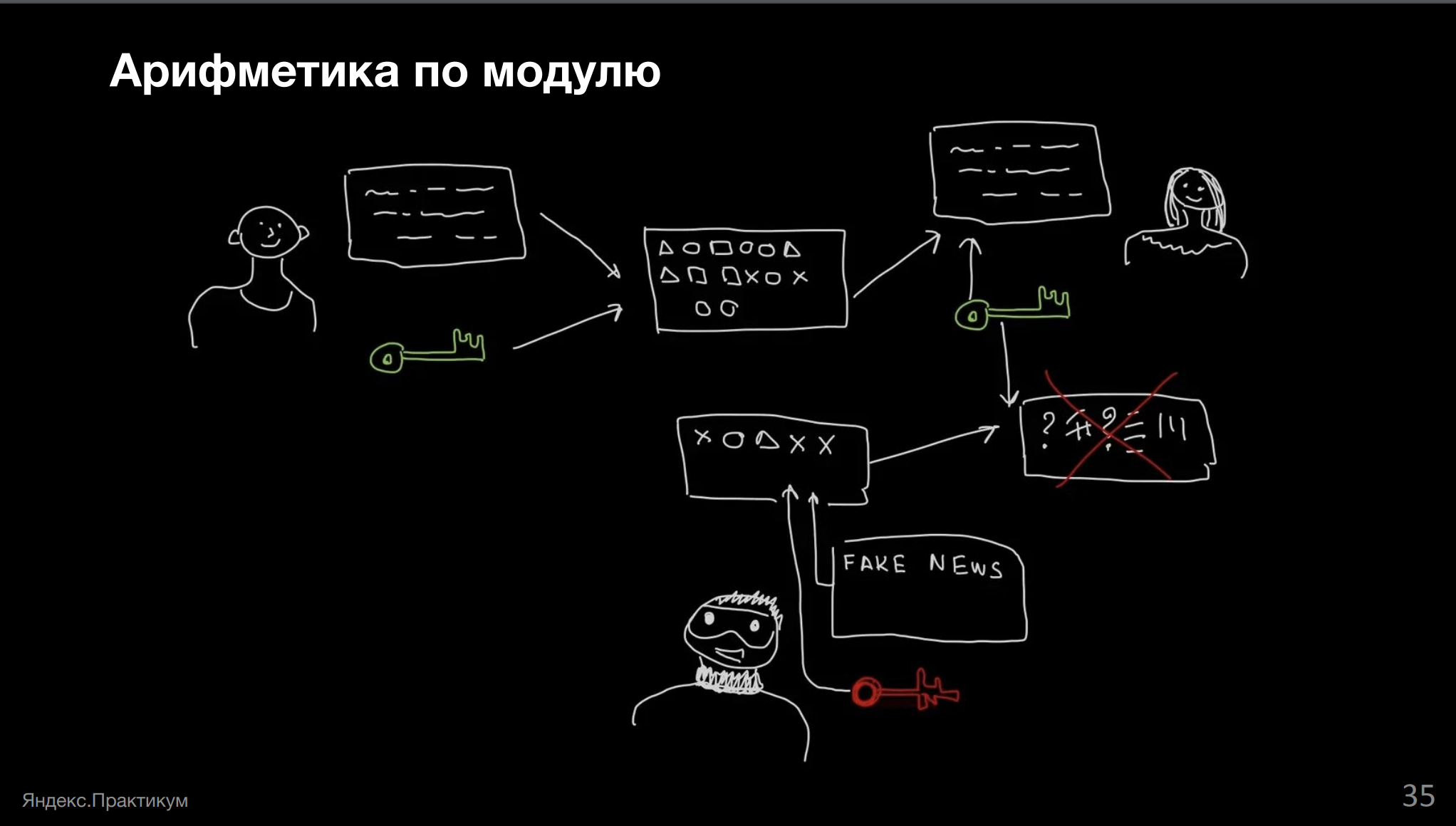
У нас есть какое-то сообщение, к которому мы добавляем ключ и считаем специальную чек-сумму (отсылка к хэшам, о которых мы говорили), и отправляем письмо.
Адресат получает письмо, получает чек-сумму и сверяет, что получил всё нужное, затем раскодирует всё своим ключом и читает сообщение. Вдруг в системе появляется злоумышленник, который берёт своё вредоносное письмо, подсовывает вместо нужного, свой ключ и свою чек-сумму.
Адресат получает всё это и расшифровывает на своей стороне. Понимает, что расшифровалась какая-то фигня, чек-сумма не совпадает, всё плохо.
Нам важно брать хэш по модулю для того, чтобы не перейти за границу наших целочисленных вычислений. Помните пример с Java? Может оказаться, что наша чек-сумма разъедется потому, что вместо положительного числа у нас получится отрицательное.
Таких применений арифметики по модулю много, они встречаются регулярно, просто часто скрыты от глаз.
Как видите, на самом деле в алгоритмах куда больше интересного, чем может показаться со стороны. Сильно больше, чем можно вместить в один пост (да и в два). Если у вас есть какие-то вопросы или уточнения по тексту или видео вебинара — пишите в комментарии, буду рада ответить.