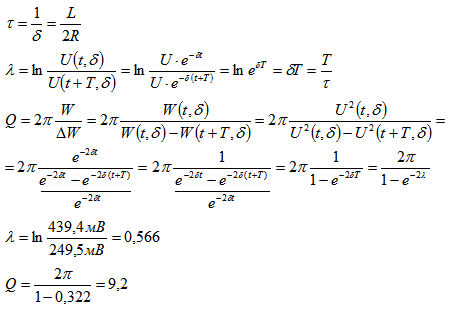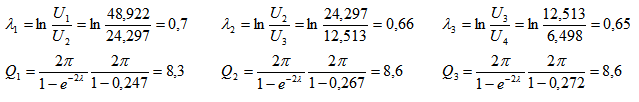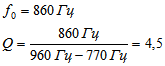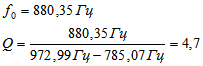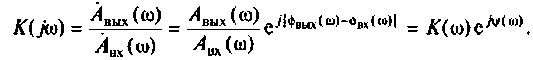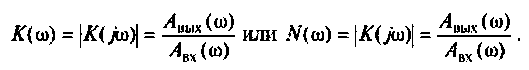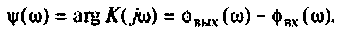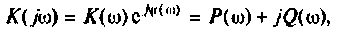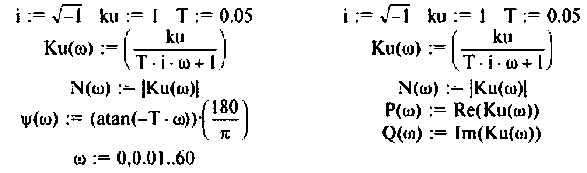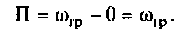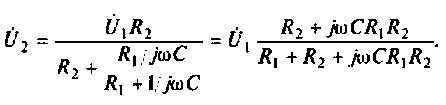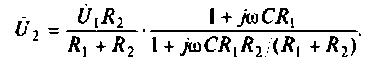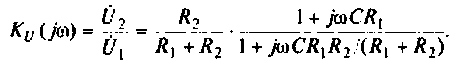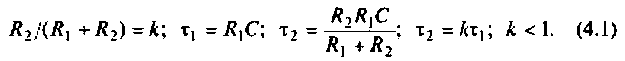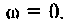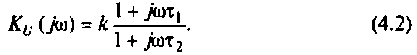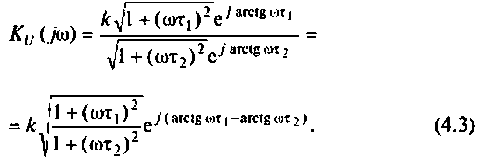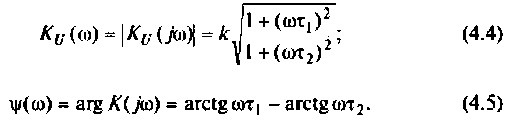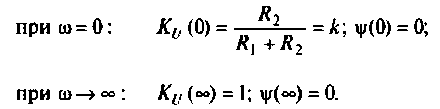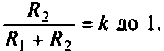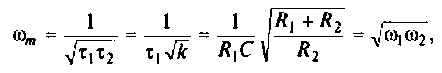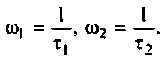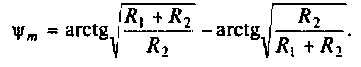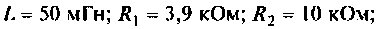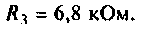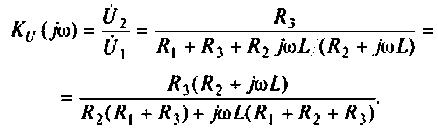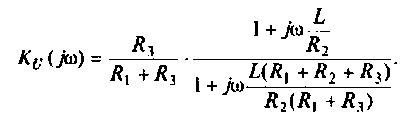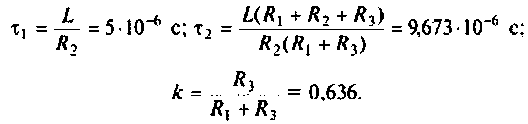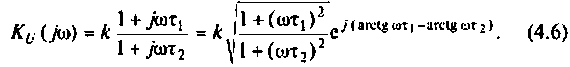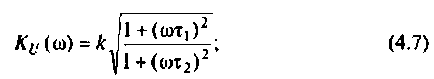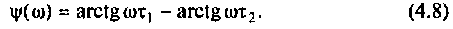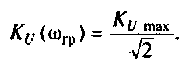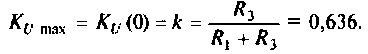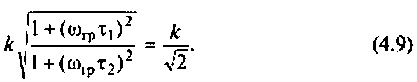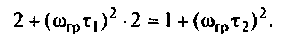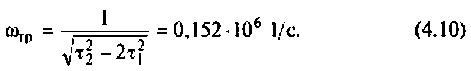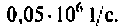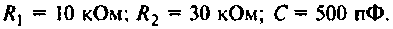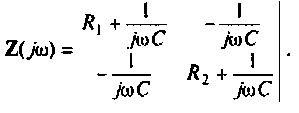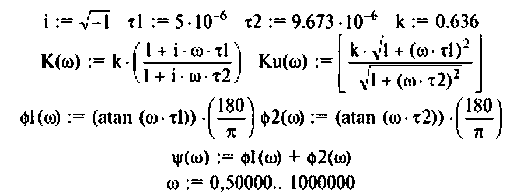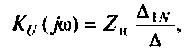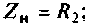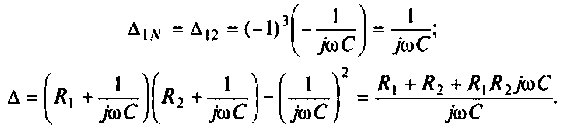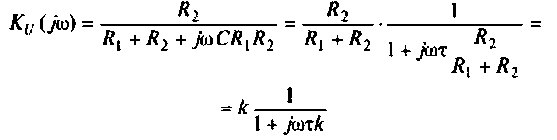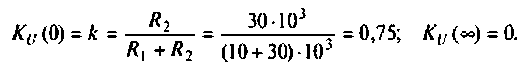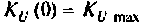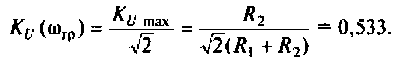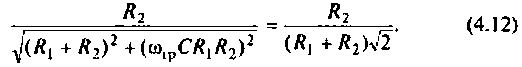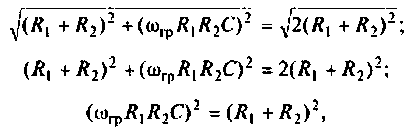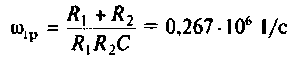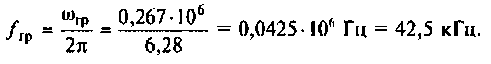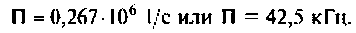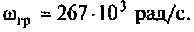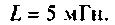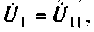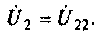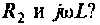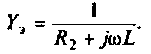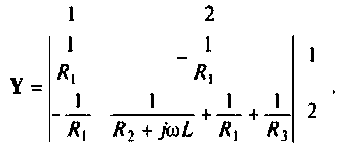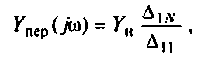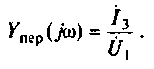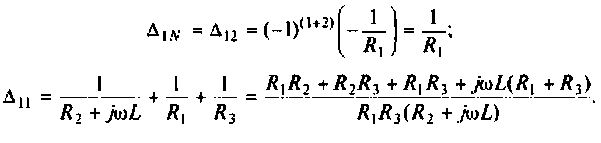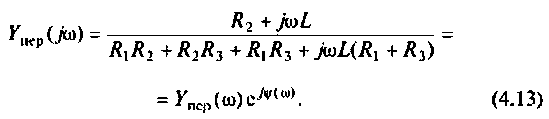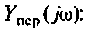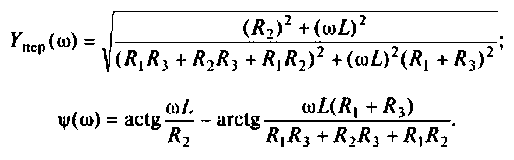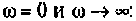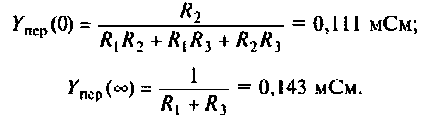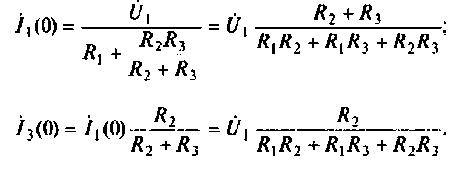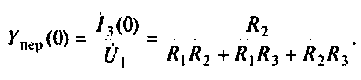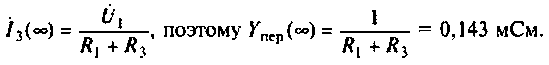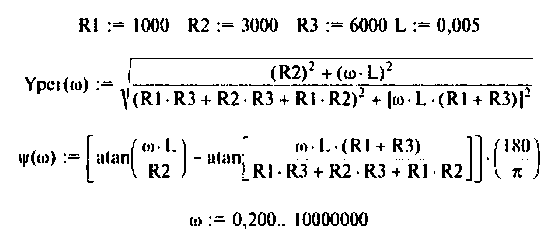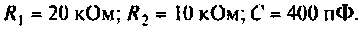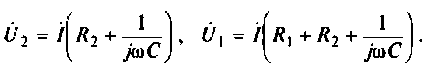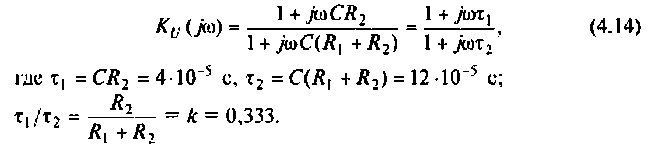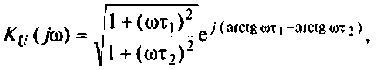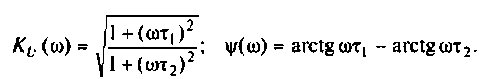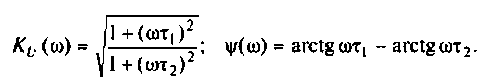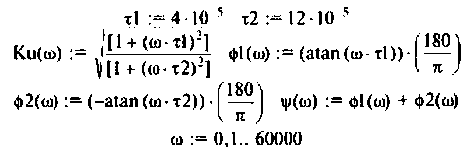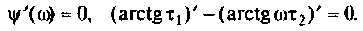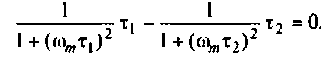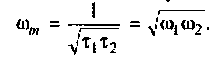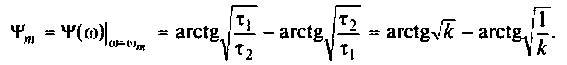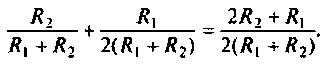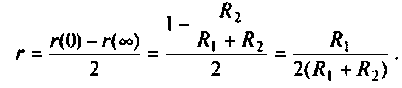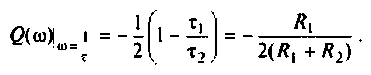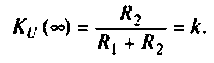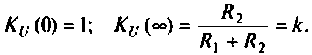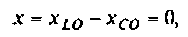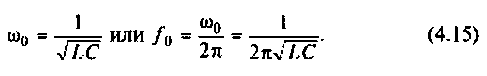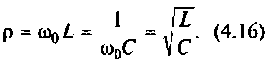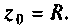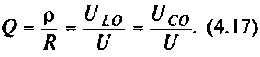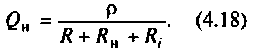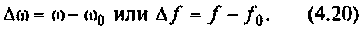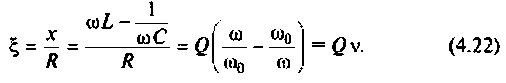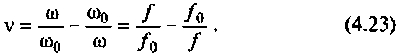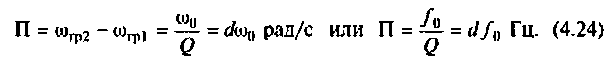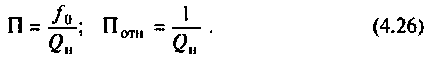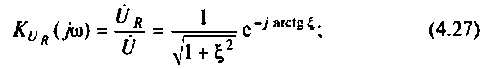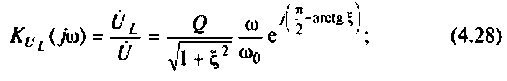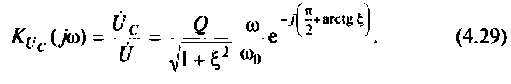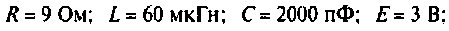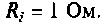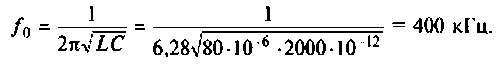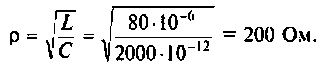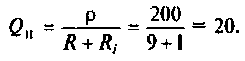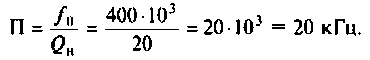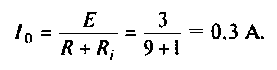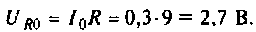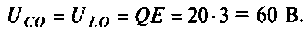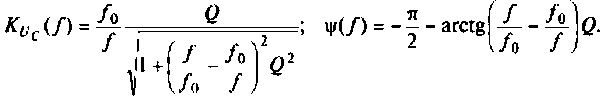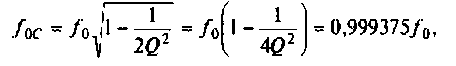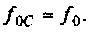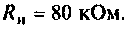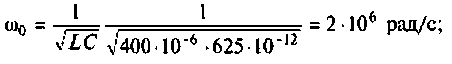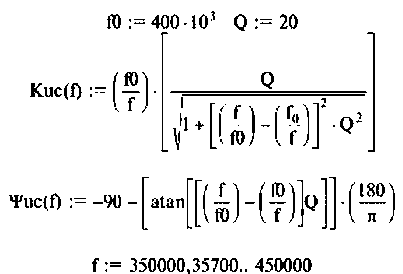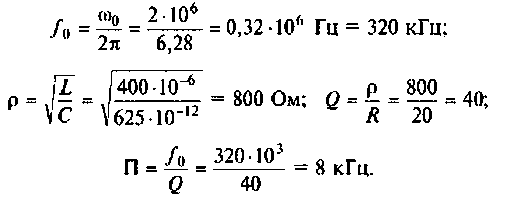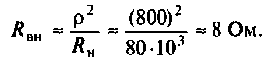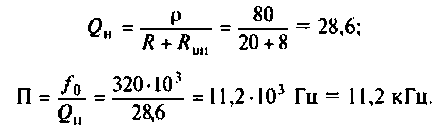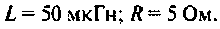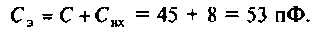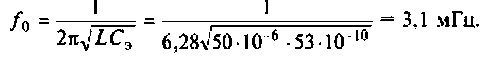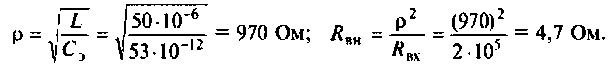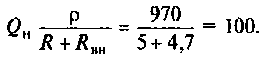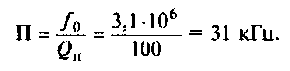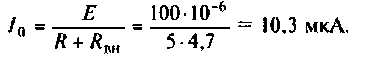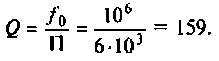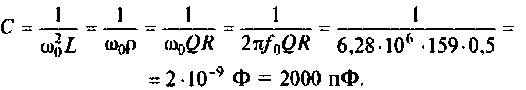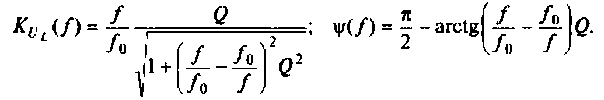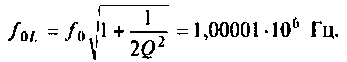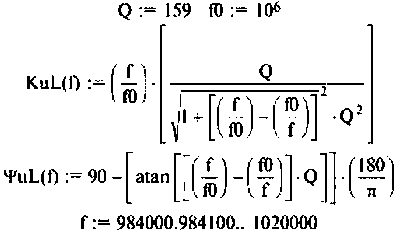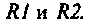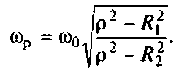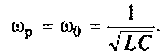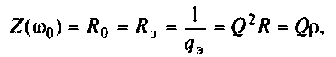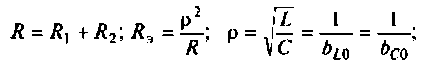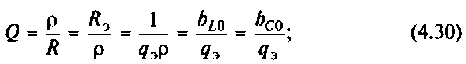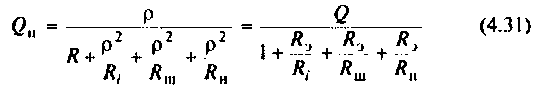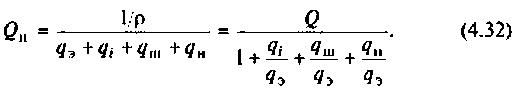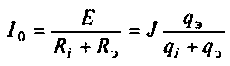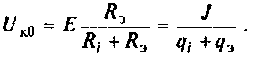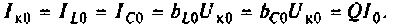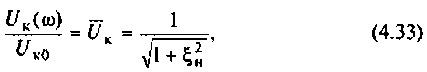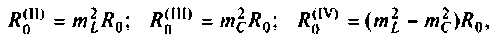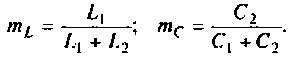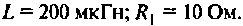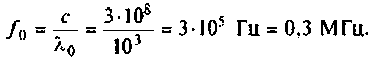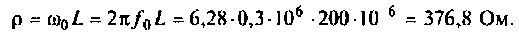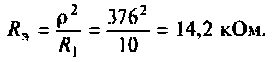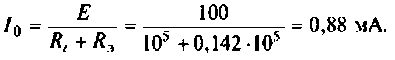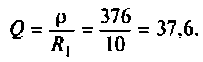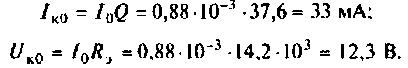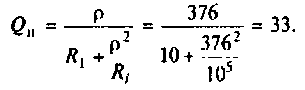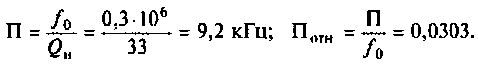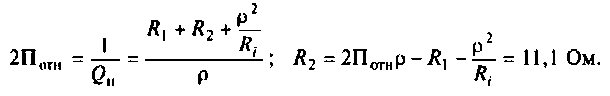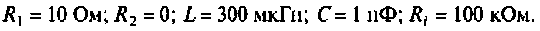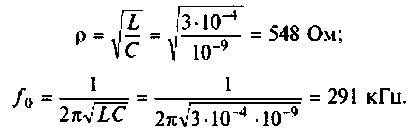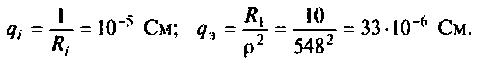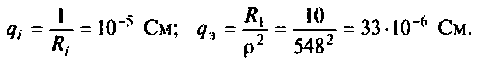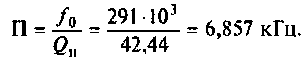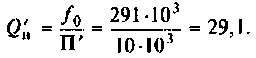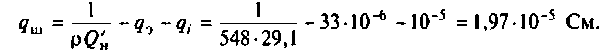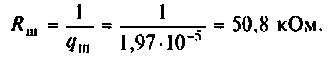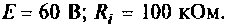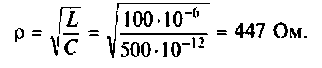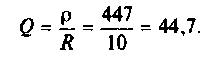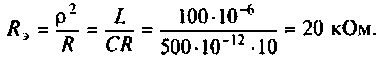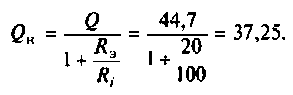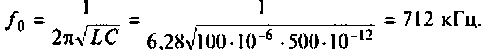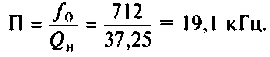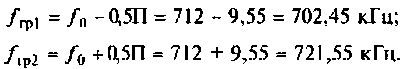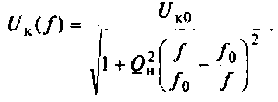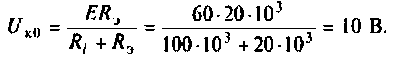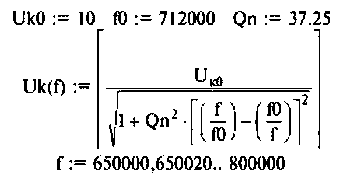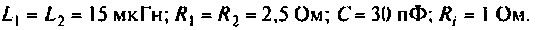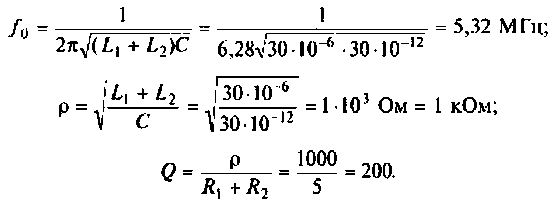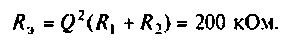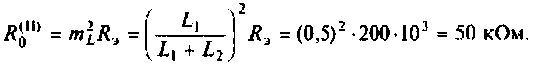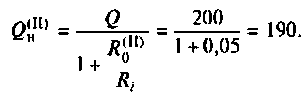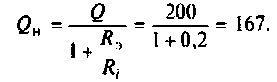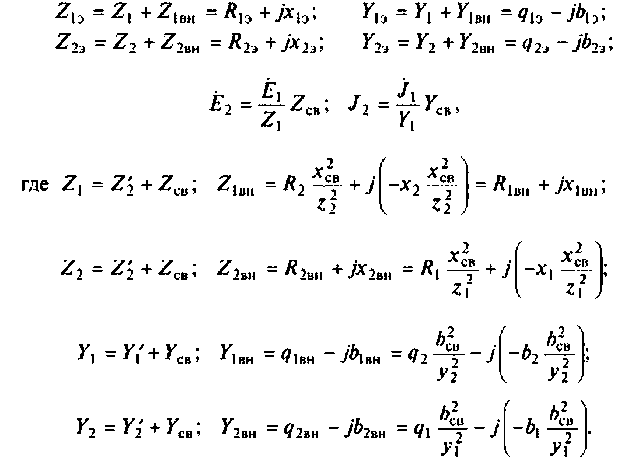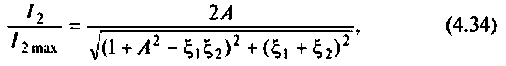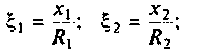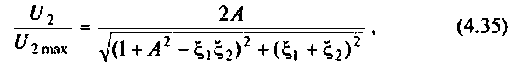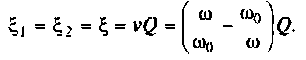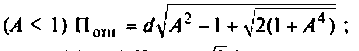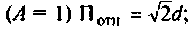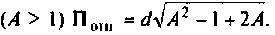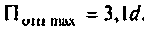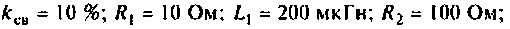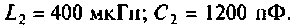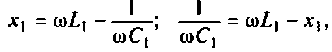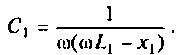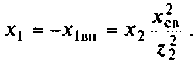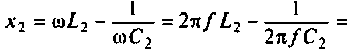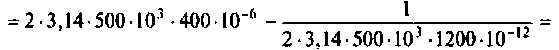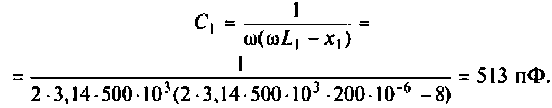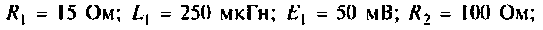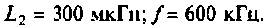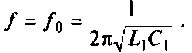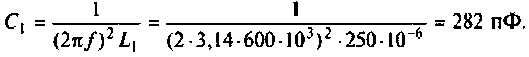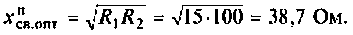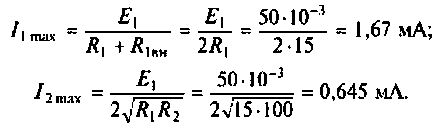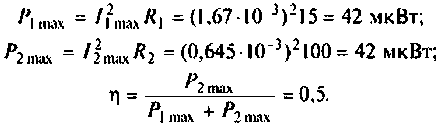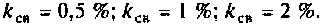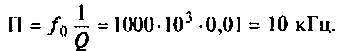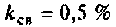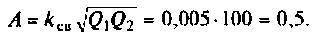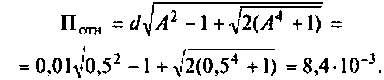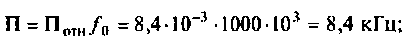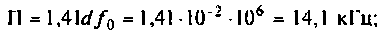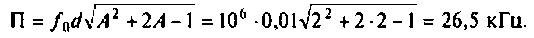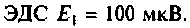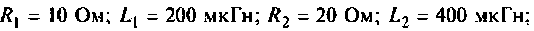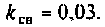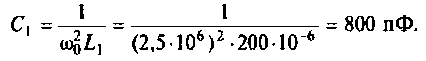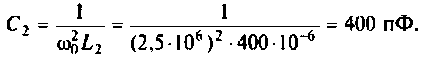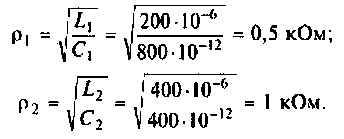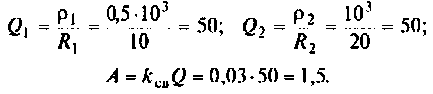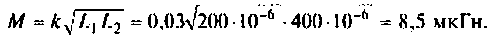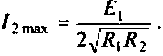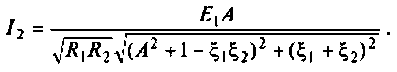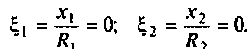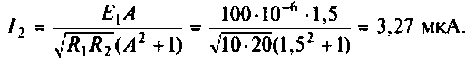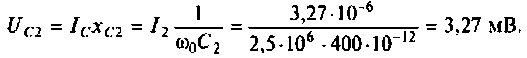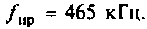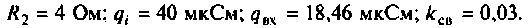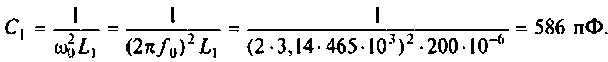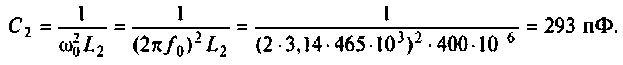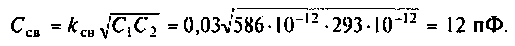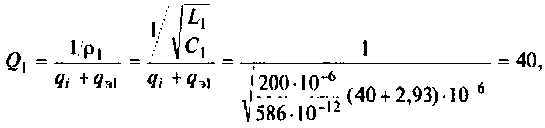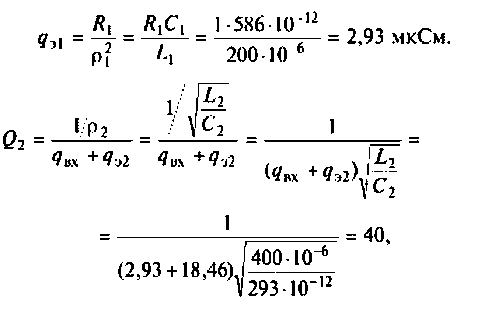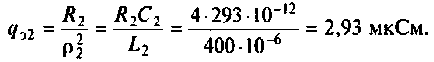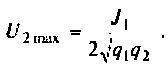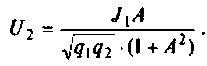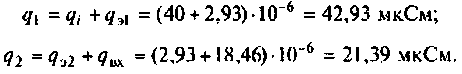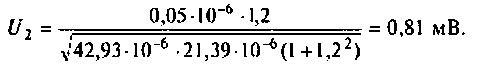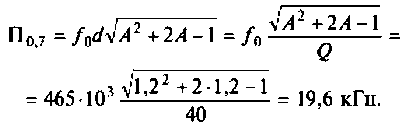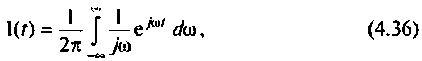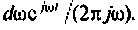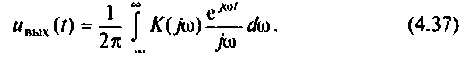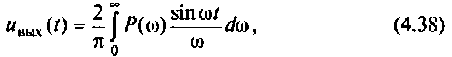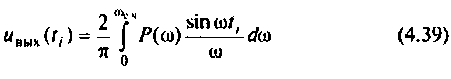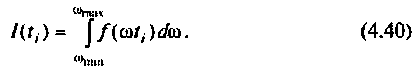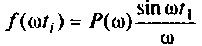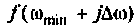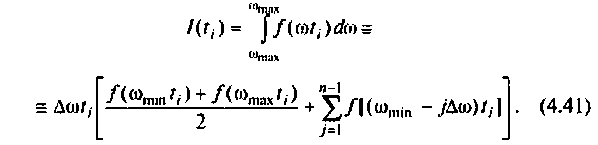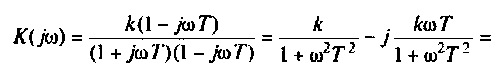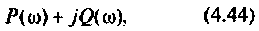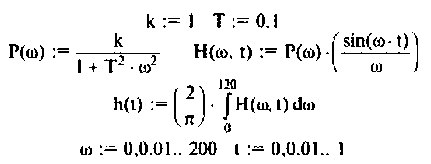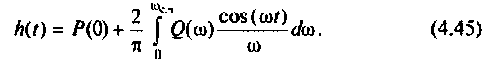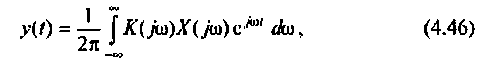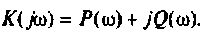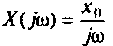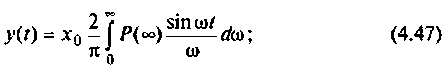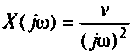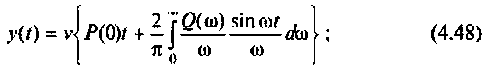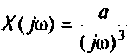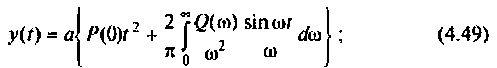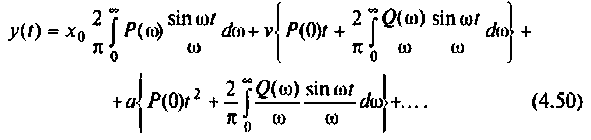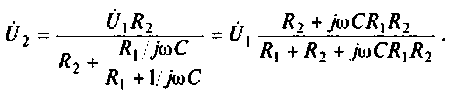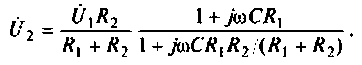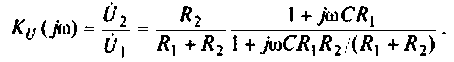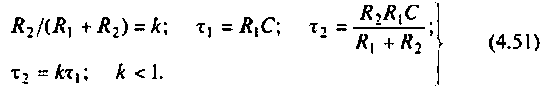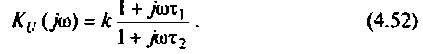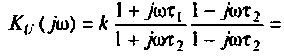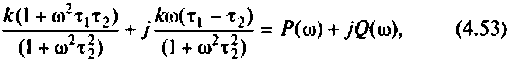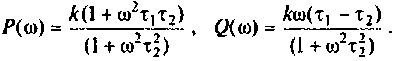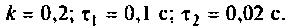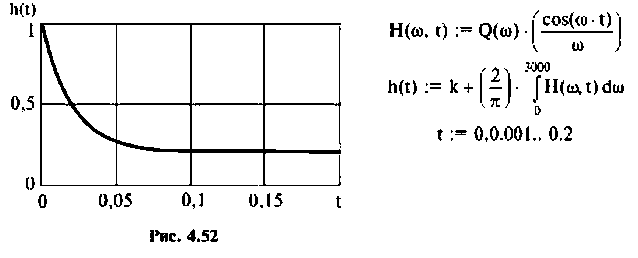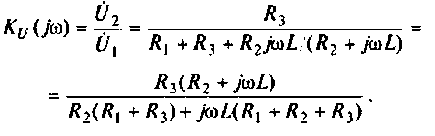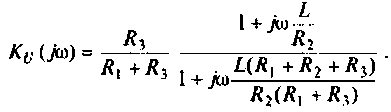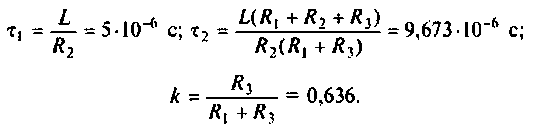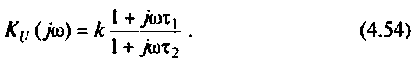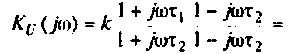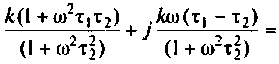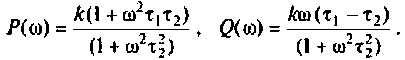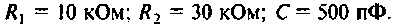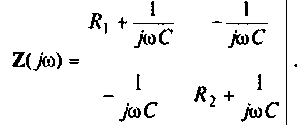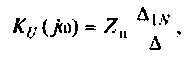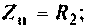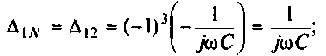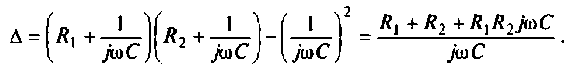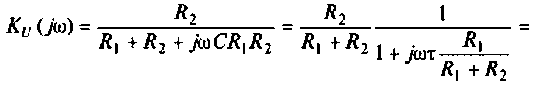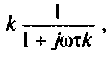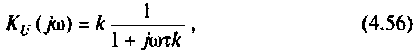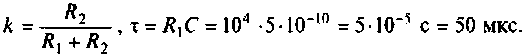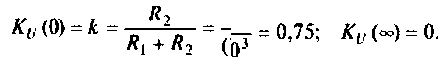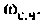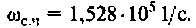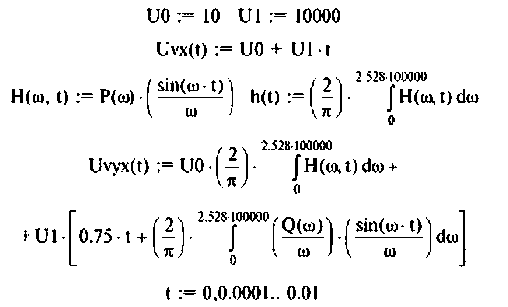Что такое добротность контура
Электрическая цепь — предназначена не только для передачи тока и напряжения от источника к потребителю. В данной электроцепи возникают определенные физические процессы, которые связаны с влиянием ее элементов на протекание данного тока.
В этой статье будет описано, что такое добротность контура. Кроме того будет приведена формула для расчета этой величины, схемы последовательного и параллельного контуров.
Определение
Физика дает следующее определение добротности. Добротностью называют параметр колебательной системы, который определяет ширину резонанса и характеризует, насколько запасы энергии в системе больше возникающих ее потерь во время изменения фазы на один радиан. Дело в том, что данный показатель определяет разницу вынужденных колебаний при резонансе с определенной амплитудой колебаний на каком-то удалении от места резонанса. При этом амплитуда вынужденных колебаний не имеет никакой зависимости от их частоты. Параметр находит применение не только при расчетах электрических цепей. Его применяют так же в механике, акустике и химии.
Добротность колебательной системы в англоязычных ресурсах называют Quality factor и обозначают буквой «Q». Данная величина является основной характеристикой всех колебательных систем, но сделать измерения данной величины невозможно, ведь ее можно только вычислить, используя различные формулы. Степень идеальности имеет прямое влияние на коэффициент потерь энергии за время одного колебательного периода. Чем меньше величина, тем выше потери самой энергии. Данное значение обратно пропорционально скорости затухания собственных колебаний системы.
Получается, что колебательный контур является разницей между входящим реактивным сопротивлением и выходящим активным. Если в колебательном контуре имеется емкость C, индуктивность L и нагрузка R, то для расчета Q используется формула:
В данной формуле за резонансную частоту электроцепи ω0 отвечает показатель 1/R.
Параметр добротности измеряется при настройке генератора электросигналов на частоту резонансных колебаний. Сама частота резонанса равна максимальному выходному напряжению такой цепи.
Параллельный контур
Добротность любого параллельного колебательного контура предполагает наличие цепи, в которой имеется емкость, нагрузка и индуктивность, соединенные параллельно. Они образуют так называемую RLC-схему.
Определяющая величина для такой схемы — это проводимость конденсатора с катушкой. Именно она суммируется при расчетах и является реактивной проводимостью параллельного колебательного контура. На резонансной частоте проводимость катушки с конденсатором будут равны, а общая разница при этом равняется 0. Для расчета такой цепи используется формула:
При этом стоит учитывать следующее:
- Не принимается во внимание емкостная паразитная характеристика катушки индуктивности, но учитывается добротность индуктивного элемента. Она соответствует выражению:
- Также учитывается добротность конденсатора, использующегося в такой электроцепи. Потери в конденсаторе связаны с наличием диэлектрика в его конструкции. Добротность конденсатора вместе с имеющимися потерями, напрямую связаны с потерями энергии на его диэлектрике tgδ. Данный коэффициент определяем с помощью такого выражения:
- На резонансной частоте к переменному току прилагается бесконечное сопротивление.
- В реальной RLC-цепи отсутствует бесконечное сопротивление, но этот параметр при увеличении сопротивления контура значительно снижается.
В параллельном колебательном контуре резонансная частота является той частотой, при которой реактивное сопротивление равняется 0, а величина входящего сопротивления является активным. Отсюда можно сделать вывод, что отсутствует фазовый сдвиг между током и напряжением.
Последовательный контур
Для последовательного колебательного контура характерно наличие последовательного соединения емкости с индуктивностью. При этом эти два элемента не влияют на потери энергии в цепи и являются идеальными элементами.
Потери в данной схеме вызваны только наличием активной нагрузки. Ниже представлен график амплитудно-частотной характеристики такой схемы.
Для такой цепи сопротивление катушки и конденсатора являются паразитными, приводят к появлению резонанса. Данный резонанс выравнивает или обнуляет сопротивления, оставляя только влияние активной нагрузки R от резистора. При этом добротность такой электроцепи определяется, как разницу напряжений на источнике тока и выходах катушки/конденсатора. В этом случае Q определяют с помощью следующего выражения:
В данной формуле:
- С — емкость конденсатора.
- L — индуктивность катушки.
- R — потери сопротивления.
Для примера попробуем решить следующую задачу. В цепи имеется катушка индуктивности L=100 мГн с сопротивлением R=100 Ом, которая соединена последовательно с конденсатором емкостью C=0.07 мкФ. Найдите резонансную частоту ω0, характеристическое сопротивление и добротность колебательного контура.
Вычисляем резонансную частоту контура:
Определяем характеристическое сопротивление:
Конечный шаг — вычисление добротности контура:
Заключение
В статье было дано краткое описание, что такое добротность контура и чему параметр равен для различных вариантов контура (параллельного, последовательного). Данная характеристика цепи и ее составных элементов играет ключевое значение при определении потерь от включения в нее различных конденсаторов, катушек и активных резисторов. С помощью добротности можно определить разницу между входным и выходным напряжениями электроцепи.
Видео по теме
Методы определения добротности
Пользуясь
определением добротности, можно показать,
что
,
(9)
RП
= r + R + RL,
где RП
– полное сопротивление цепи; r
– внутреннее сопротивление источника
тока; R
– сопротивление, включенное в контур;
RL
– активное сопротивление катушки
индуктивности.
1. Расчет
теоретического значения добротности.
Добротность контура Qтеор
можно рассчитать по формуле (9), зная
параметры электрической цепи RП,
L
и C.
2. Определение
добротности по измерениям резонансного
напряжения U0
рез
и амплитуды вынуждающей ЭДС 0.
Соотношение (8) при малых коэффициентах
затухания принимает вид
,
откуда
.
(10)
3. Определение
добротности по ширине резонансной
кривой.
Шириной резонансной кривой называется
разность частот, при которых достигается
эффективное значение резонансного
напряжения на конденсаторе, равное (см.
рис. 3)
.
Разность этих
частот
= 2
– 1
является
полосой пропускания контура.
Энергия, запасенная
в контуре при резонансе, на границах
полосы пропускания уменьшается в два
раза.
Пользуясь
соотношениями (9) и (10) и преобразуя
уравнение (5), получаем, что с достаточной
степенью точности
.
(11)
Таким
образом, зная
и рез,
можно вычислить добротность контура.
Расчет добротности
этим методом производится с помощью
полученной экспериментально резонансной
кривой в координатах U0
, .
По ней определяются для
значения
1
и 2
слева и справа от рез.
Вместо рез
и циклических частот 1
и 2
используются соответствующие частоты
генератора
.
(12)
Метод измерения и описание аппаратуры
Для выполнения
работы используется простейший
колебательный контур из последовательно
соединенных катушки индуктивности L,
конденсатора C
и сопротивления R.
Резонансные кривые снимают при различных
сопротивлениях, включенных в контур.
Наблюдение за изменением амплитуды
колебаний на конденсаторе производится
с помощью электронного осциллографа.
Для этого сигнал с конденсатора подается
на вход осциллографа, и при изменении
частоты генератора измеряется амплитуда
напряжения. При этом диапазон частот
выбирается достаточно широким в обе
стороны по отношению к резонансной
частоте. Резонансная частота соответствует
наибольшей амплитуде измеряемого
напряжения при заданном сопротивлении
контура. Определение добротности контура
производится двумя из вышеописанных
способов: по ширине резонансной кривой
и по отношению резонансного напряжения
к амплитуде вынуждающей ЭДС. Полученные
результаты позволяют вычислить омическое
сопротивление контура и оценить значение
внутреннего сопротивления генератора.
Порядок выполнения работы
-
Включите генератор
синусоидальных колебаний и электронный
осциллограф и соберите схему для
измерений в соответствии с указаниями
на стенде. -
Рассчитайте
собственную частоту контура по формуле
.
Параметры L,
C,
RL,
r
контура
даны на стенде. Значения L,
C
и f0
запишите в
табл. 1.
-
Определите по
осциллографу амплитуды вынужденных
колебаний напряжения U0,
снимаемого с конденсатора в делениях
масштабной сетки на экране осциллографа,
при фиксированных значениях частоты
F
генератора в выбранном диапазоне частот
при R1.
Полученные данные занесите в табл. 1. -
Повторите опыт
(пункт 3) при другом сопротивлении R2,
включенном в контур. -
Не изменяя
настройки генератора определите
амплитуду колебаний ЭДС генератора,
соответствующую резонансной частоте,
полученной экспериментально в п. 3,4.
Для этого установите на генераторе
резонансную частоту, выход генератора
подключите непосредственно к входу
электронного осциллографа с помощью
переключателя на стенде, и зафиксируйте
амплитуду сигнала 0.
Результат занесите в табл. 1 и табл. 2. -
По данным табл.
1 постройте резонансные кривые при
различных сопротивлениях контура R1
и R2. -
На каждой
резонансной кривой отметьте уровень,
соответствующий 0,7U0
рез.
Таблица 1
|
№ |
Частота |
U0, |
|
|
п/п |
F, |
R1 |
R2 |
|
1 2 … 11 |
С
= … Ф; f0
= … КГц;
L
= … Гн; 0
= … В.
Соседние файлы в папке 2000
- #
09.06.201525.6 Кб260.DOC
- #
09.06.2015182.78 Кб2701.DOC
- #
09.06.2015304.64 Кб2602.DOC
- #
09.06.2015189.95 Кб2603.DOC
- #
09.06.2015293.89 Кб4604.DOC
Что такое добротность колебательного контура?
как измерить добротность в радиолюбительских условиях.
«Добротность обозначается символом Q (от английского quality factor) и является тем параметром колебательной системы,
который определяет ширину резонанса и характеризует, во сколько раз запасы энергии в системе больше, чем потери энергии за
время изменения фазы на 1 радиан.
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность
колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания
»
— авторитетно учит нас Википедия.
Да уж. Напустили тумана ироды — без поллитры не разберёшься. А ведь придётся, раз впряглись.
Для начала возьмём ёжика. Хорошее животное! Хотя выдающимся умом не обладает, но думаю, что и оно в курсе, что
«quality factor» — это показатель качества колебательного контура и в первую очередь, конструктивного качества катушки индуктивности.
Теперь возьмём женщину в теле — добротную женщину. Таких женщин рисовали художники 18-го, 19-го веков, а поэты писали: «Её
выпуклости меня восхищают, её впуклости сводят с ума».
Так вот. К чему это я?
А к тому, что для получения в сухом остатке высокодобротного колебательного контура, придётся поискать в загашнике и высококачественный
конденсатор с низким током утечки, и катушку индуктивности — крепкую, добротную и красивую, словно выпавшую из картины
венецианского мастера в Пушкинском музее.
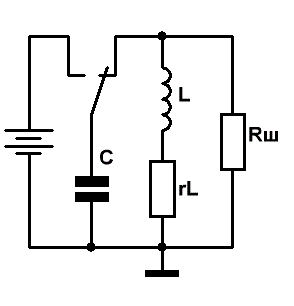
Приведём эквивалентную схему колебательного контура.
Здесь L и C — собственные индуктивность и ёмкость компонентов, входящих в состав колебательного
контура,
rL — сопротивление катушки, эквивалентное потерям электрической энергии в проводе катушки индуктивности,
Rш — сумма сопротивлений, обусловленных потерями в изоляции провода, каркасе, экране, сердечнике катушки индуктивности,
а также потерями, вызванные наличием токов утечки в конденсаторе.
Рис.1
При подключении к контуру внешних цепей, параллельно Rш добавляется дополнительное сопротивление Rн, вносимое этими внешними цепями.
По большому счёту, на Рис.1 не хватает ещё одной ёмкости, равной сумме паразитных ёмкостей катушки индуктивности, внешних цепей и
паразитной ёмкости монтажа. На высоких частотах эти привнесённые ёмкости могут иметь существенные величины, соизмеримые с ёмкостью самого
контурного конденсатора. На добротность эти ёмкости существенного влияния не оказывают, но при расчёте резонансной частоты их необходимо
учитывать и суммировать со значением основной ёмкости С.
Теперь давайте разберёмся, что такое «скорость затухания собственных колебаний в системе» и, каким боком она связана с добротностью.
Для начала мысленно спаяем схему, нарисованную на Рис.1, и замкнём переключатель на батарейку (в левое по схеме положение).
Конденсатор С зарядится до уровня, равного напряжению питания.
Теперь перещёлкнем переключатель в правое по схеме положение.
Благодаря энергии, запасённой в конденсаторе, в образовавшейся LC-цепи возникнут свободные колебания на частоте резонанса
колебательного контура, равной fо= 1/2π√LС.
Поскольку у нас ни с какой стороны не вечный двигатель — свободные колебания затухают, причём скорость затухания зависит от потерь
в конденсаторе и катушке индуктивности: чем они меньше, тем медленнее затухание.
Число колебаний от момента возбуждения свободных колебаний до момента, когда их амплитуда уменьшится в еπ = 23,14 раза,
как раз и будет числено равняться добротности контура Q.
Число периодов свободных колебаний в контуре можно подсчитать счётчиком импульсов и таким образом узнать добротность
колебательного контура, генератор сигналов в этом случае не нужен.
Собственно говоря, на таком принципе и строится большинство промышленных измерителей добротности.
Вспоминаем дальше: «Добротность является тем параметром колебательной системы, который определяет ширину резонанса».
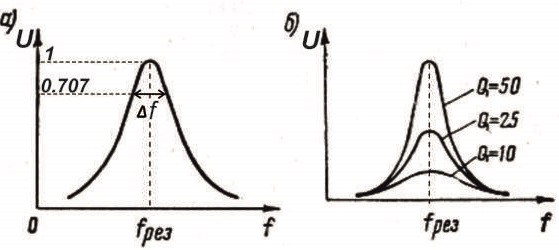
Рисуем резонансную кривую (амплитудно частотную характеристику) колебательного контура.
По частотной характеристике условно определяется полоса пропускания контура Δf.
При этом сделано допущение, что напряжение внутри этой полосы имеет право снижаться до уровня 0,707 от максимального.
Исходя из этого, формула для определения добротности приобретает следующий вид:
Q = f рез/Δf
.
Рис.2
Из формулы естественным образом вытекает, что чем выше добротность — тем уже полоса пропускания резонансного контура,
соответственно, чем ниже — тем шире.
А как измерить добротность контура, не прибегая к изготовлению специальных устройств, в домашней лаборатории?
1. Если речь идёт о низких (звуковых) частотах, то тут всё просто.
В этом случае, Q равна отношению реактивного сопротивления индуктивного или ёмкостного характера (характеристического сопротивления)
к полному последовательному сопротивлению потерь в резонансном контуре. В виду того, что конденсаторы на данных частотах практически не
вносят потерь, то добротность контура равна добротности катушки индуктивности, величина которой напрямую зависит от активного сопротивления
катушки.
А поскольку данное сопротивление можно легко измерить обычным омметром, то имеет полный смысл проделать эту не сильно замысловатую
манипуляцию, после чего перейти на страницу ссылка на страницу и в первой таблице произвести расчёт
добротности. Естественным образом, подразумевается, что катушка намотана на соответствующем для данных частот сердечнике, не вносящих
существенных потерь в работу колебательного контура.
2. На высоких частотах (радиочастотах) значение активного сопротивления катушки может составлять доли ома, к
тому же возможно проявление влияния добротности конденсатора на общую добротность цепи, поэтому такими же примитивными
методами, как в случае НЧ обойтись не удастся.
Рискну сделать осторожное предположение, что в радиолюбительской лаборатории у нас затерялся высокочастотный генератор с 50-омным
выходом и такой же высокочастотный осциллограф, или, на худой конец, измеритель ВЧ напряжений.
В этом случае мы воспользуемся ещё одним определением Q. Добротность резонансного контура равна фактору увеличения напряжения и
может быть выражена отношением напряжения, развиваемого на реактивных элементах к входному напряжению, поданному последовательно с
контуром.
Спаяем пару резисторов.
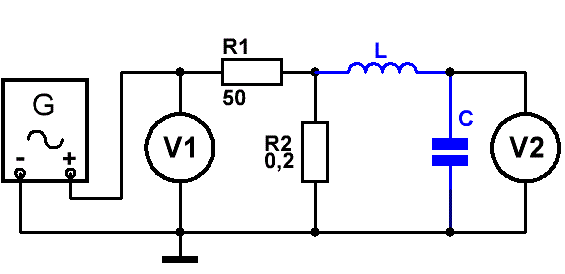
Добротность измеряется при настройке генератора сигналов на частоту резонанса контура, соответствующую максимальному выходному
напряжению.
Добротность Q рассчитывается как отношение выходного напряжения на резонансном контуре к напряжению, поданному на него.
В нашем случае
Q = 250
x V2/V1 .
Рис.3
Так как в случае высокодобротных элементов, сопротивление контура на резонансной частоте может превышать значение в сотню
килоом, для корректного измерения добротности, входные импедансы измерителя ВЧ напряжений, либо осциллографа должны превышать
это значение как минимум на порядок.
Все наши рассуждения и формулы корректны для ненагруженных параллельных колебательных контуров, то есть для случаев, когда на выходе
отсутствует реальная нагрузка.
В реальной схеме контур связан с источником колебаний и нагрузкой, которые вносят в него дополнительные потери, снижающие добротность.
Эквивалентная добротность Q параллельного колебательного контура с учётом этих потерь вычисляется по следующей формуле:
Q = Q0
x Rш/(Rш+Rо) , где
Q0 — добротность ненагруженного контура,
Rш — шунтирующее сопротивление, равное R(источника) ll R(нагрузки),
Rо — эквивалентное сопротивление ненагруженного контура, равное сопротивлению контура на резонансной частоте,
значение которого можно посчитать на той же странице ссылка на страницу во 2-ой таблице.
А на следующей странице порассуждаем на тему: что надо сделать, чтобы намотать катушку с максимально-возможной добротностью.
Методы измерения добротности электрического колебательного контура
Эффект резонанса находит своё применение в решении различных технических задач. Одной из таких задач была симуляция резонанса вибростенда электрическим колебательным контуром. Подбор элементов для колебательного контура осуществляется с целью добиться резонанса на заданной частоте с заданной добротностью. Резонансная частота и добротность определяются по нижеприведённым формулам. Для подтверждения расчетной частоты резонанса или добротности требуются практические методы с использованием измерительных приборов. Преимущество виртуальной лаборатории ZETLab в том, что она содержит в себе широкий спектр программ для различных измерений, которые можно использовать для проверки теоретических расчетов.
Принципиальная схема последовательного колебательного контура
Параметры схемы, приведённой на рисунке 1, вычисляются по следующим формулам:
Резонансная частота электрического колебательного контура
Добротность электрического колебательного контура
Примечание: в формулы для расчета подставляются не паспортные данные элементов (по которым их возможно выбирали), а реальные, которые были измерены с помощью соответствующих измерительных приборов.
Теоретический расчет
R=16 Ом,
L=18 мГн,
C=1,75 мкФ
Резонансная частота
Добротность
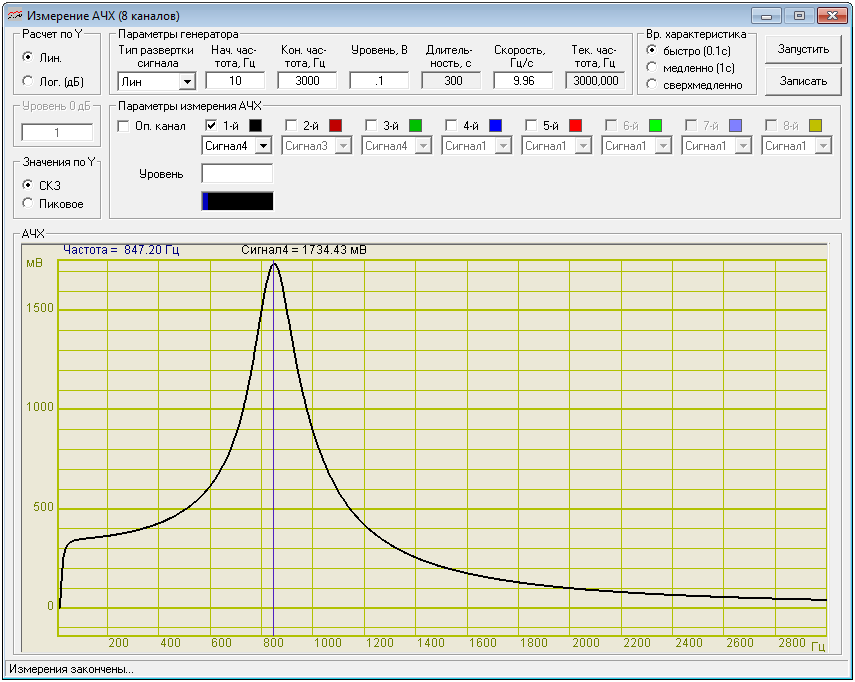
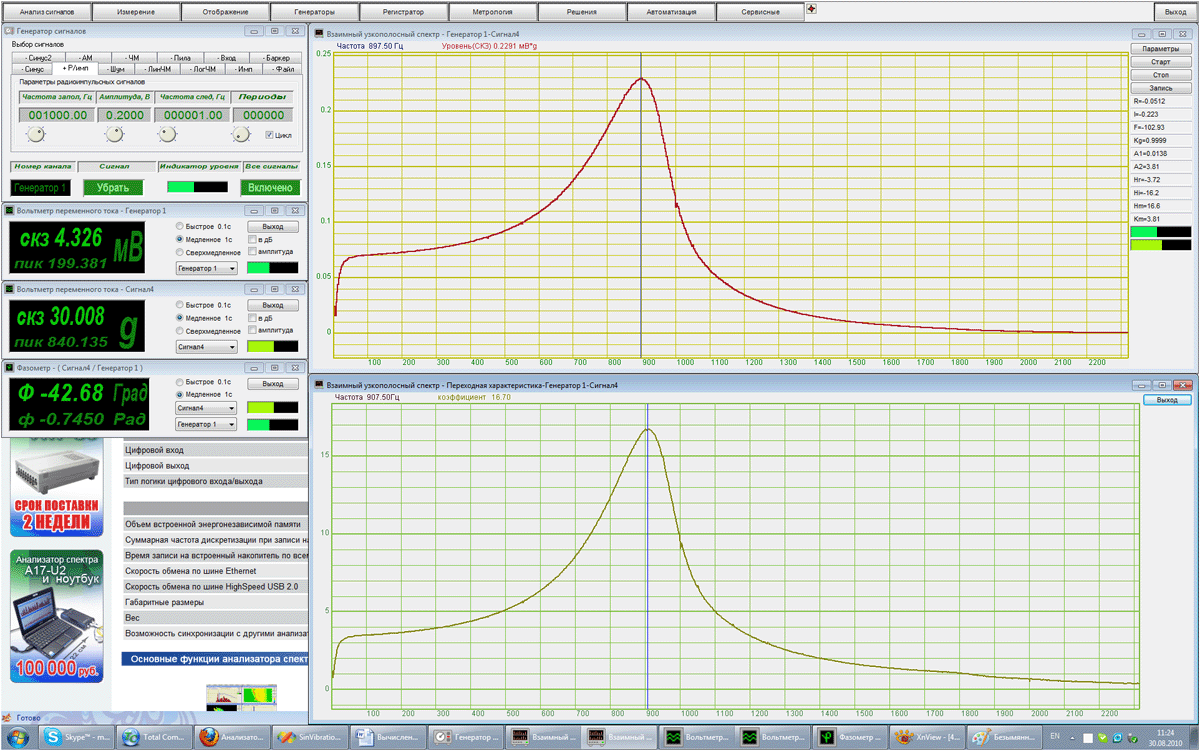
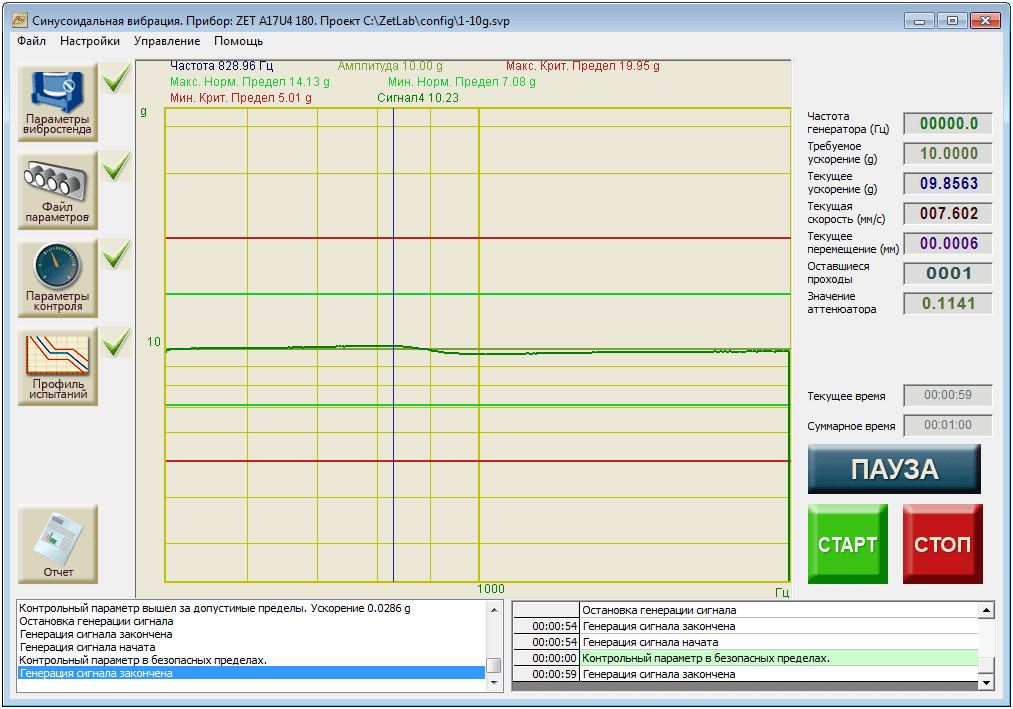
Программа «Измерение АЧХ (8 каналов)»
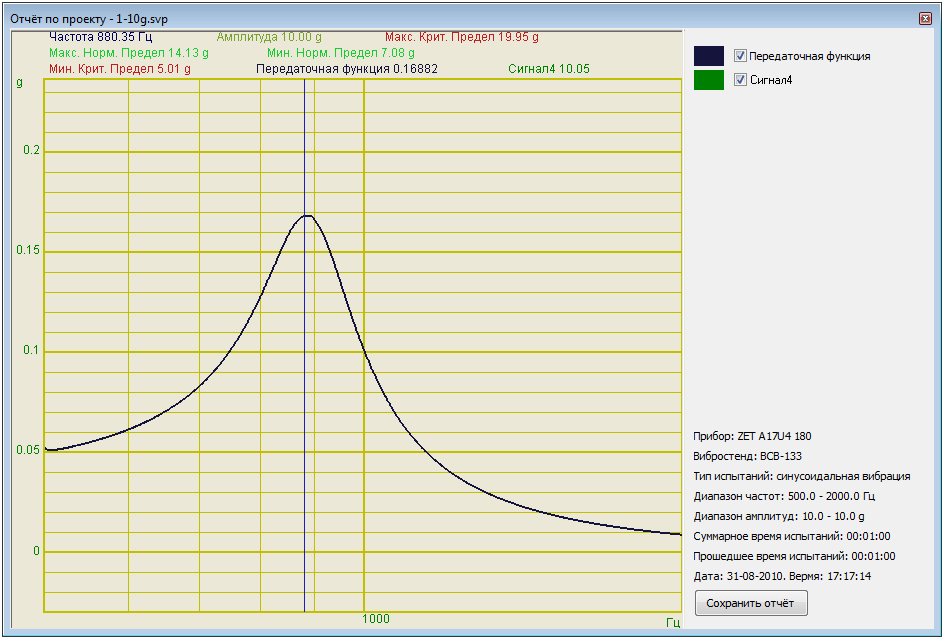
График АЧХ электрического резонансного контура
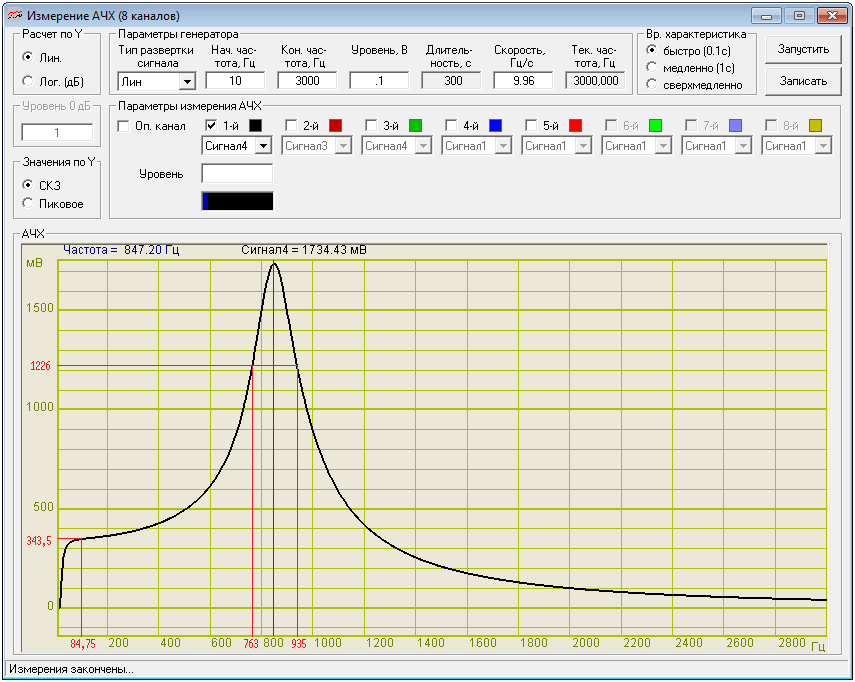
Измерение добротности по графику АЧХ
По графику АЧХ колебательного контура определяем частоту резонанса курсорными измерениями: f0 = 847 Гц.
Добротность электрического колебательного контура обратно пропорциональна разности относительных частот, соответствующих значениям относительного напряжения 1/√2 (относительно резонансной частоты и резонансного напряжения):
Кроме того добротность может быть вычислена как отношение напряжения в пике резонанса к входному напряжению.
На частоте менее 10% от резонансной частоты напряжение на конденсаторе будет составлять более 99% от входного напряжения. Соответственно ошибка, которую внесёт метод вычисления добротности, составит менее 1%.
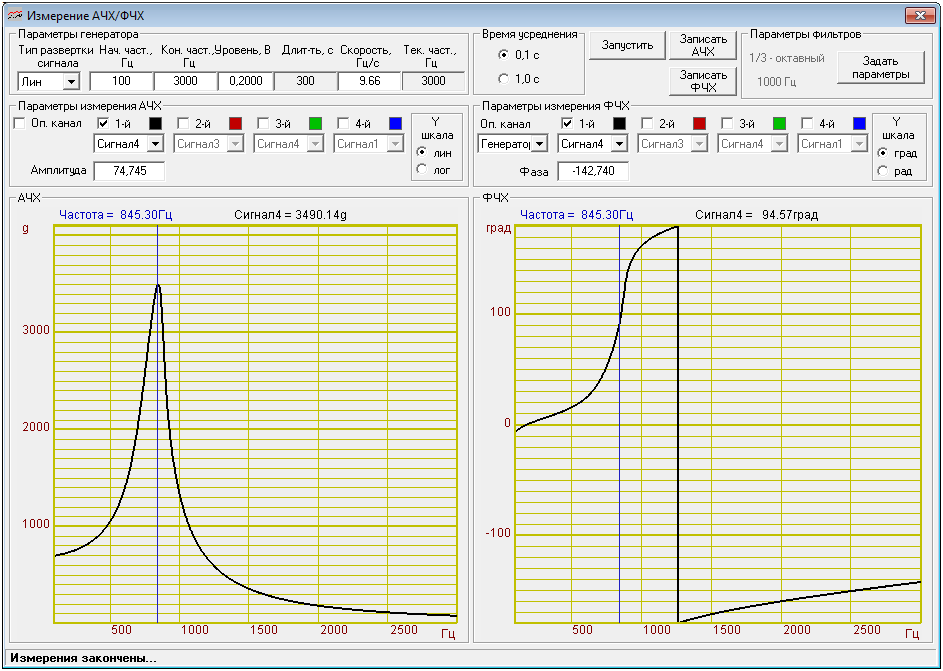
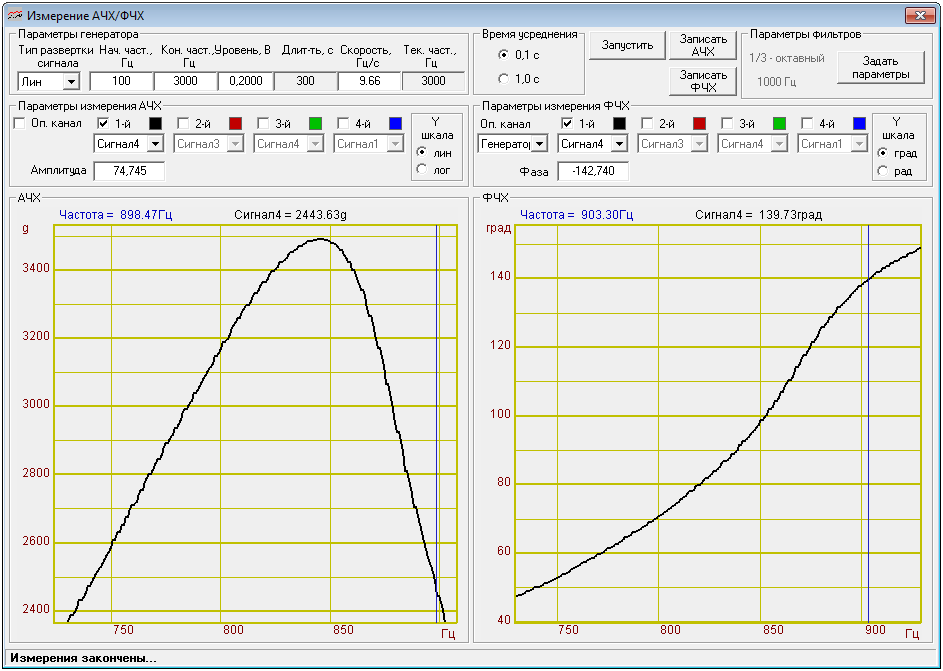
Программа «Измерение АЧХ-ФЧХ (4 канала)»
Как известно из радиотехники, полосу пропускания колебательного контура можно найти из частотных характеристик, отмечая граничные частоты, по уровню 1/v2 от максимума модуля амплитудной характеристики для последовательного колебательного контура или максимума сопротивления для параллельного контура. Можно также измерить полосу пропускания резонатора по фазово-частотной характеристике электрического импеданса как разность между частотами, соответствующими сдвигу фаз ±45° от фазы в точке резонанса. Отношение резонансной частоты к ширине полосы пропускания есть добротность колебательной системы.
Гафики измеренных АЧХ и ФЧХ
f0 = 845,3 Гц
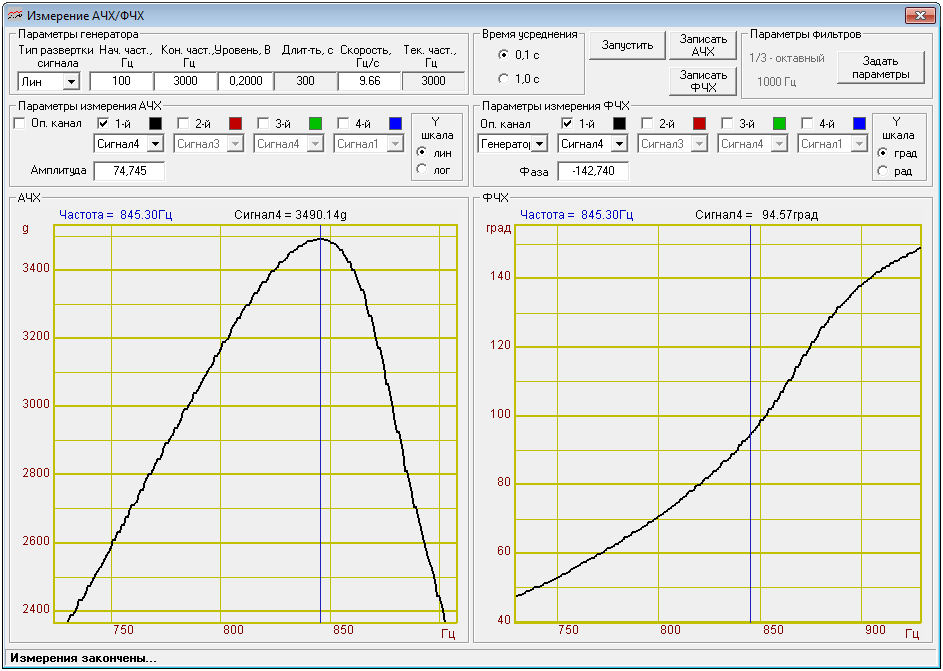
Измерение добротности по АЧХ
АЧХ: f2=898,5 Гц ФЧХ: f2=903,3 Гц
АЧХ: f1=739 Гц ФЧХ: f1=738 Гц
Измерение добротности по ФЧХ
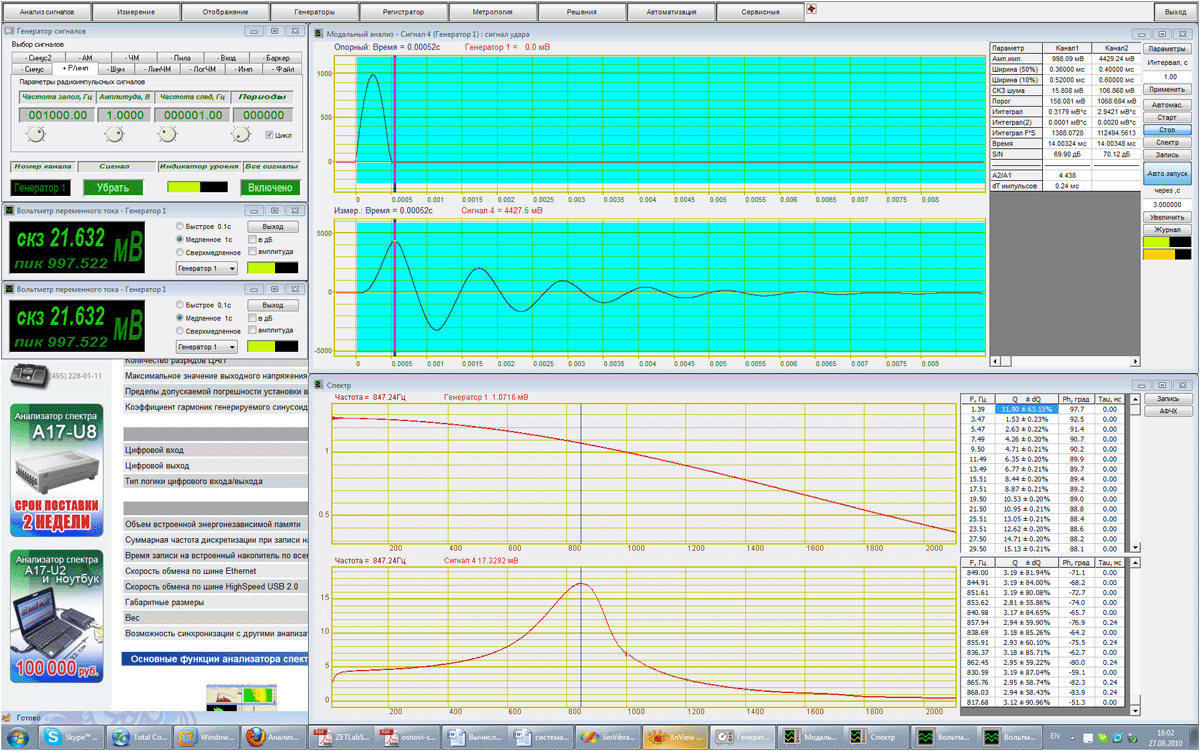
Модальный анализ
Измерение резонанса с помощью программы «Модальный анализ»
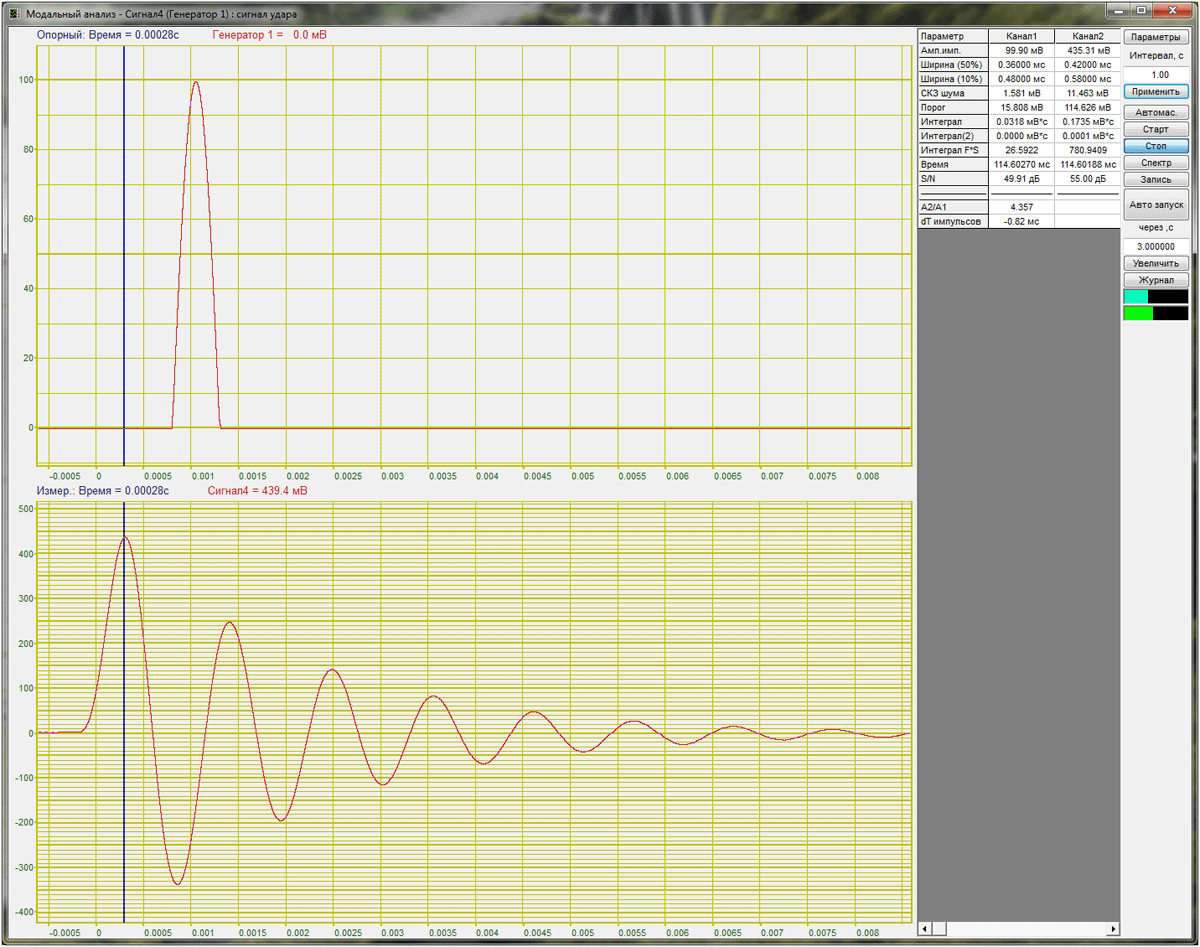
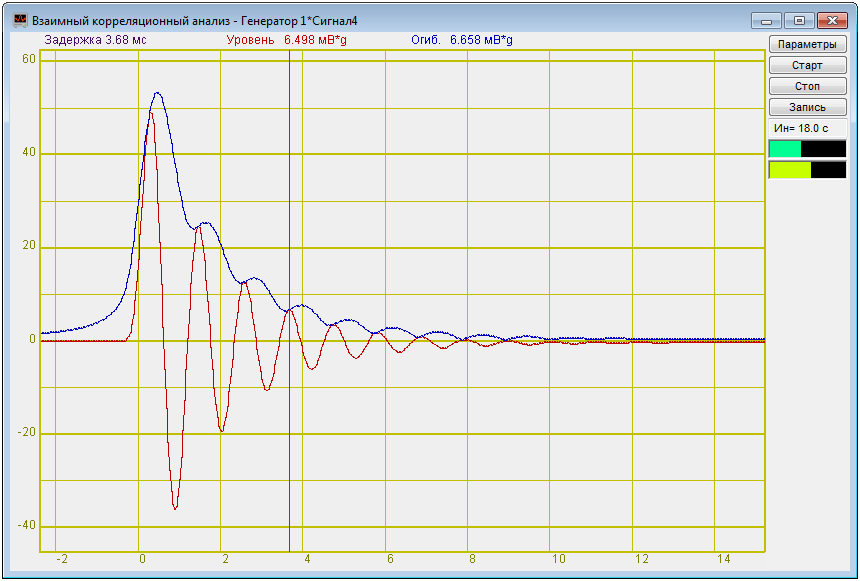
Затухающие колебания на выходе электрического колебательного контура
Если на вход системы подать дельта-импульс, то на выходе будет импульсная характеристика системы. Дельта-импульс эмулируется радио-импульсом высокой частоты с 0 периодов (полуволна).
Характеристики колебательного контура:
τ — время релаксации колебаний — время, в течение которого амплитуда колебаний уменьшится в e раз.
λ — логарифмический декремент затухания — логарифм отношения двух последовательных амплитуд колебаний.
Q — добротность контура — отношение энергии запасённой в контуре к убыли энергии за один период колебаний умноженное на 2π.
Взаимный узкополосный спектр, передаточная функция H1
Вычисления по взаимному узкополосному спектру:
Вычисления по переходной характеристике:
Взаимный узкополосный спектр генератора и измерительного канала
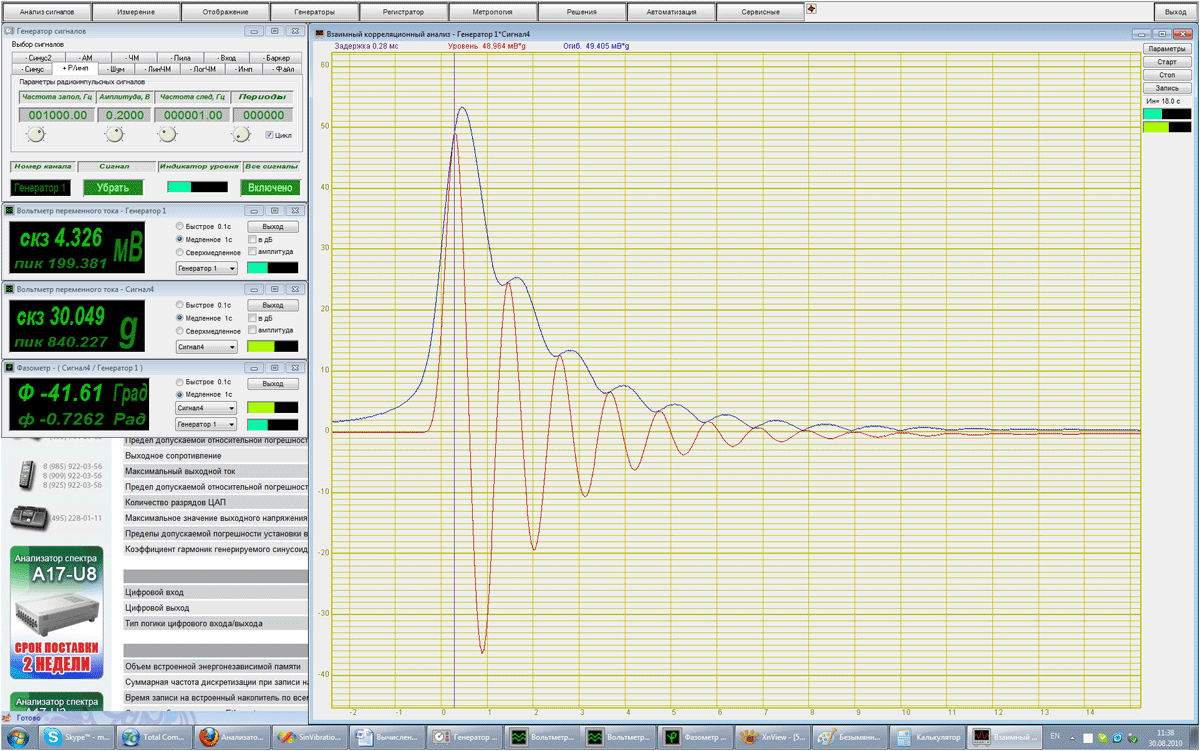
Корреляционная функция (белый шум и радиоимпульс)
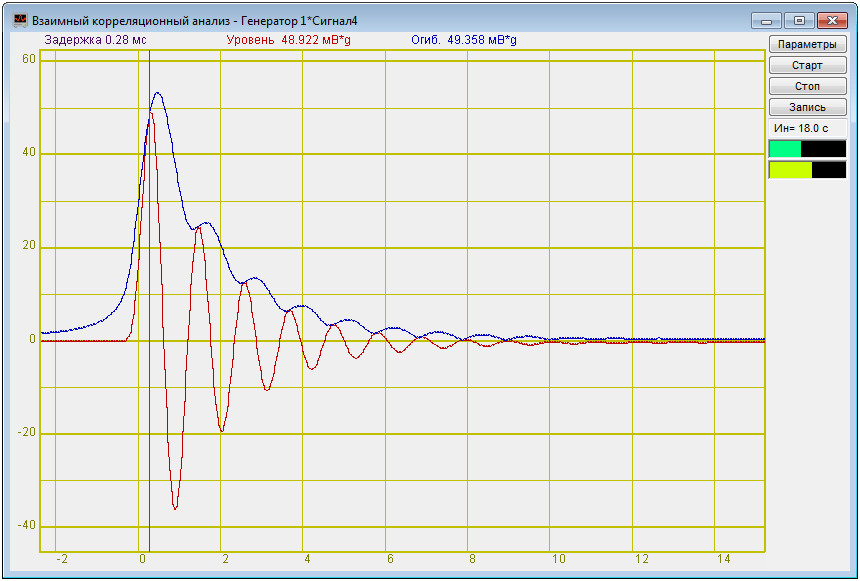
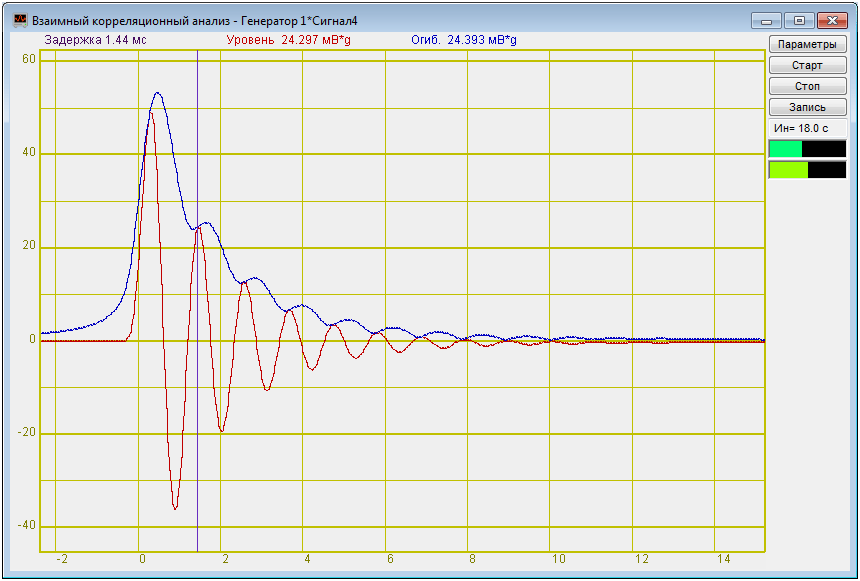
Корреляционная функция сигнала генератора и выхода колебательного контура
U1=48,922 мВ·g
U2=24,297 мВ·g
U3=12,513 мВ·g
U4=6,498 мВ·g
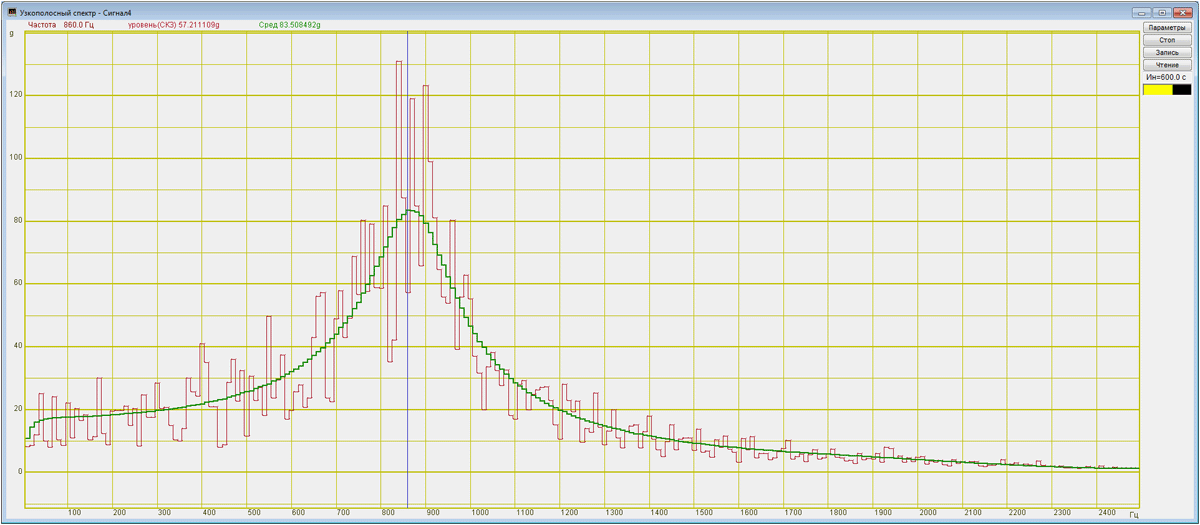
Узкополосный спектр
Применяя те же самые формулы, что и для АЧХ находим характеристики системы:
Узкополосный спектр широкополосного шума с усреднением за 600 секунд
Проведение виброиспытаний на системе с резонансом
Узкополосный спектр широкополосного шума с усреднением за 600 секунд
Узкополосный спектр широкополосного шума с усреднением за 600 секунд
Результаты, полученные в ходе испытаний:
Содержание:
Частотные методы анализа электрических цепей:
Частотные характеристики являются компонентами комплексных функций цепи.
Комплексная функция цепи (КФЦ)
Амплитудно-частотная характеристика (АЧХ)
Фазочастотная характеристика (ФЧХ)
Амплитудно-фазовая частотная характеристика (АФЧХ) (комплексная функция цепи)
где 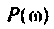
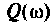
Комплексные функции простых цепей можно рассчитать непосредственно по закону Ома.
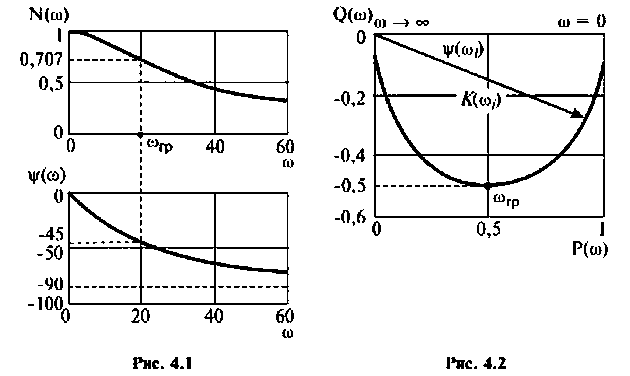
На рис.4.1 показаны АЧХ и ФЧХ, а на рис.4.2 — АФЧХ простейшей интегрирующей цепи (апериодического звена). По АЧХ определяют полосу пропускания
Полосой пропускания П называется диапазон частот, на границах которого мощность сигнала уменьшается в 2 раза, а амплитуда (действующее значение) напряжения (тока) — в 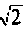
Полоса пропускания может измеряться в радианах в секунду 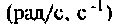
Например, для простой интегрирующей цепи полоса пропускания (см. рис. 4.1)
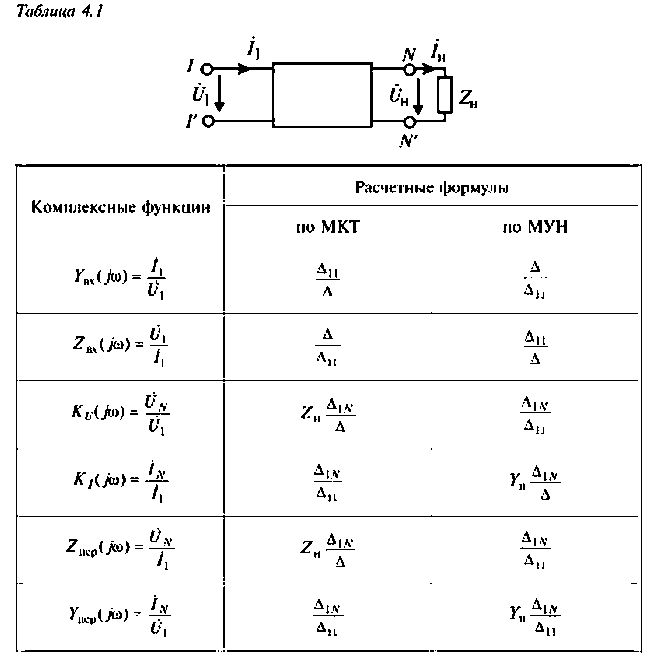
Для сложных цепей КФЦ рассчитывают по MKT или МУН. В табл. 4.1 приведены соотношения для расчета КФЦ, выраженные через определитель и алгебраические дополнения матрицы контурных сопротивлений и узловых проводимостей.
Частотные характеристики цепей с одним реактивным элементом
Примеры решения типовых задач:
Пример 4.2.1.
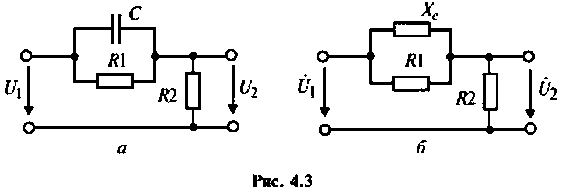
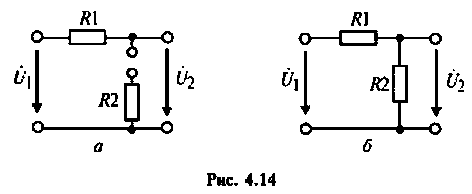
Определить комплексный коэффициент передачи по напряжению для дифференцирующего RC-контура (рис.4.3, а), рассчитать и построить графики АЧХ и ФЧХ.
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.3, б).
2. Определим комплексное напряжение на выходе цепи в виде
Преобразуем полученное выражение, вынеся зa скобки в числителе и знаменателе члены, не содержащие 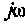
Следовательно.
Введем обозначения:
Величина 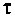
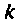
С учетом принятых обозначений
Для получения аналитических выражений АЧХ и ФЧХ запишем комплексную функцию в показательной форме.
Так как выражение (4.2) есть отношение двух полиномов, то удобно числитель и знаменатель записать отдельно в показательной форме, а затем разделить:
3. Из (4.3) запишем АЧХ и ФЧХ соответственно:
4. Построим график АЧХ и ФЧХ качественно по двум точкам. Для этого рассчитаем значения 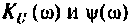
График АЧХ 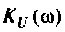
График функции ФЧХ 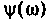
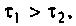
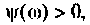
Исследуя функцию (4.5) на экстремум, можно показать, что она имеет максимум на частоте
где
Подставляя 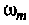
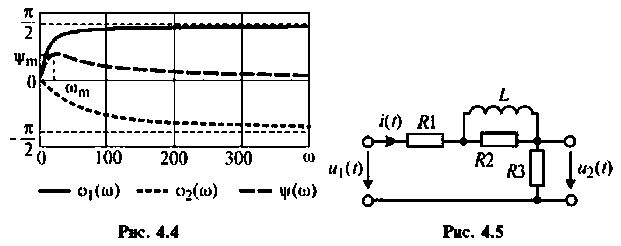
Графики АЧХ и ФЧХ изображены на рис. 4.4.
Пример 4.2.2.
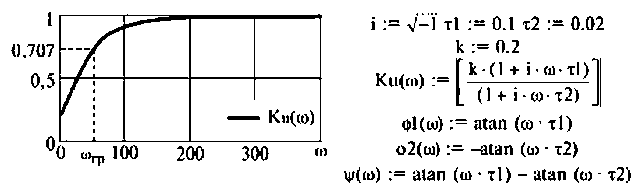
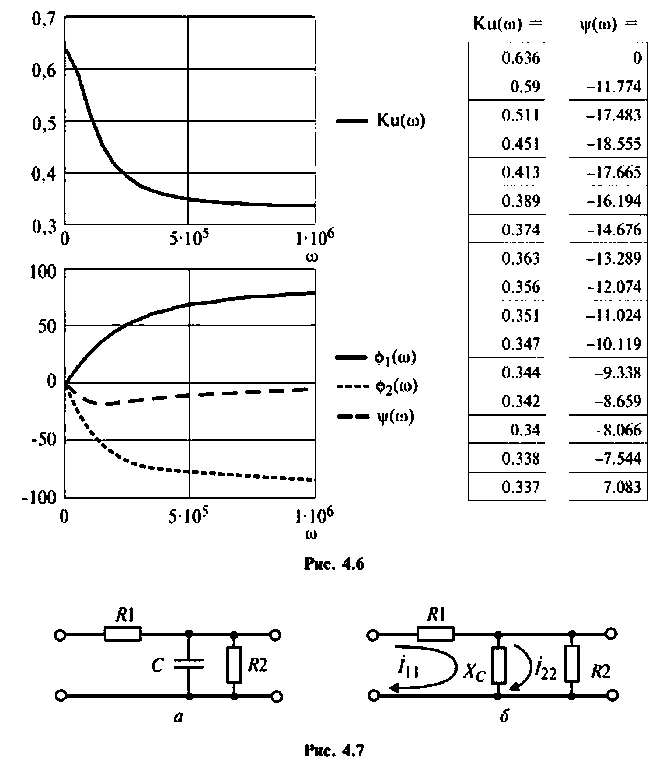
Для электрической цепи, изображенной на рис. 4.5, определить АЧХ 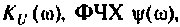
Решение
1. Найдем комплексную функцию К(; (/ш) но формуле делителя напряжения
Преобразуем полученное выражение к виду
Обозначим:
Следовательно,
Отсюда: АЧХ
ФЧХ
2. Рассчитаем граничную частоту. По определению
Из (4.7) найдем
Следовательно,
Из уравнения (4.9) получаем, что
Отсюда
3. Построим график функций.
Вычислим значения (4.7) и (4.8) для частот с дискретностью
Графики и таблицы выполним в среде Mathcad (рис. 4.6).
Пример 4.2.3.
Определить комплексный коэффициент передачи интегрирующей цепи (рис. 4.7, а), используя метод контурных токов. Построить в среде Mathcad график АЧХ, определить полосу пропускания.
Параметры цепи:
Решение
1. Представим цепь комплексной схемой замещения (рис. 4.7, б). Данная цепь имеет два независимых контура. Ток 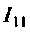
2.Составим матрицы контурных сопротивлений для двух независимых контуров
3.Определим комплексный коэффициент передачи, используя соотношение, приведенное в табл. 4.1.
где сопротивление нагрузки равно
Подставляя найденные выражения, получаем
или
где
4. Рассчитаем 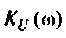
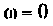
Объяснить полученные результаты можно, рассуждая так: на нулевой частоте (режим постоянного тока) сопротивление емкости бесконечно велико, ток в ней равен нулю, что эквивалентно разрыву этой ветви. При этом цепь становится резистивным делителем напряжения с передаточной функцией 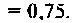
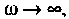
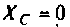
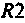
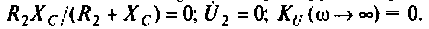
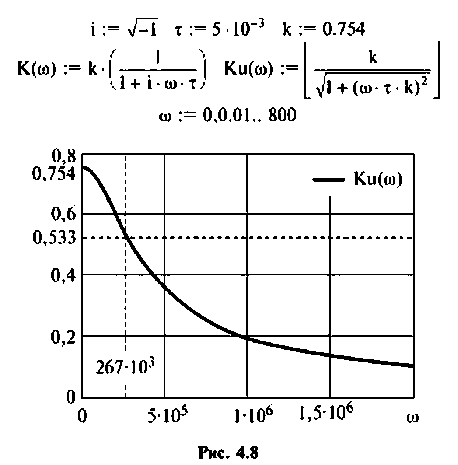
По полученным выражениям строим график АЧХ (рис. 4.8) и среде Mathcad.
5. Определяем полосу пропускания. По определению
Поэтому из (4.11) имеем
После преобразований уравнения (4.12) получаем
откуда
или
Следовательно, цепь имеет полосу пропускания
На рис. 4.8 указана граничная частота
Данная цепь представляет собой фильтр нижних частот с полосой пропускания 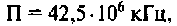

Пример 4.2.4.
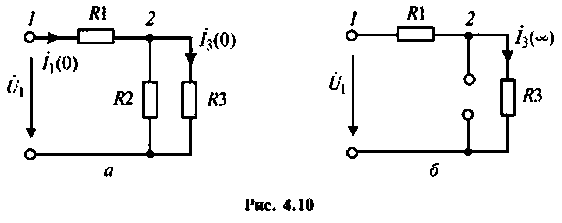
Найти комплексную передаточную проводимость 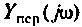
Параметры цепи: 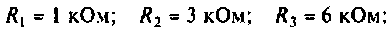
Определить АЧХ и ФЧХ, построить их графики в среде Mathcad.
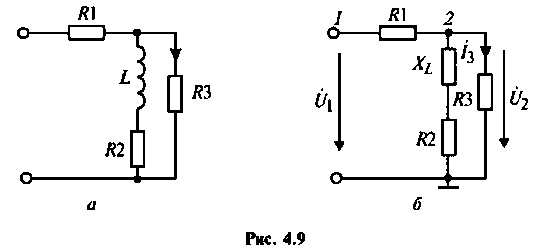
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.9, б). Схема имеет два независимых узла. В данном случае
2. Составим матрицу узловых проводимостей. При определении собственной проводимости узлов необходимо помнить, что собственная проводимость ветви, состоящей из последовательно включенных пассивных элементов, находится из соотношения 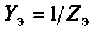
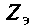
В начале рассчитывают комплексное сопротивление этой ветви, 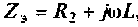
Составим матрицу проводимостей цепи 1 2
Как видим, общие проводимости узлов взяты со знаком минус, так как узловые напряжения 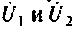
3.Определим комплексную передаточную проводимость по соотношению, приведенному в табл. 4.1
где 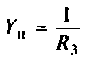
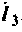
Найдем алгебраические дополнения:
После подстановки найденных значений получим
Для определении АЧХ и ФЧХ запишем выражения для модуля и аргумента
4. Рассчитаем значения 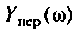
Примечание. Эти значения можно найти без вывода аналитического выражения для 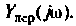
Учитывая, что 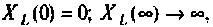
Для первой схемы:
Следовательно,
Аналогично для второй схемы получим
При расчете сложных схем такой прием можно применять для проверки правильности полученного аналитического выражения КФЦ.
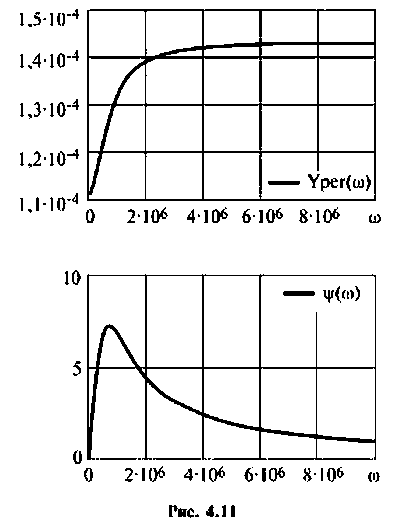
Из (4.13) видно, что функция наметен монотонной, но для качественного построения графика АЧХ (рис. 4.11) необходимо воспользоваться ПЭВМ, например построить функцию в среде Mathcad.
Пример 4.2.5.
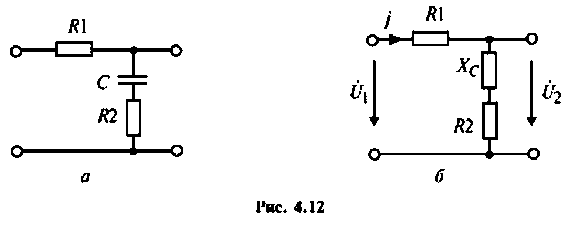
Для интегрирующего RС-контура (рис.4.12,а) определить комплексный коэффициент передачи по напряжению, рассчитать АЧХ, ФЧХ, ВЧХ, МЧХ. Построить графики АЧХ, ФЧХ. АФЧХ, если
Решение
1. Составим комплексную схему замещения цепи (рис. 4.12, б).
2. Определим 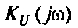
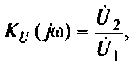
Следовательно.
3. Для нахождения АЧХ и ФЧХ комплексную функцию 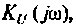
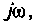
Найдем модуль (АЧХ) и аргумент (ФЧХ) комплексной функции;
Для определения вещественной и мнимой частотных характеристик запишем КФЦ в алгебраической форме. Для этого умножим и разделим (4.14) на комплексно-сопряженный знаменатель:
4. Для приближенного построения графиков АЧХ, ФЧХ. АФХ найдем значения 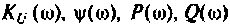
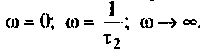
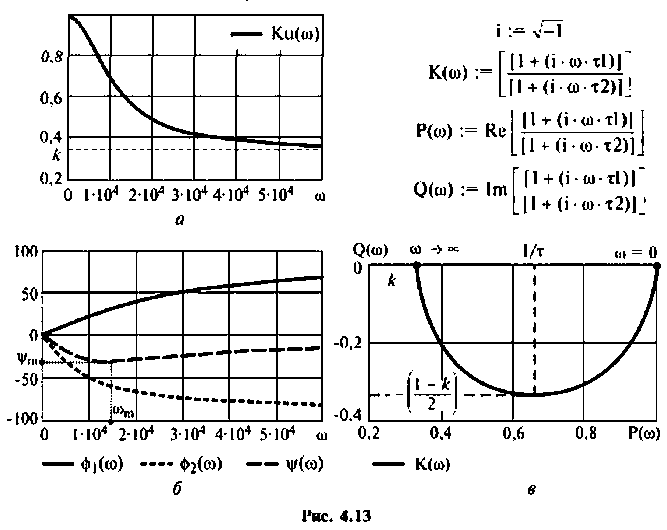
Для более точного и наглядного представления графиков воспользуемся ПЭВМ и математической средой Mathcad.
Графики характеристик приведены на рис. 4.13.
АЧХ представляет монотонно убывающую функцию (рис. 4.13, а).
ФЧХ принимает отрицательные значения, т.е. контур вносит фазовое отставание, а на частоте 
Взяв производную, получим
Решая полученное уравнение относительно 
Подставляя 
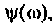
АФХ (рис. 4.13, в) представляет собой полуокружность, расположенную в 4-м квадрате. Центр окружности находится на оси 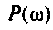
Радиус окружности нетрудно определить из соотношения:
МЧХ:
Отрицательное значение 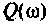
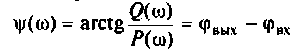
5. Проверка расчетов АЧХ. Воспользуемся эквивалентными схемами цепи для частот 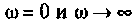
На частоте 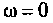
При 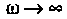
Подставляя эти значения частот в аналитическое выражение (4.14) для 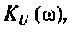
Следовательно, расчет АЧХ выполнен верно.
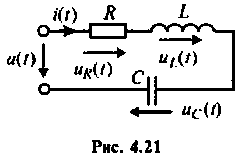
Частотные характеристики последовательного колебательного контура
Основные теоретические сведения:
В последовательном колебательном контуре (рис. 4.21) возникает резонанс напряжений, если выполняется условие
т. е. 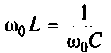
Резонансная частота
Волновое сопротивление контура
Сопротивление контура при резонансе
Собственная добротность контура
Добротность нагруженного контура
Затухание контура
Абсолютная расстройка
Относительная расстройка
Обобщенная расстройка
Фактор расстройки:
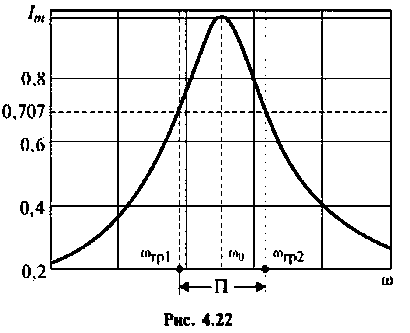
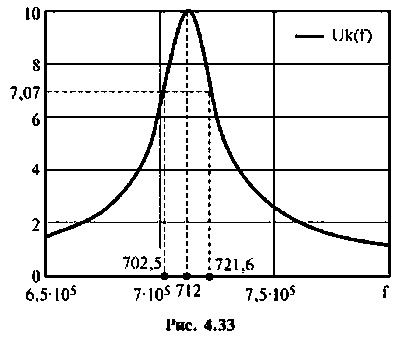
Абсолютная полоса пропускания (рис. 4.22)
Относительная полоса пропускания
Для нагруженного контура:
Комплексные коэффициенты передачи по напряжению:
на активном сопротивлении
на индуктивности
на емкости
Примеры решения типовых задач:
Пример 4.3.1.
Последовательный колебательный контур (рис. 4.23) подключен к источнику напряжению. Контур настроен в резонанс.
Параметры цепи:
Определить резонансную частоту, волновое сопротивление. добротность и полосу пропускания, ток и напряжения на элементах контура.
Построить АЧХ и ФЧХ по напряжению на конденсаторе в среде Mathcad.
Решение
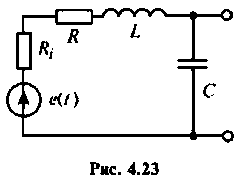
1. Определяем резонансную частоту контура
2. Находим волновое сопротивление контура
3. Вычисляем добротность нагруженного контура
4. Определяем полосу пропускания
5. Рассчитываем ток и напряжения на элементах контура при резонансе
Напряжение на R равно
Напряжения на реактивных элементах
6. Рассчитаем АЧХ и ФЧХ комплексного коэффициента передачи напряжения с емкости.
Учитывая (4.22), из (4.29) получим:
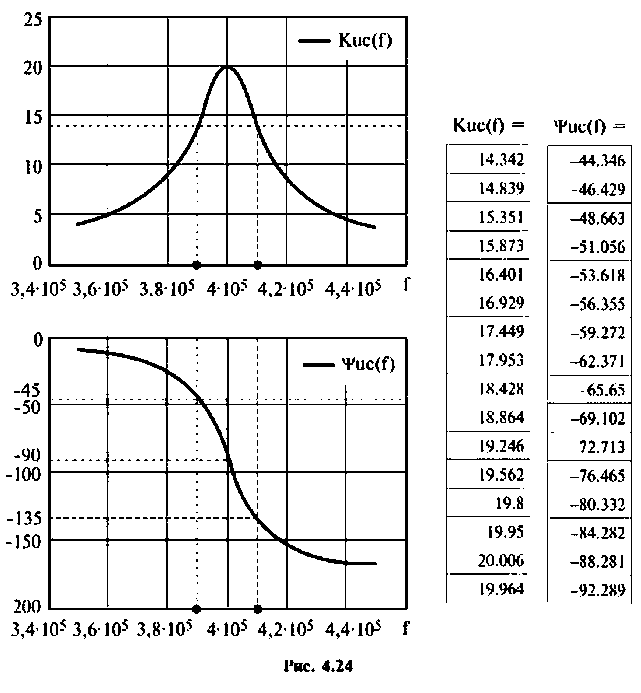
Для построения графиков АЧХ и ФЧХ, выполнения расчетов используем среду Mathcad. АЧХ, ФЧХ в виде графиков и таблиц приведены на рис. 4.24.
Следует заметить, что максимум А11Х достигается на частоте
т.е. при 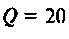
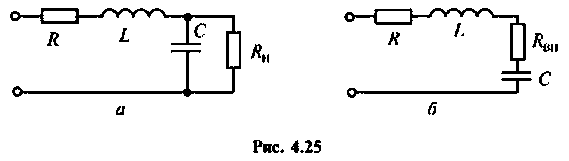
Задача 4.3.2.
К последовательному колебательному контуру (рис. 4.25) с параметрами 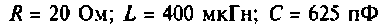
Определить собственную добротность и добротность нагруженного контура, полосу пропускания нагруженного и ненагруженного контура.
Решение
1. Рассчитаем вторичные параметры ненагруженного контура:
2.Определим вторичные параметры наруженного контура. Так как сопротивление нагрузки активное, причем 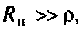
Для определения добротности рассчитаем сопротивление 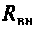
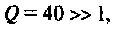
Следовательно,
Вывод. Подключение нагрузки ухудшает добротность контура, что приводит к расширению полосы пропускания.
Пример 4.3.3.
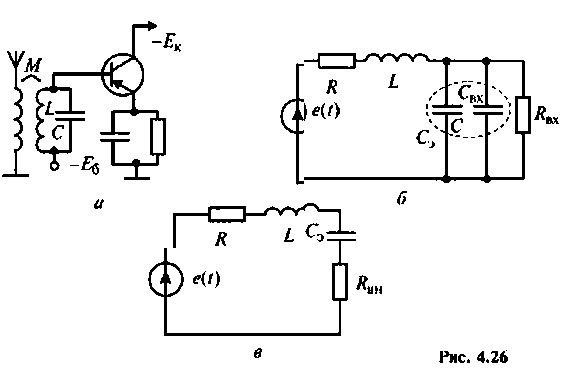
На рис. 4.26, а изображена входная цепь приемника, а на рис. 4.26, б — ее эквивалентная схема. Известны входное сопротивление и входная емкость транзистора входного каскада УВЧ: 
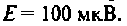
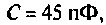
Определить абсолютную полосу пропускания и ток в контуре на резонансной частоте.
Решение
1. Определяем эквивалентную емкость контура
2. Рассчитываем резонансную частоту контура
3. Находим волновое сопротивление и сопротивление, вносимое в контур за счет транзистора усилителя (рис. 4.26, в):
4. Определяем добротность нагруженного контура
5. Рассчитаем абсолютную полосу пропускания нагруженного контура
6. Находим ток в контуре
Пример 4.3.4.
Рассчитать емкость последовательного колебательного контура, если резонансная частота контура 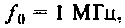
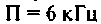
Построить АЧХ и ФЧХ комплексного коэффициента передачи напряжения с индуктивности в среде Mаthcad.
Решение
1. Определим требуемую добротность контура
2. Рассчитаем емкость конденсатора. Из формулы 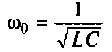
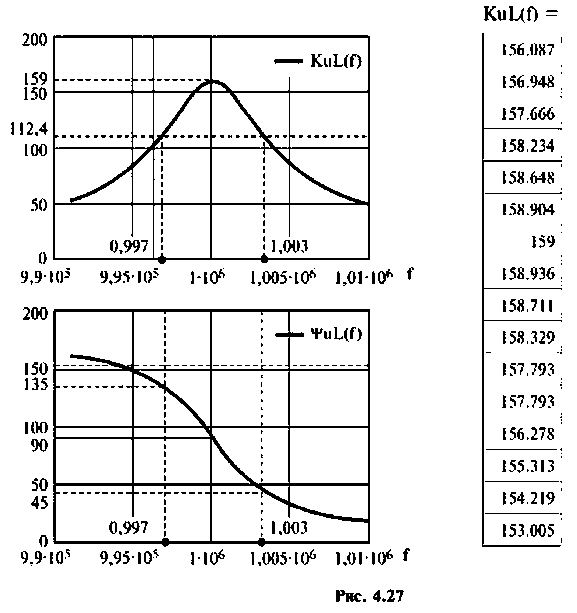
3. Рассчитаем АЧХ и ФЧХ.
Воспользуемся комплексным коэффициентом передачи напряжения с индуктивности по формуле (4.28). Учитывая 4.22), запишем:
Вычислим значения функций на частотах:
Определим частоту, при которой АЧХ имеет максимум
Смещением частоты 
Результаты расчетов АЧХ и ФЧХ б графическом и табличном видах приведены на рис. 4.27.
Частотные характеристики параллельного колебательного контура
Основные теоретические сведения:
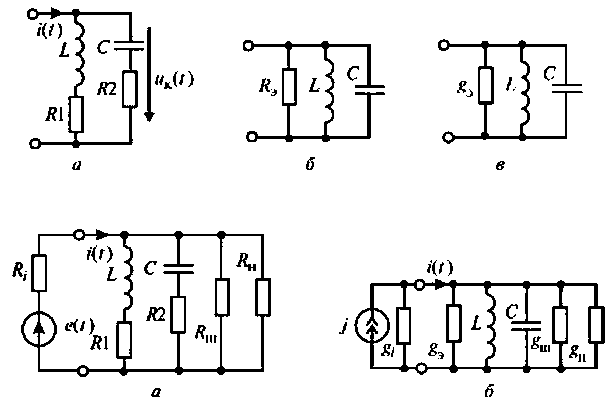
Параллельный колебательный контур образуется путем параллельного соединения катушки индуктивности и конденсатора. Оба элемента, кроме основного эффекта (запасания энергии), имеют потери энергии. В расчетной схеме (рис. 4.29, а) тепловые потери в элементах учтены включением условных сопротивлений
где резонансная частота колебаний
Для реального контура 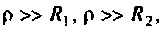
При резонансе сопротивление контура является активным, поэтому ток 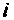
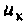
Сопротивление параллельного колебательного контура при резонансе максимально и равно (без учета внешней цепи)
где
Добротность 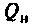
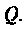
или через их проводимости
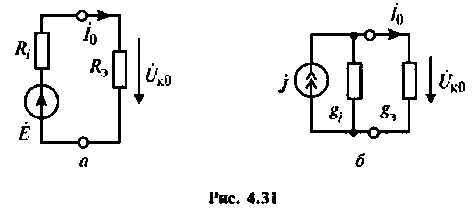
Важными параметрами цепи при резонансе являются токи в ветвях и напряжение на контуре. Ток в обшей ветви (ток источника) при резонансе минимален и равен (см. рис. 4.31)
При этом напряжение на контуре максимально и равно
Токи в индуктивности и в емкости при резонансе равны по значению и противоположны по направлению. Они образуют замкнутый ток в контуре, равный
Частотные свойства параллельного колебательного контура обычно оценивают по нормированной АЧХ
где 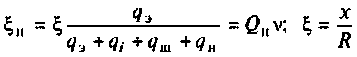
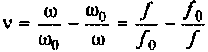
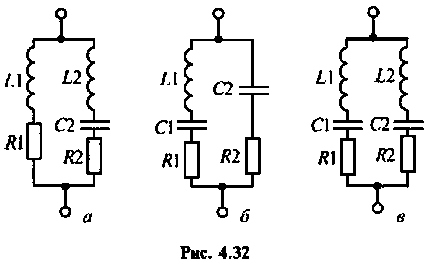
Параллельный контур, показанный на рис. 4.29, имеет по одной реактивности в ветвях. Такой контур называется простым или контуром I вида. Для уменьшения шунтирующего действия внешних цепей часто применяют сложные параллельные контуры.
На рис. 4.32, а, б, в показаны контуры II, (III и IV) видов, соответственно.
Главной особенностью этих контуров является то, что их резонансное сопротивление меньше резонансного сопротивления простого контура с такими же параметрами.
Сопротивление контуров (рис.4.32) при резонансе рассчитывается по формулам, соответственно:
где 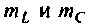
Примеры решения типовых задач:
Пример 4.4.1.
Параллельный контур (см. рис. 4.29, а) подключен к источнику с параметрами 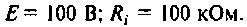
Параметры катушки индуктивности:
Определить действующие значения тока в контуре, тока на входе цепи и напряжения на контуре при резонансе, абсолютную и относительную полосы пропускания контура, добавочное сопротивление необходимое для расширения полосы пропускания в 2 раза.
Решение
1. Определим резонансную частоту колебания
2. Рассчитаем волновое сопротивление
3. Определим сопротивление контура при резонансе
4. Найдем действующее значение тока на входе контура (см. рис. 4.31, а) при резонансе
5. Определим соответственную добротность контура
6. Найдем ток в контуре и напряжение на нем:
7. Определим добротность нагруженного контура
8. Рассчитаем абсолютную и относительную полосы пропускания:
9. Определяем добавочное cопротивление 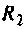
Пример 4.4.2.
Рассчитать полосу пропускания колебательного контура (см. рис. 4.30, а).
Дано:
Определить сопротивление 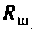
Решение
1. Рассчитаем волновое сопротивление и резонансную частоту контура:
2.Рассчитаем добротность цепи без шунта. Воспользуемся трехветвевой эквивалентной схемой цепи и соотношением (4.32). Найдем проводимость элементов схемы:
Тогда
3. Определим полосу пропускания
4. Найдем сопротивление шунта, необходимою для расширения полосы до 10 кГц,
В этом случае добротность цепи должна быть равна
Тогда из (4.32) получаем
Следовательно, сопротивление шунта должно быть равно
Пример 4.4.3.
Параллельный колебательный контур с параметрами: 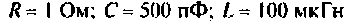
Определить собственную добротность контура, добротность нагруженного контура, абсолютную полосу пропускания и граничные частоты полосы пропускания. Построить резонансную кривую по напряжению на ЭВМ.
Решение
1. Определим волновое сопротивление контура
2. Рассчитаем собственную добротность контура
3. Найдем сопротивление контура при резонансе
4. Определим добротность нагруженного контура по формуле (4.31)
5. Рассчитаем резонансную частоту
6. Найдем полосу пропускания
7. Определим граничные частоты полосы пропускания:
8. Построим резонансную характеристику контура но напряжению. Из выражения (4.33) запишем
Напряжение па контуре при резонансе
Для построения резонансной характеристики задаемся характерными значениями частот: 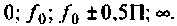
Пример 4.4.4.
Определить резонансную частоту, эквивалентное сопротивление при резонансе и добротность сложного контура (рис. 4.32, а), подключенного к источнику напряжения.
Дано:
Решение
1. Определим резонансную частоту и сопротивление параллельного контура при резонансе:
Сопротивление контура при резонансе
2. Рассчитаем эквивалентное сопротивление сложного контура II вида
3. Найдем добротность нагруженного контура II вида
Сравним значения 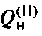
Вывод. За счет неполного включения индуктивности 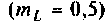
Частотные характеристики связанных колебательных контуров
Основные теоретические сведения:
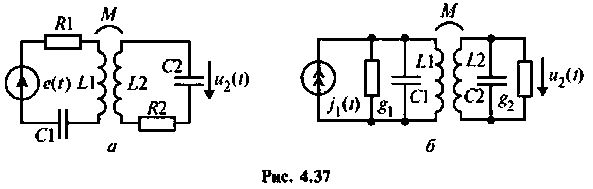
С целью повышения коэффициента прямоугольности АЧХ контуров применяют связанные контуры последовательного и параллельного питания (рис. 4.37, а, б).
Частотные характеристики связанных контуров рассмотрим на примере системы из двух контуров.
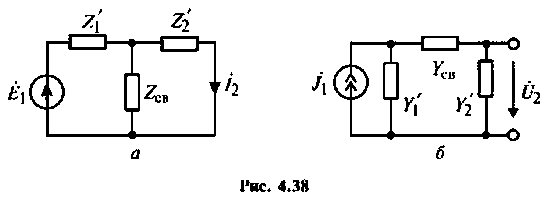
Эквивалентные схемы связанных контуров
Во всех случаях систему связанных контуров можно представить в виде Т- или П-образной эквивалентной схемы (рис. 4.38).
Количественной характеристикой связи является сопротивление связи 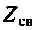
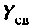
Удобным параметром для оценки связи является коэффициент связи
В случае реактивной связи для Т-образной схемы
Для П-образной схемы
где — сопротивление (проводимость) связи;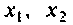
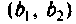
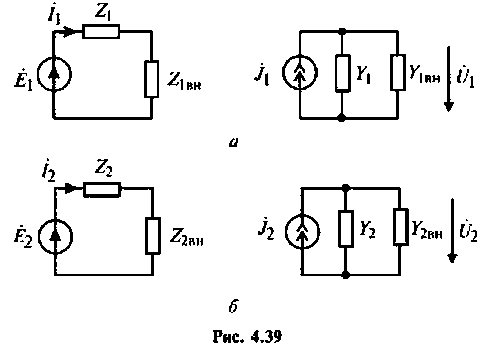
Для этого используют понятия вносимого сопротивления 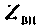
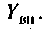
Резонансы в связанных контурах:
При настройке контуров в резонанс добиваются максимального тока (напряжения) во вторичном контуре.
Настройка связанных контуров может производиться различными способами, поэтому различают шесть резонансов. В табл. 4.3, 4.4 приведены виды и условия резонансов, способы настройки и соотношения для токов (напряжений) в связанных контурах последовательного (параллельного) питания.
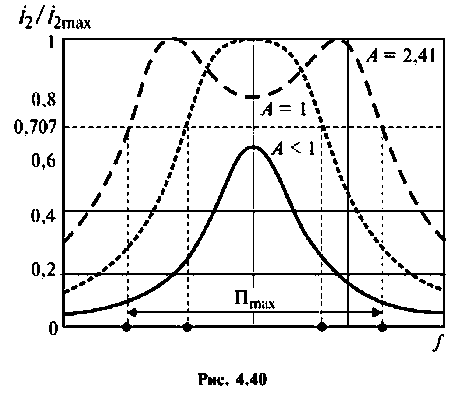
Резонансные характеристики связанных контуров:
Для двух неидентичных связанных контуров: последовательного питания
где
параллельного питания:
где 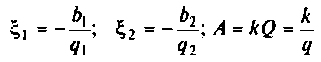
Если контуры идентичны, то обобщенная расстройка
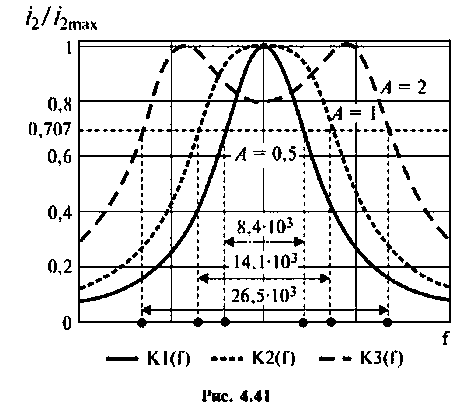
На рис. 4.40 приведены резонансные характеристики при различных факторах связи.
Относительная полоса пропускания:
а) связь слабая
б) связь критическая
в) связь сильная
При 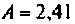
Примеры решения типовых задач:
Пример 4.5.1.
В системе двух индуктивно связанных контуров (см. рис.4.37,а) известны следующие параметры: коэффициент связи
Определить емкость 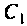
Решение
Емкость конденсатора 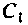
отсюда
Определим реактивное сопротивление 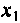
Peaктивное сопротивление второго контура
Рассчитаем полное сопротивление второго контура
Определим сопротивление связи контуров
Следовательно
Находим емкость первого контура
Пример 4.5.2.
Рассчитать емкости связанных контуров (см. рис. 4.37,а) и оптимальное сопротивление связи, если система настроена и полный резонанс. Определить токи, мощности в контурах при этом режиме, а также КПД системы.
Дано:
Решение
1. Определим емкость конденсатора 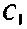
Отсюда
2. Сопротивление оптимальной связи при полном резонансе
3. Рассчитаем токи в первом и втором контурах при полном резонансе
4. Определим активные мощности в первом и втором контурах и КПД связанных контуров:
Пример 4.5.3.
На рис. 4.37, а показана система из двух идентичных связанных контуров с параметрами: 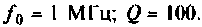
Решение
1. Определим полосу пропускания одиночного контура
2. Рассчитаем полосу пропускания системы связанных контуров:
1) определим параметр связи для
Таким образом при 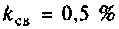
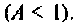
Абсолютная полоса пропускания (рис. 4.41, резонансная кривая А = 0,5)
2) при 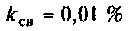
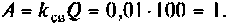
3) если 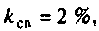
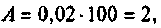
Рассчитаем полосу пропускания для этого случая.
Вид резонансных кривых по току и полоса пропускания для критической и сильной связи показаны на рис. 4.41, кривые А = 1 и А = 2.
Пример 4.5.4.
Антенный контур (см. рис. 4.37,б) индуктивно связан с входным контуром усилителя высокой частоты. Оба контура настроены в резонанс на частоту 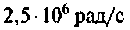
Дано:
Входное сопротивление УВЧ считать бесконечно большим.
Определить емкости и добротности контуров, их взаимную индуктивность, а также ток и напряжение на емкости во вторичном контуре.
Решение
1.Емкости контуров определим из формулы резонансной частоты. Емкость конденсатора первого контура
Емкость конденсатора второго контура
2. Рассчитаем волновое сопротивление контуров:
3. Рассчитаем добротности контуров и параметр связи:
4. Определим взаимную индуктивность двух связанных контуров
5. Рассчитаем ток во вторичном контуре. Известно (см. табл. 4.3), что при полном резонансе
Тогда, учитывая, что контуры настроены в резонанс, то из (4.34) получаем
Оба контура по условию настроены в резонанс, поэтому расстройки равны нулю:
С учетом этого рассчитаем ток во втором контуре
6. Найдем напряжение на конденсаторе вторичного контура
Пример 4.5.5.
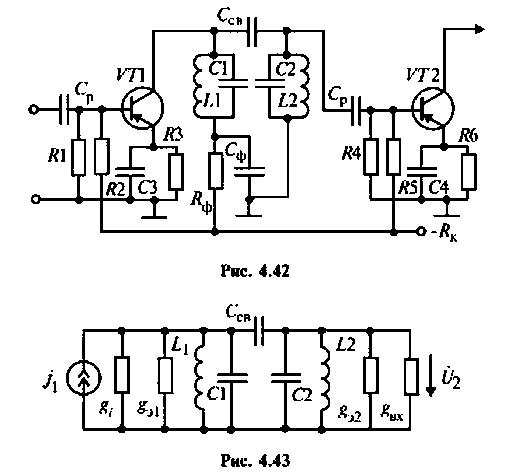
На рис. 4.42 приведена схема одного каскада УПЧ радиоприемника, в котором избирательность обеспечивается двумя связанными контурами с емкостной связью. Оба контура настроены в резонанс на промежуточную частоту
Эквивалентная схема этого каскада (рис. 4.43) имеет следующие параметры: 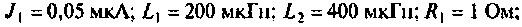
Определить емкости и добротности контуров, емкость связи, напряжение на емкости во вторичном контуре, а также полосу пропускания каскада УПЧ.
Решение
1. Из формулы резонансной частоты найдем емкость первого контура. С учетом влияния выходной емкости транзистора 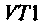
Емкость второго контура с учетом влияния входной емкости транзистора 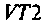
2. Определим емкость связи
3. Рассчитаем добротности нагруженных контуров при отсутствии связи между ними. Для расчета воспользуемся формулой (4.31)
где
где
4. Рассчитаем параметр связи
5. Рассчитаем напряжение на втором контуре. Известно (см. табл. 4.4), что при полном резонансе
Тогда, учитывая, что контуры настроены в резонанс 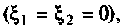
Найдем проводимость контуров
Тогда
6. Рассчитаем полосу пропускания каскадов УПЧ. учитывая, что А = 1,2.
Частотные методы расчета и построения переходных и установившихся процессов в электрических цепях
Основные теоретические сведения:
Зная частотную характеристику электрической цепи 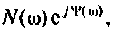
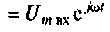
где 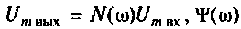
С помощью частотной характеристики электрической цели можно не только определить выходную величину цепи в установившемся режиме при гармоническом входном воздействии, но и найти реакцию цепи в переходном процессе на произвольное воздействие 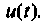
Найдем реакцию цепи на единичную ступенчатую функцию (т.е. найдем переходную функцию цепи), используя ее частотную характеристику. Как известно, интеграл Фурье для единичной ступенчатой функции имеет вид
т.е. единичная ступенчатая функция может быть представлена как бесконечная сумма элементарных колебаний вида
Каждому из этих колебаний соответствует выходное колебание 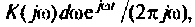
Представляя 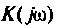
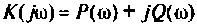
где 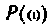
Построение переходной функции с помощью вещественной частотной характеристики методами численного интегрирования:
Выражение (4.38) позволяет вычислить переходную функцию ЭЦ и определить качество переходного процесса. Однако интегрирование этого выражения аналитическими методами — задача весьма трудоемкая, а чаще всего просто практически невыполнимая. С применением современных ЭВМ и методов численного интегрирования (метод прямоугольников, трапеций, метод Симпсона и др.) эта задача существенно упрощается, ее решение сводится к составлению программы для ПЭВМ. В инженерной практике интегрирование достаточно осуществлять в области существенных частот от 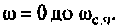

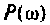
В результате интегрирования получают совокупность значений 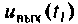
В качестве примера построения алгоритма численного интегрирования рассмотрим интегрирование с точки зрения простоты вычислений и точности результата. Сущность метода заключается в следующем. Пусть необходимо вычислить определенный интеграл
Вид подынтегральной функции, соответствующей выражению
при фиксированном времени 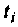
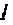
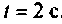
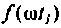
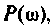
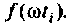
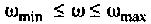
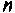
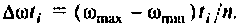
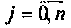

Очевидно, что погрешность численного интегрирования зависит и от выбора числа интервалов 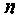
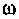
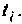
При этом одно полное колебание подынтегральной функции представляется не менее чем шестнадцатью трапециями.
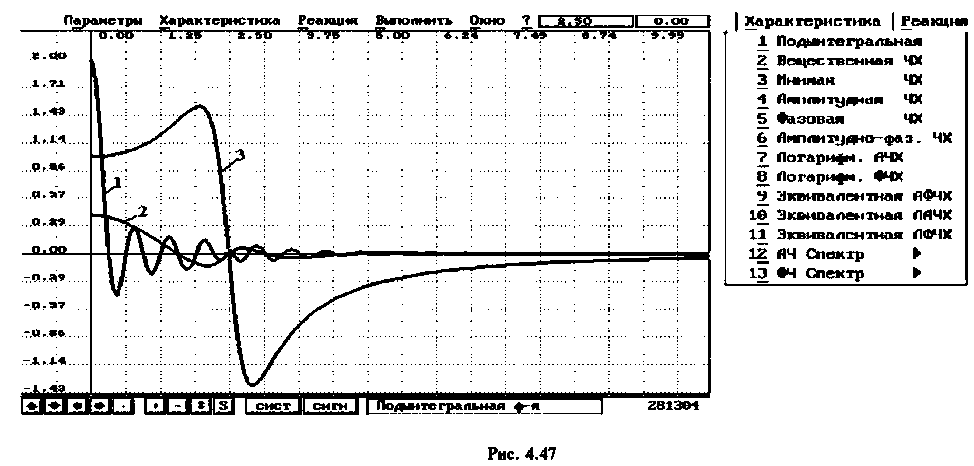
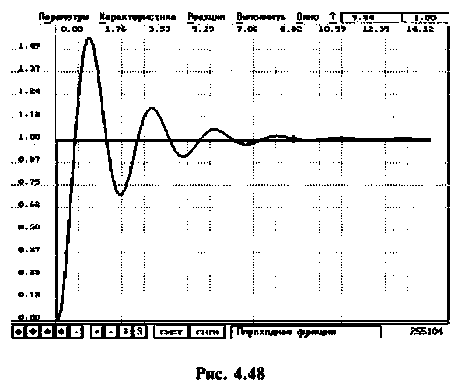
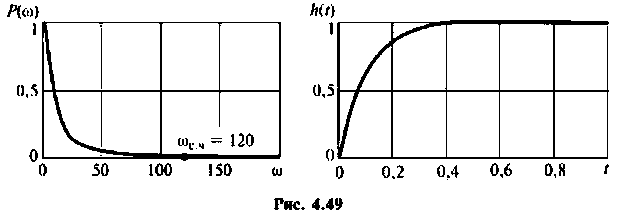
В качестве примера для построения переходной функции возьмем электрическую цепь, ВЧХ которой была построена и приведена на рис. 4.47 (кривая 3). На рис. 4.48 приведена переходная функция этой сложной электрической цепи.
Переходная функция на рис. 4.48 получена с помощью пакета ПП «Сигнал» [5].
Для вычисления интеграла (4.39) необходимо определить значение частоты для верхнего предела интегрирования 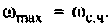
Алгебраическая форма КФ
где 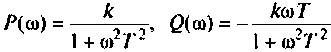
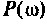
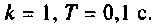
Из графика ВЧХ видно, что при 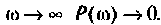
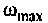
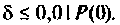
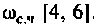
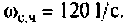
Для случая электрических цепей с дифференцирующими свойствами может оказаться, что при 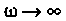
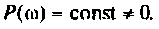
Приведенный пример наглядно показывает, что использование частотных характеристик для построения временных характеристик с помощью ЭВМ существенно расширяет возможности частотных методов анализа электрических цепей.
Спектральный метод расчета и построения выходных величин электрических цепей при сложных входных воздействиях:
Применение частотных методов при анализе и синтезе электрических цепей с требуемыми динамическими характеристиками и использованием ЭВМ позволяет не только строить переходные характеристики, но и строить реакцию цепи на любые детерминированные воздействия, оценивать их в установившихся режимах.
Математической основой частотных методов анализа электрических цепей и систем автоматического управления является обратное преобразование Фурье, позволяющее получать изображение выходного сигнала системы y(t) с помощью вещественной и мнимой частотных характеристик систем. В свою очередь, по вещественной или мнимой частотным характеристикам можно построить переходный процесс выходной величины и оценить реакцию цепи в переходном и установившемся режимах.
Как известно, реакция системы определяется по формуле обратного преобразования Фурье [4]
где
После соответствующих преобразований выражение (4.46) примет вид:
I) для ступенчатой входной функции 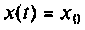
2) для линейной входной функции 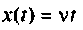
y{t) = vP(0)t+±l
2 r0(
Л» И
(4.48)
О)
3) для параболической входной функции 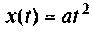
4) для полиномиального воздействия вида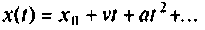
Применение ЭВМ и численных методов интегрирования позволяет отказаться от графических и табличных методов построения переходных и других необходимых функций в электрических цепях.
Примеры решения типовых задач:
Пример 4.6.1.
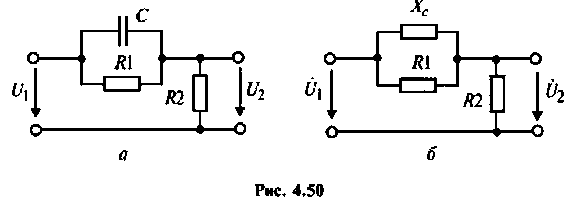
Определить комплексный коэффициент передачи по напряжению для дифференцирующего 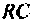
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.50, б).
2. Определим комплексное напряжение на выходе цепи в виде
Преобразуем полученное выражение, вынеся за скобки в числителе и знаменателе члены, не содержащие 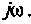
Следовательно
Введем обозначения:
Величина 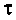
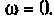
Для получения аналитических выражений ВЧХ и МЧХ запишем комплексную функцию и алгебраической форме
где
Примем:
Для определения частоты 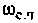
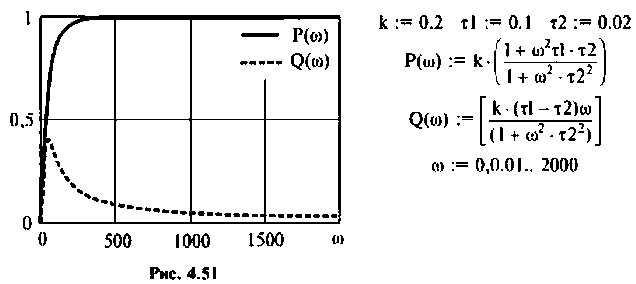
Из частотных характеристик КПФ принимаем 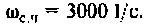
Переходная функция, показанная на рис.4.52, соответствует дифференцирую щему фазоопережающему контуру, который широко применяется в электронных и радиотехнических устройствах, системах автоматического управления.
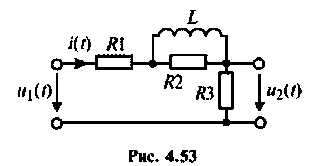
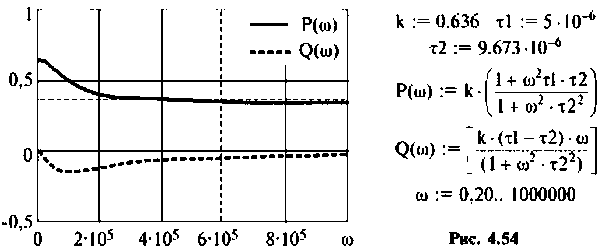
Пример 4.6.2.
Для электрической цепи, изображенной на рис, 4.53, определить КПФ 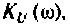
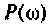
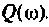
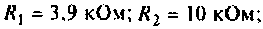
Решение
1. Найдем комплексную функцию 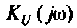
Преобразуем полученное выражение к виду
Обозначим:
Следовательно,
Для получения аналитических выражений ВЧХ и МЧХ запишем комплексную функцию и алгебраической форме
где
Для определения частоты 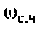
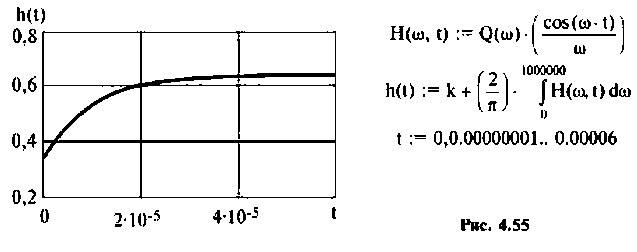
По виду ВЧХ и МЧХ определяем, что для построения переходной функции необходимо применить МЧХ. Примем из графика МЧХ 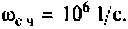
Из рис. 4.55 видно, что переходная функция соответствует интегрирующему контуру.
Пример 4.6.3.
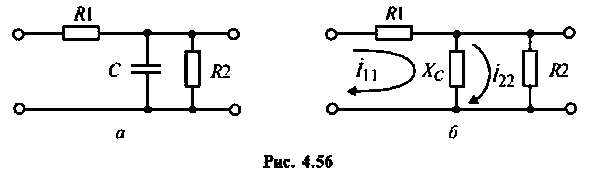
Определить комплексный коэффициент передачи интегрирующей цепи (рис. 4.56, а), используя метод контурных токов. Построить в среде Mathcad графики АЧХ, ВЧХ, МЧХ. Рассчитать и построить эпюру входного и выходного напряжения, если на вход цепи поступает напряжение вида 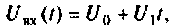
Параметры цепи:
Решение
1.Представим цепь комплексной схемой замещения (рис. 4.56, б). Данная цепь имеет два независимых контура. Ток 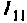
2.Составим матрицы контурных сопротивлений для двух независимых контуров
3.Определим комплексный коэффициент передачи, используя соотношение, приведенное в табл. 4.1.
где сопротивление нагрузки
Подставляя найденные выражения, получаем
т.е.
где
4. Рассчитаем 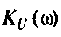
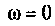
Объяснить полученные результаты можно, рассуждая так: на нулевой частоте (режим постоянного тока) сопротивление емкости бесконечно велико, ток в ней равен нулю, что эквивалентно разрыву этой ветви. При этом цепь становится резистивным делителем напряжения с передаточной функцией 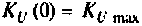
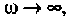
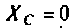
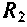
5.Определим выражения для АЧХ, ВЧХ, МЧХ. Представим КГ1Ф (4.55) в алгебраической форме
где 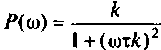
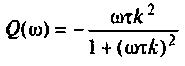
Амплитудно-частотную характеристику запишем в виде
6. В среде Mathcad построим частотные характеристики и определим
По ВЧХ на рис. 4.57 определяем, что существенная частота
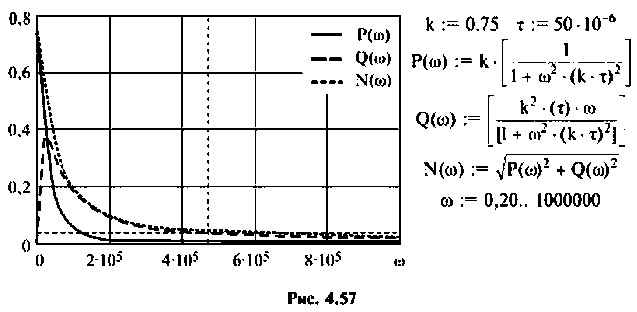
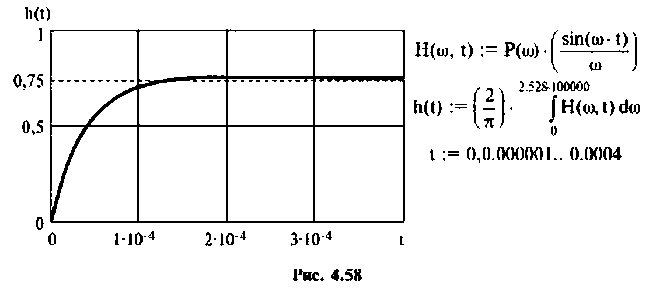
7. Построим переходную функцию электрической цепи, которая представлена на рис. 4.58.
Переходная функция электрической цепи соответствует апериодическому звену.
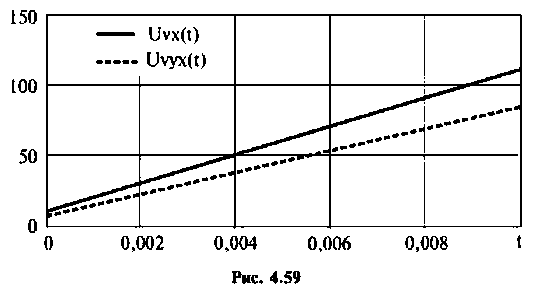
8. Построим реакцию электрической цепи на напряжение, изменяющееся но линейному закону (рис. 4.59).
- Операторные передаточные функции
- Свободные колебания в пассивных электрических цепях
- Цепи с распределёнными параметрами
- Волновые параметры длинной линии
- Энергетические характеристики двухполюсников
- Комплексные функции электрических цепей
- Гармонические колебания в колебательном контуре
- Частотные характеристики линейных электрических цепей