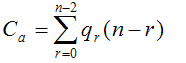The online calculator allows you to quickly build a truth table for an arbitrary Boolean function or its
vector, calculate perfect disjunctive and perfect conjunctive normal forms, find function representation in the form of the Zhegalkin polynomial, build a K-Map (Karnaugh Map), and classify the function by classes of Post (Post Emil Leon).
How to use the calculator
- Enter in the field logic function (for example, x1 ∨ x2) or its vector (for example, 10110101)
- Specify the actions to be performed using the switches
- Specify whether the output of the solution is required by the «With solution (By the steps)» switch
- Click the «Let’s go» button
Symbols used
As variables, the letters of the Latin alphabet are used, as well as numbers written after the letter (variable index).
Thus, the variable names will be: a,
x, a1, B, X, X1, Y1, A123
and so on.
To record logical operations you can use
both normal keyboard characters (*, +, !, ^,
->, =), and symbols established in literature (∧, ∨,
¬, ⊕, →, ≡). If your keyboard does not have the desired
operation symbol, then use the calculator keyboard (if it is not visible, press «Show Keyboard»),
where both all logical operations and a set of the most commonly used variables are available.
To change the order of operations round brackets are used ().
The designations of logical operations
- AND:
&•∧* - OR:
∨+ - NOT:
¬! - Exclusive OR (XOR):
⊕^ - Implication:
->→=> - Equivalence:
=~≡<=> - Schaeffer stroke:
↑| - Pierce Arrow:
↓
What the calculator can do
- Build a truth table of the function
- Build a truth table by a binary vector
- Construct a perfect conjunctive normal form (CNF)
- Construct a perfect disjunctive normal form (DNF)
- Construct the Zhegalkin polynomial (by Pascal, triangle, and undefined coefficients methods)
- Determine whether a function belongs to each of the five Post’s classes
- Build K-Map (Karnaugh Map)
- Minimize CNF and DNF
- Looking for fictitious variables
What is a Boolean function
Boolean function f(x1, x2, ... xn) — is any function of n variables x1, x2, … xn,
in which its arguments take one of two values:
either 0 or 1, and the function itself takes values 0 or 1.
That is, it is a rule by which an arbitrary set of zeros and ones is assigned the value 0 or 1.
Read more about Boolean functions on Wikipedia.
What is a truth table?
Truth table — is a table describing a logical function,
namely reflecting all values of the function for all possible values of its arguments.
The table consists of n+1 columns and 2n rows, where n is the number of variables used.
The first n columns contain all possible values of arguments (variables) of the function,
and the n+1th column contains values of the function that it takes on a given set of arguments.
Quite often there is a variant of the table in which the number of columns is equal to n + the number of logical
operations. In such a table also the first n columns are filled with sets of arguments, and the remaining columns
are filled with values of subfunctions included into the record of the function, which allows to simplify the calculation of the final
value of the function at the expense of already intermediate calculations.
Logical operations
A logical operation is an operation on statements that allows you to make new statements by combining
simpler ones. Conjunction (∧ or &), disjunction (∨ or |) are commonly referred to as basic operations,
implication (→), negation (¬), equivalence (=), exclusive OR (⊕).
Truth table of logical operations
How to set a logic function
There are many ways to specify a Boolean function:
- truth table
- characteristic sets
- value vector
- Gray’s matrix
- formulas
Let’s look at some of them:
To define a function by a vector of values, you must write a vector of 2n zeros and ones,
where n is the number of arguments on which the function depends.
For example, a function of two arguments can be defined as follows: 0001 (AND operation), 0111 (OR operation).
To define a function as a formula, you need to write a mathematical expression consisting of function arguments and logical operations.
For example, we can specify the following function: a∧b ∨ b∧c ∨ a∧c
Ways to represent a Boolean function
You can use formulas to get a huge variety of functions, and with different formulas
you can get the same function. Sometimes it can be very useful to know how to construct a particular function,
using only a small set of given operations, or using as few arbitrary operations as possible.
Let’s look at the basic ways of defining Boolean functions:
- Perfect disjunctive normal form (DNF)
- Perfect conjunctive normal form (CNF)
- Algebraic Normal Form (ANF, Zhegalkin polynomial)
Disjunctive normal form (DNF)
A simple conjunction is a conjunction of some finite set of variables,
or their negations, with each variable occurring no more than once.
A disjunctive normal form (DNF) is a disjunction of simple conjunctions.
A perfect disjunctive normal form (DNF) is a DNF with respect to some given finite set of variables,
each conjunction of which includes all variables of this set.
For example, DNF is the function ¬abc ∨ ¬a¬bc
∨ ac, but it is not a disjunctive normal form because the last conjunction lacks the variable b.
Conjunctive normal form (CNF)
A simple disjunction is a disjunction of one or more variables, or their negations,
with each variable included no more than once.
Conjunctive normal form (CNF) is a conjunction of simple disjunctions.
A perfect conjunctive normal form (CNF) is a CNF with respect to some given finite set of variables,
each disjunction of which includes all variables of this set.
For example, the CNF is the function (a ∨ b) ∧ (a ∨ b ∨ c),
but it is not an SNF because the first disjunction lacks the variable c.
Algebraic Normal Form (ANF, Zhegalkin polynomial)
Algebraic normal form, Zhegalkin polynomial is a form of representation of logical function in the form of polynomial with coefficients of 0 and 1, where conjunction operation is used as product and exclusive OR is used as addition.
Examples of Zhegalkin polynomials: 1, a, a⊕b, ab⊕a⊕b⊕1
Algorithm for constructing an DNF for a Boolean function
- Construct a truth table for the function
- Find all sets of arguments on which the function takes value 1
- Write simple conjunctions for each of the sets according to the following rule: if in a set the variable
takes value 0, it enters the conjunction with negation, otherwise without negation - Combine all simple conjunctions with a disjunction
Algorithm of CNF construction for a Boolean function
- Build a truth table for the function
- Find all sets of arguments on which the function takes the value 0
- Write simple disjunctions for each of the sets according to the following rule: if in a set the variable
takes value 1, it enters the disjunction with negation, otherwise without negation - Combine all simple disjunctions with a conjunction
Algorithm for constructing the Zhegalkin polynomial of a Boolean function
There are several methods of constructing the Zhegalkin polynomial, in this article we will consider the most convenient and simple
of all.
- Construct a truth table for the function
- Add a new column to the truth table and write in 1, 3, 5… cells of the values from the same rows
of the previous column of the truth table, and to the values in lines 2, 4, 6… add modulo two
values from correspondingly 1, 3, 5… lines. - Add a new column to the truth table and overwrite the values of 1, 2, 5, 6, 9, 10…
lines, and to 3, 4, 7, 8, 11, 12… lines add the overwritten values similarly to the previous point. - Repeat each time doubling the number of transferred and added elements until the length equals the number of rows in the table.
- Write out Boolean sets where the value of the last column is one
- Write the names of variables corresponding to the set instead of the ones in the sets (for the zero set write
one) and join them using the exclusive OR operation.
Examples of constructing different representations of logical functions
Let us construct perfect disjunctive and disjunctive normal forms and the Zhegalkin polynomial
for the function of three variables F = ¬ab∨¬bc∨ca
1. Let’s build a truth table for the function
Construction of a perfect disjunctive normal form:
Let’s find the sets on which the function takes a true value: { 0, 0, 1 } { 0, 1, 0 }
{ 0, 1, 1 } { 1, 0, 1 } { 1, 1, 1 }
Let us match the found sets with elementary conjunctions for all variables, and if a variable
in the set takes value 0, it will be written with negation:
K1: { 0, 0, 1 } — ¬a¬bc
K2: { 0, 1, 0 } — ¬ab¬c
K3: { 0, 1, 1 } — ¬abc
K4: { 1, 0, 1 } — a¬bc
K5: { 1, 1, 1 } — abc
Combine conjunctions using disjunction and get a perfect disjunctive normal form:
K1 ∨ K2 ∨ K3 ∨ K4 ∨ K5 = ¬a¬bc ∨ ¬ab¬c ∨ ¬abc ∨ a¬bc ∨ abc
Construction of a perfect conjunctive normal form:
Find the sets on which the function takes a false value: { 0, 0, 0 } { 1, 0, 0 }
{ 1, 1, 0 }
Let us match the found sets with elementary disjunctions for all variables, and if a variable
in the set takes value 1, it will be written with negation:
D1: { 0, 0, 0 } — a∨b∨c
D2: { 1, 0, 0 } — ¬a∨b∨c
D3: { 1, 1, 0 } — ¬a∨¬b∨c
Combine disjunctions with conjunctions and obtain a perfect conjunctive normal form:
D1 ∧ D2 ∧ D3 = (a∨b∨c) ∧ (¬a∨b∨c)
∧ (¬a∨¬b∨c)
Construction of the Zhegalkin polynomial:
Add a new column to the truth table and write in lines 1, 3, 5, and 7 the values from the same lines
in the previous column of the truth table, and add the values in lines 2, 4, 6 and 8 modulo 2 with the values
from lines 1, 3, 5, and 7 correspondingly:
Add a new column to the truth table and write in lines 1 and 2, 5 and 6 the values from the same lines
of the previous column in the truth table, and add the values in lines 3 and 4, 7 and 8 modulo 2 with the values
from lines 1 and 2, 5 and 6 correspondingly:
Add a new column to the truth table and write in rows 1, 2, 3, and 4 the values from the same rows of the previous
column of the truth table, and add the values in lines 5, 6, 7 and 8 modulo 2 with the values from
correspondingly in lines 1, 2, 3, and 4:
The final result is the following table:
Write out the sets, on which the resulting vector takes a unit value, and instead of the units in the sets write
the names of variables corresponding to the set (for the zero set write one):
{ 0, 0, 1 } — c, { 0, 1, 0 } — b, { 0, 1, 1 } —
bc, { 1, 1, 0 } — ab, { 1, 1, 1 } — abc
Combining these conjunctions using the exclusive or operation, we obtain the Zhegalkin polynomial:
c⊕b⊕bc⊕ab⊕abc
Построение таблицы истинности. СДНФ. СКНФ. Полином Жегалкина.
Онлайн калькулятор позволяет быстро строить таблицу истинности для произвольной булевой функции или её вектора, рассчитывать совершенную дизъюнктивную и совершенную конъюнктивную нормальные формы, находить представление функции в виде полинома Жегалкина, строить карту Карно и классифицировать функцию по классам Поста.
Калькулятор таблицы истинности, СКНФ, СДНФ, полинома Жегалкина
введите функцию или её вектор
Скрыть клавиатуру
∨
∧
¬
⊕
→
≡
↓
↑
0
1
a
b
c
x
y
z
(
)
X1
X2
X3
X4
X5
X6
Показать настройки
Таблица истинности
СКНФ
СДНФ
Полином Жегалкина
Классификация Поста
Минимизация, карта Карно
Фиктивные переменные
С решением
Построить
Построено таблиц, форм:
Как пользоваться калькулятором
- Введите в поле логическую функцию (например, x1 ∨ x2) или её вектор (например, 10110101)
- Укажите действия, которые необходимо выполнить с помощью переключателей
- Укажите, требуется ли вывод решения переключателем «С решением»
- Нажмите на кнопку «Построить»
Видеоинструкция к калькулятору
Используемые символы
В качестве переменных используются буквы латинского и русского алфавитов (большие и маленькие), а также цифры, написанные после буквы (индекс переменной). Таким образом, именами переменных будут: a, x, a1, B, X, X1, Y1, A123 и так далее.
Для записи логических операций можно использовать
как обычные символы клавиатуры (*, +, !, ^, ->, =), так и символы, устоявшиеся в литературе (∧, ∨, ¬, ⊕, →, ≡). Если на вашей клавиатуре отсутствует нужный символ операции, то используйте клавиатуру калькулятора (если она не видна, нажмите «Показать клавиатуру»), в которой доступны как все логические операции, так и набор наиболее часто используемых переменных.
Для смены порядка выполнения операций используются круглые скобки ().
Обозначения логических операций
- И (AND):
&•∧* - ИЛИ (OR):
∨+ - НЕ (NOT):
¬! - Исключающее ИЛИ (XOR):
⊕^ - Импликация:
->→=> - Эквивалентность:
=~≡<=> - Штрих Шеффера:
↑| - Стрелка Пирса:
↓
Что умеет калькулятор
- Строить таблицу истинности по функции
- Строить таблицу истинности по двоичному вектору
- Строить совершенную конъюнктивную нормальную форму (СКНФ)
- Строить совершенную дизъюнктивную нормальную форму (СДНФ)
- Строить полином Жегалкина (методами Паскаля, треугольника, неопределённых коэффициентов)
- Определять принадлежность функции к каждому из пяти классов Поста
- Строить карту Карно
- Минимизировать ДНФ и КНФ
- Искать фиктивные переменные
Что такое булева функция
Булева функция f(x1, x2, ... xn) — это любая функция от n переменных x1, x2, … xn, в которой её аргументы принимают одно из двух значений: либо 0, либо 1, и сама функция принимает значения 0 или 1. То есть это правило, по которому произвольному набору нулей и единиц ставится в соответствие значение 0 или 1. Подробнее про булевы функции можно посмотреть на Википедии.
Что такое таблица истинности?
Таблица истинности — это таблица, описывающая логическую функцию, а именно отражающую все значения функции при всех возможных значениях её аргументов. Таблица состоит из n+1 столбцов и 2n строк, где n — число используемых переменных. В первых n столбцах записываются всевозможные значения аргументов (переменных) функции, а в n+1-ом столбце записываются значения функции, которые она принимает на данном наборе аргументов.
Довольно часто встречается вариант таблицы, в которой число столбцов равно n + число используемых логических операций. В такой таблице также первые n столбцов заполнены наборами аргументов, а оставшиеся столбцы заполняются значениями подфункций, входящих в запись функции, что позволяет упростить расчёт конечного значения функции за счёт уже промежуточных вычислений.
Логические операции
Логическая операция — операция над высказываниями, позволяющая составлять новые высказывания путём соединения более простых. В качестве основных операций обычно называют конъюнкцию (∧ или &), дизъюнкцию (∨ или |), импликацию (→), отрицание (¬), эквивалентность (=), исключающее ИЛИ (⊕).
Таблица истинности логических операций
Как задать логическую функцию
Есть множество способов задать булеву функцию:
- таблица истинности
- характеристические множества
- вектор значений
- матрица Грея
- формулы
Рассмотрим некоторые из них:
Чтобы задать функцию через вектор значений необходимо записать вектор из 2n нулей и единиц, где n — число аргументов, от которых зависит функция. Например, функцию двух аргументов можно задать так: 0001 (операция И), 0111 (операция ИЛИ).
Чтобы задать функцию в виде формулы, необходимо записать математическое выражение, состоящее из аргументов функции и логических операций. Например, можно задать такую функцию: a∧b ∨ b∧c ∨ a∧c
Способы представления булевой функции
С помощью формул можно получать огромное количество разнообразных функций, причём с помощью разных формул можно получить одну и ту же функцию. Иногда бывает весьма полезно узнать, как построить ту или иную функцию, используя лишь небольшой набор заданных операций или используя как можно меньше произвольных операций. Рассмотрим основные способы задания булевых функций:
- Совершенная дизъюнктивная нормальная форма (СДНФ)
- Совершенная конъюнктивная нормальная форма (СКНФ)
- Алгебраическая нормальная форма (АНФ, полином Жегалкина)
Совершенная дизъюнктивная нормальная форма (ДНФ)
Простая конъюнкция — это конъюнкция некоторого конечного набора переменных, или их отрицаний, причём каждая переменная встречается не более одного раза.
Дизъюнктивная нормальная форма (ДНФ) — это дизъюнкция простых конъюнкций.
Совершенная дизъюнктивная нормальная форма (СДНФ) — ДНФ относительно некоторого заданного конечного набора переменных, в каждую конъюнкцию которой входят все переменные данного набора.
Например, ДНФ является функция ¬abc ∨ ¬a¬bc ∨ ac, но не является СДНФ, так как в последней конъюнкции отсутствует переменная b.
Совершенная конъюнктивная нормальная форма (КНФ)
Простая дизъюнкция — это дизъюнкция одной или нескольких переменных, или их отрицаний, причём каждая переменная входит в неё не более одного раза.
Конъюнктивная нормальная форма (КНФ) — это конъюнкция простых дизъюнкций.
Совершенная конъюнктивная нормальная форма (СКНФ) — КНФ относительно некоторого заданного конечного набора переменных, в каждую дизъюнкцию которой входят все переменные данного набора.
Например, КНФ является функция (a ∨ b) ∧ (a ∨ b ∨ c), но не является СДНФ, так как в первой дизъюнкции отсутствует переменная с.
Алгебраическая нормальная форма (АНФ, полином Жегалкина)
Алгебраическая нормальная форма, полином Жегалкина — это форма представления логической функции в виде полинома с коэффициентами вида 0 и 1, в котором в качестве произведения используется операция конъюнкции, а в качестве сложения — исключающее ИЛИ.
Примеры полиномов Жегалкина: 1, a, a⊕b, ab⊕a⊕b⊕1
Алгоритм построения СДНФ для булевой функции
- Построить таблицу истинности для функции
- Найти все наборы аргументов, на которых функция принимает значение 1
- Выписать простые конъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 0, то она входит в конъюнкцию с отрицанием, а иначе без отрицания
- Объединить все простые конъюнкции с помощью дизъюнкции
Алгоритм построения СКНФ для булевой функции
- Построить таблицу истинности для функции
- Найти все наборы аргументов, на которых функция принимает значение 0
- Выписать простые дизъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 1, то она входит в дизъюнкцию с отрицанием, а иначе без отрицания
- Объединить все простые дизъюнкции с помощью конъюнкции
Алгоритм построения полинома Жегалкина булевой функции
Есть несколько методов построения полинома Жегалкина, в данной статье рассмотрим наиболее удобный и простой из всех.
- Построить таблицу истинности для функции
- Добавить новый столбец к таблице истинности и записать в 1, 3, 5… ячейки значения из тех же строк предыдущего столбца таблицы истинности, а к значениям в строках 2, 4, 6… прибавить по модулю два значения из соответственно 1, 3, 5… строк.
- Добавить новый столбец к таблице истинности и переписать в новый столбец значения 1, 2, 5, 6, 9, 10… строк, а к 3, 4, 7, 8, 11, 12… строкам аналогично предыдущему пункту прибавить переписанные значения.
- Повторить действия каждый раз увеличивая в два раза количество переносимых и складываемых элементов до тех пор, пока длина не станет равна числу строк таблицы.
- Выписать булевы наборы, на которых значение последнего столбца равно единице
- Записать вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора записать единицу) и объединить их с помощью операции исключающего ИЛИ.
Примеры построения различных представлений логических функций
Построим совершенные дизъюнктивную и дизъюнктивную нормальные формы, а также полином Жегалкина для функции трёх переменных F = ¬ab∨¬bc∨ca
1. Построим таблицу истинности для функции
Построение совершенной дизъюнктивной нормальной формы:
Найдём наборы, на которых функция принимает истинное значение: { 0, 0, 1 } { 0, 1, 0 } { 0, 1, 1 } { 1, 0, 1 } { 1, 1, 1 }
В соответствие найденным наборам поставим элементарные конъюнкции по всем переменным, причём если переменная в наборе принимает значение 0, то она будет записана с отрицанием:
K1: { 0, 0, 1 } — ¬a¬bc
K2: { 0, 1, 0 } — ¬ab¬c
K3: { 0, 1, 1 } — ¬abc
K4: { 1, 0, 1 } — a¬bc
K5: { 1, 1, 1 } — abc
Объединим конъюнкции с помощью дизъюнкции и получим совершенную дизъюнктивную нормальную форму:
K1 ∨ K2 ∨ K3 ∨ K4 ∨ K5 = ¬a¬bc ∨ ¬ab¬c ∨ ¬abc ∨ a¬bc ∨ abc
Построение совершенной конъюнктивной нормальной формы:
Найдём наборы, на которых функция принимает ложное значение: { 0, 0, 0 } { 1, 0, 0 } { 1, 1, 0 }
В соответствие найденным наборам поставим элементарные дизъюнкции по всем переменным, причём если переменная в наборе принимает значение 1, то она будет записана с отрицанием:
D1: { 0, 0, 0 } — a∨b∨c
D2: { 1, 0, 0 } — ¬a∨b∨c
D3: { 1, 1, 0 } — ¬a∨¬b∨c
Объединим дизъюнкции с помощью конъюнкции и получим совершенную конъюнктивную нормальную форму:
D1 ∧ D2 ∧ D3 = (a∨b∨c) ∧ (¬a∨b∨c) ∧ (¬a∨¬b∨c)
Построение полинома Жегалкина:
Добавим новый столбец к таблице истинности и запишем в 1, 3, 5 и 7 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 2, 4, 6 и 8 сложим по модулю два со значениями из соответственно 1, 3, 5 и 7 строк:
Добавим новый столбец к таблице истинности и запишем в 1 и 2, 5 и 6 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 3 и 4, 7 и 8 сложим по модулю два со значениями из соответственно 1 и 2, 5 и 6 строк:
Добавим новый столбец к таблице истинности и запишем в 1 2, 3 и 4 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 5, 6, 7 и 8 сложим по модулю два со значениями из соответственно 1, 2, 3 и 4 строк:
Окончательно получим такую таблицу:
Выпишем наборы, на которых получившийся вектор принимает единичное значение и запишем вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора следует записать единицу):
{ 0, 0, 1 } — c, { 0, 1, 0 } — b, { 0, 1, 1 } — bc, { 1, 1, 0 } — ab, { 1, 1, 1 } — abc
Объединяя полученные конъюнкции с помощью операции исключающего или, получим полином Жегалкина: c⊕b⊕bc⊕ab⊕abc
Онлайн всего: 1
Гостей: 1
Пользователей: 0
Главная » Примеры решения задач » Онлайн калькулятор
Логические выражения |
|
Калькулятор для нахождения сокращенных дизъюнктивных нормальных форм ( ДНФ ) , минимальных конъюнктивных нормальных форм ( КНФ ), составления таблицы истинности и построение диаграммы Эйлера-Венна множеств (бесплатно). Множества или выражения обозначаем большими буквами латинского алфавита A,B,C,D и т.д. A’ — штрихом обозначаем дополнения множеств (в данном случае дополнение множества A) && — конъюнкция ( логическое «И» ) || — дизъюнкция ( логическое «ИЛИ» ) ! — отрицание (ставим впереди выражения, пример !A) cap — пересечение множеств cup — объединение множеств (сложение множеств) A&!B — обозначаем разность множеств A∖B=A-B A=>B — импликация «Если …., то» A<=>B — эквивалентность |
Поможем с решением ваших задач и контрольных! |
Категория: Онлайн калькулятор | Просмотров: 455092 | Добавил: Admin | Теги: логические выражения, онлайн калькулятор | Рейтинг: 2.8/91 |
Решение
$$b wedge c wedge neg a$$
$$b wedge c wedge neg a$$
Таблица истинности
+---+---+---+--------+ | a | b | c | result | +===+===+===+========+ | 0 | 0 | 0 | 0 | +---+---+---+--------+ | 0 | 0 | 1 | 0 | +---+---+---+--------+ | 0 | 1 | 0 | 0 | +---+---+---+--------+ | 0 | 1 | 1 | 1 | +---+---+---+--------+ | 1 | 0 | 0 | 0 | +---+---+---+--------+ | 1 | 0 | 1 | 0 | +---+---+---+--------+ | 1 | 1 | 0 | 0 | +---+---+---+--------+ | 1 | 1 | 1 | 0 | +---+---+---+--------+
$$b wedge c wedge neg a$$
$$b wedge c wedge neg a$$
Уже приведено к КНФ
$$b wedge c wedge neg a$$
Уже приведено к ДНФ
$$b wedge c wedge neg a$$
Калькулятор
Метод Квайна
В основе две операции:
где под p понимается некоторая элементарная конъюнкция.
Теорема.
Если в СДНФ какой-либо переключательной функции выполнить все возможные операции неполного попарного склеивания и элементарного поглощения, то в результате получится СкДНФ(сокращенная дизъюнктивная нормальная форма), эквивалентная исходной функции.
Итерационый алгоритм. Задача в нахождении по полной системе импликант (конституэнт единицы) полной системы простых импликант.
Алгоритм:
- Исходным является множество конституэнт единицы функции — импликанты нулевого ранга.
- Выполняются все возможные операции неполного попарного склеивания для элементарных конъюнкций длины n. (где n-кол-во аргументов).
Согласно соотношениям «a.» и «b.» результат — дополнительная импликанта p.
- Выполняются все возможные операции элементарного поглощения для элементарных конъюнкций длины n-1. (общая часть «p» имеет длину n-1)
- В результате получилось множество элементарных конъюнкций, разделяемых на два подмножества(по длине):
- подмножество элементарных конъюнкций длины n (оставшиеся)
- подмножество элементарных конъюнкций длины n-1
Элементарные конъюнкции длины n не участвовали в склеивания, а, следовательно, и в поглощении (т.к. поглощаются собственной частью те, которые участвовали в склеивании).
Следовательно, подмножество элементарных конъюнкций длины n входит в множество простых импликант (импликант нулевого ранга). - Если множество элементарных конъюнкций длины n-1 не пусто, то выполняются шаги со второго для конъюнкций длины n-1 и т.д.
Алгоритм завершается, когда подмножество является пустым, либо нельзя выполнить ни одной операции неполного попарного склеивания.
Таким образом, получаем систему простых импликант функции.
Нахождение тупиковых ДНФ
Стратегическая задача нахождения приведенной системы простых импликант заключается в нахождении наилучших покрытий единиц функции простыми импликантами.
Для системы простых импликант для заданной функции может быть получено несколько приведенных систем. Следует считать, что среди них есть такая, которая дает тупиковую нормальную форму минимальной длины.
Алгоритм нахождения приведенных систем простых импликант также является переборным. Задача в том, чтобы обеспечить направленный перебор. Для этого алгоритм строится в виде итерационной процедуры, которая содержит следующие шаги:
- Находятся такие единицы функции, которые покрываются только какой-то одной импликантой из системы простых импликант (для каждой единицы считаем сколько ее покрывает импликант и отмечаем их).
Этим импликанты образуют, так называемое, ядро функции. Такие импликанты будут входить в приведенную систему простых импликант. Следовательно, конъюнкции будут входить во все ТДНФ( в том числе минимальные).
- Исключаются из рассмотрения все единицы функции, покрываемые ядром.
- Осталось множество непокрытых ядром единицы функции и множество простых импликант, которые не вошли в ядро.
Повторяем шаг 1 и шаг 2 для оставшихся множеств (находится псевдоядро). Но перед повторением должен быть дополнительный шаг, который уменьшает перебор. (выкидываем из тех, которые покрывают одни и те же единицы(из оставшихся) ту импликанту, которая имеет наибольшую длину)
И так далее до тех пор, пока не будут покрыты все единицы функции.
Велика вероятность, что на каком-то шаге не найдется ни одной единицы функции, которая покрывается одной импликантой. В этом случае ищется наилучшее (наименьшей длины) покрытие оставшихся единиц функции методом перебора:
Если единица функции покрывается импликантами A,B,C,…
- Пусть A входит в ТДНФ, а B,C,… нет.
- Пусть В входит в ТДНФ, а A,C,… нет.
- Пусть C входит в ТДНФ, а A,B,… нет.
- …
Таким образом, получаем множество ТДНФ. Затем выбираем из них ДНФ наименьшей длины — получаем {МДНФ}.
Пример минимизации переключательной функции методом Квайна
Функция задана вектором: 883F. Запишем 16-ричное число 883F в двоичной виде в столбец значений функции таблицы истинности.
| Набор> | Значение исходной функции | Набор> | Значение исходной функции |
| 0000 | 1 | 1000 | 0 |
| 0001 | 0 | 1001 | 0 |
| 0010 | 0 | 1010 | 1 |
| 0011 | 0 | 1011 | 1 |
| 0100 | 1 | 1100 | 1 |
| 0101 | 0 | 1101 | 1 |
| 0110 | 0 | 1110 | 1 |
| 0111 | 0 | 1111 | 1 |
Цена ДНФ является суммой длин всех входящих в нее конъюнкций.
Минимизация функции методом Квайна.
На данном шаге все импликанты участвовали в операциях попарного неполного склеивания и были поглощены своими собственными частями. Поэтому простые импликанты на этом шаге не получены.
В результате на данном шаге получаем простые импликанты: ,
В результате на данном шаге получаем простые импликанты: ,
СкДНФ: v
v
v
Нахождение тупиковых форм.
Обозначения:
- Единицы ДНФ, покрываемые импликантами СкДНФ, обозначаются «+».Импликанты, попадающие в ядро помечаются «*».
- Единицы функции, которые покрываются только какой-то одной импликантой из системы простых импликант, помечаются “>”.
- Единицы функции, покрываемые ядром, но не покрываемые только какой-то одной импликантой из системы простых импликант, помечаются “>>”.
| > |
>> |
> |
> |
>> |
> |
>> |
>> |
|
| + | + | |||||||
| + | + | |||||||
| + | + | + | + | |||||
| + | + | + | + |
Ядро: v
v
МДНФ: v
v
, цена=7
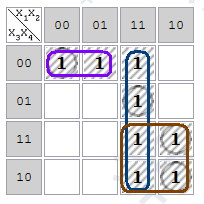
Графический метод минимизации — Карты Карно
Карты Карно — это графическое представление операций попарного неполного склеивания и элементарного поглощения.
Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции.
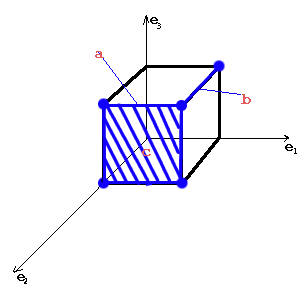
Карты Карно — определенная плоская развертка n-мерного булева куба.
Строится таблица истинности функции определенным образом. Каждая клетка таблицы соответствует вполне определенной вершине булева куба. Нулевые значения не записываются.
Карта Карно для функции 4-х переменных:
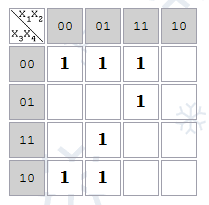
Карта Карно рассматривается как поверхность фигуры под названием тор («бублик»).
p-клетки — клетки карты Карно, соответствующие единичному значению функции.
Соседние наборы — наборы, которые различаются только одним аргументом (одной орбитой).
Любой паре соседних наборов в Карте Карно соответствуют соседние клетки.
Две соседние p-клетки на карте Карно дают импликанту первого ранга. Например, клетки 1100 и 1101 отличаются только значением переменной x3, следовательно, они дают импликанту 1
2
4.
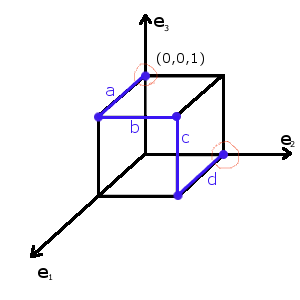
Две соседние импликанты первого ранга образуют импликанту второго ранга.
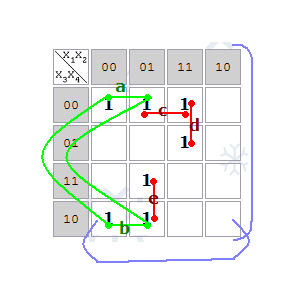
На этой карте соседние клетки образуют импликанты a,b,c,d,e. При этом импликанты a и b являются соседними, поэтому они образуют импликанту второго ранга.
Если функция имеет 5 переменных, то рисуются 2 Карты Карно: для x5=0 и для x5=1. Если 6 переменных — 4 Карты, так чтобы в соседних картах соседние клетки имели одинаковые координаты:
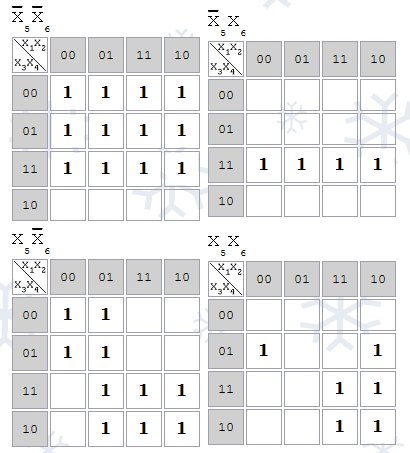
Соседние p-клетки, соответствующие импликанте образуют компактную группу.
Количество p-клеток в компактной группе является степенью двойки.
Задача минимизации переключательной функции с помощью карт Карно заключается в нахождении импликант высшего ранга (соответствующих компактным группам наибольшей размерности), покрывающих p-клетки функции наилучшим образом.
Если на картах Карно выделить все компактные группы наибольшей размерности, то дизъюнкция соответствующих конъюнкций даст СкДНФ.
Пример минимизации функции 4-х переменных методом Карт Карно
Компактных групп размера 4 — 2
Компактных групп размера 2 — 2
Нахождение тупиковых форм.
Обозначения:
Цветом выделены компактные группы наибольшей размерности, вошедшие в ядро.
Ядро: v
v
МДНФ: v
v
, цена=7
Машинно-ориентированные методы минимизации переключательных функций.
Основаны на применении соответствующих алгебр(или соответствующих алгебраический преобразований).
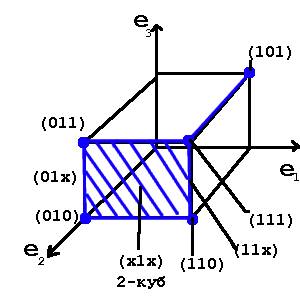
Вопрос 1. Интервальная форма задания функции. Постановка задачи минимизации.
Геометрический представление: (отображение функции на n-мерный булев куб)
Любому набору значений аргументов соответствует элементарная конъюнкция, содержащая все эти переменные — конституента единицы.
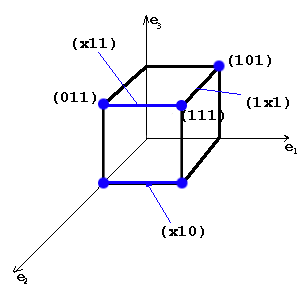
Те вершины n-мерного булева куба, в которых функция принимает единичное значение называются 0-кубами.
Два 0-куба образуют 1-куб, если соответствующие булевы вектора(их координаты) отличаются между собой значением только одной координаты(или одной компоненты). Эти координаты носят название свободной координаты. Обозначение x, остальные координаты 0-куба называются связанными и имеют либо 1, либо 0 значение. 0-кубы, образующие 1-куб называются его гранями. Два 1-куба образуют 2-куб, если свободная координата у них одинакова и они различаются значением только одной связанной компоненты.( 1-кубы — грани соответствующего 2-куба).
…
И так далее до n-куба( в случае тавтологии).
В общем случае, r-куб-это такой куб в булевом пространстве, у которого r свободных компонент и n-r связанных компонент.
Пример:
(1x1xx1) — 3-куб
(1x1x01),(1x1x11)- два 2-куба. Они являются гранями этого 3-куба(образуют его).
Если для какой-то функции взять все возможные кубы одинаковой размерности, то получаем множество кубов(или комплекс кубов).
Kr(f) — комплекс r-кубов функции f/
Для некоторой функции всегда есть комплекс
(Если Kn(f) содержит куб, то f — константа 1
оператор граней:
Cr=(a1a2…an-1an)-куб,
где a∈{0,1,x}, тогда для этого куба можно вычислить грани этого куба. Грани куба:
| ∂ip(a1a2…an-1an)= | a1a2…ai-1 p ai+1…an-1an, ai=x, p∈{0;1} | |
| ∅, ai ≠ x |
где C-получаемый куб.
При ai=x есть две грани (вместо i-ой либо 0, либо 1).
Оператор сограней
позволяет вычислить куб большей размерности, гранью которого может быть этот куб.
| δi(a1a2…an-1an)= | a1a2…ai-1 x ai+1…an-1an, ai≠x, Cr+1⊆K(f) | |
| ∅, ai=x, Cr+1⊄K(f) |
Подмножество вершин булева куба, соответствующие кубу размерности r называется интервалом булева пространства ранга r. (интервал 1 ранга — 1×1, интервал 2 ранга — x1x)
Для нашего примера:
K0(f)={101,110,111,010,011}
K1(f)={01x,11x,1×1,x11,x10}
K2(f)={x1x}
В общем случае комплекс кубов определенного ранга не является покрытием исходной функции(за исключением K0).
В нашем примере K2 не является покрытием, хотя K1 — покрытие.
K(f)=K0∪K1∪K2 — для нашей функции
Куб большей размерности покрывает кубы меньшей размерности, если они могут быть получены из него последовательным применением оператора граней.
(x1x) имеет грани (01x) и (11x), которые имеют грани : (010),(011) и (110),(111)
Если взять интервал булева пространства, то аналитически его можно описать в виде соответствующих элементарных конъюнкций.
Некоторый комплекс кубов — L, таких, что каждая вершина из комплекса K0(f) включена по крайней мер в один из кубов комплекса L, называется покрытием комплекса K функции f.
Каждое покрытие комплекса K(f) определяет некоторую ДНФ переключательной функции.
Покрытие можно рассматривать (с точки зрения реализации), как двухуровневую схему.
| Аргументы (0-ой уровень) | конъюнктивные члены(элементарные конъюнкции) (1-ый уровень) | дизъюнкция (2-ой уровень) |
Не учитывается инверсия аргументов на нулевом уровне.
Минимизация
Цена r-куба: c=n-r — число связанных переменных, количество символов в элементарной конъюнкции(совпадает с ценой в смысле Квайне)
—цена покрытия, где qr-количество кубов размерности r в покрытии L.
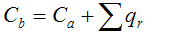
Задача минимизации: Найти такое покрытие L комплекса K(f), цена которого будет минимальна — минимизация в смысле Квайне.
Задача решается алгебраически, вводится свой математический аппарат. Это аппарат исчисления кубических комплексов (задает операции над кубами).
Каждая операция проходит в два этапа:
I Этап. Предварительное вычисление путем покоординатной обработки кубов по правилам, задаваемым с помощью таблиц покоординатной обработки.
II Этап. Окончательный.
Зададим операции над кубами:
a = (a1 a2 … an)
b = (b1 b2 … bn)
- Операция *: c=a*b
По содержанию * — это нахождение куба некоторой размерности r, грани которого содержаться в кубах a и b.
ci=ai*bi 0 1 x 0 0 y 0 1 y 1 1 x 0 1 x a*b = ∅, если ∑αici>1 c, если ∑αici≤1 где αici = 0, ci≠y 1, ci=y c = ([a1*b1] … [an*bn]).
При чем, если результат операции — y, то y заменяется на x.
(101)*(111)
после предварительной обработки:
=(1y1)
Окончательный вариант:
=(1×1)(x11)*(101)=(1×1)
(x10) (101) (1yy) ∅ — нет общих граней - Операция пересечения кубов.
c = a ∩ b
покоординатно!
ci=ai∩bi 0 1 x 0 0 ∅ 0 1 ∅ 1 1 x 0 1 x a ∩ b = ∅, если ∃i (ai∩bi = ∅ c в противном случае Пересечение — нахождение общей части булева пространства, покрываемой этими кубами (т.е. куба или грани какого-то уровня)
(1×1)∩(x1x)=(111) - Операция вычитания кубов (#).
ci=ai#bi 0 1 x 0 z y z 1 y z z x 1 0 z * и ∪ обладают свойством коммутативности, но a#b ≠ b#a !
Операция вычитания кубов удаляет из куба a общую часть кубов уменьшаемого и вычитаемого (т.е. пересечение кубов a и b).
В результате вычитания можем иметь несколько кубов.
Если куб a входит в куб b, то результат — ∅
Пример:
a#b = (1×1)#(x11) = (z0z) = (101)
c#b = (1xx)#(x11) = (z00) = {(10x),(1×0)}
Нахождение множества простых импликант
K(f)=K0∪K1∪…∪Ki∪…∪Kn-1 — комплекс K функции f
z⊆K является простой импликантой этого комплекса, если δi(z)=∅ (δi — оператор сограней), то есть не существует какого-либо другого куба, который бы включал в себя исходный куб z.
Z(f)={z} — множество импликант для функции f
Необходимо получить весь комплекс K функции f, используя операторы граней и сограней.
Берем куб z из K и проверяем, есть ли какой-то куб, гранью которого является рассматриваемый.
Операция *(«звездочка») позволяет получить множество Z — кубов, соответствующих простым импликантам функции.
Алгоритм (*) — нахождение множества кубов, соответствующих простым импликантам функции.
Предположим есть некоторый комплекс Ĉ0, являющийся покрытием комплекса K(f), т.е.
- Ĉ0(f) — неупорядоченное покрытие
причем одна и та же единица функции может покрываться несколькими кубами - C0 = Ĉ0 — {c1 | c1 ∈ Ĉ0 ∧ c2 ∈ Ĉ0 ∧ c1 ⊆ c2}
(тоже, что и поглощение в методе Квайне) - C0*C0 попарно
- в результате 3) находится множество 0-кубов:
Z0 = { c0 | c0 * C0 не содержит никаких 1-кубов }
— это такие кубы, которые в результате операции * не дают никаких 1-кубов - вычисляется Ĉ1:
Ĉ1 = C0 ∪ (C0*C0) - C1 = Ĉ1 — { c | c ⊆ d, c,d∈Ĉ1 } — {0-кубы, получившиеся в результате операции *, и Z0}
( (1×1)*(x11)= (111) ) - C1 * C1
- Z1
- Ĉ2
- C2 (удаляем 0-кубы и 1-кубы)
и так далее (итерационный процесс)
Ĉ0(f) — исходное покрытие K(f)
C1(f) и т.д. в общем случае покрытием функции не являются
C1(f) ∪ Z0 ⊆ K — является покрытием K(f)
Алгоритм заканчивается, когда на каком-то шаге получаем множество C, содержащее один куб.
Результат — множество Z — множество простых импликант.
Z = ∪Zi
Алгоритм извлечения
ИЗ множества простых импликант извлечь те (выбрать такое подмножество кубов) простые импликанты, которые:
- Является покрытием исходного множества кубов функции;
- С минимальной ценой покрытия, если покрытий несколько.
Для решения этой задачи исходные данные фактически — исходный комплекс функции, то есть некоторый исходный комплекс K0(f) и Z(f).
Определение: возьмем некоторую вершину d∈K0. Говорят, что эта вершина является обособленной вершиной комплекса на множестве простых импликант Z, если существует такой куб z∈Z, что вершина d накрывается только этой импликантой z.
Такая импликанта будет простая. Вершина d называется различающей. А импликанта получила название экстремаль.
Любое минимальное покрытие содержит экстремали нулевого ранга.
Пример:
Различающие вершины: (0;0;1) и (0;1;0)
E0={ a, d}, осталось покрыть одну вершину — (1;1;1)
Задача минимизации: необходимо найти все обособленные вершины и выделить импликанты, накрывающие эти обособленные вершины.
Такие импликанты образуют множество экстремалей.
Задача решается, если известно K0(f), то есть все вершины.
В общем случае задачи минимизации функция задана некоторым комплексом K(f), который состоит не только из 0-кубов. Тогда можно найти все 0-кубы и решить задачу, а можно и не находить.
- Некоторая простая импликанта e∈Z является экстремалью, если e∩K ≠ e∩U'(e,Z)∩K, а e∩K ≠ ∅,
U'(e,Z) = U(e,Z) — e,
U(e,Z) = { z | z∈Z, Z∩e ≠ ∅}.
Z — множество простых импликант,
U(e,Z) — окрестность куба e, т.е. все простые импликанты из Z, которые имеют общие части с импликантой e.
U'(e,Z) — окрестность без самой импликанты.Функция может быть не полностью определена:
L — комплекс, где функция определена и равна 1,
D — комплекс, где значение функции не определено,
тогда K=L∪D.
но чаще экстремали вычисляют по одному соотношению:
- [e#(Z-e)]∩K≠∅
e#(Z-e) — те вершины булева куба, которые накрываются только e и не накрываются всех оставшейся частью Z.
+ эти вершины присутствуют в комплексе K (или L для неполностью определенной функции)Если из простой импликанты e удалить все подкубы (Z-e), и остается, по крайней мере, одна вершина булева куба, которая содержится в исходном комплексе функции, то оставшиеся вершины является выделенными, или отмеченными.
Алгоритм нахождения экстремалей также итерационный.
Нахождение множества экстремалей
- Каждая простая импликанта проверяется на наличие в ней выделенной вершины, т.е. вычисляется e#(Z-e), если результат вычитания кубов не пустой, то такая импликанта может быть экстремалью.
Как правило, вычитание e#(Z-e) сводится в таблицу.
- Каждый кандидат на экстремаль проверяется на пересечение с комплексом единичных значений функции.
Если результат пересечения не пустой, значит в L (комплексе единичных значений) имеются обособленные вершины, а e является экстремалью.
Получаем множество экстремалей нулевого ранга — E0 = {e}. В смысле Квайна оно соответствует ядру функции.
- Находим
1 = Z0 — E0
Т.е. из множества простых импликант удаляем множество экстремалей нулевого ранга.
Находим L1 = L0 # E0, т.е. находятся все вершины, не покрытые экстремалями.
1 — оставшаяся часть множества простых импликант, неупорядоченное множество простых импликант.
Операция, которая позволяет сократить в последующем перебор и исключить из
i не максимальные кубы — упорядочивание.
Пусть u∈
1, v∈
1. Говорят, что u1 удовлетворяет условию u∩L1 ⊆ v∩L1.
( вершины из L1, покрываемые u, покрываются и кубов v )В этом случае из кубов u,v выбираем при упорядочивание куб v.
Если кубы разной размерности, а вершины покрывают одинаковые — то оставляем куб большей размерности ( цена = n — r ).
Таким образом,
1 => Z1 (находится Z1 — упорядоченной множество оставшихся простых импликант), применением процедуры упорядочивания.
- Остались Z1 и L1
(Z1,L1) => E1 по тому же алгоритму.
Затем
2 => Z2; L2 = L1#E1; (Z2,L2) => E2 и т.д.
Два варианта окончания алгоритма:
- L = ∅ => покрытие единственное
E = ∪Ei - L ≠ ∅ Если проверка на экстремальность не дает результата, т.е. ни одна простая импликанта не содержит квазеопорных вершин, а операция упорядочивания не дает результата.
Пример:
В этом случае не остается никакого другого варианта решения, кроме волюнтаристского.
Берется любая простая импликанта, для которой выдвигается две гипотезы (Алгоритм ветвления):
- простая импликанта входит в минимальное покрытие
e∈E
находим Li+1=Li#{e}, упорядочиваем Z и вновь применяем алгоритм извлечения (возможно еще ветвление). - простая импликанта не входит в минимальное покрытие
e∉E
удаляем e из Zi (находимi+1), упорядочиваем
i+1 => Zi+1
Li+1 = Li
И применяем алгоритм извлечения.
Таким образом, при ветвление получаем множество покрытий, сравниваем по цене и выбираем наименьшей.
- простая импликанта входит в минимальное покрытие
Все вычисления в ручном варианте сводятся к вычислениям над таблицами.
Минимизация функции методом кубических покрытий.
Рассмотрим комплекс кубов К(f) = L D, где L – множество единичных наборов, D – множество наборов, на которых ДНФ не определена.
Будем выполнять операцию «*» для получения множества простых импликант.
| 0000 | 0010 | 0100 | 0110 | 1010 | 1100 | 1101 | 1110 | |
| 0000 | — | 00×0 | 0x00 | Ø | Ø | Ø | Ø | Ø |
| 0010 | 00×0 | — | Ø | 0x10 | x010 | Ø | Ø | Ø |
| 0100 | 0x00 | Ø | — | 01×0 | Ø | x100 | Ø | Ø |
| 0110 | Ø | 0x10 | 01×0 | — | Ø | Ø | Ø | x110 |
| 1010 | Ø | x010 | Ø | Ø | — | Ø | Ø | 1×10 |
| 1100 | Ø | Ø | x100 | Ø | Ø | — | 110x | 11×0 |
| 1101 | Ø | Ø | Ø | Ø | Ø | 110x | — | Ø |
| 1110 | Ø | Ø | Ø | x110 | 1×10 | 11×0 | Ø | — |
Z0=Ø
Ĉ1=C0∪(C0*C0)
C1=>
| 00×0 | 0x00 | 0x10 | x010 | 01×0 | x100 | x110 | 1×10 | 110x | 11×0 | |
| 00×0 | — | 0000 | 0010 | 0010 | 0xx0 | 0x00 | 0x10 | x010 | Ø | Ø |
| 0x00 | 0000 | — | 0xx0 | 00×0 | 0100 | 0100 | 01×0 | Ø | x100 | x100 |
| 0x10 | 0010 | 0xx0 | — | 0010 | 0110 | 01×0 | 0110 | xx10 | Ø | x110 |
| x010 | 0010 | 00×0 | 0010 | — | 0x10 | Ø | xx10 | 1010 | Ø | 1×10 |
| 01×0 | 0xx0 | 0100 | 0110 | 0x10 | — | 0100 | 0110 | x110 | x100 | x1x0 |
| x100 | 0x00 | 0100 | 01×0 | Ø | 0100 | — | x1x0 | 11×0 | 1100 | 1100 |
| x110 | 0x10 | 01×0 | 0110 | xx10 | 0110 | x1x0 | — | 1110 | 11×0 | 1110 |
| 1×10 | x010 | Ø | xx10 | 1010 | x110 | 11×0 | 1110 | — | 11×0 | 1110 |
| 110x | Ø | x100 | Ø | Ø | x100 | 1100 | 11×0 | 11×0 | — | 1100 |
| 11×0 | Ø | x100 | x110 | 1×10 | x1x0 | 1100 | 1110 | 1110 | 1100 | — |
Z1=
Ĉ2=C1∪(C1*C1)
C2=>
| 0xx0 | xx10 | x1x0 | |
| 0xx0 | — | 0x10 | 01×0 |
| xx10 | 0x10 | — | x110 |
| x1x0 | 01×0 | x110 | — |
Z2=
Ĉ3=C2∪(C2*C2)
C3=>Ø
Z = Z0∪Z1∪Z2
Z=>
Нахождение тупиковых форм.
| 110x | 0xx0 | xx10 | x1x0 | ||
|
110x |
— |
110x |
110x |
1101 |
v |
|
0xx0 |
0xx0 |
— |
0x00 |
0000 |
v |
|
xx10 |
xx10 |
1×10 |
— |
1010 |
v |
|
x1x0 |
x110 |
1110 |
Ø | — |
E0:
L1=L0#E0
| 110x | 0xx0 | xx10 | |
|
0000 |
0000 |
1010 |
Ø |
L1:Ø


Z1:
E:
МДНФ: v
v
, цена=7
Содержание
- Постановка задачи
- Решение задачи
- Анализ переключательной функции
- Метод Квайна
- Карты Карно
- Кубические покрытия
- Анализ полученных результатов
- Список литературы
1. Постановка задачи
Минимизировать переключательную функцию шести аргументов. Функция задана в виде наборов, на которых значения функции равны единице либо не определены. Наборы задаются в шестнадцатеричной системе счисления. В скобках заданы наборы, на которых значение функции не определено:
y => (2) v (3B) v (20) v (21) v (1D) v (6) v (1B) v (D) v (24) v (2C) v (23) v (B) v 36 v 1C v 3A v 7 v A v 8 v 10 v 38 v 12 v 15 v 5 v 1F v 3F v 1A v 17 v 3E v 3D v 39 v 9 v 37 v 19 v 2A v 11 v 18 v 4 v 3C v 2E v 29 v 0 v 2D v 28 v 25 v 14 v 1E
Необходимо выполнить следующие задачи:
- Доопределить функцию нулями, минимизировать полученную функцию методом Квайна;
- Доопределить функцию единицами и произвести минимизацию, используя карты Карно;
- Минимизировать исходную функцию методом кубических покрытий;
- Проанализировать полученные результаты;
2. Решение задачи
2.1 Анализ переключательной функции
Представим исходную последовательность в виде таблицы истинности.
Исходная последовательность:
(2) v (3B) v (20) v (21) v (1D) v (6) v (1B) v (D) v (24) v (2C) v (23) v (B) v 36 v 1C v 3A v 7 v A v 8 v 10 v 38 v 12 v 15 v 5 v 1F v 3F v 1A v 17 v 3E v 3D v 39 v 9 v 37 v 19 v 2A v 11 v 18 v 4 v 3C v 2E v 29 v 0 v 2D v 28 v 25 v 14 v 1E
| Набор | Значение исходной функции | Набор | Значение исходной функции |
|---|---|---|---|
| x1x2x3x4x5x6 | x1x2x3x4x5x6 | ||
| 000000 | 1 | 100000 | ? |
| 000001 | 0 | 100001 | ? |
| 000010 | ? | 100010 | 0 |
| 000011 | 0 | 100011 | ? |
| 000100 | 1 | 100100 | ? |
| 000101 | 1 | 100101 | 1 |
| 000110 | ? | 100110 | 0 |
| 000111 | 1 | 100111 | 0 |
| 001000 | 1 | 101000 | 1 |
| 001001 | 1 | 101001 | 1 |
| 001010 | 1 | 101010 | 1 |
| 001011 | ? | 101011 | 0 |
| 001100 | 0 | 101100 | ? |
| 001101 | ? | 101101 | 1 |
| 001110 | 0 | 101110 | 1 |
| 001111 | 0 | 101111 | 0 |
| 010000 | 1 | 110000 | 0 |
| 010001 | 1 | 110001 | 0 |
| 010010 | 1 | 110010 | 0 |
| 010011 | 0 | 110011 | 0 |
| 010100 | 1 | 110100 | 0 |
| 010101 | 1 | 110101 | 0 |
| 010110 | 0 | 110110 | 1 |
| 010111 | 1 | 110111 | 1 |
| 011000 | 1 | 111000 | 1 |
| 011001 | 1 | 111001 | 1 |
| 011010 | 1 | 111010 | 1 |
| 011011 | ? | 111011 | ? |
| 011100 | 1 | 111100 | 1 |
| 011101 | ? | 111101 | 1 |
| 011110 | 1 | 111110 | 1 |
| 011111 | 1 | 111111 | 1 |
‘?’ обозначено значение наборов, на которых функция не определена.
Цена ДНФ является суммой длин всех входящих в нее конъюнкций.
2.2 Минимизация функции методом Квайна.
Доопределим функцию нулями, получим конституэнты единицы, затем выполним операции попарного неполного склеивания и элементарного поглощения.
|
|
На данном шаге все импликанты участвовали в операциях попарного неполного склеивания и были поглощены своими собственными частями. Поэтому простые импликанты на этом шаге не получены.
|
|
В результате на данном шаге получаем простые импликанты:
x2x3x4x5x6 , x1x2x4x5x6
|
|
В результате на данном шаге получаем простые импликанты:
x1x3x5x6 , x1x4x5x6 , x1x3x4x5 , x1x3x4x6 , x1x2x3x5 , x1x2x4x5 , x1x2x4x6 , x1x2x5x6 , x2x4x5x6 , x2x3x4x5 , x1x3x5x6 , x1x3x5x6 , x1x2x4x5 , x1x2x3x5 , x1x2x3x4
|
В результате на данном шаге получаем простые импликанты:
x3x4x5 , x3x4x6 , x2x3x6
СкДНФ:
x2x3x4x5x6 v x1x2x4x5x6 v x1x3x5x6 v x1x4x5x6 v x1x3x4x5 v x1x3x4x6 v x1x2x3x5 v x1x2x4x5 v x1x2x4x6 v x1x2x5x6 v x2x4x5x6 v x2x3x4x5 v x1x3x5x6 v x1x3x5x6 v x1x2x4x5 v x1x2x3x5 v x1x2x3x4 v x3x4x5 v x3x4x6 v x2x3x6
Нахождение тупиковых форм.
Обозначения:
- Единицы ДНФ, покрываемые импликантами СкДНФ, обозначаются «+».Импликанты, попадающие в ядро помечаются «*».
- Единицы функции, которые покрываются только какой-то одной импликантой из системы простых импликант, помечаются “>”.
- Единицы функции, покрываемые ядром, но не покрываемые только какой-то одной импликантой из системы простых импликант, помечаются “>>”.
|
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
|
| x2x3x4x5x6 | + | + | ||||||||||||||||||||||||||||||||
| x1x2x4x5x6 | + | + | ||||||||||||||||||||||||||||||||
| x1x3x5x6 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x4x5x6 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x3x4x5 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x3x4x6* | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x3x5 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x4x5 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x4x6* | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x5x6 | + | + | + | + | ||||||||||||||||||||||||||||||
| x2x4x5x6 | + | + | + | + | ||||||||||||||||||||||||||||||
| x2x3x4x5 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x3x5x6 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x3x5x6* | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x4x5* | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x3x5 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x3x4 | + | + | + | + | ||||||||||||||||||||||||||||||
| x3x4x5* | + | + | + | + | + | + | + | + | ||||||||||||||||||||||||||
| x3x4x6* | + | + | + | + | + | + | + | + | ||||||||||||||||||||||||||
| x2x3x6 | + | + | + | + | + | + | + | + |
Ядро: x1x3x4x6 v x1x2x4x6 v x1x3x5x6 v x1x2x4x5 v x3x4x5 v x3x4x6
До упорядочивания:
|
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
|
| x2x3x4x5x6 | + | ||||||||||
| x1x2x4x5x6 | + | + | |||||||||
| x1x3x5x6 | + | + | + | ||||||||
| x1x4x5x6 | + | ||||||||||
| x1x3x4x5 | + | + | |||||||||
| x1x2x3x5 | + | + | |||||||||
| x1x2x4x5 | + | ||||||||||
| x1x2x5x6 | + | + | |||||||||
| x2x4x5x6 | + | ||||||||||
| x2x3x4x5 | + | + | |||||||||
| x1x3x5x6 | + | + | |||||||||
| x1x2x3x5 | + | + | |||||||||
| x1x2x3x4 | + | + | |||||||||
| x2x3x6 | + | + | + |
После упорядочивания:
|
x1x2x3x4x5x6> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
|
| x1x2x4x5x6* | + | + | |||||||||
| x1x3x5x6* | + | + | + | ||||||||
| x1x2x3x5* | + | + | |||||||||
| x1x2x5x6 | + | + | |||||||||
| x2x3x4x5* | + | + | |||||||||
| x1x3x5x6 | + | + | |||||||||
| x1x2x3x5 | + | + | |||||||||
| x2x3x6 | + | + | + |
Псевдоядро: x1x2x4x5x6 v x1x3x5x6 v x1x2x3x5 v x2x3x4x5
До упорядочивания:
| x1x2x3x4x5x6 | x1x2x3x4x5x6 | x1x2x3x4x5x6 | |
| x1x2x5x6 | + | ||
| x1x3x5x6 | + | ||
| x1x2x3x5 | + | + | |
| x2x3x6 | + | + |
После упорядочивания:
| x1x2x3x4x5x6> | x1x2x3x4x5x6>> | x1x2x3x4x5x6> | |
| x1x2x3x5* | + | + | |
| x2x3x6* | + | + |
Псевдоядро: x1x2x3x5 v x2x3x6
МДНФ: x1x3x4x6 v x1x2x4x6 v x1x3x5x6 v x1x2x4x5 v x3x4x5 v x3x4x6 v x1x2x4x5x6 v x1x3x5x6 v x1x2x3x5 v x2x3x4x5 v x1x2x3x5 v x2x3x6, цена=46
2.3 Минимизация функции методом Карт Карно.
Дополним функцию единицами и построим Карты Карно.
Компактных групп размера 16 — 1
Компактных групп размера 8 — 9
Компактных групп размера 4 — 13
Компактных групп размера 2 — 1
Нахождение тупиковых форм.
Обозначения:
Ядро: x1x2x3x4x6 v x1x2x4x5 v x1x4x6 v x1x3x4 v x1x2x5 v x1x3x6 v x2x3
Псевдоядро: x1x2x3x4 v x1x3x4x6
Псевдоядро: x1x2x5
Псевдоядро: x3x5x6
МДНФ: x1x2x3x4x6 v x1x2x4x5 v x1x4x6 v x1x3x4 v x1x2x5 v x1x3x6 v x2x3 v x1x2x3x4 v x1x3x4x6 v x1x2x5 v x3x5x6, цена=37
2.4 Минимизация функции методом кубических покрытий.
Рассмотрим комплекс кубов К(f) = L D, где L – множество единичных наборов, D – множество наборов, на которых ДНФ не определена.
Будем выполнять операцию «*» для получения множества простых импликант.
| K(f) = |
|
=> C0 => |
|
| 000000 | 000010 | 000100 | 000101 | 000110 | 000111 | 001000 | 001001 | 001010 | 001011 | 001101 | 010000 | 010001 | 010010 | 010100 | 010101 | 010111 | 011000 | 011001 | 011010 | 011011 | 011100 | 011101 | 011110 | 011111 | 100000 | 100001 | 100011 | 100100 | 100101 | 101000 | 101001 | 101010 | 101100 | 101101 | 101110 | 110110 | 110111 | 111000 | 111001 | 111010 | 111011 | 111100 | 111101 | 111110 | 111111 | |
| 000000 | — | 0000×0 | 000×00 | Ø | Ø | Ø | 00×000 | Ø | Ø | Ø | Ø | 0x0000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000010 | 0000×0 | — | Ø | Ø | 000×10 | Ø | Ø | Ø | 00×010 | Ø | Ø | Ø | Ø | 0x0010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000100 | 000×00 | Ø | — | 00010x | 0001×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000101 | Ø | Ø | 00010x | — | Ø | 0001×1 | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | Ø | 0x0101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000110 | Ø | 000×10 | 0001×0 | Ø | — | 00011x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000111 | Ø | Ø | Ø | 0001×1 | 00011x | — | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 001000 | 00×000 | Ø | Ø | Ø | Ø | Ø | — | 00100x | 0010×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 001001 | Ø | Ø | Ø | Ø | Ø | Ø | 00100x | — | Ø | 0010×1 | 001×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 001010 | Ø | 00×010 | Ø | Ø | Ø | Ø | 0010×0 | Ø | — | 00101x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 001011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0010×1 | 00101x | — | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 001101 | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | 001×01 | Ø | Ø | — | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010000 | 0x0000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | — | 01000x | 0100×0 | 010×00 | Ø | Ø | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01000x | — | Ø | Ø | 010×01 | Ø | Ø | 01×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010010 | Ø | 0x0010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0100×0 | Ø | — | Ø | Ø | Ø | Ø | Ø | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010100 | Ø | Ø | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010×00 | Ø | Ø | — | 01010x | Ø | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010101 | Ø | Ø | Ø | 0x0101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010×01 | Ø | 01010x | — | 0101×1 | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010111 | Ø | Ø | Ø | Ø | Ø | 0x0111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0101×1 | — | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 011000 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | Ø | Ø | Ø | Ø | 01×000 | Ø | Ø | Ø | Ø | Ø | — | 01100x | 0110×0 | Ø | 011×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 011001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | Ø | 01×001 | Ø | Ø | Ø | Ø | 01100x | — | Ø | 0110×1 | Ø | 011×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø |
| 011010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | 01×010 | Ø | Ø | Ø | 0110×0 | Ø | — | 01101x | Ø | Ø | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø |
| 011011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0110×1 | 01101x | — | Ø | Ø | Ø | 011×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11011 | Ø | Ø | Ø | Ø |
| 011100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | 011×00 | Ø | Ø | Ø | — | 01110x | 0111×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø |
| 011101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | Ø | Ø | 01×101 | Ø | Ø | 011×01 | Ø | Ø | 01110x | — | Ø | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø |
| 011110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | 0111×0 | Ø | — | 01111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | Ø |
| 011111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | 011×11 | Ø | 0111×1 | 01111x | — | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 |
| 100000 | x00000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | — | 10000x | Ø | 100×00 | Ø | 10×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 100001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10000x | — | 1000×1 | Ø | 100×01 | Ø | 10×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 100011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1000×1 | — | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 100100 | Ø | Ø | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×00 | Ø | Ø | — | 10010x | Ø | Ø | Ø | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 100101 | Ø | Ø | Ø | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×01 | Ø | 10010x | — | Ø | Ø | Ø | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 101000 | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×000 | Ø | Ø | Ø | Ø | — | 10100x | 1010×0 | 101×00 | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 101001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×001 | Ø | Ø | Ø | 10100x | — | Ø | Ø | 101×01 | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø |
| 101010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1010×0 | Ø | — | Ø | Ø | 101×10 | Ø | Ø | Ø | Ø | 1×1010 | Ø | Ø | Ø | Ø | Ø |
| 101100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×100 | Ø | 101×00 | Ø | Ø | — | 10110x | 1011×0 | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø |
| 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×101 | Ø | 101×01 | Ø | 10110x | — | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø |
| 101110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 101×10 | 1011×0 | Ø | — | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | Ø |
| 110110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | — | 11011x | Ø | Ø | Ø | Ø | Ø | Ø | 11×110 | Ø |
| 110111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11011x | — | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11×111 |
| 111000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | — | 11100x | 1110×0 | Ø | 111×00 | Ø | Ø | Ø |
| 111001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | 11100x | — | Ø | 1110×1 | Ø | 111×01 | Ø | Ø |
| 111010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1010 | Ø | Ø | Ø | Ø | Ø | 1110×0 | Ø | — | 11101x | Ø | Ø | 111×10 | Ø |
| 111011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1110×1 | 11101x | — | Ø | Ø | Ø | 111×11 |
| 111100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | Ø | 111×00 | Ø | Ø | Ø | — | 11110x | 1111×0 | Ø |
| 111101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | Ø | 111×01 | Ø | Ø | 11110x | — | Ø | 1111×1 |
| 111110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | 11×110 | Ø | Ø | Ø | 111×10 | Ø | 1111×0 | Ø | — | 11111x |
| 111111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11×111 | Ø | Ø | Ø | 111×11 | Ø | 1111×1 | 11111x | — |
Z0=Ø
Ĉ1=C0∪(C0*C0)
C1=>
| 0000×0, 000×00, 00×000 0x0000, x00000, 000×10 00×010, 0x0010, 00010x 0001×0, 0x0100, x00100 0001×1, 00×101, 0x0101 x00101, 00011x, 0x0111 00100x, 0010×0, 0x1000 x01000, 0010×1, 001×01 0x1001, x01001, 00101x 0x1010, x01010, 0x1011 0x1101, x01101, 01000x 0100×0, 010×00, 01×000 010×01, 01×001, 01×010 01010x, 01×100, 0101×1 01×101, 01×111, x10111 01100x, 0110×0, 011×00 x11000, 0110×1, 011×01 x11001, 01101x, 011×10 x11010, 011×11, x11011 01110x, 0111×0, x11100 0111×1, x11101, 01111x x11110, x11111, 10000x 100×00, 10×000, 1000×1 100×01, 10×001, 10010x 10×100, 10×101, 10100x 1010×0, 101×00, 1×1000 101×01, 1×1001, 101×10 1×1010, 10110x, 1011×0 1×1100, 1×1101, 1×1110 11011x, 11×110, 11×111 11100x, 1110×0, 111×00 1110×1, 111×01, 11101x 111×10, 111×11, 11110x 1111×0, 1111×1, 11111x |
| 0000×0 | 000×00 | 00×000 | 0x0000 | x00000 | 000×10 | 00×010 | 0x0010 | 00010x | 0001×0 | 0x0100 | x00100 | 0001×1 | 00×101 | 0x0101 | x00101 | 00011x | 0x0111 | 00100x | 0010×0 | 0x1000 | x01000 | 0010×1 | 001×01 | 0x1001 | x01001 | 00101x | 0x1010 | x01010 | 0x1011 | 0x1101 | x01101 | 01000x | 0100×0 | 010×00 | 01×000 | 010×01 | 01×001 | 01×010 | 01010x | 01×100 | 0101×1 | 01×101 | 01×111 | x10111 | 01100x | 0110×0 | 011×00 | x11000 | 0110×1 | 011×01 | x11001 | 01101x | 011×10 | x11010 | 011×11 | x11011 | 01110x | 0111×0 | x11100 | 0111×1 | x11101 | 01111x | x11110 | x11111 | 10000x | 100×00 | 10×000 | 1000×1 | 100×01 | 10×001 | 10010x | 10×100 | 10×101 | 10100x | 1010×0 | 101×00 | 1×1000 | 101×01 | 1×1001 | 101×10 | 1×1010 | 10110x | 1011×0 | 1×1100 | 1×1101 | 1×1110 | 11011x | 11×110 | 11×111 | 11100x | 1110×0 | 111×00 | 1110×1 | 111×01 | 11101x | 111×10 | 111×11 | 11110x | 1111×0 | 1111×1 | 11111x | |
| 0000×0 | — | 000000 | 000000 | 000000 | 000000 | 000010 | 000010 | 000010 | 000×00 | 000xx0 | 000×00 | 000×00 | Ø | Ø | Ø | Ø | 000×10 | Ø | 00×000 | 00x0x0 | 00×000 | 00×000 | Ø | Ø | Ø | Ø | 00×010 | 00×010 | 00×010 | Ø | Ø | Ø | 0x0000 | 0x00x0 | 0x0000 | 0x0000 | Ø | Ø | 0x0010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | x00000 | x00000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000×00 | 000000 | — | 000000 | 000000 | 000000 | 000xx0 | 0000×0 | 0000×0 | 000100 | 000100 | 000100 | 000100 | 00010x | 00010x | 00010x | 00010x | 0001×0 | Ø | 00×000 | 00×000 | 00×000 | 00×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0000 | 0x0000 | 0x0x00 | 0x0000 | Ø | Ø | Ø | 0x0100 | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | x00x00 | x00000 | Ø | Ø | Ø | x00100 | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00×000 | 000000 | 000000 | — | 000000 | 000000 | 0000×0 | 00x0x0 | 0000×0 | 000×00 | 000×00 | 000×00 | 000×00 | Ø | Ø | Ø | Ø | Ø | Ø | 001000 | 001000 | 001000 | 001000 | 00100x | 00100x | 00100x | 00100x | 0010×0 | 0010×0 | 0010×0 | Ø | Ø | Ø | 0x0000 | 0x0000 | 0x0000 | 0xx000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x1000 | 0x1000 | 0x1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | x00000 | x0x000 | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x01000 | x01000 | x01000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x0000 | 000000 | 000000 | 000000 | — | 000000 | 0000×0 | 0000×0 | 0x00x0 | 000×00 | 000×00 | 0x0x00 | 000×00 | Ø | Ø | Ø | Ø | Ø | Ø | 00×000 | 00×000 | 0xx000 | 00×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010000 | 010000 | 010000 | 010000 | 01000x | 01000x | 0100×0 | 010×00 | 010×00 | Ø | Ø | Ø | Ø | 01×000 | 01×000 | 01×000 | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | x00000 | x00000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x00000 | 000000 | 000000 | 000000 | 000000 | — | 0000×0 | 0000×0 | 0000×0 | 000×00 | 000×00 | 000×00 | x00x00 | Ø | Ø | Ø | Ø | Ø | Ø | 00×000 | 00×000 | 00×000 | x0x000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0000 | 0x0000 | 0x0000 | 0x0000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100000 | 100000 | 100000 | 10000x | 10000x | 10000x | 100×00 | 100×00 | Ø | 10×000 | 10×000 | 10×000 | 10×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000×10 | 000010 | 000xx0 | 0000×0 | 0000×0 | 0000×0 | — | 000010 | 000010 | 0001×0 | 000110 | 0001×0 | 0001×0 | 00011x | Ø | Ø | Ø | 000110 | 00011x | Ø | 00×010 | Ø | Ø | Ø | Ø | Ø | Ø | 00×010 | 00×010 | 00×010 | Ø | Ø | Ø | Ø | 0x0010 | Ø | Ø | Ø | Ø | 0x0010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00×010 | 000010 | 0000×0 | 00x0x0 | 0000×0 | 0000×0 | 000010 | — | 000010 | Ø | 000×10 | Ø | Ø | Ø | Ø | Ø | Ø | 000×10 | Ø | 0010×0 | 001010 | 0010×0 | 0010×0 | 00101x | Ø | Ø | Ø | 001010 | 001010 | 001010 | 00101x | Ø | Ø | Ø | 0x0010 | Ø | Ø | Ø | Ø | 0xx010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0x1010 | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | x01010 | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x0010 | 000010 | 0000×0 | 0000×0 | 0x00x0 | 0000×0 | 000010 | 000010 | — | Ø | 000×10 | Ø | Ø | Ø | Ø | Ø | Ø | 000×10 | Ø | Ø | 00×010 | Ø | Ø | Ø | Ø | Ø | Ø | 00×010 | 0xx010 | 00×010 | Ø | Ø | Ø | 0100×0 | 010010 | 0100×0 | 0100×0 | Ø | Ø | 010010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×010 | Ø | Ø | Ø | Ø | Ø | 01×010 | 01×010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00010x | 000×00 | 000100 | 000×00 | 000×00 | 000×00 | 0001×0 | Ø | Ø | — | 000100 | 000100 | 000100 | 000101 | 000101 | 000101 | 000101 | 0001xx | 0001×1 | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | 00×101 | Ø | Ø | 0x0100 | Ø | 0x0101 | Ø | Ø | 0x010x | 0x0100 | 0x0101 | 0x0101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00100 | Ø | Ø | x00101 | Ø | x0010x | x00100 | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0001×0 | 000xx0 | 000100 | 000×00 | 000×00 | 000×00 | 000110 | 000×10 | 000×10 | 000100 | — | 000100 | 000100 | 0001xx | 00010x | 00010x | 00010x | 000110 | 00011x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0100 | Ø | Ø | Ø | Ø | 0x0100 | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00100 | Ø | Ø | Ø | Ø | x00100 | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x0100 | 000×00 | 000100 | 000×00 | 0x0x00 | 000×00 | 0001×0 | Ø | Ø | 000100 | 000100 | — | 000100 | 00010x | 00010x | 0x010x | 00010x | 0001×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010×00 | 010×00 | 010100 | 010×00 | 01010x | Ø | Ø | 010100 | 010100 | 01010x | 01010x | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | 01×100 | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | x00100 | Ø | Ø | Ø | Ø | x00100 | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x00100 | 000×00 | 000100 | 000×00 | 000×00 | x00x00 | 0001×0 | Ø | Ø | 000100 | 000100 | 000100 | — | 00010x | 00010x | 00010x | x0010x | 0001×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0100 | Ø | Ø | Ø | Ø | 0x0100 | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×00 | 100100 | 100×00 | Ø | 10010x | Ø | 100100 | 100100 | 10010x | Ø | Ø | 10×100 | Ø | Ø | Ø | Ø | Ø | 10×100 | 10×100 | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0001×1 | Ø | 00010x | Ø | Ø | Ø | 00011x | Ø | Ø | 000101 | 0001xx | 00010x | 00010x | — | 000101 | 000101 | 000101 | 000111 | 000111 | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | 00×101 | Ø | Ø | Ø | Ø | 0x0101 | Ø | Ø | 0x0101 | Ø | 0x01x1 | 0x0101 | 0x0111 | 0x0111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00101 | Ø | x00101 | Ø | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00×101 | Ø | 00010x | Ø | Ø | Ø | Ø | Ø | Ø | 000101 | 00010x | 00010x | 00010x | 000101 | — | 000101 | 000101 | 0001×1 | 0001×1 | 001×01 | Ø | Ø | Ø | 001×01 | 001101 | 001×01 | 001×01 | Ø | Ø | Ø | Ø | 001101 | 001101 | Ø | Ø | Ø | Ø | 0x0101 | Ø | Ø | 0x0101 | Ø | 0x0101 | 0xx101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | 0x1101 | 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00101 | Ø | x00101 | Ø | x0x101 | Ø | Ø | Ø | Ø | x01101 | Ø | Ø | Ø | x01101 | Ø | Ø | x01101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x0101 | Ø | 00010x | Ø | Ø | Ø | Ø | Ø | Ø | 000101 | 00010x | 0x010x | 00010x | 000101 | 000101 | — | 000101 | 0001×1 | 0x01x1 | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | Ø | Ø | Ø | 0xx101 | 00×101 | 010×01 | Ø | 01010x | Ø | 010101 | 010×01 | Ø | 010101 | 01010x | 010101 | 010101 | 0101×1 | 0101×1 | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | Ø | 01×101 | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00101 | Ø | x00101 | Ø | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x00101 | Ø | 00010x | Ø | Ø | Ø | Ø | Ø | Ø | 000101 | 00010x | 00010x | x0010x | 000101 | 000101 | 000101 | — | 0001×1 | 0001×1 | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | x0x101 | Ø | Ø | Ø | Ø | 0x0101 | Ø | Ø | 0x0101 | Ø | 0x0101 | 0x0101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×01 | 10010x | Ø | 100×01 | 100101 | 100×01 | 100101 | 10010x | 100101 | Ø | Ø | Ø | Ø | 10×101 | Ø | Ø | Ø | 10×101 | Ø | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00011x | 000×10 | 0001×0 | Ø | Ø | Ø | 000110 | 000×10 | 000×10 | 0001xx | 000110 | 0001×0 | 0001×0 | 000111 | 0001×1 | 0001×1 | 0001×1 | — | 000111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0111 | Ø | 0x0111 | 0x0111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x0111 | Ø | Ø | Ø | Ø | Ø | 00011x | Ø | Ø | 0001×1 | 00011x | Ø | Ø | 000111 | 0001×1 | 0x01x1 | 0001×1 | 000111 | — | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0101×1 | Ø | Ø | 0101×1 | Ø | 010111 | 0101×1 | 010111 | 010111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | 01×111 | Ø | 01×111 | Ø | 01×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00100x | 00×000 | 00×000 | 001000 | 00×000 | 00×000 | Ø | 0010×0 | Ø | Ø | Ø | Ø | Ø | Ø | 001×01 | Ø | Ø | Ø | Ø | — | 001000 | 001000 | 001000 | 001001 | 001001 | 001001 | 001001 | 0010xx | 0010×0 | 0010×0 | 0010×1 | 001×01 | 001×01 | Ø | Ø | Ø | 0x1000 | Ø | 0x1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x100x | 0x1000 | 0x1000 | 0x1000 | 0x1001 | 0x1001 | 0x1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | Ø | Ø | x01001 | Ø | Ø | Ø | x0100x | x01000 | x01000 | x01000 | x01001 | x01001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0010×0 | 00x0x0 | 00×000 | 001000 | 00×000 | 00×000 | 00×010 | 001010 | 00×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 001000 | — | 001000 | 001000 | 0010xx | 00100x | 00100x | 00100x | 001010 | 001010 | 001010 | 00101x | Ø | Ø | Ø | Ø | Ø | 0x1000 | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x10x0 | 0x1000 | 0x1000 | Ø | Ø | Ø | 0x1010 | 0x1010 | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x010x0 | x01000 | x01000 | Ø | Ø | x01010 | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x1000 | 00×000 | 00×000 | 001000 | 0xx000 | 00×000 | Ø | 0010×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 001000 | 001000 | — | 001000 | 00100x | 00100x | 0x100x | 00100x | 0010×0 | 0x10x0 | 0010×0 | Ø | Ø | Ø | 01×000 | 01×000 | 01×000 | 011000 | Ø | 01100x | 0110×0 | Ø | 011×00 | Ø | Ø | Ø | Ø | 011000 | 011000 | 011000 | 011000 | 01100x | 01100x | 01100x | 0110×0 | 0110×0 | 0110×0 | Ø | Ø | 011×00 | 011×00 | 011×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x01000 | x01000 | xx1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | x11000 | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x01000 | 00×000 | 00×000 | 001000 | 00×000 | x0x000 | Ø | 0010×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 001000 | 001000 | 001000 | — | 00100x | 00100x | 00100x | x0100x | 0010×0 | 0010×0 | x010x0 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x1000 | 0x1000 | xx1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×000 | 10×000 | 101000 | Ø | Ø | 10100x | Ø | 101×00 | Ø | 101000 | 101000 | 101000 | 101000 | 10100x | 10100x | 1010×0 | 1010×0 | 101×00 | 101×00 | 101×00 | Ø | Ø | Ø | Ø | Ø | 1×1000 | 1×1000 | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0010×1 | Ø | Ø | 00100x | Ø | Ø | Ø | 00101x | Ø | Ø | Ø | Ø | Ø | Ø | 001×01 | Ø | Ø | Ø | Ø | 001001 | 0010xx | 00100x | 00100x | — | 001001 | 001001 | 001001 | 001011 | 00101x | 00101x | 001011 | 001×01 | 001×01 | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | 0x10x1 | 0x1001 | 0x1001 | 0x1011 | Ø | Ø | 0x1011 | 0x1011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01001 | Ø | Ø | Ø | x01001 | Ø | Ø | Ø | x01001 | x01001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 001×01 | Ø | Ø | 00100x | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | 00×101 | 001101 | 00×101 | 00×101 | Ø | Ø | 001001 | 00100x | 00100x | 00100x | 001001 | — | 001001 | 001001 | 0010×1 | Ø | Ø | 0010×1 | 001101 | 001101 | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | 0x1001 | Ø | Ø | Ø | 0x1001 | 0x1x01 | 0x1001 | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | 0x1101 | 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01001 | Ø | Ø | x01101 | x01001 | Ø | Ø | Ø | x01x01 | x01001 | Ø | Ø | x01101 | Ø | Ø | x01101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x1001 | Ø | Ø | 00100x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 001×01 | Ø | Ø | Ø | Ø | 001001 | 00100x | 0x100x | 00100x | 001001 | 001001 | — | 001001 | 0010×1 | Ø | Ø | 0x10x1 | 0x1x01 | 001×01 | 01×001 | Ø | Ø | 01100x | 01×001 | 011001 | Ø | Ø | Ø | Ø | 011×01 | Ø | Ø | 011001 | 01100x | 01100x | 01100x | 011001 | 011001 | 011001 | 0110×1 | Ø | Ø | 0110×1 | 0110×1 | 011×01 | Ø | Ø | 011×01 | 011×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01001 | Ø | Ø | Ø | x01001 | Ø | Ø | Ø | x01001 | xx1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | x11001 | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x01001 | Ø | Ø | 00100x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 001×01 | Ø | Ø | Ø | Ø | 001001 | 00100x | 00100x | x0100x | 001001 | 001001 | 001001 | — | 0010×1 | Ø | Ø | 0010×1 | 001×01 | x01x01 | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | 0x1001 | 0x1001 | xx1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×001 | Ø | 10100x | 10×001 | 10×001 | 101001 | Ø | Ø | 101×01 | 101001 | 10100x | 10100x | 10100x | 101001 | 101001 | Ø | Ø | 101×01 | Ø | Ø | 101×01 | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | 1×1001 | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00101x | 00×010 | Ø | 0010×0 | Ø | Ø | 00×010 | 001010 | 00×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0010xx | 001010 | 0010×0 | 0010×0 | 001011 | 0010×1 | 0010×1 | 0010×1 | — | 001010 | 001010 | 001011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | 0x1011 | Ø | Ø | 0x101x | 0x1010 | 0x1010 | 0x1011 | 0x1011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | x01010 | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x1010 | 00×010 | Ø | 0010×0 | Ø | Ø | 00×010 | 001010 | 0xx010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0010×0 | 001010 | 0x10x0 | 0010×0 | 00101x | Ø | Ø | Ø | 001010 | — | 001010 | 0x101x | Ø | Ø | Ø | 01×010 | Ø | 0110×0 | Ø | Ø | 011010 | Ø | Ø | Ø | Ø | Ø | Ø | 0110×0 | 011010 | 0110×0 | 0110×0 | 01101x | Ø | Ø | 011010 | 011010 | 011010 | 01101x | 01101x | Ø | 011×10 | Ø | Ø | Ø | 011×10 | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | x01010 | xx1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | x11010 | x11010 | Ø | Ø | Ø | Ø | Ø |
| x01010 | 00×010 | Ø | 0010×0 | Ø | Ø | 00×010 | 001010 | 00×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0010×0 | 001010 | 0010×0 | x010x0 | 00101x | Ø | Ø | Ø | 001010 | 001010 | — | 00101x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0x1010 | xx1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1010×0 | Ø | Ø | Ø | Ø | Ø | Ø | 1010×0 | 101010 | 1010×0 | 1010×0 | Ø | Ø | 101010 | 101010 | Ø | 101×10 | Ø | Ø | 101×10 | Ø | Ø | Ø | Ø | 1×1010 | Ø | Ø | Ø | 1×1010 | 1×1010 | Ø | Ø | Ø | Ø | Ø |
| 0x1011 | Ø | Ø | Ø | Ø | Ø | Ø | 00101x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0010×1 | 00101x | Ø | Ø | 001011 | 0010×1 | 0x10x1 | 0010×1 | 001011 | 0x101x | 00101x | — | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0110×1 | 01101x | Ø | Ø | Ø | Ø | 011×11 | Ø | 0110×1 | 01101x | Ø | Ø | 011011 | 0110×1 | 0110×1 | 011011 | 01101x | 01101x | 011011 | 011011 | Ø | Ø | Ø | 011×11 | Ø | 011×11 | Ø | 011×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11011 | Ø | x11011 | Ø | x11011 | Ø | Ø | Ø | Ø |
| 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | 00×101 | 001101 | 0xx101 | 00×101 | Ø | Ø | 001×01 | Ø | Ø | Ø | 001×01 | 001101 | 0x1x01 | 001×01 | Ø | Ø | Ø | Ø | — | 001101 | Ø | Ø | Ø | Ø | 01×101 | 011×01 | Ø | 01×101 | 01110x | 01×101 | 011101 | 0111×1 | Ø | 011×01 | Ø | 01110x | Ø | 011×01 | 011101 | 011×01 | Ø | Ø | Ø | 0111×1 | Ø | 011101 | 01110x | 01110x | 011101 | 011101 | 0111×1 | Ø | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | Ø | Ø | Ø | x01101 | Ø | Ø | Ø | x01101 | Ø | Ø | xx1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | x11101 | Ø | x11101 | Ø |
| x01101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | 00×101 | 001101 | 00×101 | x0x101 | Ø | Ø | 001×01 | Ø | Ø | Ø | 001×01 | 001101 | 001×01 | x01x01 | Ø | Ø | Ø | Ø | 001101 | — | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | 0x1101 | xx1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×101 | 101×01 | 10×101 | 10110x | 101101 | 101×01 | Ø | 10110x | Ø | 101101 | 101×01 | Ø | Ø | 101101 | 10110x | 10110x | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | 1×1101 | Ø | 1×1101 | Ø |
| 01000x | 0x0000 | 0x0000 | 0x0000 | 010000 | 0x0000 | Ø | Ø | 0100×0 | Ø | Ø | 010×00 | Ø | Ø | Ø | 010×01 | Ø | Ø | Ø | Ø | Ø | 01×000 | Ø | Ø | Ø | 01×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | — | 010000 | 010000 | 010000 | 010001 | 010001 | 0100×0 | 010x0x | 010×00 | 010×01 | 010×01 | Ø | Ø | 01x00x | 01×000 | 01×000 | 01×000 | 01×001 | 01×001 | 01×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0100×0 | 0x00x0 | 0x0000 | 0x0000 | 010000 | 0x0000 | 0x0010 | 0x0010 | 010010 | Ø | Ø | 010×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | 01×010 | Ø | Ø | Ø | Ø | 010000 | — | 010000 | 010000 | 01000x | 01000x | 010010 | 010×00 | 010×00 | Ø | Ø | Ø | Ø | 01×000 | 01x0x0 | 01×000 | 01×000 | Ø | Ø | Ø | 01×010 | 01×010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010×00 | 0x0000 | 0x0x00 | 0x0000 | 010000 | 0x0000 | Ø | Ø | 0100×0 | 0x0100 | 0x0100 | 010100 | 0x0100 | Ø | Ø | 01010x | Ø | Ø | Ø | Ø | Ø | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010000 | 010000 | — | 010000 | 010x0x | 01000x | 0100×0 | 010100 | 010100 | 01010x | 01010x | Ø | Ø | 01×000 | 01×000 | 01xx00 | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | 01×100 | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 01×000 | 0x0000 | 0x0000 | 0xx000 | 010000 | 0x0000 | Ø | Ø | 0100×0 | Ø | Ø | 010×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x1000 | 011000 | 0x1000 | Ø | Ø | 01100x | Ø | Ø | 0110×0 | Ø | Ø | Ø | Ø | 010000 | 010000 | 010000 | — | 01000x | 01x00x | 01x0x0 | 010×00 | 01xx00 | Ø | Ø | Ø | Ø | 011000 | 011000 | 011000 | 011000 | 01100x | 01100x | 01100x | 0110×0 | 0110×0 | 0110×0 | Ø | Ø | 011×00 | 011×00 | 011×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | x11000 | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010×01 | Ø | Ø | Ø | 01000x | Ø | Ø | Ø | Ø | 0x0101 | Ø | 01010x | Ø | 0x0101 | 0x0101 | 010101 | 0x0101 | Ø | 0101×1 | Ø | Ø | Ø | Ø | Ø | Ø | 01×001 | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | 010001 | 01000x | 010x0x | 01000x | — | 010001 | Ø | 010101 | 01010x | 010101 | 010101 | 0101×1 | 0101×1 | 01×001 | Ø | Ø | Ø | 01×001 | 01xx01 | 01×001 | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | Ø | 01×101 | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 01×001 | Ø | Ø | Ø | 01000x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010×01 | Ø | Ø | Ø | 0x1001 | Ø | 01100x | Ø | 0x1001 | 0x1001 | 011001 | 0x1001 | Ø | Ø | Ø | 0110×1 | 011×01 | Ø | 010001 | 01000x | 01000x | 01x00x | 010001 | — | Ø | 010×01 | Ø | 010×01 | 01xx01 | Ø | Ø | 011001 | 01100x | 01100x | 01100x | 011001 | 011001 | 011001 | 0110×1 | Ø | Ø | 0110×1 | 0110×1 | 011×01 | Ø | Ø | 011×01 | 011×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | x11001 | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 01×010 | 0x0010 | Ø | Ø | 0100×0 | Ø | 0x0010 | 0xx010 | 010010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0110×0 | Ø | Ø | Ø | Ø | Ø | 0x1010 | 011010 | 0x1010 | 01101x | Ø | Ø | 0100×0 | 010010 | 0100×0 | 01x0x0 | Ø | Ø | — | Ø | Ø | Ø | Ø | Ø | Ø | 0110×0 | 011010 | 0110×0 | 0110×0 | 01101x | Ø | Ø | 011010 | 011010 | 011010 | 01101x | 01101x | Ø | 011×10 | Ø | Ø | Ø | 011×10 | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | x11010 | x11010 | Ø | Ø | Ø | Ø | Ø |
| 01010x | Ø | 0x0100 | Ø | 010×00 | Ø | Ø | Ø | Ø | 0x010x | 0x0100 | 010100 | 0x0100 | 0x0101 | 0x0101 | 010101 | 0x0101 | Ø | 0101×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | 010x0x | 010×00 | 010100 | 010×00 | 010101 | 010×01 | Ø | — | 010100 | 010101 | 010101 | 0101×1 | 0101×1 | Ø | Ø | 01×100 | Ø | Ø | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | 01x10x | 01×100 | 01×100 | 01×101 | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 01×100 | Ø | 0x0100 | Ø | 010×00 | Ø | Ø | Ø | Ø | 0x0100 | 0x0100 | 010100 | 0x0100 | Ø | Ø | 01010x | Ø | Ø | Ø | Ø | Ø | 011×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01110x | Ø | 010×00 | 010×00 | 010100 | 01xx00 | 01010x | Ø | Ø | 010100 | — | 01010x | 01x10x | Ø | Ø | 011×00 | 011×00 | 011100 | 011×00 | Ø | 01110x | Ø | Ø | 0111×0 | Ø | Ø | Ø | 011100 | 011100 | 011100 | 01110x | 01110x | 0111×0 | 0111×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | Ø | x11100 | x11100 | Ø | Ø |
| 0101×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0101 | Ø | 01010x | Ø | 0x01x1 | 0x0101 | 010101 | 0x0101 | 0x0111 | 010111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | 010×01 | Ø | 01010x | Ø | 010101 | 010×01 | Ø | 010101 | 01010x | — | 010101 | 010111 | 010111 | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | Ø | Ø | Ø | 01×111 | Ø | 01×101 | Ø | Ø | 01x1x1 | 01×101 | 01×111 | Ø | 01×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0101 | Ø | 01010x | Ø | 0x0101 | 0xx101 | 010101 | 0x0101 | Ø | 0101×1 | Ø | Ø | Ø | Ø | Ø | 0x1101 | 011×01 | Ø | Ø | Ø | Ø | Ø | 011101 | 0x1101 | 010×01 | Ø | 01010x | Ø | 010101 | 01xx01 | Ø | 010101 | 01x10x | 010101 | — | 01x1x1 | 0101×1 | 011×01 | Ø | 01110x | Ø | 011×01 | 011101 | 011×01 | Ø | Ø | Ø | 0111×1 | Ø | 011101 | 01110x | 01110x | 011101 | 011101 | 0111×1 | Ø | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | x11101 | Ø | x11101 | Ø |
| 01×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0111 | Ø | 0101×1 | Ø | 0x0111 | 010111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×11 | 0111×1 | Ø | Ø | Ø | Ø | Ø | 0101×1 | Ø | Ø | 0101×1 | Ø | 010111 | 01x1x1 | — | 010111 | Ø | Ø | Ø | Ø | 011×11 | 0111×1 | Ø | 011×11 | 01111x | Ø | 011111 | 011×11 | 0111×1 | 01111x | Ø | 011111 | 0111×1 | 011111 | 01111x | 011111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | x1x111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 | Ø | Ø | x11111 | x11111 |
| x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0111 | Ø | 0101×1 | Ø | 0x0111 | 010111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0101×1 | Ø | Ø | 0101×1 | Ø | 010111 | 0101×1 | 010111 | — | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | 01×111 | Ø | 01×111 | Ø | x1x111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 110111 | 11011x | 110111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11×111 | Ø | Ø | 11×111 | 11×111 |
| 01100x | Ø | Ø | 0x1000 | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x100x | 0x1000 | 011000 | 0x1000 | 0x1001 | 0x1001 | 011001 | 0x1001 | Ø | 0110×0 | Ø | 0110×1 | 011×01 | Ø | 01x00x | 01×000 | 01×000 | 011000 | 01×001 | 011001 | 0110×0 | Ø | 011×00 | Ø | 011×01 | Ø | Ø | — | 011000 | 011000 | 011000 | 011001 | 011001 | 011001 | 0110xx | 0110×0 | 0110×0 | 0110×1 | 0110×1 | 011x0x | 011×00 | 011×00 | 011×01 | 011×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x1100x | x11000 | x11000 | x11001 | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0110×0 | Ø | Ø | 0x1000 | 01×000 | Ø | Ø | 0x1010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x10x0 | 011000 | 0x1000 | Ø | Ø | 01100x | Ø | 0x1010 | 011010 | 0x1010 | 01101x | Ø | Ø | 01×000 | 01x0x0 | 01×000 | 011000 | Ø | 01100x | 011010 | Ø | 011×00 | Ø | Ø | Ø | Ø | 011000 | — | 011000 | 011000 | 0110xx | 01100x | 01100x | 011010 | 011010 | 011010 | 01101x | 01101x | 011×00 | 011xx0 | 011×00 | Ø | Ø | 011×10 | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | x110x0 | x11000 | Ø | Ø | x11010 | x11010 | Ø | Ø | Ø | Ø | Ø |
| 011×00 | Ø | Ø | 0x1000 | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x1000 | 011000 | 0x1000 | Ø | Ø | 01100x | Ø | Ø | 0110×0 | Ø | Ø | 01110x | Ø | 01×000 | 01×000 | 01xx00 | 011000 | Ø | 01100x | 0110×0 | 01×100 | 011100 | Ø | 01110x | Ø | Ø | 011000 | 011000 | — | 011000 | 01100x | 011x0x | 01100x | 0110×0 | 011xx0 | 0110×0 | Ø | Ø | 011100 | 011100 | 011100 | 01110x | 01110x | 0111×0 | 0111×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | Ø | x11000 | x11000 | x11x00 | Ø | Ø | Ø | Ø | Ø | x11100 | x11100 | Ø | Ø |
| x11000 | Ø | Ø | 0x1000 | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x1000 | 011000 | xx1000 | Ø | Ø | 01100x | Ø | Ø | 0110×0 | Ø | Ø | Ø | Ø | 01×000 | 01×000 | 01×000 | 011000 | Ø | 01100x | 0110×0 | Ø | 011×00 | Ø | Ø | Ø | Ø | 011000 | 011000 | 011000 | — | 01100x | 01100x | x1100x | 0110×0 | 0110×0 | x110x0 | Ø | Ø | 011×00 | 011×00 | x11x00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | 1×1000 | 1×1000 | 111000 | Ø | 11100x | Ø | 1110×0 | Ø | Ø | 111×00 | Ø | Ø | Ø | Ø | Ø | 111000 | 111000 | 111000 | 11100x | 11100x | 1110×0 | 1110×0 | Ø | 111×00 | 111×00 | Ø | Ø |
| 0110×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | 01100x | Ø | 0x10x1 | 0x1001 | 011001 | 0x1001 | 0x1011 | 01101x | Ø | 011011 | 011×01 | Ø | 01×001 | Ø | Ø | 01100x | 01×001 | 011001 | 01101x | Ø | Ø | Ø | 011×01 | 011×11 | Ø | 011001 | 0110xx | 01100x | 01100x | — | 011001 | 011001 | 011011 | 01101x | 01101x | 011011 | 011011 | 011×01 | Ø | Ø | 011xx1 | 011×01 | 011×11 | Ø | 011×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | x110x1 | x11001 | x11011 | Ø | x11011 | Ø | Ø | Ø | Ø |
| 011×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | 01×101 | Ø | Ø | Ø | 0x1001 | Ø | 01100x | Ø | 0x1001 | 0x1x01 | 011001 | 0x1001 | Ø | Ø | Ø | 0110×1 | 011101 | 0x1101 | 01×001 | Ø | Ø | 01100x | 01xx01 | 011001 | Ø | 01×101 | 01110x | 01×101 | 011101 | 0111×1 | Ø | 011001 | 01100x | 011x0x | 01100x | 011001 | — | 011001 | 0110×1 | Ø | Ø | 011xx1 | 0110×1 | 011101 | 01110x | 01110x | 011101 | 011101 | 0111×1 | Ø | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | x11001 | x11x01 | Ø | Ø | Ø | x11101 | Ø | x11101 | Ø |
| x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | 01100x | Ø | 0x1001 | 0x1001 | 011001 | xx1001 | Ø | Ø | Ø | 0110×1 | 011×01 | Ø | 01×001 | Ø | Ø | 01100x | 01×001 | 011001 | Ø | Ø | Ø | Ø | 011×01 | Ø | Ø | 011001 | 01100x | 01100x | x1100x | 011001 | 011001 | — | 0110×1 | Ø | Ø | 0110×1 | x110x1 | 011×01 | Ø | Ø | 011×01 | x11x01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | 1×1001 | Ø | Ø | 11100x | 1×1001 | 111001 | Ø | Ø | Ø | Ø | Ø | 111×01 | Ø | Ø | Ø | Ø | 111001 | 11100x | 11100x | 111001 | 111001 | 1110×1 | Ø | 1110×1 | 111×01 | Ø | 111×01 | Ø |
| 01101x | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0110×0 | Ø | 0x1011 | Ø | 0110×1 | Ø | 0x101x | 011010 | 0x1010 | 011011 | Ø | Ø | Ø | 01×010 | Ø | 0110×0 | Ø | 0110×1 | 011010 | Ø | Ø | Ø | Ø | 011×11 | Ø | 0110xx | 011010 | 0110×0 | 0110×0 | 011011 | 0110×1 | 0110×1 | — | 011010 | 011010 | 011011 | 011011 | Ø | 011×10 | Ø | 011×11 | Ø | 011x1x | 011×10 | 011×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | x11011 | Ø | x1101x | x11010 | x11011 | Ø | Ø | Ø | Ø |
| 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0110×0 | Ø | Ø | Ø | Ø | Ø | 0x1010 | 011010 | 0x1010 | 01101x | Ø | Ø | Ø | 01×010 | Ø | 0110×0 | Ø | Ø | 011010 | Ø | 0111×0 | Ø | Ø | 01111x | Ø | 0110×0 | 011010 | 011xx0 | 0110×0 | 01101x | Ø | Ø | 011010 | — | 011010 | 011x1x | 01101x | 0111×0 | 011110 | 0111×0 | 01111x | Ø | 011110 | 011110 | 01111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | x11110 | Ø | x11110 | Ø | Ø | x11010 | Ø | Ø | Ø | x11010 | x11x10 | Ø | Ø | x11110 | Ø | x11110 |
| x11010 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0110×0 | Ø | Ø | Ø | Ø | Ø | 0x1010 | 011010 | xx1010 | 01101x | Ø | Ø | Ø | 01×010 | Ø | 0110×0 | Ø | Ø | 011010 | Ø | Ø | Ø | Ø | Ø | Ø | 0110×0 | 011010 | 0110×0 | x110x0 | 01101x | Ø | Ø | 011010 | 011010 | — | 01101x | x1101x | Ø | 011×10 | Ø | Ø | Ø | 011×10 | x11x10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1010 | Ø | 1110×0 | Ø | Ø | 1×1010 | 111010 | Ø | Ø | Ø | Ø | 111×10 | Ø | 111×10 | Ø | 1110×0 | 111010 | 1110×0 | 11101x | Ø | 111010 | 111010 | 11101x | Ø | 111×10 | Ø | 111×10 |
| 011×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | 0x1011 | Ø | 0110×1 | Ø | 0x1011 | 01101x | Ø | 011011 | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | 0110×1 | 01101x | Ø | Ø | 01×111 | 0111×1 | 011111 | 01×111 | 0110×1 | 01101x | Ø | Ø | 011011 | 011xx1 | 0110×1 | 011011 | 011x1x | 01101x | — | 011011 | 0111×1 | 01111x | Ø | 011111 | 0111×1 | 011111 | 01111x | 011111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 | Ø | Ø | Ø | x11011 | Ø | x11011 | Ø | x11x11 | Ø | Ø | x11111 | x11111 |
| x11011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1011 | Ø | 0110×1 | Ø | 0x1011 | 01101x | Ø | 011011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0110×1 | 01101x | Ø | Ø | Ø | Ø | 011×11 | Ø | 0110×1 | 01101x | Ø | Ø | 011011 | 0110×1 | x110x1 | 011011 | 01101x | x1101x | 011011 | — | Ø | Ø | Ø | 011×11 | Ø | 011×11 | Ø | x11x11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1110×1 | Ø | 11101x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 111×11 | 1110×1 | 11101x | Ø | 111011 | 1110×1 | 111011 | 11101x | 111011 | Ø | Ø | 111×11 | 111×11 |
| 01110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | 0x1101 | 01×101 | Ø | Ø | Ø | Ø | Ø | 011×00 | Ø | Ø | 0x1101 | 011×01 | Ø | Ø | Ø | Ø | Ø | 011101 | 0x1101 | Ø | Ø | 01×100 | 011×00 | 01×101 | 011×01 | Ø | 01x10x | 011100 | 01×101 | 011101 | 0111×1 | Ø | 011x0x | 011×00 | 011100 | 011×00 | 011×01 | 011101 | 011×01 | Ø | 0111×0 | Ø | 0111×1 | Ø | — | 011100 | 011100 | 011101 | 011101 | 0111xx | 0111×0 | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | x11101 | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | x11101 | Ø | Ø | Ø | x1110x | x11100 | x11101 | Ø |
| 0111×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×00 | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | Ø | 01110x | Ø | Ø | Ø | 01×100 | 011×00 | Ø | Ø | 011×10 | 01×100 | 011100 | Ø | 01110x | 01111x | Ø | 011×00 | 011xx0 | 011100 | 011×00 | Ø | 01110x | Ø | 011×10 | 011110 | 011×10 | 01111x | Ø | 011100 | — | 011100 | 0111xx | 01110x | 011110 | 011110 | 01111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | x11110 | Ø | x11110 | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | x11110 | Ø | x11100 | x111x0 | Ø | x11110 |
| x11100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01110x | Ø | Ø | Ø | 01×100 | 011×00 | Ø | Ø | Ø | 01×100 | 011100 | Ø | 01110x | Ø | Ø | 011×00 | 011×00 | 011100 | x11x00 | Ø | 01110x | Ø | Ø | 0111×0 | Ø | Ø | Ø | 011100 | 011100 | — | 01110x | x1110x | 0111×0 | x111x0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | 1×1100 | 111×00 | Ø | Ø | Ø | Ø | 1×1100 | 1×1100 | 111100 | 11110x | 1111×0 | Ø | 1111×0 | Ø | 111×00 | 111×00 | 111100 | Ø | 11110x | Ø | 1111×0 | Ø | 111100 | 111100 | 11110x | 1111×0 |
| 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | 01×101 | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | Ø | 0x1101 | 011×01 | Ø | Ø | Ø | Ø | 011×11 | 011101 | 0x1101 | Ø | Ø | Ø | Ø | 01×101 | 011×01 | Ø | 01×101 | 01110x | 01x1x1 | 011101 | 011111 | 01×111 | 011×01 | Ø | 01110x | Ø | 011xx1 | 011101 | 011×01 | 011×11 | 01111x | Ø | 011111 | 011×11 | 011101 | 0111xx | 01110x | — | 011101 | 011111 | 01111x | 011111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | x11111 | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | x11111 | x11101 | Ø | x111x1 | x11111 |
| x11101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | 011×01 | Ø | Ø | Ø | Ø | Ø | 011101 | xx1101 | Ø | Ø | Ø | Ø | 01×101 | 011×01 | Ø | 01×101 | 01110x | 01×101 | 011101 | 0111×1 | Ø | 011×01 | Ø | 01110x | Ø | 011×01 | 011101 | x11x01 | Ø | Ø | Ø | 0111×1 | Ø | 011101 | 01110x | x1110x | 011101 | — | 0111×1 | Ø | x111x1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | Ø | 1×1101 | 111×01 | Ø | Ø | 1×1101 | Ø | 11110x | 111101 | Ø | Ø | Ø | 1111×1 | 111×01 | Ø | 11110x | 111×01 | 111101 | Ø | Ø | 1111×1 | 111101 | 11110x | 111101 | 1111×1 |
| 01111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | 011×11 | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | 0111×0 | 01×111 | 0111×1 | 011111 | 01×111 | Ø | 011×10 | 0111×0 | Ø | 011×11 | 0111×1 | Ø | 011x1x | 011110 | 011×10 | 011111 | 011×11 | 0111xx | 011110 | 0111×0 | 011111 | 0111×1 | — | 011110 | 011111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | Ø | x11110 | x11111 | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | x11111 | Ø | x11110 | x11111 | x1111x |
| x11110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | 0111×0 | Ø | Ø | 01111x | Ø | Ø | 011×10 | 0111×0 | Ø | Ø | Ø | Ø | 011×10 | 011110 | x11x10 | 01111x | Ø | 0111×0 | 011110 | x111x0 | 01111x | Ø | 011110 | — | x1111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | 111×10 | Ø | 1×1110 | 1111×0 | Ø | 111110 | 11×110 | 111110 | 11111x | Ø | 111×10 | 1111×0 | Ø | Ø | 111×10 | 111110 | 11111x | 1111×0 | 111110 | 11111x | 111110 |
| x11111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×11 | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | 0111×1 | 011111 | x1x111 | Ø | Ø | Ø | Ø | 011×11 | 0111×1 | Ø | 011×11 | 01111x | Ø | 011111 | x11x11 | 0111×1 | 01111x | Ø | 011111 | x111x1 | 011111 | x1111x | — | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1111×1 | 11111x | 11×111 | 11111x | 111111 | Ø | Ø | Ø | 111×11 | 1111×1 | 111×11 | 11111x | 111111 | 1111×1 | 11111x | 111111 | 111111 |
| 10000x | x00000 | x00000 | x00000 | x00000 | 100000 | Ø | Ø | Ø | Ø | Ø | Ø | 100×00 | Ø | Ø | Ø | 100×01 | Ø | Ø | Ø | Ø | Ø | 10×000 | Ø | Ø | Ø | 10×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | — | 100000 | 100000 | 100001 | 100001 | 100001 | 100x0x | 100×00 | 100×01 | 10x00x | 10×000 | 10×000 | 10×000 | 10×001 | 10×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 100×00 | x00000 | x00x00 | x00000 | x00000 | 100000 | Ø | Ø | Ø | x00100 | x00100 | x00100 | 100100 | Ø | Ø | Ø | 10010x | Ø | Ø | Ø | Ø | Ø | 10×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100000 | — | 100000 | 10000x | 100x0x | 10000x | 100100 | 100100 | 10010x | 10×000 | 10×000 | 10xx00 | 10×000 | Ø | Ø | Ø | Ø | 10×100 | 10×100 | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 10×000 | x00000 | x00000 | x0x000 | x00000 | 100000 | Ø | Ø | Ø | Ø | Ø | Ø | 100×00 | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x01000 | x01000 | 101000 | Ø | Ø | Ø | 10100x | Ø | Ø | 1010×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100000 | 100000 | — | 10000x | 10000x | 10x00x | 100×00 | 10xx00 | Ø | 101000 | 101000 | 101000 | 101000 | 10100x | 10100x | 1010×0 | 1010×0 | 101×00 | 101×00 | 101×00 | Ø | Ø | Ø | Ø | Ø | 1×1000 | 1×1000 | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 1000×1 | Ø | Ø | Ø | Ø | 10000x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100001 | 10000x | 10000x | — | 100001 | 100001 | 100×01 | Ø | 100×01 | 10×001 | Ø | Ø | Ø | 10×001 | 10×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 100×01 | Ø | Ø | Ø | Ø | 10000x | Ø | Ø | Ø | x00101 | Ø | Ø | 10010x | x00101 | x00101 | x00101 | 100101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×001 | Ø | Ø | Ø | Ø | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100001 | 100x0x | 10000x | 100001 | — | 100001 | 100101 | 10010x | 100101 | 10×001 | Ø | Ø | Ø | 10xx01 | 10×001 | Ø | Ø | 10×101 | Ø | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 10×001 | Ø | Ø | Ø | Ø | 10000x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×01 | Ø | Ø | x01001 | Ø | Ø | 10100x | x01001 | x01001 | x01001 | 101001 | Ø | Ø | Ø | Ø | Ø | 101×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100001 | 10000x | 10x00x | 100001 | 100001 | — | 100×01 | Ø | 10xx01 | 101001 | 10100x | 10100x | 10100x | 101001 | 101001 | Ø | Ø | 101×01 | Ø | Ø | 101×01 | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | 1×1001 | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 10010x | Ø | x00100 | Ø | Ø | 100×00 | Ø | Ø | Ø | x0010x | x00100 | x00100 | 100100 | x00101 | x00101 | x00101 | 100101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100x0x | 100100 | 100×00 | 100×01 | 100101 | 100×01 | — | 100100 | 100101 | Ø | Ø | 10×100 | Ø | 10×101 | Ø | Ø | Ø | 10x10x | 10×100 | 10×100 | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 10×100 | Ø | x00100 | Ø | Ø | 100×00 | Ø | Ø | Ø | x00100 | x00100 | x00100 | 100100 | Ø | Ø | Ø | 10010x | Ø | Ø | Ø | Ø | Ø | 101×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | Ø | Ø | 100×00 | 100100 | 10xx00 | Ø | 10010x | Ø | 100100 | — | 10x10x | 101×00 | 101×00 | 101100 | 101×00 | 10110x | Ø | 1011×0 | Ø | 101100 | 101100 | 101100 | 10110x | 1011×0 | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | Ø | Ø | 1×1100 | 1×1100 | Ø | Ø |
| 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00101 | Ø | Ø | 10010x | x00101 | x0x101 | x00101 | 100101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | 101×01 | Ø | Ø | Ø | Ø | x01101 | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | 100×01 | 10010x | Ø | 100×01 | 100101 | 10xx01 | 100101 | 10x10x | — | 101×01 | Ø | 10110x | Ø | 101101 | 101×01 | Ø | Ø | 101101 | 10110x | 10110x | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | 1×1101 | Ø | 1×1101 | Ø |
| 10100x | Ø | Ø | x01000 | Ø | 10×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x0100x | x01000 | x01000 | 101000 | x01001 | x01001 | x01001 | 101001 | Ø | Ø | 1010×0 | Ø | Ø | 101×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10x00x | 10×000 | 101000 | 10×001 | 10×001 | 101001 | Ø | 101×00 | 101×01 | — | 101000 | 101000 | 101000 | 101001 | 101001 | 1010×0 | 1010×0 | 101x0x | 101×00 | 101×00 | 101×01 | Ø | Ø | Ø | Ø | 1x100x | 1×1000 | 1×1000 | 1×1001 | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 1010×0 | Ø | Ø | x01000 | Ø | 10×000 | Ø | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x010x0 | x01000 | 101000 | Ø | Ø | Ø | 10100x | x01010 | x01010 | 101010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | 1×1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×000 | 10×000 | 101000 | Ø | Ø | 10100x | Ø | 101×00 | Ø | 101000 | — | 101000 | 101000 | 10100x | 10100x | 101010 | 101010 | 101×00 | 101xx0 | 101×00 | Ø | 101×10 | Ø | Ø | Ø | 1×1000 | 1x10x0 | 1×1000 | Ø | Ø | 1×1010 | 1×1010 | Ø | Ø | Ø | Ø | Ø |
| 101×00 | Ø | Ø | x01000 | Ø | 10×000 | Ø | Ø | Ø | Ø | Ø | Ø | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x01000 | x01000 | 101000 | Ø | Ø | Ø | 10100x | Ø | Ø | 1010×0 | Ø | Ø | 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | Ø | Ø | 10×000 | 10xx00 | 101000 | Ø | Ø | 10100x | 10×100 | 101100 | 10110x | 101000 | 101000 | — | 101000 | 101x0x | 10100x | 101xx0 | 1010×0 | 101100 | 101100 | 101100 | 10110x | 1011×0 | Ø | Ø | Ø | 1×1000 | 1×1000 | 1x1x00 | Ø | Ø | Ø | Ø | Ø | 1×1100 | 1×1100 | Ø | Ø |
| 1×1000 | Ø | Ø | x01000 | Ø | 10×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x01000 | xx1000 | 101000 | Ø | Ø | Ø | 10100x | Ø | Ø | 1010×0 | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | x11000 | x11000 | 111000 | Ø | Ø | 11100x | Ø | Ø | 1110×0 | Ø | Ø | Ø | Ø | 111×00 | Ø | Ø | Ø | Ø | Ø | 10×000 | 10×000 | 101000 | Ø | Ø | 10100x | Ø | 101×00 | Ø | 101000 | 101000 | 101000 | — | 10100x | 1x100x | 1010×0 | 1x10x0 | 101×00 | 101×00 | 1x1x00 | Ø | Ø | Ø | Ø | Ø | 111000 | 111000 | 111000 | 11100x | 11100x | 1110×0 | 1110×0 | Ø | 111×00 | 111×00 | Ø | Ø |
| 101×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | 10×101 | Ø | Ø | x01001 | Ø | Ø | 10100x | x01001 | x01x01 | x01001 | 101001 | Ø | Ø | Ø | Ø | x01101 | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | 10×001 | Ø | 10100x | 10×001 | 10xx01 | 101001 | 10×101 | 10110x | 101101 | 101001 | 10100x | 101x0x | 10100x | — | 101001 | Ø | Ø | 101101 | 10110x | 10110x | 101101 | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | 1×1001 | 1x1x01 | Ø | Ø | Ø | 1×1101 | Ø | 1×1101 | Ø |
| 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01001 | Ø | Ø | 10100x | x01001 | x01001 | xx1001 | 101001 | Ø | Ø | Ø | Ø | Ø | 101×01 | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | 11100x | x11001 | x11001 | 111001 | Ø | Ø | Ø | Ø | 1110×1 | Ø | Ø | Ø | Ø | 111×01 | Ø | Ø | Ø | 10×001 | Ø | 10100x | 10×001 | 10×001 | 101001 | Ø | Ø | 101×01 | 101001 | 10100x | 10100x | 1x100x | 101001 | — | Ø | Ø | 101×01 | Ø | Ø | 1x1x01 | Ø | Ø | Ø | Ø | 111001 | 11100x | 11100x | 111001 | 111001 | 1110×1 | Ø | 1110×1 | 111×01 | Ø | 111×01 | Ø |
| 101×10 | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | 1010×0 | Ø | Ø | Ø | Ø | x01010 | x01010 | 101010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | Ø | Ø | Ø | 1010×0 | Ø | Ø | Ø | Ø | 1011×0 | Ø | 1010×0 | 101010 | 101xx0 | 1010×0 | Ø | Ø | — | 101010 | 1011×0 | 101110 | 1011×0 | Ø | 101110 | Ø | 1×1110 | Ø | Ø | 1×1010 | Ø | Ø | Ø | 1×1010 | 1x1x10 | Ø | Ø | 1×1110 | Ø | 1×1110 |
| 1×1010 | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | 1010×0 | Ø | Ø | Ø | Ø | x01010 | xx1010 | 101010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | 1110×0 | Ø | Ø | Ø | x11010 | x11010 | 111010 | Ø | 11101x | Ø | Ø | Ø | Ø | Ø | Ø | 111×10 | Ø | Ø | Ø | 1010×0 | Ø | Ø | Ø | Ø | Ø | Ø | 1010×0 | 101010 | 1010×0 | 1x10x0 | Ø | Ø | 101010 | — | Ø | 101×10 | Ø | Ø | 1x1x10 | Ø | 111×10 | Ø | 1110×0 | 111010 | 1110×0 | 11101x | Ø | 111010 | 111010 | 11101x | Ø | 111×10 | Ø | 111×10 |
| 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×100 | Ø | x01101 | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | 101×00 | Ø | x01101 | Ø | 101×01 | Ø | Ø | Ø | Ø | x01101 | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | 1×1101 | Ø | Ø | Ø | Ø | 10×100 | 101×00 | Ø | 10×101 | 101×01 | 10x10x | 101100 | 101101 | 101x0x | 101×00 | 101100 | 101×00 | 101101 | 101×01 | 1011×0 | Ø | — | 101100 | 101100 | 101101 | 1011×0 | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | 1×1101 | Ø | Ø | Ø | 1x110x | 1×1100 | 1×1101 | Ø |
| 1011×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 101×00 | Ø | Ø | Ø | Ø | Ø | Ø | 101×10 | Ø | Ø | 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | 1×1110 | Ø | Ø | 10×100 | 101×00 | Ø | Ø | Ø | 10×100 | 101100 | 10110x | 101×00 | 101xx0 | 101100 | 101×00 | 10110x | Ø | 101110 | 101×10 | 101100 | — | 101100 | 10110x | 101110 | Ø | 1×1110 | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | 1×1110 | Ø | 1×1100 | 1x11x0 | Ø | 1×1110 |
| 1×1100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 101×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | 111×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | x11100 | 111100 | Ø | 11110x | Ø | 1111×0 | Ø | Ø | 10×100 | 101×00 | Ø | Ø | Ø | 10×100 | 101100 | 10110x | 101×00 | 101×00 | 101100 | 1x1x00 | 10110x | Ø | 1011×0 | Ø | 101100 | 101100 | — | 1x110x | 1x11x0 | Ø | 1111×0 | Ø | 111×00 | 111×00 | 111100 | Ø | 11110x | Ø | 1111×0 | Ø | 111100 | 111100 | 11110x | 1111×0 |
| 1×1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | 101×01 | Ø | Ø | Ø | Ø | xx1101 | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | 111×01 | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | 11110x | x11101 | 111101 | Ø | Ø | 1111×1 | Ø | Ø | Ø | Ø | 10×101 | 101×01 | 10×101 | 10110x | 101101 | 101×01 | Ø | 10110x | Ø | 101101 | 1x1x01 | Ø | Ø | 101101 | 10110x | 1x110x | — | Ø | Ø | Ø | 1111×1 | 111×01 | Ø | 11110x | 111×01 | 111101 | Ø | Ø | 1111×1 | 111101 | 11110x | 111101 | 1111×1 |
| 1×1110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 101×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | 111×10 | Ø | Ø | Ø | x11110 | 1111×0 | Ø | Ø | x11110 | 111110 | 11111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1011×0 | Ø | Ø | 101×10 | 1011×0 | Ø | Ø | Ø | 101110 | 1x1x10 | 1011×0 | 101110 | 1x11x0 | Ø | — | 11×110 | 111110 | 11111x | Ø | 111×10 | 1111×0 | Ø | Ø | 111×10 | 111110 | 11111x | 1111×0 | 111110 | 11111x | 111110 |
| 11011x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | x10111 | 110111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11×110 | 11×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11×110 | — | 110110 | 110111 | Ø | Ø | Ø | Ø | Ø | Ø | 11×110 | 11×111 | Ø | 11×110 | 11×111 | 11x11x |
| 11×110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11011x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | 111×10 | Ø | Ø | Ø | x11110 | 1111×0 | Ø | Ø | x11110 | 111110 | 11111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | 111×10 | Ø | 1×1110 | 1111×0 | Ø | 111110 | 110110 | — | 11x11x | Ø | 111×10 | 1111×0 | Ø | Ø | 111×10 | 111110 | 11111x | 1111×0 | 111110 | 11111x | 111110 |
| 11×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | x1x111 | 110111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 | 111×11 | Ø | Ø | Ø | x11111 | 1111×1 | x11111 | 11111x | 111111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1111×1 | 11111x | 110111 | 11x11x | — | Ø | Ø | Ø | 111×11 | 1111×1 | 111×11 | 11111x | 111111 | 1111×1 | 11111x | 111111 | 111111 |
| 11100x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | Ø | Ø | x11001 | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x1100x | x11000 | x11000 | 111000 | x11001 | x11001 | 111001 | Ø | Ø | 1110×0 | Ø | 1110×1 | Ø | Ø | 111×00 | Ø | 111×01 | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | 1×1001 | Ø | Ø | Ø | 1x100x | 1×1000 | 1×1000 | 111000 | 1×1001 | 111001 | Ø | 1110×0 | Ø | Ø | 111×00 | 111×01 | Ø | Ø | Ø | Ø | — | 111000 | 111000 | 111001 | 111001 | 1110xx | 1110×0 | 1110×1 | 111x0x | 111×00 | 111×01 | Ø |
| 1110×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | Ø | Ø | Ø | Ø | Ø | x11010 | 1×1010 | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | x110x0 | x11000 | 111000 | Ø | Ø | 11100x | x11010 | x11010 | 111010 | Ø | 11101x | Ø | Ø | 111×00 | Ø | Ø | Ø | 111×10 | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | 1x10x0 | 1×1000 | 111000 | Ø | 11100x | 1×1010 | 111010 | Ø | Ø | 111×00 | Ø | 111×10 | Ø | 111×10 | Ø | 111000 | — | 111000 | 1110xx | 11100x | 111010 | 111010 | 11101x | 111×00 | 111xx0 | Ø | 111×10 |
| 111×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | x11000 | x11000 | x11x00 | 111000 | Ø | Ø | 11100x | Ø | Ø | 1110×0 | Ø | Ø | x11100 | x11100 | 111100 | Ø | 11110x | Ø | 1111×0 | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | 1×1100 | Ø | 1×1000 | 1×1000 | 1x1x00 | 111000 | Ø | 11100x | Ø | 1110×0 | 1×1100 | 1×1100 | 111100 | 11110x | 1111×0 | Ø | 1111×0 | Ø | 111000 | 111000 | — | 11100x | 111x0x | 1110×0 | 111xx0 | Ø | 111100 | 111100 | 11110x | 1111×0 |
| 1110×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | 1×1001 | Ø | Ø | Ø | x11011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | 11100x | x110x1 | x11001 | 111001 | x11011 | Ø | 11101x | x11011 | 111011 | Ø | Ø | Ø | Ø | 111×01 | Ø | Ø | 111×11 | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | 1×1001 | Ø | Ø | 11100x | 1×1001 | 111001 | Ø | 11101x | Ø | Ø | Ø | 111×01 | Ø | Ø | Ø | 111×11 | 111001 | 1110xx | 11100x | — | 111001 | 111011 | 11101x | 111011 | 111×01 | Ø | 111xx1 | 111×11 |
| 111×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | 1×1001 | Ø | Ø | Ø | Ø | x11101 | 1×1101 | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | x11001 | Ø | Ø | 11100x | x11001 | x11x01 | 111001 | Ø | Ø | Ø | Ø | 1110×1 | x11101 | Ø | 11110x | x11101 | 111101 | Ø | Ø | 1111×1 | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | 1×1101 | 1×1001 | Ø | Ø | 11100x | 1x1x01 | 111001 | Ø | Ø | 1×1101 | Ø | 11110x | 111101 | Ø | Ø | Ø | 1111×1 | 111001 | 11100x | 111x0x | 111001 | — | 1110×1 | Ø | 111xx1 | 111101 | 11110x | 111101 | 1111×1 |
| 11101x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | 1×1010 | x11011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | 1110×0 | x11011 | Ø | 1110×1 | x1101x | x11010 | 111010 | x11011 | 111011 | Ø | Ø | Ø | Ø | Ø | Ø | 111×10 | 111×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1010 | Ø | 1110×0 | Ø | 1110×1 | 1×1010 | 111010 | Ø | Ø | Ø | Ø | 111×10 | Ø | 111×10 | 111×11 | 1110xx | 111010 | 1110×0 | 111011 | 1110×1 | — | 111010 | 111011 | Ø | 111×10 | 111×11 | 111x1x |
| 111×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | 1×1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | 1110×0 | Ø | Ø | Ø | x11010 | x11x10 | 111010 | Ø | 11101x | Ø | x11110 | 1111×0 | Ø | Ø | x11110 | 111110 | 11111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1010 | Ø | 1110×0 | Ø | Ø | 1x1x10 | 111010 | Ø | 1×1110 | 1111×0 | Ø | 111110 | 11×110 | 111110 | 11111x | 1110×0 | 111010 | 111xx0 | 11101x | Ø | 111010 | — | 111x1x | 1111×0 | 111110 | 11111x | 111110 |
| 111×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 | 11×111 | Ø | Ø | Ø | Ø | x11011 | Ø | 1110×1 | x11011 | Ø | 11101x | x11x11 | 111011 | Ø | Ø | Ø | x11111 | 1111×1 | x11111 | 11111x | 111111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1110×1 | Ø | 11101x | Ø | Ø | Ø | 1111×1 | 11111x | 11×111 | 11111x | 111111 | 1110×1 | 11101x | Ø | 111011 | 111xx1 | 111011 | 111x1x | — | 1111×1 | 11111x | 111111 | 111111 |
| 11110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | 1×1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | x11101 | Ø | Ø | Ø | Ø | x11100 | 111×00 | Ø | x11101 | 111×01 | Ø | Ø | Ø | Ø | Ø | x1110x | x11100 | 111100 | x11101 | 111101 | Ø | 1111×0 | 1111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | 1×1101 | Ø | Ø | 1×1100 | 111×00 | 1×1101 | 111×01 | Ø | Ø | 1x110x | 1×1100 | 111100 | 111101 | 1111×0 | Ø | 1111×0 | 1111×1 | 111x0x | 111×00 | 111100 | 111×01 | 111101 | Ø | 1111×0 | 1111×1 | — | 111100 | 111101 | 1111xx |
| 1111×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | 111×00 | Ø | Ø | Ø | Ø | x11110 | 111×10 | Ø | Ø | x11100 | x111x0 | 111100 | Ø | 11110x | x11110 | 111110 | 11111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | 1×1100 | 111×00 | Ø | Ø | 1×1110 | 111×10 | 1×1100 | 1x11x0 | 111100 | 11110x | 111110 | 11×110 | 111110 | 11111x | 111×00 | 111xx0 | 111100 | Ø | 11110x | 111×10 | 111110 | 11111x | 111100 | — | 1111xx | 111110 |
| 1111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | 1×1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | x11111 | 11×111 | Ø | Ø | Ø | Ø | Ø | x11101 | 111×01 | Ø | Ø | Ø | x11111 | 111×11 | x11101 | Ø | 11110x | x111x1 | 111101 | x11111 | 11111x | 111111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | Ø | 1×1101 | 111×01 | Ø | Ø | 1×1101 | Ø | 11110x | 111101 | 11111x | 11×111 | 11111x | 111111 | 111×01 | Ø | 11110x | 111xx1 | 111101 | 111×11 | 11111x | 111111 | 111101 | 1111xx | — | 111111 |
| 11111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 | 11×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | 111×10 | x11111 | 111×11 | Ø | x11110 | 1111×0 | x11111 | 1111×1 | x1111x | 111110 | 111111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | 111×10 | Ø | 1×1110 | 1111×0 | 1111×1 | 111110 | 11x11x | 111110 | 111111 | Ø | 111×10 | 1111×0 | 111×11 | 1111×1 | 111x1x | 111110 | 111111 | 1111xx | 111110 | 111111 | — |
Z1=
Ĉ2=C1∪(C1*C1)
C2=>
| 000xx0, 00x0x0, 0x00x0 0x0x00, x00x00, 0xx000 x0x000, 0xx010, 0001xx 0x010x, x0010x, 0x01x1 0xx101, x0x101, 0010xx 0x100x, x0100x, 0x10x0 x010x0, xx1000, 0x10x1 0x1x01, x01x01, xx1001 0x101x, xx1010, xx1101 010x0x, 01x00x, 01x0x0 01xx00, 01xx01, 01x10x 01x1x1, x1x111, 0110xx 011x0x, x1100x, 011xx0 x110x0, x11x00, 011xx1 x110x1, x11x01, 011x1x x1101x, x11x10, x11x11 0111xx, x1110x, x111x0 x111x1, x1111x, 100x0x 10x00x, 10xx00, 10xx01 10x10x, 101x0x, 1x100x 101xx0, 1x10x0, 1x1x00 1x1x01, 1x1x10, 1x110x 1x11x0, 11x11x, 1110xx 111x0x, 111xx0, 111xx1 111x1x, 1111xx |
| 000xx0 | 00x0x0 | 0x00x0 | 0x0x00 | x00x00 | 0xx000 | x0x000 | 0xx010 | 0001xx | 0x010x | x0010x | 0x01x1 | 0xx101 | x0x101 | 0010xx | 0x100x | x0100x | 0x10x0 | x010x0 | xx1000 | 0x10x1 | 0x1x01 | x01x01 | xx1001 | 0x101x | xx1010 | xx1101 | 010x0x | 01x00x | 01x0x0 | 01xx00 | 01xx01 | 01x10x | 01x1x1 | x1x111 | 0110xx | 011x0x | x1100x | 011xx0 | x110x0 | x11x00 | 011xx1 | x110x1 | x11x01 | 011x1x | x1101x | x11x10 | x11x11 | 0111xx | x1110x | x111x0 | x111x1 | x1111x | 100x0x | 10x00x | 10xx00 | 10xx01 | 10x10x | 101x0x | 1x100x | 101xx0 | 1x10x0 | 1x1x00 | 1x1x01 | 1x1x10 | 1x110x | 1x11x0 | 11x11x | 1110xx | 111x0x | 111xx0 | 111xx1 | 111x1x | 1111xx | |
| 000xx0 | — | 0000×0 | 0000×0 | 000×00 | 000×00 | 000000 | 000000 | 000010 | 0001×0 | 000100 | 000100 | 0001xx | 00010x | 00010x | 00x0x0 | 00×000 | 00×000 | 00x0x0 | 00x0x0 | 00×000 | Ø | Ø | Ø | Ø | 00×010 | 00×010 | Ø | 0x0x00 | 0x0000 | 0x00x0 | 0x0x00 | Ø | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00x00 | x00000 | x00x00 | Ø | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00x0x0 | 0000×0 | — | 0000×0 | 000000 | 000000 | 00×000 | 00×000 | 00×010 | 000xx0 | 000×00 | 000×00 | Ø | Ø | Ø | 0010×0 | 001000 | 001000 | 0010×0 | 0010×0 | 001000 | 0010xx | 00100x | 00100x | 00100x | 001010 | 001010 | Ø | 0x0000 | 0xx000 | 0xx0x0 | 0xx000 | Ø | Ø | Ø | Ø | 0x10x0 | 0x1000 | 0x1000 | 0x10x0 | 0x10x0 | 0x1000 | Ø | Ø | Ø | 0x1010 | 0x1010 | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | x0x000 | x0x000 | Ø | Ø | x01000 | x01000 | x010x0 | x010x0 | x01000 | Ø | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x00x0 | 0000×0 | 0000×0 | — | 0x0000 | 000000 | 0x0000 | 000000 | 0x0010 | 000xx0 | 0x0x00 | 000×00 | Ø | Ø | Ø | 00x0x0 | 0xx000 | 00×000 | 0xx0x0 | 00x0x0 | 0xx000 | Ø | Ø | Ø | Ø | 0xx010 | 0xx010 | Ø | 010000 | 010000 | 0100×0 | 010000 | 01000x | 010×00 | Ø | Ø | 01x0x0 | 01×000 | 01×000 | 01x0x0 | 01x0x0 | 01×000 | Ø | Ø | Ø | 01×010 | 01×010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | x00000 | x00000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x0x00 | 000×00 | 000000 | 0x0000 | — | 000×00 | 0x0000 | 000000 | 0x00x0 | 000100 | 0x0100 | 000100 | 0x010x | 0x010x | 00010x | 00×000 | 0xx000 | 00×000 | 0xx000 | 00×000 | 0xx000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010×00 | 010000 | 010000 | 010×00 | 010x0x | 010100 | 01010x | Ø | 01×000 | 01xx00 | 01×000 | 01xx00 | 01×000 | 01xx00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | 01×100 | 01×100 | Ø | Ø | x00x00 | x00000 | x00x00 | Ø | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x00x00 | 000×00 | 000000 | 000000 | 000×00 | — | 000000 | x00000 | 0000×0 | 000100 | 000100 | x00100 | 00010x | 00010x | x0010x | 00×000 | 00×000 | x0x000 | 00×000 | x0x000 | x0x000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0x00 | 0x0000 | 0x0000 | 0x0x00 | Ø | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×00 | 100000 | 100×00 | 100x0x | 100100 | 10xx00 | 10×000 | 10xx00 | 10×000 | 10xx00 | Ø | Ø | 10×100 | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0xx000 | 000000 | 00×000 | 0x0000 | 0x0000 | 000000 | — | 00×000 | 0xx0x0 | 000×00 | 0x0x00 | 000×00 | Ø | Ø | Ø | 001000 | 0x1000 | 001000 | 0x1000 | 001000 | 0x1000 | 0x100x | 0x100x | 00100x | 0x100x | 0x10x0 | 0x10x0 | Ø | 010000 | 01×000 | 01×000 | 01×000 | 01x00x | 01xx00 | Ø | Ø | 011000 | 011000 | 011000 | 011000 | 011000 | 011000 | 01100x | 01100x | 01100x | 0110×0 | 0110×0 | 0110×0 | Ø | 011×00 | 011×00 | 011×00 | Ø | Ø | x00000 | x0x000 | x0x000 | Ø | Ø | x01000 | xx1000 | x01000 | xx1000 | xx1000 | Ø | Ø | Ø | Ø | Ø | x11000 | x11000 | x11000 | Ø | Ø | Ø |
| x0x000 | 000000 | 00×000 | 000000 | 000000 | x00000 | 00×000 | — | 00x0x0 | 000×00 | 000×00 | x00x00 | Ø | Ø | Ø | 001000 | 001000 | x01000 | 001000 | x01000 | x01000 | 00100x | 00100x | x0100x | x0100x | 0010×0 | x010x0 | Ø | 0x0000 | 0xx000 | 0xx000 | 0xx000 | Ø | Ø | Ø | Ø | 0x1000 | 0x1000 | xx1000 | 0x1000 | xx1000 | xx1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100000 | 10×000 | 10×000 | 10x00x | 10xx00 | 101000 | 101000 | 101000 | 101000 | 101000 | 10100x | 1010×0 | 101×00 | 101×00 | Ø | 1×1000 | 1×1000 | 1×1000 | Ø | Ø | Ø |
| 0xx010 | 000010 | 00×010 | 0x0010 | 0x00x0 | 0000×0 | 0xx0x0 | 00x0x0 | — | 000×10 | Ø | Ø | Ø | Ø | Ø | 001010 | 0x10x0 | 0010×0 | 0x1010 | 001010 | 0x10x0 | 0x101x | Ø | Ø | Ø | 0x1010 | 0x1010 | Ø | 0100×0 | 01x0x0 | 01×010 | 01x0x0 | Ø | Ø | Ø | Ø | 011010 | 0110×0 | 0110×0 | 011010 | 011010 | 0110×0 | 01101x | 01101x | Ø | 011010 | 011010 | 011010 | 01101x | 011×10 | Ø | 011×10 | Ø | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | xx1010 | Ø | Ø | xx1010 | Ø | Ø | Ø | x11010 | Ø | x11010 | Ø | x11010 | Ø |
| 0001xx | 0001×0 | 000xx0 | 000xx0 | 000100 | 000100 | 000×00 | 000×00 | 000×10 | — | 00010x | 00010x | 0001×1 | 000101 | 000101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | 00×101 | Ø | Ø | Ø | 00×101 | 0x010x | Ø | Ø | 0x0100 | 0x0101 | 0x010x | 0x01x1 | 0x0111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x0010x | Ø | x00100 | x00101 | x0010x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x010x | 000100 | 000×00 | 0x0x00 | 0x0100 | 000100 | 0x0x00 | 000×00 | Ø | 00010x | — | 00010x | 0x0101 | 0x0101 | 000101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0xx101 | 00×101 | Ø | Ø | Ø | 0xx101 | 01010x | 010x0x | 010×00 | 010100 | 010101 | 01010x | 010101 | 0101×1 | Ø | 01x10x | Ø | 01×100 | Ø | 01×100 | 01×101 | Ø | 01×101 | Ø | Ø | Ø | Ø | 01x10x | 01x10x | 01×100 | 01×101 | Ø | x0010x | Ø | x00100 | x00101 | x0010x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x0010x | 000100 | 000×00 | 000×00 | 000100 | x00100 | 000×00 | x00x00 | Ø | 00010x | 00010x | — | 000101 | 000101 | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | x0x101 | Ø | Ø | Ø | x0x101 | 0x010x | Ø | Ø | 0x0100 | 0x0101 | 0x010x | 0x0101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10010x | 100x0x | 100100 | 100101 | 10010x | 10x10x | Ø | 10×100 | Ø | 10×100 | 10×101 | Ø | 10x10x | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x01x1 | 0001xx | Ø | Ø | 0x010x | 00010x | Ø | Ø | Ø | 0001×1 | 0x0101 | 000101 | — | 0x0101 | 000101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0xx101 | 00×101 | Ø | Ø | Ø | 0xx101 | 010101 | 010×01 | Ø | 01010x | 010101 | 010101 | 0101×1 | 010111 | Ø | 01×101 | Ø | Ø | Ø | Ø | 01x1x1 | Ø | 01×101 | 01×111 | Ø | Ø | 01×111 | 01x1x1 | 01×101 | Ø | 01x1x1 | 01×111 | x00101 | Ø | Ø | x00101 | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø |
| 0xx101 | 00010x | Ø | Ø | 0x010x | 00010x | Ø | Ø | Ø | 000101 | 0x0101 | 000101 | 0x0101 | — | 00×101 | 001×01 | 0x1x01 | 001×01 | Ø | Ø | Ø | 0x1x01 | 0x1101 | 001101 | 0x1x01 | Ø | Ø | 0x1101 | 010101 | 01xx01 | Ø | 01x10x | 01×101 | 01×101 | 01×101 | 01x1x1 | 011×01 | 011101 | 011×01 | 01110x | Ø | 01110x | 011101 | 011×01 | 011101 | 0111×1 | Ø | Ø | 0111×1 | 011101 | 011101 | 01110x | 011101 | 0111×1 | x00101 | Ø | Ø | x0x101 | x0x101 | x01101 | Ø | Ø | Ø | Ø | xx1101 | Ø | xx1101 | Ø | Ø | Ø | x11101 | Ø | x11101 | Ø | x11101 |
| x0x101 | 00010x | Ø | Ø | 00010x | x0010x | Ø | Ø | Ø | 000101 | 000101 | x00101 | 000101 | 00×101 | — | 001×01 | 001×01 | x01x01 | Ø | Ø | Ø | 001×01 | 001101 | x01101 | x01x01 | Ø | Ø | x01101 | 0x0101 | Ø | Ø | Ø | 0xx101 | 0xx101 | 0xx101 | Ø | Ø | 0x1101 | Ø | Ø | Ø | Ø | 0x1101 | Ø | xx1101 | Ø | Ø | Ø | Ø | 0x1101 | xx1101 | Ø | xx1101 | Ø | 100101 | 10xx01 | 10x10x | 10×101 | 10×101 | 101101 | 101×01 | 10110x | Ø | 10110x | 101101 | Ø | 101101 | 10110x | Ø | Ø | 1×1101 | Ø | 1×1101 | Ø | 1×1101 |
| 0010xx | 00x0x0 | 0010×0 | 00x0x0 | 00×000 | 00×000 | 001000 | 001000 | 001010 | Ø | Ø | Ø | Ø | 001×01 | 001×01 | — | 00100x | 00100x | 0010×0 | 0010×0 | 001000 | 0010×1 | 001001 | 001001 | 001001 | 00101x | 001010 | 001×01 | Ø | 0x100x | 0x10x0 | 0x1000 | 0x1001 | Ø | Ø | Ø | 0x10xx | 0x100x | 0x100x | 0x10x0 | 0x10x0 | 0x1000 | 0x10x1 | 0x10x1 | 0x1001 | 0x101x | 0x101x | 0x1010 | 0x1011 | Ø | Ø | Ø | Ø | Ø | Ø | x0100x | x01000 | x01001 | Ø | x0100x | x0100x | x010x0 | x010x0 | x01000 | x01001 | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x100x | 00×000 | 001000 | 0xx000 | 0xx000 | 00×000 | 0x1000 | 001000 | 0x10x0 | Ø | Ø | Ø | Ø | 0x1x01 | 001×01 | 00100x | — | 00100x | 0x1000 | 001000 | 0x1000 | 0x1001 | 0x1001 | 001001 | 0x1001 | 0x10xx | 0x10x0 | 0x1x01 | 01x00x | 01100x | 011000 | 011000 | 011001 | 011x0x | 011×01 | Ø | 01100x | 01100x | 01100x | 011000 | 011000 | 011000 | 011001 | 011001 | 011001 | 0110xx | 0110xx | 0110×0 | 0110×1 | 011x0x | 011x0x | 011×00 | 011×01 | Ø | Ø | x0100x | x01000 | x01001 | Ø | x0100x | xx100x | x01000 | xx1000 | xx1000 | xx1001 | Ø | Ø | Ø | Ø | x1100x | x1100x | x11000 | x11001 | Ø | Ø |
| x0100x | 00×000 | 001000 | 00×000 | 00×000 | x0x000 | 001000 | x01000 | 0010×0 | Ø | Ø | Ø | Ø | 001×01 | x01x01 | 00100x | 00100x | — | 001000 | x01000 | x01000 | 001001 | 001001 | x01001 | x01001 | 0010xx | x010x0 | x01x01 | Ø | 0x100x | 0x1000 | 0x1000 | 0x1001 | Ø | Ø | Ø | 0x100x | 0x100x | xx100x | 0x1000 | xx1000 | xx1000 | 0x1001 | xx1001 | xx1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10x00x | 10100x | 101000 | 101001 | 101x0x | 10100x | 10100x | 101000 | 101000 | 101000 | 101001 | 1010×0 | 101x0x | 101×00 | Ø | 1x100x | 1x100x | 1×1000 | 1×1001 | Ø | Ø |
| 0x10x0 | 00x0x0 | 0010×0 | 0xx0x0 | 0xx000 | 00×000 | 0x1000 | 001000 | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | 0010×0 | 0x1000 | 001000 | — | 0010×0 | 0x1000 | 0x10xx | 0x100x | 00100x | 0x100x | 0x1010 | 0x1010 | Ø | 01×000 | 011000 | 0110×0 | 011000 | 01100x | 011×00 | Ø | Ø | 0110×0 | 011000 | 011000 | 0110×0 | 0110×0 | 011000 | 0110xx | 0110xx | 01100x | 011010 | 011010 | 011010 | 01101x | 011xx0 | 011×00 | 011xx0 | Ø | 011×10 | Ø | x01000 | x01000 | Ø | Ø | x01000 | xx1000 | x010x0 | xx10x0 | xx1000 | Ø | xx1010 | Ø | Ø | Ø | x110x0 | x11000 | x110x0 | Ø | x11010 | Ø |
| x010x0 | 00x0x0 | 0010×0 | 00x0x0 | 00×000 | x0x000 | 001000 | x01000 | 001010 | Ø | Ø | Ø | Ø | Ø | Ø | 0010×0 | 001000 | x01000 | 0010×0 | — | x01000 | 0010xx | 00100x | x0100x | x0100x | 001010 | x01010 | Ø | Ø | 0x1000 | 0x10x0 | 0x1000 | Ø | Ø | Ø | Ø | 0x10x0 | 0x1000 | xx1000 | 0x10x0 | xx10x0 | xx1000 | Ø | Ø | Ø | 0x1010 | xx1010 | xx1010 | Ø | Ø | Ø | Ø | Ø | Ø | 10×000 | 101000 | 101000 | 10100x | 101×00 | 101000 | 101000 | 1010×0 | 1010×0 | 101000 | 10100x | 101010 | 101×00 | 101xx0 | Ø | 1x10x0 | 1×1000 | 1x10x0 | Ø | 1×1010 | Ø |
| xx1000 | 00×000 | 001000 | 0xx000 | 0xx000 | x0x000 | 0x1000 | x01000 | 0x10x0 | Ø | Ø | Ø | Ø | Ø | Ø | 001000 | 0x1000 | x01000 | 0x1000 | x01000 | — | 0x100x | 0x100x | x0100x | xx100x | 0x10x0 | xx10x0 | Ø | 01×000 | 011000 | 011000 | 011000 | 01100x | 011×00 | Ø | Ø | 011000 | 011000 | x11000 | 011000 | x11000 | x11000 | 01100x | x1100x | x1100x | 0110×0 | x110x0 | x110x0 | Ø | 011×00 | x11x00 | x11x00 | Ø | Ø | 10×000 | 101000 | 101000 | 10100x | 101×00 | 101000 | 1×1000 | 101000 | 1×1000 | 1×1000 | 1x100x | 1x10x0 | 1x1x00 | 1x1x00 | Ø | 111000 | 111000 | 111000 | 11100x | 1110×0 | 111×00 |
| 0x10x1 | Ø | 0010xx | Ø | Ø | Ø | 0x100x | 00100x | 0x101x | Ø | Ø | Ø | Ø | 0x1x01 | 001×01 | 0010×1 | 0x1001 | 001001 | 0x10xx | 0010xx | 0x100x | — | 0x1001 | 001001 | 0x1001 | 0x1011 | 0x101x | 0x1x01 | 01×001 | 011001 | 0110xx | 01100x | 011001 | 011×01 | 011xx1 | 011×11 | 0110×1 | 011001 | 011001 | 0110xx | 0110xx | 01100x | 0110×1 | 0110×1 | 011001 | 011011 | 011011 | 01101x | 011011 | 011xx1 | 011×01 | Ø | 011xx1 | 011×11 | Ø | x01001 | Ø | x01001 | Ø | x01001 | xx1001 | Ø | Ø | Ø | xx1001 | Ø | Ø | Ø | Ø | x110x1 | x11001 | Ø | x110x1 | x11011 | Ø |
| 0x1x01 | Ø | 00100x | Ø | Ø | Ø | 0x100x | 00100x | Ø | 00×101 | 0xx101 | 00×101 | 0xx101 | 0x1101 | 001101 | 001001 | 0x1001 | 001001 | 0x100x | 00100x | 0x100x | 0x1001 | — | 001×01 | 0x1001 | 0x10x1 | Ø | 0x1101 | 01xx01 | 011001 | 01100x | 011x0x | 011×01 | 011101 | 011101 | 0111×1 | 011001 | 011×01 | 011001 | 011x0x | 01100x | 011x0x | 011×01 | 011001 | 011×01 | 011xx1 | 0110×1 | Ø | 011xx1 | 011101 | 011101 | 01110x | 011101 | 0111×1 | Ø | x01001 | Ø | x01x01 | x01101 | x01x01 | xx1001 | Ø | Ø | Ø | xx1x01 | Ø | xx1101 | Ø | Ø | x11001 | x11x01 | Ø | x11x01 | Ø | x11101 |
| x01x01 | Ø | 00100x | Ø | Ø | Ø | 00100x | x0100x | Ø | 00×101 | 00×101 | x0x101 | 00×101 | 001101 | x01101 | 001001 | 001001 | x01001 | 00100x | x0100x | x0100x | 001001 | 001×01 | — | x01001 | 0010×1 | Ø | x01101 | Ø | 0x1001 | Ø | Ø | 0x1x01 | 0x1101 | 0x1101 | Ø | 0x1001 | 0x1x01 | xx1001 | Ø | Ø | Ø | 0x1x01 | xx1001 | xx1x01 | Ø | Ø | Ø | Ø | 0x1101 | xx1101 | Ø | xx1101 | Ø | 10xx01 | 101001 | 101x0x | 101×01 | 101101 | 101×01 | 101001 | 101x0x | 10100x | 101x0x | 101×01 | Ø | 101101 | 10110x | Ø | 1×1001 | 1x1x01 | Ø | 1x1x01 | Ø | 1×1101 |
| xx1001 | Ø | 00100x | Ø | Ø | Ø | 0x100x | x0100x | Ø | Ø | Ø | Ø | Ø | 0x1x01 | x01x01 | 001001 | 0x1001 | x01001 | 0x100x | x0100x | xx100x | 0x1001 | 0x1001 | x01001 | — | 0x10x1 | Ø | xx1x01 | 01×001 | 011001 | 01100x | 01100x | 011001 | 011×01 | 011×01 | Ø | 011001 | 011001 | x11001 | 01100x | x1100x | x1100x | 011001 | x11001 | x11001 | 0110×1 | x110x1 | Ø | x110x1 | 011×01 | x11x01 | Ø | x11x01 | Ø | 10×001 | 101001 | 10100x | 101001 | 101×01 | 101001 | 1×1001 | 10100x | 1x100x | 1x100x | 1×1001 | Ø | 1x1x01 | Ø | Ø | 111001 | 111001 | 11100x | 111001 | 1110×1 | 111×01 |
| 0x101x | 00×010 | 001010 | 0xx010 | Ø | Ø | 0x10x0 | 0010×0 | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | 00101x | 0x10xx | 0010xx | 0x1010 | 001010 | 0x10x0 | 0x1011 | 0x10x1 | 0010×1 | 0x10x1 | — | 0x1010 | Ø | Ø | 0110xx | 011010 | 0110×0 | 0110×1 | Ø | 011×11 | 011×11 | 01101x | 0110xx | 0110xx | 011010 | 011010 | 0110×0 | 011011 | 011011 | 0110×1 | 01101x | 01101x | 011010 | 011011 | 011x1x | Ø | 011×10 | 011×11 | 011x1x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | xx1010 | Ø | Ø | xx1010 | Ø | Ø | Ø | x1101x | Ø | x11010 | x11011 | x1101x | Ø |
| xx1010 | 00×010 | 001010 | 0xx010 | Ø | Ø | 0x10x0 | x010x0 | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | 001010 | 0x10x0 | x010x0 | 0x1010 | x01010 | xx10x0 | 0x101x | Ø | Ø | Ø | 0x1010 | — | Ø | Ø | 0110×0 | 011010 | 0110×0 | Ø | Ø | Ø | Ø | 011010 | 0110×0 | x110x0 | 011010 | x11010 | x110x0 | 01101x | x1101x | Ø | 011010 | x11010 | x11010 | x1101x | 011×10 | Ø | x11x10 | Ø | x11x10 | Ø | 1010×0 | 1010×0 | Ø | Ø | 1010×0 | 1x10x0 | 101010 | 1×1010 | 1x10x0 | Ø | 1×1010 | Ø | 1x1x10 | 111×10 | 111010 | 1110×0 | 111010 | 11101x | 111010 | 111×10 |
| xx1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | 0xx101 | x0x101 | 0xx101 | 0x1101 | x01101 | 001×01 | 0x1x01 | x01x01 | Ø | Ø | Ø | 0x1x01 | 0x1101 | x01101 | xx1x01 | Ø | Ø | — | 01×101 | 011×01 | Ø | 01110x | 011101 | 011101 | 011101 | x111x1 | 011×01 | 011101 | x11x01 | 01110x | Ø | x1110x | 011101 | x11x01 | x11101 | 0111×1 | Ø | Ø | x111x1 | 011101 | x11101 | x1110x | x11101 | x111x1 | 10×101 | 101×01 | 10110x | 101101 | 101101 | 101101 | 1x1x01 | 10110x | Ø | 1x110x | 1×1101 | Ø | 1×1101 | 1x110x | 1111×1 | 111×01 | 111101 | 11110x | 111101 | 1111×1 | 111101 |
| 010x0x | 0x0x00 | 0x0000 | 010000 | 010×00 | 0x0x00 | 010000 | 0x0000 | 0100×0 | 0x010x | 01010x | 0x010x | 010101 | 010101 | 0x0101 | Ø | 01x00x | Ø | 01×000 | Ø | 01×000 | 01×001 | 01xx01 | Ø | 01×001 | Ø | Ø | 01×101 | — | 01000x | 010000 | 010×00 | 010×01 | 01010x | 010101 | 0101×1 | 01x00x | 01xx0x | 01x00x | 01xx00 | 01×000 | 01xx00 | 01xx01 | 01×001 | 01xx01 | Ø | Ø | Ø | Ø | 01x10x | 01x10x | 01×100 | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 01x00x | 0x0000 | 0xx000 | 010000 | 010000 | 0x0000 | 01×000 | 0xx000 | 01x0x0 | Ø | 010x0x | Ø | 010×01 | 01xx01 | Ø | 0x100x | 01100x | 0x100x | 011000 | 0x1000 | 011000 | 011001 | 011001 | 0x1001 | 011001 | 0110xx | 0110×0 | 011×01 | 01000x | — | 01×000 | 01×000 | 01×001 | 01xx0x | 01xx01 | Ø | 01100x | 01100x | 01100x | 011000 | 011000 | 011000 | 011001 | 011001 | 011001 | 0110xx | 0110xx | 0110×0 | 0110×1 | 011x0x | 011x0x | 011×00 | 011×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x1100x | Ø | x11000 | x11000 | x11001 | Ø | Ø | Ø | Ø | x1100x | x1100x | x11000 | x11001 | Ø | Ø |
| 01x0x0 | 0x00x0 | 0xx0x0 | 0100×0 | 010000 | 0x0000 | 01×000 | 0xx000 | 01×010 | Ø | 010×00 | Ø | Ø | Ø | Ø | 0x10x0 | 011000 | 0x1000 | 0110×0 | 0x10x0 | 011000 | 0110xx | 01100x | Ø | 01100x | 011010 | 011010 | Ø | 010000 | 01×000 | — | 01×000 | 01x00x | 01xx00 | Ø | Ø | 0110×0 | 011000 | 011000 | 0110×0 | 0110×0 | 011000 | 0110xx | 0110xx | 01100x | 011010 | 011010 | 011010 | 01101x | 011xx0 | 011×00 | 011xx0 | Ø | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | x110x0 | x11000 | Ø | x11010 | Ø | Ø | Ø | x110x0 | x11000 | x110x0 | Ø | x11010 | Ø |
| 01xx00 | 0x0x00 | 0xx000 | 010000 | 010×00 | 0x0x00 | 01×000 | 0xx000 | 01x0x0 | 0x0100 | 010100 | 0x0100 | 01010x | 01x10x | Ø | 0x1000 | 011000 | 0x1000 | 011000 | 0x1000 | 011000 | 01100x | 011x0x | Ø | 01100x | 0110×0 | 0110×0 | 01110x | 010×00 | 01×000 | 01×000 | — | 01xx0x | 01×100 | 01x10x | Ø | 011000 | 011×00 | 011000 | 011×00 | 011000 | 011×00 | 011x0x | 01100x | 011x0x | 011xx0 | 0110×0 | 011xx0 | Ø | 011100 | 011100 | 011100 | 01110x | 0111×0 | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | x11000 | x11x00 | Ø | Ø | x11100 | x11100 | Ø | x11000 | x11x00 | x11x00 | Ø | Ø | x11100 |
| 01xx01 | Ø | Ø | 01000x | 010x0x | Ø | 01x00x | Ø | Ø | 0x0101 | 010101 | 0x0101 | 010101 | 01×101 | 0xx101 | 0x1001 | 011001 | 0x1001 | 01100x | Ø | 01100x | 011001 | 011×01 | 0x1x01 | 011001 | 0110×1 | Ø | 011101 | 010×01 | 01×001 | 01x00x | 01xx0x | — | 01×101 | 01×101 | 01x1x1 | 011001 | 011×01 | 011001 | 011x0x | 01100x | 011x0x | 011×01 | 011001 | 011×01 | 011xx1 | 0110×1 | Ø | 011xx1 | 011101 | 011101 | 01110x | 011101 | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | x11x01 | Ø | x11101 | Ø | Ø | x11001 | x11x01 | Ø | x11x01 | Ø | x11101 |
| 01x10x | 0x0100 | Ø | 010×00 | 010100 | 0x0100 | 01xx00 | Ø | Ø | 0x010x | 01010x | 0x010x | 010101 | 01×101 | 0xx101 | Ø | 011x0x | Ø | 011×00 | Ø | 011×00 | 011×01 | 011101 | 0x1101 | 011×01 | Ø | Ø | 011101 | 01010x | 01xx0x | 01xx00 | 01×100 | 01×101 | — | 01×101 | 01x1x1 | 011x0x | 01110x | 011x0x | 011100 | 011×00 | 011100 | 011101 | 011×01 | 011101 | 0111xx | Ø | 0111×0 | 0111×1 | 01110x | 01110x | 011100 | 011101 | 0111xx | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | x11101 | Ø | x1110x | x11100 | Ø | Ø | x1110x | x11100 | x11101 | Ø | x1110x |
| 01x1x1 | Ø | Ø | Ø | 01010x | Ø | Ø | Ø | Ø | 0x01x1 | 010101 | 0x0101 | 0101×1 | 01×101 | 0xx101 | Ø | 011×01 | Ø | Ø | Ø | Ø | 011xx1 | 011101 | 0x1101 | 011×01 | 011×11 | Ø | 011101 | 010101 | 01xx01 | Ø | 01x10x | 01×101 | 01×101 | — | 01×111 | 011xx1 | 011101 | 011×01 | 0111xx | Ø | 01110x | 0111×1 | 011xx1 | 011101 | 011111 | 011×11 | 01111x | 011111 | 0111×1 | 011101 | 0111xx | 0111×1 | 011111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | x11101 | Ø | x1x111 | Ø | x11101 | Ø | x111x1 | x11111 | x111x1 |
| x1x111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0111 | 0101×1 | Ø | 010111 | 01x1x1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×11 | 0111×1 | Ø | Ø | 011×11 | Ø | x111x1 | 0101×1 | Ø | Ø | Ø | 01x1x1 | 01x1x1 | 01×111 | — | 011×11 | 0111×1 | Ø | 01111x | Ø | Ø | 011111 | x11x11 | x111x1 | 011111 | x11x11 | x1111x | x11111 | 011111 | x111x1 | x1111x | x11111 | x11111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1111×1 | 11111x | 1111×1 | 11111x | 11×111 | 111×11 | 1111×1 | 11111x | 111111 | 111111 | 111111 |
| 0110xx | Ø | 0x10x0 | 01x0x0 | 01×000 | Ø | 011000 | 0x1000 | 011010 | Ø | Ø | Ø | Ø | 011×01 | Ø | 0x10xx | 01100x | 0x100x | 0110×0 | 0x10x0 | 011000 | 0110×1 | 011001 | 0x1001 | 011001 | 01101x | 011010 | 011×01 | 01x00x | 01100x | 0110×0 | 011000 | 011001 | 011x0x | 011xx1 | 011×11 | — | 01100x | 01100x | 0110×0 | 0110×0 | 011000 | 0110×1 | 0110×1 | 011001 | 01101x | 01101x | 011010 | 011011 | 011xxx | 011x0x | 011xx0 | 011xx1 | 011x1x | Ø | Ø | Ø | Ø | Ø | Ø | x1100x | Ø | x110x0 | x11000 | x11001 | x11010 | Ø | Ø | Ø | x110xx | x1100x | x110x0 | x110x1 | x1101x | Ø |
| 011x0x | Ø | 0x1000 | 01×000 | 01xx00 | Ø | 011000 | 0x1000 | 0110×0 | Ø | 01x10x | Ø | 01×101 | 011101 | 0x1101 | 0x100x | 01100x | 0x100x | 011000 | 0x1000 | 011000 | 011001 | 011×01 | 0x1x01 | 011001 | 0110xx | 0110×0 | 011101 | 01xx0x | 01100x | 011000 | 011×00 | 011×01 | 01110x | 011101 | 0111×1 | 01100x | — | 01100x | 011×00 | 011000 | 011×00 | 011×01 | 011001 | 011×01 | 011xxx | 0110xx | 011xx0 | 011xx1 | 01110x | 01110x | 011100 | 011101 | 0111xx | Ø | Ø | Ø | Ø | Ø | Ø | x1100x | Ø | x11000 | x11x00 | x11x01 | Ø | x1110x | x11100 | Ø | x1100x | x11x0x | x11x00 | x11x01 | Ø | x1110x |
| x1100x | Ø | 0x1000 | 01×000 | 01×000 | Ø | 011000 | xx1000 | 0110×0 | Ø | Ø | Ø | Ø | 011×01 | Ø | 0x100x | 01100x | xx100x | 011000 | xx1000 | x11000 | 011001 | 011001 | xx1001 | x11001 | 0110xx | x110x0 | x11x01 | 01x00x | 01100x | 011000 | 011000 | 011001 | 011x0x | 011×01 | Ø | 01100x | 01100x | — | 011000 | x11000 | x11000 | 011001 | x11001 | x11001 | 0110xx | x110xx | x110x0 | x110x1 | 011x0x | x11x0x | x11x00 | x11x01 | Ø | Ø | 1x100x | 1×1000 | 1×1001 | Ø | 1x100x | 11100x | 1×1000 | 111000 | 111000 | 111001 | 1110×0 | 111x0x | 111×00 | Ø | 11100x | 11100x | 111000 | 111001 | 1110xx | 111x0x |
| 011xx0 | Ø | 0x10x0 | 01x0x0 | 01xx00 | Ø | 011000 | 0x1000 | 011010 | Ø | 01×100 | Ø | Ø | 01110x | Ø | 0x10x0 | 011000 | 0x1000 | 0110×0 | 0x10x0 | 011000 | 0110xx | 011x0x | Ø | 01100x | 011010 | 011010 | 01110x | 01xx00 | 011000 | 0110×0 | 011×00 | 011x0x | 011100 | 0111xx | 01111x | 0110×0 | 011×00 | 011000 | — | 0110×0 | 011×00 | 011xxx | 0110xx | 011x0x | 011×10 | 011010 | 011×10 | 011x1x | 0111×0 | 011100 | 0111×0 | 0111xx | 011110 | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | x110x0 | x11x00 | Ø | x11x10 | x11100 | x111x0 | x11110 | x110x0 | x11x00 | x11xx0 | Ø | x11x10 | x111x0 |
| x110x0 | Ø | 0x10x0 | 01x0x0 | 01×000 | Ø | 011000 | xx1000 | 011010 | Ø | Ø | Ø | Ø | Ø | Ø | 0x10x0 | 011000 | xx1000 | 0110×0 | xx10x0 | x11000 | 0110xx | 01100x | Ø | x1100x | 011010 | x11010 | Ø | 01×000 | 011000 | 0110×0 | 011000 | 01100x | 011×00 | Ø | Ø | 0110×0 | 011000 | x11000 | 0110×0 | — | x11000 | 0110xx | x110xx | x1100x | 011010 | x11010 | x11010 | x1101x | 011xx0 | x11x00 | x11xx0 | Ø | x11x10 | Ø | 1×1000 | 1×1000 | Ø | Ø | 1×1000 | 111000 | 1x10x0 | 1110×0 | 111000 | 11100x | 111010 | 111×00 | 111xx0 | 111×10 | 1110×0 | 111000 | 1110×0 | 1110xx | 111010 | 111xx0 |
| x11x00 | Ø | 0x1000 | 01×000 | 01xx00 | Ø | 011000 | xx1000 | 0110×0 | Ø | 01×100 | Ø | Ø | 01110x | Ø | 0x1000 | 011000 | xx1000 | 011000 | xx1000 | x11000 | 01100x | 011x0x | Ø | x1100x | 0110×0 | x110x0 | x1110x | 01xx00 | 011000 | 011000 | 011×00 | 011x0x | 011100 | 01110x | Ø | 011000 | 011×00 | x11000 | 011×00 | x11000 | — | 011x0x | x1100x | x11x0x | 011xx0 | x110x0 | x11xx0 | Ø | 011100 | x11100 | x11100 | x1110x | x111x0 | Ø | 1×1000 | 1x1x00 | Ø | 1×1100 | 1x1x00 | 111000 | 1x1x00 | 111000 | 111×00 | 111x0x | 111xx0 | 111100 | 111100 | 1111×0 | 111000 | 111×00 | 111×00 | 111x0x | 111xx0 | 111100 |
| 011xx1 | Ø | Ø | Ø | Ø | Ø | 01100x | Ø | 01101x | Ø | 01×101 | Ø | 01x1x1 | 011101 | 0x1101 | 0x10x1 | 011001 | 0x1001 | 0110xx | Ø | 01100x | 0110×1 | 011×01 | 0x1x01 | 011001 | 011011 | 01101x | 011101 | 01xx01 | 011001 | 0110xx | 011x0x | 011×01 | 011101 | 0111×1 | 011111 | 0110×1 | 011×01 | 011001 | 011xxx | 0110xx | 011x0x | — | 0110×1 | 011×01 | 011×11 | 011011 | 011x1x | 011×11 | 0111×1 | 011101 | 0111xx | 0111×1 | 011111 | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | x11x01 | Ø | x11101 | Ø | x11111 | x110x1 | x11x01 | Ø | x11xx1 | x11x11 | x111x1 |
| x110x1 | Ø | Ø | Ø | Ø | Ø | 01100x | Ø | 01101x | Ø | Ø | Ø | Ø | 011×01 | Ø | 0x10x1 | 011001 | xx1001 | 0110xx | Ø | x1100x | 0110×1 | 011001 | xx1001 | x11001 | 011011 | x1101x | x11x01 | 01×001 | 011001 | 0110xx | 01100x | 011001 | 011×01 | 011xx1 | x11x11 | 0110×1 | 011001 | x11001 | 0110xx | x110xx | x1100x | 0110×1 | — | x11001 | 011011 | x11011 | x1101x | x11011 | 011xx1 | x11x01 | Ø | x11xx1 | x11x11 | Ø | 1×1001 | Ø | 1×1001 | Ø | 1×1001 | 111001 | Ø | 1110xx | 11100x | 111001 | 11101x | 111×01 | Ø | 111×11 | 1110×1 | 111001 | 1110xx | 1110×1 | 111011 | 111xx1 |
| x11x01 | Ø | Ø | Ø | Ø | Ø | 01100x | Ø | Ø | Ø | 01×101 | Ø | 01×101 | 011101 | xx1101 | 0x1001 | 011001 | xx1001 | 01100x | Ø | x1100x | 011001 | 011×01 | xx1x01 | x11001 | 0110×1 | Ø | x11101 | 01xx01 | 011001 | 01100x | 011x0x | 011×01 | 011101 | 011101 | x111x1 | 011001 | 011×01 | x11001 | 011x0x | x1100x | x11x0x | 011×01 | x11001 | — | 011xx1 | x110x1 | Ø | x11xx1 | 011101 | x11101 | x1110x | x11101 | x111x1 | Ø | 1×1001 | Ø | 1x1x01 | 1×1101 | 1x1x01 | 111001 | Ø | 11100x | 111x0x | 111×01 | Ø | 111101 | 11110x | 1111×1 | 111001 | 111×01 | 111x0x | 111×01 | 111xx1 | 111101 |
| 011x1x | Ø | 0x1010 | 01×010 | Ø | Ø | 0110×0 | Ø | 011010 | Ø | Ø | Ø | 01×111 | 0111×1 | Ø | 0x101x | 0110xx | Ø | 011010 | 0x1010 | 0110×0 | 011011 | 011xx1 | Ø | 0110×1 | 01101x | 011010 | 0111×1 | Ø | 0110xx | 011010 | 011xx0 | 011xx1 | 0111xx | 011111 | 011111 | 01101x | 011xxx | 0110xx | 011×10 | 011010 | 011xx0 | 011×11 | 011011 | 011xx1 | — | 01101x | 011×10 | 011×11 | 01111x | 0111xx | 011110 | 011111 | 01111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | x11x10 | Ø | x11110 | x1111x | x1101x | Ø | x11x10 | x11x11 | x11x1x | x1111x |
| x1101x | Ø | 0x1010 | 01×010 | Ø | Ø | 0110×0 | Ø | 011010 | Ø | Ø | Ø | Ø | Ø | Ø | 0x101x | 0110xx | Ø | 011010 | xx1010 | x110x0 | 011011 | 0110×1 | Ø | x110x1 | 01101x | x11010 | Ø | Ø | 0110xx | 011010 | 0110×0 | 0110×1 | Ø | 011×11 | x11x11 | 01101x | 0110xx | x110xx | 011010 | x11010 | x110x0 | 011011 | x11011 | x110x1 | 01101x | — | x11010 | x11011 | 011x1x | Ø | x11x10 | x11x11 | x11x1x | Ø | Ø | Ø | Ø | Ø | Ø | 1110xx | 1×1010 | 111010 | 1110×0 | 1110×1 | 111010 | Ø | 111×10 | 111x1x | 11101x | 1110xx | 111010 | 111011 | 11101x | 111x1x |
| x11x10 | Ø | 0x1010 | 01×010 | Ø | Ø | 0110×0 | Ø | 011010 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0110×0 | Ø | 011010 | xx1010 | x110x0 | 01101x | Ø | Ø | Ø | 011010 | x11010 | Ø | Ø | 0110×0 | 011010 | 011xx0 | Ø | 0111×0 | 01111x | x1111x | 011010 | 011xx0 | x110x0 | 011×10 | x11010 | x11xx0 | 011x1x | x1101x | Ø | 011×10 | x11010 | — | x11x1x | 011110 | x111x0 | x11110 | x1111x | x11110 | Ø | Ø | Ø | Ø | Ø | Ø | 1110×0 | 1x1x10 | 111010 | 111xx0 | Ø | 111×10 | 1111×0 | 111110 | 111110 | 111010 | 111xx0 | 111×10 | 111x1x | 111×10 | 111110 |
| x11x11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01101x | Ø | Ø | Ø | 01×111 | 0111×1 | Ø | 0x1011 | 0110×1 | Ø | 01101x | Ø | Ø | 011011 | 011xx1 | Ø | x110x1 | 011011 | x1101x | x111x1 | Ø | 0110×1 | 01101x | Ø | 011xx1 | 0111×1 | 011111 | x11111 | 011011 | 011xx1 | x110x1 | 011x1x | x1101x | Ø | 011×11 | x11011 | x11xx1 | 011×11 | x11011 | x11x1x | — | 011111 | x111x1 | x1111x | x11111 | x11111 | Ø | Ø | Ø | Ø | Ø | Ø | 1110×1 | Ø | 11101x | Ø | 111xx1 | 111x1x | 1111×1 | 11111x | 111111 | 111011 | 111xx1 | 111x1x | 111×11 | 111×11 | 111111 |
| 0111xx | Ø | Ø | Ø | 01×100 | Ø | 011×00 | Ø | 011×10 | Ø | 01x10x | Ø | 01x1x1 | 011101 | 0x1101 | Ø | 011x0x | Ø | 011xx0 | Ø | 011×00 | 011xx1 | 011101 | 0x1101 | 011×01 | 011x1x | 011×10 | 011101 | 01x10x | 011x0x | 011xx0 | 011100 | 011101 | 01110x | 0111×1 | 011111 | 011xxx | 01110x | 011x0x | 0111×0 | 011xx0 | 011100 | 0111×1 | 011xx1 | 011101 | 01111x | 011x1x | 011110 | 011111 | — | 01110x | 0111×0 | 0111×1 | 01111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | x11101 | x11110 | x1110x | x111x0 | x1111x | Ø | x1110x | x111x0 | x111x1 | x1111x | x111xx |
| x1110x | Ø | Ø | Ø | 01×100 | Ø | 011×00 | Ø | Ø | Ø | 01x10x | Ø | 01×101 | 011101 | xx1101 | Ø | 011x0x | Ø | 011×00 | Ø | x11x00 | 011×01 | 011101 | xx1101 | x11x01 | Ø | Ø | x11101 | 01x10x | 011x0x | 011×00 | 011100 | 011101 | 01110x | 011101 | x111x1 | 011x0x | 01110x | x11x0x | 011100 | x11x00 | x11100 | 011101 | x11x01 | x11101 | 0111xx | Ø | x111x0 | x111x1 | 01110x | — | x11100 | x11101 | x111xx | Ø | Ø | 1×1100 | 1×1101 | 1x110x | 1x110x | 111x0x | 1×1100 | 111×00 | 111100 | 111101 | 1111×0 | 11110x | 111100 | 1111xx | 111x0x | 11110x | 111100 | 111101 | 1111xx | 11110x |
| x111x0 | Ø | Ø | Ø | 01×100 | Ø | 011×00 | Ø | 011×10 | Ø | 01×100 | Ø | Ø | 01110x | Ø | Ø | 011×00 | Ø | 011xx0 | Ø | x11x00 | Ø | 01110x | Ø | Ø | 011×10 | x11x10 | x1110x | 01×100 | 011×00 | 011xx0 | 011100 | 01110x | 011100 | 0111xx | x1111x | 011xx0 | 011100 | x11x00 | 0111×0 | x11xx0 | x11100 | 0111xx | Ø | x1110x | 011110 | x11x10 | x11110 | x1111x | 0111×0 | x11100 | — | x111xx | x11110 | Ø | Ø | 1×1100 | Ø | 1×1100 | 1×1100 | 111×00 | 1x11x0 | 111xx0 | 111100 | 11110x | 111110 | 111100 | 1111×0 | 111110 | 111xx0 | 111100 | 1111×0 | 1111xx | 111110 | 1111×0 |
| x111x1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | 01x1x1 | 011101 | xx1101 | Ø | 011×01 | Ø | Ø | Ø | Ø | 011xx1 | 011101 | xx1101 | x11x01 | 011×11 | Ø | x11101 | 01×101 | 011×01 | Ø | 01110x | 011101 | 011101 | 0111×1 | x11111 | 011xx1 | 011101 | x11x01 | 0111xx | Ø | x1110x | 0111×1 | x11xx1 | x11101 | 011111 | x11x11 | x1111x | x11111 | 0111×1 | x11101 | x111xx | — | x11111 | Ø | Ø | Ø | 1×1101 | 1×1101 | 1×1101 | 111×01 | Ø | Ø | 11110x | 111101 | 11111x | 111101 | 1111xx | 111111 | 111xx1 | 111101 | 1111xx | 1111×1 | 111111 | 1111×1 |
| x1111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | Ø | Ø | 01×111 | 0111×1 | Ø | Ø | Ø | Ø | 011×10 | Ø | Ø | 011×11 | 0111×1 | Ø | Ø | 011x1x | x11x10 | x111x1 | Ø | Ø | 011×10 | 0111×0 | 0111×1 | 0111xx | 011111 | x11111 | 011x1x | 0111xx | Ø | 011110 | x11x10 | x111x0 | 011111 | x11x11 | x111x1 | 01111x | x11x1x | x11110 | x11111 | 01111x | x111xx | x11110 | x11111 | — | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | 111×10 | 1111×0 | 1111×1 | 111110 | 1111xx | 111110 | 11111x | 111x1x | 1111xx | 111110 | 111111 | 11111x | 11111x |
| 100x0x | x00x00 | x00000 | x00000 | x00x00 | 100×00 | x00000 | 100000 | Ø | x0010x | x0010x | 10010x | x00101 | x00101 | 100101 | Ø | Ø | 10x00x | Ø | 10×000 | 10×000 | Ø | Ø | 10xx01 | 10×001 | Ø | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | — | 10000x | 100×00 | 100×01 | 10010x | 10xx0x | 10x00x | 10xx00 | 10×000 | 10xx00 | 10xx01 | Ø | 10x10x | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 10x00x | x00000 | x0x000 | x00000 | x00000 | 100000 | x0x000 | 10×000 | Ø | Ø | Ø | 100x0x | Ø | Ø | 10xx01 | x0100x | x0100x | 10100x | x01000 | 101000 | 101000 | x01001 | x01001 | 101001 | 101001 | Ø | 1010×0 | 101×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1x100x | Ø | 1×1000 | 1×1000 | Ø | 1×1001 | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10000x | — | 10×000 | 10×001 | 10xx0x | 10100x | 10100x | 101000 | 101000 | 101000 | 101001 | 1010×0 | 101x0x | 101×00 | Ø | 1x100x | 1x100x | 1×1000 | 1×1001 | Ø | Ø |
| 10xx00 | x00x00 | x0x000 | x00000 | x00x00 | 100×00 | x0x000 | 10×000 | Ø | x00100 | x00100 | 100100 | Ø | Ø | 10x10x | x01000 | x01000 | 101000 | x01000 | 101000 | 101000 | Ø | Ø | 101x0x | 10100x | Ø | 1010×0 | 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | 1×1000 | 1x1x00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | 1×1100 | Ø | Ø | 100×00 | 10×000 | — | 10xx0x | 10×100 | 101×00 | 101000 | 101×00 | 101000 | 101×00 | 101x0x | 101xx0 | 101100 | 101100 | Ø | 1×1000 | 1x1x00 | 1x1x00 | Ø | Ø | 1×1100 |
| 10xx01 | Ø | Ø | Ø | Ø | 100x0x | Ø | 10x00x | Ø | x00101 | x00101 | 100101 | x00101 | x0x101 | 10×101 | x01001 | x01001 | 101001 | Ø | 10100x | 10100x | x01001 | x01x01 | 101×01 | 101001 | Ø | Ø | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | Ø | 1×1001 | 1x1x01 | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | 1×1101 | Ø | 100×01 | 10×001 | 10xx0x | — | 10×101 | 101×01 | 101001 | 101x0x | 10100x | 101x0x | 101×01 | Ø | 101101 | 10110x | Ø | 1×1001 | 1x1x01 | Ø | 1x1x01 | Ø | 1×1101 |
| 10x10x | x00100 | Ø | Ø | x00100 | 100100 | Ø | 10xx00 | Ø | x0010x | x0010x | 10010x | x00101 | x0x101 | 10×101 | Ø | Ø | 101x0x | Ø | 101×00 | 101×00 | Ø | x01101 | 101101 | 101×01 | Ø | Ø | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | 1×1101 | Ø | Ø | Ø | Ø | Ø | 1x110x | 1×1100 | 1×1101 | Ø | 10010x | 10xx0x | 10×100 | 10×101 | — | 10110x | 101x0x | 101100 | 101×00 | 101100 | 101101 | 1011×0 | 10110x | 101100 | Ø | Ø | 1x110x | 1×1100 | 1×1101 | Ø | 1x110x |
| 101x0x | Ø | x01000 | Ø | Ø | 10xx00 | x01000 | 101000 | Ø | Ø | Ø | 10x10x | Ø | x01101 | 101101 | x0100x | x0100x | 10100x | x01000 | 101000 | 101000 | x01001 | x01x01 | 101×01 | 101001 | Ø | 1010×0 | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1x100x | Ø | 1×1000 | 1x1x00 | Ø | 1×1001 | 1x1x01 | Ø | Ø | Ø | Ø | Ø | 1x110x | 1×1100 | 1×1101 | Ø | 10xx0x | 10100x | 101×00 | 101×01 | 10110x | — | 10100x | 101×00 | 101000 | 101×00 | 101×01 | 101xx0 | 10110x | 101100 | Ø | 1x100x | 1x1x0x | 1x1x00 | 1x1x01 | Ø | 1x110x |
| 1x100x | Ø | x01000 | Ø | Ø | 10×000 | xx1000 | 101000 | Ø | Ø | Ø | Ø | Ø | Ø | 101×01 | x0100x | xx100x | 10100x | xx1000 | 101000 | 1×1000 | xx1001 | xx1001 | 101001 | 1×1001 | Ø | 1x10x0 | 1x1x01 | Ø | x1100x | x11000 | x11000 | x11001 | Ø | Ø | Ø | x1100x | x1100x | 11100x | x11000 | 111000 | 111000 | x11001 | 111001 | 111001 | Ø | 1110xx | 1110×0 | 1110×1 | Ø | 111x0x | 111×00 | 111×01 | Ø | 10x00x | 10100x | 101000 | 101001 | 101x0x | 10100x | — | 101000 | 1×1000 | 1×1000 | 1×1001 | 1x10x0 | 1x1x0x | 1x1x00 | Ø | 11100x | 11100x | 111000 | 111001 | 1110xx | 111x0x |
| 101xx0 | Ø | x010x0 | Ø | Ø | 10xx00 | x01000 | 101000 | x01010 | Ø | Ø | 10×100 | Ø | Ø | 10110x | x010x0 | x01000 | 101000 | x010x0 | 1010×0 | 101000 | Ø | Ø | 101x0x | 10100x | x01010 | 101010 | 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | 1x10x0 | 1x1x00 | Ø | Ø | Ø | Ø | 1×1010 | 1x1x10 | Ø | Ø | 1×1100 | 1x11x0 | Ø | 1×1110 | 10xx00 | 101000 | 101×00 | 101x0x | 101100 | 101×00 | 101000 | — | 1010×0 | 101×00 | 101x0x | 101×10 | 101100 | 1011×0 | 1×1110 | 1x10x0 | 1x1x00 | 1x1xx0 | Ø | 1x1x10 | 1x11x0 |
| 1x10x0 | Ø | x010x0 | Ø | Ø | 10×000 | xx1000 | 101000 | xx1010 | Ø | Ø | Ø | Ø | Ø | Ø | x010x0 | xx1000 | 101000 | xx10x0 | 1010×0 | 1×1000 | Ø | Ø | 10100x | 1x100x | xx1010 | 1×1010 | Ø | Ø | x11000 | x110x0 | x11000 | Ø | Ø | Ø | Ø | x110x0 | x11000 | 111000 | x110x0 | 1110×0 | 111000 | Ø | 1110xx | 11100x | x11010 | 111010 | 111010 | 11101x | Ø | 111×00 | 111xx0 | Ø | 111×10 | 10×000 | 101000 | 101000 | 10100x | 101×00 | 101000 | 1×1000 | 1010×0 | — | 1×1000 | 1x100x | 1×1010 | 1x1x00 | 1x1xx0 | 111×10 | 1110×0 | 111000 | 1110×0 | 1110xx | 111010 | 111xx0 |
| 1x1x00 | Ø | x01000 | Ø | Ø | 10xx00 | xx1000 | 101000 | Ø | Ø | Ø | 10×100 | Ø | Ø | 10110x | x01000 | xx1000 | 101000 | xx1000 | 101000 | 1×1000 | Ø | Ø | 101x0x | 1x100x | Ø | 1x10x0 | 1x110x | Ø | x11000 | x11000 | x11x00 | Ø | x11100 | Ø | Ø | x11000 | x11x00 | 111000 | x11x00 | 111000 | 111×00 | Ø | 11100x | 111x0x | Ø | 1110×0 | 111xx0 | Ø | x11100 | 111100 | 111100 | 11110x | 1111×0 | 10xx00 | 101000 | 101×00 | 101x0x | 101100 | 101×00 | 1×1000 | 101×00 | 1×1000 | — | 1x1x0x | 1x1xx0 | 1×1100 | 1×1100 | 1111×0 | 111000 | 111×00 | 111×00 | 111x0x | 111xx0 | 111100 |
| 1x1x01 | Ø | Ø | Ø | Ø | Ø | Ø | 10100x | Ø | Ø | Ø | 10×101 | Ø | xx1101 | 101101 | x01001 | xx1001 | 101001 | Ø | 10100x | 1x100x | xx1001 | xx1x01 | 101×01 | 1×1001 | Ø | Ø | 1×1101 | Ø | x11001 | Ø | Ø | x11x01 | x11101 | x11101 | 1111×1 | x11001 | x11x01 | 111001 | Ø | 11100x | 111x0x | x11x01 | 111001 | 111×01 | Ø | 1110×1 | Ø | 111xx1 | x11101 | 111101 | 11110x | 111101 | 1111×1 | 10xx01 | 101001 | 101x0x | 101×01 | 101101 | 101×01 | 1×1001 | 101x0x | 1x100x | 1x1x0x | — | Ø | 1×1101 | 1x110x | 1111×1 | 111001 | 111×01 | 111x0x | 111×01 | 111xx1 | 111101 |
| 1x1x10 | Ø | x01010 | Ø | Ø | Ø | Ø | 1010×0 | xx1010 | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | 1010×0 | xx1010 | 101010 | 1x10x0 | Ø | Ø | Ø | Ø | xx1010 | 1×1010 | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | 11111x | x11010 | Ø | 1110×0 | x11x10 | 111010 | 111xx0 | Ø | 11101x | Ø | x11x10 | 111010 | 111×10 | 111x1x | x11110 | 1111×0 | 111110 | 11111x | 111110 | Ø | 1010×0 | 101xx0 | Ø | 1011×0 | 101xx0 | 1x10x0 | 101×10 | 1×1010 | 1x1xx0 | Ø | — | 1x11x0 | 1×1110 | 111110 | 111010 | 111xx0 | 111×10 | 111x1x | 111×10 | 111110 |
| 1x110x | Ø | Ø | Ø | Ø | 10×100 | Ø | 101×00 | Ø | Ø | Ø | 10x10x | Ø | xx1101 | 101101 | Ø | Ø | 101x0x | Ø | 101×00 | 1x1x00 | Ø | xx1101 | 101101 | 1x1x01 | Ø | Ø | 1×1101 | Ø | Ø | Ø | x11100 | x11101 | x1110x | x11101 | 1111×1 | Ø | x1110x | 111x0x | x11100 | 111×00 | 111100 | x11101 | 111×01 | 111101 | Ø | Ø | 1111×0 | 1111×1 | x1110x | 11110x | 111100 | 111101 | 1111xx | 10x10x | 101x0x | 101100 | 101101 | 10110x | 10110x | 1x1x0x | 101100 | 1x1x00 | 1×1100 | 1×1101 | 1x11x0 | — | 1×1100 | 1111xx | 111x0x | 11110x | 111100 | 111101 | 1111xx | 11110x |
| 1x11x0 | Ø | Ø | Ø | Ø | 10×100 | Ø | 101×00 | Ø | Ø | Ø | 10×100 | Ø | Ø | 10110x | Ø | Ø | 101×00 | Ø | 101xx0 | 1x1x00 | Ø | Ø | 10110x | Ø | Ø | 1x1x10 | 1x110x | Ø | Ø | Ø | x11100 | Ø | x11100 | Ø | 11111x | Ø | x11100 | 111×00 | x111x0 | 111xx0 | 111100 | Ø | Ø | 11110x | x11110 | 111×10 | 111110 | 11111x | x111x0 | 111100 | 1111×0 | 1111xx | 111110 | 10×100 | 101×00 | 101100 | 10110x | 101100 | 101100 | 1x1x00 | 1011×0 | 1x1xx0 | 1×1100 | 1x110x | 1×1110 | 1×1100 | — | 111110 | 111xx0 | 111100 | 1111×0 | 1111xx | 111110 | 1111×0 |
| 11x11x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 111×10 | 1111×1 | Ø | Ø | Ø | Ø | Ø | Ø | x1x111 | 11×111 | Ø | Ø | Ø | x11110 | 111×10 | 1111×0 | x11111 | 111×11 | 1111×1 | x1111x | 111x1x | 111110 | 111111 | x1111x | 1111xx | 111110 | 111111 | 11111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | 111×10 | 1111×0 | 1111×1 | 111110 | 1111xx | 111110 | — | 111x1x | 1111xx | 111110 | 111111 | 11111x | 11111x |
| 1110xx | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x1100x | 1x100x | x110x0 | 1x10x0 | 111000 | x110x1 | x11001 | 1×1001 | 111001 | x1101x | 111010 | 111×01 | Ø | x1100x | x110x0 | x11000 | x11001 | Ø | Ø | 111×11 | x110xx | x1100x | 11100x | x110x0 | 1110×0 | 111000 | x110x1 | 1110×1 | 111001 | x1101x | 11101x | 111010 | 111011 | Ø | 111x0x | 111xx0 | 111xx1 | 111x1x | Ø | 1x100x | 1×1000 | 1×1001 | Ø | 1x100x | 11100x | 1x10x0 | 1110×0 | 111000 | 111001 | 111010 | 111x0x | 111xx0 | 111x1x | — | 11100x | 1110×0 | 1110×1 | 11101x | 111xxx |
| 111x0x | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | Ø | Ø | Ø | Ø | Ø | x11101 | 1×1101 | Ø | x1100x | 1x100x | x11000 | 1×1000 | 111000 | x11001 | x11x01 | 1x1x01 | 111001 | Ø | 1110×0 | 111101 | Ø | x1100x | x11000 | x11x00 | x11x01 | x1110x | x11101 | 1111×1 | x1100x | x11x0x | 11100x | x11x00 | 111000 | 111×00 | x11x01 | 111001 | 111×01 | Ø | 1110xx | 111xx0 | 111xx1 | x1110x | 11110x | 111100 | 111101 | 1111xx | Ø | 1x100x | 1x1x00 | 1x1x01 | 1x110x | 1x1x0x | 11100x | 1x1x00 | 111000 | 111×00 | 111×01 | 111xx0 | 11110x | 111100 | 1111xx | 11100x | — | 111×00 | 111×01 | 111xxx | 11110x |
| 111xx0 | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | x110x0 | 1x10x0 | 111000 | Ø | Ø | Ø | 11100x | x11010 | 111010 | 11110x | Ø | x11000 | x110x0 | x11x00 | Ø | x11100 | Ø | 11111x | x110x0 | x11x00 | 111000 | x11xx0 | 1110×0 | 111×00 | Ø | 1110xx | 111x0x | x11x10 | 111010 | 111×10 | 111x1x | x111x0 | 111100 | 1111×0 | 1111xx | 111110 | Ø | 1×1000 | 1x1x00 | Ø | 1×1100 | 1x1x00 | 111000 | 1x1xx0 | 1110×0 | 111×00 | 111x0x | 111×10 | 111100 | 1111×0 | 111110 | 1110×0 | 111×00 | — | 111xxx | 111×10 | 1111×0 |
| 111xx1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | 1×1101 | Ø | x11001 | 1×1001 | Ø | Ø | 11100x | x110x1 | x11x01 | 1x1x01 | 111001 | x11011 | 11101x | 111101 | Ø | x11001 | Ø | Ø | x11x01 | x11101 | x111x1 | 111111 | x110x1 | x11x01 | 111001 | Ø | 1110xx | 111x0x | x11xx1 | 1110×1 | 111×01 | x11x11 | 111011 | 111x1x | 111×11 | x111x1 | 111101 | 1111xx | 1111×1 | 111111 | Ø | 1×1001 | Ø | 1x1x01 | 1×1101 | 1x1x01 | 111001 | Ø | 1110xx | 111x0x | 111×01 | 111x1x | 111101 | 1111xx | 111111 | 1110×1 | 111×01 | 111xxx | — | 111×11 | 1111×1 |
| 111x1x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | 1×1010 | 1110×0 | x11011 | Ø | Ø | 1110×1 | x1101x | 111010 | 1111×1 | Ø | Ø | x11010 | Ø | Ø | Ø | x11111 | 111111 | x1101x | Ø | 1110xx | x11x10 | 111010 | 111xx0 | x11x11 | 111011 | 111xx1 | x11x1x | 11101x | 111×10 | 111×11 | x1111x | 1111xx | 111110 | 111111 | 11111x | Ø | Ø | Ø | Ø | Ø | Ø | 1110xx | 1x1x10 | 111010 | 111xx0 | 111xx1 | 111×10 | 1111xx | 111110 | 11111x | 11101x | 111xxx | 111×10 | 111×11 | — | 11111x |
| 1111xx | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | 1×1101 | Ø | Ø | Ø | Ø | Ø | 111×00 | Ø | x11101 | 1×1101 | 111×01 | Ø | 111×10 | 111101 | Ø | Ø | Ø | x11100 | x11101 | x1110x | x111x1 | 111111 | Ø | x1110x | 111x0x | x111x0 | 111xx0 | 111100 | x111x1 | 111xx1 | 111101 | x1111x | 111x1x | 111110 | 111111 | x111xx | 11110x | 1111×0 | 1111×1 | 11111x | Ø | Ø | 1×1100 | 1×1101 | 1x110x | 1x110x | 111x0x | 1x11x0 | 111xx0 | 111100 | 111101 | 111110 | 11110x | 1111×0 | 11111x | 111xxx | 11110x | 1111×0 | 1111×1 | 11111x | — |
Z2=
Ĉ3=C2∪(C2*C2)
C3=>
| 0xx0x0, 0x10xx, xx100x xx10x0, xx1x01, 01xx0x 011xxx, x110xx, x11x0x x11xx0, x11xx1, x11x1x x111xx, 10xx0x, 1x1x0x 1x1xx0, 111xxx |
| 0xx0x0 | 0x10xx | xx100x | xx10x0 | xx1x01 | 01xx0x | 011xxx | x110xx | x11x0x | x11xx0 | x11xx1 | x11x1x | x111xx | 10xx0x | 1x1x0x | 1x1xx0 | 111xxx | |
| 0xx0x0 | — | 0x10x0 | 0x1000 | 0x10x0 | 0x100x | 01×000 | 0110×0 | 0110×0 | 011000 | 0110×0 | 0110xx | 011010 | 011xx0 | x0x000 | xx1000 | xx10x0 | x110x0 |
| 0x10xx | 0x10x0 | — | 0x100x | 0x10x0 | 0x1001 | 01100x | 0110xx | 0110xx | 01100x | 0110×0 | 0110×1 | 01101x | 011xxx | x0100x | xx100x | xx10x0 | x110xx |
| xx100x | 0x1000 | 0x100x | — | xx1000 | xx1001 | 01100x | 01100x | x1100x | x1100x | x11000 | x11001 | x110xx | x11x0x | 10100x | 1x100x | 1×1000 | 11100x |
| xx10x0 | 0x10x0 | 0x10x0 | xx1000 | — | xx100x | 011000 | 0110×0 | x110x0 | x11000 | x110x0 | x110xx | x11010 | x11xx0 | 101000 | 1×1000 | 1x10x0 | 1110×0 |
| xx1x01 | 0x100x | 0x1001 | xx1001 | xx100x | — | 011×01 | 011×01 | x11001 | x11x01 | x11x0x | x11x01 | x11xx1 | x11101 | 101×01 | 1x1x01 | 1x1x0x | 111×01 |
| 01xx0x | 01×000 | 01100x | 01100x | 011000 | 011×01 | — | 011x0x | 01100x | 011x0x | 011×00 | 011×01 | 011xxx | 01110x | Ø | x11x0x | x11x00 | x11x0x |
| 011xxx | 0110×0 | 0110xx | 01100x | 0110×0 | 011×01 | 011x0x | — | 0110xx | 011x0x | 011xx0 | 011xx1 | 011x1x | 0111xx | Ø | x11x0x | x11xx0 | x11xxx |
| x110xx | 0110×0 | 0110xx | x1100x | x110x0 | x11001 | 01100x | 0110xx | — | x1100x | x110x0 | x110x1 | x1101x | x11xxx | 1x100x | 11100x | 1110×0 | 1110xx |
| x11x0x | 011000 | 01100x | x1100x | x11000 | x11x01 | 011x0x | 011x0x | x1100x | — | x11x00 | x11x01 | x11xxx | x1110x | 1x1x0x | 111x0x | 111×00 | 111x0x |
| x11xx0 | 0110×0 | 0110×0 | x11000 | x110x0 | x11x0x | 011×00 | 011xx0 | x110x0 | x11x00 | — | x11xxx | x11x10 | x111x0 | 1x1x00 | 111×00 | 111xx0 | 111xx0 |
| x11xx1 | 0110xx | 0110×1 | x11001 | x110xx | x11x01 | 011×01 | 011xx1 | x110x1 | x11x01 | x11xxx | — | x11x11 | x111x1 | 1x1x01 | 111×01 | 111xxx | 111xx1 |
| x11x1x | 011010 | 01101x | x110xx | x11010 | x11xx1 | 011xxx | 011x1x | x1101x | x11xxx | x11x10 | x11x11 | — | x1111x | Ø | 111xxx | 111×10 | 111x1x |
| x111xx | 011xx0 | 011xxx | x11x0x | x11xx0 | x11101 | 01110x | 0111xx | x11xxx | x1110x | x111x0 | x111x1 | x1111x | — | 1x110x | 11110x | 1111×0 | 1111xx |
| 10xx0x | x0x000 | x0100x | 10100x | 101000 | 101×01 | Ø | Ø | 1x100x | 1x1x0x | 1x1x00 | 1x1x01 | Ø | 1x110x | — | 101x0x | 101×00 | 1x1x0x |
| 1x1x0x | xx1000 | xx100x | 1x100x | 1×1000 | 1x1x01 | x11x0x | x11x0x | 11100x | 111x0x | 111×00 | 111×01 | 111xxx | 11110x | 101x0x | — | 1x1x00 | 111x0x |
| 1x1xx0 | xx10x0 | xx10x0 | 1×1000 | 1x10x0 | 1x1x0x | x11x00 | x11xx0 | 1110×0 | 111×00 | 111xx0 | 111xxx | 111×10 | 1111×0 | 101×00 | 1x1x00 | — | 111xx0 |
| 111xxx | x110x0 | x110xx | 11100x | 1110×0 | 111×01 | x11x0x | x11xxx | 1110xx | 111x0x | 111xx0 | 111xx1 | 111x1x | 1111xx | 1x1x0x | 111x0x | 111xx0 | — |
Z3=
Ĉ4=C3∪(C3*C3)
C4=>
| x11xxx | |
| x11xxx | — |
Z4=
Ĉ5=C4∪(C4*C4)
C5=>Ø
Z = Z0∪Z1∪Z2∪Z3∪Z4
Z=>
| 1000×1, 000xx0, 0x0x00 x00x00, x0x000, 0001xx 0x010x, x0010x, 0x01x1 0xx101, x0x101, 01x1x1 x1x111, 11x11x, 0xx0x0 0x10xx, xx100x, xx10x0 xx1x01, 01xx0x, 10xx0x 1x1x0x, 1x1xx0, x11xxx |
Нахождение тупиковых форм.
| 1000×1 | 000xx0 | 0x0x00 | x00x00 | x0x000 | 0001xx | 0x010x | x0010x | 0x01x1 | 0xx101 | x0x101 | 01x1x1 | x1x111 | 11x11x | 0xx0x0 | 0x10xx | xx100x | xx10x0 | xx1x01 | 01xx0x | 10xx0x | 1x1x0x | 1x1xx0 | x11xxx | ||
|
1000×1 |
— |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
100011 |
100011 |
100011 |
100011 |
v |
|
000xx0 |
000xx0 |
— |
000×10 |
000×10 |
000×10 |
000010 |
000010 |
000010 |
000010 |
000010 |
000010 |
000010 |
000010 |
000010 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
0x0x00 |
0x0x00 |
010×00 |
— |
010×00 |
010×00 |
010×00 |
010000 |
010000 |
010000 |
010000 |
010000 |
010000 |
010000 |
010000 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
x00x00 |
x00x00 |
100×00 |
100×00 |
— |
100100 |
100100 |
100100 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
x0x000 |
x0x000 |
x01000 |
x01000 |
x01000 |
— |
x01000 |
x01000 |
x01000 |
x01000 |
x01000 |
x01000 |
x01000 |
x01000 |
x01000 |
101000 |
101000 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
0001xx |
0001xx |
0001×1 |
0001×1 |
0001×1 |
0001×1 |
— |
000111 |
000111 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
0x010x |
0x010x |
0x0101 |
0x0101 |
0x0101 |
0x0101 |
010101 |
— |
010101 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
x0010x |
x0010x |
x00101 |
x00101 |
x00101 |
x00101 |
100101 |
100101 |
— |
100101 |
100101 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
0x01x1 |
0x01x1 |
0x01x1 |
0x01x1 |
0x01x1 |
0x01x1 |
0101×1 |
010111 |
010111 |
— |
010111 |
010111 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
0xx101 |
0xx101 |
0xx101 |
0xx101 |
0xx101 |
0xx101 |
0x1101 |
0x1101 |
0x1101 |
0x1101 |
— |
011101 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
x0x101 |
x0x101 |
x0x101 |
x0x101 |
x0x101 |
x0x101 |
x01101 |
x01101 |
x01101 |
x01101 |
101101 |
— |
101101 |
101101 |
101101 |
101101 |
101101 |
101101 |
101101 |
Ø | Ø | Ø | Ø | Ø | Ø | |
|
01x1x1 |
01x1x1 |
01x1x1 |
01x1x1 |
01x1x1 |
01x1x1 |
01x1x1 |
01×111 |
01×111 |
011111 |
011111 |
011111 |
— | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
x1x111 |
x1x111 |
x1x111 |
x1x111 |
x1x111 |
x1x111 |
x1x111 |
x1x111 |
x1x111 |
x11111 |
x11111 |
x11111 |
111111 |
— | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11×110 |
— |
11×110 |
11×110 |
11×110 |
11×110 |
11×110 |
11×110 |
11×110 |
11×110 |
110110 |
110110 |
v |
|
0xx0x0 |
0xx0x0 |
0x10x0 |
0x10x0 |
0x10x0 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
— |
010010 |
010010 |
010010 |
010010 |
010010 |
010010 |
010010 |
010010 |
010010 |
v |
|
0x10xx |
0x10xx |
0x10xx |
0x10xx |
0x10xx |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
— |
0x1011 |
0x1011 |
0x1011 |
0x1011 |
0x1011 |
0x1011 |
0x1011 |
001011 |
v |
|
xx100x |
xx100x |
xx100x |
xx100x |
xx100x |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
1×1001 |
— |
1×1001 |
Ø | Ø | Ø | Ø | Ø | Ø | |
|
xx10x0 |
xx10x0 |
xx10x0 |
xx10x0 |
xx10x0 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
1×1010 |
1×1010 |
1×1010 |
— |
1×1010 |
1×1010 |
1×1010 |
1×1010 |
Ø | Ø | |
|
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
1×1001 |
111101 |
111101 |
— |
111101 |
111101 |
Ø | Ø | Ø | |
|
01xx0x |
01xx0x |
01xx0x |
01xx01 |
01xx01 |
01xx01 |
01xx01 |
01×001 |
01×001 |
01×001 |
01×001 |
01×001 |
01×001 |
01×001 |
01×001 |
01×001 |
010001 |
010001 |
010001 |
010001 |
— |
010001 |
010001 |
010001 |
010001 |
v |
|
10xx0x |
10xx00 |
10xx00 |
10xx00 |
101×00 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
— | Ø | Ø | Ø | |
|
1x1x0x |
1x1x0x |
1x1x0x |
1x1x0x |
1x1x0x |
1x1x01 |
1x1x01 |
1x1x01 |
1x1x01 |
1x1x01 |
1x1x01 |
1×1001 |
1×1001 |
1×1001 |
1×1001 |
1×1001 |
1×1001 |
111101 |
111101 |
1×1100 |
1×1100 |
111100 |
— | Ø | Ø | |
|
1x1xx0 |
1x1xx0 |
1x1xx0 |
1x1xx0 |
1x1xx0 |
1x1x10 |
1x1x10 |
1x1x10 |
1x1x10 |
1x1x10 |
1x1x10 |
1x1x10 |
1x1x10 |
1x1x10 |
1×1010 |
1×1010 |
1×1010 |
1×1010 |
101110 |
101110 |
101110 |
101110 |
101110 |
— |
101110 |
v |
|
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xx0 |
x11xx0 |
x11xx0 |
x11xx0, x11x10, x1101x |
x11x00, x110x0, 011xx0 |
x11100, 111×00, 1110×0 |
x11100, 111×00, 1110×0 |
x11100 |
x11100 |
x11100 |
111100 |
111100 |
011110 |
011110 |
— | v |
E0:
L1=L0#E0
| 11x11x | 0xx0x0 | 01xx0x | 1x1xx0 | x11xxx | |
|
000000, 000100, 000101 |
000000, 000100, 000101 |
000100, 000101, 000111 |
000100, 000101, 000111 |
000100, 000101, 000111 |
000100 |
L1:

До упорядочивания:
| 000100 | 000101 | 000111 | 001001 | 010111 | 100101 | 101001 | 101101 | |
| 1000×1 | ||||||||
| 000xx0 | + | |||||||
| 0x0x00 | + | |||||||
| x00x00 | + | |||||||
| x0x000 | ||||||||
| 0001xx | + | + | + | |||||
| 0x010x | + | + | ||||||
| x0010x | + | + | + | |||||
| 0x01x1 | + | + | + | |||||
| 0xx101 | + | |||||||
| x0x101 | + | + | + | |||||
| 01x1x1 | + | |||||||
| x1x111 | + | |||||||
| 0x10xx | + | |||||||
| xx100x | + | + | ||||||
| xx10x0 | ||||||||
| xx1x01 | + | + | + | |||||
| 10xx0x | + | + | + | |||||
| 1x1x0x | + | + |
После упорядочивания:
| 000100 | 000101 | 000111 | 001001 | 010111 | 100101 | 101001 | 101101 | |
| 0001xx | + | + | + | |||||
| x0010x | + | + | + | |||||
| 0x01x1 | + | + | + | |||||
| x0x101 | + | + | + | |||||
| xx1x01 | + | + | + | |||||
| 10xx0x | + | + | + |

Z1:
| 0001xx | x0010x | 0x01x1 | x0x101 | xx1x01 | 10xx0x | ||
|
0001xx |
— |
00011x |
000110 |
000110 |
000110 |
000110 |
v |
|
x0010x |
10010x |
— |
10010x |
100100 |
100100 |
Ø | |
|
0x01x1 |
0101×1 |
0101×1 |
— |
0101×1 |
0101×1 |
0101×1 |
v |
|
x0x101 |
x01101 |
x01101 |
x01101 |
— | Ø | Ø | |
|
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1001 |
— |
x11001 |
v |
|
10xx0x |
10xx0x |
10x00x |
10x00x |
10x00x |
10×000 |
— | v |
E1:
L2=L1#E1
| 0x01x1 | xx1x01 | |
|
000100 |
000100 |
000100 |
L2:

До упорядочивания:
| 000100 | 100101 | |
| 0001xx | + | |
| x0010x | + | + |
| x0x101 | + | |
| 10xx0x | + |
После упорядочивания:
| 000100 | 100101 | |
| x0010x | + | + |
| 10xx0x | + |

Z2:
| x0010x | 10xx0x | ||
|
x0010x |
— |
00010x |
v |
|
10xx0x |
10x00x |
— | v |
E2:
L3=L2#E2
| x0010x | |
|
000100 |
Ø |
L3:Ø


Z3:
E:
МДНФ:x1x2x4x5 v x1x4x6 v x1x2x5 v x1x3x6 v x2x3 v x1x3x4x6 v x3x5x6 v x2x3x4x5, цена=26
3. Анализ полученных результатов
Все результаты:
Результат метода Квайна
f1 = x1x3x4x6 v x1x2x4x6 v x1x3x5x6 v x1x2x4x5 v x3x4x5 v x3x4x6 v x1x2x4x5x6 v x1x3x5x6 v x1x2x3x5 v x2x3x4x5 v x1x2x3x5 v x2x3x6, цена=46
Результат метода Карно
f2 = x1x2x3x4x6 v x1x2x4x5 v x1x4x6 v x1x3x4 v x1x2x5 v x1x3x6 v x2x3 v x1x2x3x4 v x1x3x4x6 v x1x2x5 v x3x5x6, цена=37
Результат метода Кубических покрытий
f3 = x1x2x4x5 v x1x4x6 v x1x2x5 v x1x3x6 v x2x3 v x1x3x4x6 v x3x5x6 v x2x3x4x5, цена=26
| Набор | Исходная | После Квайна | После Карно | После Кубических покрытий |
| x1x2x3x4x5x6 | f0 | f1 | f2 | f3 |
| 000000 | 1 | 1 | 1 | 1 |
| 000001 | 0 | 0 | 0 | 0 |
| 000010 | ? | 0 | 1 | 1 |
| 000011 | 0 | 0 | 0 | 0 |
| 000100 | 1 | 1 | 1 | 1 |
| 000101 | 1 | 1 | 1 | 1 |
| 000110 | ? | 0 | 1 | 0 |
| 000111 | 1 | 1 | 1 | 1 |
| 001000 | 1 | 1 | 1 | 1 |
| 001001 | 1 | 1 | 1 | 1 |
| 001010 | 1 | 1 | 1 | 1 |
| 001011 | ? | 0 | 1 | 0 |
| 001100 | 0 | 0 | 0 | 0 |
| 001101 | ? | 0 | 1 | 1 |
| 001110 | 0 | 0 | 0 | 0 |
| 001111 | 0 | 0 | 0 | 0 |
| 010000 | 1 | 1 | 1 | 1 |
| 010001 | 1 | 1 | 1 | 1 |
| 010010 | 1 | 1 | 1 | 1 |
| 010011 | 0 | 0 | 0 | 0 |
| 010100 | 1 | 1 | 1 | 1 |
| 010101 | 1 | 1 | 1 | 1 |
| 010110 | 0 | 0 | 0 | 0 |
| 010111 | 1 | 1 | 1 | 1 |
| 011000 | 1 | 1 | 1 | 1 |
| 011001 | 1 | 1 | 1 | 1 |
| 011010 | 1 | 1 | 1 | 1 |
| 011011 | ? | 0 | 1 | 1 |
| 011100 | 1 | 1 | 1 | 1 |
| 011101 | ? | 0 | 1 | 1 |
| 011110 | 1 | 1 | 1 | 1 |
| 011111 | 1 | 1 | 1 | 1 |
| 100000 | ? | 0 | 1 | 0 |
| 100001 | ? | 0 | 1 | 0 |
| 100010 | 0 | 0 | 0 | 0 |
| 100011 | ? | 0 | 1 | 0 |
| 100100 | ? | 0 | 1 | 1 |
| 100101 | 1 | 1 | 1 | 1 |
| 100110 | 0 | 0 | 0 | 0 |
| 100111 | 0 | 0 | 0 | 0 |
| 101000 | 1 | 1 | 1 | 1 |
| 101001 | 1 | 1 | 1 | 1 |
| 101010 | 1 | 1 | 1 | 1 |
| 101011 | 0 | 0 | 0 | 0 |
| 101100 | ? | 0 | 1 | 1 |
| 101101 | 1 | 1 | 1 | 1 |
| 101110 | 1 | 1 | 1 | 1 |
| 101111 | 0 | 0 | 0 | 0 |
| 110000 | 0 | 0 | 0 | 0 |
| 110001 | 0 | 0 | 0 | 0 |
| 110010 | 0 | 0 | 0 | 0 |
| 110011 | 0 | 0 | 0 | 0 |
| 110100 | 0 | 0 | 0 | 0 |
| 110101 | 0 | 0 | 0 | 0 |
| 110110 | 1 | 1 | 1 | 1 |
| 110111 | 1 | 1 | 1 | 1 |
| 111000 | 1 | 1 | 1 | 1 |
| 111001 | 1 | 1 | 1 | 1 |
| 111010 | 1 | 1 | 1 | 1 |
| 111011 | ? | 0 | 1 | 1 |
| 111100 | 1 | 1 | 1 | 1 |
| 111101 | 1 | 1 | 1 | 1 |
| 111110 | 1 | 1 | 1 | 1 |
| 111111 | 1 | 1 | 1 | 1 |
АНАЛИЗ
По таблице истинности видно, что минимизация функции проведена верно.
В результате минимизации получили минимальные дизъюнктивные нормальные формы:
- Доопределив функцию нулями, методом Квайна получили МДНФ цены 46
- Доопределив функцию единицами, методом карт Карно получили МДНФ цены 37
- Доопределяя функцию по ходу выполнения алгоритма, методом кубических покрытий получили МДНФ цены 26
Метод кубических покрытий приводит к наименьшей МДНФ. Это связано с тем, что минимизируется не полностью определенная функция. В результате минимальная форма принимает на наборах, на которых исходная функция не определена, такие значения, которые соответствуют наиболее оптимальному покрытию. Из всех методов наиболее трудоемким оказывается также метод кубических покрытий, но он удобен для программной реализации минимизации. Наименее трудоемким оказался метод Квайне.
4 Список литературы
- http://www.google.com/search?q=минимизация+переключательных+функций
- file:///C:/Users/Viktor/Desktop/tmp2/minsf/index.html#24