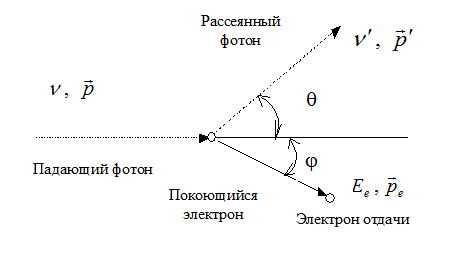
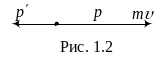Эффект Комптона
является результатом упругого столкновения
рентгеновского фотона со свободным
электроном. Изменение длины волны Δλ
фотона при рассеянии его на угол
определяется выражением
Δλ = λ׳
— λ
= λк
(1- cos
),
где
=2,43пм
— комптоновская длина волна,
—
масса покоя электрона.
При рассеянии
выполняются законы сохранения энергии
и импульса
,
,
где
и
— соответственно энергия налетающего
и рассеянного фотона,
и
— энергия покоя и полная энергия электрона,
и
— импульс налетающего и рассеянного
фотона соответственно,
-импульс электрона отдачи.
Примеры решения задач
Задача 1.
Фотон испытал рассеяние на покоившемся
свободном электроне. Найти импульс
налетавшего фотона, если энергия
рассеянного фотона равна кинетической
энергии электрона отдачи при угле φ=
/2
между направлениями их разлета.
Решение
Кинетическая
энергия Т
электрона отдачи на основании закона
сохранения энергии равна разности между
энергией ε падающего фотона и энергией
ε’
рассеянного фотона
Т =
—
.
По условию задачи
Т =
,
значит,
= 2
,
или
hс/λ
= 2hс/λ׳
,
откуда λ
/ λ’ = 0,5, а с
учетом формулы p
= h/λ
, p׳/p
= 0,5.
В
оспользуемся законом сохранения
импульса, в соответствии с которым
.
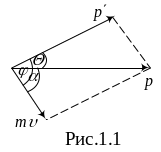
Построим векторную
диаграмму. Угол φ = 90° между направлениями
разлета рассеянного фотона и электрона
отдачи складывается из углов
и α (рис.1.1),
т.е. φ
=
+ α. Но α=arcsin
(p‘/p)=30°,
и, следовательно,
= φ – α
=60° .
Учитывая, что на
основании формулы Комптона λ=0,5λк,
получаем
p=h/0,5λк=2m0с=1,02МэВ/с
.
З
адача 2. Определить
импульс электрона отдачи при эффекте
Комптона, если фотон с энергией, равной
энергии покоя электрона, был рассеян
под углом
= 180°.
Решение
Используя формулы
для энергии и импульса фотона, определяем
длину волны и импульс падающего фотона.
Так как по условию
= hc/λ
=m0с2
,
то
λ = h
/ m0с,
а p
= h
/ λ = m0с.
В соответствии с
формулой Комптона для данного случая
λ׳
– λ
= λк (1
– cos
1800)
= 2λк,
откуда длина волны
рассеянного фотона равна
λ׳
=
2λк +
λ = 2h
/(m0
с) + h
/ (m0
с) = 3h
/ (m0
с).
Величина его
импульса
p‘
= h
/ λ׳
=
m0с/3.
Для нахождения
импульса электрона отдачи построим
векторную диаграмму импульсов (рис.1.2).
По закону сохранения импульса
или
.
Из полученного
уравнения найдем
m
= 3,64∙10-22
кг∙м/с.
Задачи для самостоятельного решения и контрольных заданий
1. Рентгеновские
лучи с длиной волны
= 0,2Å
испытывают комптоновское рассеяние
под углом 90°. Найти: 1) изменение длины
волны рентгеновских лучей при рассеянии;
2) энергию электрона отдачи. [0,024
Å, 6,7
кэВ]
2. При комптоновском
рассеянии энергия падающего фотона
распределяется поровну между рассеянным
фотоном и электроном отдачи. Угол
рассеяния равен
/2.
Найти энергию и импульс рассеянного
фотона. [0,258
МэВ,
кг
м/с]
3. Рентгеновские
лучи с длиной волны
= 0,708 Å
испытывают комптоновское рассеяние на
парафине. Найти длину волны рентгеновских
лучей, рассеянных в направлениях: 1)
/2;
2)
.
[0,732 Å, 0,756 Å]
4. Рентгеновское
излучение длиной волны
=55,8пм
рассеивается плиткой графита. Определить
частоту света, рассеянного под углом
=60°
к направлению падающего пучка света.
[5,26
Гц]
5. Энергия падающего
фотона равна энергии покоя электрона.
Определить энергию рассеянного фотона,
если угол рассеяния
равен 1) 60°; 2) 90°; 3) 180°.[743МэВ,
0,258МэВ,
171МэВ]
6. Фотон с энергией
=0,25МэВ
рассеялся на свободном электроне.
Энергия рассеянного фотона равна 0,2
МэВ.
Определить угол рассеяния. [600]
7. Угол рассеяния
фотона равен 90°. Угол отдачи электрона
равен 30°. Определить энергию падающего
фотона. [0,37МэВ]
8. Длина волны
света, падающего на вещество со свободными
электронами,
=0,003
нм. Какую энергию приобретут электроны
отдачи при рассеянии кванта под углом
=60°?
[0,117 МэВ]
9. Поток жестких
рентгеновских лучей (λ
=24пм)
при соударении со свободным электроном
передал ему 9% своей энергии. Определить
длину волны рассеянного рентгеновского
излучения. [26,4
пм]
10. Изменение длины
волны рентгеновских лучей при комптоновском
рассеянии равно 2,4пм.
Вычислить угол рассеяния и величину
энергии, переданной при этом электрону
отдачи, если длина волны рентгеновских
лучей до взаимодействия 10 пм.
[24,3 эВ]
11. Какая доля
энергии фотона приходится при эффекте
Комптона на электрон отдачи, если
рассеяние фотона происходит на угол
180°? Энергия фотона до рассеяния равна
0,255МэВ.
[0,5]
12. Узкий пучок
монохроматического рентгеновского
излучения падает на рассеивающее
вещество. При этом длины волн излучения,
рассеянного под углами, равными 600
и 1200,
отличаются друг от друга в n=2
раза. Считая,
что рассеяние происходит на свободных
электронах, найти длину волны падающего
излучения. [1,2
пм]
13. Фотон с
длиной волны,
равной 6,0пм,
рассеялся под прямым углом на покоившемся
свободном электроне. Найти частоту
рассеянного
фотона и кинетическую энергию электрона
отдачи. [v=3,55∙1020
с-1;
Т=60кэВ]
14. Фотон с энергией
0.46МэВ
рассеялся под углом 120° на покоившемся
свободном электроне. Определить
относительное изменение частоты фотона.
[0,57]
15. Определить угол
,
под которым был рассеян гамма-квант с
энергией
=1,02МэВ
при эффекте Комптона, если кинетическая
энергия электрона отдачи Т=0,51МэВ.
[60°]
16. Найти энергию
налетающего фотона, если известно, что
при рассеянии под углом 90° на покоившемся
свободном электроне последний приобрел
энергию 300 кэВ.
[0,57 МэВ]
17. Фотон с энергией
1,
равной энергии покоя электрона, испытывает
комптоновское рассеяние на свободном
электроне. Определить: а) максимально
возможное изменение длины волны фотона;
б) максимальную энергию и импульс
электрона отдачи; в) энергию и импульс
электрона отдачи при условии, что фотон
рассеивается под углом 90°.
[а)
4.810-6мкм;
б) 0.34 МэВ, 3.63∙10-22
кг м/с; в) 0.256 МэВ, 3∙10-22
кг м/с]
18.
Рентгеновский фотон с энергией εф
= 20 кэВ претерпевает комптоновское
рассеяние на свободном электроне на
угол
= 90º. Чему равна энергия электрона отдачи?
[756 эВ]
19. Рентгеновское
излучение с длиной волны λ=10пм
рассеивается свободными электронами.
Определите максимальную длину волны
рентгеновского излучения в рассеянном
пучке. [12,4
пм]
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В сегодняшней статье решаем задачи по физике. Тема – эффект Комптона.
Подпишитесь на наш телеграм, там много полезных материалов для учебы. А если хотите скидку, ищите ее на нашем втором канале для клиентов.
Нужна помощь?
Доверь свою работу кандидату наук!
Задачи на тему «эффект Комптона»
Не знаете, с чего начать решение? Вот вам общая памятка по решению физических задач и более 40 формул, держите их под рукой!
Кстати, у нас есть еще и справочник с теорией. Нужна теория по эффекту Комптона? Пожалуйста!
Задача на эффект Комптона №1
Условие
Узкий пучок монохроматического рентгеновского излучения падает на рассеивающее вещество. Найти угол комптоновского рассеяния, если длина волны излучения увеличилась на 1 пм.
Решение
Запишем формулу эффекта Комптона:
λ’-λ=2λсеsin2θ2
Отсюда найдем искомый угол θ:
θ=2acrsin∆λ2λec=2arcsin1·10-122·2,4263·10-12=53,95°
Ответ: θ=53,95°.
Задача на эффект Комптона №2
Условие
Гамма-излучение с длиной волны 0,83·10-13 м рассеялось на свободных протонах под углом 180°. Найти энергию фотона после рассеяния.
Решение
По формуле эффекта Комптона:
λ’=λ+λpc·1-cosθ
Отсюда:
λ’=0,83·10-13+1,3214·10-15·1—1≈8,56·10-14 м
Выразим энергию через длину волны:
Е’=hcλ’=6,62·10-34·3·1088,56·10-14=2,32·10-12Дж
Ответ: 2,32 пДж
Задача на эффект Комптона №3
Условие
В результате комптоновского рассеяния под углом 174° длина волны фотона стала равной 8 пм. Во сколько раз уменьшилась частота фотона?
Решение
Из формулы для эффекта Комптона найдем:
λ’-λ=λес·1-cosθλ=λ’-λec·1-cosθλ=8·10-12-2,4263·10-121—0,9945≈3,16·10-12 м
Частоту фотона после рассеяния найдем из формулы для длины волны:
λ=сϑϑ=сλ=3·1083,16·10-12=94,87·1018 Гц
Частота фотона до рассеивания:
ϑ’=сλ’=3·1088·10-12=37,47·1018 Гц
Отсюда:
ϑϑ’=94,8737,47≈2,5
Ответ: уменьшилась в 2,5 раза.
Задача на эффект Комптона №4
Условие
В результате эффекта Комптона фотон с энергией ε1=1,02 МэВ рассеян на свободных электронах на угол θ=150°. Определить энергию рассеянного фотона.
Решение
Согласно формуле Комптона изменение длины волны фотона при рассеянии на свободном электроне:
∆λ=hcE01-cosθ
Здесь E0 – энергия покоя электрона.
С учетом того, что ε=hϑ=hcλ и λ=hcε, первую формулу можно переписать в следующем виде:
hcε-hcε1=hcε01-cosθ
Отсюда можно найти энергию рассеянного фотона ε2:
1ε2-1ε1=1-cosθE0ε2=ε1E0E0+ε11-cosθ
Энергия покоя электрона равна E0=mc2
Подставим значения и рассчитаем:
Е0=9,11·10-31·9·1016=8,199·10-14 Дж=0,511·106 эВ=0,511 МэВε2=1,02·0,5110,511+1,021-сos150°=0,216 МэВ
Ответ: 0,216 МэВ.
Задача на эффект Комптона №5
Условие
При каком угле рассеивания фотонов происходит максимально возможное изменение длины волны?
Решение
Длина волны рассеянного фотона в результате эффекта Комптона возрастает тем больше, чем больше угол рассеивания фотона. Максимально возможное значение этого угла θ=180°, т.е. фотон меняет направление движения на противоположное. Тогда формула Комптона принимает вид:
λ’-λ=2λс
Ответ: 180°.
Нужно больше задач? Не проблема! Вот, например, задачи на фотоэффект.
Вопросы на тему «эффект Комптона»
Вопрос 1. В чем суть эффекта Комптона?
Ответ. Эффект Комптона – явление, сопровождающее рассеяние электромагнитного излучения на свободных (слабосвязанных) электронах атома, приводящее к изменению его частоты (длины волны).
Вопрос 2. Какие закономерности существуют для комптоновского рассеяния?
Ответ. Комптоновское рассеяние подчиняется следующим закономерностям:
- рассеянное излучение обладает высокой интенсивностью для веществ с малым атомным весом и малой интенсивностью для веществ с большим атомным весом;
- при увеличении угла рассеяния интенсивность рассеянного излучения в эффекте Комптона возрастает (интенсивность при классическом рассеянии падает с увеличением угла рассеяния);
- смещение длины волны рассеянного излучения зависит от угла рассеяния;
- при одинаковых углах рассеяния величина смещения одна и та же для всех рассеивающих веществ.
Вопрос 3. Что такое комптоновская длина волны?
Ответ. Комптоновская длина волны является постоянной величиной для частицы, на которой происходит рассеяние электромагнитного излучения.
λс=hmc
Здесь m – масса частицы, на которой происходит рассеяние.
Вопрос 4. Запишите формулу Комптона.
Ответ. Формула комптона имеет вид:
∆λ=λ’-λ=λс1-cosθ
Здесь λ – длина волны падающего излучения, λ’– длина волны рассеянного излучения, θ – угол рассеяния, λс – комптоновская длина волны.
Вопрос 5. Какую премию получил Комптон за открытие данного эффекта?
Ответ. В 1927 году Комптон (совместно с Вильсоном) получил Нобелевскую премию.
Посмотри примеры работ и убедись, что мы поможем на совесть!
Нужна помощь в решении задач? В профессиональном сервисе для учащихся вам помогут решить любую, хоть с тремя звездочками. Обращайтесь в любое время.
Рис.3 — Панель управления
Для удобства использования элементы контроля и управления объединены в отдельные группы.
Угол измерения.
При нажатии кнопки «Задать угол», выполняется та же команда, что и при выборе пункта меню «Модель_Задать угол». Случайным образом задается угол измерения, и Детектор соответствующим образом поворачивается. Значение угла в градусах отображается элементом управления, расположенным слева от кнопки.
Регистрация.
Кнопка «Источник вкл./выкл.» запускает и останавливает работу модели. При запуске включается Индикатор измерений, расположенный справа от метки «Регистрация». По окончанию измерений Индикатор выключается. Количество зарегистрированных на текущий момент частиц отображается на панели слева от кнопки «Источник вкл./выкл.».
Создать отчет.
Кнопка «Создать отчет» запускает программу Microsoft Word и создает по заложенному в программу шаблону документ отчета. В этом документе в соответствии с заданием пользователи обрабатывают и анализируют результаты измерений и создают отчет о проделанной работе.
Выход.
Кнопка «Выход» закрывает Главную форму и завершает работу приложения. При выполнении измерений эта команда блокируется.
Для удобства пользователей все основные команды элементов Панели управления продублированы в Главном меню программы.
Проведение эксперимента
При проведении модельного эксперимента пользователю необходимо руководствоваться заданием, и выполнить следующую последовательность операций:
· Установить угол измерения с помощью кнопки «Задать угол».
· Кнопкой «Источник вкл./выкл.» запустить модель и начать измерения. Индикатор измерений при этом включится.
· Дождаться завершения процесса измерений, при этом Индикатор измерений выключится и в Журнале результатов появится новая строка.
Обработка и оформление результатов
Для обработки данных и составления отчета необходимо:
· Кнопкой «Создать отчет» сформировать и открыть документ отчета.
· Скопировать результаты измерений в буфер обмена с помощью команды Контекстного меню «Копировать список»
· Вставить результаты в документ отчета
· Выполнить соответствующие расчеты и оформить отчет
· Сохранить файл отчета на диске
· Закрыть форму отчета
По завершению работы необходимо закрыть главную форму и выйти из программы.
Литература
1. С. Э. Фриш, А. В. Тиморева, Курс общей физики т. 3, Гос. изд. технико-теоретической литературы, Москва, 1952.
2. Дж. Б. Мэрион, Физика и физический мир, Мир, Москва, 1975.
ЛАБОРАТОРНАЯ РАБОТА 3
Изучение рассеяния рентгеновских лучей
Цель работы – исследование рассеяния рентгеновских лучей веществом.
После выполнения данной работы студенты должны:
· уяснить сущность эффекта Комптона;
· определять длину волны рассеянного рентгеновского излучения при разных углах рассеяния и энергию отдачи комптоновского электрона.
1. Краткая теория
Изучение рассеяния рентгеновских лучей с энергией 20–50 кэВ явилось важным этапом в становлении квантовой теории вещества. Обнаружение Комптоном изменения длины волны рентгеновского излучения при его рассеянии веществом, содержащим легкие атомы, подтвердило универсальный характер соотношения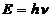 
. До опытов Комптона полагалось, что данное соотношение применимо только для оптической области частот. Теперь же мы получили прямые доказательства того, что фотонную структуру имеет и более высокочастотное электромагнитное излучение. Кроме того, эксперименты Комптона дают дополнительные доказательства справедливости специальной теории относительности.
С классической точки зрения рентгеновское излучение представляет собой электромагнитные волны, которые при взаимодействии с атомами вещества способны вызвать вынужденные колебания электронов. При этом естественно ожидать, что частота рассеянного излучения должна совпадать с частотой падающего излучения. Однако, экспериментально было обнаружено, что при рассеянии рентгеновских и гамма–лучей длина волны в спектре рассеянного излучения кроме первоначальной длины волны возбуждающего излучения появляется более длинные волны. Анализ этого явления, названного в последствии эффектом Комптона, позволило А. Комптону установить следующее:
· в рассеянном излучении присутствуют как первоначальная длина волны возбуждающего излучения, так и длина волны, смещенная в сторону более длинных волн;
· величина смещения зависит от угла рассеяния и возрастает при его увеличении;
· при увеличении угла рассеяния интенсивность несмещенной линии падает, а интенсивность смещенной линии возрастает;
· особенности этого явления объясняются, предположив, что рентгеновское излучение имеет чисто корпускулярную природу.
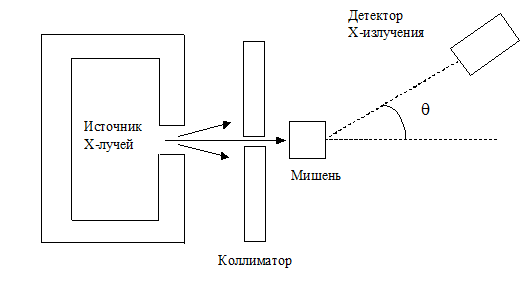
Рассмотрим более подробно явление рассеяние жестких рентгеновских лучей в графите, выполненные А. Комптоном в 1922 г. Схема опыта показана на рис.1. В опыте Комптона рентгеновские лучи, возникающие в трубке с молибденовым антикатодом при разности потенциалов 50 кВ, рассеивались в графитовой мишени. Длина волны падающего излучения отвечала так называемой Мо К–линии с длиной волны 0,7 
=0,7×10-8 см, что соответствует энергии около 20 кэВ. Эта энергия весьма высока по сравнению с энергией связи почти всех электронов атома углерода.
Рис. 1 — Схема эксперимента Комптона
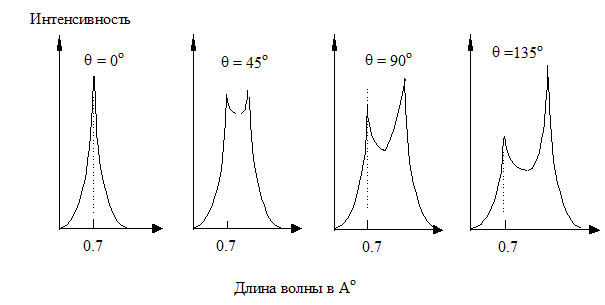
Экспериментальные спектры рассеяния при разных углах рассеяния q представлены на рис.2.
Рис. 2 — Экспериментальные спектры рассеяния
В спектре рассеянного излучения присутствует две линии: одна линия идентична по своим свойствам рассеиваемому излучению, а вторая линия имеет длину волны, которая зависит от угла рассеяния и сдвинута относительно длины волны падающего излучения в длинноволновую область.
Происхождение первой линии легко понять, исходя из волновых представлений падающего излучения. Первичное излучение заставляет электроны атомов вещества колебаться со своей собственной частотой n, и осциллирующие электроны являются источником излучения той же частоты n. В этом процессе происходит лишь временное изменение состояния атома, и электроны не испускаются. Можно ожидать, что такого рода рассеяние будут испытывать главным образом сильно связанные электроны атома, располагающихся на внутренних электронных оболочках (рис.3).
Рис. 3 — Рассеяние первичного излучения сильносвязанными электронами внутренних оболочек и слабосвязанными электронами внешних электронных оболочек атома
Электроны, располагающиеся на внешних электронных оболочках имеют малые энергии связи (10 – 100 эВ) по сравнению с энергией рентгеновского излучения. В таких условиях можно ожидать, что процесс рассеяния рентгеновского излучения будет происходить как на свободных электронах и они могут быть выброшены из атома в процессе рассеяния. В опытах Комптона удалось зарегистрировать электроны отдачи и показать, что электрон отдачи и рассеянное излучение коррелированы друг с другом. Поэтому именно рассеяние на внешних электронах отвечает за появление новой длинноволновой компоненты.
Для количественного анализа рассеяния А. Комптон применил квантовую теорию, согласно которой электромагнитное излучение представляется как состоящее из потока фотонов с энергией E = hn.
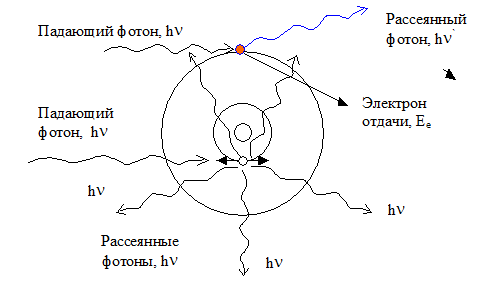
Согласно квантовой теории явление рассеяния рентгеновского излучения можно рассматривать как результат упругого столкновения рентгеновского фотона с почти свободным электроном. При этом фотон передает электрону часть своей энергии и часть своего импульса в соответствии с законами сохранения энергии и импульса. Кинематика рассеяния рентгеновского фотона на свободном электроне показана на рис.4.
Рис. 4 — Кинематика комптоновского рассеяния на свободном электроне
Фотон с частотой n и энергией 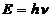сталкивается с покоящимся электроном, масса которого равна 
, а полная энергия электрона до столкновения или энергия покоя – 
.
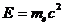
После столкновения возникает фотон с частотой 
, движущийся под углом q к направлению движения первичного фотона, и электрона отдачи, обладающего энергией Ee и импульсом 
и образующий угол j с первичным направлением.