Как найти длину в метрах физика

В физике следует различать траекторию, путь и перемещение.

Длина пути измеряется в системе СИ в метрах, в СГС (сантиметр, грамм, секунда) — в сантиметрах. Применяются и другие единицы измерения длины, в том числе внесистемные (дюйм, фут, ярд, миля и т.д.).

При движении без ускорения путь равен произведению скорости на расстояние:

$S = v cdot (t_2 — t_1) = v cdot Delta t$,

где $v_0$ – скорость тела, $t_2$ — момент времени окончания движения, $t_1$ — момент времени начала движения, $Delta t$ — время движения. График зависимости пути от времени на координатной плоскости в случае такого, называемого равномерным, движения является прямой линией.

Если равноускоренное движение начато с нулевой скорости и известно ускорение, то формула пути имеет вид

$S = frac{a cdot t^{2}}{2}$

где $a$ – ускорение тела.

Объединив два условия, получим общую формулу нахождения пути при равноускоренном движении с произвольной начальной скоростью:

$S = frac{a cdot t^2}{2} + v_0 cdot Delta t$.

Если движение не равномерное и известна средняя скорость движения, то путь можно выразить и другим способом:

$S = v_{ср.} cdot Delta t$,

где $v_{ср.}$ — средняя скорость движения.

На практике движение бывает равномерным или равноускоренным лишь на небольших фрагментах пути, поэтому для вычисления его длины траекторию разбивают на участки, где тело движется по простым закономерностям, вычисляют длину каждого из них и суммируют. Если известна траектория, то ее разбивают на фрагменты, каждый из которых имеет простую геометрическую форму. Сложив их длины, можно найти путь.

Знаете ответ?

План урока:

Измерить – значит сравнить

Числа «карлики» и числа «великаны»

Как измерить длину. Погрешности измерений

Площадь и ее измерение

Измерение объема. Мензурка

Измерить – значит, сравнить

На помощь человеку приходят числа, используя которые можно было сравнить предметы по величине. Так в одном известном мультфильме длину удава измеряли в «попугаях», сравнивая величину удава с длиной попугая.

Из мультфильма «38 попугаев». 

Длина удава 38 «попугаев». Понятно, что удав в 38 раз длиннее попугая. Но попугаи бывают разными. Если взять другого попугая, тот же удав будет, например, 45 «попугаев». Что делать?

Нужно найти тело, принимаемое за единицу измерения, с которой сравниваются другие тела.

В практической деятельности человеку приходится часто измерять длину, массу и время. В разных странах вводились разные единицы измерения этих величин. Существовали такие единицы, как «лошадиная сила», локоть, бочка. Но ведь и локоть, и бочка могут быть разными, поэтому о точности выполнения работы говорилось приблизительно.

(Источник)

Сравнивать нужно только однородные физические величины. Длину тела нужно сравнивать с длиной другого тела, а массу тела – только с массой другого тела, принятого за единицу измерения. Так массу удава из мультфильма можно было сравнить с массой обезьянки. Удав имеет массу 195 «обезьянок». Что бы это значило?

Выход был найден, когда ввели систему единиц СИ. Чтобы измерить любую величину, нужно сравнить ее с однородной величиной, принятой за единицу. Как же выбирают эти единицы?

Наиболее распространено измерение длины, размеров пройденного пути, расстояния. Все эти величины измеряются в метрах. Один метр получили следующим образом. Взяли одну сорока миллионную часть меридиана, который проходит через столицу Франции – Париж. Длину этой части и приняли за 1 метр. На стержне, изготовленном из иридия и платины, нанесли два деления, расстояние между которыми равно одному метру. Такой сплав меньше всего подвержен температурному влиянию, которое может изменить длину тела. Это стержень и есть эталон длины, с которым сравнивают единицу длины во многих странах мира. Метровые линейки – это многочисленные копии эталона, которыми как раз и можно пользоваться.

Эталон длины

(Источник)

Первый эталон метра был изготовлен из латуни в 1795 г. С 1960 г. используется изготовленный с помощью электронных технологий эталон из сплава иридия и платины.  

Существует и эталон массы, равный одному килограмму. Он также изготовлен из сплава иридия и платины.

(Источник)

Эталоны длины и массы хранятся в г. Севр, вблизи Парижа, где располагается Международная палата мер и весов. В 1960 году метр начали сравнивать с величинами, относящимися к разделу «Световые явления». Подробности о свете изучаются в старших классах.

Со светом связана и единица времени – 1 секунда. А до 1960 года (год введения СИ) за основу подсчета времени брали время оборота Земли вокруг Солнца – 1 год, который по календарю состоит из 12 месяцев. Месяцы делятся на сутки – время полного оборота Земли вокруг своей оси, сутки — 24 часа, в каждом из которых 60 минут. А одна шестидесятая часть минуты и есть одна секунда.

Время «хранят» при помощи очень точных часов – устройств, предназначенных для измерения времени. Действие любых часов основано на повторяющихся процессах – колебаниях. Чем меньше период (время одного полного колебания), тем часы более точные.

     При изучении быстро протекающих процессов требуется измерять миллиардные и еще более мелкие доли секунды. Для этого служат атомные часы.

(Источник)

Ученик седьмого класса, конечно же, умеет измерять длину и время, массу продуктов определяют продавцы с помощью весов.

По мере изучения физики будет идти знакомство с различными физическими величинами, способами и приборами их измерения. А сейчас надо знать:

• чтобы измерить физическую величину, ее надо сравнить с однородной величиной, принятой за единицу;
• за основу физических величин берутся эталонные значения, то есть образец сравнения.
• для всех величин существуют свои способы, устройства и единицы измерения.

Числа «карлики» и числа «великаны»

Солнечная система.                                                        Лапка мухи под микроскопом. 

Чтобы достать до Альфа Центавры, звезды, ближайшей к Солнечной системе, надо со скоростью света (300 000 км/с) лететь четыре года. Расстояния до небесных тел огромны.

К звездам. (Источник)

Если определить расстояние от Земли до Солнца, то оно выразится числом 150 000 000 000 м. А бывают числа с еще большим количеством нулей. Масса Земли в килограммах выражается числом с 24 нулями. Такие числа называют «гигантами». Их записывать и использовать очень неудобно.

Существует способ краткой записи больших чисел в виде степени. Например, 1 000 000 = 10⁶. 10 – основание, а 6 – показатель степени.

Используя этот способ, расстояние от нашей планеты до Солнца запишется так:

150 000 000 000 = 15 ∙ 10¹⁰ м – это промежуток называется астрономической единицей (1 а.е.) и служит единицей сравнения в Солнечной системе.

До Альфа-Центавры расстояние в 270 000 а.е., или 4 световых года. Световой год – это тоже астрономическая единица измерения расстояния. Астрономия – наука о космосе и космических телах. (1 св. год = 9,46 ∙ 10¹⁵ м = 68 000а.е.).

Фото двойной звезды Альфа созвездия Центавра. (Источник)

Большие числа записываются при помощи кратных приставок. Например, километр – это тысяча метров, килограмм – тысяча граммов. Приставка «кило» обозначает «тысяча». Есть и другие приставки, которые обозначают умножение величины на число, кратное десяти. Примеры и форма записи даны в таблице кратных приставок.

Используя эти приставки можно записывать очень большие числа.

1 а.е. = 150 000 000 000 м = 150 ∙ 10⁹ м = 150Гм;

1 св. год = 9 460 000 000 000 м = 9,46 ∙ 10¹² м = 9,46 Тм;

А теперь о числах – «карликах». Если сделать попытку измерить толщину одного листа книги, то сразу это не получится. Надо действовать по простому плану:

• отобрать в книге некоторое число страниц N (N = 100, например);
• измерить толщину L этих страниц (пусть L = 11 мм);
• найти толщину одной страницы d по формуле d = L/N.

Получится d = 0,11 мм = 0, 00011 м. Это число очень маленькое.

Такой способ измерения малых величин называется методом рядов. Он достаточно прост.

Размеры пшена.                                           Толщина проволоки. 

Но существуют и гораздо меньшие величины. Маленькие числа, так называемые «карлики», также записывают при помощи степеней или дольных приставок. (С приставками деци, санти, милли знакомятся еще в начальной школе).

Число меньше единицы, поэтому показатель степени – отрицательное число. Оно показывает количество цифр после запятой. Например, 0, 00011 м = 11 ∙ 10^-5 м.

Число 0,00000625 можно записать по-разному, применяя степень:

625 ∙ 10^-8, 62,5 ∙ 10^-7, 6,25 ∙ 10^-6 и т. д.

Очень маленькие числа по-другому можно записывать, используя таблицу дольных приставок.

Например, при изготовлении сверхточных приборов (телескопов, микроскопов и др.), детали ошлифовываются до очень гладкой поверхности. Неровности должны быть меньше 2,5 ∙ 10^-6 м или 2,5 мкм.

Большие и маленькие числа помогают человеку в различных отраслях деятельности: в науке, промышленности, медицине и т.д.

Как измерить длину. Погрешности измерений

На практике измерить длину отрезка достаточно просто:

• Приложить линейку к отрезку.
• Совместить ноль с началом отрезка.
• Определить число, соответствующее концу отрезка.
• Записать результат измерения.    

В приведенном примере длина отрезка 9,9 см. Как точен этот результат? Он точен до 1 мм, так как на линейке нет меньших делений. Не надо путать значения слов «штрих» и «деление».

(Источник)

Численное значение самого маленького деления шкалы прибора называется ценой деления.

Чтобы определить цену деления прибора (например, линейки), нужно взять любые два рядом стоящие числа и их разность поделить на число делений между ними (т.е. промежутков между штрихами).

Цена деления линейки = (7 см – 6 см)/10 = 0,1 см = 1 мм.

И чтобы начать измерение, прежде всего надо найти цену деления прибора, который используется в данном случае. Любое измерение дает некоторую погрешность, зависящую от качества прибора. Поэтому ее называют погрешностью прибора.

Шкалы различных приборов. (Источник)

Известно, что измерить какую-то величину – это значит сравнить ее с эталоном. На практике пользуются не эталонами, а специальными приборами (линейка, часы и др.), которые являются копиями с эталонов, изготовленными с определенной точностью. Абсолютно точных измерений не бывает. При использовании линейки допускается погрешность отсчета, которая равна половине цены деления прибора (0,5 мм). Сумма погрешностей прибора и отсчета называется абсолютной погрешностью. Она равна цене деления прибора.

Абсолютная погрешность обозначается значком Δ (дельта). Для школьной линейки Δ = 1 мм. Δ показывает, на сколько совершается ошибка при использовании того или иного прибора. Для более точных измерений используется штангенциркуль. В устройстве штангенциркуля заложено две шкалы, неподвижная (Δ = 1 мм) и подвижная (Δ = 0,1 мм).

                               
Штангенциркуль.                                           Микрометр.  

А вот при помощи микрометра, где используется не перемещение шкалы, а ее вращение измерить длину можно с точностью до 0,01 мм. Но это еще не предел. В очень точных технологиях определяются размеры с точностью до 10^-7м, в научных разработках точность возрастает во много раз. Но для этого нужны сверхточные приборы.

На практике, используя приборы, необходимо учитывать качество измерения. Величина, которая помогает это учесть, называется относительной погрешностью σ (сигма) и выражается в процентах.

σ = Δ / L ( L – измеренная величина)

     Пример: Требуется замерить длину L отрезка различными приборами: 1) линейкой, 2) штангенциркулем и 3) микрометром. Длина отрезка получилась 55 мм. Какова относительная погрешность этих трех измерений?

 1) Δ₁ = 1 мм, L = 55 ± 1 мм, σ₁ = 1 мм / 55 мм ≈ 0,018 (1,8%);

   2) Δ₂ = 0,1 мм, L = 55 ± 0,1 мм, σ₂ = 0,1 мм / 55мм ≈ 0,0018 (0,18);

   3) Δ₃ = 0,01 мм, L = 55 ± 0,01 мм, σ₃ = 0,01 мм / 55мм ≈ 0,00018 (0,018%).

Как видно, более точный прибор (микрометр) дает меньший процент ошибки.

Для каждого конкретного измерения в технике, практической деятельности человека и в науке существует своя точность измерения, в соответствии с которой применяются измерительные приборы.

Площадь и ее измерение

С измерением длин очень тесно связано измерение площадей. Из математики известны формулы площадей квадрата и прямоугольника. У квадрата все стороны равны, поэтому достаточно измерить одну сторону, а у прямоугольника противоположные стороны равны, поэтому надо знать длину и ширину. Площадь обозначается буквой S, и формулы для расчета площадей следующие:

S_кв = a², S_пр = а ∙ в. Единицей измерения площади является квадратный метр (м²).

Для измерения малых площадей применяются см² и мм², а большие площади – в км². В сельском хозяйстве для измерения земельных участков используют внесистемные единицы: гектар (га) – для больших, ар (а) или «сотка» — для небольших (приусадебных или дачных) участков земли. 1га = 10 000 м², 1 а = 100 м².

Очень часто на практике имеют дело с различными кругами. Это может быть цирковая арена, крышка стола, разрез ствола дерева. Формула нахождения площади круга: S = πR². (π (пи) – это бесконечная дробь ≈ 3,14 подробно изучается в курсе алгебры).

Арена цирка.                                    Круглый стол.                            Спил дерева.  

А как определить площадь, ограниченную произвольной кривой линией? Такая площадь может быть у озера, полянки в лесу, листочка с дерева.

Существует правило нахождения площади тел произвольной формы:

• Разбить всю поверхность на равные квадраты с известной площадью.
• Подсчитать количество целых квадратов.
• Подсчитать число нецелых квадратов и поделить это число на два. (Это будет примерное количество целых квадратов).
• Сложить результаты пунктов 2 и 3.
• Умножить площадь одного квадрата на общее число целых квадратов.

Площадь больших территорий изображают в условном масштабе или фотографируют, применяют прием разбиения на квадраты и находят площадь фотографии. Используя масштаб вычисляют реальную площадь поверхности.

Довольно часто площадь приходится находить в географии. Каждое государство, область, город имеют свои площади. В строительстве – любое здание имеет площадь, которую необходимо знать строителям. В сельском хозяйстве ведется постоянный учет площадей для посевных культур.

Измерение объема. Мензурка

При измерении пространства нужно перейти к трем измерениям, так как представление о пространстве дает объем. Известны формулы объемов параллелепипеда, куба, шара, цилиндра.

(Источник)

Объем любого тела измеряется в кубических метрах (есть кратные и дольные единицы). Из математики известны формулы объемов:

V_пар = а ∙ в ∙ с (произведение длины, ширины и высоты),

V_к = а³ (а — ребро куба),

V_цил = π ∙ r² ∙ h (r — радиус основания, h – высота цилиндра),

V_ш = 4/3 π ∙ R³ (R – радиус шара).

О вычислении объемов более сложной, но правильной, формы рассказывается в старших классах. А как определить объем, например, камня, форма которого может быть самой различной? Для измерения объемов таких тел используется специальный и очень простой прибор, который называется мензурка (или измерительный цилиндр). Это стеклянный сосуд с делениями. При помощи этого цилиндра легко найти объемы сыпучих тел и жидкостей. Для этого достаточно их засыпать вещество или налить в мензурку жидкость и, зная цену деления, определить объем.

(Источник)

На мензурке обычно ставится единица измерения в миллилитрах. Литр – это широко применяемая единица объема, равная одной тысячной кубического метра. 1 мл = 1 см³ = 10^-6 м³.

Определить объем камня или любого другого тела неправильной формы с помощью мензурки можно при условии, что тело имеет размеры, позволяющие опустить его в мензурку.

(Источник)

Налить в мензурку воду и зафиксировать ее объем. Прикрепить тело неправильной формы к нити. Осторожно опустить полностью в воду. Уровень воды поднимется ровно на столько, чему равен объем тела.

Пользуясь измерительным цилиндром, нельзя забывать, что это прибор, имеющий шкалу, а значит, результат получится с погрешностью.

Основной единицей длины служит метр (м). Первоначально за образец (эталон) метра было принято расстояние между двумя штрихами на специально изготовленном платино-иридиевом стержне длины 102 см, хранящемся в Международном бюро мер и весов в Париже (рис. 14). Материал и форма сечения стержня н условия его хранения были выбраны так, чтобы наилучшим образом обеспечить неизменность образца. В частности, были приняты меры для поддержания постоянной температуры стержня. Тщательно выполненные вторичные эталоны — копии этого образца — хранятся в институтах мер и весов разных стран.

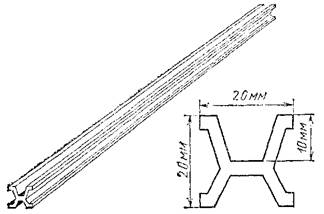Рис. 14. Первоначальный эталон метра (общий вид и сечение)

Предполагалось изготовить образец метра равным одной сорокамиллионной части длины земного меридиана. Когда выяснилась недостаточная точность измерений на земной поверхности, то не стали заменять изготовленный образец или вносить поправки на основе более точных измерений, а решили сохранить сам образец в качестве единицы длины. Этот образец примерно на 0,2 мм меньше, чем 1/40 000 000 часть меридиана.

Кроме этой основной единицы, в науке и технике применяют и другие единицы — десятичные кратные и дольные от метра:

• километр (1 км=1000 м);
• сантиметр (1 см=0,01 м);
• миллиметр (1 мм=0,001 м);
• микрометр (1 мкм=0,001 мм=0,000001 м);
• нанометр (1 нм=0,000000001 м).

В Англии, США и некоторых других странах широко распространены так называемые английские меры длины:

• дюйм = 25,4 мм;
• фут = 12 дюймов = 304.8 мм;
• миля сухопутная («статутная») = 1609 м;
• миля морская («адмиралтейская») = 1852 м (длина одной минуты дуги земного меридиана).

Старые русские меры длины составляли:

• вершок = 4,445 см;
• аршин = 28 дюймов = 16 вершков = 0,7112 м;
• сажень = 3 аршина = 2,1336 м;
• верста = 500 сажен = 1,0668 км;
• русская миля = 7 верст = 7,4676 км.

Обилие разных единиц длины (а также и единиц других физических величин) весьма неудобно на практике. Поэтому были разработаны международные стандартные определения единиц всех физических величин. Сборник этих определений называют системой единиц СИ (от слов Systeme Internationale — Международная система). С 1963 г. в СССР и ряде других стран СИ рекомендована для применения во всех областях науки и техники.

Согласно этой системе метр определен как длина, равная 1 650 763,73 длины волны оранжевого света, излучаемого специальной лампой, в которой под действием электрического разряда светится газ криптон-86. Число длин воли выбрано так, чтобы эта единица длины совпадала возможно точнее с парижским метром. Поэтому за единицу и не была выбрана длина, на которой укладывалось бы какое-либо круглое число (например, один миллион) длин волн. Эту новую единицу длины можно воспроизводить (оптическим путем) с большей точностью, чем архивный образец. Очень удобно, что для воспроизведения единицы длины не нужно обращаться к какому-то единственному хранящемуся образцу, а достаточно изготовить специальную криптоновую лампу и наблюдать испускаемый ею свет.

На практике для измерения длины, в том числе и для измерения расстояний между двумя положениями точки на траектории, применяют копии вторичных эталонов: стержни, линейки или ленты с делениями, равными длине эталона, либо его части (сантиметры, миллиметры). При измерении начало измерительной линейки совмещают с одним концом измеряемого отрезка и отмечают то ее деление, против которого окажется второй конец отрезка. Если второй конец не совпадает ни с одним из делений линейки, то «на глаз» оценивают, на какой доле расстояния между делениями он оказался.

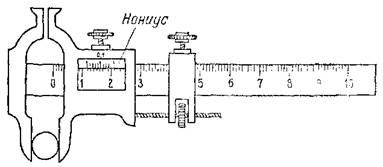Рис. 15. Штангенциркуль с нониусом

Для уменьшения неизбежной ошибки отсчета применяют различные вспомогательные приспособления. На рис. 15 изображено одно из них — нониус, установленный на штангенциркуле. Нониус представляет собой добавочную шкалу, передвигаемую вдоль основной шкалы. Деления ноииуса меньше деления основной шкалы на 0,1 их размера; например, если деление основной шкалы равно 1 мм, то деление нониуса равно 0,9 мм. На рисунке видно, что диаметр измеряемого шарика больше 11 мм, но меньше 12 мм. Чтобы найти, сколько десятых долей миллиметра составляет остающаяся дробная часть деления, смотрят, который из штрихов нониуса совпадает с каким-нибудь из штрихов основной шкалы. На нашем рисунке это девятый штрих нониуса. Значит, восьмой, седьмой и т. д. штрихи нониуса окажутся впереди ближайших к ним предыдущих штрихов основной шкалы на 0,1 мм, 0,2 мм и т. д., а начальный штрих нониуса окажется на 0,9 мм впереди ближайшего к нему предыдущего штриха основной шкалы. Отсюда следует, что диаметр шара равен стольким целым миллиметрам, сколько их укладывается от начала основной шкалы до начала шкалы нониуса (11 мм), и стольким десятым долям миллиметра, сколько делений нониуса укладывается от начала шкалы нониуса до совпадающих штрихов (0,9 мм). Итак, измеряемый диаметр шарика равен 11,9 мм.

Таким образом, нониус позволяет измерять расстояния с точностью до 1/10 деления шкалы.