In electrical engineering, electrical length is a dimensionless parameter equal to the physical length of an electrical conductor such as a cable or wire, divided by the wavelength of alternating current at a given frequency traveling through the conductor.[1][2][3] In other words, it is the length of the conductor measured in wavelengths. It can alternately be expressed as an angle, in radians or degrees, equal to the phase shift the alternating current experiences traveling through the conductor.[1][3]
Electrical length is defined for a conductor operating at a specific frequency or narrow band of frequencies. It is determined by the construction of the cable, so different cables of the same length operating at the same frequency can have different electrical lengths. A conductor is called electrically long if it has an electrical length much greater than one; that is it is much longer than the wavelength of the alternating current passing through it, and electrically short if it is much shorter than a wavelength. Electrical lengthening and electrical shortening means adding reactance (capacitance or inductance) to an antenna or conductor to increase or decrease the electrical length,[1] usually for the purpose of making it resonant at a different resonant frequency.
This concept is used throughout electronics, and particularly in radio frequency circuit design, transmission line and antenna theory and design. Electrical length determines when wave effects become important in a circuit. Ordinary lumped element electric circuits only work well for alternating currents at frequencies for which the circuit is electrically small (electrical length much less than one). For frequencies high enough that the wavelength approaches the size of the circuit (the electrical length approaches one) the lumped element model on which circuit theory is based becomes inaccurate, and transmission line techniques must be used.[4]: p.12–14
Definition[edit]
Electrical length is defined for conductors carrying alternating current (AC) at a single frequency or narrow band of frequencies. An alternating electric current of a single frequency 
is an oscillating sine wave which repeats with a period of 
.[5] This current flows through a given conductor such as a wire or cable at a particular phase velocity 
. It takes time for later portions of the wave to reach a given point on the conductor so the spacial distribution of current and voltage along the conductor at any time is a moving sine wave. After a time equal to the period 
a complete cycle of the wave has passed a given point and the wave repeats; during this time a point of constant phase on the wave has traveled a distance of
so 
(Greek lambda) is the wavelength of the wave along the conductor, the distance between successive crests of the wave.
The electrical length 
of a conductor with a physical length of 
at a given frequency is the number of wavelengths or fractions of a wavelength of the wave along the conductor; in other words the conductor’s length measured in wavelengths[6][1][2]
The phase velocity at which electrical signals travel along a transmission line or other cable depends on the construction of the line. Therefore, the wavelength corresponding to a given frequency varies in different types of lines, thus at a given frequency different conductors of the same physical length can have different electrical lengths.
Phase shift definition[edit]
In radio frequency applications, when a delay is introduced due to a conductor, it is often the phase shift 
, the difference in phase of the sinusoidal wave between the two ends of the conductor, that is of importance.[5] The length of a sinusoidal wave is commonly expressed as an angle, in units of degrees (with 360° in a wavelength) or radians (with 2π radians in a wavelength). So alternately the electrical length can be expressed as an angle which is the phase shift of the wave between the ends of the conductor[1][3][5]
Significance[edit]
The electrical length of a conductor determines when wave effects (phase shift along the conductor) are important.[4]: p.12–14 If the electrical length is much less than one, that is the physical length of a conductor is much shorter than the wavelength, say less than one tenth of the wavelength (
) it is called electrically short. In this case the voltage and current are approximately constant along the conductor, so it acts as a simple connector which transfers alternating current with negligible phase shift. In circuit theory the connecting wires between components are usually assumed to be electrically short, so the lumped element circuit model is only valid for alternating current when the circuit is electrically small, much smaller than a wavelength.[4]: p.12–14 [5] When the electrical length approaches or is greater than one, transmission line techniques (the distributed-element model) must be used.
Velocity factor[edit]
In a vacuum an electromagnetic wave (radio wave) travels at the speed of light 
2.9979×108 meters per second, and very close to this speed in air, so the free space wavelength of the wave is 
.[5] (in this article free space variables are distinguished by a subscript 0) Thus a physical length of a radio wave in space or air has an electrical length of
wavelengths.
In the SI system of units, empty space has a permittivity of 
8.854×10−12 F/m (farads per metre) and a magnetic permeability of 
1.257×10−6 H/m (henries per meter). These universal constants determine the speed of light[5][7]
Equivalent circuit of a lossless transmission line. 
and 
represent the inductance and capacitance per unit length of a small section of line
In cables and transmission lines an electrical signal travels at a rate determined by the effective shunt capacitance and series inductance per unit length of the transmission line
Each cycle of the alternating current takes time to charge the capacitance between the conductors, and the rate of change of the current is slowed by the series inductance of the wires; this determines the phase velocity at which the wave moves along the line. Some transmission lines consist only of bare metal conductors, if they are far away from other high permittivity materials their signals propagate at very close to the speed of light, 
. In most transmission lines the material construction of the line slows the velocity of the signal so it travels at a reduced phase velocity[5]
where 
(kappa) is a dimensionless number between 0 and 1 called the velocity factor (VF), characteristic of the type of line, equal to the ratio of signal velocity in the line to the speed of light.[8][9][6]
Most transmission lines contain a dielectric material (insulator) filling some or all of the space in between the conductors. The permittivity 
or dielectric constant of that material increases the distributed capacitance in the cable, which reduces the velocity factor below unity. If there is a material with high magnetic permeability (
) in the line such as steel or ferrite which increases the distributed inductance , it can also reduce , but this is almost never the case. If all the space around the transmission line conductors containing the near fields was filled with a material of permittivity and permeability , the phase velocity on the line would be[5]
The effective permittivity and permeability per unit length of the line are frequently given as dimensionless constants; relative permittivity: 
and relative permeability: 
equal to the ratio of these parameters compared to the universal constants 
and 
so the phase velocity is
So the velocity factor of the line is
In many lines only a fraction of the space surrounding the line is occupied by a solid dielectric. With only part of the electromagnetic field effected by the dielectric, there is less reduction of the wave velocity. In this case an effective permittivity 
can be calculated which if it filled all the space around the line would give the same phase velocity. This is computed as a weighted average of the relative permittivity of free space, unity, and that of the dielectric:
where the fill factor F expresses the effective proportion of space around the line occupied by dielectric.
In most transmission lines there are no materials with high magnetic permeability, so 
and 
and so
(no magnetic materials)
Since the electromagnetic waves travel slower in the line than in free space, the wavelength of the wave in the transmission line is shorter than the free space wavelength by the factor kappa: 
. Therefore, more wavelengths fit in a transmission line of a given length than in the same length of wave in free space, so the electrical length of a transmission line is longer than the electrical length of a wave of the same frequency in free space[5]
Transmission lines[edit]
| Type of line | Velocity factor κ[10] |
Velocity of signal in cm per ns |
|
|---|---|---|---|
| Parallel line, air dielectric |
 |
.95 | 29 |
| Parallel line, polyethylene dielectric (Twin lead) |
 |
.85 | 28 |
| Coaxial cable, polyethylene dielectric |
 |
.66 | 20 |
| Twisted pair, CAT-5 |  |
.64 | 19 |
| Stripline | .50 | 15 | |
| Microstrip |  |
.50 | 15 |
Ordinary electrical cable suffices to carry alternating current when the cable is electrically short; the electrical length of the cable is small compared to one, that is when the physical length of the cable is small compared to a wavelength, say .[11]
As frequency gets high enough that the length of the cable becomes a significant fraction of a wavelength, 
, ordinary wires and cables become poor conductors of AC.[4]: p.12–14 Impedance discontinuities at the source, load, connectors and switches begin to reflect the electromagnetic current waves back toward the source, creating bottlenecks so not all the power reaches the load. Ordinary wires act as antennas, radiating the power into space as radio waves, and in radio receivers can also pick up radio frequency interference (RFI).
To mitigate these problems, at these frequencies transmission line is used instead. A transmission line is a specialized cable designed for carrying electric current of radio frequency. The distinguishing feature of a transmission line is that it is constructed to have a constant characteristic impedance along its length and through connectors and switches, to prevent reflections. This also means AC current travels at a constant phase velocity along its length, while in ordinary cable phase velocity may vary. The velocity factor depends on the details of construction, and is different for each type of transmission line. However the approximate velocity factor for the major types of transmission lines is given in the table.
Electrical length is widely used with a graphical aid called the Smith chart to solve transmission line calculations. A Smith chart has a scale around the circumference of the circular chart graduated in wavelengths and degrees, which represents the electrical length of the transmission line.
The equation for the voltage as a function of time along a transmission line with a matched load, so there is no reflected power, is
where
- is the peak voltage along the line
- is the angular frequency of the alternating current in radians per second
- is the wavenumber, equal to the number of radians of the wave in one meter
- is the distance along the line
- is time
In a matched transmission line, the current is in phase with the voltage, and their ratio is the characteristic impedance 
of the line
Antennas[edit]
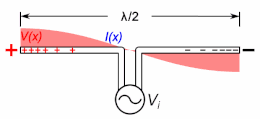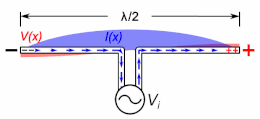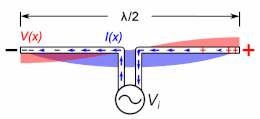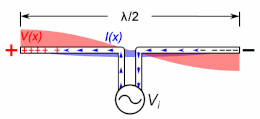
A half-wave dipole antenna showing the standing waves of voltage (red) and current (blue) on the antenna. The antenna is resonant at the frequency at which the electrical length is equal to 
An important class of radio antenna is the thin element antenna in which the radiating elements are conductive wires or rods. These include monopole antennas and dipole antennas, as well as antennas based on them such as the whip antenna, T antenna, mast radiator, Yagi, log periodic, and turnstile antennas. These are resonant antennas, in which the radio frequency electric currents travel back and forth in the antenna conductors, reflecting from the ends.
If the antenna rods are not too thick (have a large enough length to diameter ratio), the current along them is close to a sine wave, so the concept of electrical length also applies to these.[3] The current is in the form of two oppositely directed sinusoidal traveling waves which reflect from the ends, which interfere to form standing waves. The electrical length of an antenna, like a transmission line, is its length in wavelengths of the current on the antenna at the operating frequency.[1][12][13][4]: p.91–104 An antenna’s resonant frequency, radiation pattern, and driving point impedance depend not on its physical length but on its electrical length.[14] A thin antenna element is resonant at frequencies at which the standing current wave has a node (zero) at the ends (and in monopoles an antinode (maximum) at the ground plane). A dipole antenna is resonant at frequencies at which it’s electrical length is a half wavelength (
)[12] or a multiple of it. A monopole antenna is resonant at frequencies at which its electrical length is a quarter wavelength (
) or a multiple of it.
Resonant frequency is important because at frequencies at which the antenna is resonant the input impedance it presents to its feedline is purely resistive. If the resistance of the antenna is matched to the characteristic resistance of the feedline, it absorbs all the power supplied to it, while at other frequencies it has reactance and reflects some power back down the line toward the transmitter, causing standing waves (high SWR) on the feedline. Since only a portion of the power is radiated this causes inefficiency, and can possibly overheat the line or transmitter. Therefore, transmitting antennas are usually designed to be resonant at the transmitting frequency; and if they cannot be made the right length they are electrically lengthened or shortened to be resonant (see below).
End effects[edit]
Reduction factor of physical length of a resonant dipole from a half-wavelength electrical length as a function of element thickness
A thin-element antenna can be thought of as a transmission line with the conductors separated,[15] so the near-field electric and magnetic fields extend further into space than in a transmission line, in which the fields are mainly confined to the vicinity of the conductors. Near the ends of the antenna elements the electric field is not perpendicular to the conductor axis as in a transmission line but spreads out in a fan shape (fringing field).[16] As a result, the end sections of the antenna have increased capacitance, storing more charge, so the current waveform departs from a sine wave there, decreasing faster toward the ends.[17] When approximated as a sine wave, the current does not quite go to zero at the ends; the nodes of the current standing wave, instead of being at the ends of the element, occur somewhat beyond the ends.[18] Thus the electrical length of the antenna is longer than its physical length.
The electrical length of an antenna element also depends on the length-to-diameter ratio of the conductor.[19][15][20][21] As the ratio of the diameter to wavelength increases, the capacitance increases, so the node occurs farther beyond the end, and the electrical length of the element increases.[19][20] When the elements get too thick, the current waveform becomes significantly different from a sine wave, so the entire concept of electrical length is no longer applicable, and the behavior of the antenna must be calculated by electromagnetic simulation computer programs like NEC.
As with a transmission line, an antenna’s electrical length is increased by anything that adds shunt capacitance or series inductance to it, such as the presence of high permittivity dielectric material around it. In microstrip antennas which are fabricated as metal strips on printed circuit boards, the dielectric constant of the substrate board increases the electrical length of the antenna. Proximity to the Earth or a ground plane, nearby grounded towers, metal structural members, guy lines and the capacitance of insulators supporting the antenna also increase the electrical length.[20]
These factors, called «end effects», cause the electrical length of an antenna element to be somewhat longer than the length of the same wave in free space. In other words, the physical length of the antenna at resonance will be somewhat shorter than the resonant length in free space (one-half wavelength for a dipole, one-quarter wavelength for a monopole).[19][20] As a rough generalization, for a typical dipole antenna, the physical resonant length is about 5% shorter than the free space resonant length.[19][20]
Electrical lengthening and shortening[edit]
In many circumstances for practical reasons it is inconvenient or impossible to use an antenna of resonant length. An antenna of nonresonant length at the operating frequency can be made resonant by adding a reactance, a capacitance or inductance, either in the antenna itself or in a matching network between the antenna and its feedline.[20] A nonresonant antenna appears at its feedpoint electrically equivalent to a resistance in series with a reactance. Adding an equal but opposite type of reactance in series with the feedline will cancel the antenna’s reactance; the combination of the antenna and reactance will act as a series resonant circuit, so at its operating frequency its input impedance will be purely resistive, allowing it to be fed power efficiently at a low SWR without reflections.
In a common application, a monopole antenna with an electrical length shorter than a quarter-wavelength (
), or a dipole antenna shorter than a half-wavelength () will have capacitive reactance. Adding an inductor (coil of wire), called a loading coil, at the feedpoint in series with the antenna, with inductive reactance equal to the antenna’s capacitive reactance at the operating frequency, will cancel the capacitance of the antenna, so the combination of the antenna and coil will be resonant at the operating frequency. An antenna shorter than resonant length is called electrically short, and since adding inductance is equivalent to increasing the electrical length, this technique is called electrically lengthening the antenna. This is the usual technique for matching an electrically short transmitting antenna to its feedline, so it can be fed power efficiently. However, an electrically short antenna that has been lengthened in this way still has the same radiation pattern; it does not radiate as much power, and therefore has lower gain than a full-sized antenna.
Conversely, an antenna longer than resonant length at its operating frequency, such as a monopole longer than a quarter wavelength but shorter than a half wavelength, will have inductive reactance. This can be cancelled by adding a capacitor of equal but opposite reactance at the feed point to make the antenna resonant. This is called electrically shortening the antenna.
Scaling properties of antennas[edit]
Two antennas that are similar (scaled copies of each other), fed with different frequencies, will have the same radiation resistance and radiation pattern and fed with equal power will radiate the same power density in any direction if they have the same electrical length at the operating frequency; that is, if their lengths are in the same proportion as the wavelengths.[22][4]: p.12–14
This means the length of antenna required for a given antenna gain scales with the wavelength (inversely with the frequency), or equivalently the aperture scales with the square of the wavelength.
Electrically short antennas[edit]
An electrically short conductor, much shorter than one wavelength, makes an inefficient radiator of electromagnetic waves. As the length of an antenna is made shorter than its fundamental resonant length (a half-wavelength for a dipole antenna and a quarter-wavelength for a monopole), the radiation resistance the antenna presents to the feedline decreases with the square of the electrical length, that is the ratio of physical length to wavelength, 
. As a result, other resistances in the antenna, the ohmic resistance of metal antenna elements, the ground system if present, and the loading coil, dissipate an increasing fraction of transmitter power as heat. A monopole antenna with an electrical length below .05 or 18° has a radiation resistance of less than one ohm, making it very hard to drive.
A second disadvantage is that since the capacitive reactance of the antenna and inductive reactance of the required loading coil do not decrease, the Q factor of the antenna increases; it acts electrically like a high Q tuned circuit. As a result, the bandwidth of the antenna decreases with the square of electrical length, reducing the data rate that can be transmitted. At VLF frequencies even the huge toploaded wire antennas that must be used have bandwidths of only ~10 hertz, limiting the data rate that can be transmitted.
Regimes of electromagnetics[edit]
The field of electromagnetics is the study of electric fields, magnetic fields, electric charge, electric currents and electromagnetic waves. Classic electromagnetism is based on the solution of Maxwell’s equations. These equations are mathematically difficult to solve in all generality, so approximate methods have been developed that apply to situations in which the electrical length of the apparatus is very short (
) or very long (
). Electromagnetics is divided into three regimes or fields of study depending on the electrical length of the apparatus, that is the physical length of the apparatus compared to the wavelength 
of the waves:[4]: p.21 [23][24][25] Completely different apparatus is used to conduct and process electromagnetic waves in these different wavelength ranges
- Circuit theory: When the wavelength of the electrical oscillations is much larger than the physical size of the circuit (), say ,[26] the action occurs in the near field. The phase of the oscillations and therefore the current and voltage can be approximated as constant along the length of connecting wires. Also little energy is radiated in the form of electromagnetic waves, the power radiated by a conductor as an antenna is proportional to the electrical length squared . So the electrical energy remains in the wires and components as quasistatic near-field electric and magnetic fields. Therefore, the approximation of the lumped element model can be used, and electric currents oscillating at these frequencies can be processed by electric circuits consisting of lumped circuit elements such as resistors, capacitors, inductors, transformers, transistors, and integrated circuits linked by ordinary wires. Mathematically Maxwell’s equations reduce to circuit theory (Kirchhoff’s circuit laws).
- , Distributed-element model (microwave theory): When the wavelength of the waves is of the same order of magnitude as the size of the equipment (), as it is in the microwave part of the spectrum, full solutions of Maxwell’s equations must be used. At these frequencies, wires are replaced by transmission lines and waveguide and lumped elements are replaced by resonant stubs, irises, and cavity resonators. Often only a single mode (wave pattern) is propagating through the apparatus, which simplifies the mathematics. A modification of circuit theory called the distributed-element model can often be used, in which extended objects are regarded as electrical circuits with capacitance, inductance and resistance distributed along their length. A graphical aid called the Smith chart is often used to analyze transmission lines.
- , Optics: When the wavelength of the electromagnetic wave is much smaller than the physical size of the equipment that manipulates it (), say , most of the path of the waves is in the far field. In the far field, the electric and magnetic fields cannot be separated but propagate together as an electromagnetic wave. Unlike in the case of microwaves, the number of modes propagating is usually large. Since little of the energy is stored in the quasistatic (induction) electric or magnetic fields at the surface boundaries between media (called evanescent fields in optics), the concepts of voltage, current, capacitance, and inductance have little meaning and are not used, and the medium is characterized by its index of refraction , absorption, permittivity , permeability , and dispersion. At these frequencies electromagnetic waves are manipulated by optical elements such as lenses, mirrors, prisms, optical filters and diffraction gratings. Maxwell’s equations can be approximated by the equations of geometrical optics.
Historically, electric circuit theory and optics developed as separate branches of physics until at the end of the 19th century James Clerk Maxwell’s electromagnetic theory and Heinrich Hertz’s discovery that light was electromagnetic waves unified these fields as branches of electromagnetism.
Definition of variables[edit]
| Symbol | Unit | Definition |
|---|---|---|
 |
meter−1 | Wavenumber of wave in conductor 
|
|
farads / meter | Permittivity per meter of the dielectric in cable |
|
farads / meter | Permittivity of free space, a fundamental constant |
|
farads / meter | Effective relative permittivity per meter of cable |
|
none | Relative permittivity of the dielectric in cable |
|
none | Velocity factor of current in conductor 
|
|
meter | Wavelength of radio waves in conductor |
 |
meter | Wavelength of radio waves in free space |
|
henries / meter | Effective magnetic permeability per meter of cable |
|
henries / meter | Permeability of free space, a fundamental constant |
|
none | Relative permeability of dielectric in cable |
 |
none | Index of refraction of dielectric material |
 |
none | Constant = 3.14159 |
|
radians or degrees | Phase shift of current between the ends of the conductor |
 |
radians / second | Angular frequency of alternating current 
|
|
meters / second | Speed of light in vacuum |
|
farads / meter | Shunt capacitance per unit length of the conductor |
|
hertz | Frequency of radio waves |
 |
none | Fill factor of a transmission line, the fraction of space filled with dielectric |
|
none | Electrical length of conductor |
 |
none | Electrical length of electromagnetic wave of length l in free space |
|
meter | Length of the conductor |
|
henrys / meter | Inductance per unit length of the conductor |
|
second | Period of radio waves |
 |
second | time |
|
meters / second | phase velocity of current in conductor |
 |
meter | distance along conductor |
References[edit]
- ^ a b c d e f
«Electrical length». ATIS Telecom Glossary. Alliance for Telecommunications Industry Solutions website. 2019. Retrieved 24 December 2022. ANSI (American National Standards Institute) accredited definition - ^ a b Kaiser, Kenneth L. (2004). Electromagnetic Compatibility Handbook. CRC Press. pp. 3.1–3.2. ISBN 9780849320873.
- ^ a b c d Weik, Martin (2012). Communications Standard Dictionary. Springer. p. 283. ISBN 9781461304296.
- ^ a b c d e f g Schmitt, Ron (2002). Electromagnetics Explained: A Handbook for Wireless RF, EMC, and High-Speed Electronics. Newnes. ISBN 9780750674034.
- ^ a b c d e f g h i Paul, Clayton R. (2011). Transmission Lines in Digital and Analog Electronic Systems. Wiley. pp. 6–11. ISBN 9781118058244.
- ^ a b Drollinger, Francis J. (1980). Ground Radio Communications Specialist: Vol. 7 — Auxiliary circuits and systems. US Air Force Technical Training School. pp. 16–18.
- ^ Rao, R. S. (2012). Electromagnetic Waves and Transmission Lines. PHI Learning. p. 445. ISBN 9788120345157.
- ^ Carr, Joseph J. (1997). Microwave & Wireless Communications Technology. Newnes. p. 51. ISBN 0750697075.
- ^ Amlaner, Charles J. Jr. (March 1979). «The design of antennas for use in radio telemetry». A Handbook on Biotelemetry and Radio Tracking: Proceedings of an International Conference on Telemetry and Radio Tracking in Biology and Medicine, Oxford, 20–22 March 1979. Elsevier. p. 260. Retrieved 23 November 2013.
- ^ Keller, Reto B. (2022). Design for Electromagnetic Compatibility-In a Nutshell. Springer International. p. 39. ISBN 9783031141867.
- ^ Keller, Reto (2018). «Chapter 5: Transmission lines». Electromagnetic compatibility knowledge base. Academy of EMC website. Retrieved 24 December 2022.
- ^ a b Radioman 3 & 2, US Navy Training Course NAVPERS 10228-E. Bureau of Naval Personnel, US Navy. 1967. p. 131.
- ^ Singh, Yaduvir (2011). Electro Magnetic Field Theory. Dorling Kindersley. p. 451. ISBN 9788131760611.
- ^ Griffith, B. Whitfield (2000). Radio-electronic Transmission Fundamentals. Noble Publishing. pp. 335–337. ISBN 9781884932137.
- ^ a b US Air Force Manual 52-19: Antenna Systems. US Air Force. 1953. pp. 104–105.
- ^ Schelkunoff, Sergei A.; Friis, Harold T. (1952). Antennas: Theory and Practice. John Wiley and Sons. p. 245.
- ^ Rudge, Alan W.; Milne, K. (1982). The Handbook of Antenna Design, Vol. 2. IET. p. 564. ISBN 9780906048870.
- ^ The effect of this on the antenna is equivalent to the current wave moving along the antenna at a phase velocity lower than the speed of light , as in a transmission line, and some sources explain it this way. However, this is not a physically correct description
- ^ a b c d Lewis, Geoff (2013). Newnes Communications Technology Handbook. Elsevier. p. 46. ISBN 9781483101026.
- ^ a b c d e f The A.R.R.L. Antenna Book, 5th Ed. American Radio Relay League. 1949. pp. 27–28.
- ^ Carr, Joseph (2001). Antenna Toolkit, 2nd Ed. Elsevier. pp. 52–54. ISBN 9780080493886.
- ^ Levin, Boris (2019). Wide-Range Antennas. CRC Press. p. 26. ISBN 9781351043229.
- ^ Azadeh, Mohammad (2009). Fiber Optics Engineering. Springer Science and Business Media. p. 11. ISBN 9781441903044.
- ^ Pozar, David M. (2011). Microwave Engineering, 4th Ed. Wiley Global Education. pp. 1–2. ISBN 9781118213636.
- ^ Karmel, Paul R.; Colef, Gabriel D.; Camisa, Raymond L. (1998). Introduction to Electromagnetic and Microwave Engineering. John Wiley and Sons. pp. 1–2. ISBN 9780471177814.
- ^ Clark, Alan Robert; Fourie, Andre P. C. (2001). Antennas in Practice (PDF). Poynting Innovations. p. 3. ISBN 0620276193.
|
m = ρ * V ρ — плотность V — объём m — масса V = S * l S — площадь, например площадь поперечного сечения провода l — искомая длина, например длина провода Подставляем вместо в первую формулу вместо объёма произведение S*l. Получаем: m=ρ*S*l Находим отсюда l: l=m/(ρ*S) Можно записать и так l=m/ρ/S, но выглядит это менее понятно. А можно и так: l=1/(ρ*S/m) модератор выбрал этот ответ лучшим
Массу разделить на площадь и разделить на плотность.
Andrei 9 лет назад Для определения длины проводника необходимо его массу поделить на произведение его плотности и площади поперечного сечения, при этом обратите внимание на единицы измерения величин, чтобы не вышло так что плотность у Вас кг, а масса в г., или с длинной что то не так!
Помощни к 7 лет назад На счет массы не знаю, но длину можно найти при помощи площади, сопротивления и плотности. Для этого нужно сопротивление умножить на площадь и поделить все это на плотность. Вот смотрите подробнее на рисунке:
Знаете ответ? |
Длина проводника по сопротивлению
Определить длину проводника если известно, материал, сопротивление и сечение проводника.
Общее сопротивление проводника связано с его удельным сопротивлением, длиной и сечением формулой:
R= r*l / S
отсюда длина l = RS / r,
Где:
- S — сечение проводника в мм2
- R — сопротивление проводника в Ом,
- r — удельное сопротивление (обозначается буковой «ро»)
- l — расчетная длина проводника (в метрах)
Расчет производить исходя из температуры проводника +20 °C
Поделиться в соц сетях:
Популярные сообщения из этого блога
Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi Как найти тангенс фи, если известен косинус фи формула: tg φ = (√(1-cos²φ))/cos φ Калькулятор онлайн — косинус в тангенс cos φ: tg φ: Поделиться в соц сетях: Найти синус φ, если известен тангенс φ Найти косинус φ, если известен тангенс φ
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о «Использование сердечного индекса Руфье в медико-спортивном контроле». Проба Руфье — представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор — онлайн tg φ: cos φ: ± Поделиться в соц сетях:
Основные формулы по физике — ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
Формулы электричества и магнетизма. Изучение основ электродинамики традиционно начинается с электрического поля в вакууме. Для вычисления силы взаимодействия между двумя точными зарядами и вычисления напряженности электрического поля, созданного точечным зарядом, нужно уметь применять закон Кулона. Для вычисления напряженностей полей, созданных протяженными зарядами (заряженной нитью, плоскостью и т.д.), применяется теорема Гаусса. Для системы электрических зарядов необходимо применять принцип
При изучении темы «Постоянный ток» необходимо рассмотреть во всех формах законы Ома и Джоуля-Ленца При изучении «Магнетизма» необходимо иметь в виду, что магнитное поле порождается движущимися зарядами и действует на движущиеся заряды. Здесь следует обратить внимание на закон Био-Савара-Лапласа. Особое внимание следует обратить на силу Лоренца и рассмотреть движение заряженной частицы в магнитном поле.
Электрические и магнитные явления связаны особой формой существования материи — электромагнитным полем. Основой теории электромагнитного поля является теория Максвелла.
Смотрите также основные формулы оптики
Таблица основных формул электричества и магнетизма
|
Физические законы, формулы, переменные |
Формулы электричество и магнетизм |
||||
|
Закон Кулона: |
|
||||
|
Напряженность электрического поля: где Ḟ — сила, действующая на заряд q0 , находящийся в данной точке поля. |
|
||||
|
Напряженность поля на расстоянии r от источника поля: 1) точечного заряда 2) бесконечно длинной заряженной нити с линейной плотностью заряда τ: 3) равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда σ: 4) между двумя разноименно заряженными плоскостями |
|||||
|
Потенциал электрического поля: где W — потенциальная энергия заряда q0 . |
|
||||
|
Потенциал поля точечного заряда на расстоянии r от заряда: |
|
||||
|
По принципу суперпозиции полей, напряженность: |
|
||||
|
Потенциал: где Ēi и ϕi — напряженность и потенциал в данной точке поля, создаваемый i-м зарядом. |
|
||||
|
Работа сил электрического поля по перемещению заряда q из точки с потенциалом ϕ1 в точку с потенциалом ϕ2 : |
|
||||
|
Связь между напряженностью и потенциалом 1) для неоднородного поля: 2) для однородного поля: |
|
||||
|
Электроемкость уединенного проводника: |
|
||||
|
Электроемкость конденсатора: где U = ϕ1 — ϕ2 — напряжение. |
|
||||
|
Электроемкость плоского конденсатора: где S — площадь пластины (одной) конденсатора, d — расстояние между пластинами. |
|
||||
|
Энергия заряженного конденсатора: |
|
||||
|
Сила тока: |
|
||||
|
Плотность тока: где S — площадь поперечного сечения проводника. |
|
||||
|
Сопротивление проводника: ρ — удельное сопротивление; l — длина проводника; S — площадь поперечного сечения. |
|
||||
|
Закон Ома 1) для однородного участка цепи: 2) в дифференциальной форме: 3) для участка цепи, содержащего ЭДС: где ε — ЭДС источника тока, R и r — внешнее и внутреннее сопротивления цепи; 4) для замкнутой цепи: |
|||||
|
Закон Джоуля-Ленца 1) для однородного участка цепи постоянного тока: 2) для участка цепи с изменяющимся со временем током: |
|
||||
|
Мощность тока: |
|
||||
|
Связь магнитной индукции и напряженности магнитного поля: где B — вектор магнитной индукции, |
|
||||
|
Магнитная индукция (индукция магнитного поля): 2) поля бесконечно длинного прямого тока 3) поля, созданного отрезком проводника с током ɑ1 и ɑ2 — углы между отрезком проводника и линией, соединяющей концы отрезка и точкой поля; |
|||||
|
Сила Лоренца: по модулю |
|
||||
|
Поток вектора магнитной индукции (магнитный поток через площадку S): |
|
||||
|
Потокосцепление (полный поток): |
|
||||
|
Закон Фарадея-Ленца: |
|
||||
|
ЭДС самоиндукции: |
|
||||
|
Индуктивность соленоида: где n — число витков на единицу длины соленоида, |
|
||||
|
Энергия магнитного поля: |
|
||||
|
Заряд, протекающий по замкнутому контуру при изменении магнитного потока через контур: где ∆Ф = Ф2 – Ф1 — изменение магнитного потока, R — сопротивление контура. |
|
||||
|
Работа по перемещению замкнутого контура с током I в магнитном поле: |
|
,
Поделитесь ссылкой с друзьями:
Похожие таблицы
Комментарии:
В телекоммуникациях и электротехнике, электрическая длина ( или длина фазы ) относится к длине электрического проводника с точки зрения фазового сдвига, вносимого передачей по этому проводнику на некоторой частоте.
Содержание
- 1 Использование термина
- 2 Длина фазы
- 3 Коэффициент скорости
- 4 Антенны
- 4.1 Изменение электрической длины под нагрузкой
- 4.2 Преимущества
- 4.3 Недостатки
- 4.4 Техническая реализация
- 4.4.1 Применение
- 5 См. Также
- 6 Ссылки
- 7 Дополнительная литература
Использование термина
В зависимости от конкретного контекста термин » электрическая длина «используется вместо простой физической длины для включения одного или нескольких из следующих трех понятий:
- Когда речь идет о количестве длин волн или фазе, участвующих в прохождении волны через В частности, сегмент линии передачи, можно просто указать эту электрическую длину, в то время как определение физической длины, частоты или коэффициента скорости опускается. В этом случае электрическая длина обычно выражается как N длин волн или как фаза φ, выраженная в градусах или радианах. Таким образом, в микрополосковой схеме можно указать закороченный шлейф с фазовой длиной 60 °, которая будет соответствовать разным физическим длинам при применении к разным частотам. Или можно рассмотреть 2-метровую секцию коаксиального кабеля, электрическая длина которой составляет одну четверть длины волны (90 °) на частоте 37,5 МГц, и спросить, какой становится ее электрическая длина, когда цепь работает на другой частоте.
- Из-за к коэффициенту скорости конкретной линии передачи, например, время прохождения сигнала по кабелю определенной длины равно времени прохождения через большее расстояние при движении со скоростью света. Таким образом, импульс, посланный по 2-метровому участку коаксиального кабеля (коэффициент скорости которого составляет 67%), достигнет конца коаксиального кабеля одновременно с тем же импульсом, который поступит на конец оголенного провода длиной 3 метра (по которому он распространяется со скоростью света), и можно сказать, что 2-метровая секция коаксиального кабеля имеет электрическую длину 3 метра или электрическую длину 1/2 длины волны на 50 МГц (поскольку радиоволна 50 МГц имеет длину волны 6 метров).
- Поскольку резонансные антенны обычно указываются в терминах электрической длины их проводников (например, полуволнового диполя ), получение такой электрической длины в общих чертах приравнивается к с электрическим резонансом, то есть чисто резистивным импедансом на входе антенны, как обычно желательно. Например, антенна, которая была сделана слишком длинной, будет иметь индуктивное сопротивление, которое можно скорректировать, физически укоротив антенну. Основываясь на этом понимании, распространенный жаргон в торговле антеннами относится к достижению резонанса (устранение реактивного сопротивления) на выводах антенны как электрическое сокращение этой слишком длинной антенны (или электрическое удлинение слишком короткой антенны), когда электрическая согласующая сеть (или антенный тюнер ) выполнил эту задачу без физического изменения длины антенны. Хотя терминология очень неточна, это использование широко распространено, особенно применительно к использованию нагрузочной катушки в нижней части короткого монополя (вертикальной или штыревой антенны ) для «электрически удлинить» его и добиться электрического резонанса, видимого через нагрузочную катушку.
Длина фазы
Первое использование термина «электрическая длина» предполагает синусоидальную волну некоторой частоты, или, по крайней мере, узкополосный сигнал с центром вокруг некоторой частоты f. Синусоидальная волна будет повторяться с периодом T = ⁄ f. Частота f будет соответствовать определенной длине волны λ вдоль конкретного проводника. Для проводников (таких как неизолированный провод или заполненный воздухом коаксиальный ), которые передают сигналы со скоростью света c, длина волны определяется как λ = ⁄ f. Расстояние L вдоль этого проводника соответствует N длинам волн, где N; = ⁄ λ.
На рисунке справа видно, что показанная волна имеет длину N = 1,5 длины волны. Гребень волны в начале графика, движущийся вправо, появится в конце через время 1,5 T. Электрическая длина этого сегмента называется «1,5 длины волны» или, выраженная в виде фазового угла, «540 °» (или 3 π радиан), где N длин волн соответствует φ = 360 ° • N (или φ = 2π • N радианы). В приложениях радиочастоты, когда задержка вводится из-за линии передачи, часто имеет значение фазовый сдвиг φ, поэтому определение конструкции с точки зрения фазы или электрической длины позволяет адаптировать эта конструкция на произвольную частоту за счет использования длины волны λ, применяемой к этой частоте.
Коэффициент скорости
В линии передачи сигнал распространяется со скоростью, контролируемой эффективной емкостью и индуктивностью на единицу длины ЛЭП. Некоторые линии передачи состоят только из неизолированных проводов, и в этом случае их сигналы распространяются со скоростью света, c. Чаще сигнал распространяется с пониженной скоростью κc, где κ — коэффициент скорости, число меньше 1, представляющее отношение этой скорости к скорости света.
Большинство линий передачи содержат диэлектрический материал ( изолятор), заполняющий часть или все пространство между проводниками. Относительная диэлектрическая проницаемость или диэлектрическая постоянная этого материала увеличивает распределенную емкость в кабеле, что снижает коэффициент скорости ниже единицы. Также возможно уменьшение κ из-за относительной проницаемости (μ r { displaystyle mu _ { text {r}}}) этого материала, что увеличивает распределенную индуктивность, но этого почти никогда не бывает. Теперь, если заполнить пространство диэлектриком с относительной диэлектрической проницаемостью ϵ r { displaystyle epsilon _ { text {r}}}, то скорость плоской электромагнитной волны уменьшится на коэффициент скорости:
- κ = vpc = 1 ϵ r μ r ≈ 1 ϵ r { displaystyle kappa = { frac {v_ {p}} {c}} = { frac {1} { sqrt { epsilon _ { text {r}} mu _ { text {r}}}}} приблизительно { frac {1} { sqrt { epsilon _ { text {r}}}}}}.
.Этот пониженный коэффициент скорости также применяется к распространению сигналов по проводам, погруженным в большое пространство, заполненное этим диэлектриком. Однако, когда только часть пространства вокруг проводников заполнена этим диэлектриком, скорость волны меньше уменьшается. Часть электромагнитной волны, окружающей каждый проводник, «чувствует» действие диэлектрика, а часть находится в свободном пространстве. Затем можно определить эффективную относительную диэлектрическую проницаемость ϵ eff { displaystyle epsilon _ { text {eff}}}, которая затем предсказывает коэффициент скорости согласно
- κ = 1 ϵ эфф { displaystyle kappa = { frac {1} { sqrt { epsilon _ { text {eff}}}}}}
ϵ eff { displaystyle epsilon _ { text {eff}}}вычисляется как средневзвешенное значение относительной диэлектрической проницаемости свободного пространства (1) и диэлектрической проницаемости:
- ϵ eff = (1 — F) + F ϵ r { displaystyle epsilon _ { text {eff}} = (1-F) + F epsilon _ { text {r}}}
где коэффициент заполнения F выражает эффективную долю пространства, на которое влияет диэлектрик.
В случае коаксиального кабеля, где весь объем между внутренним проводником и экраном заполнен диэлектриком, коэффициент заполнения равен единице, поскольку электромагнитная волна ограничена в этот регион. В других типах кабелей, таких как двухжильный, коэффициент заполнения может быть намного меньше. В любом случае, любой кабель, предназначенный для радиочастот, будет иметь коэффициент скорости (а также его характеристический импеданс ), указанный производителем. В случае коаксиального кабеля, где F = 1, коэффициент скорости определяется исключительно типом используемого диэлектрика, как указано здесь.
. Например, типичный коэффициент скорости для коаксиального кабеля составляет 0,66, что соответствует диэлектрическая проницаемость 2,25. Предположим, мы хотим послать сигнал 30 МГц по короткому участку такого кабеля и задержать его на четверть волны (90 °). В свободном пространстве эта частота соответствует длине волны λ 0 = 10 м, поэтому для задержки 0,25 λ потребуется электрическая длина 2,5 м. Если применить коэффициент скорости 0,66, то физическая длина кабеля составит 1,67 м.
Коэффициент скорости также применяется к антеннам в тех случаях, когда антенные проводники (частично) окружены диэлектриком. Это особенно относится к микрополосковым антеннам, таким как патч-антенна. Волны на микрополоске зависят в основном от диэлектрика печатной платы под ними, но также и от воздуха над ними (из-за краевых эффектов следа). Таким образом, их коэффициенты скорости зависят не напрямую от диэлектрической проницаемости материала печатной платы, а от эффективной диэлектрической проницаемости ϵ eff { displaystyle epsilon _ { text {eff}}}, которая часто указывается для материал печатной платы (или может быть рассчитан). Обратите внимание, что коэффициент заполнения и, следовательно, ϵ eff { displaystyle epsilon _ { text {eff}}}в некоторой степени зависят от ширины следа по сравнению с толщиной платы.
Антенны
Хотя существуют определенные конструкции широкополосных антенн, многие антенны классифицируются как резонансные и работают в соответствии с конструкцией на определенной частоте. Это особенно относится к радиовещательным станциям и системам связи, которые ограничены одной частотой или узкой полосой частот. Сюда входят дипольные и монопольные антенны и все конструкции на их основе (Yagi, дипольные или монопольные решетки, свернутый диполь и т. д.). В дополнение к направленному усилению в лучевых антеннах, страдающих от проектной частоты, полное сопротивление точки питания антенны очень чувствительно к сдвигам частоты. Особенно для передачи антенна часто предназначена для работы на резонансной частоте. На резонансной частоте по определению этот импеданс представляет собой чистое сопротивление, которое соответствует характеристическому импедансу линии линии передачи и выходного (или входное) сопротивление передатчика (или приемника). На частотах, отличных от резонансной, импеданс включает некоторое реактивное сопротивление (емкость или индуктивность ). Можно использовать антенный тюнер , чтобы отменить это реактивное сопротивление (и изменить сопротивление, чтобы оно соответствовало линии передачи), однако этого часто избегают в качестве дополнительного осложнения (и его необходимо контролировать на антенная сторона линии передачи).
Условием резонанса в монопольной антенне является то, что элемент должен быть нечетным кратным четверти длины волны λ / 4. В дипольной антенне оба ведомых проводника должны быть такой длины, чтобы общая длина диполя составляла (2N + 1) λ / 2.
Электрическая длина антенного элемента, как правило, отличается от его физической длины. Например, увеличение диаметра проводника или наличие поблизости металлических предметов уменьшит скорость волн в элемент, увеличивающий электрическую длину.
Антенна, которая короче своей резонансной длины, описывается как «электрически короткая» и проявляет емкостное реактивное сопротивление. Точно так же антенна, длина которой превышает ее резонансную длину, описывается как «электрически длинная» и демонстрирует индуктивное реактивное сопротивление.
, изменяющее электрическую длину путем загрузки
нагрузочной катушки в антенне мобильного телефона, установленной на крыше автомобиля. Катушка позволяет антенне быть короче четверти длины волны и при этом оставаться резонансной.
Эффективную электрическую длину антенны можно изменить без изменения ее физической длины, добавив реактивное сопротивление, (индуктивность или емкость ) последовательно с ним. Это называется согласованием по сосредоточенному сопротивлению или нагрузкой.
Например, несимметричная антенна, такая как металлический стержень, питаемый с одного конца, будет резонансным, если ее электрическая длина равна четверти длины волны λ / 4 используемой частоты.. Если антенна короче четверти длины волны, импеданс точки питания будет включать емкостное реактивное сопротивление ; это вызывает отражения на фиде и рассогласование на передатчике или приемнике, даже если резистивная составляющая импеданса правильная. Чтобы нейтрализовать емкостное реактивное сопротивление, индуктивность, называемая нагрузочной катушкой, вставляется между линией питания и выводом антенны. Выбор индуктивности с тем же реактивным сопротивлением, что и (отрицательное) емкостное реактивное сопротивление, видимое на выводе антенны, отменяет эту емкость, и антенная система (антенна и катушка) снова будет резонансной. Линия питания имеет чисто резистивный импеданс. Поскольку антенна, которая была слишком короткой, теперь кажется резонансной, добавление загрузочной катушки иногда называют «электрическим удлинением» антенны.
Точно так же импеданс точки питания монопольной антенны длиннее λ / 4 (или диполя с плечами длиннее λ / 4) будет включать индуктивное реактивное сопротивление. Конденсатор, включенный последовательно с антенной, может нейтрализовать это реактивное сопротивление, чтобы сделать его резонансным, что можно назвать «электрическим сокращением» антенны.
Индуктивная нагрузка широко используется для уменьшения длины штыревых антенн в портативных радиостанциях, таких как рации и коротковолновые антенны в автомобилях, в соответствии с физическими требованиями.
Вертикальная антенна, которая может иметь любую желаемую высоту: примерно менее половины длины волны частоты, на которой работает антенна. Эти антенны могут работать как передающие, так и как приемные.
Преимущества
Электрическое удлинение позволяет создавать более короткие антенны. Он применяется, в частности, для антенн для VLF, длинноволновых и средневолновых передатчиков. Поскольку эти радиоволны имеют длину от нескольких сотен метров до многих километров, мачтовые излучатели необходимой высоты не могут быть реализованы с экономической точки зрения. Он также широко используется для штыревых антенн на портативных устройствах, таких как рации, что позволяет использовать антенны намного короче стандартной четверти длины волны. Наиболее широко используемым примером является резиновая антенна-утенок.
Недостатки
Электрическое удлинение уменьшает полосу пропускания антенны, если другие меры фазы не предпринято. Электрически удлиненная антенна менее эффективна, чем эквивалентная полноразмерная антенна.
Техническая реализация
Есть две возможности реализации электрического удлинения.
- переключение в индуктивных катушках в серии с антенной
- переключение на металлических поверхностях, известное как емкость крыши, на концах антенн, которые образуют конденсаторы — земля.
Часто оба показателя сочетаются. Катушки, включенные последовательно, иногда необходимо размещать в середине конструкции антенны. Кабина, установленная на высоте 150 метров на Blosenbergturm в Beromünster, представляет собой такую конструкцию, в которой установлен удлинительный змеевик для питания верхней части башни (Blosenbergturm дополнительно имеет кольцевой конденсатор на крыше)
Применение
Передающие антенны передатчиков, работающих на частотах ниже длинноволнового диапазона радиовещания, всегда применяют электрическое удлинение. Его часто применяют в вещательных антеннах длинноволновых радиовещательных станций. Однако для передающих антенн NDB широко применяется электрическое удлинение, поскольку в них используются антенны, высота которых значительно меньше четверти излучаемой длины волны.
Слева характеристики, построенные по экспериментально полученным данным о координатах с логарифмической абсциссой. Справа антенна с увеличенной эффективной индуктивностью между двумя точками в соответствии с хорошо известной работой цепей с шунтирующей настройкой, отрегулированной несколько вне резонанса.
См. Также
- Антенный тюнер
- Электрически малая антенна
- Нагрузочная катушка
- Монопольная антенна
Ссылки
- Terman, Frederick Emmons (1943). Справочник радиоинженера. Макгроу-Хилл. п. 773.
- Краус, Джон Д. (1988). Антенны (PDF) (2-е изд.). Макгроу-Хилл. п. 413. ISBN 0-07-035422-7 .
- Баланис, Константин А. (1997). Теория антенн. Джон Вили и сыновья. Стр. 151. ISBN 0-471-59268-4 .
Дополнительная литература
- A. Никль, США Патент 2125804 «Антенна». (Подано 25 мая 1934 г.; выдано 2 августа 1938 г.)
- Уильям У. Браун, США Патент 2,059,186 «Антенная конструкция». (Подана 25 мая 1934 г.; выдана 27 октября 1936 г.)
- Роберт Б. Доум, США Патент 2101674, «Антенна». (Подано 25 мая 1934 г.; опубликовано 7 декабря 1937 г.)
- Слюсар В.И. 60 лет теории электрически малых антенн.// Труды 6-й Международной конференции по теории и технике антенн, 17-21 сентября, 2007, Севастополь, Украина. — Стр. 116 — 118. [2 impression