К этой странице обращались 1110 раз.
Текст страницы доступен по условиям лицензии GNU Free Documentation License. Материалы могут быть скопированы при условии указания активной ссылки на источник копирования в теле статьи (на той же странице). В отдельных случаях могут действовать условия лицензии Creative Commons Attribution-ShareAlike (CC BY-SA 3.0), информацию об этом можно просмотреть на странице обсуждения или в истории правок. В частности, условия лицензии CC BY-SA 3.0 действуют в отношении статей, перенесенных из Википедии, Викии/Fandom и Руниверсалиса (указание на факт переноса всегда есть в истории правок статьи или на ее странице обсуждения).
В текстах могут упоминаться организации, признанные на территории Российской Федерации террористическими и/или в отношении которых судом принято вступившее в законную силу решение о запрете деятельности — см. полный список, а также деятельность которых запрещена по решению суда — см. полный список.
Собственно, хотел я найти, для себя, формулу длину синусоиды.
Пятница, вечер… Я попытаюсь… Вам доказать? … убедить Вас в том, что..?
что Вы поставили перед собой совсем неинтересную задачу, и получили совсем неинтересный ответ на неё.
Подобные соображения я уже высказывал на форуме; более того, ко мне как бы присоединился один из модераторов. Но я не буду искать его или моих предыдущих постов, выскажусь заново.
Курица — не птица, синусоида — не кривая
!
Искать длину синусоиды — мартышкин труд. Не надо этого делать!
Синусоида обычно — график некой функции
. Например, 


Хорошо, пусть не ток/напряжение как функция времени, а что-то другое. Может, тогда получится что-то поприличнее, геометрически более осмысленная модель? Ну, давайте придумаем процесс вроде 
а, но я до этого сразу не допёр.
Ну ладно, возьмём «реальную кривую», не «график функции». И что, сразу всё будет клёво интегрироваться? В элементарных функциях?
Нет, конечно. Возьмём банальный эллипс, который обычно выступает как кривая, и иногда как «график». Даже для него длина кривой сводится к эллиптическим функциям.
Но, заметим, — продвинутые справочники по математике приводят для длины дуги эллипса и точную формулу (в терминах эллиптических интегралов), и формулу приближённую. Но им не приходит в голову приводить что-то подобное для синусоиды.
Понимаете, Ummagumma
, я бы не позволил себе обозначить Ваш интерес к длине кривой как «на самом деле неинтересно» (или бессмысленно), если бы речь шла о какой-нибудь брахистохроне, трактрисе, конике, циклоиде, и прочая. Меня именно сиснусоида напрягла.
Заинтересуйтесь кем-нибудь другой.
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
andrey-750 |
Заголовок сообщения: Длина синусоиды
|
||
|
Помогите вычислить длину синусоиды за период, если амплитуда — А, а период — N. Т.е. длина графика Y=A*sin(2Pi*X/N) Спасибо.
|
||
| Вернуться к началу |
|
||
|
andrey-750 |
Заголовок сообщения: Re: Длина синусоиды
|
|
Я не спрашивал про длину сигнала. Я спрашивал про длину кривой.
|
|
| Вернуться к началу |
|
|
vorvalm |
Заголовок сообщения: Re: Длина синусоиды
|
|
Длина кривой линии в прямоугольных координатах выражается интегралом [math]L=int_A^Bsqrt{dx^2+dy^2}[/math] Синусоиду надо разделить на 4 участка, т.е.[math]A = 0,[/math][math]B = pi|2[/math]
|
|
| Вернуться к началу |
|
| За это сообщение пользователю vorvalm «Спасибо» сказали: XP9K |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
МНК для синусоиды
в форуме Численные методы |
Integer |
5 |
969 |
23 июн 2014, 11:02 |
|
Построение синусоиды в exel
в форуме Microsoft Excel |
FDR |
1 |
2552 |
01 сен 2013, 10:54 |
|
Расчет длины затухающей синусоиды
в форуме Оптика и Волны |
azel405 |
4 |
1669 |
29 янв 2014, 23:27 |
|
Рекурсивное вычисление коррекции синусоиды
в форуме Дифференциальное исчисление |
dorringtorr |
0 |
283 |
06 дек 2016, 18:37 |
|
Написать формулу соответствующую графику синусоиды
в форуме Тригонометрия |
Reddington |
14 |
438 |
22 июл 2021, 14:23 |
|
Как получена приближенная формула длины синусоиды?
в форуме Ряды |
rt7 |
14 |
546 |
25 фев 2021, 22:32 |
|
Длина дуги
в форуме Интегральное исчисление |
351w |
6 |
308 |
02 дек 2017, 17:19 |
|
Длина дуги
в форуме Интегральное исчисление |
tanyhaftv |
10 |
694 |
03 май 2018, 23:24 |
|
Длина дуги
в форуме Интегральное исчисление |
tanyhaftv |
6 |
295 |
18 апр 2018, 17:08 |
|
Длина кривой
в форуме Интегральное исчисление |
Jugalator |
10 |
320 |
06 апр 2018, 00:06 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 2 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB
Длина дуги синусоиды — это число, характеризующее протяжённость дуги синусоиды в единицах измерения длины.
Обозначения
Введём обозначения:
x1 — первая точка дуги;
x2 — вторая точка дуги;
y=sinx — уравнение синусоиды;
E(k,t) — эллиптический интеграл II рода;
Lsin — длина дуги синусоиды.
Формула
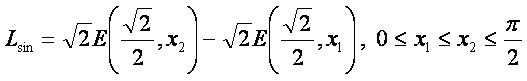
- Длина полной (от 0 до π) арки синусоиды равна Lарк.sin=2√2E(√2/2,π/2).
Вывод формулы
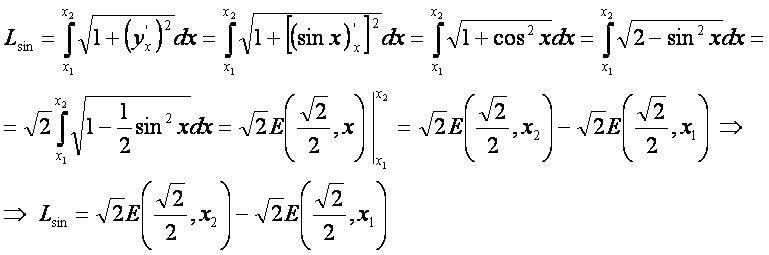
- Для вывода используется формула «длина дуги плоской кривой» в прямоугольной системе координат.
- Для нахождения интеграла используется эллиптический интеграл II рода.
Другие кривые:
Ссылки
- Храбров А. И. Немного об эллиптических интегралах. http://www.math.spbu.ru/analysis/f-doska/ellint.pdf
- Участник:Logic-samara
линии нарисованной чем? пикселями? карандашом? какой такой линии? что ты несешь?
- Показать ответ
- Ссылка
Ответ на:
комментарий
от theNamelessOne 03.09.13 18:38:46 MSK
ехал сёдня на велике у которого спидометр и линейка сбилась обнаружил что он намерил 2.5 круг как 4.
это если считать что я ехал по прямому кругу . а если я ехал по синусоиде по кругу . при какой ширине трека(и возможной амплетуде) и частоте колебание колеса вокруг средней линии по синусоиде спидометр может быть исправным?
- Показать ответы
- Ссылка
Ответ на:
комментарий
от stevejobs 03.09.13 18:41:18 MSK
пусть масштаб x1 y1
есть синусоида от 0 до 2pi
в каком отношении длина участка синусоиды( образованой y=sin(x) ) от 0 до 2pi к отрезку абцисы от 0 до 2pi
★★☆
(03.09.13 18:44:22 MSK)
Последнее исправление: qulinxao 03.09.13 18:45:33 MSK
(всего
исправлений: 1)
- Ссылка
Ответ на:
комментарий
от morse 03.09.13 18:44:43 MSK
её развёртка при равномерном прокрутке ленты когда карандаш движется по окружности равномерно.
- Ссылка
Можно дать оценку 7.6400
Deleted
(03.09.13 18:56:07 MSK)
- Ссылка
примерно 7.64
★★☆☆☆
(03.09.13 18:56:39 MSK)
- Ссылка
считается элементарно: длина участка кривой f(x) при приращении dx равен по теореме Пифагора sqrt(dx^2+f'(x)^2dx^2) = sqrt(1+f'(x)^2)dx. теперь интегрируй данное выражение от 0 до 2pi.
получится int(sqrt(1+cos(x)^2),x=0..2*Pi);
И да, интеграл неберущийся.
★★☆☆☆
(03.09.13 18:58:43 MSK)
Последнее исправление: dikiy 03.09.13 19:02:23 MSK
(всего
исправлений: 2)
- Показать ответы
- Ссылка
Ответ на:
комментарий
от morse 03.09.13 18:44:43 MSK
не единичная, а с диаметром pi
jcd ★★★★★
(03.09.13 19:00:41 MSK)
- Ссылка
Ответ на:
комментарий
от dikiy 03.09.13 18:58:43 MSK
т.е такая элементарная задача не по зубам школьному году когда знакомят с синусоидой/косинусоидой (5-6 класс) и основным уравнением s**2+c**2=1
????
★★☆
(03.09.13 19:05:06 MSK)
Последнее исправление: qulinxao 03.09.13 19:05:48 MSK
(всего
исправлений: 1)
- Показать ответы
- Ссылка
Ответ на:
комментарий
от qulinxao 03.09.13 19:05:06 MSK
Ответ на:
комментарий
от morse 03.09.13 18:44:43 MSK
это единичная окружность, не?
Лол. А ничего, что период 2pi, минимум -1, максимум 1.
Sadler ★★★
(03.09.13 19:07:20 MSK)
- Ссылка
Ответ на:
комментарий
от qulinxao 03.09.13 18:43:06 MSK
а если я ехал по синусоиде по кругу
спидометр может быть исправным
но тебя посадят не за превышение, а за пьянство!
- Ссылка
Ответ на:
комментарий
от qulinxao 03.09.13 19:05:06 MSK
т.е такая элементарная задача не по зубам школьному году когда знакомят с синусоидой/косинусоидой (5-6 класс) и основным уравнением s**2+c**2=1
не по зубам совершенно. это матан первого курса инженеров.
★★☆☆☆
(03.09.13 19:10:19 MSK)
- Показать ответы
- Ссылка
Ответ на:
комментарий
от dikiy 03.09.13 19:10:19 MSK
Если дать википедию, то по зубам: ищем график синуса, затем эллипс, затем периметр эллипса.
Sadler ★★★
(03.09.13 19:12:38 MSK)
- Показать ответ
- Ссылка
Ответ на:
комментарий
от qulinxao 03.09.13 18:43:06 MSK
ехал сёдня на велике у которого спидометр и линейка сбилась обнаружил что он намерил 2.5 круг как 4.
это если считать что я ехал по прямому кругу . а если я ехал по синусоиде по кругу . при какой ширине трека(и возможной амплетуде) и частоте колебание колеса вокруг средней линии по синусоиде спидометр может быть исправным?
циклическая частота будет равна ~1.85. А значит обычная 0.29Гц.
//fix короче, ты двигался по синусоиде sin(1.85 x). А какая это частота — сами разбирайтесь 
★★☆☆☆
(03.09.13 19:14:27 MSK)
Последнее исправление: dikiy 03.09.13 19:19:03 MSK
(всего
исправлений: 1)
- Показать ответ
- Ссылка
Ответ на:
комментарий
от Sadler 03.09.13 19:12:38 MSK
Если дать википедию, то по зубам: ищем график синуса, затем эллипс, затем периметр эллипса.
агащаз. Чтобы посчитать интеграл надо хотя бы какой-нить CAS уметь пользоваться. Ну или современным калькулятором.
★★☆☆☆
(03.09.13 19:15:35 MSK)
- Показать ответы
- Ссылка
Ответ на:
комментарий
от jcd 03.09.13 19:07:08 MSK
7.64040
———————-
L = int_{0}^{2pi}frac{1}{cos(arctan(cos x))} , dx
(и wolfram integrator)
- Показать ответ
- Ссылка
Ответ на:
комментарий
от dikiy 03.09.13 19:15:35 MSK
Не надо считать интеграл, надо найти приближенную формулу. Очевидно же, что там не эллипс, но примерно, с погрешностью, можно считать, что это эллипс и, опять же, с погрешностью, юзать приблизительную формулу периметра эллипса.
На самом деле там вот такая штука.
Sadler ★★★
(03.09.13 19:19:06 MSK)
- Показать ответы
- Ссылка
Ответ на:
комментарий
от dikiy 03.09.13 19:16:36 MSK
Ответ на:
комментарий
от dikiy 03.09.13 19:15:35 MSK
я к тому , что когда придумываеш задачку из «реальной жизни» оказывается что школьных трюков не всегда достаточно.
т.е неберущийся т.е длина синуса не элементарная функция??? хм.
а может как нить школьным курсом можно обойтись для получения аналитически ответа?
- Показать ответы
- Ссылка
Ответ на:
комментарий
от Sadler 03.09.13 19:19:06 MSK
Не надо считать интеграл, надо найти приближенную формулу. Очевидно же, что там не эллипс, но примерно, с погрешностью, можно считать, что это эллипс и, опять же, с погрешностью, юзать приблизительную формулу периметра эллипса.
если уж считать руками этот интеграл, то с помощью ряда Тейлора. А-то вы еще «яйцами» измерять начнете.
★★☆☆☆
(03.09.13 19:21:30 MSK)
- Показать ответ
- Ссылка
Ответ на:
комментарий
от Sadler 03.09.13 19:19:06 MSK
это график длины(алгебраической т.е отрицательные значения вычитаются) графика синуса от нуля до x?
хм тока ведь длина то монотонно растёт так что график должне тоже «неубывать»
- Показать ответ
- Ссылка
Ответ на:
комментарий
от dikiy 03.09.13 19:21:30 MSK
Ответ на:
комментарий
от Sadler 03.09.13 19:23:54 MSK
Ответ на:
комментарий
от qulinxao 03.09.13 19:19:48 MSK
а может как нить школьным курсом можно обойтись для получения аналитически ответа?
аналитический ответ получить нельзя. Интеграл этот неберущийся не в смысле для школьников неберущийся, а в смысле, что вообще неберущийся. Его можно считать только приближенно.
школьным курсом тут, увы — не обойтись. Хотя бы потому, что даже если ты посчитаешь каким-то раком длину линии sin(x) (например ниткой померяешь), то потом же тебе все равно надо решить задачу по нахождению такого параметра k в sin(kx), чтобы int(sqrt(1+k^2*cos(x)^2),0..2*pi) был равен нужному числу.
А это уже численные методы, ряды Тейлора и другой матан.
★★☆☆☆
(03.09.13 19:24:59 MSK)
- Показать ответы
- Ссылка
Ответ на:
комментарий
от qulinxao 03.09.13 19:23:15 MSK
это график длины(алгебраической т.е отрицательные значения вычитаются) графика синуса от нуля до x?
Это я разрезал полный период синусоиды на две половины и одну сместил влево на pi, чтобы получилось подобие эллипса. Затем посчитал по формуле для эллипса с погрешностью в пару процентов =) Чит, да.
Sadler ★★★
(03.09.13 19:25:24 MSK)
- Ссылка
Ответ на:
комментарий
от qulinxao 03.09.13 19:24:46 MSK
ну если приближённо , как её оценить?
А вот задача оценки погрешности уже не для школьника. Здесь без интегралов будет сложно. Так что только на глазок.
Sadler ★★★
(03.09.13 19:26:36 MSK)
Последнее исправление: Sadler 03.09.13 19:30:50 MSK
(всего
исправлений: 2)
- Показать ответы
- Ссылка
Ответ на:
комментарий
от qulinxao 03.09.13 19:19:48 MSK
оказывается что школьных трюков не всегда достаточно
Программировать учат в 5 или в каком там классе. На бейсике посчитать примерную длину этой линии несложно.
PolarFox ★★★★★
(03.09.13 19:28:56 MSK)
- Показать ответы
- Ссылка
Ответ на:
комментарий
от PolarFox 03.09.13 19:28:56 MSK
Ответ на:
комментарий
от PolarFox 03.09.13 19:28:56 MSK
Программировать учат в 5 или в каком там классе. На бейсике посчитать примерную длину этой линии несложно.
прочти собственную задачу в начале треда. Подсчет интеграла — это далеко не самое сложное там.
★★☆☆☆
(03.09.13 19:32:14 MSK)
- Показать ответ
- Ссылка
Ответ на:
комментарий
от Sadler 03.09.13 19:30:21 MSK
s = 0.0
x0 = 0.0
y0 = 0.0
FOR x1 = 0 to PI*2 STEP 0.01
y1 = SIN(x1)
s = s + SQRT((x0 - x1)^2 + (y0 - y1)^2)
x0 = x1
y0 = y1
NEXT
PRINT s
PolarFox ★★★★★
(03.09.13 19:33:42 MSK)
- Ссылка
Ответ на:
комментарий
от dikiy 03.09.13 19:32:14 MSK
Это где про велосипед и пьяного велосипедиста? Там два параметра (амплитуда и частота), тут уже с BASIC будет трудно.
Так что берём VisualBasic, пишем весьма похожую программу и двигаем два слайдера, пока 2.5 не превратится в 4.
PolarFox ★★★★★
(03.09.13 19:36:58 MSK)
- Показать ответ
- Ссылка
Ответ на:
комментарий
от dikiy 03.09.13 19:14:27 MSK
ах да, натупил: 1.85sin(x) надо. или sin(1.89x) например.
★★☆☆☆
(03.09.13 19:37:01 MSK)
Последнее исправление: dikiy 03.09.13 19:42:22 MSK
(всего
исправлений: 2)
- Ссылка
Ответ на:
комментарий
от jcd 03.09.13 19:19:25 MSK
я затупил
Подумал, что это такая шутка.
i-rinat ★★★★★
(03.09.13 19:37:12 MSK)
- Ссылка
Ответ на:
комментарий
от PolarFox 03.09.13 19:36:58 MSK
Так что берём VisualBasic, пишем весьма похожую программу и двигаем два слайдера, пока 2.5 не превратится в 4.
не отличается от измерения нитками 
лучше взять octave и сделать одну команду:
octave:29> fzero(@(k) quad(@(x) sqrt(1+k^2*cos(k*x)^2),0,2*pi)/2/pi-1.6,1)
ans = 1.8926
octave:30>
★★☆☆☆
(03.09.13 19:39:09 MSK)
Последнее исправление: dikiy 03.09.13 19:41:55 MSK
(всего
исправлений: 2)
- Показать ответ
- Ссылка
Ответ на:
комментарий
от dikiy 03.09.13 19:24:59 MSK
я понял что функция длины синусы не имеет аналитической записи подобно интегралу exp(x**2).
но может для полного периода из каких других соображений можно получить ?
т.е у нас же начальная задаче не получить функцию по которой для любого момента знать путь .
а всеголиш получить длину полного периода(ну или четверти /половины) ?
- Показать ответы
- Ссылка
Ответ на:
комментарий
от dikiy 03.09.13 19:39:09 MSK
sqrt(1+k^2*cos(k*x)^2),0,2*pi)/2/pi-4/2.5,1)/2/pi
Если не вглядываться, похоже на программу на Malbolge.
PolarFox ★★★★★
(03.09.13 19:43:40 MSK)
- Ссылка
Ответ на:
комментарий
от qulinxao 03.09.13 19:43:02 MSK
но может для полного периода из каких других соображений можно получить ?
нет.
★★☆☆☆
(03.09.13 19:47:18 MSK)
- Показать ответ
- Ссылка
Ответ на:
комментарий
от dikiy 03.09.13 19:47:18 MSK
Ответ на:
комментарий
от qulinxao 03.09.13 19:49:31 MSK
через Гамма-функцию емнип как-то. Мне реально лень лазить искать сейчас 
★★☆☆☆
(03.09.13 19:52:54 MSK)
- Ссылка
Ответ на:
комментарий
от qulinxao 03.09.13 19:43:02 MSK
а всеголиш получить длину полного периода(ну или четверти /половины) ?
Задача как раз не в этом, а в том, чтобы найти параметр k в sin(kx) или в k*sin(x). А тут уже числа могут быть совершенно потолочными.
★★☆☆☆
(03.09.13 19:54:19 MSK)
- Ссылка
Ответ на:
комментарий
от qulinxao 03.09.13 19:49:31 MSK
Вот вам очень точное приближение для длины дуги синусоиды для любого расстояния: y = 1.21601586016669*x + 0.103124670820249*sin(2.00011089891195*x) — 0.000168863395023369.
Sadler ★★★
(03.09.13 19:55:07 MSK)
Последнее исправление: Sadler 03.09.13 19:57:31 MSK
(всего
исправлений: 2)
- Показать ответ
- Ссылка
Я не понял, тебе что надо? Криволинейный интеграл dl по синусоиде?
Дык, это вроде как получается int_0^{2pi} frac{dx}{cosatancos x }
Лень упрощать.
(03.09.13 19:57:32 MSK)
- Показать ответ
- Ссылка
Ответ на:
комментарий
от Sadler 03.09.13 19:55:07 MSK
т.е длина синусоиды полного периода длиней прямой в 1.216 раз. хм.
формула через интерграл разложения в ряд косинуса двойного угла?
- Показать ответ
- Ссылка
Ответ на:
комментарий
от Anon 03.09.13 19:57:32 MSK
я анализ универского курса если и знал то уже и забыл , ибо дискретка и прочая конкретная.
удивился обнаружив , что предположение о синусоидальном движении относительно разделительной(произвольной прямой паралельной краям дороги) приводит к недостаточности школьного курса математики для решения — какое было перемещение.
т.е вот это вот очередное подтверждение, что школьный набор не замкнут 
- Показать ответ
- Ссылка
Ответ на:
комментарий
от qulinxao 03.09.13 19:59:17 MSK
Да, в 1.216 + небольшая погрешность. Формула получена с помощью генетического программирования.
Есть ещё одна, если хотите: y = 1.216*x + 0.1032*sin(2*x) — 0.002204*sin(4*x). Действительно очень похоже на какой-то ряд.
Sadler ★★★
(03.09.13 20:02:57 MSK)
- Показать ответы
- Ссылка
Вы не можете добавлять комментарии в эту тему. Тема перемещена в архив.