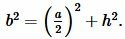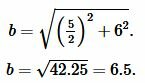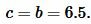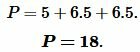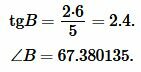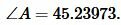Как посчитать стороны равнобедренного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать стороны равнобедренного треугольника
Чтобы посчитать чему равны стороны равнобедренного треугольника воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить длины сторон равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):
для стороны a:
- длину основания (b) и угол α
- длину основания (b) и угол β
- длину основания (b) и высоту (h)
для стороны b:
- длину двух равных сторон (a) и угол α
- длину двух равных сторон (a) и угол β
- длину двух равных сторон (a) и высоту (h)
Введите их в соответствующие поля и получите результат.
Как посчитать сторону a равнобедренного треугольника
Если известна сторона b и угол α
Чему равна сторона a равнобедренного треугольника если длина основания
b =
, а угол
α =?
Ответ:
a =
0
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол α?
Формула
a = b/2⋅cos α
Пример
Если сторона b = 10 см, а ∠α = 30°, то:
a = 10/2⋅cos 30° = 10/(2⋅0.8660) = 5.77см
Если известна сторона b и угол β
Чему равна сторона a равнобедренного треугольника если длина основания
b =
, а угол
β =?
Ответ:
a =
0
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол β?
Формула
a = b/2⋅sin β/2
Пример
Если сторона b = 10 см, а ∠β = 30°, то:
a = 10/2⋅sin 15 = 10/(2⋅0.2588) = 19.31см
Если известна сторона b и высота h
Чему равна сторона a равнобедренного треугольника если длина основания
b =
, а высота
h =?
Ответ:
a =
0
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и высота h?
Формула
a = √1/b2 + h2
Пример
Если сторона b = 10 см, а высота h = 20 см, то:
a = √1/102 + 202 = √0.01+400 = 20.61см
Как посчитать сторону b (основание) равнобедренного треугольника
Если известна сторона a и угол α
Чему равна сторона b равнобедренного треугольника если длина стороны
a =
, а угол
α =?
Ответ:
b =
0
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол α?
Формула
b = 2⋅a⋅cos α
Пример
Если сторона a = 10 см, а ∠α = 30°, то:
b = 2⋅10⋅cos 30° = 2⋅10⋅0.8660 = 17.32см
Если известна сторона a и угол β
Чему равна сторона b равнобедренного треугольника если длина стороны
a =
, а угол
β =?
Ответ:
b =
0
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол β?
Формула
b = 2⋅a⋅sin β/2
Пример
Если сторона a = 10 см, а ∠β = 40°, то:
b = 2⋅10⋅sin 40/2 = 2⋅10⋅0.342 = 6.84см
Если известна сторона a и высота h
Чему равна сторона b равнобедренного треугольника если длина стороны
a =
, а высота
h =?
Ответ:
b =
0
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и высота h?
Формула
b = 2⋅√a2 — h2 , h < a
Пример
Если сторона a = 10 см, а высота h = 5 см, то:
b = 2⋅√102 — 52 = 2⋅√75 = 17.32см
См. также
Все формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b):
Формулы длины равных сторон , (a):
- Подробности
-
Автор: Administrator
-
Опубликовано: 11 октября 2011
-
Обновлено: 13 августа 2021
Как посчитать стороны равнобедренного треугольника
Онлайн калькулятор
Чтобы вычислить длины сторон равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):
- длину основания (b) и угол α
- длину основания (b) и угол β
- длину основания (b) и высоту (h)
- длину двух равных сторон (a) и угол α
- длину двух равных сторон (a) и угол β
- длину двух равных сторон (a) и высоту (h)
Введите их в соответствующие поля и получите результат.
Как посчитать сторону a равнобедренного треугольника
Если известна сторона b и угол α
Чему равна сторона a равнобедренного треугольника если длина основания , а угол
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол α?
Формула
Пример
Если сторона b = 10 см, а ∠α = 30°, то:
Если известна сторона b и угол β
Чему равна сторона a равнобедренного треугольника если длина основания , а угол
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол β?
Формула
Пример
Если сторона b = 10 см, а ∠β = 30°, то:
a = 10 /2⋅sin 15 = 10/(2⋅0.2588) = 19.31см
Если известна сторона b и высота h
Чему равна сторона a равнобедренного треугольника если длина основания , а высота
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и высота h?
Формула
Пример
Если сторона b = 10 см, а высота h = 20 см, то:
a = √ 1 /10 2 + 20 2 = √ 0.01+400 = 20.61см
Как посчитать сторону b (основание) равнобедренного треугольника
Если известна сторона a и угол α
Чему равна сторона b равнобедренного треугольника если длина стороны , а угол
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол α?
Формула
Пример
Если сторона a = 10 см, а ∠α = 30°, то:
b = 2⋅10⋅cos 30° = 2⋅10⋅0.8660 = 17.32см
Если известна сторона a и угол β
Чему равна сторона b равнобедренного треугольника если длина стороны , а угол
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол β?
Формула
Пример
Если сторона a = 10 см, а ∠β = 40°, то:
Если известна сторона a и высота h
Чему равна сторона b равнобедренного треугольника если длина стороны , а высота
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и высота h?
Формула
b = 2⋅ √ a 2 — h 2 , h
Пример
Если сторона a = 10 см, а высота h = 5 см, то:
Все формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
Равнобедренный треугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти неизвестные элементы (стороны, углы) а также периметр, площадь, высоты равнобедренного треугольника. Теоретическую часть и численные примеры смотрите ниже.
Открыть онлайн калькулятор
Определение равнобедренного треугольника
Определение 1 (Евклид). Треугольник, в котором длины двух сторон равны между собой называется равнобедренным треугольником.
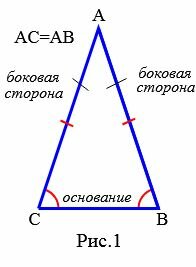
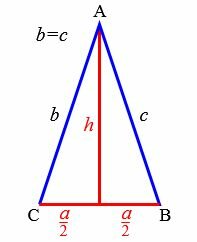
Равные стороны равнобедренного трекугольника называются боковыми сторонами. Третья сторона равнобедренного треугольника называется основанием треугольника (Рис.1).
Угол между боковыми сторонами равнобедненного треугольника (( small angle A ) ) называется вершинным углом. Углы между основанием и боковыми сторонами (( small angle B, angle C ) ) называются углами при основании.
Существует более общее определение равнобедненого треугольника:
Определение 2 (Современная трактовка). Треугольник, в котором длины хотя бы двух сторон равны между собой называется равнобедренным треугольником.
Из определения 2 следует, что равносторонний треугольник является частным случаем равнобедренного треугольника. Действительно, в качестве равных сторон можно взять любые две стороны равностороннего треугольника, а третья сторона будет основанием.
Теорема о равнобедренном треугольнике
Теорема 1. Углы, прилежащие к основанию равнобедренного треугольника равны.
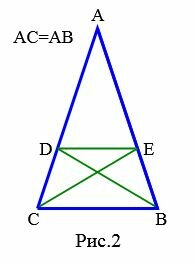
Доказательство (доказательство Прокла). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.2). Докажем, что ( small angle B= angle C. ) Возьмем любую точку D на стороне AC и точку E на стороне AB так, чтобы AD=AE. Проведем отрезки DE, CE, BD. Треугольники ABD и ACE равны по двум сторонам и углу между ними: AE=AD, AC=AB, угол ( small angle A ) общий (см. статью на странице Треугольники. Признаки равенства треугольников). Отсюда следует:
| ( small angle ACE=angle ABD.) | (2) |
Из ( small AB=AC) и ( small AD=AE ) следует:
Рассмотрим треугольники CBE и BCD. Они равны по трем сторонам: ( small CE=BD,) ( small CD=BE ,) сторона ( small BC ) общая. Отсюда следует, что
| ( small angle ECB= angle DBC. ) | (4) |
Из (2) и (4) следует, что ( small angle B= angle C. )
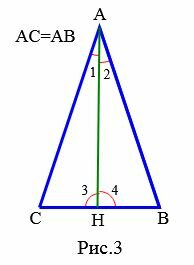
Доказательство (Вариант 2). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.3). Проведем биссектрису ( small AH ) треугольника. Тогда ( small angle CAH=angle BAH. ) Докажем, что ( small angle B= angle C. ) Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона ( small AH ) общая, ( small angle CAH=angle BAH. ) Отсюда следует: ( small angle B= angle C. )
Свойства равнобедренного треугольника
Теорема 2. В равнобедренном треугольнике биссектриса проведенная к основанию является медианой и высотой.
Доказательство. Рассмотрим равнобедренный треугольник ABC, где AB=AC, а AH− биссектриса треугольника (Рис.3). Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона ( small AH ) общая, ( small angle 1=angle 2. ) Тогда ( small CH=HB, ) ( small angle 3=angle 4. ) Равенство ( small CH=HB ) означает, что ( small AH ) является также медианой треугольника ABC. Углы ( small angle 3) и ( angle 4 ) смежные. Следовательно их сумма равна 180° и, поскольку эти углы равны, то каждый из этих углов равен 90°. Тогда ( small AH ) является также высотой треугольника ( small ABC. ) Поскольку высота ( small AH ) перпендикулярна к ( small BC ) и ( small CH=HB, ) то ( small AH ) является также серединным перпендикуляром к основанию равнобедренного треугольника.
Мы доказали, что биссектриса, медиана, высота и серединный перпендикуляр равнобедренного треугольника, проведенные к основанию совпадают.
Исходя из теоремы 2 можно сформулировать следующие теоремы, доказательство которых аналогично доказательству теоремы 2:
Теорема 3. В равнобедренном треугольнике медиана проведенная к основанию является биссектрисой и высотой.
Теорема 4. В равнобедренном треугольнике высота проведенная к основанию является биссектрисой и медианой.
Признаки равнобедренного треугольника
Признак 1. Если в треугольнике две стороны равны, то треугольник является равнобедренным.
Признак 1 следует из определения 1.
Признак 2. Если в треугольнике два угла равны, то треугольник является равнобедренным.
Доказательство признака 2 смотрите в статье Соотношения между сторонами и углами треугольника (Следствие 2. Признак равнобедренного треугольника).
Признак 3. Если в треугольнике высота проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
Доказательство. Пусть в треугольнике ( small ABC ) ( small AH ) является высотой и медианой (Рис.4). Тогда ( small angle 3=angle4=90°, ) ( small CH=HB. ) Треугольники ( small AHC ) и ( small AHB ) равны по двум сторонам и углу между ними (первый признак равенства треугольников): ( small AH ) − общая сторона, ( small CH=HB, ) ( small angle 3=angle4. ) Следовательно ( small AB=AC. )
Признак 4. Если в треугольнике высота проведенная к одной стороне совпадает с биссектрисой проведенной к этой же стороне, то треугольник является равнобедренным.
Доказательство. Пусть в треугольнике ( small ABC ) ( small AH ) является высотой и биссектрисой (Рис.4). Тогда ( small angle 3=angle4=90°, ) ( small angle 1=angle2. ) Треугольники ( small AHC ) и ( small AHB ) равны по стороне и прилежащим двум углам (второй признак равенства треугольников): ( small AH ) − общая сторона, ( small angle 1=angle 2, ) ( small angle 3=angle4. ) Следовательно ( small AB=AC. )
Признак 5. Если в треугольнике биссектриса проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
Доказательство (Вариант 1). Пусть в треугольнике ( small ABC ) ( small AH ) является биссектрисой и медианой (Рис.5). Тогда
| ( small angle 1=angle2, ) ( small CH=HB. ) | (5) |
Применим теорему синусов для треугольника ( small AHC ):
| ( small frac <large CH><large sin angle 1>= frac <large AH><large sin angle C>. ) | (6) |
Применим теорему синусов для треугольника ( small AHB ):
| ( small frac <large HB><large sin angle 2>= frac <large AH><large sin angle B>. ) | (7) |
тогда, из (5), (6), (7) получим:
| ( small frac <large AH><large sin angle C>= frac <large AH><large sin angle B>. ) | (8) |
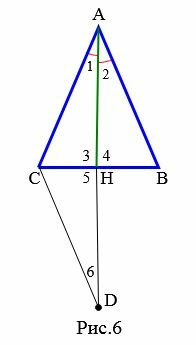
Следовательно ( small sin angle C= sin angle B. ) Поскольку сумма всех углов треугольника равна 180°, то нам интересует синус углов от 0 до 180°. Учитывая это получим, что синусы углов равны в двух случаях: 1) ( small angle C= angle B, ) 2) ( small angle C= 180° — angle B. ) Поскольку сумма двух углов треугольника меньше 180°: ( small angle C + angle B Доказательство (Вариант 2). Пусть в треугольнике ( small ABC ) ( small AH ) является биссектрисой и медианой, т.е. ( small angle 1=angle 2, ) ( small CH=HB ) (Рис.6). На луче ( small AH ) отложим отрезок ( small HD ) так, чтобы ( small AH=HD. ) Соединим точки ( small C ) и ( small D. )
Треугольники ( small AHB ) и ( small DHC ) равны по двум сторонам и углу между ними (первый признак равенства треугольников). Действительно: ( small AH=HD, ) ( small CH=HB, ) ( small angle 4=angle 5 ) (углы 4 и 5 вертикальные). Тогда ( small AB=CD, ) ( small angle 6=angle 2. ) Отсюда ( small angle 6=angle 1. ) Получили, что треугольник ( small CAD ) равнобедренный (признак 2). Тогда ( small AC=CD. ) Но ( small AB=CD ) и, следовательно ( small AB=AC. ) Получили, что треугольник ( small ABC ) равнобедренный.
1. Признак равенства равнобедренных треугольников по основанию и боковой стороне
Если основание и боковая сторона одного равнобедренного треугольника соответственно равны основанию и боковой стороне другого равнобедненного треугольника, то эти треугольники равны.
Действительно. Поскольку треугольник равнобедренный, то боковые стороны равны. То есть три стороны одного равнобедренного треугольника соответственно равны трем сторонам другого равнобедненного треугольника. А по третьему признаку равенства треугольников, эти треугольники равны.
2. Признак равенства равнобедренных треугольников по боковой стороне и углу при вершине
Если боковая сторона и угол при вершине одного равнобедренного треугольники соответственно равны боковой стороне и углу при вершине другого равнобедренного треугольника, то такие треугольники равны.
Действительно. Так как боковые стороны равнобедненного треугольника равны, то имеем: две стороны и угол между ними одного треугольника соотвественно равны двум сторонам и углу между ними другого треугольника. Тогда по первому признаку равенства треугольников, эти реугольники равны.
3. Признак равенства равнобедренных треугольников по основанию и углу при основании
Если основание и угол при основании равнобедренного треугольника соответственно равны основанию и углу при основании другого равнобедренного треугольника, то такие треугольники равны.
Доказательство. В равнобедренном треугольнике углы при основании равны. тогда имеем: основание и две углы одного равнобедненного треугольника равны основанию и двум углам другого равнобедненного треугольника. Тогда эти треугольники равны по второму признаку равенства треугольников.
Задачи и решения
Задача 1. Известны основание ( small a=5 ) и высота ( small h=6 ) равнобедренного треугольника. Найти углы, боковые стороны, периметр, площадь.
Решение. Найдем боковые стороны ( small b ) и ( small c ) равнобедренного треугольника. Воспользуемся теоремой Пифагора:
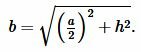 |
(9) |
Подставляя значения ( small a ) и ( small h ) в (9), получим:
Боковая сторона ( small c ) равнобедренного треугольника равна:
Найдем периметр треугольника. Периметр треугольника равен сумме длин его сторон:
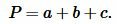 |
(10) |
Подставляя значения ( small a=5, ) ( small b=6.5 ) и ( small c=6.5 ) в (10), получим:
Найдем угол ( small B ) равнобедренного треугольника:
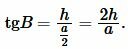 |
(11) |
Подставляя значения ( small a=5, ) ( small h=6 ) в (11), получим:
Тогда угол ( small C ) равнобедренного треугольника равен:
Поскольку сумма всех углов треугольника равна 180°, то имеем:
Площадь треугольника можно вычислить из формулы:
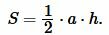 |
(12) |
Подставляя значения ( small a=5, ) ( small h=6 ) в (12), получим:
http://www-formula.ru/lengthpartiesisoscelestriangle
http://matworld.ru/geometry/ravnobedrennyj-treugolnik.php
Информация по назначению калькулятора
Треугольник — это одна из основных геометрических фигур: многоугольник с тремя углами (или вершинами) и тремя сторонами (или ребрами), которые являются прямыми отрезками.
В евклидовой геометрии любые три неколлинеарные точки определяют треугольник и единственную плоскость, то есть двумерное декартово пространство.
Сумма длин любых двух сторон треугольника всегда превышает длину третьей стороны. Это и есть неравенство треугольника.
Треугольники могут быть классифицированы в соответствии с относительной длиной их сторон:
⇒ В равностороннем треугольнике все стороны имеют одинаковую длину. Равносторонний треугольник также является равноугольным многоугольником, т.е. все его внутренние углы равны, а именно 60° — это правильный многоугольник.
⇒ В равнобедренном треугольнике две стороны имеют одинаковую длину. Равнобедренный треугольник также имеет два совпадающих угла (а именно, углы, противоположные совпадающим сторонам). Равносторонний треугольник — это равнобедренный треугольник, но не все равнобедренные треугольники являются равносторонними треугольниками.
⇒ В скалярном треугольнике все стороны имеют разную длину. Внутренние углы в скалярном треугольнике все разные.
Треугольники также могут быть классифицированы в соответствии с их внутренними углами:
⇒ Прямоугольный треугольник имеет один внутренний угол 90° (прямой угол). Сторона, противоположная прямому углу, является гипотенузой; это самая длинная сторона в прямоугольном треугольнике. Две другие стороны — катеты треугольника.
⇒ Тупой треугольник имеет один внутренний угол, больший 90° (тупой угол).
⇒ Острый треугольник имеет внутренние углы, которые все меньше 90° (три острых угла). Равносторонний треугольник — это острый треугольник, но не все острые треугольники являются равносторонними треугольниками.
⇒ Наклонный треугольник имеет только углы, которые меньше или больше 90°. Следовательно, это любой треугольник, который не является прямоугольным треугольником.
Онлайн калькулятор поможет найти параметры треугольника, такие как:
- Длины сторон
- Углы
- Высота
- Периметр
- Площадь
- Медианы
- Биссектрисы
- Радиус Вписанной и Описанной окружностей
- Диаметр Вписанной и Описанной окружностей
- Длина Вписанной и Описанной окружностей
- Площадь Вписанной и Описанной окружностей
— равны в равностороннем треугольнике
— также равны в равностороннем треугольнике
— это прямая линия, проходящая через вершину и перпендикулярная противоположной стороне (т. е. образующая прямой угол с ней)
— равен сумме всех 3х сторон (P=AB+BC+AC)
— равна половине произведения высоты и стороны к которой построена высота (S=1/2 * H * AC)
Enter any two known values for an isosceles triangle to calculate the edge lengths, altitude, angles, area, perimeter, inradius, and circumradius.
Solution:
| side a: |
3 |
| base b: |
5 |
| angle α: |
33.557° | 0.5857 rad |
| angle β: |
112.89° | 1.97 rad |
| height h: |
1.658 |
| area: |
4.146 |
| perimeter: |
11 |
| inradius: |
0.7538 |
| circumradius: |
2.714 |
Type of Triangle:
obtuse isosceles triangle
Learn how we calculated this below
scroll down
On this page:
-
Calculator
-
What is an Isosceles Triangle?
-
Types of Isosceles Triangles
-
How to Calculate Edge Lengths of an Isosceles Triangle
-
How to Calculate the Angles of an Isosceles Triangle
-
How to Calculate Area and Perimeter
What is an Isosceles Triangle?
An isosceles triangle is a triangle that has two sides of equal length. The third side is often referred to as the base. Isosceles triangles are typically considered to have exactly two sides of equal length.
However, sometimes they are referred to as having at least two sides of equal length. The equilateral triangle, for example, is considered a special case of the isosceles triangle.
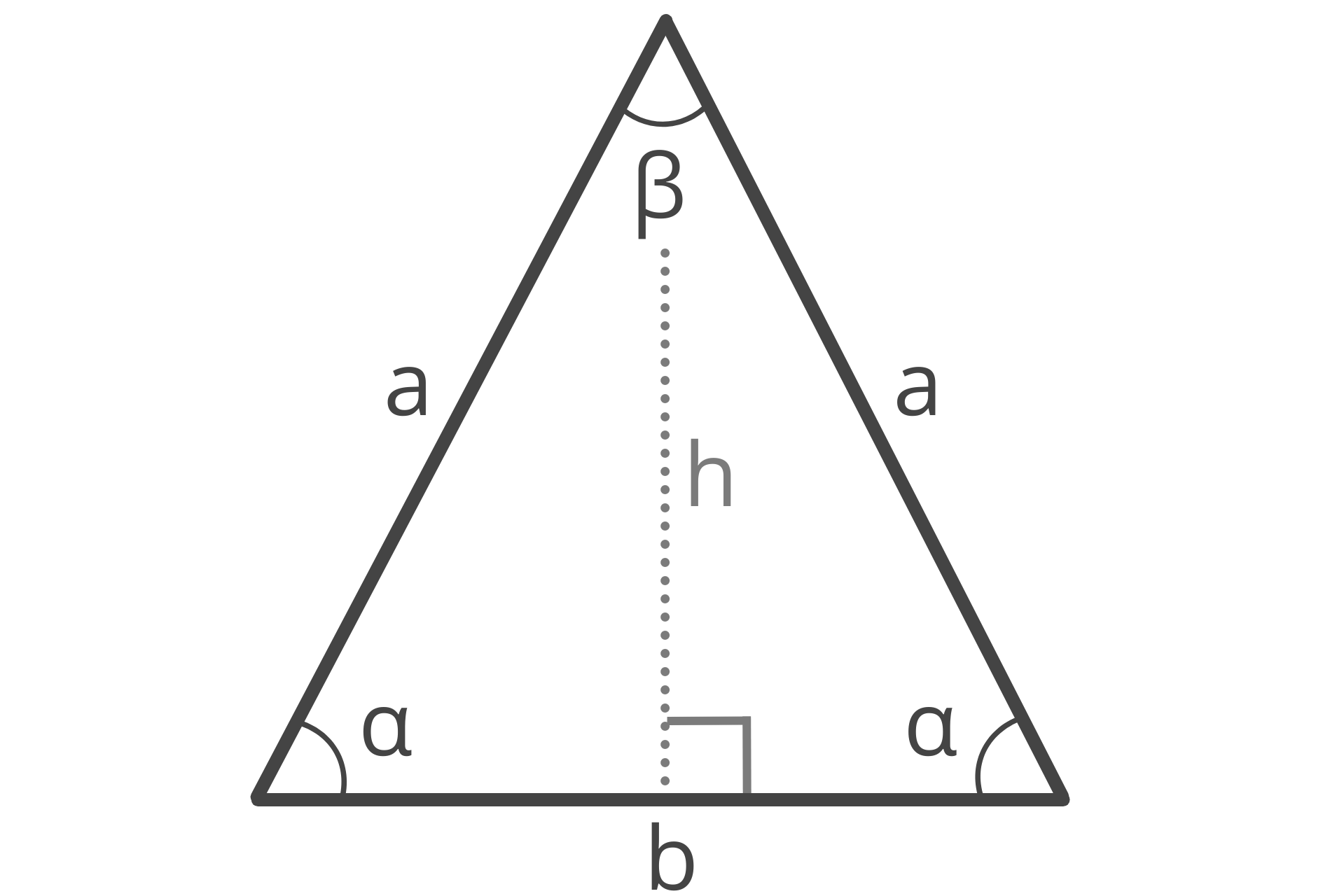
The two interior angles adjacent to the base are called the base angles, while the interior angle opposite the base is called the vertex angle. When references are made to the angles of a triangle, they are most commonly referring to the interior angles.
Because the side lengths opposite the base angles are of equal length, the base angles are also identical. Note, this means that any reference made to side length a applies to either of the identical side lengths as they are equal, and any reference made to base angle α applies to either of the base angles as they are also identical.

Types of Isosceles Triangles
There are four types of isosceles triangles: acute, obtuse, equilateral, and right.
An acute isosceles triangle is an isosceles triangle with a vertex angle less than 90°, but not equal to 60°.
An obtuse isosceles triangle is an isosceles triangle with a vertex angle greater than 90°.
An equilateral triangle is a special case of isosceles triangles. Note, in an equilateral triangle, all three interior angles are identical to one another, and all three side lengths are equal to one another.
Thus, the vertex angle of an equilateral triangle is equal to 60°, as are the base angles. Try our equilateral triangle calculator.
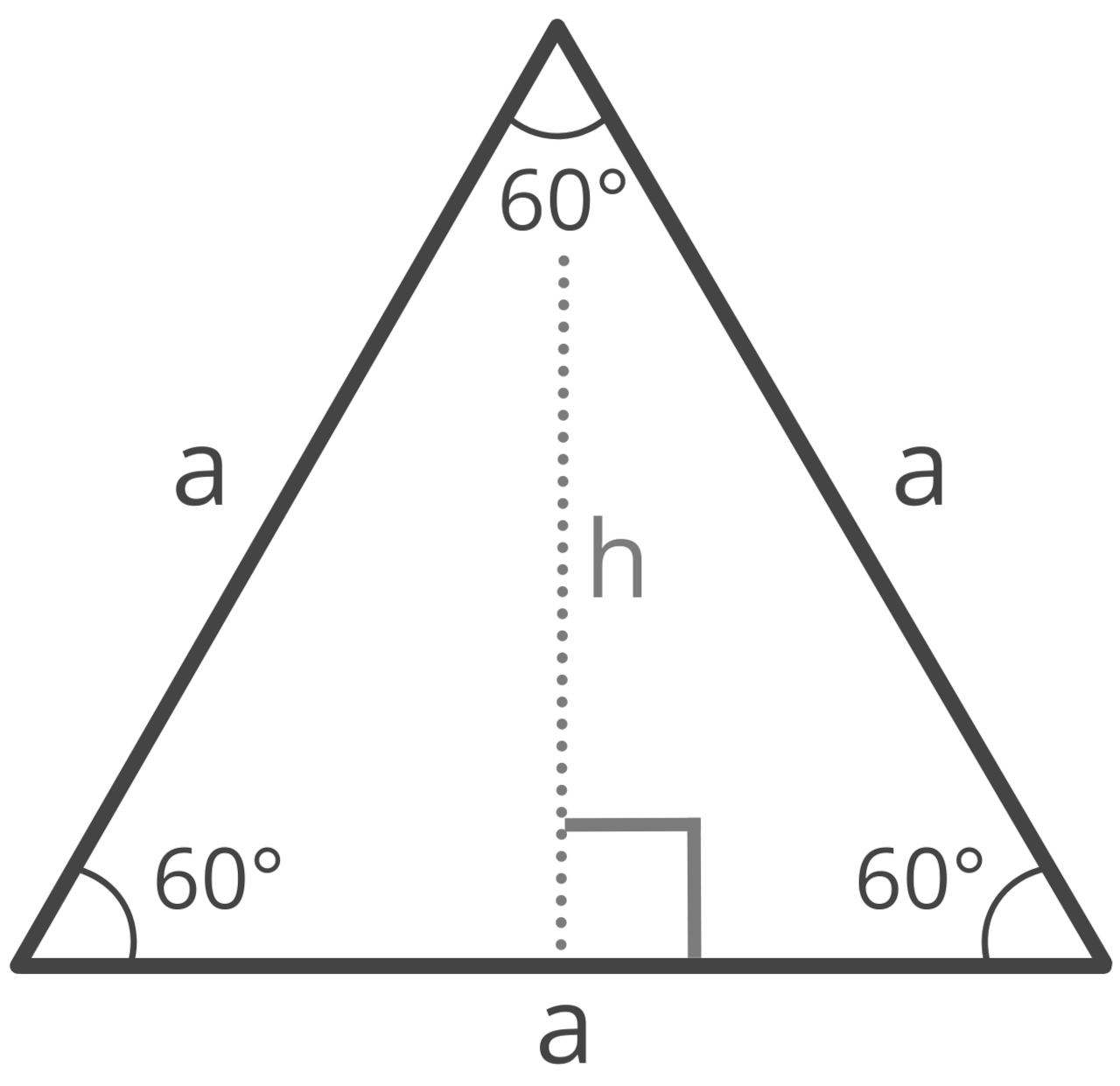
A right isosceles triangle is an isosceles triangle with a vertex angle equal to 90°, and base angles equal to 45°. This is also referred to as a 45 45 90 special right triangle.
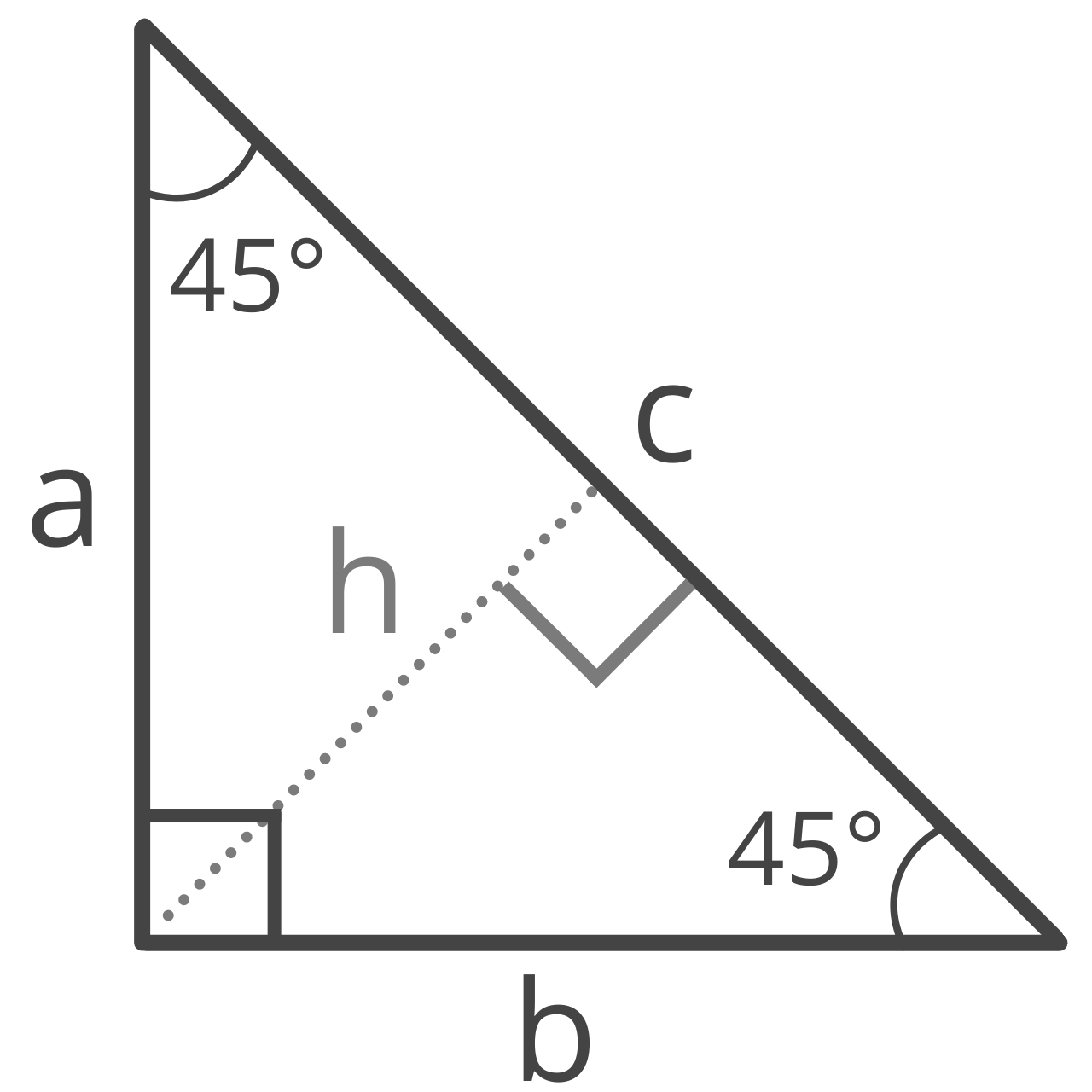
We have a special right triangle calculator to calculate this type of triangle.
How to Calculate Edge Lengths of an Isosceles Triangle
Given the height, or altitude, of an isosceles triangle and the length of one of the sides or the base, it’s possible to calculate the length of the other sides.
Find the Base Length
Use the following formula derived from the Pythagorean theorem to solve the length of the base side:
b = 2a² – h²
The base length b is equal to 2 times the square root of quantity leg a squared minus the height h squared.
Find the Leg Length
Use the following formula also derived from the Pythagorean theorem to solve the length of side a:
a = h² + (b ÷ 2)²
The side length a is equal to the square root of the quantity height h squared plus one-half of base b squared.
How to Calculate the Angles of an Isosceles Triangle
Given any angle in an isosceles triangle, it is possible to solve the other angles.
Find the Base Angle
Use the following formula to solve either of the base angles:
α = 180° – β / 2
The base angle α is equal to quantity 180° minus vertex angle β, divided by 2.
Find the Vertex Angle
Use the following formula to solve the vertex angle:
β = 180° – 2α
The vertex angle β is equal to 180° minus 2 times the base angle α.
How to Calculate Area and Perimeter
Given the side lengths of an isosceles triangle, it is possible to solve the perimeter and area using a few simple formulas.
Find the Perimeter
You can find the perimeter of an isosceles triangle using the following formula:
p = 2a + b
Thus, the perimeter p is equal to 2 times side a plus base b.
Find the Semiperimeter
Given the perimeter, you can find the semiperimeter. The semiperimeter s is equal to half the perimeter.
s = p / 2
Find the Area
You can find the area of an isosceles triangle using the formula:
A = s(s – a)(s – a)(s – b)
The area A is equal to the square root of the semiperimeter s times semiperimeter s minus side a times semiperimeter s minus a times semiperimeter s minus base b.
This is known as Heron’s formula.