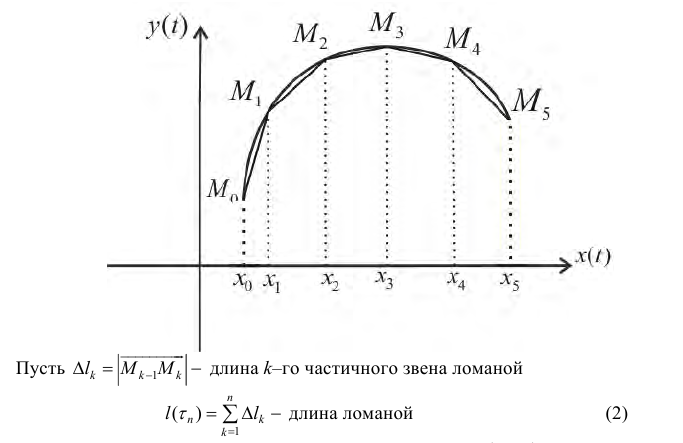
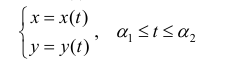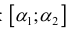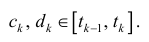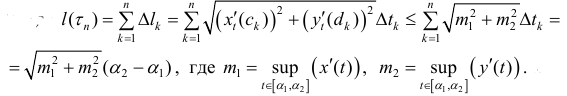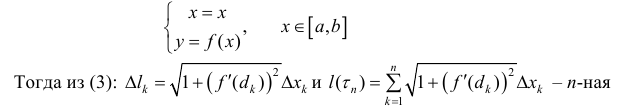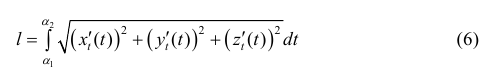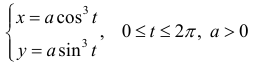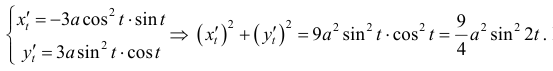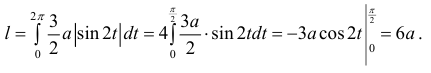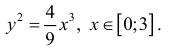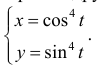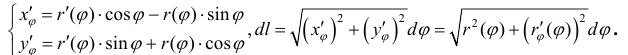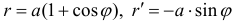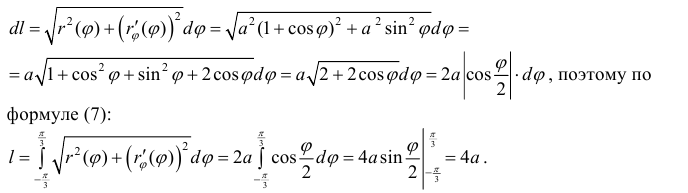Длину дуги получают интегрированием дифференциала дуги от первой точки к конечной. Сложность вычислений заключается в том, что кривая, как правило, заданная двумя или и тремя уравнениями изменения координат по осям, а интегрирование нужно свести к одной координате. Для этого нужно найти дифференциал дуги.
Формулы дифференциалу дуги для пространственных и плоских кривых, заданных явно и параметрически хорошо расписаны.
Их здесь повторять не будем, а лишь выделим цветом в формулах.
Когда известен дифференциал дуги, интеграл вычисляют всеми возможными способами:
непосредственное интегрирование, замена переменных, интегрирования частями.
Часть методов дальше применим для решения заданий.
Пример 1 Найти длину дуги пространственной кривой:
x=3t, y=3t2, z=2t3, от точки O(0,0,0) к точке A(3,3,2).
Решение: Найдем производные по переменной t от заданных функций x=x(t), y=y(t) и z=z(t):
x’=3, y’=6t, z’=6t2.
Производные нам нужны для нахождения дифференциала дуги ds заданной кривой:
Эта формула справедлива для всех пространственных кривых, заданных параметрически.
Следующим шагом определим пределы интегрирования.
Чтобы их найти нужно в уравнение пространственной кривой
подставить две точки О, А.
Складываем уравнение на определение пределов изменения параметра t:
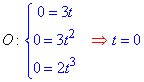
При решении установили, что параметр должен принадлежать интервалу 0≤t≤1.
Вычислим длину дуги заданной кривой, при 0≤t≤1:
Интеграл найти не трудно, поскольку под корнем легко выделить квадрат, а дальше уже имеем дело с квадратичной функцией, которую легко интегрировать.
Дальше рассмотрим более сложные задания в которых вычисление производных и дифференциала дуги усложняется.
Пример 2 Найти длину дуги пространственной кривой (a>0) :
(x-y)2=a(x+y), x2-y2=9/8-z2, от точки O(0,0,0) к точке A(x0,y0,z0).
Решение: В подобных примерах целесообразно сделать замену переменных:
Тогда заданное уравнение (x-y)2=a(x+y) приобретет вид:
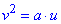
Отсюда
Подобные превращения выполняем для второго уравнения кривой
x2-y2=9/8-z2, или (x-y)(x+y)=9/8-z2:
отсюда
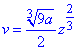
Имеем 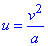
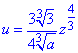
Найдем производные по переменной z от функций u=u(z) и v=v(z):
после упрощений получим такие конечные значения
Запишем как изменяется z от точки O(0,0,0) к точке A(x0, y0, z0):
0≤z≤z0.
Следующим шагом найдем дифференциал дуги ds по формуле:
Под корнем выделили полный квадрат, поэтому дифференциал упростился.
Через интеграл вычисляем длину дуги кривой:
Найти интеграл в этом случае тоже не складывает больших трудностей.
Окончательно получим
Значение функций в точке A(x0, y0, z0):
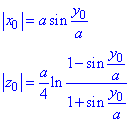
Найдем производные по переменной y функций x=x(y), z=z(y):
За свойством логарифма превратим логарифм дроби в разницу логарифмов
Такой прием поможет при вычислении производной составленной функции
Запишем пределы интегрирования y, когда точка проходит значение от O(0,0,0) к A(x0, y0, z0):
0≤y≤y0.
Дифференциал дуги ds кривой вычислим по формуле:
Длину дуги пространственной кривой найдем по формуле:
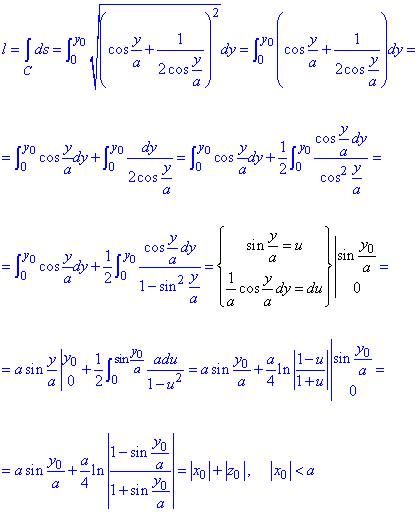
В интеграле сделали замену переменных и интегрировали частями.
Пример 4 Вычислить длину дуги пространственной кривой (a>0, c>0) :
x2+y2=cz, y/x=tg (z/c), от точки O(0,0,0) к точке A(x0, y0, z0).
Решение: Перейдем к полярной системе координат с помощью формул перехода:
Превращаем первое уравнение кривой
дальше второе
Из формул видим насколько проще стали уравнения кривой.
Запишем все три пространственные координаты через параметр угла φ:
здесь переменная пробегает значение 0≤φ≤z0/c, поскольку φ=z/c.
Запишем производные по переменной φ для функций x=x(φ), y=y(φ) но z=z(φ):
Вычислим дифференциал дуги ds кривой по формуле:
Не забывайте в подобных заданиях выделять полный квадрат под корнем.
Без этого Вы не сможете найти интеграла.
Через интеграл найдем длину дуги пространственной кривой:
Из приведенных примеров можно сделать вывод, что сложность вычисления криволинейных интегралов имеет место лишь в выборе системы координат, нахождении производных и дифференциалов дуг.
Найти интеграл в большинстве случаев достаточно легко, сложные задания, как правило, преподаватели Вам не дадут вычислять.
При вычислении любой длины следует помнить, что это величина конечная, то есть просто число. Если имеется в виду длина дуги кривой, то такая задача решается с помощью определенного интеграла (в плоском случае) или криволинейного интеграла первого рода (по длине дуги). Дуга АВ будет обозначаться UАВ.
Первый случай (плоский). Пусть UАВ задана плоской кривой y = f(x). Аргумент функции изменятся в пределах от а до b и она непрерывно дифференцируема этом отрезке. Найдем длину L дуги UАВ (см. рис. 1а). Для решения этой задачи разбейте рассматриваемый отрезок на элементарные отрезки ∆xi, i=1,2,…,n. В результате UАВ разобьется на элементарные дуги ∆Ui, участков графика функции y=f(x) на каждом из элементарных отрезков. Найдете длину ∆Li элементарной дуги приближенно, заменив ее соответствующей хордой. При этом можно приращения заменить дифференциалами и использовать теорему Пифагора. После вынесения из квадратного корня дифференциала dx получите результат, приведенный на рисунке 1b.
Как вычислить длину кривой
Второй случай (дуга UАВ задана параметрически). x=x(t), y=y(t), tє[α,β]. Функции x(t) и y(t) имеют непрерывные производные на отрезке этом отрезке. Найдите их дифференциалы. dx=f’(t)dt, dy=f’(t)dt. Подставьте эти дифференциалы в формулу для вычисления длины дуги в первом случае. Вынесите dt из квадратного корня под интегралом, положите х(α)=а, x(β)=b и придете к формуле для вычисления длины дуги в данном случае (см. рис. 2а).
Третий случай. Дуга UАВ графика функции задана в полярных координатах ρ=ρ(φ) Полярный угол φ при прохождении дуги изменяется от α до β. Функция ρ(φ)) имеет непрерывную производную на отрезке ее рассмотрения. В такой ситуации проще всего использовать данные, полученные на предыдущем шаге. Выберите φ в качестве параметра и подставьте в уравнения связи полярных и декартовых координат x=ρcosφ y=ρsinφ. Продифференцируйте эти формулы и подставьте квадраты производных в выражение на рис. 2а. После небольших тождественных преобразований, основанных в основном, на применении тригонометрического тождества (cosφ)^2+(sinφ)^2=1, получите формулу для вычисления длины дуги в полярных координатах (см. рис.2b).
Четвертый случай (пространственная кривая, заданная параметрически). x=x(t), y=y(t), z=z(t) tє[α,β]. Строго говоря, здесь следует применить криволинейный интеграл первого рода (по длине дуги). Криволинейные интегралы вычисляют переводом их в обычные определенные. В результате ответ останется практическим таким же как и случае два, с тем лишь отличием, что под корнем появится добавочное слагаемое – квадрат производной z’(t) (см рис. 2с).
Примеры:
Пример 1. Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у=ƒ(х), где а≤х≤ b.
Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю. Покажем, что если функция у=ƒ(х) и ее производная у’ = ƒ'(х) непрерывны на отрезке [а; b], то кривая АВ имеет длину, равную
Применим схему I (метод сумм).
1. Точками х0 = а, х1…, хn = b (х0 < x1 < …< хn) разобьем отрезок [а; b] на n частей (см. рис. 183). Пустьэтим точкам соответствуют точки М0 = А, M1,…,Mn =В на кривой АВ. Проведем хорды М0M1, M1M2,…, Мn-1Мn, длины которых обозначим соответственно через ΔL1, AL2,…, ΔLn. Получим ломаную M0M1M2 … Mn-ιMn, длина которой равна Ln=ΔL1 + ΔL2+…+ ΔLn =
2. Длину хорды (или звена ломаной) ΔL1 можно найти по теореме Пифагора из треугольника с катетами Δxi и Δуi:
По теореме Лагранжа о конечном приращении функции Δуi=ƒ'(сi)•Δхi, где ci є (xi-1;xi). Поэтому
а длина всей ломаной M0M1… Мn равна
3.Длина l кривой АВ, по определению, равна
.
Заметим, что при ΔLi→0 также и Δxi →0 ΔLi =и, следовательно, |Δxi|<ΔLi).
Функция непрерывна на отрезке [а; b], так как, по условию, непрерывна функция ƒ'(х). Следовательно, существует предел интегральной суммы (41.4), когда max Δxi→ 0:
Таким образом,или в сокращенной записи l =
Если уравнение кривой АВ задано в параметрической форме
где x(t) и y(t) — непрерывныефункции с непрерывными производными и х(а) = а, х(β) = b, то длина l кривой АВ находится по формуле
Формула (41.5) может быть получена из формулы (41.3) подстановкой x = x(t),dx = x'(t)dt,
Пример 2. Определить длину окружности x2 + y2 = r2. Решение. Вычислим сначала длину четвертой части окружности, лежащей в первом квадранте. Тогда уравнение дуги AB будет, откуда
,следовательно,
Длина всей окружности L = 2πr.
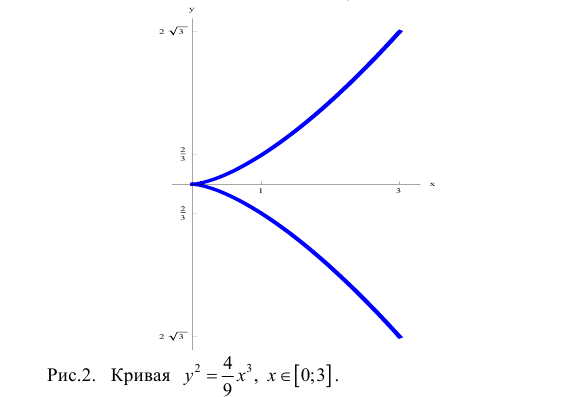
Пример 3. Найти длину дуги кривой y2 = x3 от x = 0 до x = 1 (y > 0). Решение. Дифференцируя уравнение кривой, найдем y’ = (3/2)x1/2, откуда
Пример 4. Пусть кривая лежит в плоскости x0y и описывается уравнением y = f(x).
Для нахождения длины дуги этой кривой, заключенной между точками с абсциссами a и b, разобьем дугу на столь малые элементы, чтобы каждый из них можно было аппроксимируовать прямолинейным участком (см. рисунок 1).
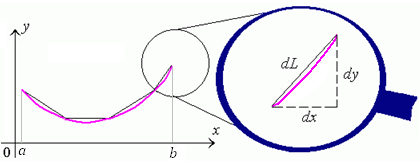
Рис. 1. Аппроксимация элемента дуги кривой прямолинейным участком.
Длину dL бесконечно малого участка можно выразить через dx и dy с помощью теоремы Пифагора:
 |
(1) |
где y ‘ – производная функции y = f(x) по переменной x.
Длина дуги равна сумме длин составляющих ее элементов:
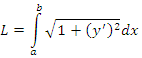 . . |
Пример 5.
На рис. 114 даны две проекции пространственной кривой l. Чтобы определить длину кривой, необходимо осуществить ее спрямление. Спрямление пространственной кривой, заданной ортогональными проекциями, осуществляется следующим путем:
1. Спрямляем горизонтальную проекцию кривой А’В’ в [А1В1]. Для этого намечаем на l’ ряд точек 1′, 2′, 3′, … так, чтобы дуги, заключенные между этими точками, мало отличались по длине от стягивающих их хорд. Откладываем длины хорд |А’1’|, |1’2’|, |2’3’|, … , |6’В’| на горизонтальной прямой а в последовательности, которую они занимали на проекции кривой.
2. Из точек А0, 10, 20, 30, … , В]0 прямой а восставляем перпендикуляры и отмечаем точки их пересечения с горизонтальными прямыми, проведенными через соответствующие фронтальные проекции точек А», 1″, 2″, 3″, … , В».
3. Полученные точки пересечения А0, 10, 20, 30, , В0 укажут вершины ломаной линии, выпрямив которую, получим отрезок [A01B01], равный длине пространственной кривой с точностью аппроксимации дуг кривой их хордами.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
- Дайте определение пространственной и плоской кривой.
- Что называется порядком алгебраической кривой и как можно определить его, если кривая (плоская или пространственная) задана графически?
- Перечислите свойства кривой линии, инвариантные относительно параллельного проецирования.
- Назовите «особые точки» кривой и дайте их определение.
- Что такое соприкасающаяся плоскость?
- Дайте определение трехгранника Френе.
- Расскажите, как можно построить касательную к плоской кривой:
- Что такое эвольвента и эволюта плоской кривой? Дайте определения и укажите основные свойства этих кривых.
- Что называется кривизной плоской кривой в данной точке? Как можно определить ее графически?
- Что такое шаг винтовой линии?
- Как построить на чертеже цилиндрическую винтовую линию?
- Как можно определить длину дуги пространственной кривой по ее ортогональным проекциям?
а) проходящую через заданную точку, не принадлежащую кривой,
б) проходящую через точку, заданную на кривой;
в) параллельную заданному направлению.
Преподаватель который помогает студентам и школьникам в учёбе.
Длина дуги кривой — определение и вычисление с примерами решения
Длина дуги кривой:
Определение 1. Рассмотрим простую кривую L на плоскости (см. § 30), заданную параметрически в виде
Разобьем отрезок
Кривая называется спрямлякмой, если множество 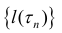
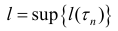
Замечание. Эквивалентное утверждение: число l называется длиной кривой L, если 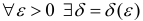
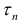
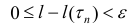
Теорема 1. Пусть x (t) и y (t) – непрерывно-дифференцируемы, тогда кривая L вида (1) – спрямляемая.
Доказательство. 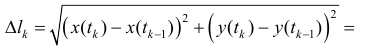
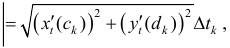
Тогда
Таким образом 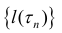
Найдем длину кривой L. Рассмотрим случай явного задания функции:
интегральная сумма для функции 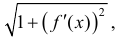
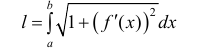
Аналогично для кривой L заданной по формулам (1)
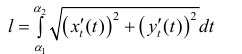
Длина l пространственной кривой L: 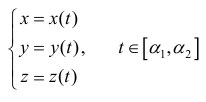
Пример 1.
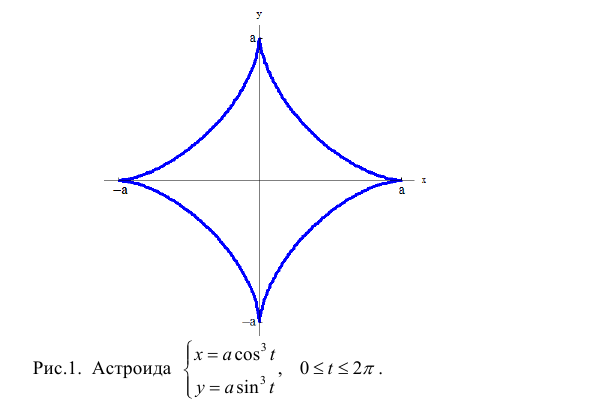
Найдем длину дуги астроиды
Решение.
По формуле (5):
Пример 2.
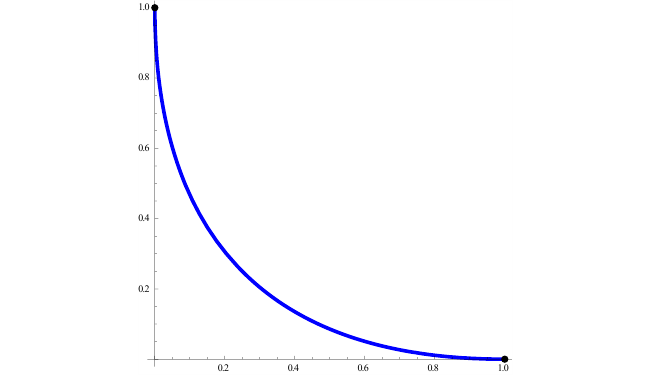
Найти длину дуги линии
Решение.
Кривая симметрична относительно оси Ох:
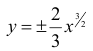
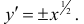
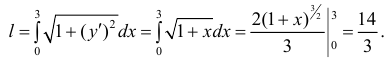
Замечание. Если кривая не является простой, необходимо учитывать возможность самоналожения участков кривой друг на друга.
Пример 3.
Найти длину кривой
Решение.
При 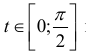
При 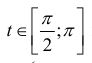
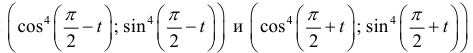
Поэтому 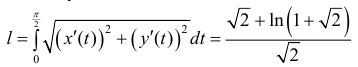
Замечание. 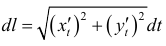
Найдем длину кривой L заданной в полярных координатах: r=r(ϕ), 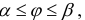
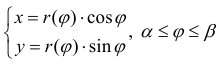
Поэтому 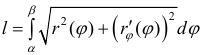
Пример 4.
Найти длину дуги части кардиоиды 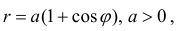
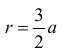
Решение.
- Геометрические фигуры и их свойства
- Основные фигуры геометрии и их расположение в пространстве
- Пространственные фигуры — виды, изображения, свойства
- Взаимное расположения прямых на плоскости
- Объем пространственных фигур
- Объёмы поверхностей геометрических тел
- Фигуры вращения: цилиндр, конус, шар
- Объем фигур вращения

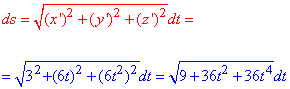
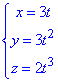
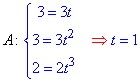
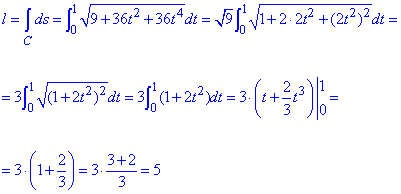
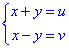
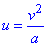

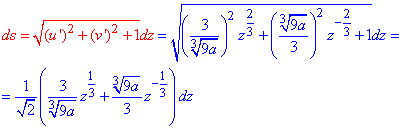
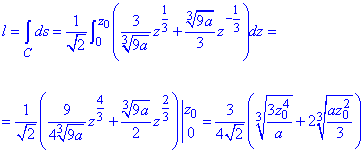
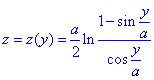
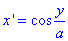
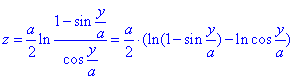
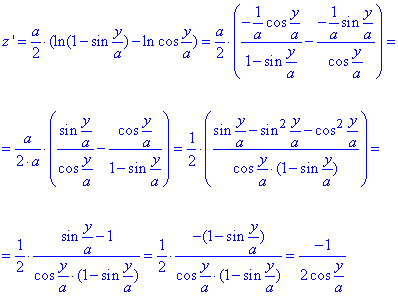
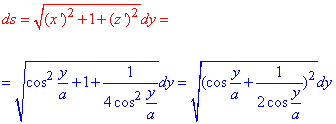
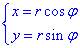
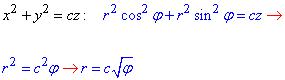
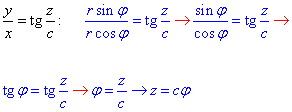
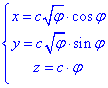
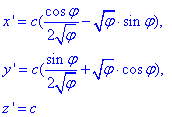
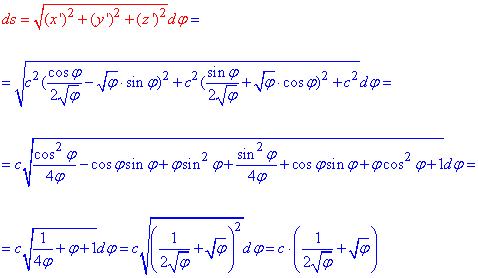
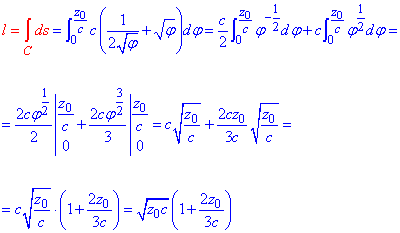
![1_5254fef39271a5254fef392758[1] 1_5254fef39271a5254fef392758[1]](https://ic.pics.livejournal.com/wrtorr/66163308/11897/11897_900.png)