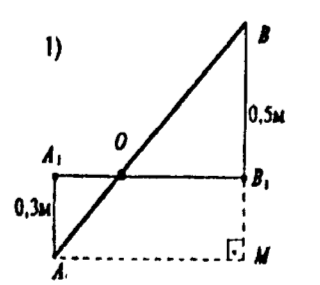
Решение.
Пусть отрезок АВ пересекает плоскость а в точке О. Спроектируем его на плоскость α. Проведем перпендикуляры ΑΑ1 и BB1
АА1 = 0,3 м, ВВ1 = 0,5 м.
Проведем через т. А прямую, параллельную А1B1. Она пересечет
продолжение отрезка ВВ1 в точке М. AM ┴ ВМ. В Δ АВМ по теореме Пифагора: AM2 = АВ2 — МВ2, но
МВ = МВ1 + ВВ1 = 0,5 + 0,3 = 0,8 (м), а АВ = 1 (м), так что
AM2 = 1 — 0,64 = 0,36 (м2); AM = 0,6 (м). Далее
так как AA1B1M — прямоугольник, то А1В1 = AM = 0,6 м.
4.5. Определение длины отрезка и углов его наклона к плоскостям проекций
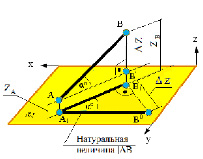
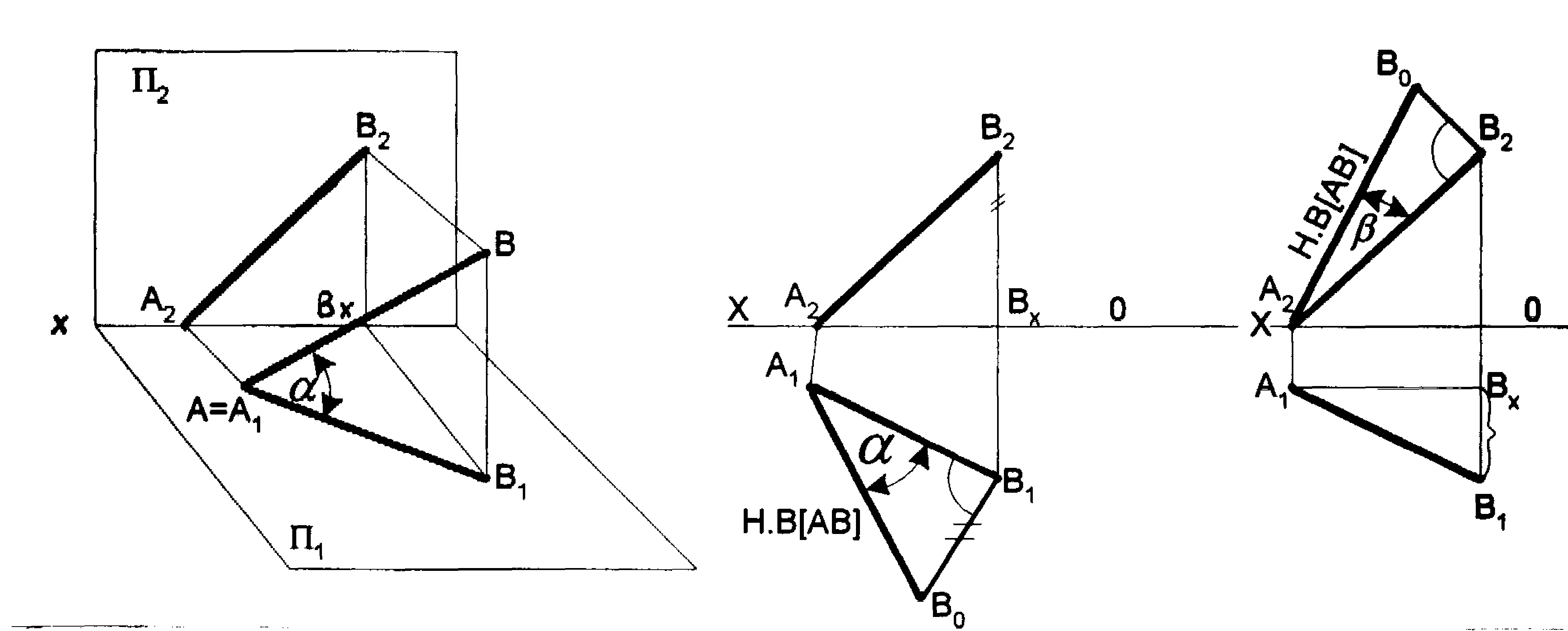
Прямая общего положения на плоскости проекций отображается с искажением (рис.4.6). Для того чтобы найти её натуральную величину, необходимо воспользоваться правилом прямоугольного треугольника, согласно которому на комплексном чертеже натуральной величиной прямой является гипотенуза прямоугольного треугольника, построенного на двух катетах. Один из этих двух катетов – это проекция рассматриваемой прямой, а вторым катетом является разность координат начала и конца этой прямой или разность координат z точек А и В (Δz = zA – zB).
Углы наклона прямой общего положения к плоскостям проекций по двум ее проекциям находят при определении действительной величины этой прямой способом прямоугольного треугольника. Если взять прямую общего положения АВ и спроецировать ее на горизонтальную плоскость проекций, а через точку А провести линию, параллельную плоскости, то в пространстве получится прямоугольный треугольник, один из катетов которого (AB’) равен длине проекции прямой АВ, а угол между прямой и этим катетом будет углом наклона заданной прямой к горизонтальной плоскости проекций (рис. 4.6), что можно подтвердить известным математическим соотношением:
tg α = BB’ / AB’ = (BB1 – B’B1) / AB’ = (zB – zA) / A1 B1.
Прямая А1В0 представляет натуральную величину прямой общего положения АВ.
Для определения натуральной величины прямой общего положения АВ и угла наклона её к плоскости проекций на эпюре (комплексном чертеже) необходимо построить прямоугольный треугольник:
— первый катет этого треугольника равен проекции прямой, на плоскости проекций;
— для построения второго катета необходимо из проекции любого конца проекции прямой линии под прямым углом к проекции провести луч, на котором отложить длину второго катета, равную разности расстояний от концов прямой до данной плоскости проекций;
— гипотенуза полученного прямоугольного треугольника будет равна действительной величине заданной прямой;
— угол наклона прямой линии к той или иной плоскости проекций равен углу между гипотенузой – натуральной величиной и катетом – проекцией прямой на эту плоскость проекций.
Углы наклона прямой линии общего положения к плоскости, всегда меньше их ортогональных проекций.
Рис. 4.6. Определение угла наклона и натуральной величины отрезка
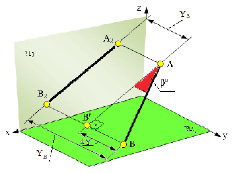
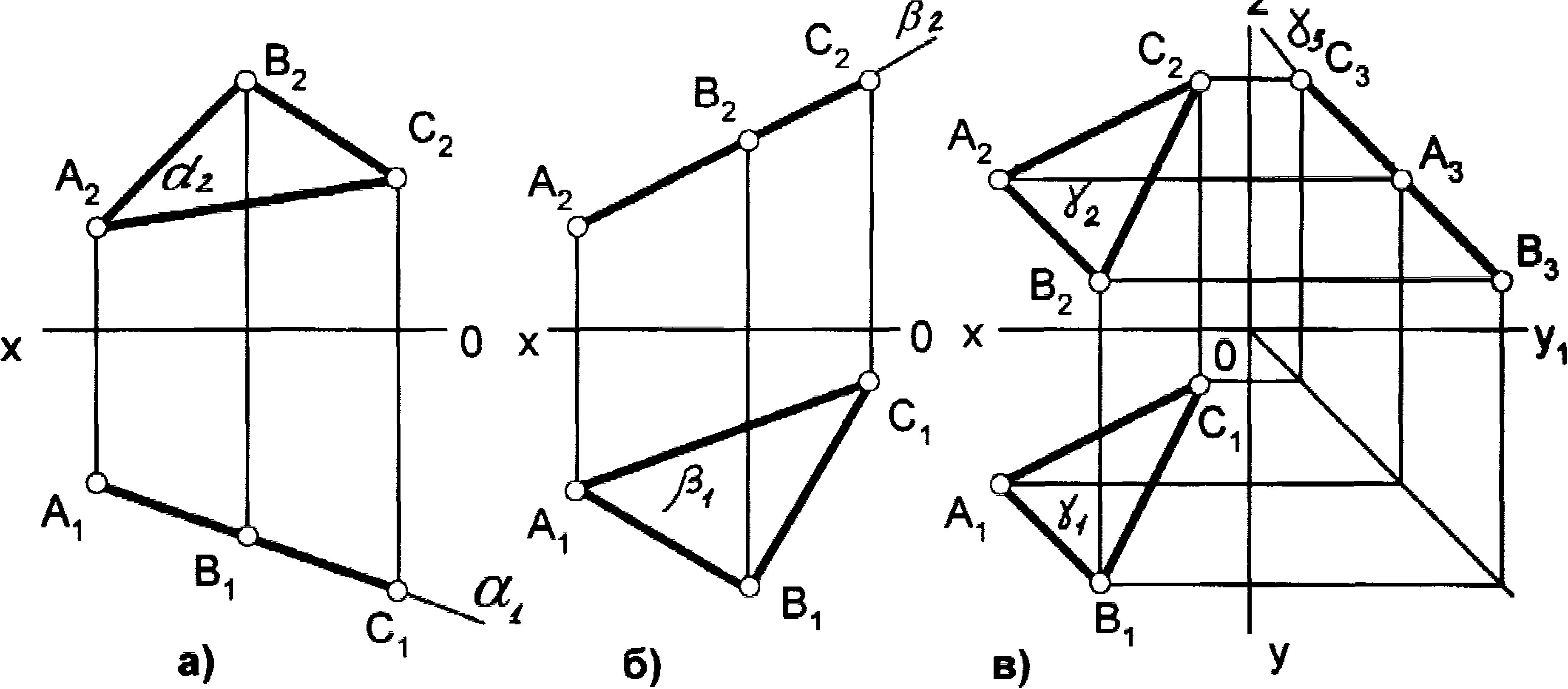
Учитывая сказанное выше и рассмотрев рис. 4.7, можно утверждать, что длина отрезка АВ равна гипотенузе треугольника, катетами которого являются фронтальная проекция отрезка А2В2 и разность координат Y точек А и В (ΔY = YB – YA). Угол этого треугольника, лежащий против катета ΔY, равен углу наклона отрезка АВ к фронтальной плоскости проекций π2 (угол β°).
По аналогии длина отрезка АВ может быть определена и как гипотенуза треугольника, катеты которого профильная проекция отрезка А3В3 и разность координат Х (Δ Х = ХА – ХВ) точек А и В. Угол γ° этого треугольника, лежащий против катета Δ Х, определяет угол наклона отрезка АВ к профильной плоскости проекций π3.
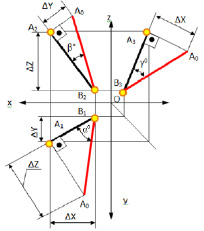
На рис. 4.8 показан пример определения натуральной (действительной) длины прямой АВ и углов её наклона к плоскостям проекций.
Рис. 4.7. Определение угла наклона и натуральной величины отрезка
Рис. 4.8. Определение длины отрезка и углов наклона к плоскостям проекций на комплексном чертеже
Угол αº, получен при построении прямоугольного треугольника на горизонтальной проекции прямой. Углы β и γ определены с использованием фронтальной и профильной проекций прямой соответственно. Натуральная величина, указанной прямой, обозначена гипотенузами прямоугольных треугольников, построенных на трёх плоскостях проекций.
Если отрезок
прямой занимает общее положение, то
определить истинную величину прямой
на плоскостях проекций нельзя. Поэтому
для определения длины отрезка по его
проекциям используют способ прямоугольного
треугольника: длина отрезка измеряется
гипотенузой прямоугольного треугольника,
одним катетом которого является проекция
отрезка на плоскость, а другим – разность
расстояний концов его до этой плоскости.
Рассмотрим прямую общего положения в
пространстве.
Рис. 9
Треугольник АВВ1–прямоугольный.
Гипотенуза АВ является натуральной
длиной отрезка (рис.
9, а), а проекция А1В1– катетом. Второй катет ВВ1определяет превышение одного конца
отрезка над другим относительно
плоскости проекций П1и проецируется
без искажения на фронтальную плоскость
проекций П2. Угол= ВАВ1– это угол наклона прямой
АВ к горизонтальной плоскости проекций.
Построения см. на
рис. 9, б.
Из точки В1
проведём перпендикуляр к проекции
А1В1, отложим на нём отрезок
В1Во= ВхВ2и
соединим прямой точки А1и Во.
Построенный треугольник А1ВоВ1=
АВВ1(рис.
9, а), так как равны их катеты и
угол между ними составляет 90°.
Следовательно, отрезок А1Во
равен отрезку АВ и угол В1А1Воопределяет угол наклона отрезка АВ к
горизонтальной плоскости проекций.
Аналогичное
построение можно сделать на фронтальной
плоскости проекций, только в качестве
второго катета нужно будет взять
разность глубин его концов В1Вх(рис. 9, в).
Определение длины
отрезка с использованием способа замены
плоскостей проекций будем рассматривать
в вузе.
Вопросы для самопроверки
1. Какое положение
может занимать прямая относительно
плоскостей проекций ?
2. Прямая общего
положения (начертить комплексный
чертёж).
3. В каком случае
прямая обращается в точку и как называются
такие прямые ? Привести пример.
4. Какие точки
называются конкурирующими ?
5. Сформулировать
признак принадлежности точки, прямой
(см.
выше).
6. Сформулировать
правило прямоугольного треугольника.
4. Плоскость
Плоскость может
быть задана аналитически (уравнением)
или графически (проекциями). Для
графического задания плоскости достаточно
построить проекции определяющих её
элементов
(рис.
10):
1) трёх точек, не
лежащих на одной прямой;
2) прямой и точки,
не лежащей на этой прямой;
3) двух пересекающихся
прямых;
4) двух параллельных
прямых;
5) любой плоской
фигурой.
Рис. 10
В зависимости от
положения плоскости относительно
плоскостей проекций различают плоскости
общего и частного положения.
Плоскость, не
перпендикулярную ни одной из основных
плоскостей проекций называют плоскостью
общего положения
(рис.
10.5).
Плоскости частного
положения можно разделить на две группы:
проецирующие и
плоскости уровня.
4.1. Проецирующие плоскости
Проецирующие
плоскости– это плоскости,
перпендикулярные к одной из плоскостей
проекций (рис.
11). К ним относятся:
1) горизонтально-проецирующая
П1;
2) фронтально-проецирующая
П2;
3) профильно-проецирующая
П3.
Рис. 11
Отличительной
особенностью проецирующих плоскостей
является то, что все геометрические
образы, принадлежащие проецирующей
плоскости, проецируются на перпендикулярную
к ней плоскость в одну прямую, совпадая
с главной проекцией (следом):
горизонтально-проецирующая
плоскость А1В1С1(рис.
11, а),
фронтально-проецирующая
плоскость А2В2С2(рис.
11, б),
профильно-проецирующая
плоскость А3В3С3(рис.
11, в).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Ответкин
- Решебники
- 10 класс
- Геометрия
- Погорелов
- Задача №38, Параграф 3
ГДЗ (готовое домашние задание из решебника) на Задача №38, § 3 по учебнику Геометрия. 10-11 классы. Учебник для общеобразовательных учреждений / А. В. Погорелов — 13-е издание. Просвещение, 2014-2017г.
Условие
Отрезок длины 1 м пересекает плоскость, концы его удалены от плоскости на 0,5 м и на 0,3 м.
Найдите длину проекции отрезка на плоскость.
Решение 1
Популярные решебники
Ваше сообщение отправлено
и скоро будет рассмотрено
ось u, если даны его длина d и угол j наклона к оси:
/3;
/3;
/2;
;
/3.
чертеже отрезки, исходящие из начала координат,
зная их проекции на координатные оси:
чертеже отрезки, имеющие началом точку M(2; -1), зная
их проекции на координатные оси:
4), М5(0; -3). Найти проекции на координатные оси
следующих отрезков:
отрезка
что его начало в точке М1(-2; 3), найти координаты его конца.
отрезка
что его конец в точке B(1; -3), найти координаты его
начала.
чертеже отрезки, исходящие оиз начала координат,
зная длину d и полярный угол q каждого из них:
/6;
/3;
/3.
чертеже отрезки, имеющие началом точку М(2; 3), зная
длину и полярный угол каждого из них (координаты
точки М декартовы):
/9;
/2ж
на координатные оси отрезков, зная длину d и
полярный угол q каждого из них:
/6;
/4.
отрезков на координатные оси. Вычислить длину
каждого из них.
отрезков на координатные оси. Вычислить длину d и
полярный угол q каждого из них.
Y=
Y=2.
8). Вычислить длину и полярный
угол слдующих отрезков:
равна 5, его проекция на ось абсцисс равна 4. Найти
проекцию этого отрезка на ось ординат при
условии, что он образует с осью ординат:
проекция на ось абсцисс равна –12. Найти
координаты конца этого отрезка при условии, что
он образует с осью ординат:
проекция на ось ординат равна 15. Найти координаты
начала этого отрезка при условии, что он образует
с осью абсцисс:
его проекцию на ось, которая составляет с осью Ox
угол q =2p /3.
проекцию отрезка
с осью Ox угол q =-p
/6.
Q(3; 1). Найти проекцию отрезка
ось, которая составляет с осью Ox угол
проекцию отрезка
точки A(5; -4), B(-7; 1) и направленную:
-4), C(-3; 4), D(-2; 2), E(10; -3). Определить расстояние d между
точками:
вершины квадрата A(3; -7) и В(-1; 4). Вычислить его
площадь.
противоположные вершины квадрата P(3; 5), Q(1; -3).
Вычислить его площадь.
правильного треугольника, две вершины которого
суть A(-3; 2), B(1; 6).
-7), В(5; -7), С(-2; 5) параллелограмма ABCD, четвертая
вершина которого D противоположна B. Определить
длины диагоналей того параллелограмма.
суть точки P(4; 9), Q(-2; 1). Вычислить площадь этого
ромба.
суть точки P(3; -4), Q(1; 2). Вычислить длину высоты
этого ромба.
А(3; -5), В(-2; -7), С(18; 1) лежат на одной прямой.
треугольник с вершинами A1(1; 1), A2(2;
3), A3(5; -1) прямоугольный.
А(2; 2), В(-1; 6), С(-5; 3), D(-2; -1) являются вершинами
квадрата.
среди внутренних углов треугольника с вершинами
M1(1; 1), M2(0; 2), M3(2; -1) тупой угол.
внутренние углы треугольника с вершинами M(-1; 3),
N(1; 2), P(0, 4) острые.
треугольника суть точки A(5; 0), B(0; 1), C(3; 3). Вычислить
его внутренние углы.
треугольника суть точки А(
его внешний угол при вершине А.
найти такую точку М, расстояние от которой до
точки N(2; -3) равнялось бы 5.
найти такую точку М, расстояние от которой до
точки N(-8; 13 равнялось бы 17.
N(5; -2); на оси абсцисс найти такую точку Р, чтобы
угол MPN был прямым.
проведена окружность, касающаяся обеих
координатных осей. Определить ее центр С и радиус
R.
окружность радиуса 5, касающаяся оси Ox.
Определить центр С окружности.
координаты точки М2, симметричной точке М1(1; 2) относительно прямой, проходящей
через точки А(1; 0), В(-1; -2).
противоположные вершины квадрата А(3; 0) и С(-4; 1).
Найти две его другие вершины.
веришны квадрата А(2; -1) и В(-1; 3). Определить две его
другие вершины.
треугольника M1(-3; 6), M2(9;
-10), M3(-5; 4). Определить центр
С и радиус R круга, описанного около этого
треугольника.