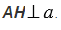Как найти длину перпендикуляра зная наклонную

Как найти длину перпендикуляра

Даны точка и прямая представленная уравнением (1) § 161. Требуется найти расстояние от точки до прямой т. е. длину перпендикуляра (см. рис. 175), опущенного из точки на прямую .

Можно сначала найти основание К перпендикуляра (§ 161, пример), затем длину отрезка Проще применить формулу (при обозначениях § 161)

т. е. в векторной форме

Числитель выражения (1а) есть площадь параллелограмма (§ 111) , а знаменатель — длина основания Следовательно, дробь равна высоте параллелограмма.

Расстояние от точки до прямой

Что называется расстоянием от точки до прямой? Как найти расстояние от точки до прямой?

Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из данной точки на прямую.

Таким образом, чтобы найти расстояние от точки до прямой, надо из точки к прямой провести перпендикуляр и найти его длину.

Например, на рисунке 1 расстояние от точки A до прямой a равно длине перпендикуляра AB, опущенного из точки A на прямую a.

Задачи на нахождение расстояния от точки до прямой сводятся к рассмотрению прямоугольного треугольника.

№ 1. Из точки к прямой проведены две наклонные, длины которых относятся как 2:3, а длины их проекций соответственно равны 2 см и 7 см. Найти расстояние от точки до прямой.

Дано: A∉a,

BC и BD — их проекции, BC=2 см, BD=7 см

1) Пусть k — коэффициент пропорциональности. Тогда AC=2k см, AD=3k см.

2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора

3) Аналогично, из треугольника ABD

4) Приравниваем правые части полученных равенств и находим k:

5) Зная k, найдем AB:

№ 2. Из точки к прямой проведены две наклонные, длины которых равны 13 см и 15 см. Найти расстояние от точки до прямой, если разность проекций наклонных равна 4 см.

Дано: A∉a,

AC и AD — наклонные, AC=13 см, AD=15 см,

BC и BD — их проекции, BD-BC=4 см

1) Пусть BC=x см, тогда BD=x+4 см.

2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора

3) Аналогично, из треугольника ABD

4) Приравниваем правые части полученных равенств и находим x:

5) Зная x, найдем AB:

№ 3. Найти расстояние от точки A до прямой a, если известно, что наклонная AF, длина которой равна c, образует с прямой a угол α.

Дано: A∉a,

Треугольник ABF — прямоугольный (так как AB — перпендикуляр к прямой a по условию). AB — катет, противолежащий углу ACB, AF — гипотенуза.

Основные сведения о перпендикуляре к прямой — что это такое, как находить

Каким будет определение положения прямой и плоскости, зависит от наличия общих точек. Если их больше одной, то прямая лежит на данной плоскости, если одна — то она ее пересекает. Если прямая не имеет с плоскостью точек пересечения, то прямая и плоскость параллельны.

Пересечение прямой линии и плоскости может происходить под разными углами. Если при пересечении между прямой и плоскостью образуется прямой угол, то такая прямая является к плоскости перпендикуляром. При этом она перпендикулярна всем прямым линиям, принадлежащим данной плоскости. Из этого свойства вытекает следующее определение.

Перпендикулярной к плоскости называется прямая линия, которая перпендикулярна всем без исключения прямым, лежащим в выбранной плоскости.

Следствием из данного определения является свойство плоскости, для которой установлено наличие перпендикуляра. Оно формулируется следующим образом: «Если плоскость перпендикулярна некоторой прямой, то она является также перпендикулярной для всех прямых, параллельных данной прямой».

В решении задач на построение перпендикуляров к плоскости в конкретной точке существует только одно решение, поскольку через определенную точку можно провести только одну прямую, занимающую по отношению к плоскости перпендикулярное положение.

О единственности такой прямой в геометрии существует доказательство.

Проведение перпендикуляра из точки к прямой

В жизни с перпендикуляром можно столкнуться часто. Например, если по двум параллельным направляющим движутся тела, то кратчайшее расстояние между ними будет лежать именно по перпендикуляру.

Допустим, на уроке ученикам дали задание построить перпендикуляр к имеющейся площади. Особым условием является то, что проходить этот перпендикуляр должен через выбранную точку. Технически задача проста. Для ее исполнения нужен чертежный треугольник, один угол у которого является прямым, то есть составляет 90°.

Приложив его к прямой таким образом, что одна из сторон, образующих прямой угол, лежит на прямой, а другая — проходит через точку с определенными координатами, необходимо соединить эту точку и прямую.

Такой отрезок будет кратчайшим соединением точки с прямой линией (и выбранной плоскостью).

Взаимное положение такого перпендикуляра и прямой обозначается специальным знаком.

Для перпендикуляра, проведенного из выбранной точки к прямой, можно определить длину. Она равна расстоянию от этой точки до точки пересечения с прямой плоскостью.

Как построить перпендикуляр к прямой

Построить перпендикуляр к прямой можно несколькими способами:

1. С помощью циркуля.

Из выбранной точки P проводим полуокружность, которая пересекается с прямой в точках A и B.

Затем тем же радиусом строим две окружности, центры которых совпадают с точками A и B. При этом окружности проходят через точку P.

Следующим шагом будет соединение точек P и Q.

На данном рисунке перпендикуляр к прямой AB — отрезок PQ.

2. Вторым способом построения перпендикуляра является использование транспортира. Чтобы провести перпендикуляр, внимательно откладываем 90° от выбранной точки на прямой, используя при этом линейку транспортира. Отрезок, соединяющий эту точку и деление 90°, является перпендикуляром к прямой в заданной точке.

3. Третий способ был описан выше. Он основан на применении чертежного треугольника и линейки. С помощью линейки проводим прямую. Прикладываем к ней прямым углом треугольник и очерчиваем этот угол с двух сторон. Один отрезок совпадает с имеющейся прямой, а второй является перпендикуляром к ней.

Пояснение на примерах

В конспектах по геометрии присутствует понятие высоты, представляющей собой перпендикуляр к одной из сторон геометрической фигуры (например, треугольника).

Высотой треугольника называется перпендикуляр, который выходит из вершины треугольника и следует к противоположной стороне (либо к продолжению этой стороны, если треугольник тупоугольный).

В данном определении содержится отличие от основной характеристики биссектрисы, которая, опускаясь на противолежащую углу сторону, не является перпендикуляром к ней.

Аналогичная ситуация с определением медианы — линии, исходящей из угла треугольника и делящей противоположную сторону на две равные части.

Высоту треугольника можно провести из любого его угла, поэтому у каждого треугольника имеется три высоты.

Существует теорема, что все три высоты треугольника пересекаются в одной точке, которая называется ортоцентром.

Используя свойство высоты треугольника о пересечении одной из его сторон под прямым углом, можно через высоту выразить формулу площади треугольника:

Уравнение для расчета высоты через площадь:

Найти через длины сторон:

h a = 2 p p — a p — b p — c a

где p — это полупериметр треугольника, который рассчитывается так:

p = a + b + c 2
Можно дать краткую характеристику еще двум способам выразить высоту треугольника: