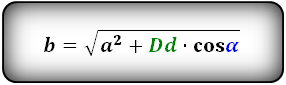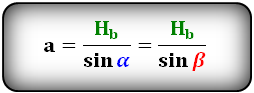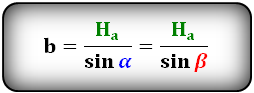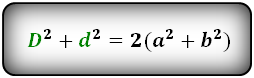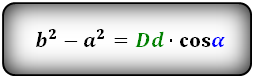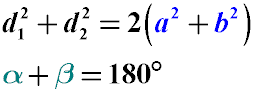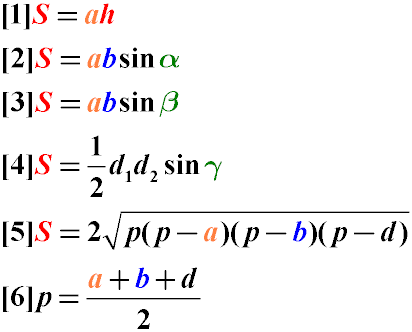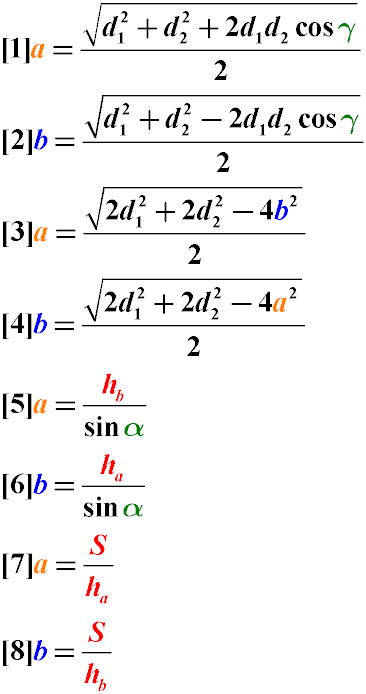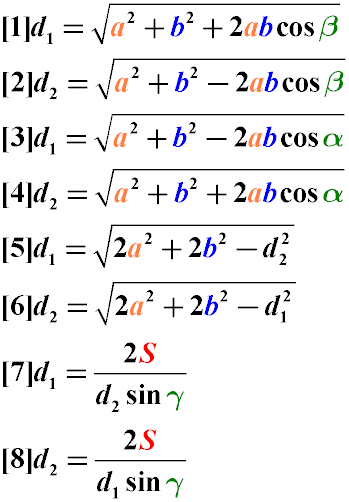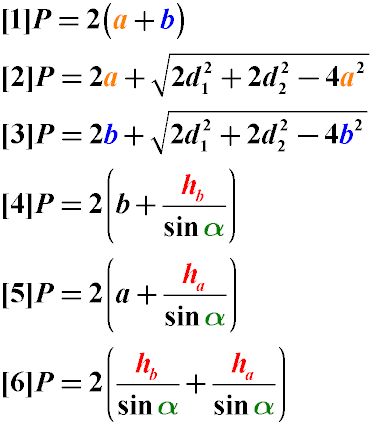Как найти длину параллелограмма если известна высота - AvtoShod.ru

Онлайн калькулятор длины сторон параллелограмма напишет подробное решение с ответом и пояснениями.
Калькулятор может:

Сторона параллелограмма через площадь и высоту.
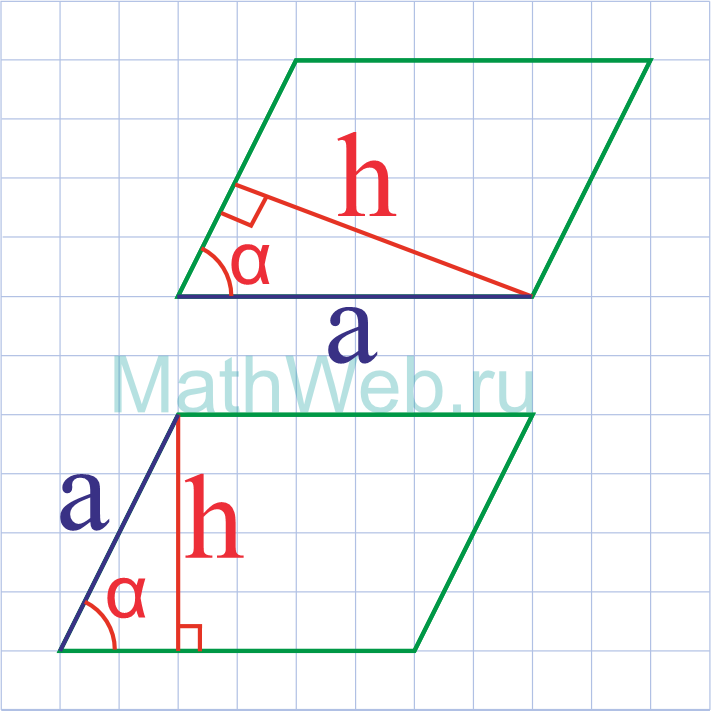
Сторона параллелограмма через высоту и угол.

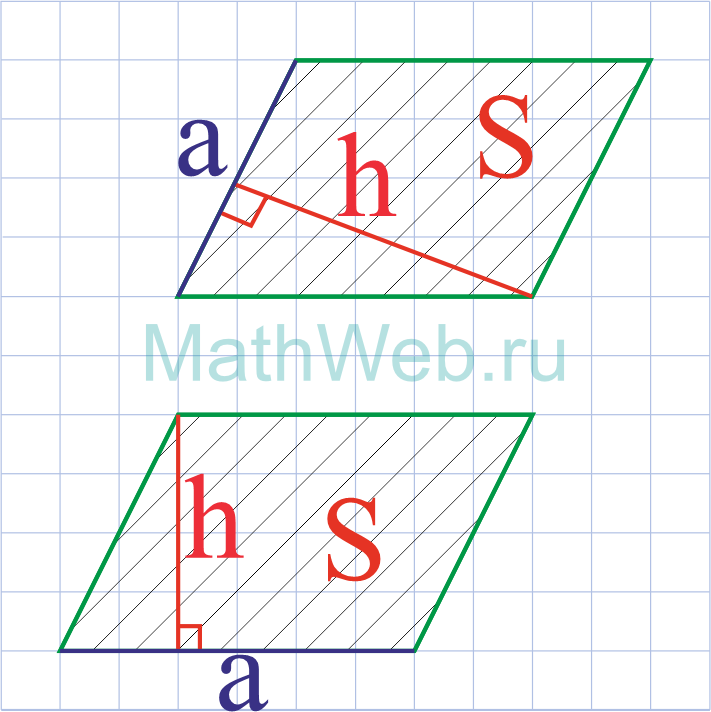
Где S — площадь параллелограмма,h — его высота.

Где h — его высота,α — острый угол.

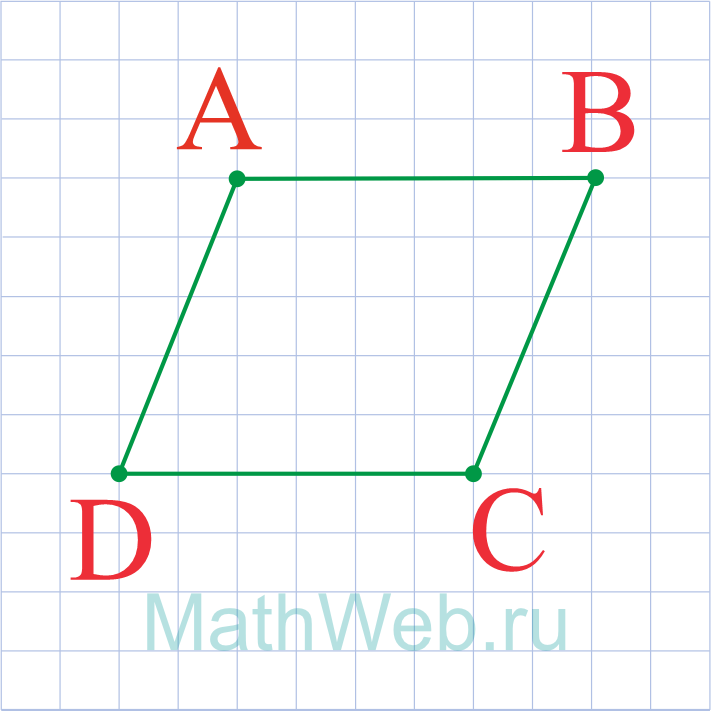
Параллелограмм- это четырехугольник у которого противоположные стороны параллельны.
Противоположные стороны параллелограмма равны.
Диагональные углы параллелограмма равны.

Как найти длину стороны параллелограмма ?

Сторона параллелограмма может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.

	a =
	a =

Источник

Как найти длину одной из сторон параллелограмма?

Чтобы найти сторону параллелограмма, необходимо наличие некоторых других значений, которые бы были известны. Далее попросту использовать одну из подходящих формул.

Например, по теореме косинусов, это формулы сторон через диагонали и находящийся между ними угол:

Другим решением, являются формулы, где стороны рассчитываются по диагонали и одной из известной стороны:

Вот еще формулы сторон параллелепипеда, через вторую сторону, диагонали и косинус угла:

Стоит напомнить и про формулы длин сторон, через высоту и синус угла:

Так же длину стороны параллелограмма, можно определить если известны площадь и высота:

Как видим, вариантов расчета высоты параллелограмма достаточно много и хотелось напомнить основные характеристики этой геометрической фигуры:

Во первых, параллелограммом называется четырехугольник, имеющий параллельно расположенные противоположные стороны , т. е. находящиеся на параллельных прямых. Квадраты, прямоугольники и ромбы, также являются параллелограммами.

система выбрала этот ответ лучшим

Для нахождения стороны параллелограмма есть более десятка разных формул (они перечислены в ответе автора Бульбозавр), но для решения задач на эту тему, далеко не всегда их можно применить.

На мой взгляд лучше всего разобрать несколько примеров и на практике увидеть, как находить сторону этой фигуры — в наших случаях с помощью уравнений.

Пример 1

Нужно найти стороны параллелограмма, если одна из сторон больше другой в два раза а периметр равен 30 см.

Даже не нужно чертить рисунок, а просто составить уравнение и решить его

периметр(30см) = 2(х+2х) откуда х=5см, следовательно одна сторона равна 5см, другая — 10см.

Пример 2

АВСД — параллелограмм, нужно найти его стороны если — ВМ перпендикуляр к АС, АМ=6см, МС=15см, ВС больше АВ на 6 см

Для решения этой задачи сначала рассматриваем два прямоугольных треугольника АВМ и ВСМ у которых общий катет h.

Согласно Пифагору

h*h=a*a-6*6=b*b-15*15 откуда b*b-a*a=(b-a)(b+a)=225-36=189

по условию задачи b-a=7 тогда b+a=189/7=27

решив эту простенькую систему уравнений найдем стороны a=10см b=17cм

Alexsandr82
[21.4K]

6 лет назад

Есть еще несколько формул которые будут скорее вспомогательными при решении задач по нахождению стороны паралелограмма но тем не менее их тоже нужно знать. Например одну из сторон паралеллограмма можно найти если известна вторая сторона и периметр фигуры по формуле:

Р = 2(а+b), тогда а = (Р/2 — b), или b = (P/2 — a), где Р — периметр, а и b — стороны.

Также можно найти сторону паралеллограмма зная его площадь и высоту опущенную на искомую сторону:

S = a*H1 = b*H2, тогда а = S/H1 или b = S/H2, где S — площадь, а — меньшая сторона паралелограмма, b — большая сторона, Н1 — высота построенная к меньшей стороне, Н2 — сторна построенная к большей стороне паралеллограмма.

Vector 60
[121]

8 месяцев назад

Существует несколько формул для вычисления сторон параллелограмма (a и b).

1) Для нахождения сторон параллелограмма можно воспользоваться длиной диагоналей, а также величиной углов между диагоналями. Формулы будут такими:

2) Если известна одна из сторон и диагонали, то другую сторону можно найти так:

3) Если известна высота и величина одного из углов, то стороны параллелограмма можно найти по таким формулам:

4) Еще можно использовать значение площади и высоты:

Stasy12
[41.5K]

более года назад

Формул, конечно много, с помощью которых можно найти сторону параллелограмма.

Например можно найти стороны паралелограмма, зная размеры диагоналей и угла между ними(формула 1и 2)

Зная длины диагоналей и одну из сторон, легко можно найти вторую(формулы 3 и 4)

Через высоту, которая опущена на сторону и угол между сторонами(формулы 5 и 6)

Зная площадь и высоту, которая опущена на

заданную сторону можно найти длину стороны(формулы 7 и 8).

Знаете ответ?

Источник

Свойства параллелограмма:

1. Противоположные стороны равны и параллельны

2. Противоположные углы равны

3. Точка пересечения диагоналей, делит их пополам

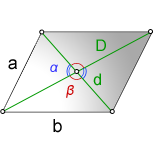
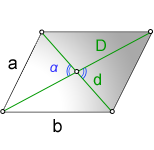
1. Формулы длины сторон через диагонали и угол между ними.

a, b — стороны параллелограмма

D — большая диагональ

d — меньшая диагональ

α, β — углы между диагоналями

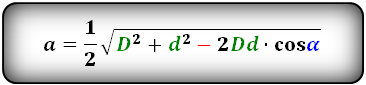
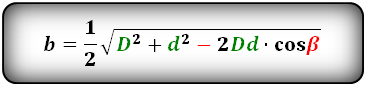
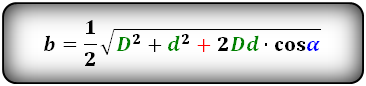
Формулы сторон параллелограмма через диагонали и угол между ними (по теореме косинусов), (a, b):

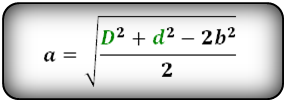
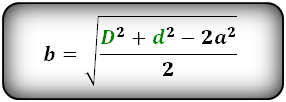
Формулы сторон параллелограмма через диагонали и сторону, (a, b):

Формулы сторон параллелограмма , (a, b):

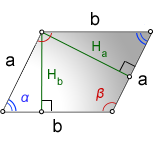
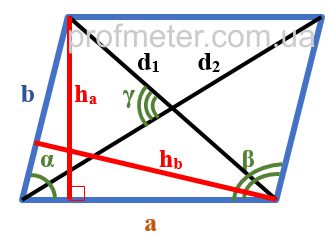
2. Формулы длины сторон параллелограмма через высоту.

a, b — стороны параллелограмма

H_b — высота на сторону b

Ha — высота на сторону a

α, β — углы параллелограмма

Формулы сторон параллелограмма через высоту, (a, b):

3. Дополнительные, интересные формулы параллелограмма:

a, b — стороны параллелограмма

D — большая диагональ

d — меньшая диагональ

α — острый угол между диагоналями

Формула суммы квадратов диагоналей:

Формула разности квадратов сторон:

Формулы площади параллелограмма

Формула периметра параллелограмма

Все формулы по геометрии

Подробности

Опубликовано: 31 октября 2011

Обновлено: 13 августа 2021

Источник

В параллелограмме противоположные стороны друг другу параллельны, а прилежащие находятся образуют определенный угол, поэтому чтобы определить большинство параметров параллелограмма нужно знать кроме сторон высоту или угол, их соединяющий. Если заданы стороны и высота, то одними из первых можно рассчитать периметр и площадь параллелограмма. Периметр параллелограмма, зная стороны, выглядит как их удвоенная сумма, а площадь является произведением высоты и стороны, на которую она опущена.
P=2(a+b)
S=ah_a=bh_b

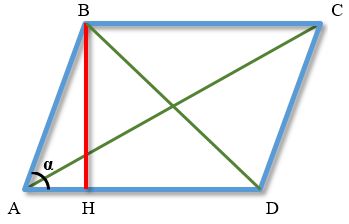
Чтобы иметь возможность продолжать расчеты, необходимо найти углы между сторонами α и β. Используя прямоугольный треугольник, образованный высотой со стороной параллелограмма, выводим их взаимосвязь в тригонометрическое отношение. Затем, зная один из углов, в зависимости от того, какая высота была дана, отнимаем его из 180 градусов, чтобы найти второй. (рис.106.1)
sin⁡α=h_b/a
sin⁡β=h_a/b
α=180°-β
β=180°-α

Зная углы и стороны, можно найти диагонали параллелограмма по теореме косинусов в треугольниках, которые они образуют со сторонами. Каждая диагональ будет равна корню из суммы квадратов сторон параллелограмма и разности удвоенного их произведения на косинус угла между ними. (рис.106.2)
d_1=√(a^2+b^2-2ab cos⁡β )
d_2=√(a^2+b^2-2ab cos⁡α )

Используя эту же теорему косинусов, можно найти угол между диагоналями в одном из четырех треугольников, образованных ими, где сторонами являются половины диагоналей и одна из сторон параллелограмма. (рис.106.3)
cos⁡γ=(〖d_1/4〗^2+〖d_2/4〗^2-a^2)/((d_1 d_2)/4)=(〖d_1〗^2+〖d_2〗^2-4a^2)/(2d_1 d_2 )
cos⁡δ=(〖d_1〗^2+〖d_2〗^2-4b^2)/(2d_1 d_2 )

Биссектрисы параллелограмма, проведенные из углов α и β, образуют равнобедренные треугольники, в которых сама биссектриса является основанием, а боковыми конгруэнтными сторонами становится меньшая сторона параллелограмма. Треугольник считается равнобедренным, так как из свойств биссектрисы и суммы углов в треугольнике следует, что углы при основании такого треугольника конгруэнтны. Используя теорему косинусов, можно найти биссектрисы параллелограмма через стороны. (рис. 106.4)
l_α=√(2a^2-2a^2 cos⁡β )=a√(2-2 cos⁡β )
l_β= b√(2-2 cos⁡α )

Источник

Учебный курс

Решаем задачи по геометрии

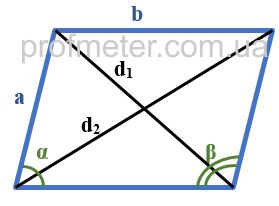
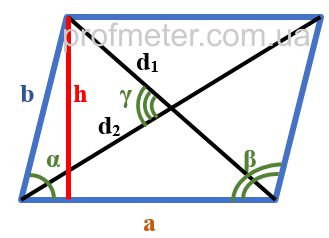
Параллелограмм — четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых.

Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Как выглядит параллелограмм

На приведенном рисунке параллелограмм обозначен синими линиями.

Элементы параллелограмма, указанные на рисунке:
ABCD — параллелограмм, у которого противолежащие стороны попарно параллельны ( AB параллельна CD, а BC параллельна AD)
BH — высота параллелограмма, опущенная из точки B на основание AD (на рисунке обозначена красным цветом)
AC и BD — диагонали параллелограмма.

Свойства параллелограмма

Противоположные стороны параллелограмма равны
Противоположные углы параллелограмма равны
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. Точка пересечения диагоналей называется центром симметрии параллелограмма
Диагональ делит параллелограмм на два равных треугольника
Сумма углов, прилежащих к одной стороне, равна 180°. (см. формулу ниже)
Сумма всех углов равна 360°
Средние линии параллелограмма пересекаются в точке пересечения его диагоналей и делятся этой точкой пополам
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон (см. формулу ниже)

Признаки параллелограмма

Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий:

Противоположные стороны попарно равны
Противоположные стороны попарно параллельны и равны
Противоположные углы попарно равны
Диагонали делятся в точке их пересечения пополам
Сумма соседних углов равна 180 градусов
Две стороны равны и параллельны

Как найти площадь параллелограмма

Формулы нахождения площади параллелограмма приведены ниже:

То есть:

Площадь параллелограмма равна произведению длины одной из его сторон на высоту, опущенную на эту сторону
Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними. Как видно из чертежа, произведение b sin α равно высоте, опущенной на другую сторону, что в итоге дает нам предыдущую формулу
Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними
Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними
Площадь параллелограмма также можно найти через формулу Герона, рассмотрев одну из диагоналей как треугольник и вычислив удвоенную площадь этого треугольника
Для нахождения полупериметра треугольника из предыдущей формулы мы используем две стороны параллелограмма и его диагональ. Поскольку каждая диагональ разбивает его на два равных треугольника, то не имеет значения, какую из диагоналей мы выберем

Как найти стороны параллелограмма

Стороны параллелограмма можно найти через:

Размеры диагоналей и угол между ними (формулы 1 и 2)
Через длины диагоналей и одну из сторон можно найти вторую (формулы 3 и 4)
Через высоту, опущенную на сторону и угол между сторонами (формулы 5 и 6)
Через площадь и высоту, опущенную на заданную сторону, можно найти величину этой стороны (Формулы 7 и

Как найти диагонали параллелограмма

Диагональ параллелограмма можно найти через длины его сторон и косинус угла между ними (Формулы 1-4)
Также диагональ может быть найдена через длины сторон и размер второй диагонали (Формулы 5-6)
Диагональ может быть найдена из площади, длины второй диагоналями и угла между ними (Формулы 7-8)

Как найти периметр параллелограмма

Периметр параллелограмма может быть найден:

через его стороны (Формула 1)
через одну из сторон и длину двух диагоналей (Формулы 2 и 3)
через сторону, высоту и угол между сторонами (Формулы 4-6)

Задачи с решениями про параллелограмм смотрите в уроках ниже:

Трапеция, описанная вокруг окружности |

Описание курса

| Параллелограмм. Задачи про площадь и стороны

Обсудить на форуме
Записаться на курсы
Обратиться к консультанту
Пройти тест
Полный список курсов обучения
Бесплатные видеоуроки
Нужна информация!

Источник

Как найти длину стороны параллелограмма ?

Как выглядит параллелограмм

Свойства параллелограмма

Признаки параллелограмма

Как найти площадь параллелограмма

Как найти стороны параллелограмма

Как найти диагонали параллелограмма

Как найти периметр параллелограмма

Не пропустите также: