1
Optorius
[13.8K]
7 месяцев назад
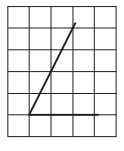
Имеются 2 точки A и B на клетчатой бумаге 1×1, необходимо найти расстояние между ними.
Для этого представим, что отрезок AB это гипотенуза, а катеты пересекаются в левом нижнем углу. Длину катетов можно посчитать по количеству клеток и рассчитать гипотенузу.
AB = кв.корень(8^2 + 6^2) = 10.
Ответ: 10.
автор вопроса выбрал этот ответ лучшим
комментировать
в избранное
ссылка
отблагодарить
Задания
Версия для печати и копирования в MS Word
Тип 12 № 4142
i
На клетчатой бумаге с размером клетки 1 × 1 отмечены точки A и B. Найдите длину отрезка AB.
Спрятать решение
Решение.
Найдём длину отрезка AB по теореме Пифагора:
Ответ: 10.
Источники:
ВПР по математике 8 класса 2021 года. Вариант 2;
ВПР по математике 8 класса 2022 года. Вариант 10.
Спрятать решение
·
Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
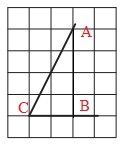
Задача № 1
На клетчатой бумаге с размером клетки 1×1 отмечены точки A и B. (Рис. 1). Найдите длину отрезка AB.
Решение
Расстояние между точками A и B удобно найти из прямоугольного треугольника (Рис. 2).
По теореме Пифагора это расстояние равно длине гипотенузы треугольника ABC, катеты которого равны 15 и 8.
Искомая длина AB равна 17.
Ответ: 17.
Задача № 2
На клетчатой бумаге с размером клетки 1×1 см изображён угол (Рис. 3). Найдите его градусную величину.
Решение
Сделаем дополнительные построения (Рис. 4).
Теперь мы видим, что изображённый на рисунке угол равен сумме прямого угла и угла 45°, поэтому он равен 135°.
Ответ: 135.
Задача № 3
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC (Рис. 4). Найдите длину его средней линии, параллельной стороне AС.
Решение
Необходимо вспомнить свойство о средней линии треугольника, которое гласит: «Средняя линия треугольника равна половине той стороны, которой она параллельна».
Длина стороны АС равна 4 (Рис. 4), поэтому искомая длина средней линии равна 2.
Ответ: 2.
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
В 18 задании необходимо найти какую-либо часть фигуры, нарисованной на клетчатой бумаге. Именно клетчатая бумага 1×1 является особенностью данного задания. Задание не сложное, необходимо внимательно посчитать количество клеток и при необходимости выполнить действие. Опять же нам понадобятся элементарные знания геометрии для успешного решения данного задания. Ниже я разобрал типичные задания.
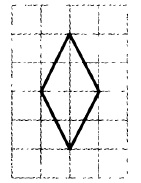
На клетчатой бумаге размером 1×1 изображён ромб. Найдите длину его большей диагонали.
Внимательно смотрим на рисунок и видим, что длина одной диагонали ромба равна 2, а второй 4. Так как нас спрашивают длину большей диагонали, то в ответе нужно указать 4.
Ответ: 4
pазбирался: Даниил Романович | обсудить разбор | оценить
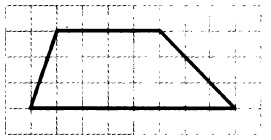
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии.
Мы знаем, что средняя линия равна полусумме оснований. Нижнее основание данной трапеции равно 8 клеткам, а верхнее – 4 клеткам. Полусумма оснований:
( 8 + 4 ) / 2 = 6
Ответ: 6
pазбирался: Даниил Романович | обсудить разбор | оценить
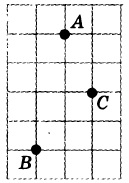
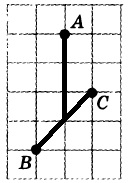
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Проведем необходимые отрезки:
Из рисунка можно вычислить длину – это 3.
Ответ: 3
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите тангенс острого угла, изображённого на рисунке.
Детализируем рисунок. Проведем вертикальную линию, которая отсекает от сторон угла 2 клетки по горизонтали . В результате получен прямоугольный ∆АВС:
Чтобы получить ответ на вопрос задачи, требуется найти tg∠C.
Согласно определению тангенса, из треугольника ∆АВС можем записать:
tg∠C=AB/BC.
По рисунку подсчитываем длины отрезков АВ и ВС (по кол-ву клеток):
АВ=4, ВС=2.
Получаем:
tg∠C=4/2=2.
Ответ: 2
pазбирался: Даниил Романович | обсудить разбор | оценить
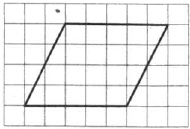
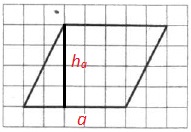
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Площадь параллелограмма вычисляется так:
S=a·ha
Обозначим a и ha на рисунке:
Теперь определим их длины по рисунку:
a=5; ha=4.
Вычисляем искомую площадь:
S=5·4=20.
Ответ: 20
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найдите площадь этого ромба.
Площадь ромба будем искать через его диагонали:
S=d1·d2/2
Линии диагоналей обозначим на рисунке красным:
Обозначим меньшую диагональ через d1, большую – через d2 (можно наоборот). Определим их длины из рисунка:
d1=8; d2=10.
Находим площадь фигуры:
S=8·10/2=40
Ответ: 40
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.
Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.
Ответ: 4
pазбирался: Даниил Романович | обсудить разбор | оценить
- ОГЭ по математике
Вебинар на тему: «Задания по геометрии в ОГЭ-2021 по математике»
Ведущая: Фридман Елена Михайловна
→ презентация к вебинару
Рассмотрены задания из ОГЭ по геометрии:
— Планиметрия. Часть 1 (задания 15 – 18);
— Задание 25 из части 2.
| № | Понятия и свойства |
| 15 | Треугольник. Медиана, высота, биссектриса, средняя линия, сумма углов, внешний угол, соотношения между сторонами и углами. Теорема косинусов. Четырехугольник. Параллелограмм (ромб, прямоугольник, квадрат), трапеция, их свойства. Признаки параллельности прямых. |
| 16 | Вписанные и описанные треугольники и четырехугольники. Касательные, хорды, углы, секущая, угол, образованный касательной и хордой, вписанный угол. Теорема синусов. |
| 17 | Площадь треугольника, четырехугольника, решение треугольника. |
| 18 | Задачи на клетчатой бумаге, площадь фигуры, центральный и вписанный углы, градусная мера дуги окружности |
| 19 | Выбор верного утверждения |
Примеры задач 25:
Связанные страницы:
Решение заданий Варианта №18 из сборника ОГЭ 2022 по математике И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.
ЧАСТЬ 1
Задание 1-5.
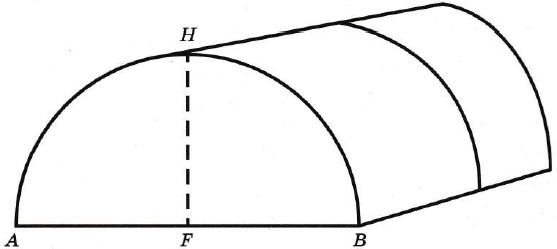
Сергей Петрович решил построить на дачном участке теплицу длиной 4 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки.
Отдельно требуется купить плёнку для передней и задней стенок теплицы. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы – одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 40 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см. Высота теплицы показана на рисунке отрезком HF.
Задание 6.
Найдите значение выражения frac{1}{frac{1}{21}+frac{1}{28}}.
Задание 7.
На координатной прямой отмечены числа х, у и z.
Какая из разностей у – z, у – x, x – z отрицательна?
1) у – z
2) у – x
3) x – z
4) ни одна из них
Задание 8.
Найдите значение выражения frac{2^{-6}cdot 2^{6}}{2^{-8}}.
Задание 9.
Решите уравнение х2 – 35 = 2х.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Задание 10.
Вероятность того, что новый утюг прослужит больше года, равна 0,94. Вероятность того, что он прослужит больше двух лет, равна 0,85. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Задание 11.
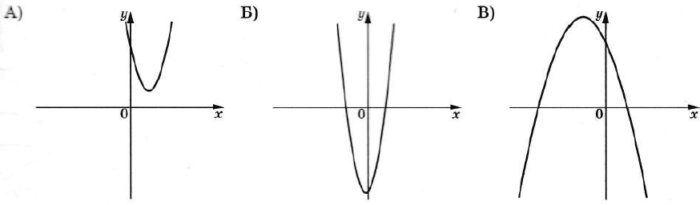
На рисунках изображены графики функций вида у = ах2 + bх + c. Установите соответствие между графиками функций и знаками коэффициентов а и с.
ГРАФИКИ
КОЭФФИЦИЕНТЫ
1) а > 0‚ с < 0
2) а < 0, с > 0
3) а > 0, с > 0
В таблице под каждой буквой укажите соответствующий номер.
Задание 12.
Работа постоянного тока (в джоулях) вычисляется по формуле A = I2Rt‚ где I – сила тока (в амперах), R – сопротивление (в омах), t – время (в секундах). Пользуясь этой формулой, найдите А (в джоулях), если t = 10 с, I = 4 A и R = 2 Ом.
Ответ задания: 320.
Задание 13.
Укажите решение неравенства
– 3 – x ≤ 4x + 7
1) (–∞; –0,8]
2) [–2; +∞)
3) (–∞; –2)
4) (–0,8; +∞)
Задание 14.
В 8:00 часы сломались и за каждый следующий час отставали на одно и то же количество минут по сравнению с предыдущим часом. В 23:00 того же дня часы отставали на 15 минут. На сколько минут отставали часы спустя 36 часа после того, как они сломались?
Ответ задания: 36.
Задание 15.
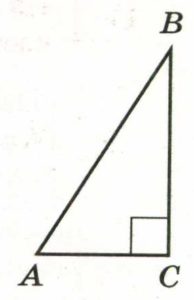
В треугольнике АВС угол С равен 90°‚ АС = 14‚ АВ = 20. Найдите sin В.
Задание 16.
В окружности с центром О отрезки АС и BD – диаметры. Угол AOD равен 108°. Найдите угол АСВ. Ответ дайте в градусах.
Задание 17.
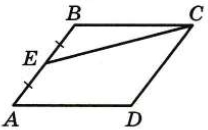
Площадь параллелограмма АВСD равна 96. Точка Е – середина стороны АВ. Найдите площадь треугольника СВЕ.
Задание 18.
На клетчатой бумаге с размером клетки 1 x 1 изображён треугольник АВС. Найдите длину его медианы, проведённой из вершины С.
Задание 19.
Какие из следующих утверждений верны?
1) Если диагонали параллелограмма равны, то он является ромбом.
2) Сумма острых углов прямоугольного треугольника равна 90 градусам.
3) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
ЧАСТЬ 2
Задание 20.
Решите уравнение х4 = (3х – 4)2.
Задание 21.
Моторная лодка прошла против течения реки 208 км и вернулась в пункт отправления, затратив на обратный путь на 5 часов меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 5 км/ч.
Ответ задания: 21.
Задание 22.
Постройте график функции y = x2 – 11x – 2|x – 5| + 30 и определите, при каких значениях m прямая у = m имеет с графиком ровно три общие точки.
Ответ задания: –0,25; 0.
Задание 23.
Прямая пересекает стороны АВ и ВС треугольника АВС в точках К и N соответственно. Известно, что АВ = 9, ВС = 12, АС = 18, АК = 5, СN = 9. Найдите длину отрезка КN.
Ответ задания: 6.
Задание 24.
Сторона АD параллелограмма АВСD вдвое больше стороны АВ. Точка G – середина стороны АD. Докажите, что BG – биссектриса угла АBС.
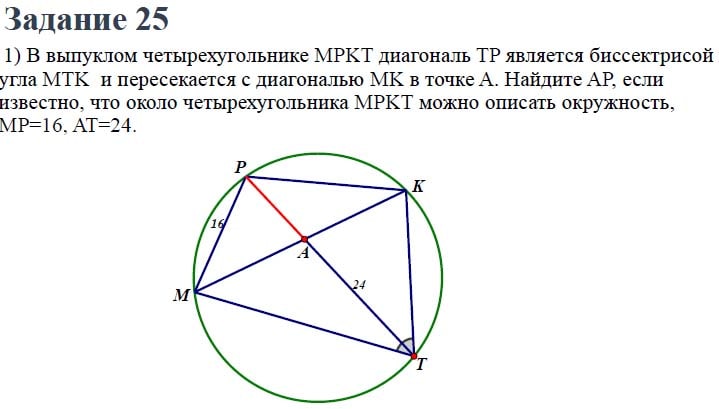
Задание 25.
В трапеции АВСD основания АD и ВС равны соответственно 34 и 2, а сумма углов при основании АD равна 90°. Найдите радиус окружности, проходящей через точки А и В и касающейся прямой СD, если АВ = 24.
Ответ задания: 13,5.
Источник варианта: Сборник ОГЭ 2022 по математике. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.7 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
Слайд 2

Текст слайда:
Задания:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Демо-версия!
Слайд 3

Текст слайда:
№1
Найдите синус угла АОВ. В ответе укажите
значение синуса, умноженное на
17
Ответ
В
А
О
Алгоритм (3):
3. Выполнить вычисления и записать ответ .
1. Вспомнить что называют синусом острого угла прямоугольного треугольника.
2. Записать формулу нахождения sinО.
Построение:
С
4
4
Слайд 4

Текст слайда:
№2
KarMaN01@yandex.ru
Информация
Слайд 5

Текст слайда:
№3
KarMaN01@yandex.ru
Информация
Слайд 6

Текст слайда:
№4
KarMaN01@yandex.ru
Информация
Слайд 7

Текст слайда:
№5
KarMaN01@yandex.ru
Информация
Слайд 8

Текст слайда:
№6
KarMaN01@yandex.ru
Информация
Слайд 9

Текст слайда:
№7
KarMaN01@yandex.ru
Информация
Слайд 10

Текст слайда:
№8
KarMaN01@yandex.ru
Информация
Слайд 11
Текст слайда:
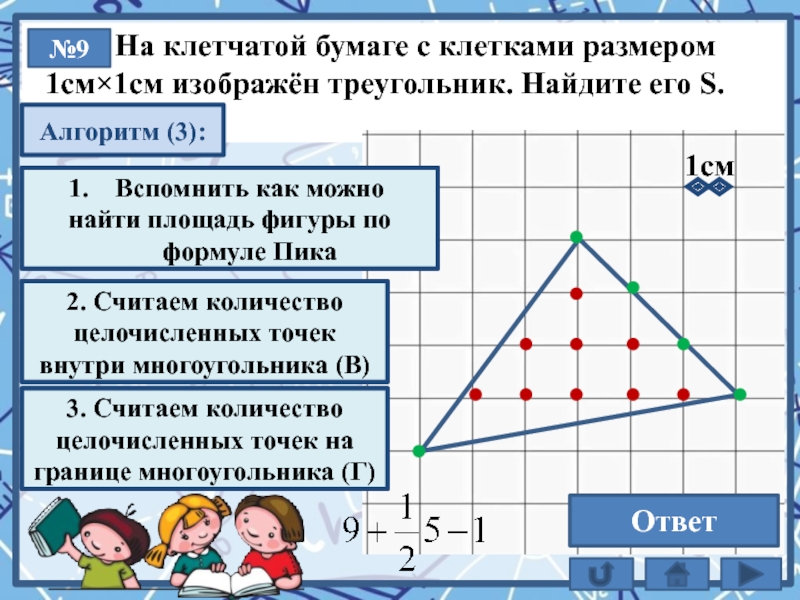
На клетчатой бумаге с клетками размером
1см×1см изображён треугольник. Найдите его S.
№9
10,5
Ответ
Алгоритм (3):
Площадь многоугоугольника с целочисленными вершинами равна сумме В + Г/2 – 1
Вспомнить как можно
найти площадь фигуры по формуле Пика
2. Считаем количество целочисленных точек внутри многоугольника (В)
1cм
3. Считаем количество целочисленных точек на границе многоугольника (Г)
Слайд 12

Текст слайда:
№10
KarMaN01@yandex.ru
Информация
Слайд 13

Текст слайда:
На клетчатой бумаге с клетками размером 1см×1см
изображён параллелограмм. Найдите его высоту,
опущенную на большую сторону.
№11
4
Ответ
Алгоритм (3):
3. Сравнить стороны и записать ответ к задаче.
1. Высота параллелограмма – перпендикуляр из вершины к противоположной стороне.
Вспомнить что называют высотой параллелограмма.
2. Провести высоты и из тр-ка АВН определить
сторону АВ
4
6
1cм
В
А
Н
Слайд 14

Текст слайда:
№12
KarMaN01@yandex.ru
Информация
Слайд 15

Текст слайда:
№13
KarMaN01@yandex.ru
Информация
Слайд 16

Текст слайда:
№14
KarMaN01@yandex.ru
Информация
Слайд 17

Текст слайда:
№15
KarMaN01@yandex.ru
Информация
Слайд 18

Текст слайда:
№16
KarMaN01@yandex.ru
Информация
Слайд 19

Текст слайда:
№17
KarMaN01@yandex.ru
Информация
Слайд 20
Текст слайда:
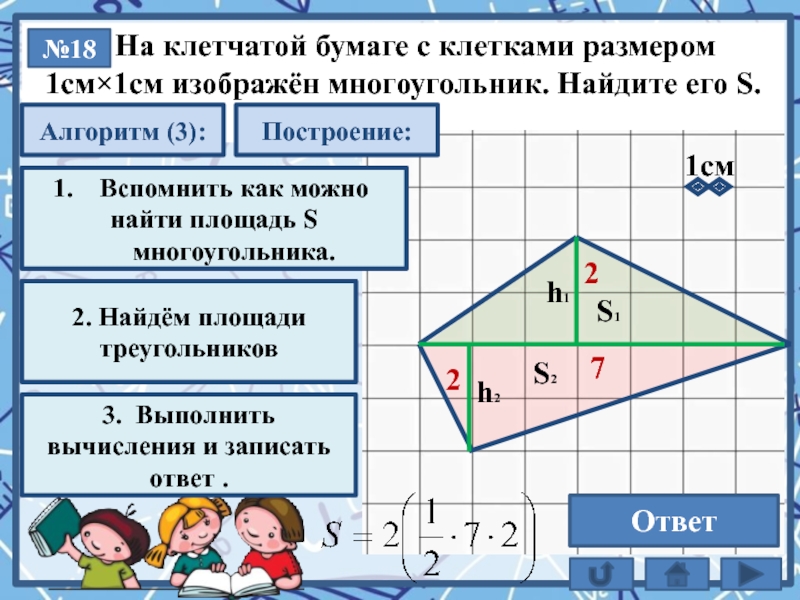
На клетчатой бумаге с клетками размером
1см×1см изображён многоугольник. Найдите его S.
№18
14
Ответ
S1
Алгоритм (3):
3. Выполнить вычисления и записать ответ .
1. Площадь многоугольника равна сумме площадей фигур из которых состоит (S1 + S2)
Вспомнить как можно
найти площадь S многоугольника.
2. Найдём площади треугольников
Построение:
h1
2
7
1cм
S2
2
h2
Слайд 21

Текст слайда:
№19
KarMaN01@yandex.ru
Информация
Слайд 22
Текст слайда:
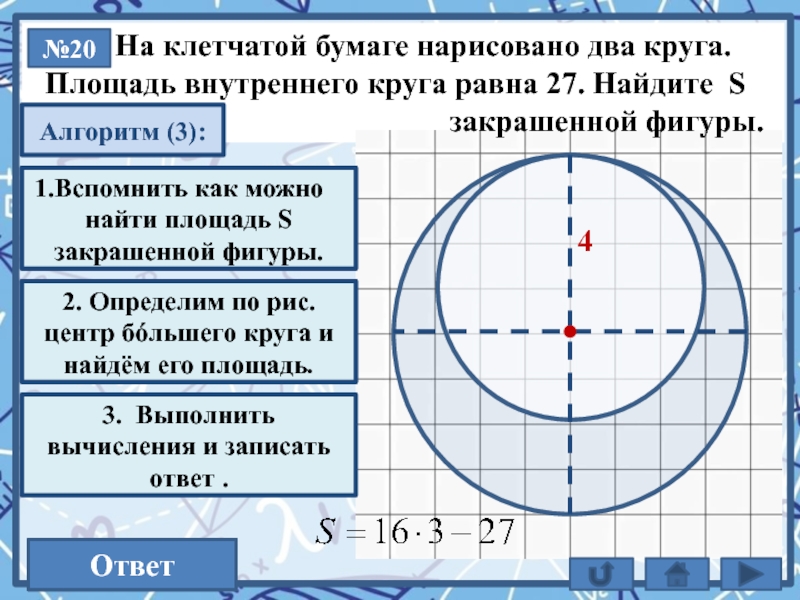
На клетчатой бумаге нарисовано два круга.
Площадь внутреннего круга равна 27. Найдите S
закрашенной фигуры.
№20
Алгоритм (3):
3. Выполнить вычисления и записать ответ .
S = Sб – Sм
Вспомнить как можно
найти площадь S закрашенной фигуры.
2. Определим по рис. центр бóльшего круга и найдём его площадь.
4
21
Ответ
Слайд 23

Текст слайда:
Уважаемые пользователи, дорогие коллеги!
Если Вам понравился ресурс, то получить полную версию
Вы можете, написав мне на электронную почту:
Пожалуйста, в письме указывайте ФИО
Описание:
Презентация состоит из 24 рабочих слайдов
В ресурсе представлено 20 задач по заявленной теме
с подробным разбором решения.
Задачи соответствуют спецификации и кодификатору к демонстрационному варианту КИМ-2020 по математике, представленного на сайте ФИПИ
Предлагаю подробный разбор заданий №8 и №10
Спасибо за интерес к работе.
Желаю Вам интересных уроков и успешных учеников!
С уважением, КарМаН
KarMaN01@yandex.ru
Слайд 24

Текст слайда:
Титульный слайд
Фон слайдов
источники
Дети в классе
Презентация на тему Задание №18 ОГЭ математика 2021 с решениями, из раздела: Образование. Эта презентация содержит 27 слайда(ов). Информативные слайды и изображения помогут Вам заинтересовать аудиторию. Скачать конспект-презентацию на данную тему можно внизу страницы, поделившись ссылкой с помощью социальных кнопок. Также можно добавить наш сайт презентаций в закладки! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них. Все права принадлежат авторам презентаций.
Слайды и текст этой презентации
Открыть в PDF
Слайд 2

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 отмечены три точки А, В и С. Найдите расстояние от точки А до прямой ВС.
ЗАДАЧА №1
Слайд 3

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 отмечены три точки А, В и С. Найдите расстояние от точки А до прямой ВС.
ЗАДАЧА №1
ОТВЕТ: 3.
Слайд 4

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен ромб. Найдите длину его большей диагонали.
ЗАДАЧА №2
Слайд 5

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен ромб. Найдите длину его большей диагонали.
ЗАДАЧА №2
ОТВЕТ: 10.
Слайд 6

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 отмечены три точки А, В и С. Найдите расстояние от точки А до середины ВС.
ЗАДАЧА №3
Слайд 7

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 отмечены три точки А, В и С. Найдите расстояние от точки А до середины ВС.
ЗАДАЧА №3
ОТВЕТ: 6.
Слайд 8

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен треугольник. Найдите его площадь.
ЗАДАЧА №4
Слайд 9

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен треугольник. Найдите его площадь.
ЗАДАЧА №4
ОТВЕТ: 21.
Слайд 10

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображена трапеция. Найдите ее площадь.
ЗАДАЧА №5
Слайд 11

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображена трапеция. Найдите ее площадь.
ЗАДАЧА №5
ОТВЕТ: 33.
Слайд 12

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображена фигура. Найдите ее площадь.
ЗАДАЧА №6
Слайд 13

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображена фигура. Найдите ее площадь.
ЗАДАЧА №6
ОТВЕТ: 26.
Слайд 14

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен параллелограмм. Найдите площадь этого параллелограмма.
ЗАДАЧА №7
Слайд 15

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен параллелограмм. Найдите площадь этого параллелограмма.
ЗАДАЧА №7
ОТВЕТ: 42.
Слайд 16

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен ромб. Найдите площадь ромба.
ЗАДАЧА №8
Слайд 17

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен ромб. Найдите площадь ромба.
ЗАДАЧА №8
ОТВЕТ: 20.
Слайд 18

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен треугольник. Найдите длину его средней линии, параллельной стороне АС.
ЗАДАЧА №9
Слайд 19

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен треугольник. Найдите длину его средней линии, параллельной стороне АС.
ЗАДАЧА №9
ОТВЕТ: 4,5.
Слайд 20

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображена трапеция. Найдите длину ее средней линии.
ЗАДАЧА №10
Слайд 21

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображена трапеция. Найдите длину ее средней линии.
ЗАДАЧА №10
ОТВЕТ: 5,5.
Слайд 22

Текст слайда:
Найти тангенс угла АОВ, изображенного на рисунке.
ЗАДАЧА №11
Слайд 23

Текст слайда:
Найти тангенс угла АОВ, изображенного на рисунке.
ЗАДАЧА №11
ОТВЕТ: 3,5.
Слайд 24

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен параллелограмм. Найдите площадь этого параллелограмма.
ЗАДАЧА №12
Слайд 25

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен параллелограмм. Найдите площадь этого параллелограмма.
ЗАДАЧА №12
ОТВЕТ: 14.
Слайд 26

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен треугольник. Найдите площадь этого треугольника.
ЗАДАЧА №13
Слайд 27

Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен треугольник. Найдите площадь этого треугольника.
ЗАДАЧА №13
ОТВЕТ: 17,5.
В задании (18) все задачи связаны с данными, которые можно увидеть на чертеже, сделанном на бумаге в клетку. Сформулируем несколько основных правил работы с такими чертежами.
Все размеры соотносим с размерами клеточки. Причём обязательно учитываем, что длины отрезков — это размеры линейные, а площади — это размеры квадратные. Если, например, указана длина стороны клеточки (3) см (или любых других единиц), то линейные размеры нужно умножать на (3), а площади — на (9). И наоборот, если обозначен размер площади клетки, то для размера линейного нужно будет извлечь из этого размера квадратный корень.
Рис. (1). Масштаб
2. Измерение размеров в клеточках
В таких задачах не даётся в условии размер стороны фигуры. Все размеры явно видны по чертежу. Посчитать линейный размер по клеточкам можно только в том случае, если отрезок проходит точно вертикально или точно горизонтально. Если линия проходит под углом к горизонту, нужно определить начало и конец линии в узлах пересечения клеток и воспользоваться теоремой Пифагора.
Рис. (2). Линейные размеры (красным зачёркнуто неправильное определение длины отрезка)
Задачи по клеточкам, в которых нужно найти площади или середину отрезка, вовсе необязательно решать с помощью формул. Можно разбить фигуру на несколько частей и найти отдельно размеры каждой из них.
Рис. (3). Площадь нескольких частей
Отрезок может начинаться либо в узле клеток, либо точно в середине. Других долей быть не может. Если нужно найти середину отрезка, проходящего под углом к горизонту, можно построить вокруг него прямоугольник по его габаритным размерам и провести вторую диагональ. Хорошо подходит при поиске расположения средней линии трапеции.
Рис. (4). Средняя линия трапеции
5. Расстояния между точками
Если на чертеже нет линий, а есть только точки, соедини их прямыми линиями. Расстояние от точки до прямой — перпендикуляр (линия под прямым углом).
Рис. (5). Расстояния между точками