Загрузить PDF
Загрузить PDF
Найти длину вертикального или горизонтального отрезка на координатной плоскости можно с помощью координат, а вот сделать это с диагональным отрезком сложнее. Длину диагонального отрезка можно вычислить по формуле, которая основана на теореме Пифагора, где гипотенузой прямоугольного треугольника является наш диагональный отрезок.[1]
С помощью этой формулы можно быстро найти длину любого отрезка на координатной плоскости.
-
1
Запишите формулу для вычисления длины. Формула:
, где
— длина отрезка,
— координаты начальной точки отрезка,
— координаты конечной точки отрезка.[2]
-
2
Найдите координаты точек отрезка. Возможно, они будут даны. Если нет, найдите их по осям Х и Y.[3]
-
3
Подставьте координаты в формулу. Будьте внимательны и подставьте значения соответствующих переменных. Две координаты
должны находится внутри первой пары скобок, а две координаты
— внутри второй пары скобок.[4]
Реклама
-
1
Выполните вычитание в скобках. Сделайте это, потому что операции в скобках имеют приоритет.[5]
-
2
Возведите в квадрат полученные значения. В нашем случае возведение в степень — это вторая по важности операция.[6]
-
3
Сложите числа под знаком корня. Делайте вычисления так, как будто работаете с целыми числами.
-
4
Вычислите длину отрезка
. Для этого извлеките корень из полученной суммы чисел.
Реклама
Советы
- Не путайте эту формулу с другими, например, с формулой для вычисления углового коэффициента или с линейным уравнением.
- Помните о порядке выполнения математических операций. Сначала вычтите, затем возведите в квадрат, затем сложите, а затем извлеките квадратный корень.
Реклама
Об этой статье
Эту страницу просматривали 24 709 раз.
Была ли эта статья полезной?
Как вычислить длину отрезка зная координаты
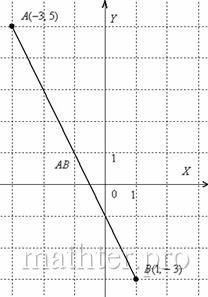
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1, а на ось Х длина проекции равна x2-x1. Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)². В данном случае |AB| является длиной отрезка.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5). Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5. А это значит, что длина нашего отрезка равна 5:1/2.
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.
Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1.
Рассчитаем длину отрезка А, для этого найдем квадратный корень:
Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1, то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61.
Отрезком обозначают ограниченный двумя точками участок прямой. Точки – концы отрезка.
Общеизвестный факт, что каждая точка А плоскости имеет свои координаты (х, у).
В данном примере вектор AB задан координатами (х2— х1, y2— y1). Квадрат длины вектора будет равен сумме квадратов его координат. Следовательно, расстояние d между точками А и В, или, что то же самое, длина вектора АВ, вычисляется согласно формуле:
Эта формула длины отрезка предоставляет возможность рассчитывать расстояние между двумя произвольными точками плоскости, при условии, что известны координаты этих точек
Вышеуказанную формулу длины отрезка можно доказать и другим способом. В системе координат заданы координаты крайних точек отрезка координатами его концов(х1y1) и (х2,у2).
Прочертим прямые лини через эти точки перпендикулярно к осям координат, в результате имеем прямоугольный треугольник. Первоначальный отрезок является гипотенузой образовавшегося треугольника. Катеты треугольника сформированы отрезками, их длиной будет проекция гипотенузы на оси координат.
Установим длину этих проекций.
На ось у длина проекции равна y2 — y1, а на ось х длина проекции равна х2 — х1. На основании теоремы Пифагора видим, что |AB|² = (y2 – y1)² + (x2 – x1)².
В рассмотренном случае |AB| выступает длиной отрезка.
Вычислим длину отрезка АВ, для этого извлечем квадратный корень. Результатом является все та же формула длины отрезков по известным координатам конца и начала.
Этот онлайн калькулятор рассчитывает длину отрезка и координаты середины отрезка (средней точки) по декартовым координатам концов отрезка. Отрезок и средняя точка отображаются на графике, также на графике показан графический способ нахождения середины отрезка.
Эта страница существует благодаря следующим персонам
Timur
- Статья : Расчет длины отрезка и координат середины отрезка по двум точкам — Автор, Переводчик en — ru
- Калькулятор : Расчет длины отрезка и координат середины отрезка по двум точкам — Автор, Переводчик en — ru
Этот онлайн калькулятор рассчитывает длину отрезка и координаты середины отрезка по введенным декартовым координатам двух точек — концов отрезка.
Формула вычисления расстояния между двумя точками и это формула длины гипотенузы прямоугольного треугольника . Координаты середины отрезка — среднее арифметическое координат точек .
Отрезок и средняя точка отображаются на графике. Также среднюю точку можно найти построением. Для этого на графике надо построить две дуги с центрами на концах отрезка и с радиусом равным длине отрезка. Затем надо построить прямую линию между точками пересечения дуг. Эта линия пересечет исходный отрезок в середине.
Длина отрезка. Расстояние между точками: онлайн-калькулятор
Чтобы найти расстояние между точками (длину отрезка) онлайн, необходимо:
- Задать размерность (плоскость или пространство).
- Ввести в поля координаты точек.
- Нажать «рассчитать».
Как найти длину отрезка (расстояние между точками) с помощью онлайн-калькулятора
Рассмотрим пример, наглядно демонстрирующий работу с онлайн-калькулятором. Найдем длину произвольного отрезка, начальная и конечная точки которого имеют координаты (1;4) и (3;0). Для этого:
- Выберем размерность (2 или 3). Калькулятор позволяет задать отрезок соответственно на плоскости, или в пространстве. В нашем конкретном примере выберем плоскость (2):
- Введем в пустые поля координаты начальной и конечной точек отрезка:
- После ввода координат остается нажать «Рассчитать» и получить ответ с решением:
Расчет длины отрезка
Отрезок — это тонкий пространственный объект имеющий конечную длину и представляющий собой цепь связанных друг с другом точек.
Длина отрезка равна квадратному корню из суммы квадратов разностей координат по каждой оси. Линия на плоскости характеризуется двумя координатами начала и конца, а линия в пространстве характеризуется тремя координатами начала и конца.
Смотрите также статью о всех геометрических фигурах (линейных 1D, плоских 2D и объемных 3D).
Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета длины отрезка, если известны координаты начала и конца отрезка. С помощью этого калькулятора вы в один клик сможете вычислить длину отрезка.
http://zaochnik.com/online-calculators/tochka-pryamaya-ploskost/dlina-otrezka-rasstoyanie-mezhdu-tochkami/
http://www.center-pss.ru/math/dlina-otrezka.htm
Как вычислить длину отрезка зная координаты
Как Найти Длину Отрезка. Чтобы найти отрезок побольше, нужно два меньших сложить. Их вычислим путем нахождения разницы координат точек по отдельной оси:
Длина вектора находится по формуле: Расстояние между двумя точками на плоскости. Auto, то попали по адресу, измерение отрезков затем по шкале разметки на линейке надо найти длину отрезка и отметить точку.
В Данном Случае Его Длину Мы Можем Найти, Применяя Теорему Пифагора.
Расстояние между двумя точками — это длина отрезка, что соединяет эти точки. Чтобы найти меньший отрезок, нужно от большого отнять другой меньший. Рассчитаем длину отрезка а, для этого найдем квадратный корень:
Если Даны Две Точки Пространства И , То Длину.
У меня есть отрезок с известными координатами концов. Auto, то попали по адресу, измерение отрезков затем по шкале разметки на линейке надо найти длину отрезка и отметить точку. Найти длину вертикального или горизонтального отрезка на координатной плоскости можно с помощью координат, а вот.
Например, Чтобы Найти Длину Отрезка, Мы Прикладываем К Нему Линейку И Сравниваем Их.
Найдем длины проекций (x и y) исходного отрезка на координатные оси. В этом случае используем формулу расстояния, т. Теперь давайте посмотрим, как найти длину отрезка, когда заданы координаты двух конечных точек.
Х = 5, У =5.
На этом отрезке есть точка. В зависимости от размерности задачи расстояние между двумя точками можно найти. Их вычислим путем нахождения разницы координат точек по отдельной оси:
Итак, В Системе Координат Начертим Отрезок С Заданными Координатами Его Концов (X1;
Длина вектора находится по формуле: Длина, как уже отмечалось, обозначается знаком модуля. Пусть отрезок задан двумя точками в плоскости координат, тогда можно найти его длину с помощью теоремы пифагора.
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и
, то длину отрезка
можно вычислить по формуле:
Если даны две точки пространства и
, то длину отрезка
можно вычислить по формуле:
Примечание: соответствующие координаты можно переставить местами: и
,
но это нестандартный вариант.
Задача 3
Даны точки и
. Найти длину отрезка
.
Решение: по соответствующей формуле:
Ответ: (единицы)
Обратите внимание на вынесение множителя из-под корня: (см. Приложение Школьные материалы). Это крайне
желательное действие, если оно возможно. Ибо будет придирка со стороны преподавателя. С высокой вероятностью.
И для наглядности снова выполню чертёж, тут есть что сказать:
Отрезок – это не вектор, а обычный ненаправленный
отрезок. И перемещать его куда-либо, конечно, нельзя.
Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину
отрезка . Но проще, конечно, использовать Калькулятор (приложен к книге).
Кстати, в ответе не забываем указать размерность: «единицы». В условии не сказано, ЧТО это – миллиметры, сантиметры, метры
или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Задание для самостоятельного решения с отрезком в пространстве:
Задача 4
Даны точки и
. Найти длину отрезка
.
Решение и ответ в конце книги.


| Оглавление |
Автор: Aлeксaндр Eмeлин