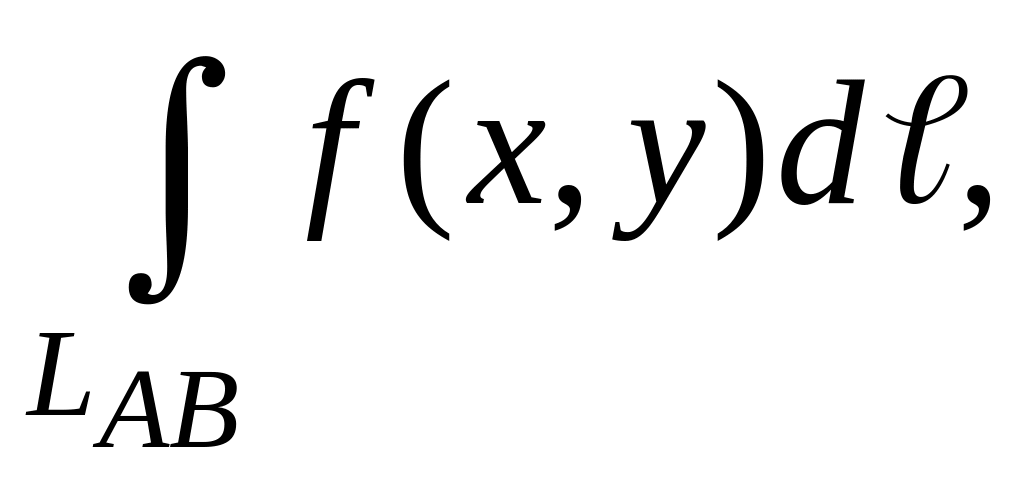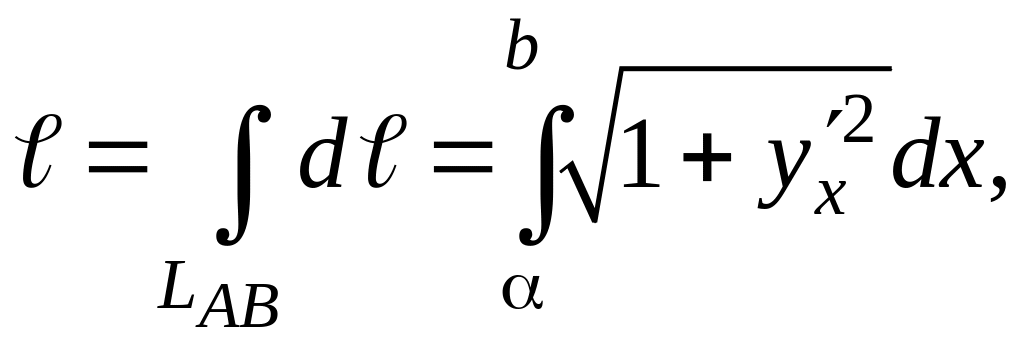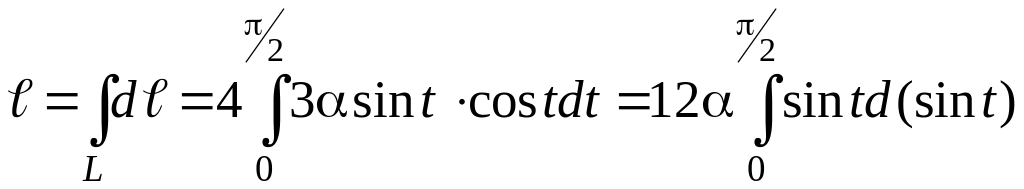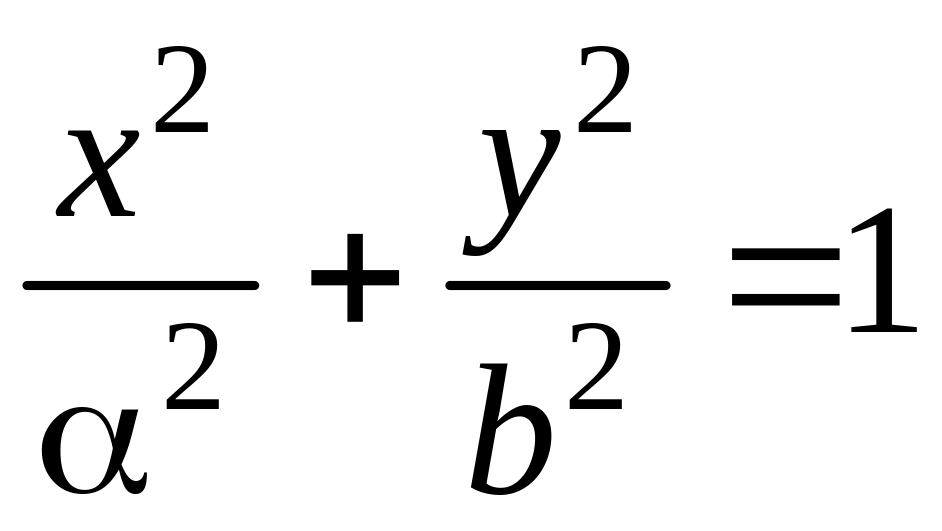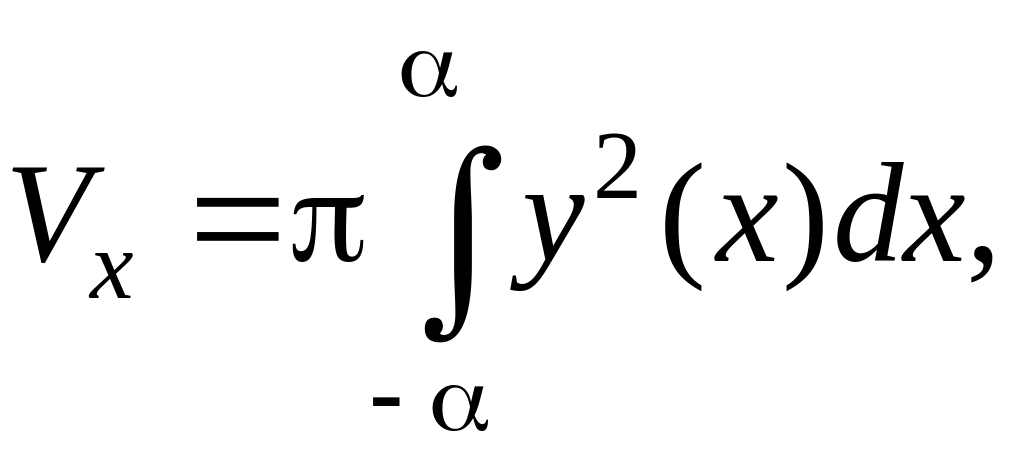Как найти длину, если известен объем
Если известен объем трехмерной геометрической фигуры, в большинстве случаев можно найти некоторые ее линейные размеры. Главный линейный размер любой фигуры – это длины ее сторон, а для сферы – радиус. Для различных типов фигур он находится по-разному.

Вам понадобится
- Объемы измеряемых фигур, свойства многогранников
Инструкция
Зная объем правильного многогранника (выпуклого многогранника, стороны которого правильные многоугольники) можно вычислить его сторону. Чтобы найти длину стороны тетраэдра (правильного четырехгранника, грани которого являются равносторонними треугольниками), умножьте его объем на 12 и разделите результат на корень квадратный из 2. Из полученного числа извлеките кубический корень.
Чтобы найти сторону куба, который является шестигранником, каждая грань которого квадрат, из его объема извлеките кубический корень. Вычислите сторону октаэдра, который состоит из 8 треугольных граней, каждая из которых является правильным треугольником, умножив его объем на 3 и поделив на корень квадратный из 2. Из полученного числа извлеките кубический корень. Найдите сторону додекаэдра, многогранника состоящего из 12 правильных пятиугольников, для чего поделите его объем на число 7,66, и извлеките из результата кубический корень.
Чтобы найти радиус шара, объем которого известен, умножьте этот объем на 3 и поделите последовательно на числа 4 и 3,14. Их полученного результат извлеките кубический корень.
Если же фигура не является правильным многогранником, то, зная ее объем, можно вычислить длины только некоторых ее элементов. Зная объем и площадь основания призмы, можно найти ее высоту. Для этого поделите значение объема на площадь основания h=V/S. Чтобы найти другие линейные элементы, нужно знать параметры площади основания, например, если это квадрат, из значения площади извлеките корень квадратный, это и будет сторона основания.
Если известен объем цилиндра, то можно найти его высоту, зная радиус. Для этого объем последовательно поделите на число 3,14 и квадрат радиуса основания. Если же известна высота, то найдите радиус основания, поделив объем на число 3,14 и значение высоты, а из результата извлеките корень квадратный.
Чтобы найти высоту пирамиды через объем, поделите его на площадь основания, а результат умножьте на число 3.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
|
ksandr97 7 лет назад
В правильной треугольной пирамиде SABC медианы основания ABC пересекаются в точке O. Площадь треугольника ABC равна 2; объём пирамиды равен 6. Найдите длину отрезка OS. Татьяна108 7 лет назад высота равна 9. Объём пирамиды равен одной третьей произведения площади основания на высоту, значит 6=1/3*2*h, откуда h=6*3:2=9 автор вопроса выбрал этот ответ лучшим комментировать
в избранное
ссылка
отблагодарить Знаете ответ? |
|
Есть интересный вопрос? Задайте его нашему сообществу, у нас наверняка найдется ответ! |
Делитесь опытом и знаниями, зарабатывайте награды и репутацию, заводите новых интересных друзей! |
Задавайте интересные вопросы, давайте качественные ответы и зарабатывайте деньги. Подробнее.. |
Статистика проекта за месяц
Новых пользователей: 4379
Создано вопросов: 15869
Написано ответов: 37355
Начислено баллов репутации: 889482
Длину
плоских кривых, заключенных между двумя
точками А
и В,
можно найти с помощью криволинейного
интеграла
если положить f(x,y)
≡ 1. В этом случае криволинейный интеграл,
также как и двойной, будет равен размерам
области интегрирования, т.е. длине части
линии LAB.
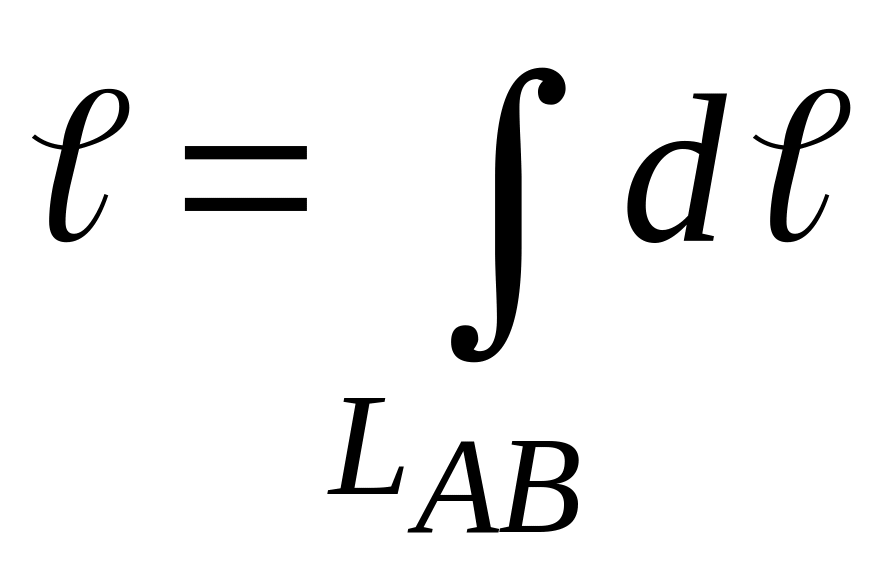
Меру
элементарной части (дифференциал длины)
— dℓ
выражают через уравнение данной линии
LAB
и переходят к линейному интегралу. Если
кривая LAB
задана в декартовой системе координат
непрерывной и дифференцируемой функцией
y
= y(x),
то вычисление ее длины сводят к вычислению
линейного интеграла вида:
где
Пределы
в линейном интеграле α
и b
– являются проекциями на ось Oх
точек линии А
и В
соответственно.
Длину
дуги АВ
кривой, заданной параметрическими
уравнениями x
= x(t);
y
= y(t),
находят по формуле
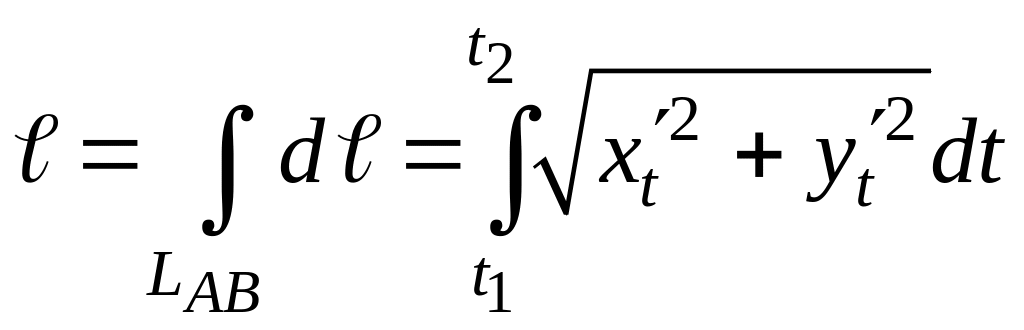
где
t1
и t2
значения параметра t
в точках А
и В.
И
наконец, длина линии LAB,
уравнение которой r
= r(φ)
задано в полярной системе координат,
равна линейному интегралу
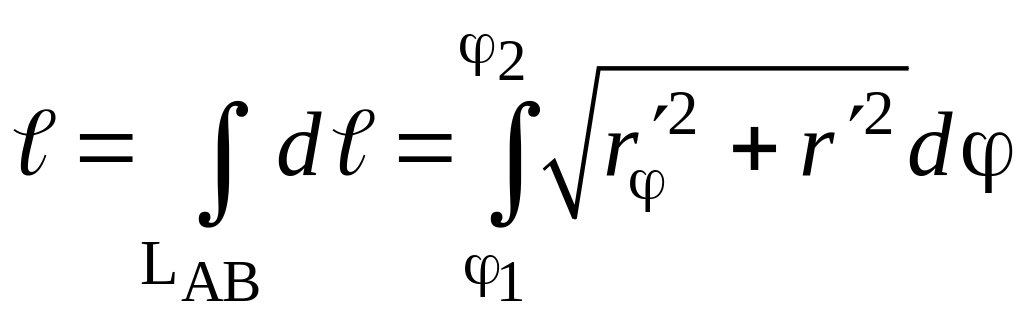
где
φ1
и φ2
полярные углы точек А
и В.
Пример
5. Найти длину
полукубической параболы y2
= x3
от точки А(0,0)
до точки В(4;8).
Решение.
Длина отрезка полукубической параболы
между точками А
и В
равна криволинейному интегралу
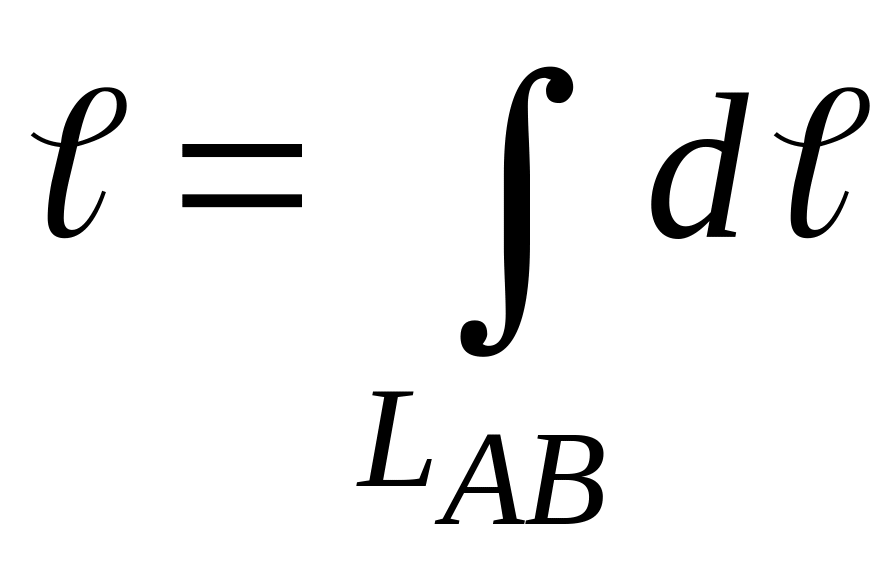
Дифференциал
длины кривой в
декартовой системе координат
выражают через ее уравнение y
= y(x)
по формуле
Найдем
его для данной линии
Переход
от криволинейного интеграла к линейному
и вычисление последнего дает искомую
длину:
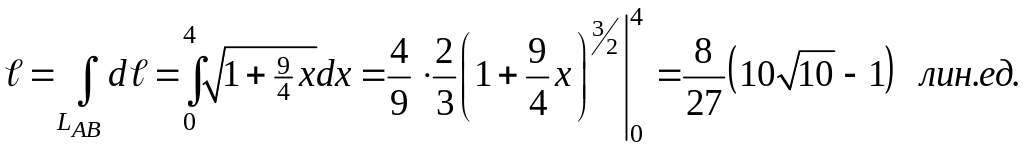
Пример
6. Найти длину
астроиды, заданную
параметрическими уравнениями
Решение.
Длину астроиды
также найдем с помощью криволинейного
интеграла
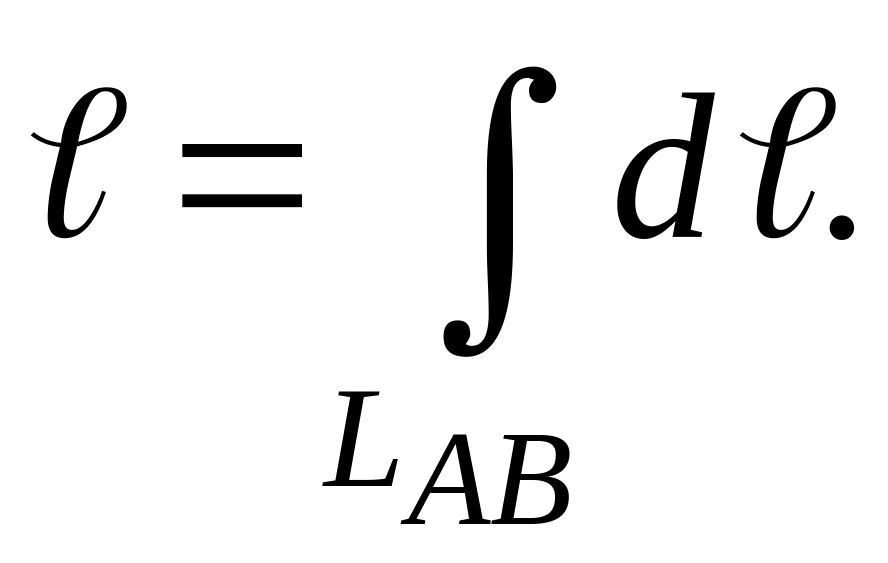
Дифференциал
длины кривой, заданной параметрически,
выражают через ее уравнение по формуле
Найдем его для
астроиды
Подставляя
найденное выражение для dℓ
в криволинейный интеграл и переходя к
линейному, получим:
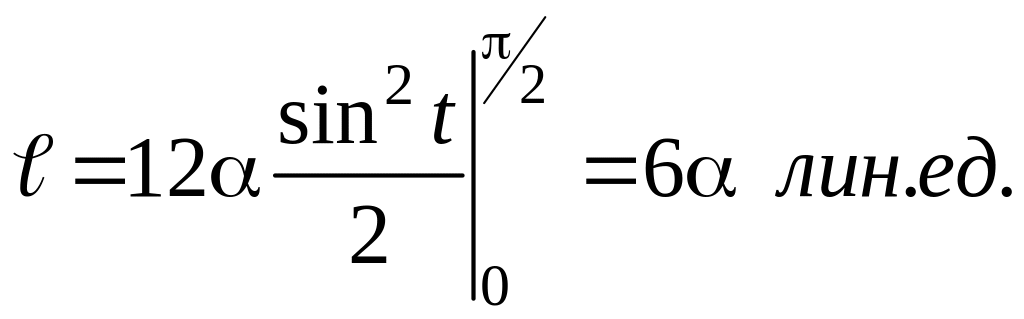
3.11.3.Вычисление объемов тел
Объем
тел, в зависимости от их формы и условий
задачи, можно находить различными
способами.В частом случае, когда известна
площадь поперечных сечений тела, его
объем вычисляют с помощью линейного
интеграла
по формуле:
где
S(x)
– площадь сечения тела плоскостью,
перпендикулярной оси Ox,
α
и b
– проекции его крайних точек на ту же
ось.
Исходя
из этой формулы, находят объем тел
вращения.
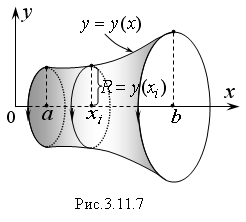
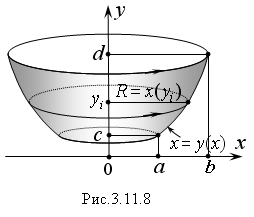
П
усть
криволинейная трапеция, ограниченная
сверху графиком непрерывной функции y
= y(x)
и прямыми x
= α,
x
= b,
вращается вокруг оси Oх
(Рис. 3.11.7).
В
результате ее вращения образуется тело.
Его плоскими сечениями, перпендикулярными
оси Oх,
являются круги с различными радиусами
R
= y(x),
площадь которых равна:
Следовательно,
объем полученного тела можно найти по
формуле
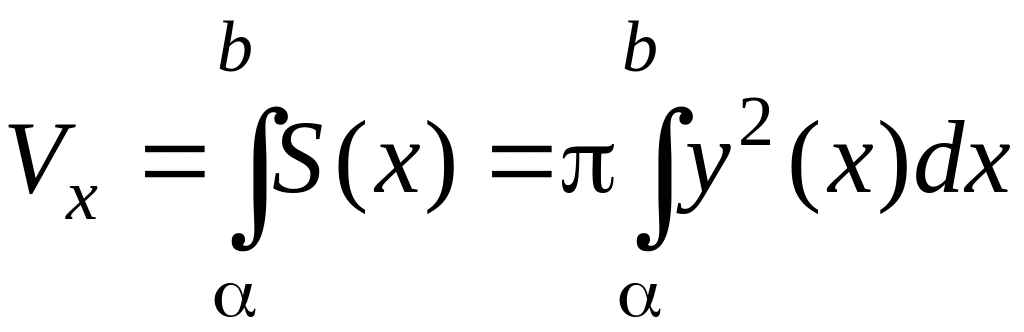
П
ри
вращении линии, ограничивающей
криволинейную трапецию, вокруг оси Oy
(Рис. 3.11.8) объем полученного тела равен:

где
x(y)
– уравнение вращающейся линии решенное
относительно переменной x.
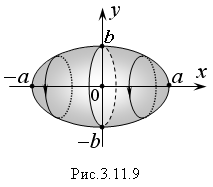
Пример
7. Найти объем
тела, полученного при вращении эллипса
относительно осей Ox
и Oy.
Р
ешение.
График эллипса
изображен на рисунке 3.11.9.
Координаты
его крайних точек по оси Oх:
x1
= –α,
x2
= α,
по оси Oy:
y1
= –b,
y2
= b.
Объем
тела, образованного вращением эллипса
относительно оси Oх,
найдем по формуле:
где
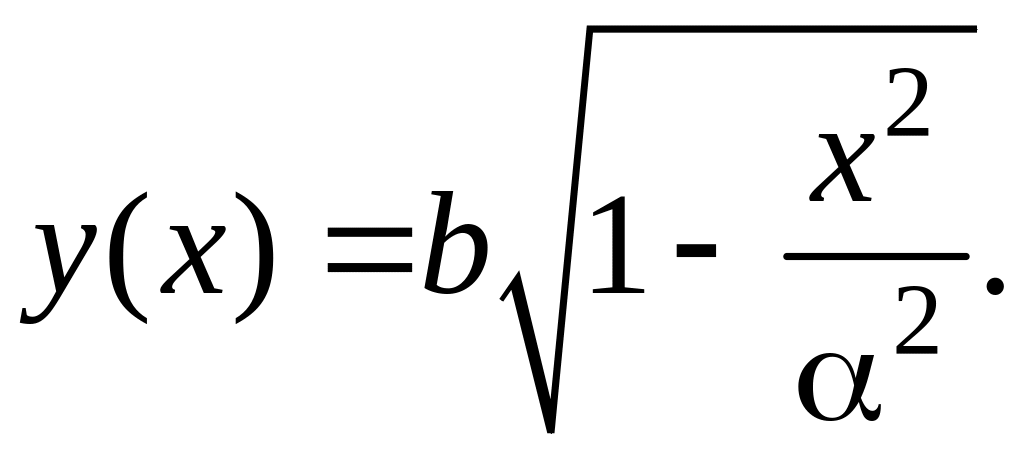
С учетом симметрии
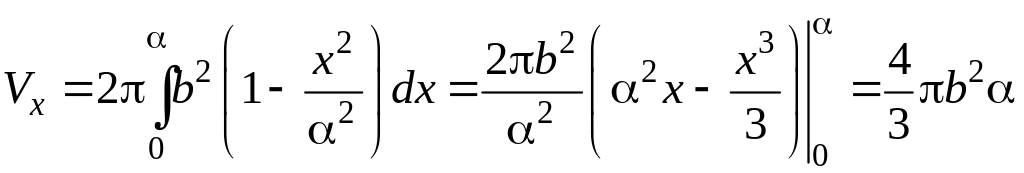
Аналогично,
вычислим объем Vy
где
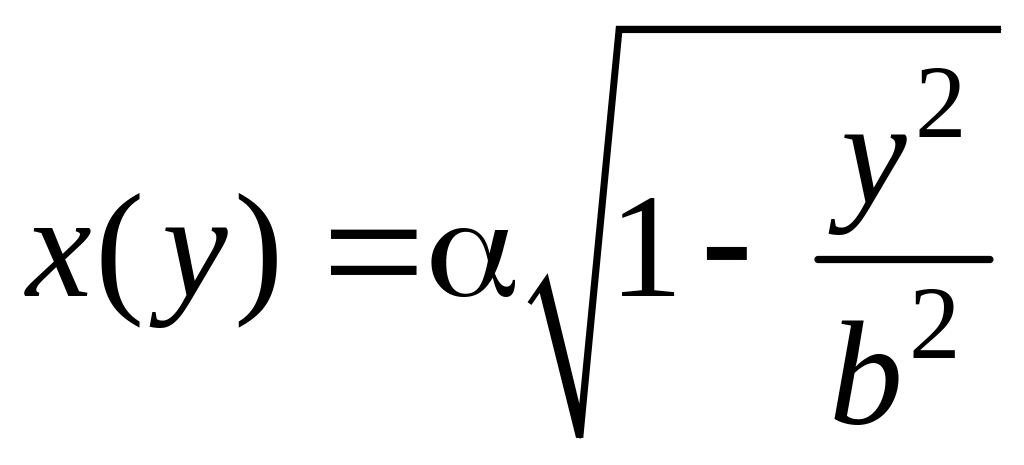
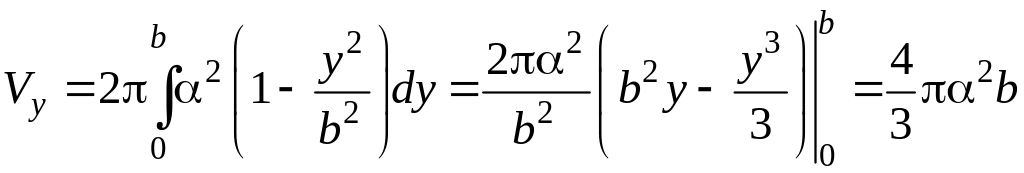
Если
α
= b,
то тела вращения относительно осей Oх
и Oy
становятся шаром, объем которого равен
.
Р
ассмотрим
теперь общий случай вычисления объемов
тел с помощью кратныx
интегралов.
Пусть
тело произвольной формы ограничено
двумя поверхностями, уравнения которых
известны:
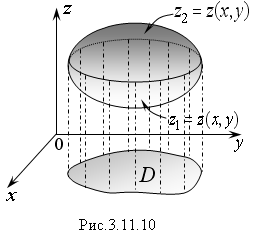
Проекцией данного тела на плоскость
xOy
является область D
(Рис. 3.11.10). Двойной интеграл по области
D
геометрически равен объему цилиндра,
построенного на этой области и
ограниченного сверху графиком
подынтегральной функции. Поэтому объем
тела, изображенного на рисунке 3.11.10,
можно представить как разность объемов
двух цилиндрических тел, или как разность
двух двойных интегралов:
В
самом общем случае объем тел произвольной
формы находят с помощью тройного
интеграла,
в котором подынтегральная функция равна
единице
Легко
заметить, что предыдущая формула является
следствием последней, в самом деле:
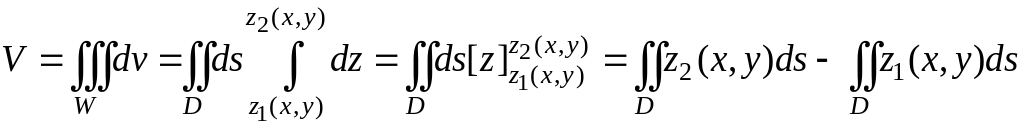
Пример
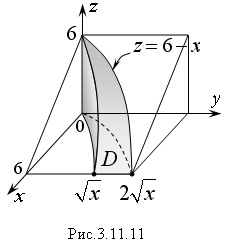
8. Найти
объем, ограниченный поверхностями:
z
= 0, z
+ x
= 6
Р
ешение.
Тело ограничено двумя цилиндрическими
поверхностями
с образующими, параллельными оси Oz,
и двумя плоскостями z
= 0, z
= 6 – x.
Искомый объем равен объему цилиндрического
тела, построенного на области D
и ограниченного сверху плоскостью z
= 6 – x
(Рис. 3.11.11). Найдем его с помощью двойного
интеграла
Переменная
x
внутри области D
изменяется от 0 до 6, а переменная y
от ее значений на линии
до значений на линии
.
Перейдем к двукратному интегрированию:
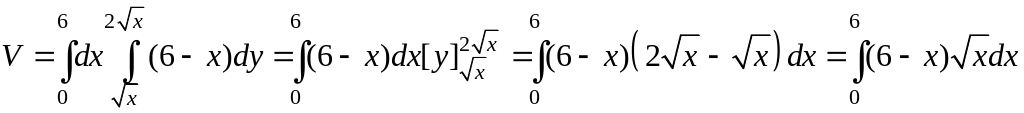
Вычисляя последний
интеграл, получим
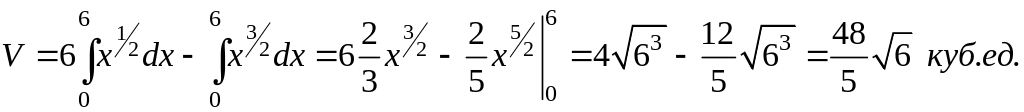
Для сравнения
найдем этот же объем с помощью тройного
интеграла
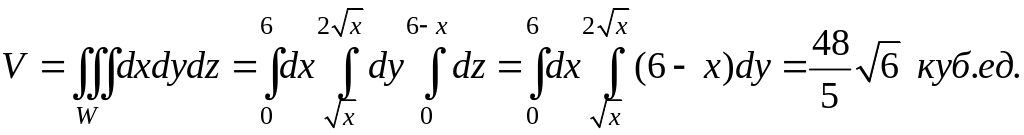
После
подстановки пределов для переменной z
мы приходим к такому же двойному
интегралу.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
0
В правильной треугольной пирамиде SABC медианы основания ABC пересекаются в точке O. Площадь треугольника ABC равна 2; объём пирамиды равен 6. Найдите длину отрезка OS.
1 ответ:
1
0
высота равна 9. Объём пирамиды равен одной третьей произведения площади основания на высоту, значит 6=1/3*2*h, откуда h=6*3:2=9
Читайте также
а) Итак, S1-сумма=2970; S2-в три раза меньше=990;
Наш ряд имеет вид a1b1+a2b2+a3b3+… +anbn, где a-это десятки, b-единицы. Получается для любого значения ab=10a+b;
Например: 45=4*10+5;
Сложим все десятки вместе: **a1+a2+a3+…+an=A*<wbr />*;
Сложим все единицы вместе: b1+b2+b3…+bn=B<wbr />;
Наша формула для S1=10A+B;
Что бы получить S2, нам надо перевернуть числа, т.е, десятки станут единицами, а единицы станут десятками, поэтому S2=A+10B;
Решим систему уравнений: S1=10A+B и S2=A+10B;
B=S1-10A;
**S2=A+10*S1-100*A;*<wbr />*
Подставим значения:
990=-99A+29700;
99A=28710;
A=290- сумма всех a;
B=70-сумма всех b;
Теперь можем найти минимальное количество чисел, поскольку максимальное возможное значение, это 99, в нём 9 десятков, поэтому n=A/9=290/9=32*(2/<wbr />9), получается минимальное количество 33 числа;
Теперь, выясним во сколько раз A>B=290/70=4*(1/7)<wbr />, получим примерно в 4.1 раза, существуют всего две комбинации, примерно удовлетворяющих нашему значению, а именно: 92 и 51;
Поскольку мы уже рассчитали минимальное количество чисел с 9 десятками, то нам будет удобнее использовать число 92 в дальнейшем.
Умножим 92 на 32 и добавим не достающее число, 92*32=2944;
2970-2944=26;
<h2>Получаем ответ: а)Наш ряд выглядит так: 92(32 раза)+26;</h2>
б) Докажем «от противного» Представим, что такое возможно, тогда наша формула S1=10A+B примет вид: 10A+B=5(A+10B);
10A+B=5(A+10B)
10A+B=5A+50B;
A=49*B/5;
A=(9*4/5)*B;
Значит, что бы такое произошло, A должно быть больше B в 9*4/5 раз. А такой комбинации не существует, поскольку, даже самое маленькое значение для B=1, а самое большое для A=9, получаем A=9/1=9;
<h2>Ответ: б)Нет;</h2>
в) Найдем наименьшее количество возможных чисел(n), для этого возьмём максимально возможно число(99) и поделим: 2970/99=30;
С использованием 9 десяток, их будет 32+доп.число. Теперь подберём такое число, в котором a=9, а b=самое маленькое число(т.е 1), теперь, наш поворот будет наиболее эффективным. Было 91, переворот: 19;
Найдём то самое доп.число, 91 умножим на 32=2912;
Вычтем из нужной суммы получившееся 2970-2912=58.
Наш ряд: 91(32 раза)+58;
Перевернём: 19(32 раза)+85;
Найдём сумму после переворота: 19*32+58=693;
<h2>Ответ: в)693;</h2>
Если мой ответ был полезен, или просто вам понравился, вы всегда сможете его поддержать, нажав на пальчик вверх. Спасибо за внимание.
Пусть Х — скорость течения реки.
По течению лодка двигалась со скоростью (4+Х)км/ч, расстояние в 15 км. преодолела за 15/(4+Х) часов.
Против течения лодка двигалась со скоростью (4-Х) км/ч, расстояние в 15 км. преодолела за 15/(4-Х) часов.
Лодка отсутствовала в пункте А 12 часов. Из них 10 часов она провела в дороге.
Составляем уравнение:
15/(4+Х)+15/(4-Х)=10
Решаем уравнение:
15(4-Х)+15(4+Х)=10(4-Х)(4+Х)
60-15Х+60+15Х=10(4-Х)(4+Х)
(4-Х)(4+Х)=12
16-Х2=12
Х2=4
Х имеет значения 2 и -2
-2 не подходит по смыслу.
Значит, скорость реки 2 км/ч
а) Посчитаем вариант, при котором сумма будет самой наименьшей. Естественно, это просто сумма первых ста чисел, т.е 1+2+3…+100. Можно считать перебирая, а можно через формулу «суммы арифметической прогрессии«.
Теперь рассчитываем сумму. S100=((1+100)/2)*1<wbr />00=5050;
Нам надо попытаться как-нибудь, заменить любое число в нашем ряду на 230. Узнаем, какой суммы нам не достаёт до заданной в условии: 5120-5050=70, ага, а какое самое большое число было в нашем ряду? Правильно, 100. Получается, самое большое число, на которое мы сможем заменить любое число из нашего ряда, это 170. А значит, числа 230 в ряду никак быть не может.
<h2>Ответ: а) Нет;</h2>
б) Возьмём, всё тот же ряд, от 1 до 100, но уберём оттуда число 14 и попытаемся заменить его другим. Например, попробуем взять самое маленькое число после 100, а именно 101 и проведём замену. Сумму первых ста чисел мы нашли, а значит, для замены, нам надо вычесть из неё 14 и прибавить новое значение 101: 5050-14+101=5137<wbr />. К сожалению в условии сказано, что сумма равна 5120, поэтому увы, нельзя исключать число 14 из нашего списка.
<h2>Ответ: б) Нет;</h2>
в) Найдём все числа кратные 14 из нашего ряда (от 1 до 100). Существует множество способов нахождения кратных значений, но в нашем случае, число не такое большое, их можно перебрать в ручную, получаем ряд, посредством сложения: 14, 28, 42, 56, 70, 84, 98. Всего 7 чисел кратных 14. Теперь попробуем заменить их на более большие значения не кратные 14, поскольку на данный момент, наша сумма составляет 5050. Заменим наибольшее кратное число на наименьшее из неиспользованных: 98 на 101;
Наша сумма станет: (101-98)+5050=5053<wbr />;
Далее, будем руководствоваться тем же методом, заменим 84 на 102;
Сумма: (102-84)+5053=5071<wbr />;
Место ещё есть, продолжаем. Заменим 70 на 103;
Сумма: (103-70)+5071=5104<wbr />;
5104, по-прежнему меньше 5120, значит идём дальше. Заменим 56 на 104;
Сумма: (104-56)+5104=5152<wbr />;
Получилось больше чем надо, а значит, нужно вернуться на шаг назад.
Тогда возьмём не 103, а какое-нибудь другое число, что бы сумма ряда стала равна 5120. Почитаем сколько не хватает: 5120-5104=16; Тогда, прибавим эти 16 единиц к числу 103, получим 119, проверим на кратность. 119/14=8.5, а значит оно не кратно. Мы заменили 3 кратных числа из 7, тогда осталось всего 4.
<h2>Ответ: в) 4;</h2>
Если мой ответ был полезен, или просто вам понравился, вы всегда сможете его поддержать, нажав на пальчик вверх. Спасибо за внимание.
1 июня 2015 году выпускники сдают ЕГЭ по математике (базовый).
4 июня 2015 года выпускники сдают ЕГЭ по математике (профильный).
В этом году наш родной Рособрнадзор решил принять беспрецедентные меры по предотвращению утечки информации и он сделал все возможное, чтобы такое никогда не произошло.
Хотя, в прошлые года все социальные сети были забиты всякими заманчивыми предложениями, но это было раньше — все меняется, главное не нарваться на недобросовестных людей, которые пользуются нашей доверчивостью.
Совет один — думайте своей головой и готовьтесь, готовьтесь, готовьтесь.
Удачной вам сдачи!
Вопрос стоит-как лучше решать? Приходит в голову только один способ решения.Пусть х-скорость первого гонщика,а у-скорость второго гонщика,t-время всего пути второго гонщика.Тогда-весь путь -60*3=180 км.Составим 4 равенства. х(t-1/6)=180-здесь 1/6-это 10 минут. у*t=180. 3n=(1/4)*у. 3(n+1)=(1/4)*х-здесь (1/4)-это 15 минут,а n-количество кругов которые сделал второй гонщик за эти 15 минут.Решая третье и четвёртое уравнения получим у+12=х.Подставляет у+12=х в первое уравнение.Получим (у+12)*(t-1/6)=y*t. Из него получим y=72t-12.Подставим во второе уравнение.Получим. (72t-12)*t=180.В получившиеся квадратном уравнении 6t^2-t-15=0 находим корни.Их -два.Один отрицательный(отбрас<wbr />ывает,не имеет смысла).Второй корень t=5/3.Далее найдём скорость второго гонщика у=72*(5/3)-12=108 км/час.Скорость первого гонщика 108+12=120 км/час.Проверка по первому. 120*(5/3-1/6)=120*(9<wbr />/6)=180 км.Ответ-скорость второго гонщика -108 км/час.

а) Как найти длину если известны объем, толщина и ширина?
б) Как найти ширину, если известны длина и площадь?