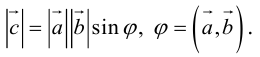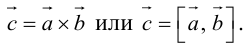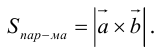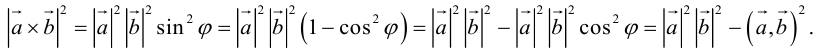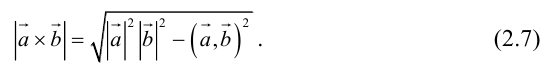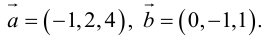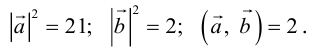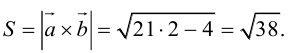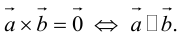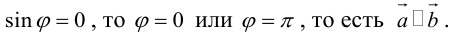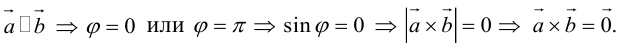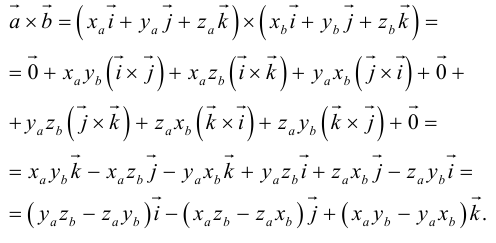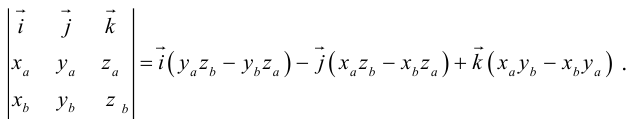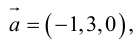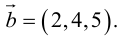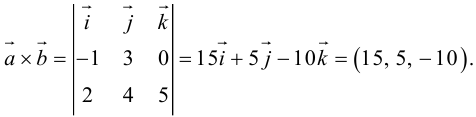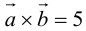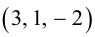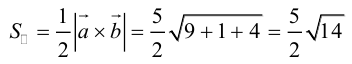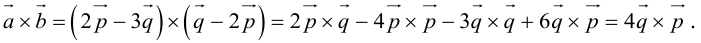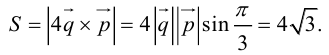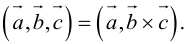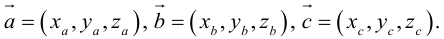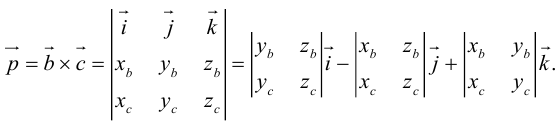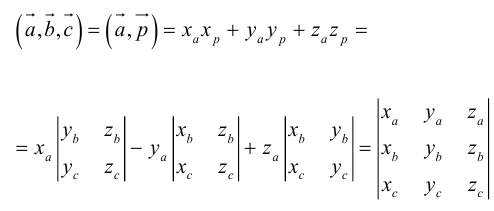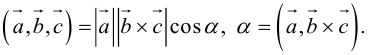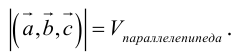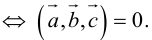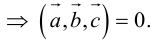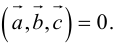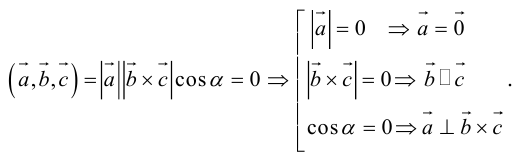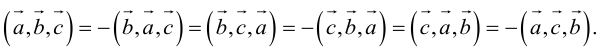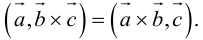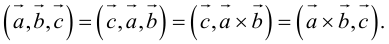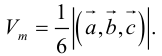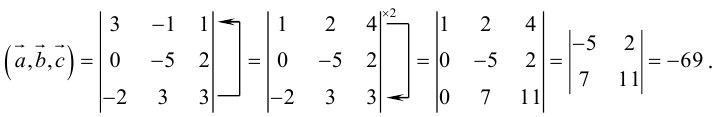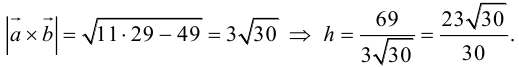Угол между векторами. Ортогональные проекции векторов
Угол между векторами
Углом между двумя ненулевыми векторами называется угол между равными им векторами, имеющими общее начало, не превосходящий по величине числа .
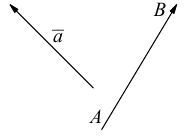
Пусть в пространстве даны два ненулевых вектора и
(рис.1.22). Построим равные им векторы
и
. На плоскости, содержащей лучи
и
, получим два угла
. Меньший из них, величина
которого не превосходит
, принимается за угол между векторами
и
.
Поскольку направление нулевого вектора не определено, то не определен и угол между двумя векторами, если хотя бы один из них нулевой. Из определения следует, например, что угол между ненулевыми коллинеарными векторами либо равен нулю (если векторы одинаково направлены), либо равен (если векторы противоположно направлены).
Ортогональные проекции векторов
Движение по любой прямой может быть в двух направлениях. Ориентированной прямой называется прямая, на которой выбрано направление, т.е. одно из направлений считается положительным, а противоположное — отрицательным. Для измерения длин отрезков на прямой задается масштабный отрезок, который принимается за единицу.
Ориентированная прямая с заданным масштабным отрезком называется осью.
Любой ненулевой вектор , принадлежащий прямой, называется направляющим вектором для данной прямой, поскольку задает на ней ориентацию. Направление вектора
принимается за положительное, а направление противоположного вектора
— за отрицательное. Кроме того, длину вектора
— можно принять за величину масштабного отрезка на этой прямой. Поэтому можно сказать, что любой ненулевой вектор определяет ось — прямую, содержащую этот вектор, задавая на ней направление и масштабный отрезок.
Ортогональной проекцией вектора на ось, задаваемую вектором
, называется его проекция на ось вдоль прямой (или вдоль плоскости), перпендикулярной данной оси. Ортогональную проекцию вектора
на ось, задаваемую вектором
, будем обозначать
.
Ортогональную проекцию вектора на прямую
(см. разд. 1.2.2 и рис. 1.13) будем обозначать
.
Ортогональную проекцию вектора а на плоскость (см. разд. 1.2.2 и рис. 1.14) будем обозначать
.
Разность между вектором и его ортогональной проекцией называют ортогональной составляющей:
— — ортогональная составляющая вектора
относительно вектора
;
— — ортогональная составляющая вектора
относительно прямой
;
— — ортогональная составляющая вектора
относительно плоскости
.
На рис. 1.23 изображены ортогональные проекции вектора :
— на прямую (или на ось
, задаваемую вектором
) вдоль прямой
(рис.1.23,а);
— на прямую (или на ось
, задаваемую вектором
) вдоль плоскости
(рис.1.23,б);
— на плоскость вдоль прямой
(рис.1.23,в).
На рис. 1.23 изображены ортогональные составляющие вектора :
— относительно оси (вектора
):
(рис.1.23,а);
— относительно плоскости (рис.1.23,в).
Для ортогональных проекций справедлива следующая теорема (см. теорему 1.1 в разд. 1.5).
Теорема 1.2 (об ортогональных проекциях вектора).
1. Если на плоскости заданы две взаимно перпендикулярные прямые и
, то любой вектор
на плоскости можно однозначно представить в виде суммы своих ортогональных проекций на эти прямые, т.е.
(рис. 1.24,а).
2. Если в пространстве заданы три попарно перпендикулярные прямые и
, пересекающиеся в одной точке, то любой вектор
в пространстве можно однозначно представить в виде суммы своих ортогональных проекций на эти прямые, т.е.
(рис. 1.24,6).
3. Квадрат длины вектора на плоскости или в пространстве равен сумме квадратов длин своих ортогональных проекций, т.е.
Первые два утверждения представляют собой частные случаи теоремы 1.1. Третье утверждение следует из теоремы Пифагора (для треугольника (рис. 1.24,а) или треугольников
и
(рис. 1.24,6)).
В формулировке теоремы 1.2 прямые можно заменить осями, задаваемыми попарно ортогональными векторами.
На рис.1.24,а проекции вектора на оси одновременно являются ортогональными составляющими:
и
. На рис. 1.24,6 вектор
является проекцией вектора
на плоскость
, содержащую прямые
и
:
, а вектор
является ортогональной составляющей вектора
относительно плоскости
.
Алгебраическое значение длины проекции
Пусть – угол между ненулевым вектором
и осью, задаваемой вектором
, т.е. угол между ненулевыми векторами
и
.
Алгебраическим значением длины ортогональной проекции вектора на ось, задаваемую вектором
, называется длина его ортогональной проекции
, взятая с положительным знаком, если угол
не превышает
, и с отрицательным знаком, если угол
больше
, т.е.:
Например, для проекций, изображенных на рис. 1.25, , поскольку угол
между векторами
и
острый, a
, так как угол
между векторами
и
тупой.
Некоторые свойства проекций векторов переносятся на алгебраические значения их длин, в частности:
1. — алгебраическое значение длины ортогональной проекции суммы векторов равно сумме алгебраических значений длин ортогональных проекций слагаемых;
2. — алгебраическое значение длины ортогональной проекции произведения вектора на число равно произведению этого числа на алгебраическое значение длины ортогональной проекции вектора
Замечания 1.4.
1. Из определения алгебраического значения длины ортогональной проекции следует (см. также рис.1.25), что , т.е. алгебраическое значение длины ортогональной проекции ненулевого вектора на ось равна произведению длины этого вектора на косинус угла между вектором и осью.
Ортогональную проекцию вектора на ось, задаваемую вектором
, можно представить в виде
Если — единичный вектор, то
.
2. Равенство можно использовать как определение косинуса угла между ненулевыми векторами
и
(или, что то же самое, косинуса угла между осями, заданными ненулевыми векторами
и
(рис. 1.26)).
3. Углом между ненулевым вектором и прямой
называется угол
между вектором
и его ортогональной проекцией
на прямую
. Величина угла
может быть найдена по формуле
4. Углом между ненулевым вектором и плоскостью
называется угол
между вектором
и его ортогональной проекцией
на плоскость
. Величина угла
может быть найдена по формуле
Пример 1.7. Основания и
равнобокой трапеции
равны
и
соответственно; точка
— середина стороны
(рис. 1.27). Найти алгебраические значения длин ортогональных проекций векторов
и
на ось, задаваемую вектором
.
Решение. Пусть — высота трапеции,
— точка пересечения прямых
и
. По свойству равнобокой трапеции
; из равенства треугольников
и
.
Обозначим через искомые алгебраические значения длин ортогональных проекций.Тогда из равенств
,
и свойства 1 алгебраических значений длин проекций следует:
Решая систему находим
, т.е.
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
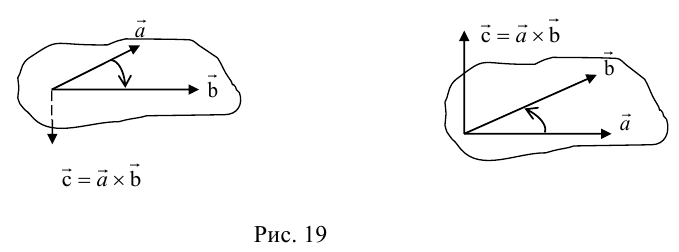
П.10. Ортогональные векторы и матрицы
Два вектора а и b размеров nx1 ортогональны между собой, если их произведение
aTb=a1b1+a2b2+…+anbn=0. (П.10.1)
Заметим, что термин ортогональны относится к двум векторам, а не к одному вектору.
Геометрически два ортогональных вектора перпендикулярны друг к другу. Это показано на рисунке П.10.1 для векторов x1T=[4, 2] и x2T=[–1, 2]. Заметим, что
x1Tx2=(4)(–1)+(2)(2)=0.
Рис. П.10.1. Два ортогональных (перпендикулярных) вектора.
Рекомендуемые материалы
Рис. П.10.2. Векторы а и b в 3-х мерном пространстве.
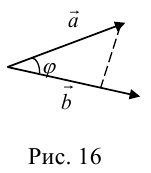
Чтобы показать, что два ортогональных вектора перпендикулярны, пусть угол между векторами а и b на рисунке П.10.2 будет q. В векторной алгебре произведение векторов аТb является их скалярным произведением. Скалярным произведением двух векторов называется число, равное произведению их длин на косинус угла между ними [Беклемишев (2006) стр.24]
аТb=
Если q =90º, то aТb=0, так как cos(90º) =0. Поэтому а и b перпендикулярны, если aТb=0.
Если аТа=1, то вектор а называется нормированным. Вектор b может быть нормирован путём деления его на свою длину 
m=b/
нормирован, так что mТm=1.
Совокупность векторов m1, m2,…, mр, которые нормированы (miТmi=1 для всех i) и взаимно ортогональны (miТmj=0 для всех i≠j; i, j=1, 2, …, р), является ортонормированной совокупностью векторов. Если матрица M= [m1, m2,…, mр] размеров рхр имеет ортонормированные столбцы, то эта матрица называется ортогональной. Поскольку элементы матрицы MТM являются произведениями столбцов M [см. пункт 1 теоремы П.2.3], то ортогональная матрица M обладает следующим свойством
MТM=I. (П.10.4)
Можно показать, что для ортогональной матрицы M также справедливо выражение
MMТ=I. (П.10.5)
Таким образом, ортогональная матрица M имеет как ортонормированные строки, так и ортонормированные столбцы. Из (П.10.4) и (П.10.5) также ясно, что если матрица M ортогональная, то MТ=M–1.
Пример П.10. Для знакомства с ортогональной матрицей, начнём с матрицы
А=
столбцы которой взаимно ортогональны, но не ортонормированы. Для нормирования столбцов матрицы необходимо элементы столбцов поделить на соответствующие длины столбцов, то есть, на 


M=
столбцы которой ортонормированы. Заметим, что строки её также ортонормированы, так что M удовлетворяет уравнениям (П.10.4) и (П.10.5).
□
Умножение вектора на ортогональную матрицу имеет эффект вращения осей. Так, если вектор х преобразуется в вектор у=Mx умножением на ортогональная матрицу M, то длина вектора у равна длине вектора х
уТу=(Mx)Т(Mx)=xТMТMx=xТIx=xТx. (П.10.5)
Следовательно, преобразование х в у является поворотом.
В лекции «5. Экономическое построение системы» также много полезной информации.
Некоторые свойства ортогональных матриц даны в следующей теореме.
Теорема П.10. Если матрица M=Mрр ортогональная, а матрица А=Арр любая квадратная, то
1. det(M)=+1 или –1,
2. det(MТAM)=det(A),
3. значение любого элемента mij матрицы M находится в интервале –1<mij<1.
Доказательство:
- det(I)=det(MТM)=det(MТ)det(M)=det(M)det(M)=[det(M)]2. Поэтому [det(M)]2=1 и det(M)=±1.
- В силу (П.9.13), определитель det(MТAM)=det(AMMТ)=det(AI)=det(A).
- Так как miТmi=1 для всех i, то имеем miТmi=
=1, а максимальное значение любого mij2 равно 1.
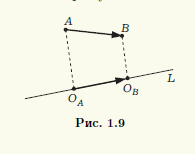
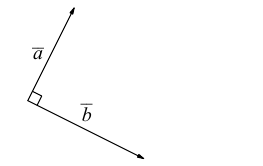
Пусть на плоскости заданы прямая L и точка A. Опустим из точки A на прямую L перпендикуляр (рис. 1.8, а). Тогда его основание (точку O) называют ортогональной проекцией точки A на прямую L. Если прямая L и точка A заданы в пространстве, то в этом случае ортогональной проекцией точки A на прямую L называют точку O пересечения прямой L с перпендикулярной ей плоскостью, проходящей через точку A (рис. 1.8, б). Если точка A лежит на прямой L, то она совпадает со своей ортогональной проекцией на L.
Для вектора — AB (на плоскости или в пространстве) можно построить ортогональные проекции на прямую L его начала и конца (рис. 1.9). Вектор OAOB, соединяющий эти проекции OA и OB и лежащий на прямой L, называют ортогональной проекцией вектора AB на прямую L.
Прямую, на которой задано одно из двух возможных направлений, называют осью. Выбранное направление на оси изображают с помощью стрелки на соответствующем конце оси. Ортогональную проекцию OAOB вектора AB на ось l можно полностью описать длиной вектора OAOB, приписав ей знак,
указывающий направление вектора. Если направление OAOB совпадает с заданным направлением оси, то берут знак плюс, а если направление вектора противоположно направлению оси, то берут знак минус. Длину вектора OAOB со знаком, определяющим направление этого вектора, называют ортогональной проекцией вектора AB на ось l и обозначают прlа.
Обратим внимание на то, что ортогональной проекцией вектора на ось является число, в то время как ортогональная проекция вектора на прямую — это вектор. Чтобы вектору соответствовало число как его проекция, на прямой нужно выбрать одно из двух возможных направлений.
Каждый ненулевой вектор l однозначно определяет ось: его можно рассматривать расположенным на некоторой прямой и задающим на ней направление. Ортогональную проекцию вектора на такую ось называют ортогональной проекцией этого вектора на направление вектора l.
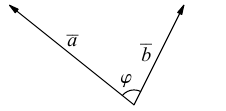
Угол между направлениями двух ненулевых векторов называют углом между этими векторами. Угол может изменяться в пределах от 0 до π. Крайние значения 0 и π отвечают коллинеарным векторам, соответственно однонаправленным и противоположно направленным. Если хотя бы один из двух векторов является нулевым, то угол между такими векторами не определен. Удобно, однако, считать, что в этом случае угол имеет произвольное значение. Так, нулевой вектор коллинеарен любому другому, что формально соответствует углу 0 (или π). Конкретное значение, приписываемое углу между нулевым вектором и каким-либо другим, выбирают исходя из ситуации.
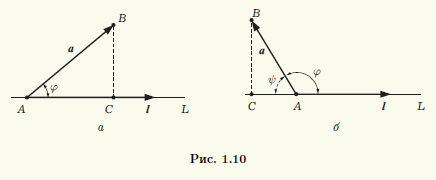
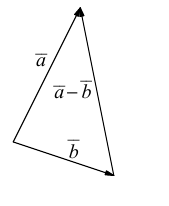
Теорема 1.1. Ортогональная проекция вектора а на направление ненулевого вектора l равна длине |а|, умноженной на косинус угла φ между векторами а и l, т.е.
прl = а|а| cos
где 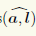
◄ Пусть вектор l лежит на прямой L, а его началом является точка A. Совместим начало вектора а с точкой A, и пусть его концом будет точка B (рис. 1.10). Построим ортогональную проекцию C точки B на прямую L. Тогда вектор AC является ортогональной проекцией вектора а = AB на прямую L.
Если угол φ между векторами а и l острый (как это показано на рис. 1.10, а), то конец вектора l и точка C лежат по одну сторону от точки A. В этом случае проекция а на направление вектора l равна длине |AC| = |AB| cosφ катета AC треугольника ABC.
Если угол φ тупой (см. рис. 1.10, б), то конец вектора l и точка C лежат по разные стороны от точки A. Это значит, что векторы AC и l имеют противоположные направления, а проекция вектора а равна — |AC|. В треугольнике ABC угол ψ, прилежащий к катету AC, равен π — φ, поэтому |AC| = |AB| cos( π — φ) = — |AB| cosφ.
Если же φ = π/2 или а = 0, то точка C совпадает с точкой A и вектор AC является нулевым вектором. Однако cosπ/2 = 0, следовательно, и в этом случае утверждение теоремы справедливо. ►
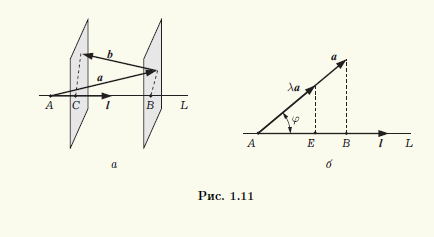
Теорема 1.2. Ортогональная проекция суммы векторов на направление ненулевого вектора равна сумме их ортогональных проекций на направление этого вектора, а при умножении вектора на число его ортогональная проекция на направление ненулевого вектора умножается на то же число:
прl(а + b) = прlа + прlb, прl(λа) — λпрlа.
◄ Доказательство следует из рис. 1.11. В случае, изображенном на рис. 1.11, а, имеем прlа = |AB|, прlb = -|BC|, прl(а + b) = |AC| = |AB| — |BC|. В случае, изображенном на рис. 1.11, б, прlа = |AB| и, если λ > 0, прl(λа) = |AE| = λ|AB|. Остальные варианты (точка C не принадлежит отрезку AB в случае а, λ ≤ 0 в случае б) рассматриваются аналогично. ►
Время на прочтение
10 мин
Количество просмотров 12K
В настоящий момент появилось достаточно большое количество библиотек дополненной реальности с богатым функционалом (ARCore, ARKit, Vuforia). Тем не менее я решил начать свой открытый проект, попутно описывая как это работает изнутри. Если повезет, то позже получится добавить какой-то особый интересный функционал, которого нет в других библиотеках. В качестве целевых платформ пока возьмем Windows и Android. Библиотека пишется на C++, и сторонние библиотеки будут задействованы по минимуму, т.е. преимущественно не будет использовано ничего готового. Фокус в статьях будет направлен на алгоритмы и математику, которые постараюсь описать максимально доступно и подробно. В этой статье пойдет речь про основы векторной алгебры.
Дополненная реальность — это совмещение виртуального мира и реального. Для этого, нам нужно представить окружающее реальное пространство в виде математической модели, понимая закономерности которой, мы сможем получить данные для совмещения. Начнем с основ векторной алгебры.
Вектора — это частный случай матриц, состоящие либо из одного столбца, либо из одной строки. Когда мы говорим о векторе, обычно имеется вектор-столбец . Но записывать вектор как столбец неудобно, поэтому будем его транспонировать —
.
Длина вектора
Первое, что мы рассмотрим — получение длины вектора — , где
— значение длины,
— наш вектор. Для примера возьмем двумерный вектор:
, где
и
— компоненты вектора, значения проекций вектора на оси двумерных координат. И мы видим прямоугольный треугольник, где
и
— это длины катетов, а
— длина его гипотенузы. По теореме Пифагора получается, что
. Значит
. Вид формулы сохраняется и для векторов большей размерности, например —
.
Скалярное произведение
Скалярное произведение векторов — это сумма произведение их компонентов: . Но так как мы знаем, что вектора — это матрицы, то тогда удобнее записать это в таком виде:
. Это же произведение можно записать в другой форме:
, где
— угол между векторами
и
(для двумерного случая эта формула доказывается через теорему косинусов). По этой формуле можно заключить, что скалярное произведение — это мера сонаправленности векторов. Ведь, если
, то
, и
— это просто произведение длин векторов. Так как
— не может быть больше 1, то это максимальное значение, которые мы можем получить, изменяя только угол
. Минимальное значение
будет равно -1, и получается при
, т.е. когда вектора смотрят в противоположные направления. Также заметим, что при
, а значит какие бы длины не имели вектора
и
, все равно
. Можно в таком случае сказать, что вектора не имеют общего направления, и называются ортогональными.
Также при помощи скалярного произведения, мы можем записать формулу длины вектора красивее: ,
.
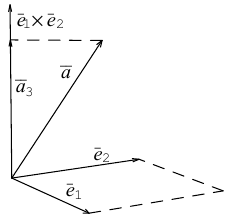
Проекция вектора на другой вектор
Возьмем два вектора: и
.
Проекцию вектора на другой вектор можно рассматривать в двух смыслах: геометрическом и алгебраическом. В геометрическом смысле проекция вектора на ось — это вектор, а в алгебраическом – число.
Вектора — это направления, поэтому их начало лежит в начале координат. Обозначим ключевые точки: — начало координат,
— конечная точка вектора
,
— конечная точка вектора
.
В геометрическом смысле мы ищем такой , чтобы конечная точка вектора (обозначим ее как —
) была ближайшей точкой к точке
, лежащей на прямой
.
Иначе говоря, мы хотим найти составляющую в
, т.е. такое значение
, чтобы
и
Расстояние между точками и
будет минимальным, если
. Получаем прямоугольный треугольник —
. Обозначим
. Мы знаем, что
по определению косинуса через соотношение сторон прямоугольного треугольника
( — гипотенуза,
— прилежащий катет).
Также возьмем скалярное произведение . Отсюда следует, что
. А значит
.
Тут вспоминаем, что — это искомый вектор
, а
—
, и получаем
. Умножаем обе части на
и получаем —
. Теперь мы знаем длину
. Вектор
отличается от вектора
длинной, но не направлением, а значит через соотношение длин можно получить:
. И мы можем вывести финальные формулы:
и
Нормализованный вектор
Хороший способ упростить работу над векторами — использовать вектора единичной длины. Возьмем вектор и получим сонаправленный вектор
единичной длины. Для этого вектор разделим на его длину:
. Эта операция называется нормализацией, а вектор — нормализованным.
Зная нормализованный вектор и длину исходного вектора, можно получить исходный вектор: .
Зная нормализованный вектор и исходный вектор, можно получить его длину: .
Хорошим преимуществом нормализованных векторов является то, что сильно упрощается формула проекции (т.к. длина равна 1, то она сокращается). Проекция вектора на
единичной длины:
Матрица поворота двумерного пространства
Предположим у нас есть некая фигура:
Чтобы ее нарисовать, заданы координаты ее вершин, от которых строятся линии. Координаты заданы в виде набора векторов следующим образом . Наша координатная сетка задана двумя осями — единичными ортогональными (перпендикулярными) векторами. В двумерном пространстве можно получить два перпендикулярных вектора к другому вектору такой же длины следующим образом:
— левый и правый перпендикуляры. Берем вектор, задающим ось
—
и ось
— левый к нему перпендикуляр —
.
Выведем новый вектор, получаемый из наших базисный векторов:
Сюрприз — он совпадает с нашим исходным вектором.
Теперь попробуем как-то изменить нашу фигуру — повернем ее на угол . Для этого повернем векторы
и
, задающих оси координат. Поворот вектора
задается косинусом и синусом угла —
. А чтобы получить вектор оси
, возьмем перпендикуляр к
:
. Выполнив эту трансформацию, получаем новую фигуру:
Вектора и
являются ортонормированным базисом, потому как вектора ортогональны между собой (а значит базис ортогонален), и вектора имеют единичную длину, т.е. нормированы.
Теперь мы говорим о нескольких системах координат — базовой системы координат (назовем ее мировой), и локальной для нашего объекта (которую мы поворачивали). Удобно объединить наш набор векторов в матрицу —
Тогда .
В итоге — .
Матрица , составляющая ортонормированный базис и описывающая поворот, называется матрицей поворота.
Также матрица поворота имеет ряд полезных свойств, которые следует иметь ввиду:
- При
, где
— единичная матрица, матрица соответствует нулевому повороту (угол
), и в таком случае локальные оси совпадают с мировыми. Как рассматривали выше, матрица никак не меняет исходный вектор.
— определитель матрицы равен 1, если у нас, как обычно бывает, правая тройка векторов.
, если тройка векторов левая.
.
.
.
, поворот не меняет длины вектора.
- зная
и
, можем получить исходный вектор
—
. Т.е. умножая вектор на матрицу поворота мы выполняем преобразование координат вектора из локальной системы координат объекта в мировую, но также мы можем поступать и наоборот — преобразовывать мировые координаты в локальную систему координат объекта, умножая на обратную матрицу поворота.
Теперь попробуем повернуть наш объект два раза, первый раз на угол , второй раз на угол
. Матрицу, полученную из угла
, обозначим как
, из угла
—
. Распишем наше итоговое преобразование:
.

Обозначим , тогда
. И из двух операций мы получили одну. Так как поворот — это линейное преобразование (описали ее при помощи одной матрицы), множество преобразований можно описать одной матрицей, что сильно упрощает над ними работу.
Масштабирование в двумерном пространстве
Масштабировать объект достаточно просто, нужно только умножить координаты точек на коэффициент масштаба: . Если мы хотим масштабировать объект на разную величину по разным осям, то формула принимает вид:
. Для удобства переведем операцию в матричный вид:
.
Теперь предположим, что нам нужно повернуть и масштабировать наш объект. Нужно отметить, что если сначала масштабировать, а затем повернуть, то результат будет отличаться, от того результата, где мы сначала повернули, а затем масштабировали:
Сначала поворот, а затем масштабирование по осям:
Сначала масштабирование по осям, а затем поворот:
Как мы видим порядок операций играет большое значение, и его нужно обязательно учитывать.
Также здесь мы также можем объединять матрицы преобразования в одну:
Хотя в данном случае, если , то
. Тем не менее, с порядком преобразований нужно быть очень аккуратным. Их нельзя просто так менять местами.
Векторное произведение векторов
Перейдем в трехмерное пространство и рассмотрим определенное на нем векторное произведение.
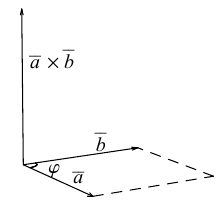
Векторное произведение двух векторов в трёхмерном пространстве — вектор, ортогональный к обоим исходным векторам, длина которого равна площади параллелограмма, образованного исходными векторами.
Для примера возьмем два трехмерных вектора — ,
. И в результате векторного произведения получим
Визуализируем данную операцию:
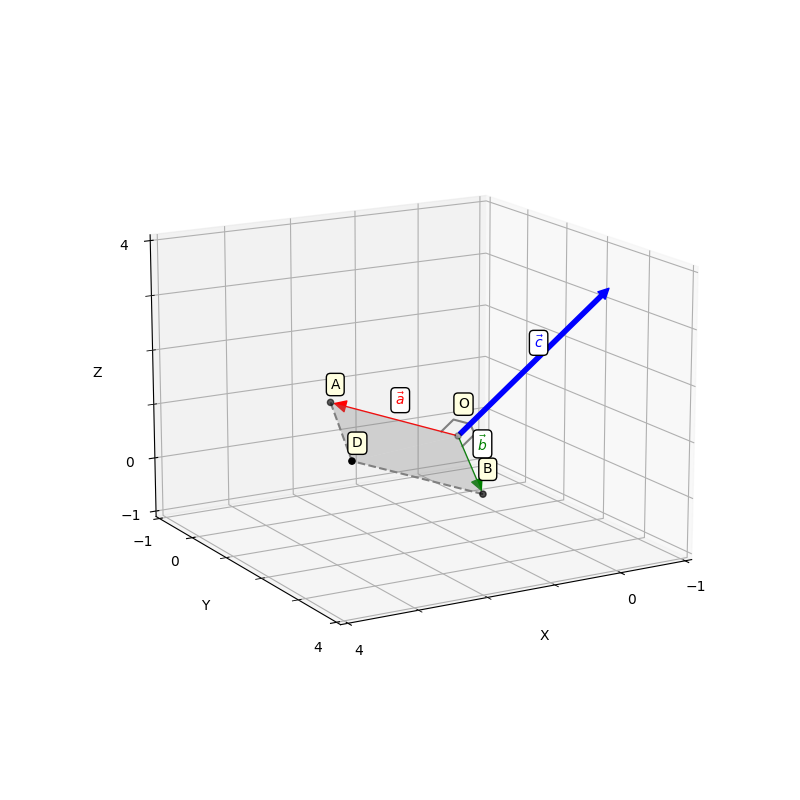
Здесь наши вектора ,
и
. Вектора начинаются с начала координат, обозначенной точкой
. Конечная точка вектора
— точка
. Конечная точка
— точка
. Параллелограмм из определения формируются точками
,
,
,
. Координаты точки
находим как —
. В итоге имеем следующие соотношения:
Два вектора образуют плоскость, а векторное произведение позволяет получить перпендикуляр к этой плоскости. Получившиеся вектора образуют образуют правую тройку векторов. Если берем обратный вектор, то получаем второй перпендикуляр к плоскости, и тройка векторов будет уже левой.
Для запоминания этой формулы удобно использовать мнемонический определитель. Пусть , и мы раскладываем определить по строке как сумму определителей миноров исходной матрицы
:
Некоторые удобные свойства данного произведения:
- Если два вектора ортогональны и нормализованы, то вектор также будет иметь единичную длину. Параллелограмм, который образуется двумя исходными векторами, станет квадратом с длинной сторон равной единице. Т.е. площадь равна единице, отсюда длина выходного вектора — единица.
Матрица поворота трехмерного пространства.
С тем, как формировать матрицу в двумерном пространстве мы разобрались. В трехмерном она формируется уже не двумя, а тремя ортогональными векторами — . По свойствам, описанным выше, можно вывести следующие отношения между этими векторам:
Вычислить вектора этих осей сложнее, чем в матрице поворота двумерного пространства. Для примера получения этих векторов рассмотрим алгоритм, который в трехмерных движках называется lookAt. Для этого нам понадобятся вектор направления взгляда — и опорный вектор для оси
—
. Сам алгоритм:
- Обычно направление камеры совпадает с осью
. Поэтому нормализуем
и получаем ось
—
.
- Получаем вектор оси
—
. В итоге у нас есть два нормализованных ортогональных вектора
и
, описывающих оси
и
, при этом ось
сонаправлена с входным вектором
, а ось
перпендикулярна к входному опорному вектору
.
- Получаем вектор оси
из полученных
и
—
.
- В итоге
В трехмерных редакторах и движках в интерфейсах часто используются углы Эйлера для задания поворота. Углы Эйлера более интуитивно понятны — это три числа, обозначающие три последовательных поворота вокруг трех основных осей . Однако, работать с ними не очень то просто. Если попробовать выразить итоговый вектор напрямую через эти повороты, то получим довольно объемную формулу, состоящую из синусов и косинусов наших углов. Есть еще пара проблем с этими углами. Первая проблема — это то, что сами по себе углы не задают однозначного поворота, так как результат зависит от того, в какой последовательности происходили повороты —
или
или как-то еще. Углы Эйлера — это последовательность поворотов, а как мы помним, смена порядка трансформаций меняет итоговый результат. Вторая проблема — это gimbal lock.
Внутри же трехмерные движки чаще всего используют кватернионы, которых мы касаться не будем.
Существуют разные способы задания поворота в трехмерном пространстве, и каждый имеет свои плюсы и минусы:
- Матрица поворота. С ней просто работать (т.к. это просто матрицы). Но есть логическая избыточность данных — все элементы матрицы связаны определенными условиями, так как количество элементов больше степеней свободы (12 элементов против трех степеней). Т.е. мы не можем взять матрицу и наполнить ее случайными числами, так при несоблюдении условий матрица просто не будет являться матрицей поворота.
- Углы Эйлера. Они интуитивно понятны, но работать с ними сложно.
- Вектор оси вращения и угол порота вокруг нее. Любой возможный поворот можно описать таким образом. Поворота вектора вокруг заданной оси рассмотрим ниже.
- Вектор поворота Родрига. Это трехмерный вектор, где нормализованный вектор представляет собой ось вращения, а длина вектора угол поворота. Этот способ задания поворота похож на предыдущий способ, но количество элементов здесь равно числу степеней свободы, и элементы не связаны между собой жесткими ограничениями. И мы можем взять трехмерный вектор с абсолютно случайными числами, и любой полученный вектор будет задавать какое-то возможное вращение.
Поворот вектора вокруг заданной оси
Теперь рассмотрим операцию, позволяющую реализовать поворот вектора вокруг оси.
Возьмем вектор — описывающий ось, вокруг которой нужно повернуть вектор
на угол
. Результирующий вектор обозначим как
. Иллюстрируем процесс:
Вектор мы можем разложить сумму векторов: вектора, параллельный к вектору
—
, и вектора, перпендикулярному к вектору к вектору
—
.
.
Вектор — это проекция вектора
на вектор
. Т.к.
— нормализованный вектор, то:
Та часть , которая принадлежит оси вращения (
) не измениться во время вращения. Повернуть нам нужно только
в плоскости перпендикулярной к
на угол
, Обозначим этот вектор как
. Тогда наш искомый вектор —
.
Вектор можем найти следующим образом:
Для того, чтобы повернуть , выведем оси
и
в плоскости, в которой будем выполнять поворот. Это должны быть два ортогональных нормализованных вектора, ортогональных к
. Один ортогональный вектор у нас уже есть —
, нормализуем его и обозначим как ось
—
.
Теперь получим вектор оси . Это должен быть вектор, ортогональный к
и
(т.е. и к
). Получить его можно через векторное произведение:
. Значит
. По свойству векторного произведения
будет равно площади параллелограмма, образуемого двумя исходными векторами (
и
). Так как вектора ортогональны, то у нас будет не параллелограмм, а прямоугольник, а значит
.
. Значит
.
Поворот двумерного вектора на угол
можно получить через синус и косинус —
. Т.к.
в координатах полученной плоскости сонаправлен с осью
, то он будет равен
. Этот вектор после поворота —
. Отсюда можем вывести:
Теперь мы можем получить наш искомый вектор:
Мы разобрались с тем, как поворачивать вектор вокруг заданной оси на заданный угол, значит теперь мы умеем использовать поворот, заданный таким образом.
Получить вектор оси вращения и угол из вектора Родрига не составляет большого труда, а значит мы теперь умеем работать и с ним тоже.
Напоминаю, что матрица поворота представляет собой три базисных вектора , а углы Эйлера — три последовательных поворота вокруг осей
,
,
. Значит мы можем взять единичную матрицу, как нулевой поворот
, а затем последовательно поворачивать базисные вектора вокруг нужных нам осей. В результате получим матрицу поворота соответствующую углам Эйлера. Например:
Также можно отдельно вывести матрицы вращения по каждой из осей ,
,
(
,
,
соответственно) и получить итоговую матрицу последовательным их умножением:
Таким же образом можно перевести вектор поворота Родрига в матрицу поворота: также поворачиваем оси матрицы поворота, полученные от единичной матрицы.
Итак, с вращением объекта разобрались. Переходим к остальным трансформациям.
Масштабирование в трехмерном пространстве
Все тоже самое что и двумерном пространстве, только матрица масштабирования принимает вид:
Перемещение объекта
До этого момента точка начала локальных координат не смещалась в мировом пространстве. Так как точка начала координат нашего объекта — это его центр, то центр объект никуда не смещался. Реализовать это смещение просто: , где
— вектор, задающий смещение.
Теперь мы умеем масштабировать объект по осям, поворачивать его и перемещать.
Объединим все одной формулой: :
Чтобы упростить формулу, мы можем, как уже делали ранее, объединить матрицы . В итоге наше преобразование описывает матрица
и вектор
. Объединение вектора
с матрицей
еще более бы упростило формулу, однако сделать в данном случае не получится, потому как сложение здесь — это не линейная операция. Тем не менее сделать это возможно, и рассмотрим этот момент уже в следующей статье.
Заключение
Для какого-то покажется, что статья описывает очевидные вещи, кому-то может показаться наоборот немного запутанной. Тем не менее это базовый фундамент, на котором будет строиться все остальное. Векторная алгебра — является фундаментом для многих областей, так что статья может вам оказаться полезной не только в дополненной реальности. Следующая статья будет уже более узконаправленной.
Содержание:
Векторная алгебра
Векторная алгебра — это раздел векторного исчисления, изучающий линейные операции с векторами и их геометрические свойства; часть линейной алгебры, занимающаяся векторными пространствами; различные векторные алгебры XIX века (например, кватернионов, бикватернионов, сплит-кватернионов).
Векторы и линейные операции над ними
Займемся теперь таким важным как в самой математике, так и в ее многочисленных приложениях, понятием вектора.
Определение: Вектором, на плоскости или в пространстве называется отрезок прямой с заданным на нем направлением, т. е. одна из его граничных точек считается начальной, а вторая — конечной.
Обозначать векторы мы будем строчными латинскими буквами
Длина отрезка, изображающего вектор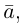
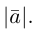
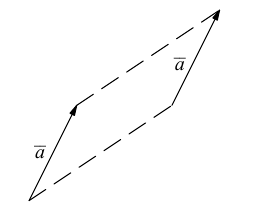
По определению, два вектора считаются равными, если один из них можно преобразовать в другой с помощью параллельного переноса.
Учитывая приведенное определение, всюду в дальнейшем мы без специальных оговорок будем перемещать вектор параллельным переносом в любую удобную для нас точку.
Два вектора 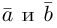
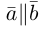
Аналогично, векторы а и b называются ортогональными (обозначение 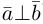
Три вектора называются компланарными, если после приведения их общему началу, они будут расположены в одной плоскости.
Углом между векторами 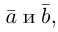
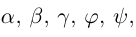
Два ненулевых вектора 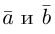
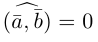
Введем теперь линейные операции над векторами.
а) Умножение числа на вектор.
Произведением действительного числа 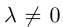
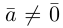
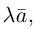
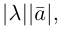
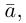
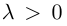
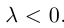
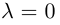
В частности, вектор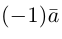
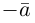
Если 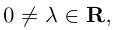
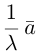
Из приведенного определения сразу же следует, что коллинеарные векторы 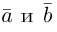
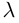
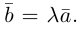
взять число 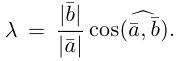
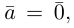
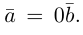
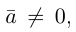
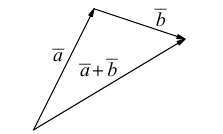
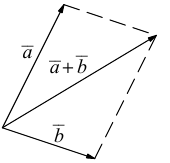
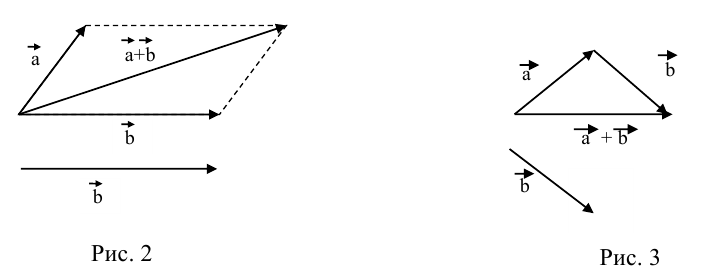
b) Сложение векторов.
Суммой двух векторов 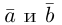
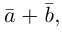
или по равносильному ему правилу параллелограмма
Вектор 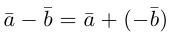
Свойства линейных операций над векторами аналогичны соответствующим свойствам действительных чисел.
Проекцией вектора 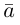
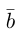
Геометрически очевидны следующие свойства проекции:
Пример №1
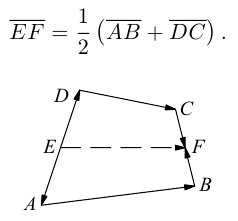
Пусть Е и F — середины сторон AD и ВС соответственно выпуклого четырехугольника ABCD. Доказать, что
Доказательство. Из четырехугольников EDCF и EABF по правил}’ сложения векторов получим:
Сложив данные равенства и учитывая, что 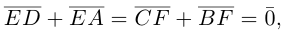
что и требовалось.
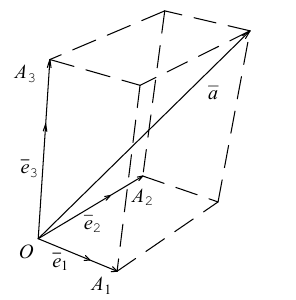
Базис и декартова система координат
Определение: Базисом на плоскости называется упорядоченная пара неколлинеарных векторов. Базисом в пространстве называется упорядоченная тройка некомпланарных векторов.
Обозначение: 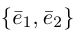
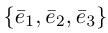
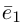
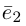
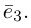
Теорема. Любой вектор единственным образом разлагается по базису, т. е. представляется в виде 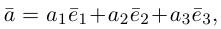
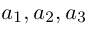
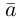
Приведем геометрическое доказательство этого утверждения.
Вектор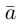
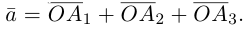
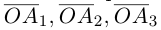
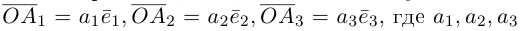
Если базис зафиксирован, то факт, что вектор а в этом базисе имеет координаты 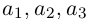
Из доказанной теоремы следует, что при выполнении линейных операций над векторами точно также преобразуются и их координаты, т. е. если 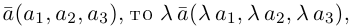
Рассмотрим теперь ортонормированный базис 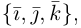
Как видно из чертежа, координаты вектора в ортонормированном базисе представляют собой проекции этого вектора на соответствующие орты. т. е.
Величины 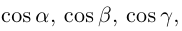
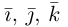
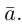
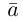
Очевидно также, что
Свяжем теперь с ортонормированным базисом декартову (прямоугольную) систему координат. Для этого поместим начала ортов в некоторую точку О, ось Ох (абсцисс) направим вдоль орта 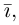
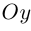
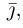
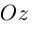
В выбранной системе координат координаты радиуса-вектора 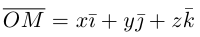
Если известны координаты начальной 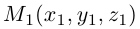
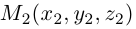
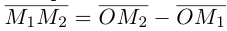
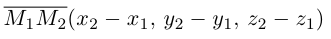
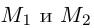
Найдем теперь координаты точки М, делящей отрезок с концами в точках 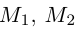
отношении 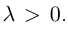
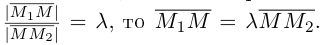
Следовательно, координаты искомой точки вычисляются по формулам:
Найдем, в частности, координаты середины отрезка. Здесь А = 1, поэтому
Пример №2
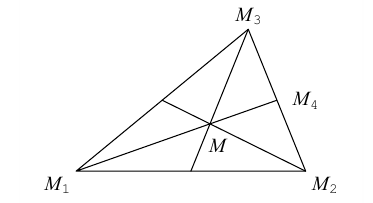
Треугольник задан координатами своих вершин 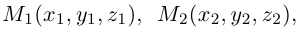
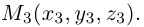
Пусть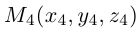
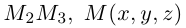
По известному свойству точки пересечения медиан 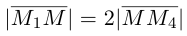
Подставив сюда найденные координаты точки 
Таким образом, координаты точки пересечения медиан треугольника равны средним арифметическим соответствующих координат его вершин.
Замечание. Базисом n-мерного пространства 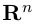
обладающая тем свойством, что любой вектор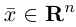
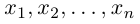
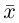
В качестве базиса в 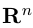
так как, очевидно, любой вектор 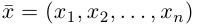
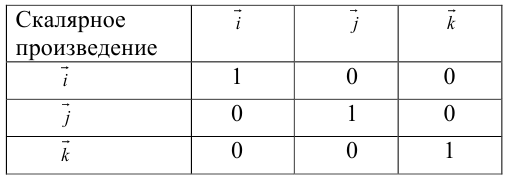
Скалярное произведение векторов
Определение: Скалярным произведением векторов 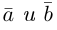
Из этого определения сразу же следует, что
и таким образом, если один из векторов имеет единичную длину, то их скалярное произведение равно проекции второго вектора на единичный.
Отметим основные свойства скалярного произведения.
Первые два и последнее свойства немедленно следуют из определения скалярного произведения, а третье и четвертое — из сформулированных в §1 свойств проекции.
Найдем теперь представление скалярного произведения в координатах. Пусть в орто-нормированном базисе 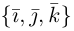
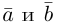
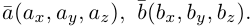
перемножим векторы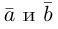
Таким образом, скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат векторов.
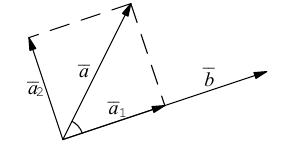
Пример №3
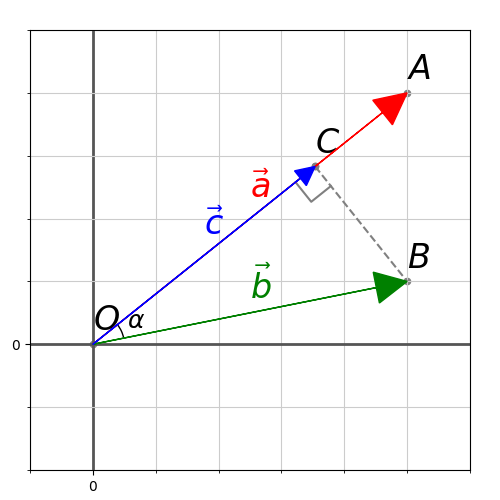
Разложить вектор 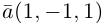
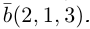
Решение.
Из чертежа следует, что 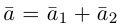
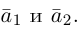
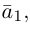
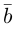
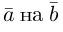
Тогда вторая ортогональная составляющая вектора 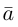
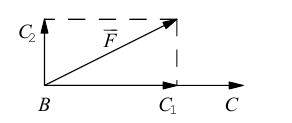
В заключение параграфа рассмотрим одно простое приложение скалярного произведения в механике. Пусть под действием постоянной силы 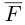
Найдем работу этой силы. Для этого разложим вектор силы 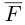
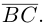
Составляющая 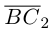
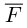
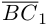
Окончательно, работа силы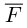
Замечание. Скалярным произведением векторов 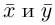
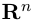
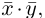
то
Несложной проверкой мы можем убедиться в том, что таким образом определенное скалярное произведение в 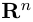
Длиной вектора 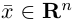
Векторы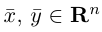
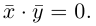
составляют ортонормированный базис пространства 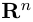
Любой вектор 
n-мерного пространства с координатами
Взяв еще одну точку 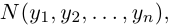
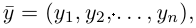
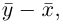
Таким образом переопределенное пространство 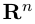
Совокупность точки О(0.0,…, 0) и ортонормированного базиса (1) называется декартовой системой координат евклидова пространства R». Точка 0(0,0,… ,0) называется, естественно, началом координат.
Векторное произведение векторов
Определение: Векторным произведением некоялинеарных векторов 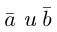

Из этого определения следует, что площадь параллелограмма, построенного на векторах 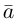
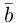

Сформулируем основные свойства векторного произведения.
Первые два свойства очевидным образом следуют из определения векторного произведения. Доказательство третьего ввиду его громоздкости мы приводить не будем.
Найдем формулу для вычисления векторного произведения в координатах. Пусть векторы 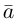
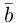
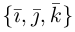
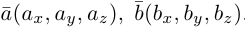
раскроем скобки в векторном произведении 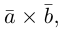
Полученный вектор мы можем записать в виде следующего символического определителя.
вычислять который удобно разложением по первой строке.
Пример №4
Найти составляющую вектора 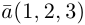
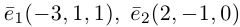
Решение.
Из чертежа видно, что искомая составляющая представляет собой вектор проекции данного вектора 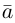

Переходим к вычислениям:
Тогда
Среди многочисленных приложений векторного произведения отметим его применение в механике при вычислении момента силы.
Итак, пусть сила 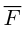
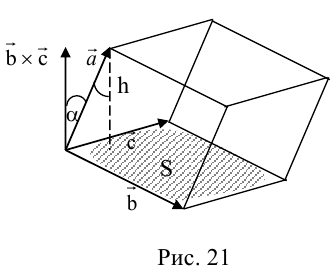
Смешанное произведение векторов
Определение: Смешанным произведением трех векторов 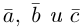
Выясним геометрический смысл смешанного произведения для тройки некомпланарных векторов.
По определению смешанного произведения
Поскольку 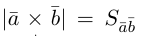
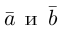
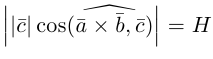
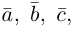
— объем параллелепипеда. Таким образом, абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих векторах.
Если векторы заданы своими координатами в ортонормированном базисе 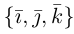
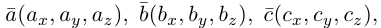
Следовательно (глава I. §2, пункт 3, свойство 7)), в координатах смешанное произведение вычисляется по формуле:
Докажем, пользуясь этой формулой, некоторые свойства смешанного произведения.
что следует из свойства 4) определителя (глава I. §2, пункт 3). Таким образом, в смешанном произведении можно менять местами знаки скалярного и векторного произведения, и поэтому для него используется более короткое обозначение 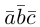
Эти свойства смешанного произведения также являются прямыми следствиями соответствующих свойств определителя.
Докажем еще одно, геометрическое свойство смешанного произведения.
Теорема. Три вектора 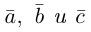
Доказательство. Докажем необходимость условия теоремы. Пусть векторы 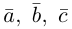
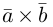
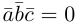
Следствие. Три вектора 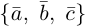
Заметим, кроме того, что, если 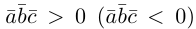
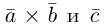
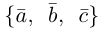
Пример №5
Доказать, что пять точек
расположены в одной плоскости.
Решение. Рассмотрим векторы 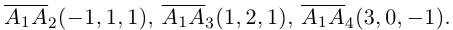
то по доказанной выше теореме эти векторы компланарны и, стало быть. точки 
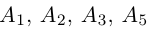
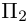
так как первая и третья строки в определителе пропорциональны. Плоскости 
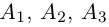
Векторы и линейные операции над ними
Определение: Вектором называется направленный отрезок (рис. 1).
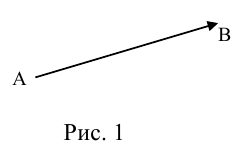
Рис. 1
Так как вектор определяется его началом и концом, то можно сформулировать эквивалентное данному определение.
Определение: Вектором называется упорядоченная пара точек.
Определение: Длина вектора 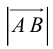
Определение: Два вектора называются равными, если они имеют равные длины и одинаково направлены. При этом одинаково направленными называются векторы, лежащие на параллельных прямых и имеющие одинаковые направления.
Из этого определения следует, что точка приложения вектора значения не имеет, то есть вектор не изменяется, если его перемещать параллельно самому себе, сохраняя длину. Такие векторы называются свободными.
Если начало и конец вектора совпадают, он называется нулевым:
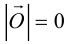
Определение: Векторы 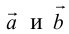
Так как направление нулевого вектора не определено, то он коллинеарен любому другому.
Определение: Векторы называются компланарными, если они параллельны одной плоскости.
Нулевой вектор компланарен любой системе компланарных векторов.
Линейные операции над векторами
Линейными называются операции сложения векторов и умножения на число.
Сложение
а) Правило параллелограмма (рис.2): начала 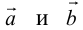
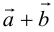
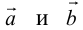
б) Правило треугольника (рис. 3): начало 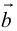
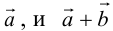
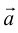
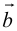
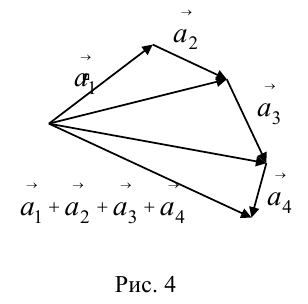
в) Правило сложения нескольких векторов (рис. 4).
Вектор 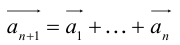
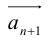
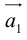
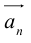
Умножение на число
Определение: Произведением вектора 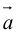
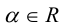
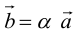
а) 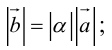
б) 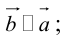
в)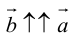
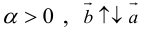
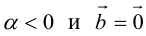
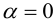
Произведение 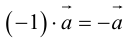
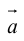
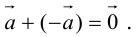
Определение: Разностью 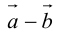
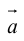
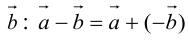
Начала 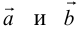
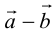
Свойства линейных операций
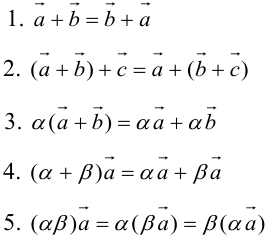
Определение: Результат конечного числа линейных операций над векторами называется их линейной комбинацией: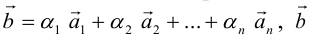
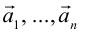
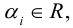
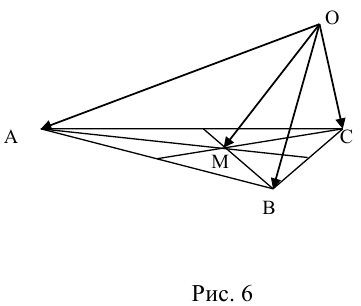
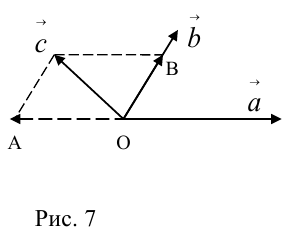
Пример №6
Пусть М – точка пересечения медиан треугольника АВС, а О – произвольная точка пространства. Представить 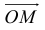
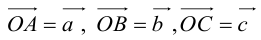
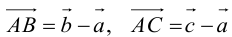
По правилу треугольника 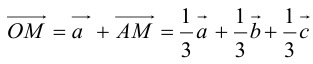
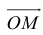
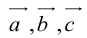
Теорема: Пусть 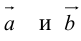
где коэффициенты (2.1) определяются единственным образом.
Представление вектора 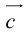
Доказательство:
- Пусть среди
есть два коллинеарных, например:
- Пусть среди
коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с
, а стороны параллельны прямым, на которых лежат
(рис. 7).
Тогда c 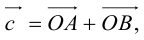
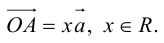
Докажем единственность разложения. Предположим, что 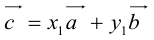
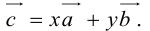
Если 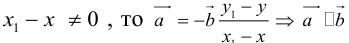
Теорема: Пусть 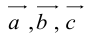
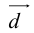
причем единственным образом.
Представление вектора 
Доказать самостоятельно.
Проекция вектора на ось
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.
Координаты вектора
Осью называется направленная прямая.
Определение: Ортом оси 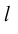
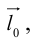
направление которого совпадает с направлением оси.
Определение: Ортогональной проекцией точки М на ось 
Определение: Ортогональной проекцией вектора 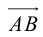
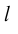
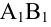
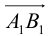
Определение: Углом между вектором и осью называется угол, на который нужно повернуть в положительном направлении ось до совпадения ее направления с направлением вектора (положительным считается поворот против часовой стрелки).
Очевидно, проекцию вектора на ось можно найти по формуле
Можно показать, что проекция линейной комбинации векторов равна та-
кой же линейной комбинации их проекций:
В частности, проекция суммы векторов равна сумме их проекций:
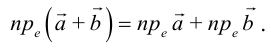
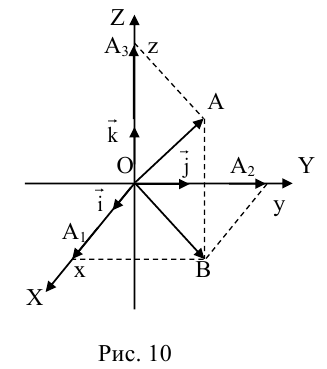
Рассмотрим прямоугольную декартову систему координат ХОY. Обозначим 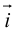
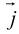

Аналогично в пространственной системе OXYZ 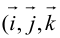
– разложение 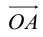
Таким образом, если задана прямоугольная декартова система координат (пдск), то со всяким пространственным вектором 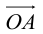
Определение: Координатами вектора 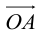
Таким образом, можно дать еще одно определение вектора.
Определение: Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).
Пример №7
Если 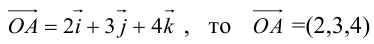
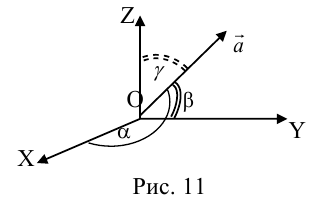
Так как, с одной стороны, вектор – объект, имеющий длину и направление, а с другой, – упорядоченная тройка чисел, то, зная длину и направление, можно определить его координаты и наоборот. Направление вектора в заданной системе координат характеризуется его направляющими косинусами (рис. 11):
Из этих формул очевидно следует основное свойство направляющих косинусов:
Если известны длина 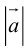
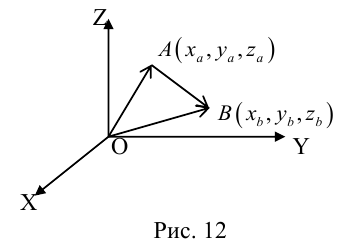
Пусть AB – произвольный вектор в системе OXYZ, OA,OB – радиус-векторы его начала и конца,
Тогда
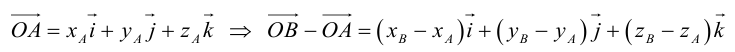
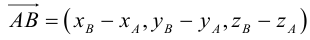
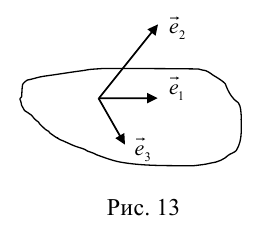
Определение: Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).
Если 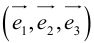
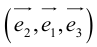
Определение: Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и длина каждого равна 1.
Такой базис принято обозначать
Из теоремы 2 следует, что всякий вектор 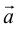
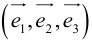
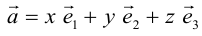
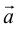
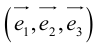
Определение: Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.
Если 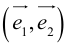
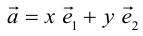
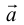
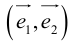
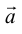
Определение: Базисом на прямой называется любой ненулевой вектор этой прямой.
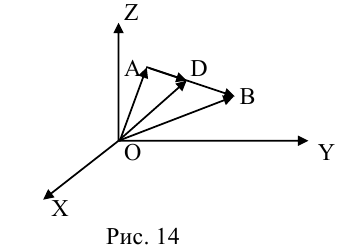
Деление отрезка в данном отношении
Рассмотрим задачу: дан отрезок AB . Найти точку D , которая делит AB в заданном отношении 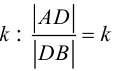
Введем прямоугольную декартову систему координат (пдск) OXYZ, тогда
Обозначим
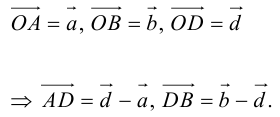
Так как 
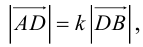
Переходя от этого векторного равенства к равенству соответствующих координат, получим:
ЗАМЕЧАНИЕ 1. Если D – середина отрезка AB , то k 1, поэтому
ЗАМЕЧАНИЕ 2. Если k < 0, 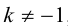
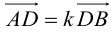
В этом случае
Скалярное произведение векторов
Определение: Скалярным произведением векторов 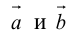
Скалярное произведение обозначается так: 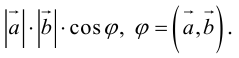
Так как 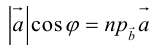
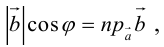
Свойства скалярного произведения
1.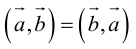
2.
Доказательство:
3.
Доказательство:
а) 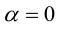
б)
в) 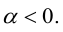
4.
Отсюда следует, что
Необходимым и достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения:
5.
Доказательство:
а) пусть
б) пусть
В первом и втором случаях один из сомножителей – нулевой вектор. Его направление не определено, поэтому можно считать, что 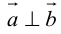
Используя свойства 4 и 5, составим таблицу вычисления скалярного произведения базисных векторов
Пусть в некоторой пдск 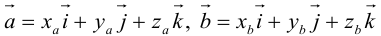
Таким образом,
Пример №8
Найти, при каком значении x векторы 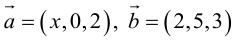
Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю (свойство 5), поэтому найдем скалярное произведение по формуле (2.5):
Пример №9
Найти угол между биссектрисой AD и медианой 
Так как 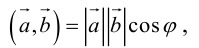
то
Найдем координаты векторов 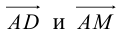
По теореме о биссектрисе внутреннего угла треугольника
Чтобы найти k , вычислим длины AC и AB :
Разделим отрезок CB в данном отношении по формулам (2.3):
отсюда
Заметим, что 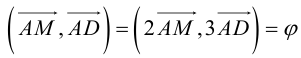
Пример №10
Найти
Воспользуемся свойствами 1–4 скалярного произведения:
Отсюда
ЗАМЕЧАНИЕ. Так как работа силы 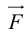
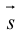
Определение векторного произведения векторов
Определение: Тройка некомпланарных векторов 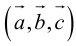
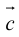
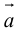
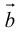
Определение: Векторным произведением вектора 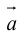
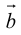
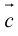
(
перпендикулярен плоскости векторов
и
).
- Направление
таково, что тройка
– правая.
Векторное произведение обозначается так:
ЗАМЕЧАНИЕ 1. Геометрический смысл векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.
Это следует из того, что площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними.
Заметим, что
Таким образом, длину вектора векторного произведения можно вычислить с помощью скалярного произведения по формуле
Пример №11
Найти площадь параллелограмма, построенного на векторах
По формуле (2.7):
ЗАМЕЧАНИЕ 2. Направление вектора 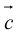
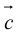
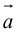
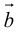
Свойства векторного произведения
1.
Доказательство:
а)пусть 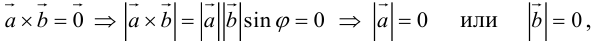
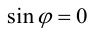
Его направление не определено, поэтому можно считать, что 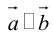
б)пусть
2. 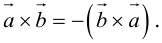
Доказательство: По определению направления векторов 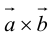
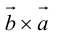
3.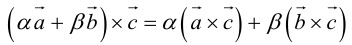
Векторное произведение также линейно и по второму сомножителю.
Используя определение и свойства 1 и 2, составим таблицу вычисления векторного произведения базисных векторов 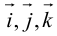
Пусть в некоторой пдск 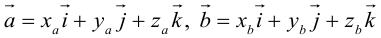
Заметим, что это выражение можно получить, вычислив символический определитель (сделать это можно по-разному, но лучше разложить по первой строке):
Таким образом,
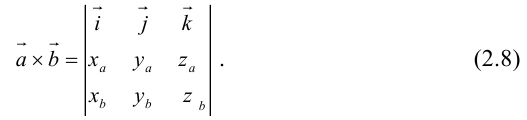
Пример №12
Вычислить векторное произведение векторов
По формуле (2.8):
Заметим, что площадь треугольника, построенного на векторах 
или
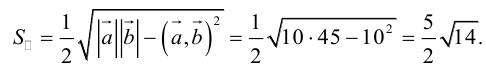
Пример №13
Вычислить площадь параллелограмма, построенного на векторах 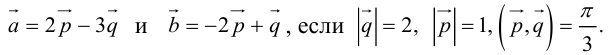
Так как 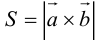
Отсюда
Определение смешанного произведения векторов
Определение: Смешанным произведением векторов 
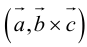
Смешанное произведение обозначается так:
Пусть в некоторой пдск
Обозначим
Тогда
по 7 свойству определителей.
Таким образом,
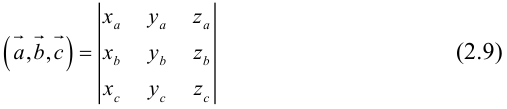
По определению скалярного произведения
Совместим начала всех трех векторов в одной точке. Тогда (рис. 21)
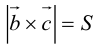
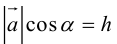
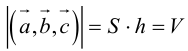
Геометрический смысл смешанного произведения: модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах-сомножителях, при этом 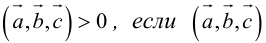
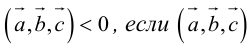
Свойства смешанного произведения
1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения: 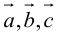
Доказательство: а) 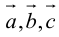
Если 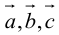
б)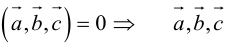
Во всех трех случаях 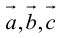
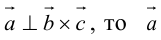
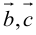
2. Круговая перестановка сомножителей в смешанном произведении не изменяет его величины. Перестановка соседних сомножителей изменяет его знак, не изменяя абсолютной величины:
Доказательство следует из формулы (2.9) и свойства 3 определителей, при этом круговая перестановка сомножителей соответствует двойной перемене строк в определителе, а потому оставляет его неизменным.
3. В смешанном произведении векторное и скалярное произведения можно менять местами:
Доказательство: из свойства 2 смешанного произведения и свойства 1 скалярного получим:
4. Смешанное произведение линейно по каждому из трех сомножителей.
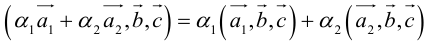
Доказательство следует из формулы (2.9) и свойств определителей.
Пример №14
Найти объем тетраэдра, построенного на векторах
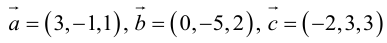
Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому
Отсюда 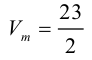
Чтобы найти высоту, воспользуемся формулой
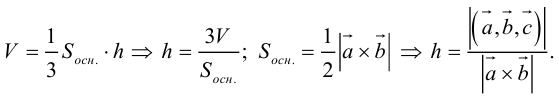
По формуле (2.7)
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Геометрия
- Аналитическая геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика



 =1, а максимальное значение любого mij2 равно 1.
=1, а максимальное значение любого mij2 равно 1.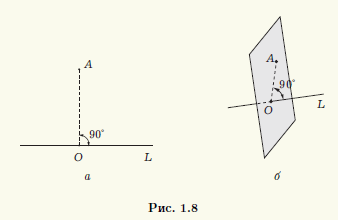








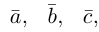
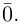
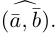
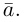
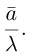
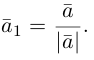
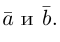
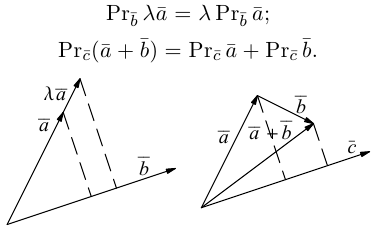
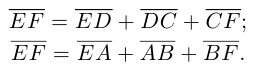
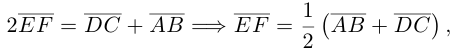
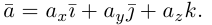
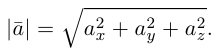

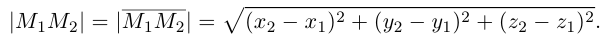
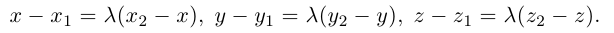
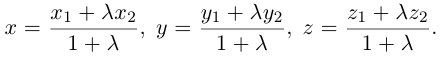
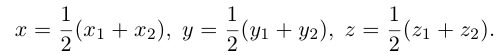
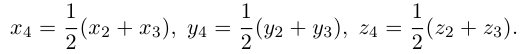
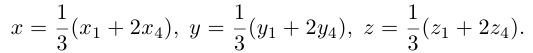
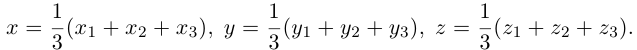


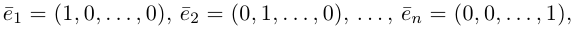
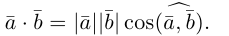
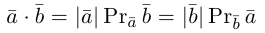
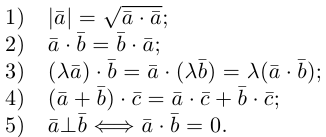
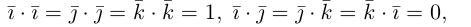
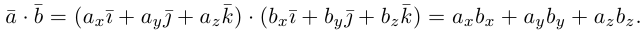
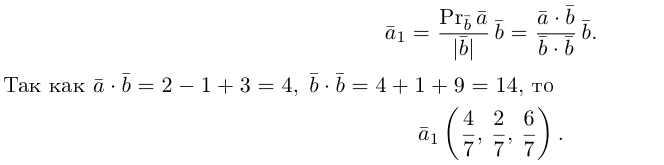
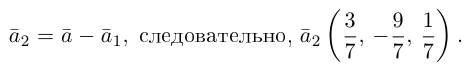
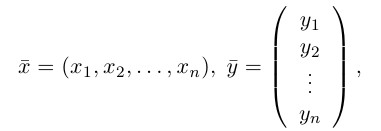
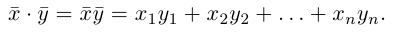
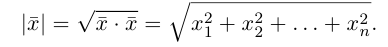
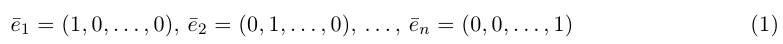
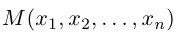

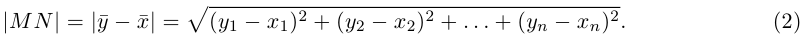
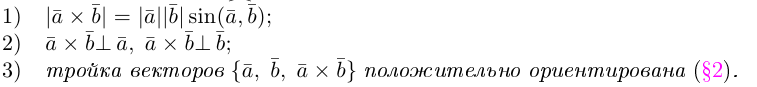
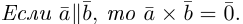
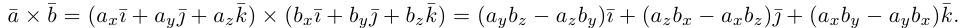
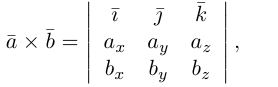
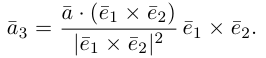
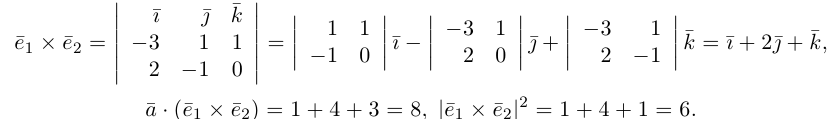
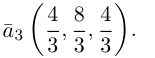
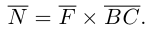
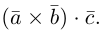
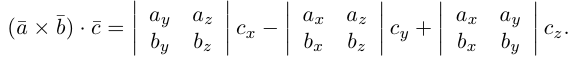
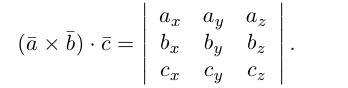
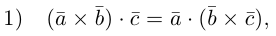
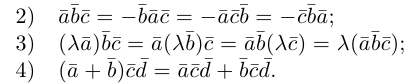
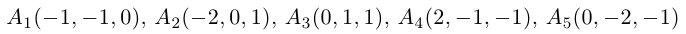
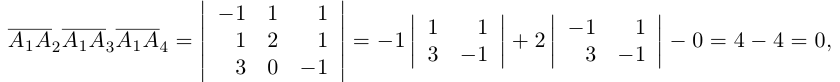
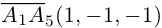
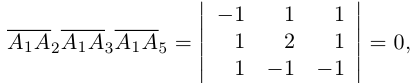

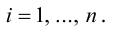
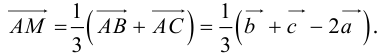
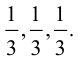
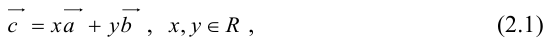
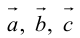 есть два коллинеарных, например:
есть два коллинеарных, например: 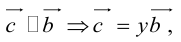
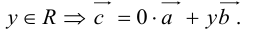
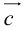 , а стороны параллельны прямым, на которых лежат
, а стороны параллельны прямым, на которых лежат 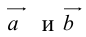 (рис. 7).
(рис. 7). 
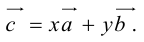
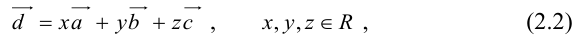
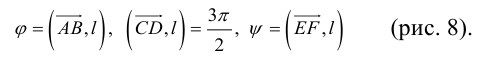
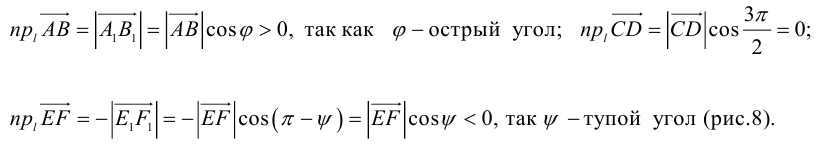
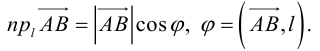
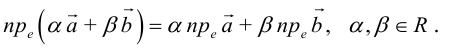
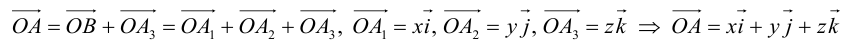
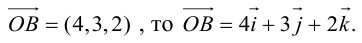
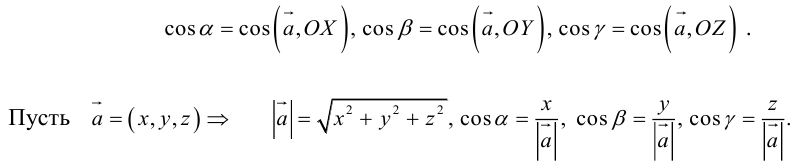
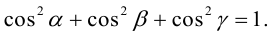
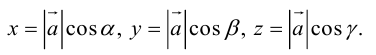
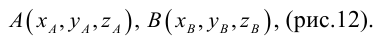
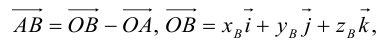
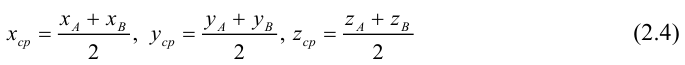
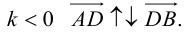
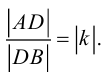
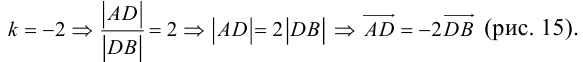
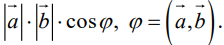
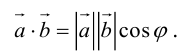
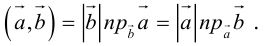
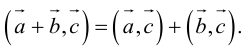
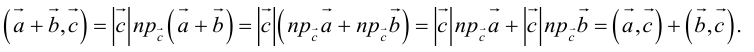
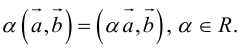
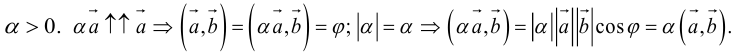
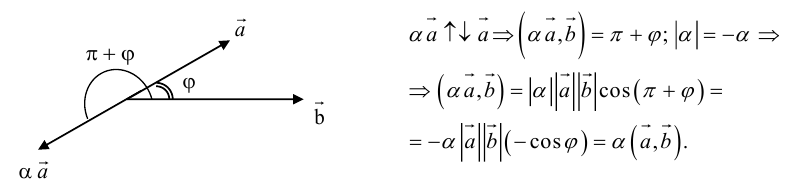
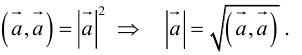
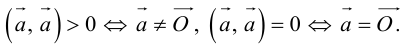
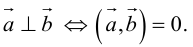
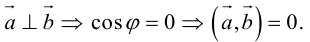
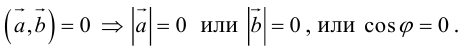
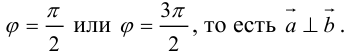
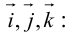
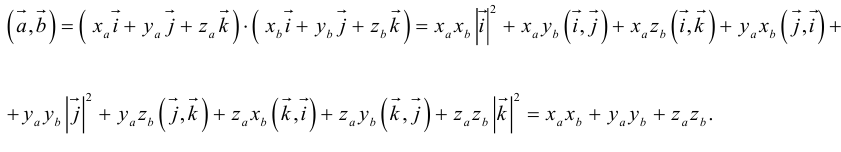

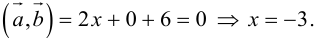
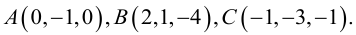

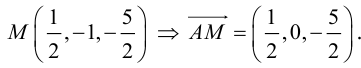
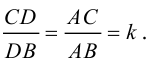
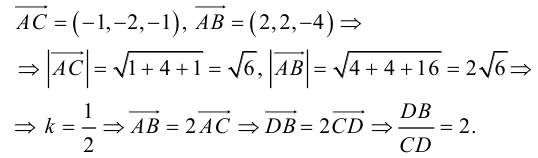
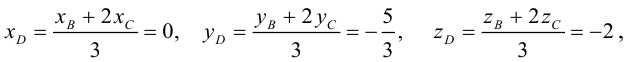
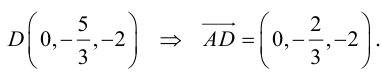
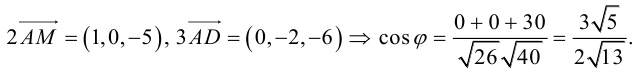
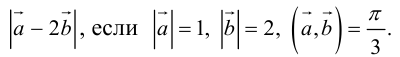
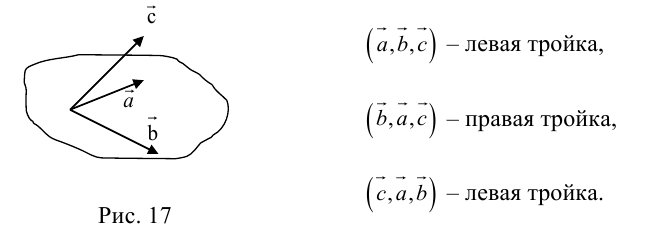
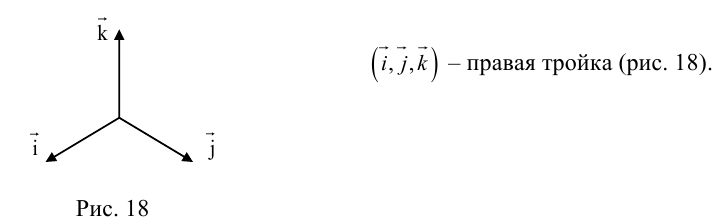
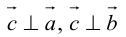 (
(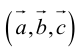 – правая.
– правая.