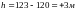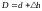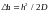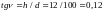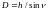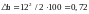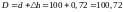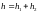1. Определение горизонтального проложения линии
По отметкам ее начальной и конечной точек
8.1.1. Цель лабораторной
работы:
определить
горизонтальную проекцию d
линии АВ
(рис. 8.1) по
отметкам ее начальной и конечной точек.
8.1.2. Приборы и
принадлежности:
ватман формата А4, калькулятор, линейка,
карандаш.
8.1.3. Порядок выполнения работы
Задание указано в
прил. 11 Л.Р. 8.1.
Пример. Длина
наклонной линии D
= 100,00 м и отметки
точек:
НА
= 120 м и НВ
= 123 м.
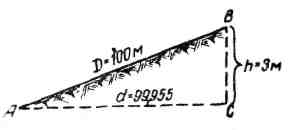
Рис.
8.1.
Горизонтальное проложение линии
Вычислить превышение
точки В над точкой А. Как видно из рисунка,
.
С учетом поправки
горизонтальное проложение будет равно:
.
(8.1)
Определить поправку
за наклон линии по формуле
.
(8.2)
где h
— превышение;
D — длина
наклонной линии.
Следует помнить,
что поправка за наклон линии всегда
отрицательна независимо от знака угла
наклона.
Тогда
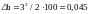
Введя поправку в
наклонную линию со знаком минус, получим
горизонтальную проекцию 100,000 м – 0,045 м
= 99,955 м.
8.1.4. К
сдаче представляют:
оформленную задачу с решением и схемой.
2. Определение наклонного расстояния по горизонтальному проложению линии, если известны отметки концов этой линии
8.2.1. Цель лабораторной
работы: определить
наклонное расстояние D
линии АВ (рис.
8.1) по горизонтальной проекции и разности
концов отметок.
8.2.2. Приборы и
принадлежности:
чертежная бумага
формата А4,
калькулятор, линейка, карандаш.
8.2.3. Порядок выполнения работы
Задание указано в
прил.11 Л.Р. 8.2 Рассмотрим на примере:
необходимо определить наклонное
расстояние D
(рис. 8.1) если горизонтальная проекция
d
= 100,00 м, а разность отметок концов линии
h=12
м.
,
(8.3)
т.е.
;
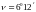
Наклонное расстояние
будет равно
,
(8.4)
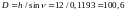
или по вышеприведенной
формуле (8.1), если ввести поправку со
знаком плюс к d
по формуле
;
(8.5)
;
.
8.2.4. К
сдаче представляют
оформленную задачу с решением и схемой.
3. Определение высоты недоступного сооружения
8.3.1.
Цель лабораторной работы: определить
высоту недоступного сооружения.
8.3.2.
Приборы и принадлежности:
теодолит, штатив, мерная лента, рейка,
полевой журнал измерения превышений.
8.3.3. Порядок выполнения работы
На
местности эту работу можно выполнить
с помощью теодолита и мерной ленты.
Теодолит располагают вблизи здания или
сооружения так, чтобы можно было измерить
расстояние от точки установки теодолита
до стены здания, а также определить
соответствующие углы наклона визирной
оси теодолита. Обработать полевой журнал
измерения превышений.
-
С
помощью нитяного дальномера измерить
расстояние d до сооружения (рис. 8.2).
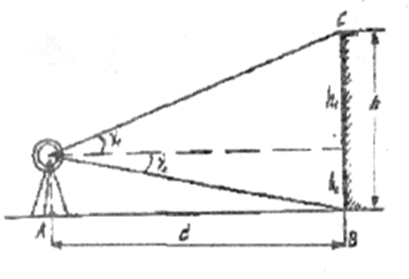
Рис.
8.2.
Определение высоты недоступного
сооружения
-
При
КП и КЛ измерить вертикальные углы ν1
и ν2
до верхней и нижней точек недоступного
сооружения; -
Определить МО
теодолита.
Формулы
для расчета превышений:
(8.6)
Результаты
измерений записать в табл. 8.1
Таблица
8.1
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Размещено 3 года назад по предмету
Математика
от nik891821
-
Ответ на вопрос
Ответ на вопрос дан
elsahlouОтвет:
5см
Пошаговое объяснение:
Наклонная является гипотенузой даного прямоугольного треугольника. Треуголиник-египктский по отношению сторон.
-
Ответ на вопрос
Ответ на вопрос дан
uncl95Пошаговое объяснение:
Длинна наклонной это гипотенуза прямоугольного треугольника
По теореме Пифагора
√4²+3²=√25=5 см
Длина наклонной 5 см
Рисунок во вложении
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
ryifa274
Вопрос по геометрии:
Найдите длину наклонной, если
её проекция 10 см, угол наклона 300
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
fenistapea408
(Длина проекции)=(длина наклонной)* cos(угла наклона).
В данном случае: 10=х*(√(3)/2), х=20/√(3)=20*√(3)/3.
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат — это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

silvewolf1
+10
Решено
7 лет назад
Геометрия
10 — 11 классы
10 класс! Из точки А к плоскости Альфа, проведен перпендикуляр и наклонная. Длина наклонной 6, и образует с плоскостью угол 30 градусов. Найти длину проекции наклонной
Смотреть ответ
1
Ответ проверен экспертом
5
(1 оценка)
2
kostichevs
7 лет назад
Светило науки — 357 ответов — 3172 помощи
AB — перпендикуляр
AC=6
∠α=30°
Решение:
ΔABC — прямоугольный
AC — гипотенуза
BC — проекция наклонной на плоскость. Найдем BC.
AB — катет, лежащий против угла 30°, значит равен половине гипотенузы:
AB=1/2AC=3
По т. Пифагора находим катет BC:
BC=√AC²-AB²=√36-9=√25=5
Ответ: 5
(1 оценка)
https://vashotvet.com/task/7057176
Под действием силы в 120 Н груз массой 12 кг перемещается вверх по наклонной плоскости. Коэффициент полезного действия наклонной плоскости 45%. Чему равна длина наклонной плоскости, если ее высота 120 см?
Сначала определим полезную работу, которая совершается при подъеме данного груза на высоту 120 см = 1,2 м. Апол = mgh = 12*10*1,2 = 144 Дж. После этого используя формулу КПД найдем полную работу. КПД = Апол/Аполн *100%, Аполн = Апол*100/45 = 320 Дж. После этого можно определить длину наклонной плоскости используя формулу работы A = F*s, где s=l (длине наклонной плоскости). l = A/F = 320/120 = 2,67 м = 267 см.
Примечание. Текст задачи взят с форума. Если Вы не нашли решения нужного типа задачи — пишите на форуме. Наверняка курс будет дополнен.
Задача.
| Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если наклонные относятся между собой как 1:2, а проекции наклонных равны 1 см и 7 см. | З точки до плоскості проведені дві похилі. Знайдіть довжини похилих, якщо похилі відносяться між собою як 1:2, а проекції похилих рівні 1 см і 7 див. |
Решение.
Обозначим заданную в условии точку как В. Пусть наклонные к плоскости пересекают плоскость в точках А и D .
Опустим из точки В перпендикуляр на данную плоскость. Обозначим точку пересечения перпендикуляра с плоскостью как С.
Отметим, что у нас образовались прямоугольные треугольники DBC и ABC с прямым углом C. Из чего следует, что по теореме Пифагора:
BC 2 + AC 2 = AB 2
и
BC 2 + CD 2 = BD 2
или
BC 2 = AB 2 — AC 2
и
BC 2 = BD 2 — CD 2
Теперь, учитывая, что левые части обоих выражений равны, получаем
AB 2 — AC 2 = BD 2 — CD 2
Подставим значения, которые известны по условию
AB 2 — 7 2 = BD 2 — 1
AB 2 — 49 = BD 2 — 1
Поскольку длины наклонных соотносятся как 1:2, обозначив длину BD как х (икс), получаем, что длина AB = 2x, откуда
4х 2 — 49 = х 2 — 1
3х 2 = 48
х 2 = 16
х = 4
Откуда длина второй наклонной равна 4 * 2 = 8 см
Ответ: 4 и 8 см.
Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если одна на 26 см больше другой, а проекции наклонных равны 12 см и 40 см.
Решение.
Обозначим заданную в условии точку как В. Пусть наклонные к плоскости пересекают плоскость в точках А и D .
Опустим из точки В перпендикуляр на данную плоскость. Обозначим точку пересечения перпендикуляра с плоскостью как С.
Отметим, что у нас образовались прямоугольные треугольники DBC и ABC с прямым углом C. Из чего следует, что по теореме Пифагора: BC 2 + AC 2 = AB 2
и
BC 2 + CD 2 = BD 2
или
BC 2 = AB 2 — AC 2
и
BC 2 = BD 2 — CD 2
Теперь, учитывая, что левые части обоих выражений равны, получаем
AB 2 — AC 2 = BD 2 — CD 2
Примем во внимание, что большая наклонная имеет большую проекцию.
Кроме того, поскольку одна наклонная на 26 см больше другой, то пусть BD = AB — 26.
Откуда AB = BD + 26
Подставим значения, которые известны по условию
(BD + 26) 2 — 40 2 = BD 2 — 12 2
BD 2 + 52BD + 676 — 1600 = BD 2 — 144
52BD = 780
BD = 15
Наклонная к прямой
Что такое наклонная к прямой? Сколько наклонных можно провести из одной точки к данной прямой? Как найти расстояние между основаниями наклонных?
Наклонной, проведенной из точки A к прямой a, называется отличный от перпендикуляра отрезок, соединяющий точку A с некоторой точкой на прямой a.
Рисунок наклонной, проведенной из данной точки к данной прямой, начинают с изображения перпендикуляра (даже если в условии задачи о перпендикуляре не упоминается).
Чтобы нарисовать наклонную, нужно соединить точку, из которой проводится наклонная, с любой точкой на данной прямой.
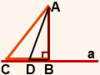
На рисунке 1 AB — перпендикуляр, проведенный из точки A к прямой a, AC — наклонная.
Точка B — основание перпендикуляра, точка C — основание наклонной AC.
Отрезок BC, соединяющий основание перпендикуляра с основанием наклонной, — проекция наклонной AC на прямую a.
Из точки к прямой можно провести бесконечно много наклонных.
Две наклонные проведенные из данной точки к данной прямой, могут быть расположены как по одну сторону от перпендикуляра, так и по разные стороны от него.
На рисунке 2 наклонные AC и AD расположены по одну сторону от перпендикуляра AB.
BC — проекция наклонной AC на прямую a,
BD — проекция наклонной AD на прямую a.
CD — расстояние между основаниями наклонных
Если наклонные расположены по одну сторону от перпендикуляра, чтобы найти расстояние между основаниями наклонных, надо найти разность между длинами их проекций.
На рисунке 3 наклонные AC и AD расположены по разные стороны от перпендикуляра AB.
BC — проекция наклонной AC на прямую a,
BD — проекция наклонной AD на прямую a.
CD — расстояние между основаниями наклонных
Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.
В следующий раз рассмотрим свойства наклонных.
2 Comments
Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.