Как найти длину линии через координаты - AvtoShod.ru

Загрузить PDF

Найти длину вертикального или горизонтального отрезка на координатной плоскости можно с помощью координат, а вот сделать это с диагональным отрезком сложнее. Длину диагонального отрезка можно вычислить по формуле, которая основана на теореме Пифагора, где гипотенузой прямоугольного треугольника является наш диагональный отрезок.^[1] С помощью этой формулы можно быстро найти длину любого отрезка на координатной плоскости.

1

Запишите формулу для вычисления длины. Формула: $d={sqrt {(x_{{2}}-x_{{1}})^{{2}}+(y_{{2}}-y_{{1}})^{{2}}}}$ , где — длина отрезка, $(x_{{1}},y_{{1}})$ — координаты начальной точки отрезка, $(x_{{2}},y_{{2}})$ — координаты конечной точки отрезка.^[2]
2

Найдите координаты точек отрезка. Возможно, они будут даны. Если нет, найдите их по осям Х и Y.^[3]
3

Подставьте координаты в формулу. Будьте внимательны и подставьте значения соответствующих переменных. Две координаты должны находится внутри первой пары скобок, а две координаты — внутри второй пары скобок.^[4]

Реклама

1

Выполните вычитание в скобках. Сделайте это, потому что операции в скобках имеют приоритет.^[5]
2

Возведите в квадрат полученные значения. В нашем случае возведение в степень — это вторая по важности операция.^[6]
3

Сложите числа под знаком корня. Делайте вычисления так, как будто работаете с целыми числами.
4

Вычислите длину отрезка . Для этого извлеките корень из полученной суммы чисел.

Реклама

Советы

Не путайте эту формулу с другими, например, с формулой для вычисления углового коэффициента или с линейным уравнением.
Помните о порядке выполнения математических операций. Сначала вычтите, затем возведите в квадрат, затем сложите, а затем извлеките квадратный корень.

Об этой статье

Эту страницу просматривали 24 603 раза.

Была ли эта статья полезной?

Источник

Download Article

You can measure the length of a vertical or horizontal line on a coordinate plane by simply counting coordinates; however, measuring the length of a diagonal line is trickier. You can use the Distance Formula to find the length of such a line. This formula is basically the Pythagorean Theorem, which you can see if you imagine the given line segment as the hypotenuse of a right triangle.^[1] By using a basic geometric formula, measuring lines on a coordinate path becomes a relatively easy task.

1

Set up the Distance Formula. The formula states that $d={sqrt {(x_{{2}}-x_{{1}})^{{2}}+(y_{{2}}-y_{{1}})^{{2}}}}$ , where equals the distance of the line, $(x_{{1}},y_{{1}})$ equal the coordinates of the first endpoint of the line segment, and $(x_{{2}},y_{{2}})$ equal the coordinates of the second endpoint of the line segment.^[2]
2

Find the coordinates of the line segment’s endpoints. These might already be given. If not, count along the x-axis and y-axis to find the coordinates.^[3]

Advertisement
3

Plug the coordinates into the Distance Formula. Be careful to substitute the values for the correct variables. The two coordinates should be inside the first set of parentheses, and the two coordinates should be inside the second set of parentheses.^[4]

1

Calculate the subtraction in parentheses. By using the order of operations, any calculations in parentheses must be completed first.^[5]
2

Square the value in parentheses. The order of operations states that exponents should be addressed next.^[6]
3

Add the numbers under the radical sign. You do this calculation as if you were working with whole numbers.^[7]
4

Solve for . To reach your final answer, find the square root of the sum under the radical sign.^[8]

Add New Question

Question

What do we call points that are on same line?

Points on the same straight line are said to be «collinear» or «colinear.»
Question

How do I simplify the square root?

Look for a perfect square inside the radical sign, find its square root, and put that square root out in front of the radical sign, indicating that it’s to be multiplied by the radical. For example: √50 = √(2 x 25) = 5√2.
Question

The rise is 4 inches. The angle is 90 degrees from the height to the base. What is the slope?

To find the slope, you have to know the horizontal distance over which the rise occurs. The 90° angle is not relevant.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

Remember the order of operations when calculating your answer. Subtract first, then square the differences, then add, and then find the square root.
Do not confuse this formula with others, like the Midpoint Formula, Slope Formula, Equation of a Line or Line Formula.

Thanks for submitting a tip for review!

About This Article

Article SummaryX

To use the distance formula to find the length of a line, start by finding the coordinates of the line segment’s endpoints. Then, plug the coordinates into the distance formula. Next, subtract the numbers in parenthesis and then square the differences. Once you’ve done that, just add the numbers that are under the radical sign and solve for d. To learn how to set up the distance formula, keep reading!

Did this summary help you?

Thanks to all authors for creating a page that has been read 500,503 times.

Did this article help you?

Источник

Длина отрезка

Отрезком называют часть прямой линии, состоящей из всех точек этой линии, которые расположены между данными двумя точками — их называют концами отрезка.

Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.

Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2). На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.

Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1, а на ось Х длина проекции равна x2-x1. Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)². В данном случае |AB| является длиной отрезка.

Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5). Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5. А это значит, что длина нашего отрезка равна 5:1/2.

Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.

Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.

Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1.

Рассчитаем длину отрезка А, для этого найдем квадратный корень:

A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²).

Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1, то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61.

Источник

Как вычислить длину отрезка зная координаты
- - Эта страница существует благодаря следующим персонам
    - Timur
Как найти длину по координатам точек.
- Длина отрезка с помощью линейки
- Метод координат на плоскости
- Метод координат в пространстве
  - Инструкция
Координаты середины отрезка — как найти? Формулы и примеры
- Что такое отрезок
- Что такое середина отрезка
- Как найти координаты середины отрезка на координатной прямой
- Как найти середину отрезка на плоскости
- Координаты середины отрезка в пространстве
- Координаты середины отрезка через радиус-векторы его концов
Как найти длину линии по формуле расстояния
- - Все ресурсы по математике для старших классов
Как найти длину отрезка, если известны координаты. Метод координат в пространстве
Что такое линейный сегмент? (Определение, формула расстояния, пример)
- Что такое линии, сегменты линий и лучи?
- Содержание
- Линейный сегмент
  - Символ сегмента линии
- Что такое линия?
  - Символ прямой линии
- Лучи
- Измерение сегментов линии
  - Пример сегмента линии
  - Координатная плоскость
- Как найти длину диагонального отрезка на координатной плоскости
- Формула расстояния

Как вычислить длину отрезка зная координаты

Источник

Длина, как уже отмечалось, обозначается знаком модуля.

Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле:

Если даны две точки пространства и , то длину отрезка можно вычислить по формуле:

Примечание: соответствующие координаты можно переставить местами: и ,

но это нестандартный вариант.

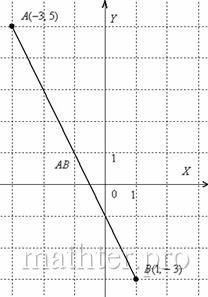
Задача 3

Даны точки и . Найти длину отрезка .

Решение: по соответствующей формуле:

Ответ: (единицы)

Обратите внимание на вынесение множителя из-под корня: (см. Приложение Школьные материалы). Это крайне

желательное действие, если оно возможно. Ибо будет придирка со стороны преподавателя. С высокой вероятностью.

И для наглядности снова выполню чертёж, тут есть что сказать:

Отрезок – это не вектор, а обычный ненаправленный

отрезок. И перемещать его куда-либо, конечно, нельзя.

Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину