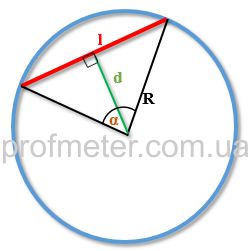
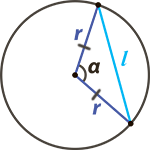
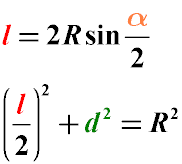Формула длины хорды окружности
Хорда — отрезок соединяющий любые две точки окружности. Диаметр окружности, самая большая хорда.
L — хорда
R — радиус окружности
O — центр окружности
α — центральный угол
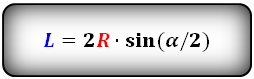
Формула длины хорды, ( L ):
Калькулятор для расчета длины хорды окружности :
Дополнительные формулы для окружности:
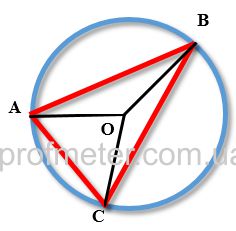
Треугольник вписанный в окружность
Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.
Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:
Площадь треугольника
S — площадь треугольника.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:
Площадь треугольника вписанного в окружность,
если известен полупериметр:
Площадь треугольника вписанного в окружность,
если известен высота и основание:
Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:
Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:
[ S = frac<1><2>ab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:
Сторона треугольника
a — сторона треугольника.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:
Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
Средняя линия треугольника
l — средняя линия треугольника.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:
Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:
[ h = b cdot sin alpha ]
Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:
Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис. - В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну. - Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора. - Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности. - Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.
Доказательство
Около любого треугольника, можно
описать окружность притом только одну.
окружность и треугольник,
которые изображены на рисунке 2.
окружность описана
около треугольника.
- Проведем серединные
перпендикуляры — HO, FO, EO. - O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника. - Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.
Как посчитать хорду окружности
Онлайн калькулятор
Хорда круга – отрезок соединяющий две точки, лежащие на окружности.
Чтобы посчитать длину хорды вам необходимо знать, чему равен радиус (r) окружности и угол (α) между двумя радиусами, образующими вместе с хордой равнобедренный треугольник (см. рис.)
Как посчитать длину хорды (градусы)
Чему равна длина хорды окружности если её радиус ,
а
Как посчитать длину хорды (радианы)
Чему равна длина хорды окружности если её радиус ,
а
Теория
Чему равна длина хорды (l) окружности если известны её радиус (r) и центральный угол (α), опирающийся на данную хорду?
Формула
Пример
Если радиус круга равен 4 см, а ∠α = 90°, то длина хорды примерно равна 5.65 см.
http://colibrus.ru/treugolnik-vpisannyy-v-okruzhnost/
http://poschitat.online/horda
Как посчитать хорду окружности
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать хорду окружности
Чтобы посчитать хорду круга (окружности) просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Хорда круга – отрезок соединяющий две точки, лежащие на окружности.
Чтобы посчитать длину хорды вам необходимо знать, чему равен радиус (r) окружности и угол (α) между двумя радиусами, образующими вместе с хордой равнобедренный треугольник (см. рис.)
Как посчитать длину хорды (градусы)
Чему равна длина хорды окружности если её радиус ,
а
угол α °
Ответ:
0
Как посчитать длину хорды (радианы)
Чему равна длина хорды окружности если её радиус ,
а
угол α рад
Ответ:
0
Теория
Чему равна длина хорды (l) окружности если известны её радиус (r) и центральный угол (α), опирающийся на данную хорду?
Формула
l = 2r⋅sinα/2
Пример
Если радиус круга равен 4 см, а ∠α = 90°, то длина хорды примерно равна 5.65 см.
См. также
| Учебный курс | Решаем задачи по геометрии |
Определение хорды Часть кривой, заключенной между двумя точками хорды, называется дугой. Плоская фигура, заключенная между дугой и ее хордой называется сегментом. Хорда, проходящая через центр окружности, называется диаметром окружности. Диаметр окружности — самая длинная хорда окружности. Свойства хорды к окружности
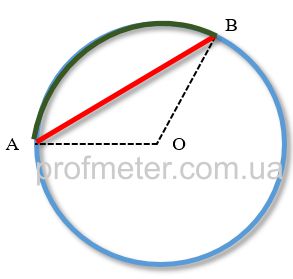
Свойства хорды и вписанного углаНа рисунке [1] вписанный угол обозначен обозначен как ACB, хорда окружности — AB
Свойства хорды и центрального углаНа рисунке [2] центральный угол обозначен как AOB, хорда как AB.
Формулы нахождения хорды Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла. Решение задач Примечание. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен. Хорды АВ и СD пересекаются в точке S, при чем AS:SB = 2:3, DS = 12см, SC = 5см, найти АВ. Решение. Согласно свойству хорд AS x SB = CS x SD, тогда 2х * 3х = 5 * 12 Откуда Ответ: 5√10 Задача. Окружность разделена на части, которые относятся как 3,5:5,5:3 и точки деления соединены между собой. Определить величину углов образовавшегося треугольника.
Решение. 3,5х + 5,5х + 3х = 360 Откуда градусные величины центральных углов равны: 90 / 2 = 45 Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ;
Задачи про окружность | Описание курса | Треугольник (Трикутник) |
Обсудить на форуме
Записаться на курсы
Обратиться к консультанту
Пройти тест
Полный список курсов обучения
Бесплатные видеоуроки
Нужна информация!
Окружность — это множество точек, которое располагается на одинаковом расстоянии от ее центра, представленного точкой.
Для любой точки L, лежащей на окружности, действует равенство OL=R. (Длина отрезка OL равняется радиусу окружности).
Окружность. Длина окружности. Касательная, дуга
Отрезок, который соединяет две точки окружности, является ее хордой. Хорда, проходящая прямо через центр окружности, является диаметром этой окружности (D). Диаметр можно вычислить по формуле: D=2R
Длина окружности вычисляется по формуле: C=2pi R
Площадь круга: S=pi R^{2}
Дугой окружности называется та ее часть, которая располагается между двух ее точек. Эти две точки и определяют две дуги окружности. Хорда CD стягивает две дуги: CMD и CLD. Одинаковые хорды стягивают одинаковые дуги.
Центральным углом называется такой угол, который находится между двух радиусов.
Длину дуги можно найти по формуле:
- Используя градусную меру: CD = frac{pi R alpha ^{circ}}{180^{circ}}
- Используя радианную меру: CD = alpha R
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
В случае, если хорды AB и CD окружности имеют пересечение в точке N, то произведения отрезков хорд, разделенные точкой N, равны между собой.
ANcdot NB = CN cdot ND
Касательная к окружности
Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью. Если же у прямой есть две общие точки, ее называют секущей.
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
AC = CB
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть.
AC^{2} = CD cdot BC
Можно сделать вывод: произведение целого отрезка первой секущей на его внешнюю часть равняется произведению целого отрезка второй секущей на его внешнюю часть.
AC cdot BC = EC cdot DC
Углы в окружности
Градусные меры центрального угла и дуги, на которую тот опирается, равны.
angle COD = cup CD = alpha ^{circ}
Вписанный угол — это угол, вершина которого находится на окружности, а стороны содержат хорды.
Вычислить его можно, узнав величину дуги, так как он равен половине этой дуги.
angle AOB = 2 angle ADB
Опирающийся на диаметр, вписанный угол, прямой.
angle CBD = angle CED = angle CAD = 90^ {circ}
Вписанные углы, которые опираются на одну дугу, тождественны.
angle ADB = angle AEB = angle AFB
Опирающиеся на одну хорду вписанные углы тождественны или их сумма равняется 180^ {circ}.
angle ADB + angle AKB = 180^ {circ}
angle ADB = angle AEB = angle AFB
На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
angle DMC = angle ADM + angle DAM = frac{1}{2} left ( cup DmC + cup AlB ight )
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
angle M = angle CBD — angle ACB = frac{1}{2} left ( cup DmC — cup AlB ight )
Вписанная окружность
Вписанная окружность — это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
- S = pr,
где:
p — полупериметр многоугольника,
r — радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
- r = frac{S}{p}
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
AB + DC = AD + BC
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
Радиус вписанной окружности вычисляется по формуле:
- r = frac{S}{p},
где p = frac{a + b + c}{2}
Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника.
В точке пересечения серединных перпендикуляров сторон этой фигуры будет находиться центр описанной окружности.
Радиус можно найти, вычислив его как радиус окружности, которая описана около треугольника, определенного любыми 3-мя вершинами многоугольника.
Есть следующее условие: окружность возможно описать около четырехугольника только, если сумма его противоположных углов равна 180^{ circ}.
angle A + angle C = angle B + angle D = 180^ {circ}
Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
Радиус описанной окружности можно вычислить по формулам:
- R = frac{a}{2 sin A} = frac{b}{2 sin B} = frac{c}{2 sin C}
- R = frac{abc}{4 S}
где:
- a, b, c — длины сторон треугольника,
- S — площадь треугольника.
Теорема Птолемея
Под конец, рассмотрим теорему Птолемея.
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
AC cdot BD = AB cdot CD + BC cdot AD
Источник: https://academyege.ru/page/okruzhnost-i-krug.html
Формула длины хорды окружности
Хорда — отрезок соединяющий любые две точки окружности. Диаметр окружности, самая большая хорда.
L — хорда
R — радиус окружности
O — центр окружности
α — центральный угол
Формула длины хорды, (L):
Калькулятор для расчета длины хорды окружности :
Дополнительные формулы для окружности:
- Подробности
-
Автор: Administrator
-
Опубликовано: 16 октября 2011
-
Обновлено: 13 августа 2021




![Хорда к окружности вместе с вписанным [1] и центральными углами [2] Хорда к окружности вместе с вписанным [1] и центральными углами [2]](https://profmeter.com.ua/upload/medialibrary/b1c/horda2.jpg)