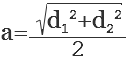Укажите размеры:
Результат:
Решение:
Ссылка на страницу с результатом:
# Теория
Ромб — это параллелограмм у которой все стороны равны, а углы непрямые.
Диагональ ромба — это прямой отрезок соединяющий вершины противоположных углов ромба.
Свойства ромба:
- Все стороны ромба равны;
- Диагонали ромба пересикаются под прямым углом;
- Диагонали ромба в точке пересечения делятся пополам;
- Сумма углов, прилежащих к одной стороне ромба, равна 180°;
- Противоположные углы ромба равны.
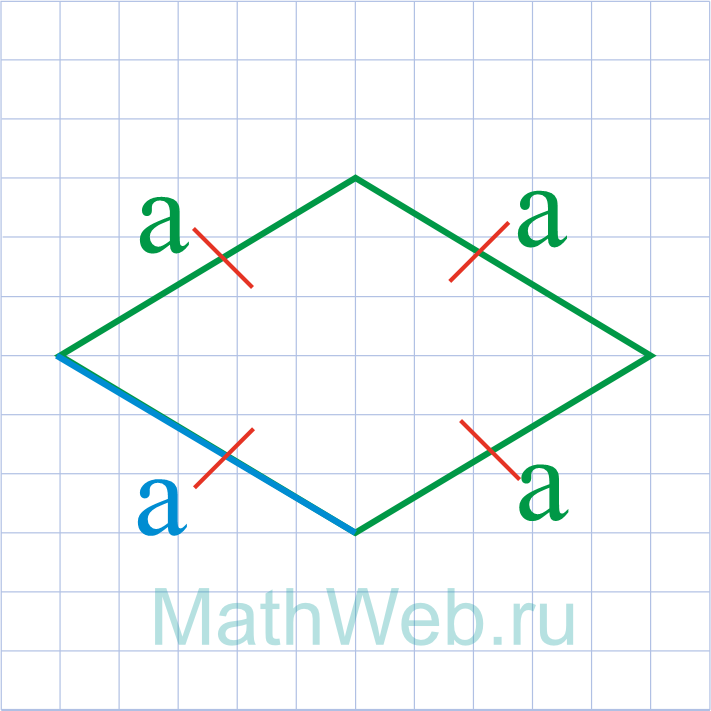
Как найти сторону ромба через диагонали
D
d
a
a
a
a
a = dfrac{ sqrt{D^2 + d^2} }{2}
- a — сторона ромба
- D — большая диагональ ромба
- d — меньшая диагональ ромба
Похожие калькуляторы:
Войдите чтобы писать комментарии
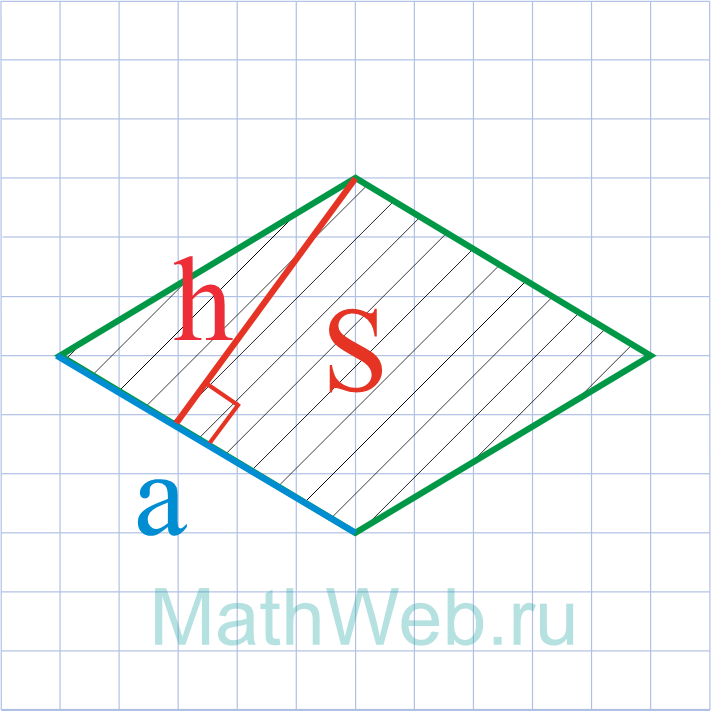
Где S — площадь ромба,h — его высота.
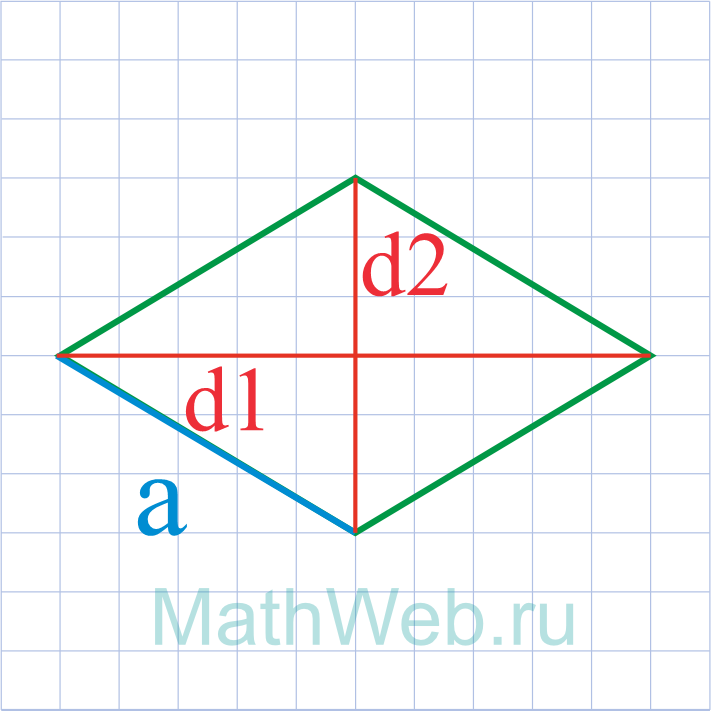
Где d1 — большая диагональ,d2 — меньшая диагональ.
Где d1 — большая диагональ,α — острый угол.
Где d2 — меньшая диагональ,β — тупой угол.
Где S — площадь ромба, α°,β° — его углы.
Где S — площадь ромба,r — радиус вписанной окружности.
Где P — периметр ромба.
- Ромб — это параллелограмм у которого все стороны равны.
- Противоположные стороны ромба параллельны.
- Все ромбы различаются между собой только размером стороны и углов.
Как найти длину стороны ромба?
Сторона ромба может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
 |
a = S h |
 |
a = √d12 ― d22 2 |
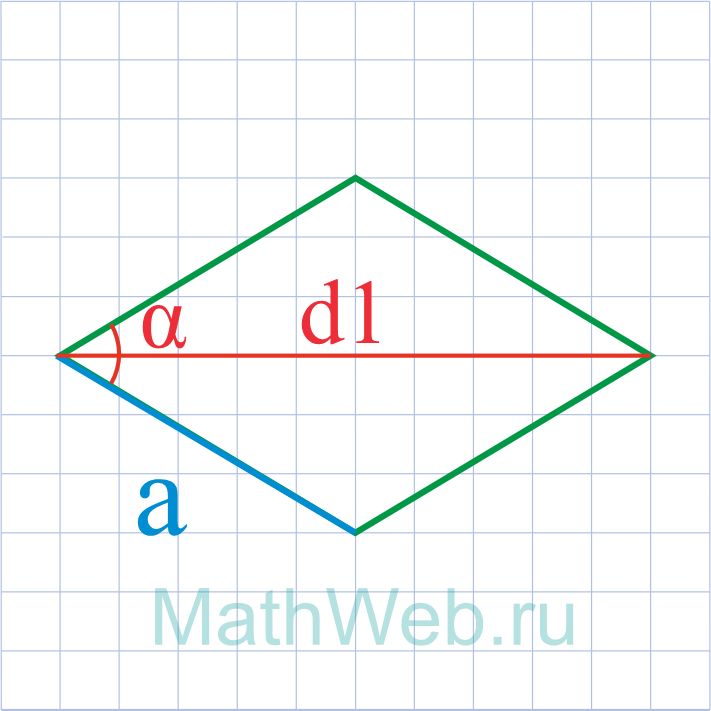 |
a = d1 √2 + 2·cos(α°) |
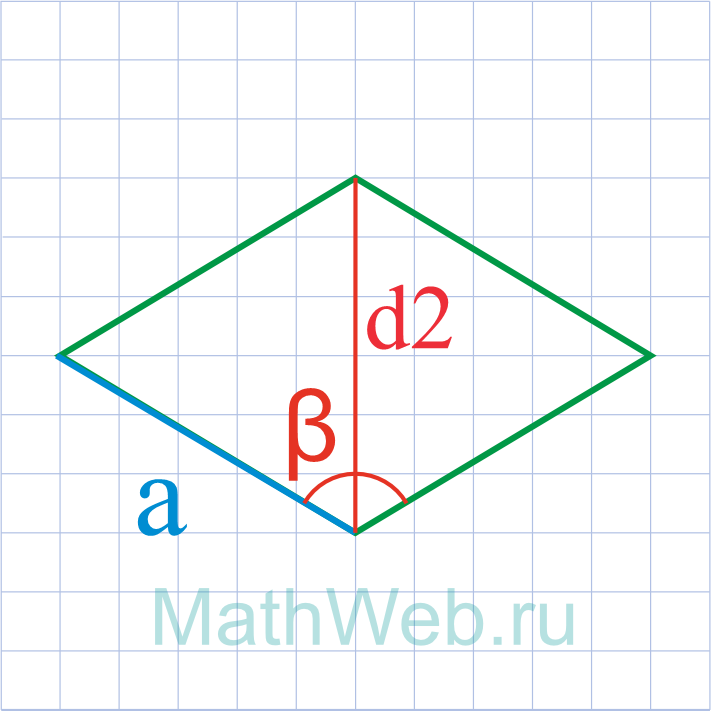 |
a = d2 √2 — 2·cos(β°) |
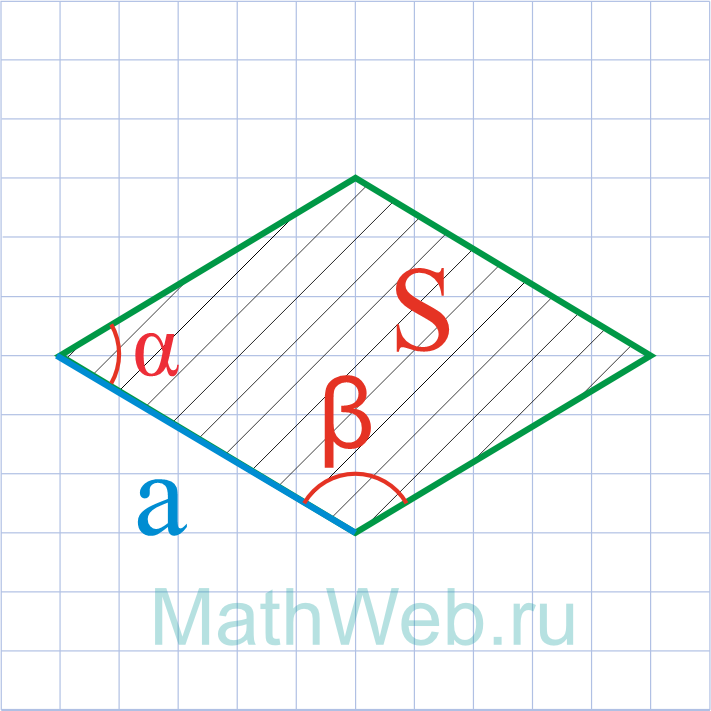 |
a = √S √sin(α°) = √S √sin(β°) |
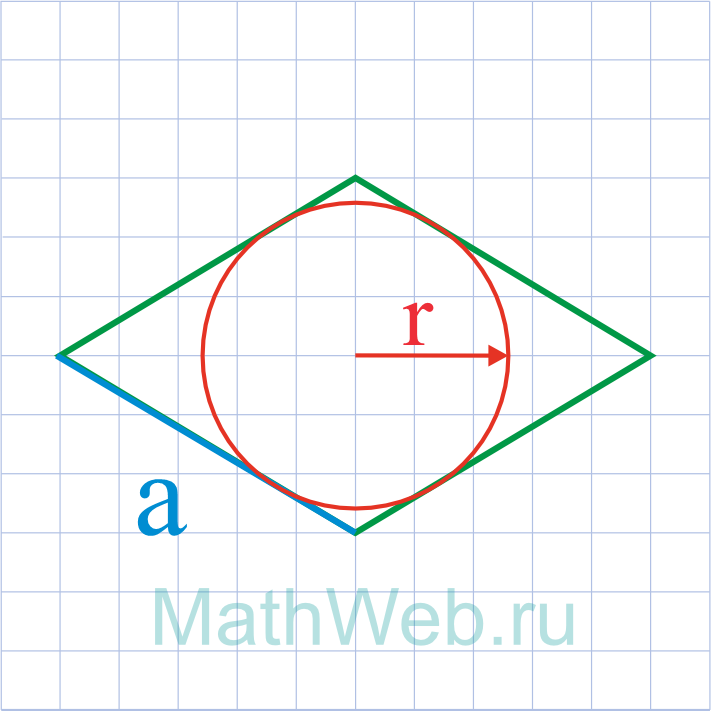 |
a = S 2r |
 |
a = P 4 |
Ромб. Формулы, признаки и свойства ромба
Определение.
Ромб — это параллелограмм, который имеет равные стороны. Если у ромба все углы прямые, тогда он называется квадратом.
Ромбы отличаются между собой размером стороны и размером углов.
Признаки ромба
Параллелограмм ABCD будет ромбом, если выполняется хотя бы одно из следующих условий:
1. Две его смежные стороны равны (отсюда следует, что все стороны равны):
АВ = ВС = СD = AD
2. Его диагонали пересекаются под прямым углом:
AC┴BD
3. Одна из диагоналей (биссектриса) делит содержащие её углы пополам:
∠BAC = ∠CAD или ∠BDA = ∠BDC
4. Если все высоты равны:
BN = DL = BM = DK
5. Если диагонали делят параллелограмм на четыре равных прямоугольных треугольника:
Δ ABO = Δ BCO = Δ CDO = Δ ADO
6. Если в параллелограмм можно вписать круг.
Основные свойства ромба
2. Диагонали перпендикулярны:
AC┴BD
3. Диагонали являются биссектрисами его углов:
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре:
AC2 + BD2 = 4AB2
5. Точка пересечения диагоналей называется центром симметрии ромба.
6. В любой ромб можно вписать окружность.
7. Центром окружности вписанной в ромб будет точка пересечения его диагоналей.
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
2. Формула стороны ромба через площадь и синус угла:
3. Формула стороны ромба через площадь и радиус вписанной окружности:
4. Формула стороны ромба через две диагонали:
5. Формула стороны ромба через диагональ и косинус острого угла (cos α) или косинус тупого угла (cos β):
6. Формула стороны ромба через большую диагональ и половинный угол:
7. Формула стороны ромба через малую диагональ и половинный угол:
8. Формула стороны ромба через периметр:
Диагонали ромба
Определение.
Диагональю ромба называется любой отрезок соединяющий две вершины противоположных углов ромба.
Ромб имеет две диагонали — длинную d1, и короткую — d2
Формулы определения длины диагонали ромба:
1. Формулы большой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d1 = a√2 + 2 · cosα
d1 = a√2 — 2 · cosβ
2. Формулы малой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d2 = a√2 + 2 · cosβ
d2 = a√2 — 2 · cosα
3. Формулы большой диагонали ромба через сторону и половинный угол:
d1 = 2a · cos(α/2)
d1 = 2a · sin(β/2)
4. Формулы малой диагонали ромба через сторону и половинный угол:
d2 = 2a · sin(α/2)
d2 = 2a · cos(β/2)
5. Формулы диагоналей ромба через сторону и другую диагональ:
d1 = √4a2 — d22
d2 = √4a2 — d12
6. Формулы диагоналей через тангенс острого tgα или тупого tgβ угла и другую диагональ:
d1 = d2 · tg(β/2)
d2 = d1 · tg(α/2)
7. Формулы диагоналей через площадь и другую диагональ:
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
Периметр ромба
Определение.
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Формула периметра ромба через сторону ромба:
P = 4a
Площадь ромба
Определение.
Площадью ромба называется пространство ограниченное сторонами ромба, т.е. в пределах периметра ромба.
Формулы определения площади ромба:
1. Формула площади ромба через сторону и высоту:
S = a · ha
2. Формула площади ромба через сторону и синус любого угла:
S = a2 · sinα
3. Формула площади ромба через сторону и радиус:
S = 2a · r
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла (tgα) или малую диагональ и тангенс тупого угла (tgβ):
Окружность вписанная в ромб
Определение.
Кругом вписанным в ромб называется круг, который примыкает ко всем сторонам ромба и имеет центр на пересечении диагоналей ромба.
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
6. Формула радиуса круга вписанного в ромб через две диагонали:
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Стороны ромба
Стороны фигур
Ромб является четырехугольником, представляет собой частный случай параллелограмма. У этого четырехугольника все стороны равны, противоположные — параллельны. У ромба 2 диагонали — большая и меньшая, они пересекаются друг с другом под прямым углом и делят углы пополам.
Если известны длины обеих диагоналей ромба, длину стороны можно рассчитать по формуле:
где где d1 — большая диагональ, d2 — меньшая диагональ, a — сторона ромба. Т.е. сторона ромба равна половине корня из суммы квадратов его диагоналей.
Расчет длины сторон ромба через диагонали
СДАМ ГИА: РЕШУ ОГЭ
Образовательный портал для подготовки к экзаменам
Математика
математика
Математика
Информатика
≡ Русский язык
Письменный экзамен
Устное собеседование
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
сайты — меню — вход — новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Справочник
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
НАШИ БОТЫ
 |
 |
На сайте что-то не так? Отключите адблок
Новости
24 мая
Обновлённая панель инструментов
1 мая
Беседы для подготовки к ОГЭ по всем предметам
1 мая
Новый сервис: можно исправить ошибки!
29 апреля
Разместили актуальные шкалы ОГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
21 апреля
Разместили варианты из заданий открытого банка ФИПИ ОГЭ по русскому языку
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
6 марта
Изменения ВПР 2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
ЧУЖОЕ НЕ БРАТЬ!
Зайчиков и Поваляев стащили наши тесты
Наша группа
Задания
Версия для печати и копирования в MS Word
Тип 18 № 348586
i
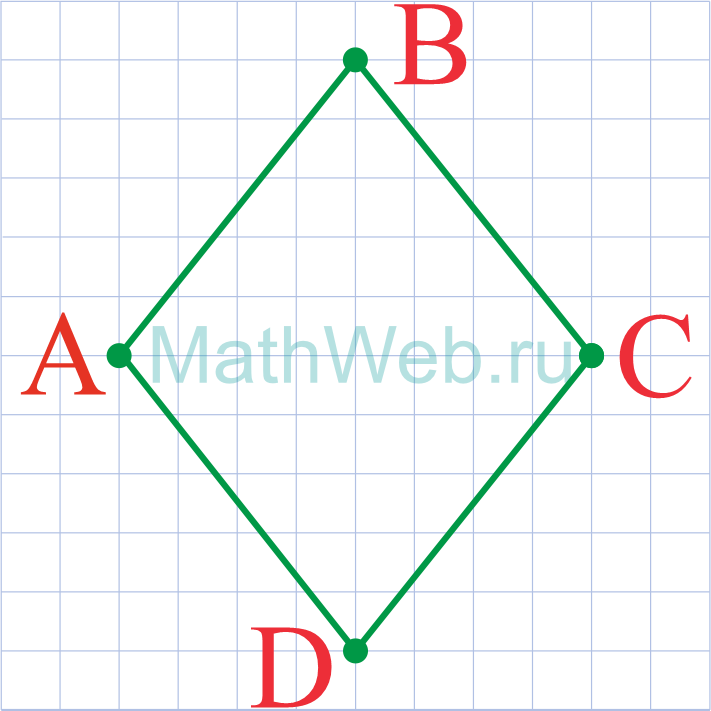
На клетчатой бумаге с размером клетки 1х1 изображён ромб. Найдите длину его большей диагонали.
Спрятать решение
Решение.
Из рисунка видно, что длина большей диагонали ромба — 6.
Ответ: 6.
Аналоги к заданию № 348446: 348586 349027 349478 … Все
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Спрятать решение
·
Прототип задания
·
Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023