Воспользуйтесь текстом «Конструкция строительной фермы», расположенным справа. Запишите свой ответ на вопрос.
Вы можете воспользоваться Online калькулятором https://www.desmos.com/scientific
Из-за обнаруженных дефектов необходимо заменить балку АС.
Измерить её непосредственно невозможно, однако, известно, что длина горизонтальной балки ВС равна 600 см.
Определите длину балки АС.
В ответе укажите приближённое значение, выраженное в сантиметрах.
Расчёт статически определимых балок
(определение реакций и построение эпюр)
Внимание! Расчёт статически неопределимых систем методом сил находится здесь.
|
В данном расчёте не задано ни одного объекта. Для создания объектов модели перейдите в раздел «Операции» |
δ ?EJEJXYαhwRauto0°180°-180°0°90°180°-90°0°180°-180°
Методическая
разработка
Формирование
математической грамотности
Автор:
Ерш Н.Н., учитель математики
1.
Комплексное
задание «Команда лыжников» (2задания).
Прочитайте текст и выполните задания 1-2.
Тренер школьной команды
лыжников для организации летних тренировок провёл опрос спортсменов, чтобы
узнать, есть ли у них скейтборды и лыжероллеры. На вопрос ответили 12 человек.
Результаты представлены в таблице 1.
Таблица
1
Наличие
скейтборда и лыжероллеров у спортсменов
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
скейтборд |
– |
+ |
+ |
+ |
– |
+ |
+ |
+ |
– |
+ |
– |
+ |
|
лыжероллеры |
+ |
+ |
– |
+ |
+ |
– |
+ |
– |
+ |
– |
+ |
– |
Обозначения: + есть, – нет
1). На основе данных таблицы 1 заполните таблицу
2, которая показывает, сколько спортсменов имеют скейтборды и сколько
спортсменов имеют лыжероллеры.
Таблица 2
Количество
снаряжения у спортсменов
|
Снаряжение |
Количество спортсменов |
|
скейтборд |
|
|
лыжероллеры |
2). На основе данных таблицы 1 составлены
следующие утверждения.
Отметьте
знаком ü
верные.
ú
У каждого спортсмена есть и лыжероллеры, и скейтборд.
ú
Если у спортсмена есть скейтборд,
то у него нет лыжероллеров.
ú
У всех спортсменов есть какое-то
снаряжение для тренировок.
ú
У всех членов команды скейтбордов
больше, чем лыжероллеров.
ú
Чтобы проводить тренировки на
лыжероллерах, нужно ещё 5 комплектов.
Характеристики
и система оценивания:
Команда
лыжников. Задание 1.
Характеристики
задания
Класс: 5
• Содержательная
область оценки: неопределённость и данные.
• Компетентностная
область оценки: применять
• Контекст:
личный
• Уровень
сложности: низкий.
• Формат
ответа: задание с несколькими краткими ответами (отдельные
поля
для ответов).
• Объект
оценки: заполнение готовой таблицы
Система
оценивания
|
Балл |
Содержание |
||||||
|
1 |
Ответ: скейтборд – 8; Таблица |
||||||
|
0 |
Дан |
Команда
лыжников. Задание 2.
Характеристики
задания
Класс: 5
• Содержательная
область оценки: неопределённость и данные
• Компетентностная
область оценки: рассуждать
• Контекст:
общественный
• Уровень
сложности: средний
• Формат
ответа: Задание с выбором нескольких верных ответов
• Объект
оценки: проверка истинности утверждений относительно
данных
таблицы, понимать логические связки «если, то», «есть», «все»,
«каждый»,
«и»
Система
оценивания
|
Балл |
Содержание |
|
2 |
Ответ: 3,4,5. Отмечены три верных |
|
1 |
Отмечены два любых |
|
0 |
Другие ответы |
__________________________________________________________________
2. Комплексное задание «Акция в магазине»
(3задания).
Прочитайте текст и выполните задания 1-3.
Ирина Петровна узнала
про акции в молочном отделе ближайшего
магазина и решила
приобрести молоко и йогурты со скидкой.
1). Ирина Петровна прочитала первое объявление:
При покупке трёх и более пакетов коровьего
молока «Бурёнка (1 л)» цена одного пакета – 50 руб.
При покупке двух и более пакетов козьего
молока «Весёлая коза (1 л)» цена одного пакета –
140 рублей.
Ирина Петровна
воспользовалась акцией и купила 3 л коровьего и 2 л
козьего молока. Какую
сумму денег она заплатила?
2). На втором объявлении Ирина Петровна
прочитала:
Акция «3 по цене 2» на йогурты фирмы «Солнышко».
Спешите. Только сегодня при покупке двух йогуртов вы
получаете третий в подарок.
Цена одного йогурта – 48 рублей.
Ирина Петровна купила
по акции 3 йогурта фирмы «Солнышко». Во сколько рублей ей обошёлся один йогурт?
3). Сколько йогуртов по акции «3 по цене 2» может
купить Ирина Петровна на 300 рублей
Характеристики
и система оценивания:
Акция в магазине.
Задание 1.
Характеристики
задания
Класс: 6
• Содержательная
область: количество
• Компетентностная
область: применять
• Контекст:
личная жизнь
• Уровень сложности:
низкий
• Формат ответа:
развернутый ответ
• Объекты оценки:
сопоставлять информацию, представленную в тексте
и на рисунке;
использовать зависимость величин для ответа на
поставленный вопрос
Система
оценивания
|
Балл |
Содержание |
|
1 |
Дан верный ответ 430 Возможное решение: 50 |
|
0 |
Другие ответы |
Акция в магазине.
Задание 2.
Характеристики
задания
Класс: 6
• Содержательная
область: количество
• Компетентностная
область: интерпретировать/ формулировать
• Контекст:
личная жизнь
• Уровень сложности:
средний
• Формат ответа:
развернутый ответ
• Объект оценки:
использовать зависимость величин для ответа на
поставленный вопрос
Система
оценивания
|
Балл |
Содержание |
|
2 |
Дан верный ответ 32р. подтвержденное Возможное объяснение: 1) она заплатила 96 2) по акции 3 штуки Значит, 48 |
|
1 |
Дан верный ответ, а |
|
0 |
Другие ответы |
Акция в магазине.
Задание 3.
Характеристики
задания
Класс: 6
• Содержательная
область: количество
• Компетентностная
область: формулировать
• Контекст:
личная жизнь
• Уровень сложности:
высокий
• Формат ответа:
развёрнутый ответ
• Объект оценки:
использовать зависимость величин для ответа на
поставленный вопрос,
выделять и учитывать в ходе рассуждений все
условия, планировать
ход решения, включающего оценку результата
вычислений (округлять
результат по недостатку по смыслу ситуации)
Система
оценивания
|
Балл |
Содержание |
|
2 |
Дан верный ответ 9 что покупать йогурты каждую оплаченную Возможное 1) По акции можно 300 : 96 3 раза за 2 3 2) 48 3 3) 300 : (48 4) 96 (оплата 2 штук 300 – 288 = 12 |
|
1 |
Дан верный ответ, а содержит неверных |
|
0 |
Другие ответы |
_______________________________________________________________________
3. Комплексное задание «Неделя математики»
(3задания).
Прочитайте текст и выполните задания 1-3.
Неделя математики
В школе при
подготовке к Неделе математики каждому из четырёх шестых классов выделили
передвижную доску, которую можно использовать с двух сторон. Рабочая площадь
доски разбита на клетки со стороной 1 дм
(10 см). Размер доски –
17 дм х 11 дм.
Каждый класс на
одной стороне доски оформил свою Математическую газету, на другой – записывал
решение конкурсных задач.
1). Доски, выделенные для каждого класса, решено
поставить вплотную друг к другу в зале вдоль стены длиной 7,5 м. Можно ли все 4
доски расположить в ряд вдоль этой стены?
2). В одном из заданий каждому классу предложили
нарисовать развёртку куба со стороной 2 дм. Какой класс справился с заданием?
Длина клетки – 1
дм
3). Все классы выполнили такое задание: «На
кондитерской фабрике, где изготавливают шоколад, решили поставить рекорд.
Сделали куб из шоколада со стороной 1 м, разрезали его на кубики со стороной 1
дм. Из этих кубиков выложили прямую дорожку, приложив кубики плотно друг к
другу».
Какой длины получилась
дорожка из шоколада?
¨
1 км
¨
100 м
¨
100 дм
¨
1000
Характеристики
и система оценивания:
Неделя математики.
Задание 1.
Характеристики
задания
Класс: 6
• Содержательная
область: количество
• Компетентностная
область: применять
• Контекст:
общественная жизнь
• Уровень сложности:
средний
• Формат ответа:
развернутый ответ
• Объект оценки:
извлекать данные из разных частей задания,
переводить единицы
длины и выполнять действия с единицами длины
Система
оценивания
|
Балл |
Содержание |
|
2 |
Дан верный ответ вычисления, которые Возможное 1) Размеры доски – 6,8 м; 6,8 м 2) 17 3) 7,5 м = 75 дм; 75 |
|
1 |
Ход решения верный, и обратно) выполнен ошибка, например, 1,7 |
|
0 |
Дан верный ответ, а можно вместить 4 |
Неделя математики.
Задание 2.
Характеристики
задания
Класс: 6
• Содержательная
область: пространство и форма
• Компетентностная
область: интерпретировать
• Контекст:
научная деятельность
• Уровень сложности:
низкий
• Формат ответа: краткий
ответ (буква)
• Объект оценки:
применять понятие «развёртка куба», учитывать
условия задания (клетка
передвижной доски имеет длину 1 дм)
Система
оценивания
|
Балл |
Содержание |
|
1 |
Выбран ответ «Б» |
|
0 |
Другие ответы |
Неделя математики.
Задание 3.
Характеристики
задания
Класс: 6
• Содержательная
область: пространство и форма
• Компетентностная
область: рассуждать
• Контекст:
научная деятельность
• Уровень сложности:
средний
• Формат ответа:
развёрнутый ответ
• Объект оценки:
применять представление об объеме куба, переводить
единицы длины
Система
оценивания
|
Балл |
Содержание |
|
2 |
Дан верный ответ (100 данный ответ. Возможное 1) Куб будет разделен Если их выложить равна 1000 дм или 2) 1 м = 10 дм,1 слой 1 дм, таких слоев длиной 1 дм. 1 |
|
1 |
Дан верный ответ, а |
|
0 |
Другие ответы. |
_______________________________________________________________________
4. Комплексное задание «Шкалы температур» (2задания).
Прочитайте текст и выполните задания 1-2.
Шкалы температур
В России для измерения температуры воздуха и тела человека используется
шкала Цельсия, а в США – шкала Фаренгейта.
Для пересчёта температурных значений пользуются формулами,
представленными в таблице:
|
Формула |
Перевод значения температуры |
|
C = (F – 32) : 1,8 |
из шкалы Фаренгейта в |
|
F = 1,8 |
из шкалы Цельсия в |
1). Турист из США планирует через два дня
прилететь в Санкт-Петербург и
просит сотрудника
российской турфирмы сообщить ему температуру в
городе в день его
прилёта.
Используя приведённые
формулы, определите, какую
температуру по шкале
Фаренгейта надо сообщить туристу из
США, если по прогнозу
погоды в городе ожидается 10°C.

2). Учащийся из России изучает английский язык в
одной из частных школ
Нью-Йорка, проживая в
американской семье. В один из учебных дней он
почувствовал себя
плохо. Врач осмотрел его и сообщил, что он не может
пойти в школу, так как
температура его тела составляет 100 °F.
Чтобы понять,
почему учащемуся следует остаться дома, определите
температуру его тела в градусах
Цельсия и оцените её в соответствии с информацией в таблице ниже.
|
Температура тела, °C |
Оценка температуры |
|
От 35 до 36,4 |
пониженная |
|
От 36,5 до 37 |
нормальная |
|
От 37,1 до 39 |
повышенная |
|
Выше 39 |
высокая |
В ответ запишите
температуру в градусах Цельсия и оценку температуры.
Характеристики
и система оценивания:
Шкалы температур.
Задание 1.
Характеристики
задания
Класс: 7
• Содержательная
область: изменение и зависимости.
• Компетентностная
область: применять
• Контекст:
образовательный
• Уровень сложности:
низкий
• Формат ответа:
задание с кратким ответом.
• Объект оценки:
работа с формулами (использование формул при
переводе значений
температур из одной шкалы в другую)
Система
оценивания
|
Балл |
Содержание |
|
1 |
Ответ: 50°F Дан верный ответ. |
|
0 |
Дан неверный ответ |
Шкалы температур.
Задание 2.
Характеристики
задания
Класс: 7
• Содержательная
область: изменение и зависимости.
• Компетентностная
область: интерпретировать
• Контекст:
образовательный
• Уровень сложности:
средний
• Формат ответа:
задание с несколькими краткими ответами (отдельные
поля для ответов)
• Объект оценки:
работа с формулами (использование формул при
переводе значений
температур из одной шкалы в другую)
Система
оценивания
|
Балл |
Содержание |
|
2 |
Ответ: А) 37°C или Б) Оба ответа даны |
|
1 |
Дан верный ответ на Ответ на вопрос Б |
|
0 |
Другие ответы. Ответ отсутствует. |
__________________________________________________________________
5. Комплексное задание «Ремонт комнаты» (2задания).
Прочитайте текст и выполните задания 1-2.
Ремонт комнаты
Семья Марии делает ремонт в её комнате. План комнаты с замерами,
которые сделала Мария,
представлен ниже.
Комната имеет неправильную форму: три прямых угла, а вместо
четвёртого угла она
имеет стену округлой формы.

Для справок:
С =2 —
длина окружности,
—
площадь круга,
где R
— радиус круга.
Считайте, что 3,14.
1). Ширина рулона меньше длины и меньше ширины
комнаты, поэтому, чтобы полностью покрыть пол комнаты, надо выложить вплотную
один к другому несколько кусков ковролина перпендикулярно стене с окном.
А) Сколько кусков ковролина придётся выложить?
Ответ:___________________
Б) Какова длина одного такого куска?
Ответ:___________________
В) Какого наименьшего количества метров
ковролина будет достаточно,
чтобы полностью
застелить пол в комнате Марии?
Ответ:___________________
2). Из-за того, что один из углов комнаты — «круглый»,
ковролин обрезают по
форме скругления.
Определите площадь остатков ковролина, получившихся в результате
скругления. Ответ дайте
в .
Запишите ответ и
приведите соответствующее решение.
Ответ:___________________________________________________________
Решение:
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Характеристики
и система оценивания:
Ремонт комнаты.
Задание 1.
Характеристики
задания
Класс: 7
• Содержательная
область: пространство и форма
• Компетентностная
область: формулировать.
• Контекст:
личный.
• Уровень сложности:
средний.
• Формат ответа:
задание с несколькими краткими ответами (отдельные поля для ответов)
• Объект оценки:
составление фигуры из заданных элементов с учётом
их линейных размеров.
Система
оценивания
|
Балл |
Содержание |
|
2 |
Ответ: А) 3; Б) 6 м; (Если наименования Даны 3 верных ответа. |
|
1 |
Даны верные ответы на ответ неверный или |
|
0 |
Другие ответы. Ответ отсутствует. |
Ремонт комнаты.
Задание 2.
Характеристики
задания
Класс: 7
• Содержательная
область: пространство и форма
• Компетентностная
область: применять.
• Контекст:
личный.
• Уровень сложности:
высокий.
• Формат ответа:
задание с развернутым ответом (в виде текста, рисунка
или и рисунка, и
текста)
• Объект оценки:
вычисление площади фигуры сложной формы,
использование свойства
аддитивности площади
Система
оценивания
|
Балл |
Содержание |
|
2 |
Ответ: 0,86 ( Пример возможного 1) 2х2 = 4 ( 2) 3,14х4:4 = 3,14 ( 3) 4-3,14 = 0,86 ( Или дано любое Дан верный ответ и |
|
1 |
Дан верный ответ ИЛИ в логически в результате которой ИЛИ дан ответ 1 ( |
|
0 |
Другие варианты. Ответ отсутствует. |
__________________________________________________________________
6. Комплексное задание «Конструкция строительной фермы» (2задания).
Прочитайте текст и выполните задания 1-2.
Конструкция
строительной фермы
Строительная ферма – это стержневая конструкция, служащая в основном
для перекрытия больших пролётов, например, при возведении мостов, промышленных
зданий, спортивных сооружений, а также для строительства небольших лёгких
павильонов и сценических конструкций.
Жёсткость конструкции
обеспечивают составляющие её треугольники.
1). Рассмотрите чертёж и укажите величины всех
углов, обозначенных цифрами 1, 2 и 3.
Угол 1 ____________________________
Угол 2 ____________________________
Угол 3 ____________________________
2). Из-за обнаруженных дефектов необходимо
заменить балку АС.
Измерить её
непосредственно невозможно. Но известно, что угол наклона балки АС с
горизонтальной балкой ВС равен , а
высота вертикальной балки АВ равна 2 м.
Определите длину
балки АС по этим данным.
Запишите ответ и
приведите соответствующее решение.
Ответ:
____________________________________________
Решение:
_____________________________________________________________________
______________________________________________________________
______________________________________________________________
______________________________________________________________
______________________________________________________________
Характеристики
и система оценивания:
Конструкция
строительной фермы. Задание 1.
Характеристики
задания
Класс: 7
• Содержательная
область: пространство и форма.
• Компетентностная
область: применять.
• Контекст:
образовательный.
•Уровень
сложности: средний.
• Формат
ответа: задание с несколькими краткими ответами (отдельные поля для
ответов).
• Объект
оценки: свойства треугольника: зависимость между сторонами
и
углами, между сторонами.
Система
оценивания
|
Балл |
Содержание |
|
2 |
Ответ: Угол 1 – Величины всех трёх |
|
1 |
Указаны верно |
|
0 |
Другие варианты |
Конструкция
строительной фермы. Задание 2.
Характеристики
задания
Класс: 7
• Содержательная
область: пространство и форма.
• Компетентностная
область: применять.
• Контекст:
образовательный.
• Уровень сложности:
повышенный.
• Формат ответа:
задание с кратким ответом и пояснением к нему.
• Объект оценки:
свойства треугольника: зависимость между сторонами
и углами, между
сторонами.
Система
оценивания
|
Балл |
Содержание |
|
2 |
Ответ: 4 м. Пример возможного АС – гипотенуза; катет гипотенузы. Дан верный ответ, |
|
1 |
Ответ дан верно, ИЛИ: дан ответ с понятий (вместо ИЛИ: не используются |
|
0 |
Другие варианты |
_________________________________________________________
7. Комплексное задание «Кулинарный колледж» (2задания).
Прочитайте текст и выполните задания 1-2.
Кулинарный
колледж
Наташа и Оля учатся в кулинарном колледже. Они изучают технологии
приготовления различных блюд.
На занятиях по теме «Каши и блюда из круп» при вычислении массы
готового продукта учащиеся считают, что:
− 1 порция – это 200 граммов готовой каши;
− из 1 кг пшённой крупы получается 4 кг готовой каши;
− для приготовления 1 кг готовой каши пшённой необходимо 0,8 л
жидкости, из которой 40% составляет вода и 60% молоко.
1). На практическом занятии Наташа и Оля получили
задание определить количество порций каши пшённой, которое можно приготовить из
3 кг пшена.
Сделайте расчёты и
приведите ответ.
Ответ:______________
порций
2). Наташа и Оля должны рассчитать, сколько литров
воды и сколько литров молока необходимо для приготовления 1 кг каши пшённой.
Сделайте расчёты и
приведите ответ.
Ответ:_____________
л. воды
_____________ л. молока
Характеристики
и система оценивания:
Кулинарный колледж. Задание 1.
Характеристики задания
Класс: 8
• Содержательная область:
Количество.
• Компетентностная область:
Применять.
• Контекст:
Образование/профессиональная деятельность
• Уровень сложности: Низкий
• Формат ответа: Задание с кратким
ответом
• Объект оценки: Отношение
пропорциональных величин, реальные
расчёты
Система
оценивания
|
Балл |
Содержание |
|
1 |
Дан верный ответ: 60 порций. |
|
0 |
Дан неверный ответ |
Кулинарный колледж. Задание 2.
Характеристики задания
Класс: 8
• Содержательная область:
Количество.
• Компетентностная область:
Формулировать
• Контекст:
Образование/профессиональная деятельность
• Уровень сложности: Низкий
• Формат ответа: Задание с
несколькими краткими ответами
• Объект оценки: Отношение
пропорциональных величин, нахождение
процента от числа, реальные расчёты
Система
оценивания
|
Балл |
Содержание |
|
1 |
Даны верные ответы: |
|
0 |
Другие ответы. |
__________________________________________________________________
8. Комплексное задание «Первая линия московского метро»
(2задания).
Прочитайте текст и выполните задания 1-2.
Первая линия московского метро
На начало 2020 года в московском метрополитене насчитывалось 14 линий,
на которых были расположены 228 станций. Большинство станций расположены под
землёй, 10 находятся на поверхности, 5 – на мостах и эстакадах.
В таблице даны
глубины заложения станций на части самой первой линии московского метро –
Сокольнической. Знак «минус» означает, что станция расположена под землей, знак
«плюс» – над поверхностью земли.
|
№ |
Название |
Глубина заложения, м |
|
1 |
Улица |
-8 |
|
2 |
Черкизовская |
-9 |
|
3 |
Преображенская |
-8 |
|
4 |
Сокольники |
-9 |
|
5 |
Красносельская |
-8 |
|
6 |
Комсомольская |
-8 |
|
7 |
Красные |
-31 |
|
8 |
Чистые |
-35 |
|
9 |
Лубянка |
-33 |
|
10 |
Охотный |
-15 |
|
11 |
Библиотека |
-12 |
|
12 |
Кропоткинская |
-13 |
|
13 |
Парк |
-11 |
|
14 |
Фрунзенская |
-42 |
|
15 |
Спортивная |
-42 |
|
16 |
Воробьёвы |
+10 |
|
17 |
Университет |
-27 |
|
18 |
Проспект |
-8 |
|
19 |
Юго-Западная |
-8 |
1). Для электронной презентации доклада о
Сокольнической линии московского метро Антону необходимо представить
статистическую информацию о глубине заложения станций на этой линии до её
продления в 2016 году.
Найдите следующие
средние характеристики (округляйте до целого):
среднее арифметическое:
_______________________
медиана:
_____________________________________
мода:
________________________________________

станций Сокольнической линии московского метро – от станции «Воробьёвы горы» до
станции «Юго-Западная».
Характеристики и система оценивания:
Первая линия московского метро. Задание 1.
Характеристики задания
Класс: 8
• Содержательная область:
Неопределённость и данные
• Компетентностная область:
Применять
• Контекст: Общественная жизнь
• Уровень сложности: Средний
• Формат ответа: Задание с
несколькими краткими ответами
• Объект оценки: Вычисление
статистических средних заданного набора данных
Система
оценивания
|
Балл |
Содержание |
|
2 |
Даны три верных среднее |
|
1 |
Верно даны два из отсутствует. |
|
0 |
Другие ответы. |
Первая линия московского метро. Задание 2.
Характеристики задания
Класс: 8
• Содержательная область:
Неопределённость и данные
• Компетентностная область:
Применять
• Контекст: Общественная жизнь
• Уровень сложности: Высокий
• Формат ответа: Задание на
построение
• Объект оценки: Построение
диаграммы
Система
оценивания
|
Балл |
Содержание |
|
1 |
Диаграмма построена |
|
0 |
Другие ответы. |
2.РАСЧЕТ МНОГОСЛОЙНОЙ ДОЩАТО-КЛЕЕНОЙ БАЛКИ
Дощато-клееные балки в виде многослойного пакета обладают рядом преимуществ перед другими составными балками:
1)работают как монолитные;
2)их возможно изготовить с поперечным сечением любых ширины и высоты;
3)отдельные доски по длине в балках стыкуются с помощью зубчатого шипа, поэтому балка не имеет стыков, ослабляющих сечение;
4)удалены пороки древесины, т. е. повышена сортность;
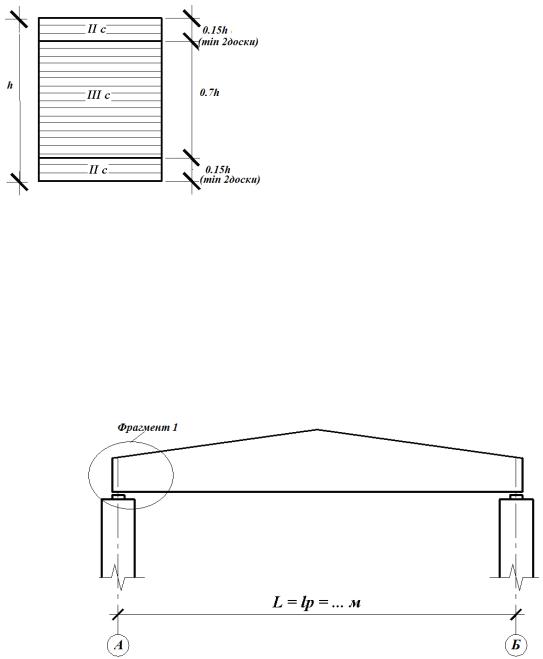
5)балки составляют из древесины одной породы разных сортов (рис.17). Второй сорт по краям сечения (в зоне действия максимальных нормальных напряжений) и III сорт в середине сечения.
Балки проектируют из пакета стандартных досок толщиной 32, 40 мм. Применение более толстых досок ведет к их растрескиванию вследствие коробления, более тонких – к
Дудорожанию изделия. Ширина досок
из условияИдостаточности опирания на балку плит покрытия.
Рис.17. Сечение дощато-клееной балки
балки назначается 150, 175, 200 мм А
Перед склеиванием доскибострагивают только по пласти с двух сторон, вследствие чего их толщинаиδ уменьшается на 4 – 7 мм.
Расчетная длина балки равна расстоянию между серединами площадок опирания (рис. 18, 19): lр = L, м.
Рис. 18. Поперечная рама
25
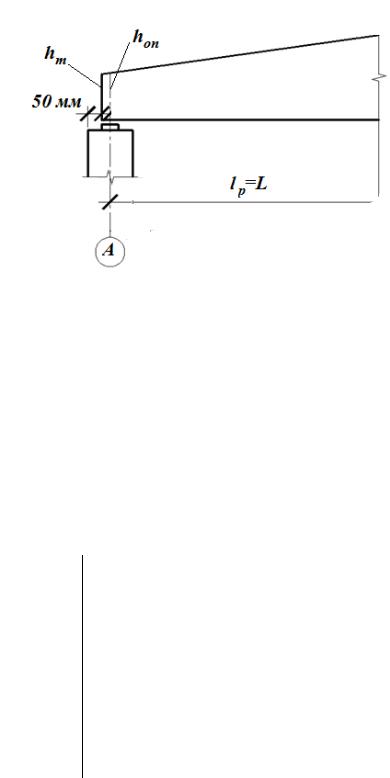
Рис. 19. Фрагмент схемы для определения расчетной длины балки
На рис.19 приведены обозначения: hт – высота двускатной балки в торце; hоп – высота двускатной балки на опоре; 50 мм – зазор, необходимый для предотвращения разрушения стыка «колонна – стеновое ограждение» при повороте торцевого сечения балки при ее изгибе от штатной нагрузки.
2.2. Определение нагрузок, действующих на балку |
||||||||||||
|
И |
||||||||||||
|
Нагрузки, действующие на балку, приведены в табл. 3. |
||||||||||||
|
Нагрузки, действующиеДна балку |
Таблица 3 |
|||||||||||
|
Вид нагрузки |
Нормативная нагрузка |
γf |
Расчетная нагрузка |
|||||||||
|
кг/м2 |
B = м, кг/м |
кг/м2 |
B = м, кг/м |
|||||||||
|
А |
||||||||||||
|
1. Постоянные: |
||||||||||||
|
— от с.в. плиты |
+ |
+ |
1,1 |
+ |
+ |
|||||||
|
и рулонной |
б |
|||||||||||
|
кровли |
+ |
+ |
+ |
+ |
||||||||
|
— от с.в. балки |
и |
1,1 |
||||||||||
|
2. Временная |
||||||||||||
|
длительно дей- |
+ |
+ |
1,4 |
+ |
+ |
|||||||
|
ствующая сне- |
С |
|||||||||||
|
говая нагрузка |
||||||||||||
|
∑ |
∑ |
|||||||||||
|
Нормативную нагрузку от собственного веса балки в предварительных |
||||||||||||
|
подсчетах (кгс/м2) можно определить по формуле |
||||||||||||
|
qн |
qн pн |
|||||||||||
|
п |
с |
. |
||||||||||
|
б |
1000 |
|||||||||||
|
1 |
||||||||||||
|
Ксв l р |
(31) |
|||||||||||
где qпн – нормативная нагрузка от веса плиты, кгс/м2; pcн – нормативная нагрузка от веса снега, кгс/м2; Kсв = 6 – коэффициент собственного веса балки, принят по [3, табл. 6.1]; lp – расчетная длина балки.
26
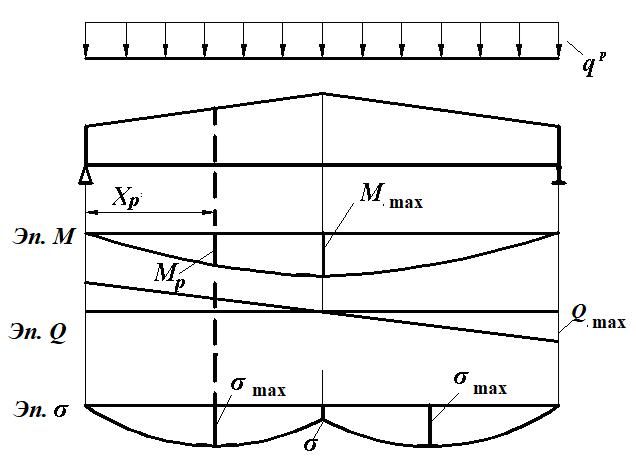
2.3. Статический расчет балки
Результаты статического расчета балки приведены на рис. 20.
|
И |
|||||||||
|
Д |
|||||||||
|
А |
|||||||||
|
б |
|||||||||
|
и |
|||||||||
|
Рис. 20. Определение расчетного сечения балки |
|||||||||
|
Максимальное значен е |
згибающего момента (кгс м) определяется по |
||||||||
|
С |
|||||||||
|
q p l 2 |
|||||||||
|
формуле M max |
р |
. Макс мальное значение поперечной силы (кгс) можно |
|||||||
|
8 |
|||||||||
|
определить по формуле Q |
q p l |
p |
. |
||||||
|
max |
2 |
||||||||
Эпюру распределения нормальных напряжений по длине балки в зависимости от высоты поперечного сечения балки необходимо построить после определения положения расчетного сечения хр, в котором действуют максимальные нормальные напряжения.
2.4. Определение высоты балки на опоре из условия прочности по касательным напряжениям
При пролетах до 18 м рекомендована ширина балки 175 мм. Толщина досок в пакете принята 40 мм (33 мм после острожки). Принятые в работе обозначения высотных размеров двускатной балки приведены на рис. 21.
27
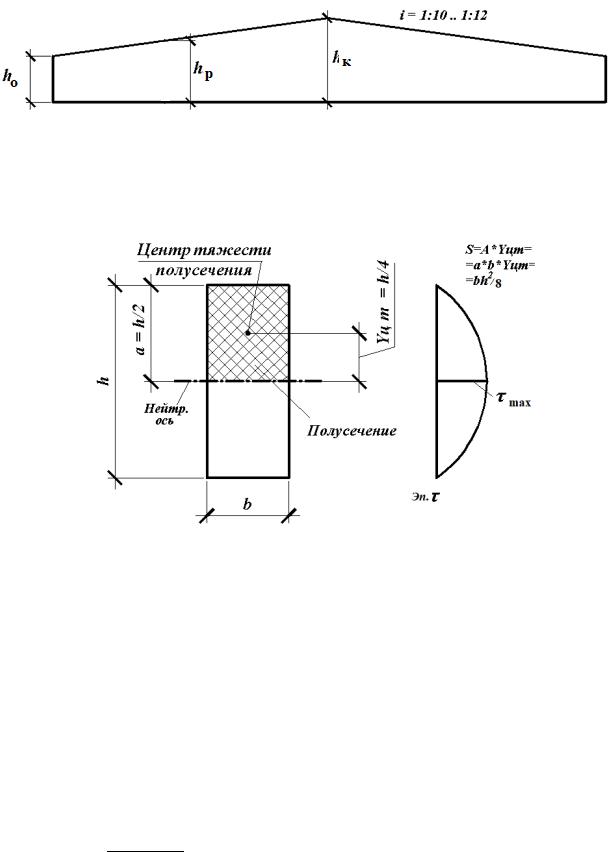
На данном рисунке и в дальнейших расчетах приняты следующие обозначения высотных размеров проектируемой двускатной балки: hк – высота балки в коньке; hо – высота балки в опорном сечении; hр – высота балки в расчетном сечении.
Рис. 21. Обозначение высотных размеров двускатной балки
Требуемую высоту поперечного сечения балки на опоре h0 (рис. 22) можно определить из условия прочности по касательным напряжениям.
|
И |
|||||||||
|
Д |
|||||||||
|
А |
|||||||||
|
С |
б |
||||||||
|
Р с. 22. Определение максимальных касательных |
|||||||||
|
инапряжений в опорном сечении балки |
|||||||||
|
Условие прочности по касательным напряжениям определено по СП [1, |
|||||||||
|
формула (18)]: |
|||||||||
|
max |
Q S |
Rск mi , |
(32) |
||||||
|
J b |
|||||||||
|
где S – статический момент сдвигаемой части опорного сечения, S |
bh2 |
||||||||
|
о |
; |
||||||||
|
8 |
|||||||||
|
J – момент инерции опорного сечения, J |
bh3 |
||||||||
|
о |
; Q – поперечная сила в |
||||||||
|
12 |
|||||||||
опорном сечении (см. рис. 20); mi – произведение коэффициентов условия
работы, mi mв mб mсл ,
n
28
здесь mв – коэффициент, учитывающий условия эксплуатации конструкции. Принимается по СП [1, табл. 7]; mб коэффициент, учитывающий высоту сечения балки. Принимается по СП [1, табл. 9]); mсл коэффициент, учитывающий толщину слоя в пакете. Принимается по СП [1, табл. 10]; n –
коэффициент учитывающий срок службы здания. Принимается по СП [1,
табл. 12].
Подставив полученные значения момента инерции и момента сопротивления в условие прочности, получим
|
Q b h2 12 |
Rск mi . |
||||||
|
8 b h3 |
|||||||
|
о |
|||||||
|
о |
|||||||
|
Откуда высота балки на опоре предварительно равна |
|||||||
|
hо |
3Q |
. |
(33) |
||||
|
2bRск mi |
|||||||
|
Предварительно высоту балки в коньке hк |
определим из заданного |
||||||
|
уклона: |
И |
||||||
|
hк = h0 + 0,5 l i. |
(34) |
||||||
|
В балках с линейно изменяющейся высотой при нагружении равномер- |
|||||||
|
р |
Дp |
||||||
|
но распределенной нагрузкой расчетным является изгибающий момент Мр, |
|
вызывающий максимальные напряжения σmax в сечении, находящемся на |
|||||||||||||
|
А |
|||||||||||||
|
расстоянии Xp от опоры (см. рис. 20). |
|||||||||||||
|
Это расстояние определяют как |
|||||||||||||
|
б |
h0 |
||||||||||||
|
и |
Х |
0,5 l |
( |
hк |
). |
(35) |
|||||||
|
При этом высота расчетного сечения |
|||||||||||||
|
С |
hp |
h0 |
iX p . |
(36) |
|||||||||
|
6 |
|||||||||||||
|
Момент в расчетном сечен и |
|||||||||||||
|
M p |
q p X |
p |
(lp X p ) . |
(37) |
|||||||||
|
2 |
|||||||||||||
|
Момент сопротивления расчетного сечения |
|||||||||||||
|
b h2 |
|||||||||||||
|
Wp |
p |
. |
(38) |
||||||||||
|
Момент инерции расчетного сечения |
|||||||||||||
|
b h3 |
|||||||||||||
|
J p |
p |
. |
(39) |
||||||||||
|
12 |
|||||||||||||
|
Статический момент расчетного сечения |
|||||||||||||
|
b h2 |
|||||||||||||
|
S p |
p |
. |
(40) |
||||||||||
|
8 |
|||||||||||||
Полученное по формуле (36) значение высоты расчетного сечения балки корректируем в сторону увеличения, компонуя его по доскам (рис. 23). Методика компоновки двускатных дощато-клееных балок по длине приведена на рис. 24.
29
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Невесомая горизонтальная балка покоится на опорах A и C. В точке B к ней прикреплен груз массой 20 кг. Расстояние AB = 8 м, BC = 2 м. Найти модули сил, с которыми опоры действуют на балку в точках A и C.
Рассмотрим универсальный алгоритм, позволяющий получить решение для подобных задач. Шаги этого алгоритма делают решение несложным и логически понятным.
Решение
Чтобы решить предложенную задачу, будем применять:
- правила составления векторных уравнений,
- понятие момента силы,
- условия равновесия тел.
Обязательно перейдите по ссылкам и ознакомьтесь со статьями. А после продолжайте читать данную статью, цепочка действий для получения ответа станет проще для понимания.
Шаг 1 — составим рисунок
Укажем на рисунке опоры и груз, действующий на балку (рис. 1).
Рис. 1. Горизонтальная невесомая балка опирается на опоры в точках A и C, в точке B к ней прикреплен груз
Примечание: Обязательно составляйте рисунок, он поможет ясно увидеть ситуацию задачи
Шаг 2 — заменим тела силами их воздействия
Заменим теперь тела, действующие на балку, силами их воздействия (рис. 2). Каждую опору заменим силой реакции опоры, а груз — силой тяжести.
Рис. 2. Балка опирается на опоры в точках A и C, в точке B к ней прикреплен груз, A – точка, через которую проходит ось вращения балки
На рисунке 2 горизонтальными стрелками отмечены плечи сил (mg) и (N_{C}). Точка A выделена красным цветом. Будем считать, что вокруг этой точки балка может вращаться, т. е. через эту точку проходит ось вращения балки.
Примечание: Силы на рисунке 2 направлены вертикально. Поэтому, для составления силового уравнения достаточно провести одну вертикальную ось.
Шаг 3 — составим условия равновесия для балки
Первое условие равновесия балки выглядит так:
[ large N_{A} + N_{C} — mg = 0 ]
( N_{A} left( H right) ) – сила реакции опоры в точке A;
( N_{C} left( H right) ) – сила реакции опоры в точке C;
( mg left( H right) ) – вес (ссылка) груза, прикрепленного к балке в точке B;
Величину ( g ) называют ускорением свободного падения.
Запишем второе условие равновесия балки. Для этого используем точку A, вокруг которой может происходить вращение балки и понятие момента силы.
[ large — N_{C} cdot AC + mg cdot AB = 0 ]
( AC left( text{м} right) ) – плечо силы реакции опоры (N_{C});
( AB left( text{м} right) ) – плечо силы (mg);
( mg left( H right) ) – вес груза, прикрепленного к балке в точке B;
Мы получили систему из двух уравнений, описывающих балку, находящуюся в покое под действием приложенных сил.
[ large boxed{ begin{cases} N_{A} + N_{C} — mg = 0 \ — N_{C} cdot AC + mg cdot AB = 0 end{cases} } ]
Решив эту систему, мы найдем две неизвестные силы (N_{A}) и (N_{C})
Примечание: Сила (mg) вращает рычаг (балку) по часовой стрелке, а сила (N_{C}) — в противоположном направлении. Из-за этого, перед величиной (N_{C}) возникает знак «минус». Подробнее об этом читайте в статье Рычаг, условие равновесия.
Шаг 4 – подставим числовые значения в полученную систему
Масса груза 20 кг. Расстояние AB = 8 м.
Найдем плечо силы (N_{C}) — расстояние AC.
AC = AB + BC — общая длина состоит из длины вех частей балки (смотрите рис. 2)
AC = 8 + 2
AC = 10 (м)
Подставим числа в систему уравнений для равновесия и получим
[ large begin{cases} N_{A} + N_{C} — 200 = 0 \ — N_{C} cdot 10 + 200 cdot 8 = 0 end{cases} ]
Из второго уравнения системы следует, что ( N_{C} = 160 ) Ньютонов.
Используем этот результат и поместим его в первое уравнение системы. Получаем:
[ large N_{A} + 160 — 200 = 0 ]
Откуда ясно, что ( N_{A} = 40 ) Ньютонов.
Ответ:
[ large begin{cases} N_{C} = 160 (H) \ N_{A} = 40 (H) end{cases} ]
Можно ли провести ось вращения через другую точку
Не обязательно в качестве точки, через которую проходит ось вращения, выбирать точку A. Можно для этих целей выбрать, к примеру, точку B (рис. 3).
Рис. 3. Балка опирается на опоры в точках A и C, в точке B к ней прикреплен груз, через точку B проходит ось вращения балки
В таком случае, получим следующую систему уравнений для равновесного положения балки
[ large boxed{ begin{cases} N_{A} + N_{C} — mg = 0 \ — N_{C} cdot BC + N_{A} cdot AB = 0 end{cases} } ]
Решая ее, получим ответ, аналогичный предыдущему случаю.
Если ось вращения проходит через точку C
Мы можем, также, в качестве точки, через которую проходит ось вращения, выбрать точку C (рис. 4).
Рис. 4. Через точку C проходит ось вращения балки, опоры расположены в точках A и C, в точке B располагается груз
Система уравнений, описывающих равновесие балки, для этого случая будет выглядеть так
[ large boxed{ begin{cases} N_{A} + N_{C} — mg = 0 \ — mg cdot BC + N_{A} cdot AC = 0 end{cases} } ]
Решение этой системы, также, позволит получить ответ для нашей задачи.
Выводы
- В качестве точки, через которую проходит ось вращения балки, можно выбирать любую из точек: A, B или C. Для каждого случая будем получать свою систему уравнений;
- Решая любую из полученных систем уравнений, сможем найти реакции опор;
- Можно, также, дополнительно задать любую другую точку на балке и выбрать ее в качестве точки, через которую будет проходить ось вращения. На ответ задачи это не повлияет и принципа решения не изменит. Важно лишь, чтобы расстояния между точками были известными;
- Иногда попадаются более сложные задачи о равновесии под действием нескольких сил. В них количество неизвестных больше количества уравнений в системе для одной оси вращения. Тогда составляем несколько систем для различных осей вращения и объединяем их в одну общую систему. Этот прием поможет решить задачу;














