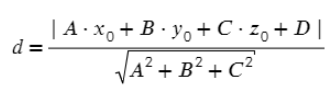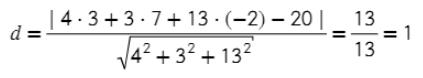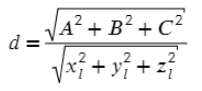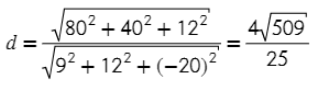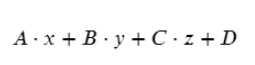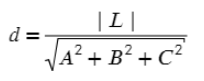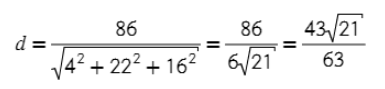Как найти дистанцию до точки

На первый взгляд может показаться, что математика сложна и коварна, но это далеко не так. Если приложить усилия к её изучению, то можно удивиться тому, насколько быстро вы измените своё мнение о ней. Давайте же разберём одну из тем, которая поможет находить расстояние от точки до точки при различных условиях. После того как вы изучите данную статью, вы можете решить предоставленные задания, чтобы лучше закрепить пройденный материал.

Математические термины

 Для начала введём некоторые определения.

Как определить расстояние между точками, находящимися на координатной прямой

Действительные числа

Рассмотрим этот способ на примере:

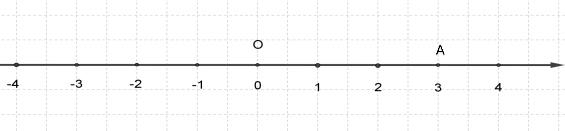
Здесь мы имеем координатную прямую OX, на которой отмечена точка A. Она произвольная, поэтому мы можем задать ей любое действительное число, пусть это будет 3.

Отрезок – это единица длины, поэтому все отрезки, что мы отложили от точки O нужно сложить, вследствие чего полученное количество единичных отрезков будет равняться длине отрезка OA. В данном случае здесь три отрезка, поэтому и ответ таков.

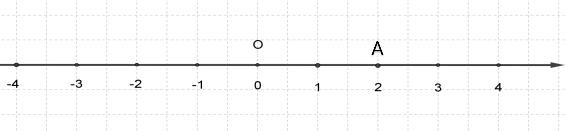
Ещё один пример, где точку отсчёта O и произвольную точку A соединяют 2 отрезка. Это значит, что расстояние длин всех единичных отрезков OA равно 2. Если же точка A будет иметь другое число, например: 6, то мы откладываем от точки O именно 6 единичных отрезков и получаем искомое расстояние.

Рациональные числа

С действительным числами всё понятно, а что делать с рациональными? Представим, что координаты точки A равны 5,5. Из этого следует, что нам нужно отложить из точки O сначала 5 единичных отрезков, то есть, целое число, а после прибавить 0,5. Иногда это кажется невозможным, ведь некоторые числа трудно представить в виде отрезка, из-за чего приходится искать самое приближенное значение числа.

Иррациональные числа

Иррациональным числам данный метод не подходит, потому как такие числа нельзя поставить на координатной прямой OX. Для примера приведём числа √5, √8, √17. Здесь можно перейти к отвлечённому представлению и посмотреть на эти числа таким образом:

• 0>A – если 0 больше A, то A имеет отрицательное значение координат: |OA| = (–A).
• 0<A – если 0 меньше A, то A имеет положительное значение координат: |OA| = (A).

Также можно сказать, что это подходит и к действительным числами. Если точка A будет находиться на начальной точке O, то и расстояние между ними будет равно 0. Здесь нужно уметь хорошо работать с рисунком, тогда всё будет понятно.

• Модуль

Важно помнить, что расстояние между точками не может быть отрицательным.

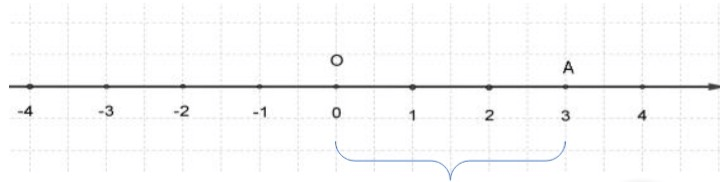
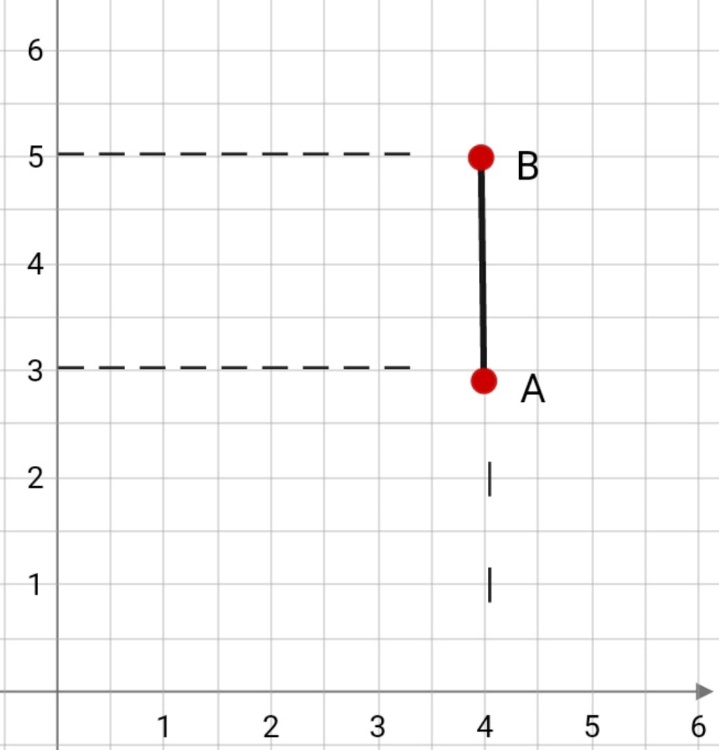
В данном случае у нас есть модуль числа A, что является расстоянием OA и это число 3.

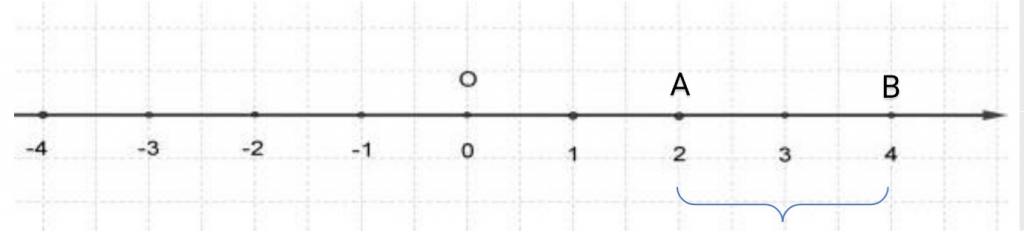
Если на координатной прямой будут точки A и B, то их расстояние нужно определить по модулю разности этих координат. Получается, чтобы найти длину отрезка AB, необходимо из числа точки B отнять число точки A:

4-2=2.

Как определить расстояние между двумя точками на плоскости

Представим прямоугольную систему координат и плоскость на ней, с находящимися там точками A и B. Далее проведём прямые от этих точек к осям Ox и Oy, как на изображении. В следствие этого образовались точки Ax и Ay, а также Bx и By.

Из этого можно вывести несколько вариантов:

• Ось Ox

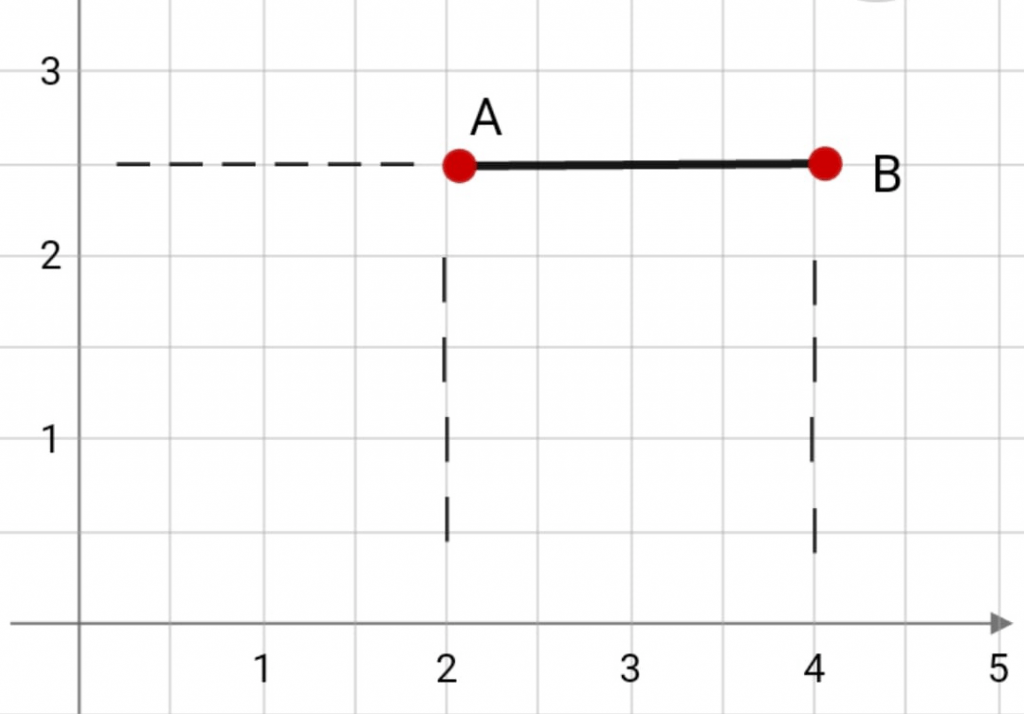
В случае расположения точек A и B на прямой, которая в свою очередь перпендикулярна оси Ox – точки A и B совпадают, а модуль AB равен модулю AyBy. Как говорилось ранее, для нахождения длины промежутка (расстояния) между двумя точками, нужно найти разность модуля заданных координат, поэтому можно сказать, что:

|AB| = |AyBy| = |yB – yA|.

При этом совпадении их расстояние равняется 0.

• Ось Oy

Теперь рассмотрим тот случай, когда прямая перпендикулярна оси Oy. Находится расстояние таким же образом, но уже с участием xB и xA: |AB| = |AxBx| = |xB – xA|.

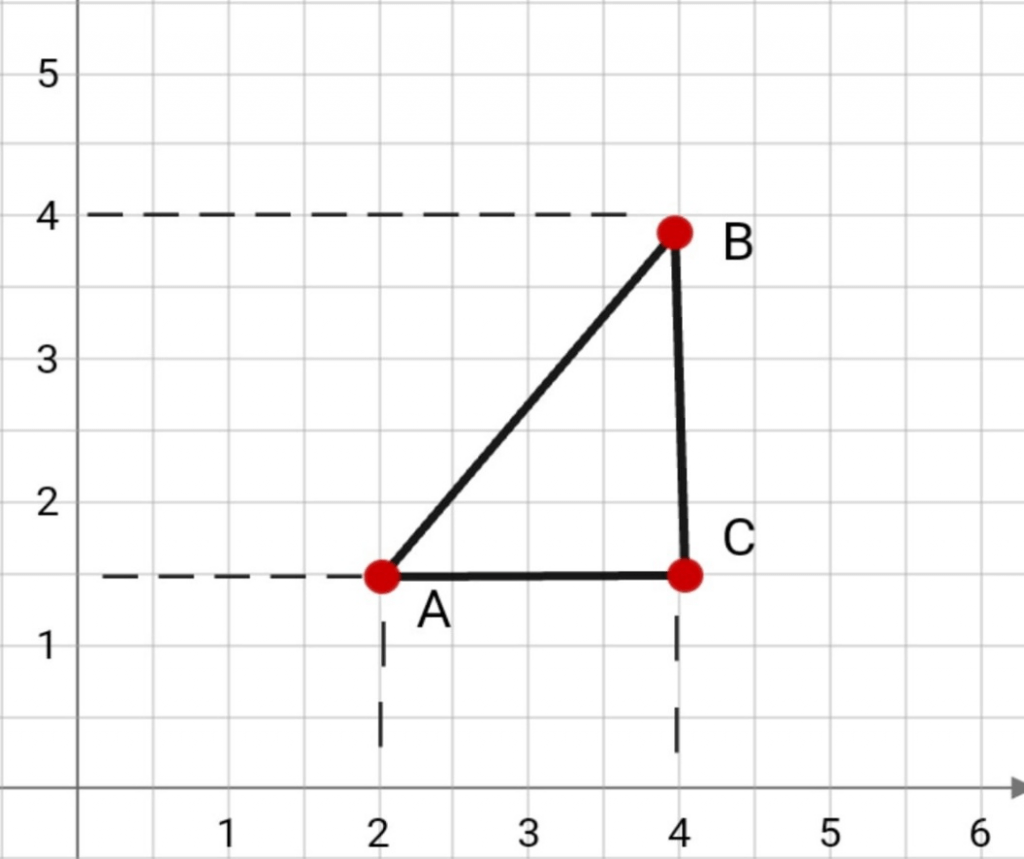
• Точки не лежат на прямой, которая перпендикулярна оси Ox и Oy

Теперь поговорим о прямоугольном треугольнике ABC. Чтобы найти расстояние на плоскости между точкой A и точкой B, необходимо воспользоваться формулой:

|AB| = √(xB – xA)² + (yB – yA)².

 Эта формула доказывает правильность ранее написанных утверждений к тем заданиям, на графиках которых точки лежат на прямой, перпендикулярной Ox и Oy.

Если точки совпадают, к ним справедливо равенство:

|AB| = √(xB – xA)² + (yB – yA)² = √0² + 0² = 0.

По рисунку видно, что:

|AC| = |AxBx|, а также |BC|=|AyBy|. Далее вспомним теорему Пифагора и с её помощью запишем равенство:

|AB|² = |AC|² + |BC|²

|AB|² = |AxBx|² + |AyBy|²

√|AxBx|² + |AyBy|²

√|xB – xA|² + |yB – yA|²

√(xB – xA)² + (yB – yA)²

Пример

Найдите расстояние между двумя точками на плоскости, если известно, что они находятся на прямоугольной системе координат со значениями: A (3, –1), а также B (X + 3, 7). Также надо найти значение действительного числа X, зная, что при них расстояние между точками будет равно 10.

Чтобы решить эту задачу, необходимо использовать формулу:

|AB| = √(xB – xA)² + (yB – yA)².

После этого действия подставляем вышеприведённые числа:

√(X + 3 – 3)² + (7 – ( – 1))² = √X² + 64.

Далее обратим внимание на то, что |AB| = 10 и составим равенство:

√X² + 64 = 10

X² + 64 = 100

X = ± 6

Ответ: |AB| = 10, при X = ±6.

Как определить расстояние между точками в пространстве

Более сложным заданием на нахождение расстояния является то, где точки расположены в пространстве, а не на плоскости.

Возьмём точки, имеющие свои координаты: A (xA, yA, zA), B (xB, yB, zB). Они размещены на прямоугольной системе координат Oxyz. Имея эти данные, мы можем приступить к поиску расстояния между этими точками.  

Итак, проведём плоскости через наши точки A и B, которые должны быть перпендикулярными осям с заданными координатами. Таким образом мы получаем точки точки проекции: Ax, Ay, Az, Bx, By, Bz. Так и получился параллелепипед, диагональ которого равна расстоянию точек.

После чего выполним такие действия:

|AxBx| = |xB – xA|

|AyBy| = |yB – yA|

|AzBz| = |zB – zA|

Теперь выполним преобразование получившегося выражения:

|AB|² = |AxBx|² + |AyBy|² + |AzBz|² = |xB – xA|² + |yB – yA|² + |zB – zA|² = (xB – xA)² + (yB – yA)² + (zB – zA)².

После всех этих действий мы можем выделить основную формулу, которая применяется для нахождения расстояния точек в пространстве:

=√(xB – xA)² + (yB – yA)² + (zB – zA)².

Её можно применять в тех случаях, когда точки располагаются на прямой, которая параллельна координатной оси или же они находятся на этой координатной оси. При совпадении точек эта формула также действительна.

Пример

Найдите расстояние между точками, которые лежат на прямоугольной системе координат в трёхмерном пространстве, координаты которых: A (2, 3, 4), а также B (-6, -1, 5).

Перейдём к решению, воспользовавшись формулой:

√(xB – xA)² + (yB – yA)² + (zB – zA)².

Подставляем имеющиеся значения:

√(–6 – 2)² + (–1 – 3)² + (5 – 4)² = √64 + 16 + 1 = √81 = 9.

Ответ: расстояние |AB| равно 9.

Задачи для самостоятельного решения

1. Задача
   Найдите расстояние между точками на плоскости, если известно, что они находятся на прямоугольной системе координат со значениями: A (2, 5), а также B (6, 4).
2. Задача
   Найдите расстояние между точками на плоскости, если известно, что они находятся на прямоугольной системе координат со значениями: A (1, 6), а также B (1, 25).
3. Задача
   Найдите расстояние между точками, которые лежат на прямоугольной системе координат в трёхмерном пространстве, координаты которых: A (1, -3, 4), а также B (4, 1, 4).
4. Задача
   Найдите расстояние между точками, которые лежат на прямоугольной системе координат в трёхмерном пространстве, координаты которых: A (2, -2, 7), а также B (6, 2, 5).

Ответы с решением:

1. Решение первой задачи

   Для решения понадобится формула:
   |AB| = √(xB – xA)² + (yB – yA)².
   Далее подставляем числа:
   |AB| = √(6 – 2)² + (4 – 5)² = √4² + (–1)² = √16 + 1 = √17.
   Ответ: |AB| равен √17.

2. Решение второй задачи

   Формула для нахождения:
   |AB| = √(xB – xA)² + (yB – yA)².
   Подставляем:
   |AB| = √(1 – 1)² + (25 – 6)² = √(0)² + (19)² = √0 + 361 = √361 = 19
   Ответ: |AB| равен 19.
3. Решение третьей задачи
   Запишем формулу:
   √(xB – xA)² + (yB – yA)² + (zB – zA)².
   Подставим числа:
   √(4 – 1)² + (1 – (–3))² + (4 – 4)² = √(3)² + (4)² + (0)² = √9 + 16 + 0 = √25 = 5.
   Ответ: |AB| равняется 5.
4. Решение четвертой задачи
   Записываем формулу для решения:
   √(xB – xA)² + (yB – yA)² + (zB – zA)²
   Заменим на координаты точек:
   √(6 – 2)² + (2 – (–2))² + (5 – 7)² = √(4)² + (4)² + (–2)² = √16 + 16 + 4= √36 = 6.
   Ответ: |AB| равняется 6.

Координатный квест: как найти координаты и расстояния без регистраций и смс

Привет, Хабр!

С вами участник профессионального сообщества NTA Алексей Майка.

Хочу поделиться своим опытом решения одной интересной задачки и описать весь проделанный путь.

Был обычный денёк, сидел я на работе и занимался своими айтишными делами. Ко мне пришел руководитель и сказал: «Нужно рассчитать дистанцию до границы регионов для этих адресов». При этом без всяких платных сервисов и API онлайн карт, и своими усилиями. Айтишник понял, айтишник принял, айтишник получил свою заветную эксельку и пошёл работать.

План работы

Вступление

Из школьных уроков географии я помнил, что для определения километража требуется знать координаты (широту и долготу) двух точек. И исходя из этого, я разделил задачу на 4 части:

• поиск координат границы;

• предобработка данных;

• поиск координат адресов;

• непосредственный расчёт расстояний между координатами.

В посте продемонстрировал весь путь решения данной задачи, небольшие нюансы, проверку результатов и непосредственно код. И, познакомив читателя с моей маленькой предысторией, расскажу об инструментах, которыми я пользовался.

В качестве основного инструмента для парсинга, обработки и расчётов я использовал Python. Средой разработки выступали Jupyter Notebook (Anaconda), PyCharm и DataSpell от компании JetBrains (дело вкуса). При работе с данным проектом использовал библиотеки Numpy, Pandas, Plotly, Geopy, Selenium.

На этом прелюдия заканчивается, переходим к сути.

Начало начал

Для расчёта дистанции до границы нужны координаты, что неудивительно, самой границы. Вручную прокликивать точки на карте мне не очень хотелось, а попытка поиска готовых координат полностью провалилась. К счастью, удалось найти json‑файл с положением границ субъектов России, среди которых и находятся нужные точки.

Для начала достаю нужные области. Импортирую библиотеки для дальнейшей работы, сохраняю данные файла в словарь (dict) и смотрю на содержимое объекта:

#Библиотека для работы с ".json"-файлами
import json 
#Библиотека для обработки и анализа данных
import pandas as pd
#Библиотека для работы с многомерными массивами
import numpy as np

# Считываем файл с координатами всех регионов
with open('data//gadm41_RUS_1.json', encoding = 'utf-8') as js:
    dict_coordin_border = json.load(js)

Видно, что json хорошо структурирован, и с ним достаточно легко работать. Названия регионов и координаты можно найти по следующим ключам:

• dict_coordin_border[‘features’] [‘properties’][‘NL_NAME_1’] — название субъекта федерации;

• dict_coordin_border[‘features’] [‘geometry’][‘coordinates’] — координаты границ субъектов.

Выделяю из данного словаря только нужные пять областей, и записываю в pandas.DataFrame данные, где:

• region — название региона;

• lon — долгота точки границы;

• lat — широта точки границы;

• sequence_number — порядковый номер записи;

• color — цвет региона.

Зачем цвет и порядковый номер? Расскажу далее, а сейчас предлагаю рассмотреть код:

Посмотреть код

df_coord_reg = pd.DataFrame()
sequence_number = 0

for regions in dict_coordin_border['features']:
    #Ставим условия для поля названия субъектов
    if regions['properties']['NL_NAME_1'] in ['Воронежскаяобласть',
                                              'Брянскаяобласть',
                                              'Курскаяобласть',
                                              'Ростовскаяобласть',
                                              'Белгородскаяобласть']:

        for list_coordin_lv_1 in regions['geometry']['coordinates']:
            for list_coordin_lv_2 in list_coordin_lv_1:
                for list_coordin_finish_lvl in list_coordin_lv_2:

                    #Заполняем df: Название региона, координаты точки границы, порядковый номер записи, цвет региона
                    if regions['properties']['NL_NAME_1'] == 'Воронежскаяобласть': color = 'purple'
                    elif regions['properties']['NL_NAME_1'] == 'Брянскаяобласть': color = 'white'
                    elif regions['properties']['NL_NAME_1'] == 'Курскаяобласть': color = 'blue'
                    elif regions['properties']['NL_NAME_1'] == 'Ростовскаяобласть': color = 'yellow'
                    elif regions['properties']['NL_NAME_1'] == 'Белгородскаяобласть': color = 'red'

                    df_coord_reg = df_coord_reg.append({'region': regions['properties']['NL_NAME_1'], #Название региона
                                                        'lon': list_coordin_finish_lvl[0], #Долгота точки границы
                                                        'lat': list_coordin_finish_lvl[1], #Широта точки границы
                                                        'sequence_number': str(sequence_number), #Порядковый номер записи
                                                        'color': color}, #Цвет региона
                                                       ignore_index = True)
                    sequence_number += 1

В итоге получается следующий dataframe:

На данном этапе я получил координаты границ регионов со всех сторон. Но это не совсем нужный результат, требуется только та часть границ, которые не совпадают друг с другом. И здесь я хочу рассказать про библиотеку plotly.

О plotly

Plotly — это графическая библиотека для интерактивной визуализации данных. С её помощью можно создавать диаграммы, гистограммы, карты распределения, 2D‑диаграммы, 3D‑графики и многое другое. Эта библиотека — сильный «зверь» для визуала, и она поможет расположить полученные точки на карте. Подробнее ознакомиться можно по ссылке.

Код ниже отображает точки на географической карте Европы:

Код

#Импортируем библиотеки для визуализации данных
import plotly.graph_objs as go

#Визуализируем на карте точки с координатами для проверки и дальнейшего анализа

fig = go.Figure(data=go.Scattergeo(                       #Scattergeo - данные, визуализируемые в виде точек географической карте
                  lon = df_coord_reg['lon'],                      #Долгота точки
                  lat = df_coord_reg['lat'],                        #Широта точки
                  mode = 'markers',                                   #Вид точки
                  marker_color  = df_coord_reg['color'],  #Цвет точки
                  text = df_coord_reg['region'] + ' ' + df_coord_reg['sequence_number']  #Текст при наведении на точку
                ),
            )

fig.update_layout(
        title = 'Субъекты РФ ',      #Задаем название карты
        geo = dict(
            scope='europe',                                   #Шаблон карты 
            landcolor = "green",                           #Цвет для стран
            countrycolor = "black",                      #Цвет границ между странами
        ),
        width=1500,                                            #Ширина карты
        height=750                                              #Высота графика
    )

Результат выполнения кода:

Как видно на рисунке, все точки находятся на своих местах. Осталось из них выбрать только точки, не являющиеся общими для регионов. Для этого я и задавал цвет областей и их порядковый номер.

Выбираю номера точек, которые находятся на границе, и перезаписываю данные в dataframe:

#Исходя из карты, выбираем следующие срезы df и записываем их в новую переменную
df_coord_border = pd.concat([df_coord_reg[11:411],
                             df_coord_reg[1278:1459],
                             df_coord_reg[974:1226],
                             df_coord_reg[3084:3157],
                             df_coord_reg[2004:2413]])

Для проверки повторно визуализирую данные и сохраняю полученные координаты в json‑файл.

Код

#Визуально проверяем полученный dataframe

fig = go.Figure(data=go.Scattergeo(lon = df_coord_border['lon'],
                                   lat = df_coord_border['lat'],
                                   mode = 'markers',
                                   marker_color  = df_coord_border['color'],
                                   text = df_coord_border['region'] + ' ' + df_coord_border['sequence_number']))
fig.update_layout(
        title = 'Субъекты РФ',
        geo = dict(
            scope='europe',
            landcolor = "green",
            countrycolor = "black",
        ),
        width=1500,                                            #Ширина карты
        height=750                                              #Высота графика
    )

#Сохраняем данные в json
df_coord_border[['lon', 'lat']].to_json('data//border.json')

Результат работы кода:

Кто? А главное, зачем?

Помните об эксельке, которую я упоминал в начале? Вот теперь пришло и её время. Создаю новую тетрадку, импортирую библиотеки, читаю xlsx‑файл. Смотрю на данные.

import pandas as pd
import numpy as np
import json

#Возьмем данные из входного файла
df_start_adress = pd.read_excel('data//starting_address.xlsx')

border_coord_df.head()

Что же получается? В файле хранятся 6 228 адресов, и, даже взглянув на эту выборку, закрадывается подозрение, что данные не имеют строгого формата. Необходимо удалить из dataframe дубликаты и проверить данные на пропуски:

#Удалим дубликаты
df_start_adress = df_start_adress.drop_duplicates()

df_start_adress

#None отсутствуют
df_start_adress.info()

#NaN,None и пустота могут быть в виде строки. Проверяем по длине строки
df_start_adress[df_start_adress['полный адрес'].str.len() <= 5]

К счастью, пропусков не наблюдается, а после удаления дубликатов dataframe сократился на 2 000 строк.

Проанализировав можно выделить несколько проблем:

1. Нет строгой типизации формата адресов. Это сильно ограничивает библиотеки и технологии, такие как запросы HTTP и бесплатные API сайтов.

1. В адресах присутствует подстрока «Адрес из Росреестра:». При проверке таких адресов в «Яндекс.Картах», выдается адрес отдела Росреестра города исходного адреса или пустой результат поиска:

1. Дублируются данные внутри ячеек. При проверке в онлайн картах данные не выдаются, или строится маршрут движения по этим адресам, точнее, путь от себя к себе:

1. Присутствуют лишние данные, которые мешают поиску.

Обработать полученные данные и привести их к одному виду показалось очень трудозатратной задачей. Проверив несколько адресов, я решил использовать сервис «Яндекс Карты». Он показал, что может работать с различными адресами и выдавать корректный результат.

Но обработать адреса все равно необходимо и избавиться хотя бы от некоторых проблем: подстрока с Росреестром и повторяющиеся данные.

Для этого применяю функцию formating_text. В функции создаю список, разбиваю строку на слова и помещаю их в список поочередно. Если данное слово уже существует в списке, то его в список не добавляю. В конце удаляю из итоговой строки «Росреестр»:

def formating_text(text):
    old_text = text.split()
    new_text = []
    for word in old_text:
        if word not in new_text:
            new_text.append(word)

    return ' '.join(new_text).replace('Адрес из Росреестра: ', '')

df_start_adress['formating_adress'] = df_start_adress['полный адрес'].apply(lambda x: formating_text(x))

Сохраняю полученный результат и перехожу к следующему этапу.

Дёшево и сердито

Самые внимательные читатели могли заметить, что для данного проекта я использовал библиотеку Selenium. Почему именно она? Она обладает преимуществами на фоне остальных библиотек и методов парсинга. Её ближайшие аналоги:

• API «Яндекс.Карт». Данная система хоть и очень удобна в использовании для этой задачи, но она не бесплатна. А мы договаривались в начале публикации, никаких дополнительных вложений.

Тарифы Яндекса

• Http/Https‑запросы. В отличие от системы, описанной выше, для запроса требуется только возможность подключения к нужному сайту. Но с моими данными написание get/ post-запросов — довольно сложная задача. К примеру, запрос https://yandex.ru/maps/213/moscow/house/mokhovaya_ulitsa_11s1 состоит из названий города, улицы и номера дома на транслите. Преобразовать входящие данные в такой формат будет непосильной задачей для меня.

Методом исключения осталась только библиотека Selenium, которая будет симулировать действие человека в браузере на сайте. Это позволит обойти системы защиты Яндекса, воспользоваться их алгоритмами обработки данных и найти координаты объекта.

Сразу скажу, здесь я не буду обучать вас данной библиотеке. Лишь разберу основной алгоритм работы скрипта, покажу некоторые нюансы и возможные методы их решения.

Подключение драйвера. В данном проекте я использовал браузер Google Chrome, и примеры будут для Google. Библиотека Selenium уже имеет в себе драйвер для работы с Google, и для его подключения просто нужно прописать команду webdriver.Chrome(). Для перехода на сайт используйте функцию get.

from selenium import webdriver
#Адрес сайта "Яндекс.Карты"
url_adress = 'https://yandex.ru/maps'

#Подключение драйвера Google
driver = webdriver.Chrome('chromedriver.exe')
#Переход на сайт
driver.get(url_adress)
time.sleep(5)

Поиск адреса. Адрес вписывается в поле формы поиска, код данного элемента «<input class=”input__control_bold” >». Для поиска элемента использовал комбинацию функций WebDriverWait и ExpectedCondition. Selenium будет производить поиск элемента, пока он не будет найден или не кончится время ожидания.

Далее заполняю найденную форму адресом с помощью функции send_keys и запускаю поиск, имитируя нажатие клавиши Enter функцией send_keys(Keys.ENTER).

from selenium.webdriver.support.ui import WebDriverWait
from selenium.webdriver.support import expected_conditions as EC
# Время ожидания
delay = 10

# Поиск формы ввода на сайте
elem_search_string = WebDriverWait(driver, delay) 
    .until(EC.presence_of_element_located(
    (By.XPATH, "//input[@class='input__control _bold']")))

# Вписываем данные в форму
elem_search_string.send_keys(adress)
# Запускаем поиск
elem_search_string.send_keys(Keys.ENTER)

Результат поиска. Если все отработало штатно, Яндекс должен выдать географические координаты адреса. С помощью уже знакомой комбинации WebDriverWait и ExpectedCondition записываю координаты в переменную:

# Поиск координат на сайте
elem_search_2 = WebDriverWait(driver, delay) 
    .until(EC.presence_of_element_located(
    (By.XPATH, "//div[@class='toponym-card-title-view__coords-badge']")))
# Запись в переменную координат адреса
coord = elem_search_2.text

Но Яндекс — не всемогущ, он не всегда находит однозначный ответ, поэтому на некоторые адреса он предлагает несколько вариантов. Как, например, здесь:

На случай таких ситуаций я брал первый предложенный вариант. Скорее всего он и будет являться нужным мне адресом:

elem_first_list = WebDriverWait(driver, delay) 
    .until(EC.presence_of_element_located(
    (By.XPATH, "//div[@class='search-snippet-view__body _type_toponym']")))
elem_first_list.click()

И напоследок очищаю форму записи:

try:
    elem_clear = WebDriverWait(driver, 2) 
        .until(EC.presence_of_element_located(
        (By.XPATH, "//a[@class='small-search-form-view__pin']")))
except:
    elem_clear = WebDriverWait(driver, 2) 
        .until(EC.presence_of_element_located(
        (By.XPATH, "//div[@class='small-search-form-view__icon _type_close']")))

Рекомендую объединить поиск координат на сайте и очистку формы записи на случай, если сервис не найдет никакого результата. Это позволит продолжить работу скрипта и не перезапускать программу.

Повторяю все вышеперечисленные действия ещё 3 000 раз и сохраняю
результат в файл.

Финишная прямая

Осталось дело за малым: рассчитать дистанцию между координатами адресов и кратчайших точек построенной границы. С этим поможет библиотека Geopy.

О Geopy 

Geopy — это сторонняя библиотека Python для определения географического местоположения. Она позволяет разработчикам Python легко находить координаты адресов, городов, стран и достопримечательностей по всему миру, используя сторонние геокодеры и другие источники данных. Ознакомиться с библиотекой можно по ссылке.

Для начала импортирую библиотеки и данные с файлов, которые получил ранее, координаты границы и адреса. Преобразую их в нужный формат для удобства в работе.

#Импортируем библиотеки
import pandas as pd
from geopy.distance import geodesic as GD 
import json
from tqdm import tqdm

#Ипортируем данные с координатами
with open("data/adress_coord.json", 'r', encoding='utf-8-sig') as ad_cor:
    adress_coord_dict = json.load(ad_cor)
    
border_coord_df = pd.read_json("data//border.json")

#Для удобства словарь с координатами адресов преобразуем в df
atress_coord_df = pd.DataFrame(adress_coord_dict.items(), columns=['adress', 'coord'])

# Преобразуем координаты границы в список
list_border_coord = list([(row['lat'], row['lon']) for index, row in border_coord_df.iterrows()])

Из библиотеки Geopy меня интересует только одна функция, которая как раз и рассчитает расстояние между двумя координатами — geodesic. Показываю, как она работает на примере:

Как видно из примера, в функцию нужно подавать широту и долготу в виде списка, множества, строки или кортежа. Главное, чтобы данные подавались попарно. В конце можно добавить единицу измерения расстояния: километры (km, kilometers), метры (m, meters), мили (mi, miles) и т. д.

Теперь пишу функцию, которая и будет считать минимальное расстояние между точками границы и адресом:

def distance_calculation(start_coord):
    list_dist = []
    for bord_coord in list_border_coord:

        #Для расчета расстояния используем функцию GD([1 координаты точки],[2 координаты точки].[единица измерения расстояния])
        dist = GD(start_coord, bord_coord).km

        #Добовляем в список результат
        list_dist.append(dist)
    
    #Возвращаем минимальную дистанцию из списке
    return min(list_dist)

tqdm.pandas()
atress_coord_df['dist_to_bor'] = atress_coord_df['coord'].progress_apply(lambda x: distance_calculation(x))

Результат:

Оценка качества

Для сдачи итоговых результатов нужно их проверить, ведь плохой результат никто не любит. Открываю Google Maps и адреса из первоначальной эксельки, расстояние до границы и линейку. И, как видно из рисунков, результаты корректны, а погрешность — в допустимых нормах.

Итог

Что я могу сказать по итогу? Задача необычная, интересная и в меру сложная. Попрактиковался с библиотеками Pandas, Selenium, Plotly и посмотрел на новую библиотеку Geopy. Результат работы корректен, а погрешность — в допустимых рамках. Санные пошли дальше в работу.

В общем, задача мне понравилась. Я получил дополнительный опыт и даже некие новые знания, и на этом я заканчиваю пост. Желаю всем удачи!)

P. S. Кстати, чуть не забыл, с кодом вы можете ознакомиться на Github.

Измерить расстояние на карте линейкой

Вы можете измерить расстояние на карте линейкой. Для этого выберите инструмент «Линейка» в правом верхнем углу карты.
С помощью данного инструмента Вы можете:

• определить расстояние на карте по прямой между точками
• отметить несколько точек на карте

Для того что бы удалить отмеченный маршрут нажмите снова по иконке «линейка». Для того, что бы отключить линейку нажмите на неё дважды.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Расстояние между точкой и плоскостью.

Расстояние между точкой и прямой.

Расстояние между двумя прямыми.

Первое, что полезно знать, это как найти расстояние от точки до плоскости: 

Значения A, B, C, D — коэффициенты плоскости

x, y, z — координаты точки

Задача. Найти расстояние между точкой А = (3; 7; −2) и плоскостью 4x + 3y + 13z — 20 = 0.

Все дано, можно сразу подставить значения в уравнение:

Задача. Найдите расстояние от точки К = (1; −2; 7) до прямой, проходящей через точки V = (8; 6; −13) и T = (−1; −6; 7).

1. Находим вектор прямой.
2. Вычисляем вектор, проходящий через искомую точку и любую точку на прямой. 
   
3. Задаем матрицу и находим определитель по двум полученным векторам в 1-ом и 2-ом пункте.
4. Расстояние получим, когда квадратный корень из суммы квадратов коэффициентов матрицы поделим на длину вектора, который задает прямую (Думаю непонятно, поэтому перейдем к конкретному примеру).

1) TV = (8−(−1); 6−(−6); -13-7) = (9; 12; −20)

2) Вектор найдем через точки K и T, хотя так же можно было бы через K и V или любую другую точку на данной прямой.

TK = (1−(−1); −2−(−6); 7-7) = (2; 4; 0)

3) Получится матрица без коэффициента D (здесь он не нужен для решения):

Если непонятно, как получить матрицу и ее определитель, смотрите здесь более подробный разбор.

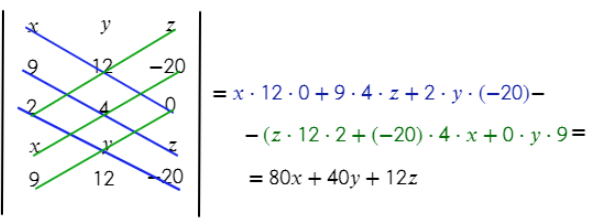
4) Плоскость получилась с коэффициентами А = 80, В = 40, С = 12,

x, y, z — координаты вектора прямой, в данном случае — вектор TV имеет координаты (9; 12; −20)

Задача. Найти расстояние между прямой, проходящей через точки Е = (1; 0; −2), G = (2; 2; −1), и прямой, проходящей через точки M = (4; −1; 4), L = (−2; 3; 0).

1. Задаем векторы обеих прямых.
2. Находим вектор, взяв по одной точке с каждой прямой.
3. Записываем матрицу из 3-х векторов (две строчки из 1-го пункта, одна строчка из 2-го) и находим ее численный определитель.
4. Задаем матрицу из двух первых векторов (в пункте 1). Первую строчку задаем как x, y, z.
5. Расстояние получим, когда разделим получившееся значение из пункта 3 по модулю на квадратный корень из суммы квадратов пункта 4. 

Перейдем к цифрам:

1) EG = (2−1; 2−0; −1−2) = (1; 2; −3)

ML = (−2−4; 3−(−1); 0−4) = (−6; 4; −4) 

2) Найдем вектор EM (можно было так же найти EL или GM, или GL).

EM = (1−4; 0−(−1); −2−4) = (−3; 1; −6)

3) Составляем матрицу из трех выше найденных векторов и находим определитель.

4) Составляем матрицу из первых двух выше найденных векторов и находим определитель 

без коэффициента D (здесь он не нужен для решения).

Вспомним, что уравнение плоскости задается так:

В нашем случае А = 4, В = 22, С = 16, D = 0.

5) Итоговая формула выглядит так, где L= −86 (из 3 пункта)

Будь в курсе новых статеек, видео и легкого математического юмора.