В этой статье вы узнаете как решить квадратное уравнение в Excel на конкретном примере. Подробно разберем решение несложно задачи с картинками.
Ход решения
Запустим программу Microsoft Office Excel. Я пользуюсь 2007 версией. Для начала объединим ячейки A1:A5 и запишем в них формулу квадратного уравнения в виде ax2+bx+c=0.Далее нам нужно возвести x в квадрат, для этого нужно сделать цифру 2 надстрочным интервалом. Выделим двойку и нажмем правой кнопкой мыши.
Получим формулу вида ax2 +bx+c=0
В ячейке A2 введем текстовое значение a= , в ячейке A3 b= и в ячейке A4 с= соответственно. Эти значения будут вводиться с клавиатуры в следующих ячейках (B2,B3,B4).
Введем текст для значений, которые будут считаться. В ячейке C2 d=, C3 x1= C4 x2=. Подстрочный интервал для xсделаем аналогично надстрочному интервалу в x2
Перейдем к вводу формул для решения
Дискриминант квадратного трехчлена равен b2-4ac
В ячейку D2 введем соответствующую формулу для возведения числа во вторую степень:
=B3^2-4*B2*B4
Квадратное уравнение имеет два корня, в случае если дискриминант больше нуля. В ячейку C3 введем формулу для x1
=ЕСЛИ(D2>0;(-B3+КОРЕНЬ(D2))/(2*B2);»Корней нет»)
Для расчета x2 введем похожую формулу, но со знаком плюс
=ЕСЛИ(D2>0;(-B3-КОРЕНЬ(D2))/(2*B2);»Корней нет»)
Соответственно при введенных значениях a,b,c сначала считается дискриминант, если его значения меньше нуля выводится сообщение «Корней нет», иначе получаем значения x1 и x2.
Защита листа в Excel
Нам нужно защитить лист, на котором мы производили расчеты. Без защиты нужно оставить ячейки, в которые можно вводить значения a,b,c, то есть ячейки B2 B3 B4. Для этого выделим данный диапазон и зайдем в формат ячеек, перейдем во вкладку Рецензирования, Защитить лист и уберем флажок с позиции Защищаемая ячейка. Нажмем кнопку OK, подтвердив внесенные изменения.
Этот диапазон ячеек будет не защищен при защите листа. Выполним защиту листа, для этого перейдем на вкладку Рецензирование пункт Защита листа. Пароль наберем 1234. Нажмем OK.
Теперь мы сможем изменять значения ячеек B2,B3,B4. При попытке изменения других ячеек мы получим сообщение следующего содержания: «Ячейка или диаграмма защищена от изменений. А так же совет по снятию защиты.
Так же вас может заинтересовать материал как закрепить область в Экселе.
Для решения квадратного уравнения необходимо знать формулу и алгоритм нахождения квадратов уравнения
Шаг 1. Организация таблицы
На первом этапе мы организуем таблицу для ввода данных коэффициентов a,b и c.
- a называют первым или старшим коэффициентом,
- b называют вторым или коэффициентом при x,
- c называют свободным членом.
Шаг 2. Проверка равенства Дискриминанта.
Для того, чтобы вычислить корни уравнения второй степени, необходимо определить значение Дискриминанта.
Формула дискриминанта
D = b2 — 4ac
Вычисление корней уравнения второй степени происходит по формулам при условии величины Дискриминанта
| Условие | D > 0 | D = 0 | D < 0 |
| Число действительных корней | корней два | корень один | Нет решения |
| Формула | X1,2=(- b ±√ (b2 — 4 * a * c)) / (2 * a) | X1=X2=-b/(2*a) |
Шаг 3. Вычисляем корни уравнения.
После определения значения Дискриминанта используем выше приведенные формулы для нахождения корней.
Находим первый корень
Находим второй корень. Формула будет отличаться только в одном знаке.
Итог: с помощью Excel можем создать единожды таблицу и формулы для решения квадратного уравнения (уравнения второй степени) и быстро их решать.
людей нашли эту статью полезной. А Вы?
Содержание
- 0.1 Шаг 1. Организация таблицы
- 0.2 Шаг 2. Проверка равенства Дискриминанта.
- 0.3 Формула дискриминанта
- 0.4 Шаг 3. Вычисляем корни уравнения.
- 1 Перейдем к вводу формул для решения
- 1.1 Защита листа в Excel
Для решения квадратного уравнения необходимо знать формулу и алгоритм нахождения квадратов уравнения
Шаг 1. Организация таблицы
На первом этапе мы организуем таблицу для ввода данных коэффициентов a,b и c.
- a называют первым или старшим коэффициентом,
- b называют вторым или коэффициентом при x,
- c называют свободным членом.
Шаг 2. Проверка равенства Дискриминанта.
Для того, чтобы вычислить корни уравнения второй степени, необходимо определить значение Дискриминанта.
Формула дискриминанта
D = b2 — 4ac
Вычисление корней уравнения второй степени происходит по формулам при условии величины Дискриминанта
| Условие | D > 0 | D = 0 | D < 0 |
| Число действительных корней | корней два | корень один | Нет решения |
| Формула | X1,2=(- b ±√ (b2 — 4 * a * c)) / (2 * a) | X1=X2=-b/(2*a) |
Шаг 3. Вычисляем корни уравнения.
После определения значения Дискриминанта используем выше приведенные формулы для нахождения корней.
Находим первый корень
Находим второй корень. Формула будет отличаться только в одном знаке.
Итог: с помощью Excel можем создать единожды таблицу и формулы для решения квадратного уравнения (уравнения второй степени) и быстро их решать.
В этой статье вы узнаете как решить квадратное уравнение на конкретном примере.
Постановка задачи: решить квадратное уравнение в Excel
Ход решения: Запустим программу Microsoft Office Excel. Я пользуюсь 2007 версией. Для начала объединим ячейки A1:A5 и запишем в них формулу квадратного уравнения в виде ax2+bx+c=0.Далее нам нужно возвести x в квадрат, для этого нужно сделать цифру 2 надстрочным интервалом. Выделим двойку и нажмем правой кнопкой мыши.
Получим формулу вида ax2 +bx+c=0
В ячейке A2 введем текстовое значение a= , в ячейке A3 b= и в ячейке A4 с= соответственно. Эти значения будут вводиться с клавиатуры в следующих ячейках (B2,B3,B4).
Введем текст для значений, которые будут считаться. В ячейке C2 d=, C3 x1= C4 x2=. Подстрочный интервал для xсделаем аналогично надстрочному интервалу в x2
Перейдем к вводу формул для решения
Дискриминант квадратного трехчлена равен b2-4ac
В ячейку D2 введем соответствующую формулу для возведения числа во вторую степень:
=B3^2-4*B2*B4
Квадратное уравнение имеет два корня, в случае если дискриминант больше нуля. В ячейку C3 введем формулу для x1
=ЕСЛИ(D2>0;(-B3+КОРЕНЬ(D2))/(2*B2);»Корней нет»)
Для расчета x2 введем похожую формулу, но со знаком плюс
=ЕСЛИ(D2>0;(-B3-КОРЕНЬ(D2))/(2*B2);»Корней нет»)
Соответственно при введенных значениях a,b,cсначала считается дискриминант, если его значения меньше нуля выводится сообщение «Корней нет», иначе получаем значения x1и x2.
Защита листа в Excel
Нам нужно защитить лист, на котором мы производили расчеты. Без защиты нужно оставить ячейки, в которые можно вводить значения a,b,c,то есть ячейки B2 B3 B4. Для этого выделим данный диапазон и зайдем в формат ячеек, перейдем во вкладку Рецензирования, Защитить лист и уберем флажок с позиции Защищаемая ячейка. Нажмем кнопку OK,подтвердив внесенные изменения.
Этот диапазон ячеек будет не защищен при защите листа. Выполним защиту листа, для этого перейдем на вкладку Рецензирование пункт Защита листа. Пароль наберем 1234. Нажмем OK.
Теперь мы сможем изменять значения ячеек B2,B3,B4. При попытке изменения других ячеек мы получим сообщение следующего содержания: «Ячейка или диаграмма защищена от изменений. А так же совет по снятию защиты.
Так же вас может заинтересовать материал как закрепить область в Экселе.
На примере квадратного уравнения х2 — 3х + 2 = 0 рассмотрим как решить квадратное уравнение в Excel.
1. В ячейки А1:А4 введите соответственно тексты
«а=», «b=», «c=», «D=».
2. В ячейки В1:ВЗ введите соответствующие значения
коэффициентов: 1; -3; 2.
3. В ячейку В4 введите формулу =В2^2-4*В1*В3
(Если все сделали правильно, то в ячейке B4 будет число 1).
4. В ячейку А5 введите текст «Есть ли корни?».
5. В ячейку В5 введите формулу =ЕСЛИ(В4=0;«х1=»;»»).
7. В ячейку В7 введите формулу = ЕСЛИ(В4>=0;«х2=»;»»),
8. В ячейку С6 введите формулу
= ЕСЛИ(В4>=0;(-В2+КОРЕНЬ(В4))/(2*В1);»»).
9. В ячейку С7 введите формулу
= ЕСЛИ(В4>=0;(-В2-КОРЕНЬ(В4))/(2*В1);»»).
A quadratic equation takes the following form:
ax2 + bx + c = y
Often you will be given the value for y and will be asked to solve for the value of x.
For example, suppose we have the following quadratic equation:
4x2 – 20x + 16 = -8
It turns out that setting x = 3 or x = 2 will solve this equation.
To solve quadratic equations in Excel, you can use the Goal Seek function.
The following step-by-step example shows how to use the Goal Seek function in practice.
Step 1: Enter the Equation
First, let’s enter some random value for x and the formula for the quadratic equation for y:
Step 2: Find the First X Value Using Goal Seek
Next, click the Data tab along the top ribbon, then click the What-If Analysis button, then Goal Seek:
In the new window that appears, specify that you’d like to set cell B2 equal to -8 by changing the value in cell A2:
Once we click OK, the Goal Seek function will automatically find the value for x that solves the equation:
Goal Seek finds that the value x=2 (assuming 1.9999 rounds to 2) solves the quadratic equation.
Step 3: Find the Second X Value Using Goal Seek
To find the second x value that solves the quadratic equation, set the initial x-value to a different number.
For example, we could choose to set the initial x-value to 4:
We can then run the Goal Seek function again and see that it finds a new solution of x=3:
Thus, the two x-values that can solve this quadratic equation are x=2 and x=3.
Additional Resources
The following tutorials explain how to perform other common tasks in Excel:
How to Solve a System of Equations in Excel
How to Plot an Equation in Excel
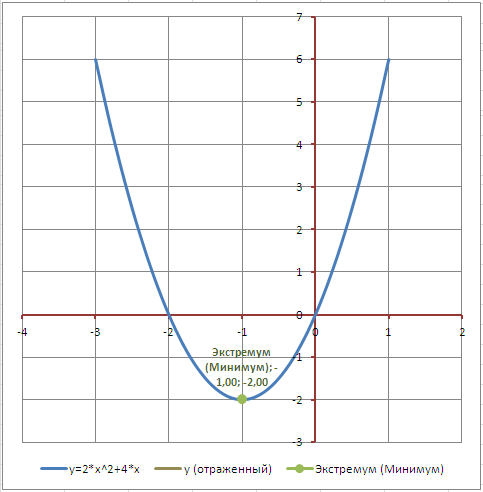
Построим график функции y=a*x^2+b*x+с (квадратное уравнение). Также рассчитаем дискриминант, найдем корни уравнения, координаты точки экстремума (максимума или минимума). Сделаем форму для сдвига и отражения графика с помощью элементов управления
формы.
Построим график функции
y=a*x^2+b*x+с
в диаграмме типа Точечная с гладкими кривыми. (см.
файл примера
лист График).
Укажем на графике точку экстремума (для этого в диаграмме создан дополнительный ряд, состоящий из 1 точки).
Коэффициенты
а, b, с
введем в отдельные ячейки, чтобы можно было быстро построить нужный график.
Строить график в диаграмме типа
Точечная с гладкими кривыми
проще, чем строить его в диаграмме типа График (см. статью
График vs Точечная диаграмма в MS EXCEL
), т.к. точку пересечения вертикальной осью горизонтальной оси можно настроить только по номеру категории (порядковый номер точки), а не по значению x (получается, что вертикальная ось y не проходит через х=0, что не удобно).
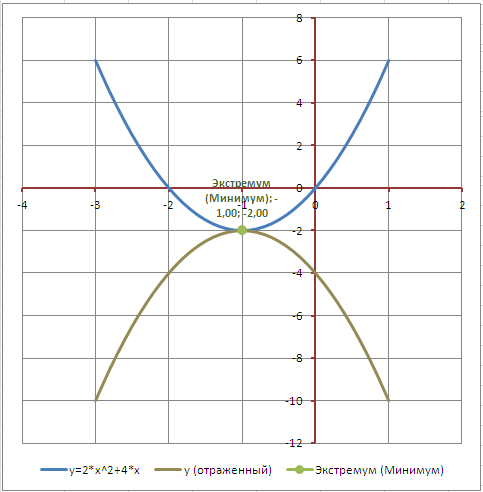
Диаграмма также может построить график, отраженный относительно горизонтальной оси (проходящей через точку экстремума).
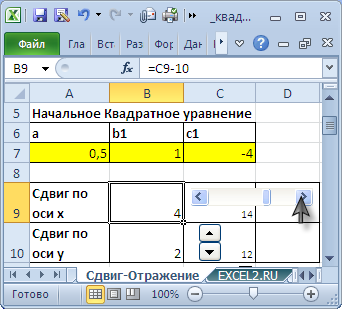
Сдвиг графика
В
файле примера
на листе Сдвиг-Отражение сделана форма для сдвига графика по координатам х и y с помощью
Элементов управления формы
.
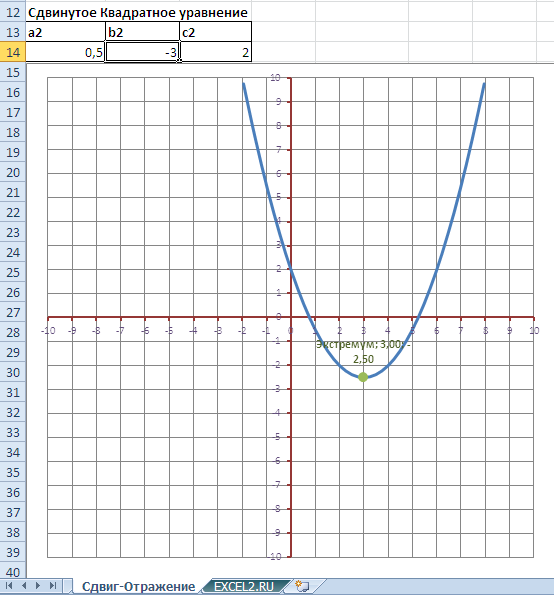
Эта форма позволяет быстро рассчитывать коэффициенты нового квадратного уравнения, полученного при сдвиге.
Форма также позволяет рассчитывать коэффициенты квадратного уравнения, полученного при горизонтальном отражении ранее сдвинутого графика (с его построением на диаграмме).
СОВЕТ
: Для начинающих пользователей EXCEL советуем прочитать статью
Основы построения диаграмм в MS EXCEL
, в которой рассказывается о базовых настройках диаграмм, а также
статью об основных типах диаграмм
.