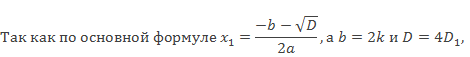Содержание:
- § 1 Понятие квадратного уравнения
- § 2 Решение квадратных уравнений
- § 3 Решение квадратного уравнения по формуле с четным вторым коэффициентом
- § 4 Краткие итоги урока
§ 1 Понятие квадратного уравнения
В этом уроке выведем формулы для решения квадратных уравнений с чётным вторым коэффициентом и научимся решать такие квадратные уравнения, используя эти формулы.
Квадратным уравнением называют уравнение вида ax2 + bx +c=0, где a называют первым или старшим коэффициентом, b – вторым коэффициентом или коэффициентом при х, с – свободным членом, х – переменная, причём a ≠ 0.
Чтобы решить квадратное уравнение, необходимо найти дискриминант D по формуле
D = b2 – 4ac
Если в квадратном уравнении коэффициент b- четное число, то это уравнение можно представить в виде ax2 + 2kx + c=0, где b=2k, k – целое число.
§ 2 Решение квадратных уравнений
Выведем формулы для решения квадратного уравнения с четным вторым коэффициентом. Для этого в основную формулу для решения квадратного уравнения вместо второго коэффициента b подставим 2k.
Найдем дискриминант.
D = b2 – 4ac = (2k)2 – 4ac = 4k2 – 4ac.
Вынесем за скобки 4 и получим D = 4(k2 – ac).
Обозначим выражение в скобках за D1. Тогда D1 = k2 – ac, а D = 4D1.
Видно, что число корней уравнения зависит от D1. Если D1 больше нуля, то уравнение имеет два корня.
Разделим числитель и знаменатель на 2. После всех преобразований формула примет вид
Корни х1 и х2 зависят только от знака квадратного корня в числителе, поэтому
А если дискриминант D1 равен нулю? Уравнение будет иметь один корень.
Вместо коэффициента b подставим 2k.
§ 3 Решение квадратного уравнения по формуле с четным вторым коэффициентом
Рассмотрим решение квадратного уравнения 5х2 –16 х + 3 = 0 как по основной формуле, так и по формуле с четным вторым коэффициентом. А затем сделаем некоторые выводы.
Итак, сначала выпишем коэффициенты a = 5, b= –16, с = 3.
Найдем дискриминант D по формуле D = b2 – 4ac.
Подставив в неё значения коэффициентов, получим D= (–16)2 – 4 ∙ 5 ∙ 3 = 196,дискриминант больше нуля D>0, значит, уравнение имеет два корня, используя соответствующие формулы, вычисляем:
Так как коэффициент b= –16 четное число, то можно решить это уравнение по формулам решения квадратного уравнения с четным вторым коэффициентом.
В нашем уравнении 5х2 –16х + 3 = 0, k = –16:2= –8.
Найдем дискриминант D1.
D1 = k2 –ac= (–8)2 – 5 ∙ 3 = 49, он больше нуля D1 >0, уравнение имеет два корня, которые находим по соответствующим формулам:
Заметим, что корни получились одинаковые х1 = 0,2; х2 = 3.
Однако есть преимущества в использовании формул решения квадратного уравнения с четным вторым коэффициентом.
Во-первых, при нахождении дискриминанта в квадрат возводится не число b, не второй коэффициент, а его половина и вычитается из этого квадрата не 4ac, а просто ac
Во-вторых, при нахождении корней в знаменателе не 2a, а просто a.
В-третьих, дискриминант, находимый по формуле с четным вторым коэффициентом, то есть D1, в 4 раза меньше дискриминанта D.
Если квадратное уравнение с четным вторым коэффициентом b=2k и с коэффициентом a= 1, т.е. является приведенным x2 + 2kx +c=0, то решить уравнение можно ещё проще. Находим дискриминант по формуле D1 = k2 – c.
Если он больше нуля D1 >0, то корни находим по формулам:
Если дискриминант равен нулю D1=0, то будет один корень х = –k.
Рассмотрим решение квадратного уравнения х2 +10 х–5600 = 0 как по основной формуле, так и по формуле решения квадратного уравнения с четным вторым коэффициентом, являющееся приведенным.
Выпишем коэффициенты a = 1, b= 10, с = – 5600.
Найдем дискриминант D по формуле D = b2 – 4ac.
D = (10)2 – 4 ∙ 1 ∙ (–5600) = 22500, D > 0, дискриминант положительный, значит, уравнение имеет два корня, используя соответствующие формулы, получим значения корней:
Так как коэффициент b = 10 четное число, то можно решить это уравнение по формуле решения квадратного уравнения с четным вторым коэффициентом. Заметим, что в уравнении коэффициент a=1.
Уравнение является приведенным.
k = 10 : 2 = 5.
Найдем дискриминант D1.
§ 4 Краткие итоги урока
Важно запомнить:
Если квадратное уравнение ax2 + bx + c = 0 с четным вторым коэффициентом, то есть второй коэффициент можно представить в виде b = 2k, k – целое число, то уравнение лучше решить по соответствующим формулам. При решении поступают следующим образом:
1.Находят дискриминант D1 по формуле D1 = k2 – ac. Значение дискриминанта зависит от коэффициентов a, k , с.
2.Сравнивают дискриминант D1 с нулём.
3.Если дискриминант больше нуля, то уравнение ax2 + 2kx +c=0 имеет два корня
Если дискриминант меньше нуля, корней нет.
4.Если квадратное уравнение ax2 + bx + c = 0 с четным вторым коэффициентом и является приведенным x2 + 2kx + c = 0, коэффициенты a= 1, b = 2k, k – целое число, то уравнение решают следующим образом:
1)Находят дискриминант D1 по формуле D1 = k2 – c.
2)Сравнивают дискриминант D1 с нулём.
3)Если дискриминант больше нуля, то уравнение x2 + 2kx +c=0 имеет два корня
Если дискриминант равен нулю, то х = –k.
Если дискриминант меньше нуля, корней нет.
Список использованной литературы:
- Макарычев Ю.Н., Н.Г. Миндюк, Нешков К.И., Суворова С.Б., под редакцией Теляковского С.А. Алгебра: учебник для 8 кл. общеобразоват. учреждений. — М.: Просвещение, 2013.
- Мордкович А.Г. Алгебра. 8 кл.: В двух частях. Ч.1: Учеб. для общеобразоват. учреждений. — М.: Мнемозина.
- Рурукин А.Н. Поурочные разработки по алгебре: 8 класс.- М.: ВАКО, 2010.
- Алгебра 8 класс: поурочные планы по учебнику Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, С.Б. Суворовой/ Авт.-сост. Т.Л. Афанасьева, Л.А. Тапилина. – Волгоград: Учитель, 2005.
Как решать квадратные уравнения по формуле четного коэффициента b
Для уравнений вида , то есть при чётном , где
вместо формулы (1) для нахождения корней можно использовать эквивалентное выражение
Действительно, подставим в вышеприведённую универсальную формулу (1) корней уравнения указанное соотношение:
Для приведённого квадратного уравнения эта формула принимает вид:
.
Также при чётном удобнее вычислять значение не целого дискриминанта, а его четверти:
или, если уравнение приведённое:
.
Все необходимые свойства при этом сохраняются:
0 Rightarrow D>0″ src=»http://upload.wikimedia.org/math/6/8/e/68eda98d8feacc2fbb9ee7adae1dc95b.png» />
(вместо знака «больше» в выражение может быть подставлены и другие знаки: «меньше» или «равно»). Подобным преобразованиям можно подвергнуть формулу для нахождения единственного корня при :
.
Обратите внимание, что для приведённого уравнения можно упростить расчёт следующим образом:
.
Отсюда следует важное и полезное правило: корнем приведённого уравнения с чётным вторым коэффициентом и равным нулю дискриминантом является половина второго коэффициента.
Эти выражения является более удобным для практических вычислений при чётном .
Квадратное уравнение с чётным вторым коэффициентом
Если в квадратном уравнении ax 2 + bx + c = 0 второй коэффициент b является чётным, то решение этого уравнения можно немного упростить. Дискриминант для такого уравнения можно вычислить по формуле D1 = k 2 − ac , а корни по формулам и .
Примеры
Решим квадратное уравнение x 2 + 6x − 16 = 0 . В нём второй коэффициент является чётным. Чтобы воспользоваться формулами для чётного коэффициента, нужно сначала узнать чему равна переменная k .
Любое четное число n можно представить в виде произведения числа 2 и числа k , то есть 2k .
Например, число 10 можно представить как 2 × 5 .
В этом произведении k = 5 .
Число 12 можно представить как 2 × 6 .
В этом произведении k = 6 .
Число −14 можно представить как 2 × (−7)
В этом произведении k = −7 .
Как видим, сомножитель 2 не меняется. Меняется только сомножитель k .
В уравнении x 2 + 6x − 16 = 0 вторым коэффициентом является число 6 . Это число можно представить как 2 × 3 . В этом произведении k = 3 . Теперь можно воспользоваться формулами для чётного коэффициента.
Найдем дискриминант по формуле D1 = k 2 − ac
Теперь вычислим корни по формулам: и .
Значит корнями уравнения x 2 + 6x − 16 = 0 являются числа 2 и −8 .
В отличие от стандартной формулы для вычисления дискриминанта ( D=b 2 − 4ac ), в формуле D1 = k 2 − ac не нужно выполнять умножение числа 4 на ac .
И в отличие от формул и формулы и не содержат в знаменателе множитель 2 что опять же освобождает нас от дополнительных вычислений.
Пример 2. Решить квадратное уравнение 5x 2 − 6x + 1=0
Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−3) . То есть k = −3 . Найдём дискриминант по формуле D1 = k 2 − ac
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и
Пример 3. Решить квадратное уравнение x 2 − 10x − 24 = 0
Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−5) . То есть k = −5 . Найдём дискриминант по формуле D1 = k 2 − ac
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и
Обычно для определения числа k поступают так: делят второй коэффициент на 2.
Действительно, если второй коэффициент b является чётным числом, то его можно представить как b = 2 k . Чтобы из этого равенства выразить сомножитель k , нужно произведение b разделить на сомножитель 2
Например, в предыдущем примере для определения числа k можно было просто разделить второй коэффициент −10 на 2
Пример 5. Решить квадратное уравнение
Коэффициент b равен . Это выражение состоит из множителя 2 и выражения . То есть оно уже представлено в виде 2k . Получается, что
Найдём дискриминант по формуле D1 = k 2 − ac
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и
При вычислении корня уравнения получилась дробь, в которой содержится квадратный корень из числа 2. Квадратный корень из числа 2 извлекается только приближённо. Если выполнить это приближённое извлечение, а затем сложить результат с 2, и затем разделить числитель на знаменатель, то получится не очень красивый ответ.
В таких случаях ответ записывают, не выполняя приближённых вычислений. В нашем случае первый корень уравнения будет равен .
Вычислим второй корень уравнения:
Вывод формул
Давайте наглядно увидим, как появились формулы для вычисления корней квадратного уравнения с чётным вторым коэффициентом.
Рассмотрим квадратное уравнение ax 2 + bx + c = 0 . Допустим, что коэффициент b является чётным числом. Тогда его можно обозначить как 2k
Заменим в уравнении ax 2 + bx + c = 0 коэффициент b на выражение 2k
Теперь вычислим дискриминант по ранее известной формуле:
Вынесем в получившемся выражении за скобки общий множитель 4
Что можно сказать о получившемся дискриминанте? При чётном втором коэффициенте он состоит из множителя 4 и выражения k 2 − ac .
В выражении 4(k 2 − ac) множитель 4 постоянен. Значит знак дискриминанта зависит от выражения k 2 − ac . Если это выражение меньше нуля, то и D будет меньше нуля. Если это выражение больше нуля, то и D будет больше нуля. Если это выражение равно нулю, то и D будет равно нулю.
То есть выражение k 2 − ac это различитель — дискриминант. Такой дискриминант принято обозначать буквой D1
Теперь посмотрим как выводятся формулы и .
В нашем уравнении ax 2 + bx + c = 0 коэффициент b заменён на выражение 2k . Воспользуемся стандартными формулами для вычисления корней. То есть формулами и . Только вместо b будем подставлять 2k . Также на забываем, что D у нас равно выражению 4(k 2 − ac)
Но ранее было сказано, что выражение k 2 − ac обозначается через D1 . Тогда в наших преобразованиях следует сделать и эту замену:
Теперь вычислим квадратный корень, расположенный в числителе. Это квадратный корень из произведения — он равен произведению корней. Остальное перепишем без изменений:
Теперь в получившемся выражении вынесем за скобки общий множитель 2
Сократим получившуюся дробь на 2
Аналогично вывóдится формула для вычисления второго корня:
8.8-3. Квадратные уравнения с чётным вторым коэффициентом
Алгебра. 8 класс. Параграф 8. Тест 3.
Вариант 1.
Решить уравнения.
1. 3x 2 -10x+3=0.
3. 5x 2 +14x-3=0.
A) -3; -0,2; B) 0,2; 3; C) -3; 0,2; D) -3; 0,5.
4. 5x 2 -18x+9=0.
A) -3; -0,6; B) -0,6; 3; C) 3; D) 0,6; 3.
5. 5x 2 -18x-8=0.
A) 0,4; 4; B) -4; -0,4; C) -0,4; 4; D) -4; 0,2.
6. 7x 2 +82x+55=0.
7. 9x 2 +12x-5=0.
9. 7(x 2 +2x-2)=(1-x)(1+x).
A) -2,5; -0,75; B) -0,75; 2,5; C) 0,75; 2,5; D) -2,5; 0,75.
10. 6x(x+4)+2x(x-1)= -15.
A) -1,5; 1,25; B) -1,5; -1,25; C) 1,25; 1,5; D) -2,5; 1,25.
Вариант 2.
Решить уравнения.
1. 3x 2 +14x-5=0.
3. 5x 2 -36x+7=0.
A) -7; 0,2; B) -0,2; 7; C) -7; 0,2; D) 0,2; 7.
4. 5x 2 -22x+8=0.
A) -4; -0,4; B) -0,4; 4; C) 0,4; 4; D) -4; 0,4.
5. 5x 2 +12x-9=0.
A) -3; 0,6; B) -3; -0,6; C) -0,6; 3; D) 0,6; 3.
6. 7x 2 +62x+48=0.
7. 9x 2 -6x-8=0.
9. 5(x 2 +x+3)=3х(9-x).
A) -1,5; -1,25; B) -1,25; 1,5; C) -1,5; 1,25; D) 1,25; 1,5.
10. 2x(x+5)+2(x 2 -18)= 6х-1.
A) -3,5; -2,5; B) 2,5; 3,5; C) -3,5; 2,5; D) -2,5; 3,5.
Квадратные уравнения решаются по формулам Виета и способом Дискриминанта(D). Начнём с того что мы должны понять как выглядит квадратное уравнение.
ax²+bx+c.
a, b и c — это какие либо цифры. а Всегда стоит перед x², b стоит перед x, а c-это свободные член и он стоит без всего(то есть просто цифра). Почему мы должны запомнить перед кем они стоят, а не просто их последовательность? Все просто, они могут стоят и в другом порядке, то есть:
bx+ax²+c.
Если бы мы просто запомнили что первое-это а второе b, а третье с, то мы бы сделали ошибку.
Теперь перейдём к самим формулам. D(Дискриминант это вспоминающий элемент) давайте его вычислим:
D=b²-4*a*c
Опять повторю, место a, b и c должны быть цифры!
После того как мы все это вычалили, у нас получается число.
Если число D:
D > 0, то уравнение имеет 2 различных корня!
D = 0, то уравнение имеет 1 корень!
D < 0, то уравнение не имеет корней!
Допустим у нас получилось что D > 0, то вычислим корни.
x₁=(-b+√D)/(2*a)
x₂=(-b-√D)/(2*a)
Вот и все, только запомните, что если D=0, корень 1.
Как найти дискрименант
В школьной программе часто приходится сталкиваться с решением квадратного уравнения типа: ax² + bx + c = 0, где а, b — первый и второй коэффициенты квадратного уравнения, с — свободный член. С помощью значения дискриминанта можно понять, есть ли у уравнения решения или нет, а если есть, то сколько.

Инструкция
Как найти дискриминант? Существует формула его нахождения: D = b² — 4ac. При этом, если D > 0, уравнение имеет два действительных корня, которые вычисляются по формулам:
x1 = (-b + VD)/2a,
x2 = (-b — VD)/2a,
где V означает квадратный корень.
Чтобы понять формулы в действии, решите несколько примеров.
Пример: x² — 12x + 35 = 0, в данном случае а = 1, b — (-12), а свободный член с — + 35. Найдите дискриминант: D = (-12)^2 — 4*1*35 = 144 — 140 = 4. Теперь найдите корни:
X1 = (-(-12) + 2)/2*1 = 7,
x2 = (-(-12) — 2)/2*1 = 5.
При а > 0, x1 < x2, при a < 0, x1 > x2, что означает если дискриминант больше нуля: существуют вещественные корни, график квадратичной функции пересекает ось ОX в двух местах.
Если D = 0, то решение одно:
x = -b/2a.
Если второй коэффициент квадратного уравнения b представляет собой четное число, то целесообразно найти дискриминант, деленный на 4. При этом формула примет следующий вид:
D/4 = b²/4 — ac.
Например, 4x^2 — 20x + 25 = 0, где a = 4, b = (- 20), с = 25. При этом D = b² — 4ac = (20)^2 — 4*4*25 = 400-400 = 0. Квадратный трехчлен имеет два равных корня, найдем их по формуле x = -b/2a = — (-20)/2*4 = 20/8 = 2,5. Если дискриминант равен нулю, значит существует один вещественный корень, график функции пересекает ось OX в одном месте. При этом, если а > 0, график располагается выше оси OX, а если a < 0, ниже этой оси.
При D < 0 вещественных корней не существует. Если дискриминант меньше нуля, значит не существует вещественных корней, а только комплексные корни, график функции не пересекает ось ОX. Комплексные числа — расширение множества вещественных чисел. Комплексное число можно представить как формальную сумму x + iy, где x и y — вещественные числа, i — мнимая единица.
Обратите внимание
В уравнении вида ax²+bx+c=0 необходимым условием является неравенство а нулю.
Если а равно единице, то уравнение называют приведенным.
Если а не равно одному, то -неприведенным. Если один из коэффициентов b, с или оба равны , то квадратное уравнение называется неполным
Источники:
- если дискриминант равен 1
- Квадратные уравнения на Сёзнайке
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.