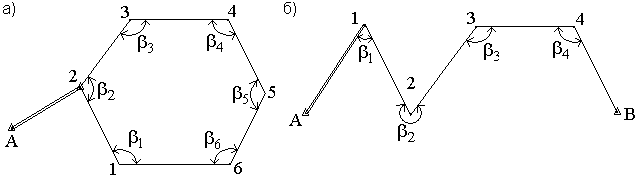
Любой теодолитный ход представляет собой построение ломаной линии на местности, которая может образовывать как замкнутую фигуру, так и оставаться в разомкнутом виде. Однако в любом из этих случаев его первостепенная задача состоит в определении координат установленных в натуре точек посредством измерения углов и длин сторон. Рассмотрим далее порядок съемки и обработки результатов теодолитного хода разомкнутого типа.
Содержание
- 1 В каких случаях прокладывают
- 2 Выполнение измерений
- 3 Обработка результатов
- 3.1 Создавайте будущее вместе с нами
- 4 Определение координат
- 5 Рекомендации к построению разомкнутого хода
В каких случаях прокладывают
Начальная и конечная точка разомкнутого хода должна быть закреплена к пункту Государственной геодезической сети (ГГС) с уже определенными координатами и углами.
Если привязка к опорной точке осуществляется только для одной стороны, такой ход называют висячим. Также достаточно часто разомкнутый ход строят внутри крупных полигонов или сетей сгущения. Это необходимо для того, чтобы в дальнейшем провести подробную съемку ситуации. В таком случае его называют диагональным.
Построение разомкнутого теодолитного хода обусловливается особенностью объекта съемки, который может представлять собой:
– автомобильные и железные дороги;
– трубопроводы;
– реки;
– линии электропередач и связи.
– другие сооружения линейного типа.
Рисунок 1. Разновидности разомкнутых теодолитных ходов
Выполнение измерений
Очень важно провести рекогносцировку и правильно заложить точки, обеспечивая между ними хорошую взаимную видимость и сохранность на период выполнения работ. Для этих целей используют колья и стержни, изготовленные из дерева, бетона или металла. Категорически запрещено устанавливать их в местах массового скопления людей. Это не только будет создавать помехи при передвижении людей, но и высок риск того, что точка будет утеряна.
В остальном же процедура выполнения данного вида работ не многим отличается от построения обычного замкнутого полигона. Ключевые различия состоят в дальнейших вычислениях.
Для измерения углов используются теодолиты, тахеометры и GPS-приемники. Важно также помнить, что качество мерных приборов могут значительно повлиять на итоговый результат, поэтому важно выполнять их компарирование. Эта процедура подразумевает сравнение длины мерного прибора с эталонной. Оно может проводиться как в лаборатории, так и в полевых условиях.
Особенно важно компарировать мерные ленты из металла, поскольку при высоких температурах он расширяется. Тканевые вообще не желательно использовать во время измерений по причине того, что они быстро растягиваются и приходят в негодность для дальнейших измерений. Помимо обычных мерных рулеток сейчас также используют и электронный светодальномер, который позволяет определить расстояние до точки при помощи нажатия всего лишь нескольких клавиш.
Обработка результатов
Поскольку разомкнутый ход представляет собой вытянутую ломаную линию, его обработка будет отличаться от вычислений, которые используют для замкнутого полигона. К тому же, изначально координаты и углы как минимум одной опорной точки уже известны.
Исходными данными для вычислений служат полученные во время съёмки:
– координаты исходных пунктов
– исходные дирекционные углы;
– измеренные углы и длины всех сторон.
Предварительные расчёты заключаются в азимутальной привязке начальной и конечной линии хода к его исходным направлениям, образованным пунктами ГГС (табл. 1)
Таблица 1. Вычисление дирекционных углов (alpha _{A1}) и (alpha _{4D}).
| (alpha _{A1}) | (alpha _{4D}) |
| (alpha _{A1′}=alpha _{AB}+gamma _{1}) (alpha _{A1}{}’=alpha _{AC}+gamma _{2}) (alpha _{A1}{}’=0,5left ( alpha _{A1}{}’+alpha _{A1}{}'{}’right )) |
(alpha _{4D}{}’=alpha _{DE}-gamma _{3}pm 180^{circ}) (alpha _{4D}{}'{}’=alpha _{DF}-gamma _{4}pm 180^{circ}) (alpha _{4D}=0,5(alpha _{4D}{}’+alpha _{4D}{}'{}’)) |
Вычисление () проводят посредством решения обратной геодезической задачи. Ее суть заключается в том, что известные значения координат исходных пунктов используют для расчета прямых и обратных дирекционных углов, которые представляют собой исходное направление.
Формула для определения горизонтального проложения через угол наклона:
(d=Scosnu ), где (S) – измеренная длина стороны; (nu) – угол наклона измеренной стороны к горизонту.
Формула определения горизонтального проложения через превышение:
(d^2=S^2 – h^2)
Итоговые вычисления включают в себя:
– определение невязок и их распределение;
– вычисление длин сторон;
– расчёт угловых величин;
– определение координат пунктов;
Обрабатывается разомкнутый теодолитный ход поэтапно и с соблюдением контроля полученных результатов. В дальнейшем они заносятся в специальные таблицы установленной формы, иначе говоря – ведомость. Очень важно проводить контроль данных с допуском, чтобы результат был максимально достоверным.
В теодолитном ходе измеряются не только горизонтальные углы (β), но и примычные (γ), а также расстояния S и углы наклона, при необходимости.
Следующим этапом будет обработка угловых данных, которую следует начать с вычисления сторон от начальной и до конечной линии:
(alpha _{1}=alpha _{н}pm 180^{circ}pm beta _{1})
(alpha _{2}=alpha _{1}pm 180^{circ}pm beta _{2})
___________________
(alpha _{2}=alpha _{n-1}pm 180^{circ}pm beta _{n})
В приведенной выше формуле +β используют для левых по ходу углов, а –β – для правых.
– последовательность передачи дирекционных углов;
Сложив уравнение, получим для определения левых угловых величин выражение:
(alpha _{к}=alpha _{н}pm n180^{circ}+Sigma beta )
– для правых:
(alpha _{к}=alpha _{н}pm n180^{circ}-Sigma beta )
Создавайте будущее вместе с нами
Присоединяйтесь к нашей команде: мы создаем финтех-сервисы для 28 млн клиентов и опережаем рынок на 5 лет. Работаем на результат и делаем больше, чем от нас ждут.
Чтобы убедится в качестве выполненных измерений необходимо определить угловую невязку. Для этого используется следующее выражение для правых угловых величин:
(f_{beta } = Sigma _{beta }-(alpha _{н}-alpha _{к})pm 180^{circ}pm Rcdot 360^{circ})
– для левых применяют формулу:
(f_{beta } = Sigma _{beta }-(alpha _{к}-alpha _{н})pm 180^{circ}pm Rcdot 360^{circ})
Выражение ( Rcdot 360^{circ}) используется в приведенных выше формулах с целью сокращения невязки полных кругов.
Далее происходит процедура определения допустимой невязки и введение поправок, что практически не отличается от вычислений в замкнутых ходах.
После их распределение выполняют уравнивание посредством введения поправок:
(nu _{beta } = – frac{f_{beta }}{n})
При этом:
(sum nu _{beta }= -f_{beta })
(beta _{испр}=beta _{изм}+nu _{beta })
(nu _{beta }) – значение поправок;
Контроль уравнивание осуществляют таким образом:
– для левых углов:
(sum beta _{испр}=(alpha _{к}-alpha _{н})pm n180^{circ}pm Rcdot 360^{circ})
– для правых:
(sum beta _{испр}=(alpha _{н}-alpha _{к})pm n180^{circ}pm Rcdot 360^{circ})
В качестве контрольного значения выступает (alpha _{к}), которое, при правильно выполненных вычислениях, должно равняться исходному:
(alpha _{выч}=alpha _{исх})
Определение координат
Теоретическая сумма приращения значений координат определяется следующим образом:
(X_{1}=X_{A}+Delta X_{A,1}) (Y_{1}=Y_{A}+Delta Y_{A,1})
(X_{2}=X_{1}+Delta X_{1,2}) (Y_{2}=Y_{1}+Delta Y_{1,2})
(X_{3}=X_{2}+Delta X_{2,3}) (Y_{3}=Y_{2}+Delta Y_{2,3})
_______________________________
(X_{B}=X_{3}+Delta X_{3,B}) (Y_{B}=Y_{3}+Delta Y_{3,B})
В данном выражении (X_{A},Y_{A},X_{B},Y_{B}) , – координаты исходных точек А и В.
Сложив части равенств, найдем теоретическое значение:
(X_{B}=X_{A}+sum Delta X)
(Y_{B}=Y_{A}+sum Delta Y)
Из данного выражения выходит:
(sum Delta X_{теор}=X_{B}-X_{A})
(sum Delta Y_{теор}=Y_{B}-Y_{A})
Следующим этапом будет определение невязки приращения координат (f_{X}) и (f_{Y}) .
(f_{X}=sum Delta X_{пр}-sum Delta X_{теор}=sum Delta X_{пр}-(X_{B}-X_{A}))
(f_{Y}=sum Delta Y_{пр}-sum Delta Y_{теор}=sum Delta Y_{пр}-(Y_{B}-Y_{A}))
Выравнивание приращений координат осуществляют через введение весовых поправок (nu _{Xi}) и (nu _{Yi}). (табл. 2). Они зависят от длины горизонтального проложения, по которому и рассчитывалась невязка, а знаки должны иметь противоположное ей значение.
Таблица 2. Уравнивание приращений координат для Х и У.
| Ось абсцисс (Х) () | Ось ординат (У) () |
| (nu _{Xi}=-tfrac{f_{X}}{sum d}d_{i}) (sum nu _{xi} = – f_{x}) (Delta X_{испр}=Delta X_{выч}+nu _{Xi}) (sum Delta X_{испр}=(X_{К}-X_{Н})) |
(nu _{Yi}=-tfrac{f_{Y}}{sum d}d_{i}) (sum nu _{yi} = – f_{y}) (Delta Y_{испр}=Delta Y_{выч}+nu _{Yi}) (sum Delta Y_{испр}=(Y_{К}-Y_{Н})) |
Вычисление координат производят по формулам с постановкой исправленных значений, которые были получены путем приращения:
(X_{выч}=X_{n-1}+Delta X_{испр})
(Y_{выч}=Y_{n-1}+Delta Y_{испр})
Если координаты рассчитаны правильно, то значение конечного и исходного значения будут совпадать:
(X_{выч}=X_{исх})
(Y_{выч}=Y_{исх})
Рекомендации к построению разомкнутого хода
- Общая длина хода на застроенных территориях должна быть в полтора раза меньше, чем на открытой местности.
- В висячих ходах допускается построение не более трех линий на застроенных территориях и не более двух на незастроенных. Расстояние между ними не должно превышать 0,1 от максимальной длины всех сторон.
Данный вид работ требует особой внимательности, поскольку для конечных результатов является полностью бесконтрольным. Его принято использовать для съемки тупиковых улиц, глухих дворов и т.д.
- Длина диагонального хода не должна превышать 0,5 от максимальной, а его погрешность не превышать 1:1000.
- Привязку осуществляют к пунктам Государственной геодезической сети 1,2,3 и 4 классов, а также пунктам сети 1 и 2 разряда.
13.Определение
дирекционных углов замкнутого и
разомкнутого теодолитного хода(вывод
формулы. Контрольные вычисления.
Теодолитные
ходы могут быть замкнутыми или
разомкнутыми.
Рис. 69. Теодолитные
ходы: замкнутый (а); разомкнутый (б).
На рис. 25 представлена
схема определения дирекционных углов
сторон теодолитного хода AB.
Известен дирекционный угол исходной
стороны α0 и
измерены геодезическим прибором
теодолитом углы β1,
β2, β3, лежащие
справа по ходу от А
к В.
Рис. 25. Схема
определения дирекционных углов сторон
теодолитного хода
Найдём дирекционные
углы α1, α2,
α3 остальных
сторон хода.
На основании
зависимости между прямыми и обратными
дирекционными углами можем написать:
α1 + β1
= α0 +
180° из данного
выражения следует, что
α1 = α0
+ 180° – β1
(1).
Аналогично
вычисляются дирекционные углы последующих
сторон теодолитного хода:
α2 + β2
= α1 +
180° →
α2 = α1
+ 180° – β2
(2)
α3 + β3
= α2 +
180° →
α3 = α2
+ 180° – β3
(3)
…………………………………………………………………….
αn
+ βn
= αn-1
+ 180° →
αn
= αn-1
+ 180° – βn
(n)
То есть, дирекционный
угол последующей стороны равен
дирекционному углу предыдущей стороны
плюс 180° и
минус угол, лежащий справа по ходу.
Для получения
контрольной формулы в выражение (2)
подставим
значение α1, из
выражения (1)
α2 = α0
+ 2 ∙ 180° – (β1
+ β2)
.
Если продолжить
аналогичные действия для последующих
сторон теодолитного хода, то
получим
αn
= α0 + n
∙ 180° – (β1
+ β2 + β3
+ … + βn)
.
или
αn
– α0 = n
∙ 180° – ∑β .
или
α0 – αn
= ∑β – n
∙ 180° .
Эта формула может
служить контрольной при вычислении
дирекционных углов по увязанным углам
β.
Если же вместо
суммы исправленных углов подставить
сумму измеренных углов ∑β,
то та же формула
позволит определить невязку fβ
измеренных углов
теодолитного хода, если дирекционные
углы α0 и
αn начальной
и конечной сторон хода известны
fβ
= ∑β – n
∙ 180° – (α0
– αn).
Иногда дирекционные
углы вычисляют по углам, лежащим слева
по ходу от А
до В
(λ1, λ2,
…, λn).
β1 = 360° –
λ1
β2 = 360° –
λ2
……………………
βn
= 360° – λn
Подставим эти
значения в выражения (1),
(2),
…, (n)
получим
α1 = α0
– 180° + λ1
α2 = α1
– 180° + λ2
……………………………
αn
= αn-1
– 180° + λn
.
Для проверки
правильности вычисления дирекционных
углов по углам λ, лежащим
слева по ходу, используют выражения
αn
– α0 =
∑λ –
n ∙ 180°
или
αn
– α0 =
∑λ +
n ∙ 180°.
Тогда невязка fβ
определяется по
формуле
fβ
= ∑λ + n
∙ 180° – (αn
– α0).
Теодолитный ход – это геодезическое построение в виде ломаной линии, вершины которой закрепляются на местности, и на них измеряются горизонтальные углы βi между сторонами хода и длины сторон Si. Закрепленные на местности точки называют точками теодолитного хода.
Построение теодолитного хода состоит из двух этапов. Это:
1. Построение ломаной линии на местности и осуществление полевых работ;
2. Математическое уравнивание хода и выполнение камеральной обработки полученных результатов.
Оба этапа выполняются строго по установленному регламенту с соблюдением норм и правил. Точность построения и обработки результатов обеспечивает правильность работы и последующую безопасность строительства или осуществления любой другой деятельности на местности. Теодолитный ход относиться к геодезическим работам цены на которые на сегодняшний день очень вариативные.
Основные виды теодолитного хода.
Теодолитный ход – это разомкнутая или замкнутая ломаная линия. В зависимости от формы построения, различают несколько видов ходов:
Разомкнутый теодолитный ход, опирающийся на два пункта с известными координатами и два дирекционных угла. Разомкнутый ход можно охарактеризовать как простую линию. Проект трассы или любого другого продолжительного участка невозможен без разомкнутой линии. Опора у нее на известные точки. В отличие от замкнутого, начало и конец располагаются в разных точках.
Разомкнутый теодолитный ход, опирающийся на один исходный пункт и один дирекционный угол — такой ход еще называют висячим. Висячий ход используют редко, потому что для его вычисления потребуется специальная формула. Суть его такова, что он имеет только начало в определенной точке координат. Конец нужно вычислять.
Замкнутый ход по своей сути является многоугольной фигурой и опирается только на один базовый пункт с установленными координатами и дирекционным углом. Вершинами стороны выступают точки, закрепленными на местности, а отрезками – расстояние между ними. Его чаще всего создают для съемки стройплощадок, жилых зданий, промышленных сооружений или земельных участков.
Диагональный (прокладывают внутри других ходов). Если необходимо заснять ровный участок, вроде строительной площадки, лучшим выбором будет полигон. На объектах вытянутого типа, вроде автодорог, принято использовать разомкнутый ход, а висячий – для съемки закрытой местности, вроде глухих улиц
Порядок выполнения работ
Как и другие геодезические мероприятия, эта процедура проводится с предварительной подготовкой для получения точных метрических данных. Немаловажную роль играет также их математическая обработка. Сами работы выполняются по принципу от общего к частному и состоят из следующих этапов:
1. Рекогносцировка местности. Оценка снимаемой территории, изучение ее особенностей. На этом этапе определяется местоположение снимаемых точек.
2. Полевая съемка. Работы непосредственно уже на местности. Выполнение линейных и угловых измерений, составление абрисов, предварительные расчеты и внесение изменений при необходимости.
3. Камеральная обработка. Завершающий этап работ, который заключается в вычислении координат замкнутого теодолитного хода и последующего составления плана и технического отсчета.
Рекогносцировка и полевые измерения выполняются непосредственно на объекте и являются наиболее трудоемкими и затратными мероприятиями. Тем не менее, от качества их проведения зависит дальнейший результат.
Обработка данных проводится уже в помещении. Сегодня она осуществляется при помощи специального программного обеспечения, хотя и ручные расчеты все также остаются актуальными и могут быть использованы геодезистом в целях проверки.
Обработка данных
Обработка результатов измерений замкнутого теодолитного хода позволит оценить качество проделанной работы и внести исправления в полученные геометрические величины. Чтобы убедится в том, что угловые и линейные измерения находятся в допуске, еще во время полевых работ выполняют первичные расчеты.
Для вычисления значений координат точек замкнутого хода используют такие данные: – координаты исходного пункта;
– исходный дирекционный угол;
– горизонтальные углы;
– длины сторон.
Уравнивание
При начале расчетов определяют теоретическую сумму углов , а потом увязывают их, распределяя между ними угловую невязку.
∑βтеор=180∘⋅(n−2)
n- количество точек полигона
fβ=∑βизм−180∘⋅(n−2)
∑βизм – значение измеренных угловых величин;
Для получения fβ, необходимо рассчитать разность между βизм, в которой присутствуют погрешности, и ∑βтеор.
В уравнивании fβ выступает как показатель точности проведенных измерительных работ, а ее значение не должно быть выше предельной величины, определяемой из следующей формулы:
fβ1=1,5tn−−√
t-точность измерительного устройства,
n – количество углов.
Уравнивание заканчивается равномерным распределением полученной невязки между угловыми величинами.
Определение дирекционных углов
При известном значении дирекционного угла (α) одной стороны и горизонтального (β) можно определить значение следующей стороны:
αn+1=αn+η
η=180∘−βпр
βпр – значение правого по ходу угла, из чего следует:
αn+1=αn+180∘−βпр
Для левого (βлев) эти знаки будут противоположными:
αn+1=αn−180∘+βлев
Поскольку значение дирекционного угла не может быть больше, чем 360∘, то из него, соответственно, отнимают 360∘. В случае с отрицательным углом, необходимо к предыдущему α добавить 180∘ и отнять значение βиспр.
Вычисление румбов
У румбов и дирекционных углов существует взаимосвязь, а определяют их по четвертям, которые носят название четырех сторон света. Как видно из табл.1. расчёты проводят согласно установленной схеме.
Таблица 1. Расчеты румба в зависимости от пределов дирекционного угла.
Приращения координат
Для приращений координат в замкнутом ходе применяют формулы, использующиеся при решении прямой геодезической задачи. Ее суть состоит в том, что по известным значениям координат исходного пункта, дирекционного угла и горизонтального приложения можно определить координаты следующего. Исходя из этого, формула приращения значений будет иметь следующий вид:
ΔX=d⋅cosα
ΔY=d⋅sinα
d-горизонтальное проложение;
α-горизонтальный угол.
Для полигона, который имеет вид замкнутой геометрической фигуры, теоретическая сумма приращений будет равняться нулю для обеих координатных осей:
∑ΔXтеор=0
∑ΔYтеор=0
Линейная невязка и невязка приращения значений координат
Несмотря на вышесказанное, случайные погрешности не позволяют алгебраическим суммам выйти в ноль, поэтому они будут равняться другим невязкам приращений координат:
fx∑ni=1ΔX1
fy∑ni=1ΔY1
Переменные fx и fy – проекции линейной невязки fp на координатной оси, которую можно рассчитать по формуле:
fp=f2x+f2y−−−−−−√
При этом fp, не должно быть боле, чем 1/2000 от доли периметра полигона, а распределения fx и fy проводится следующим образом:
δXi=−fxPdi
δYi=−fyPdi
В этих формулах δXi и δYi – поправки приращения координат.
і- номера точек;
После приращений и внесения поправок в данные измерений, проводят расчет их исправленных значений.
Вычисление координат
Когда будут произведены увязки приращений точек полигона, следует определение координат, которое осуществляют с использованием следующих формул:
Xпос=Xпр+ΔXисп
Yпос=Yпр+ΔYисп
Значения Xпос Yпос – координаты последующих пунктов, Xпр и Yпр – предыдущих.
ΔXисп и ΔYисп – исправленные приращения между этими двумя значениями.
Если координаты первой и последней точки совпадают, то обработку можно считать завершённой.
На основе полученных координат и составленных во время полевых измерений абрисов в дальнейшем составляется план теодолитного хода.