Как найти дирекционные углы линий

По
известному дирекционному углу _n
и по исправленным горизонтальным углам
_испр
вычисляются дирекционные углы остальных
сторон теодолитного хода по формулам
для правых горизонтальных углов:

– дирекционный
угол последующей стороны равен
дирекционному углу предыдущей стороны
плюс 180
и минус исправленный горизонтальный
угол правый по ходу.

Величина
дирекционного угла не может превышать
360
и быть меньше 0.
Если величина дирекционного угла больше
360,
то из результата вычислений необходимо
вычесть 360
(см. пример).

Контроль
вычисления дирекционных углов. В
замкнутом теодолитном ходе в результате
вычислений получается дирекционный
угол исходной стороны.

Пример вычисления дирекционных углов: Дирекционный угол исходной стороны 1-2 равен 4545.

;

;

;

;

При
вычислении дирекционного угла получилось
значение 40545.
Из полученного значения вычитается
360.

.

Контроль
вычисления дирекционных углов получился.

Все
результаты вычислений заносятся в
таблицу «Ведомость вычисления координат»
(табл. 6).

3.3 Вычисление приращений координат

Вычисление
приращений координат выполняется по
формулам:

,

где
d
– горизонтальное проложение (длина)
линии; 
– дирекционный угол этой линии.

Приращения
координат вычисляются с точностью два
знака после запятой.

Пример вычисления приращений координат:

;

;

;

;

.

;

;

;

;

.

Все
результаты вычисления заносятся
в табл. 6. Пример
вычисления тригонометрических функций
на калькуляторе приведен в
прил. 3.

3.4 Уравнивание линейных измерений

Разность
между суммой вычисленных приращений
координат и теоретической суммой
называется линейной невязкой хода и
обозначается f_Х
и f_Y.
Уравнивание линейных измерений
выполняется по осям Х
и Y.

Линейная невязка
вычисляется по формулам:

.

Теоретическая
сумма приращений координат зависит от
геометрии хода. В замкнутом теодолитном
ходе она равна нулю, тогда невязка равна

.

Прежде,
чем распределять невязки в приращения
координат, необходимо убедиться в их
допустимости. Для чего вычисляется
абсолютная невязка хода f_абс

и
относительная

,

где
Р
– периметр хода (сумма длин сторон), м.

Относительная
невязка сравнивается с допустимой
.

В
случае, когда полученная относительная
невязка допустима, т.е.
,
то вычисляются поправки в приращения
координат пропорционально
длинам сторон.
Невязки распределяются с обратным
знаком. Если
,
то проверяются вычисления в п.
3.3 и 3.4.

Поправки
в приращения координат _X
и _Y
вычисляются
по формулам с округлением до 0,01 м:

,

где
_X
и _Y
– поправка
в приращение по оси Х
и
Y,
соответственно, м; f_X
и f_Y
–
невязки
по осям, м; Р
–
периметр
(сумма сторон), м; d_i
–
измеренная
длина (горизонтальное проложение), м.

Знак
у поправки противоположен знаку невязки.
Поправки записываются в «Ведомость
вычисления координат». В примере (табл.
6) поправки показаны красным цветом.

После
вычисления поправок следует сделать
проверку, т.е. сложить все поправки. Если
их сумма будет равна невязке с обратным
знаком, то распределение невязки
выполнено правильно. То есть:

.

Вычисляются
исправленные приращения.

Полученные
поправки алгебраически прибавляются
к соответствующим приращениям и
получаются исправленные приращения:

.

Контроль:
сумма исправленных приращений в замкнутом
теодолитном ходе должна равняться нулю,
т.е. должно выполняться равенство:

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Чтобы понять, что такое дирекционный угол, представим на карте линию (отрезок) с начальной точкой А и конечной точкой В.
Теперь проведем из начала отрезка (точки А) луч, параллельный осевому меридиану зоны и направленный на север. И будем поворачивать этот
луч вокруг точки А по часовой стрелке до тех пор, пока он не пересечется с точкой В. Угол, на который мы повернули луч,
и будет называться дирекционным углом линии АВ.

Калькулятор угла по координатам

С помощью этого калькулятора Вы сможете производить расчет дирекционных углов линий на основе заданных координат точки стояния (А) и точки
ориентирования (В), а также рассчитывать расстояние между этими точками.

Калькулятор координат по углу и расстоянию

Этот калькулятор поможет Вам рассчитать координаты конечной точки пути на основе координат начальной точки, дирекционного угла и расстояния между точками.
Угол можно указывать как в десятичных градусах (226,27303°), так и в градусах — минутах — секундах (226° 16′ 22″).

Азимуты

Слово «азимут» иногда используется как синоним азимута для обозначения направления (показания в градусах) от одного объекта к другому. Такое использование корректно только в первом (СВ) квадранте между 0° и 90°.

Азимуты также можно считывать с юга. Национальная геодезическая служба Национального управления океанических и атмосферных исследований (NOAA) (бывшая Береговая и геодезическая служба США) всегда использует юг в качестве нулевого направления. В пожарной службе дикой природы азимут всегда считывается с северной точки.

Направление ветра

Азимут часто используется для обозначения направления ветра. Традиционно направление ветра указывается как одна из восьми точек компаса (С, СВ, В, ЮВ, Ю, ЮЗ, З, СЗ). Однако графики направления ветра и скорости часто дают значение азимута, используя 0° и 360° для севера. Ветры называются по направлению, откуда они дуют. Например, западный ветер дует с запада (или 270°), а юго-восточный ветер дует с юго-востока (135°).

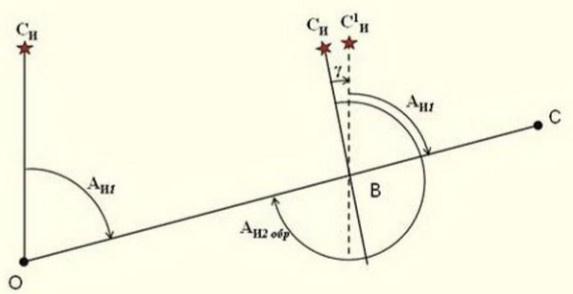
Обратный азимут и обратное визирование

Обратный азимут — это проекция азимута от начала координат до противоположной стороны азимутального круга. В азимутальном круге 360 градусов, поэтому противоположное направление будет 180 градусов (половина 360 градусов) от азимута.

Обратный азимут рассчитывается путем прибавления 180° к азимуту, если азимут меньше 180°, или вычитания 180° из азимута, если он больше 180°. Например, если азимут равен 320°, обратный азимут будет 320° — 180° = 140°. Если азимут равен 30°, обратный азимут будет равен 180° + 30° = 210°.

Обратное прицеливание — это метод прицеливания, в котором используется отсчет азимута, снятый в обратном направлении.

Компас – это инструмент, используемый для навигации и ориентации. Азимутальный компас градуирован/отмечен полным кругом в 360 градусов, который называется азимутальным кругом. Компоненты компаса включают магнитную стрелку, которая всегда указывает на магнитный север, градуированную окружность для откладывания углов от истинного севера и линию визирования для продолжения линии визирования при следовании курсу направления.

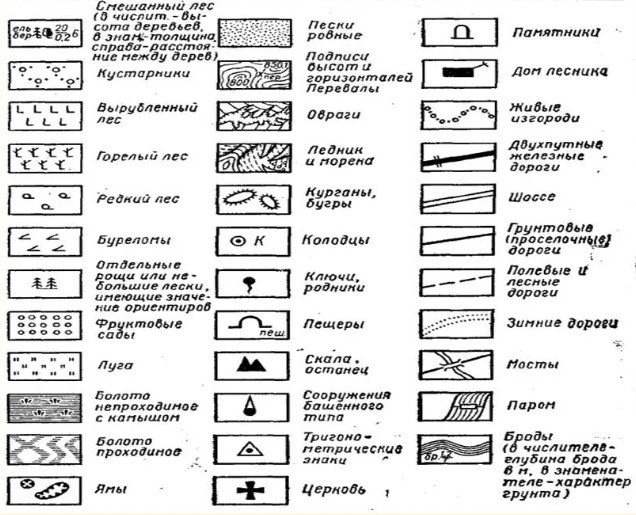
Условные знаки

Дирекционные углы и румбы

Дирекционные углы и румбы используются для ориентирования линий.

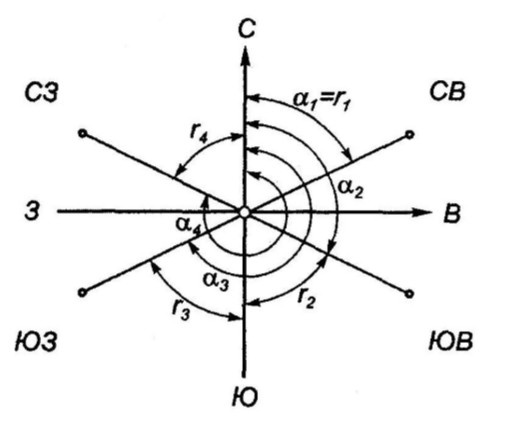
Дирекционным углом (α) линии называют угол, отсчитанный по ходу часовой стрелки от северного направления вертикальной линии километровой сетки (осевого меридиана зоны) до направления заданной линии. Пределы изменения дирекционного угла от 0º до 360º.

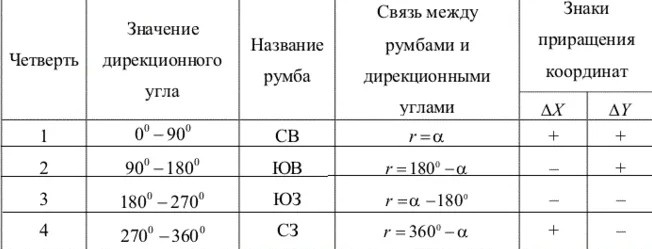
Связь между дирекционными углами и румбами зависит от четверти, в которой находится заданное направление. Перевод дирекционных углов в румбы выполняется согласно таблице ниже.

Пример перевода дирекционных углов в румбы

1. если дирекционный угол α равен 42°15′55″, тогда согласно таблице румб вычисляется по формуле r=α=42°15′55″, а название румба будет СВ;
2. если дирекционный угол α равен 100°45′11″, тогда согласно таблице румб вычисляется по формуле r=180°-α=180°-100°45′11″=79°14′49″, а название румба будет ЮВ;
3. если дирекционный угол α равен 210°17′42″, тогда согласно таблице румб вычисляется по формуле r=α-180°=210°17′42″-180°=30°17′42″, а название румба будет ЮЗ;
4. если дирекционный угол α равен 335°28′32″, тогда согласно таблице румб вычисляется по формуле r=360°-α=360°-335°28′32″=24°31′28″, а название румба будет СЗ.

Министерство образования и науки Республики
Башкортостан

Башкирский колледж архитектуры, строительства
и коммунального хозяйства

    
План – конспект

по дисциплине  «Основы геодезии»

на тему «Ориентирование линий»

Для студентов специальности 08.02.01

Строительство и
эксплуатация зданий и сооружений

Уфа -2020

ЛЕКЦИЯ 5

Тема «Ориентирование
линий»

1.     Дирекционные углы линий.

2.    
Румбы линий.

3.    
Зависимость
дирекционных углов и румбов.

4.    
Методика решения
задач на определение примычных углов.

1.     
Дирекционные углы линий.

Определение положения линий относительно сторон света
называется ориентированием.

Ориентирование заключается в том, что определяется
угол между исходным направлением и данной линией.

За исходное направление для ориентирования принимают
ось абсцисс (ось Х) или меридиан.

Для ориентирования линий служат углы, которые
называются дирекционными углами  и румбами.

Угол, составленный северным концом меридиана и данной
линией, называется дирекционным углом.

Дирекционный угол обозначается  ℒ

ЗАПОМНИТЕ!

Дирекционный угол отсчитывается

от 0 до 360˚ по ходу часовой стрелки.

                   С                                   

                                                            ℒ_1-2  = 50˚                     

                             2                      

З                 
                В

             1                  

                   Ю

             (меридиан)

Задача.

Построить угол, образованный двумя линиями, имеющими
следующие дирекционные углы

ℒ_1-2  = 160˚

ℒ_2-3  = 70˚

и определить величину этого угла.

Решение:

С

       160˚                                                                        <2=70˚+20˚=90˚

  
1

20˚   

            20˚      70˚                      3

Ю                      

          2

Дирекционный угол
заданного направления α _пр называется прямым, а
противоположного – обратным α _обр  Прямой
и обратный дирекционные углы, которые отличаются между собой на ±180˚

   С                                                                         ℒ_1-2  = 60˚

             
2                                                         ℒ_2-1 = 240˚

           60˚

1                    180˚ + 60˚ = 240˚

               
                  С                                                     ℒ_1-2   = 300˚

       
2                                                                      ℒ_2-1   = 120˚

                        1  300˚

                                     300^о
– 180^о =  120^о

                         Ю

ЗАПОМНИТЕ!

Прямой дирекционный угол отличается

от обратного на «+»  или « — » 180˚

Иногда для ориентирования линии на
местности пользуются не дирекционными углами, а румбами.

2.     
Румбы линий.

Угол, составленный ближайшим концом меридиана и данной
линией, называется румбом.

  Румб образует острый угол и  откладывается как по
ходу часовой стрелки, так и против, и обозначается    r.                          

ЗАПОМНИТЕ!

Румб имеет значение

от 0 до 90˚ и направление, в
зависимости от четверти, в которой находится данная линия

                      С                                              
r_1-2
=СВ:60˚

                                                                          
r_1-3=ЮВ:60˚

          
СЗ        60˚         2   СВ

    
З             1                В

           ЮЗ                     3  
ЮВ

                      Ю

Задача.

Построить угол, образованный двумя линиями, имеющими
следующие румбы

r _1-2  = ЮВ : 25˚

r _2-3  = СВ : 65˚

и определить величину этого угла.

Решение:

С

                    В                                                             <2=25˚+65˚=90˚

   1

                     С

25˚   

            25˚      65˚                      3

Ю                            В

З         
2

              Ю

Румб заданного направления r _пр. называется прямым, а противоположного – обратным r _обр. Прямой и
обратный румбы равны по величине и отличаются только направлением.

r_1-2
= ЮВ : 40˚

r_2
-1 = СЗ : 40˚

ЗАПОМНИТЕ!

Прямой румб отличается

от обратного  только  направлением

3.     
Зависимость
дирекционных углов и румбов.

На практике часто возникает необходимость определить румбы линий по
дирекционным углам и наоборот.

Таблица зависимости румбов и дирекционных
углов.

Пример перевода дирекционных углов в румбы

1.  
если
дирекционный угол α равен 42°, тогда согласно таблицы румб вычисляется по
формуле r=α=42°, а название румба будет СВ;

                
r = СВ: 42

2. если дирекционный угол α равен 100°, тогда
согласно таблицы румб вычисляется по формуле r=180°-α=180°-100°=80°, а название
румба будет ЮВ;              r = ЮВ: 80

3. если дирекционный угол α равен 210°,
тогда согласно таблицы румб вычисляется по формуле r=α-180°=210°-180°=30°, а
название румба будет ЮЗ;              r = ЮЗ: 30

4. если дирекционный угол α равен 335°, тогда
согласно таблицы румб вычисляется по формуле r=360°-α=360°-335°=25°, а название
румба будет СЗ.

r = СЗ: 25

4.Методика
решения задач  на определение примычных углов.

1.    
Через вершину
примычного угла, который необходимо вычислить, провести меридиан, показать
направление север и юг.

2.    
Определить, какими
линиями составлен примычный угол.

3.    
Показать известные
румбы или дирекционные углы этих линий на чертеже.

4.    
Вычислить примычный
угол.

1).     С                                                                 3).

                                                                                  
                      В₁

                    Β₁

         Ю

2).      
С

                           
В₁

          Ю

Домашнее задание

1.    
Построить линии по
заданному дирекционному углу

α_1-2 =57^о

α_2-3 =276^о

2.    
Провести линии по заданным
румбам.

r_1-2 = СВ:23^о

r_1-3 = ЮЗ:83^о

3.     По заданному дирекционному углу определить
румб линии

α_1-2 =157^о

α_3-4 =290^о

4. По заданному румбу линии определить дирекционные углы

r_1-2 = СВ:23^о

r_3-4 = ЮВ:43^о

5. Построить угол, образованный двумя линиями,
имеющими следующие румбы r_1-2 = СВ:50˚, r_2-3 = ЮВ:30˚,  и определить величину этого угла.

              
Определить примычные углы β₂ и β₃ , если

                                                                                 
r_2-3 = СВ:70˚

                                                        
3                           r_2-A
= ЮВ:60˚

               20˚                                                             
r_3-B = ЮЗ:20˚

         2        β₂                       β₃       

                                                    20˚

               60˚                           В                   

1                          
А