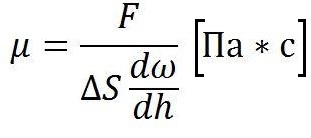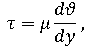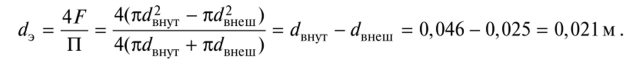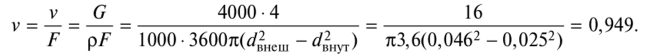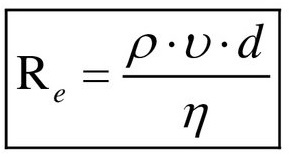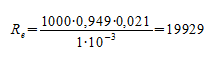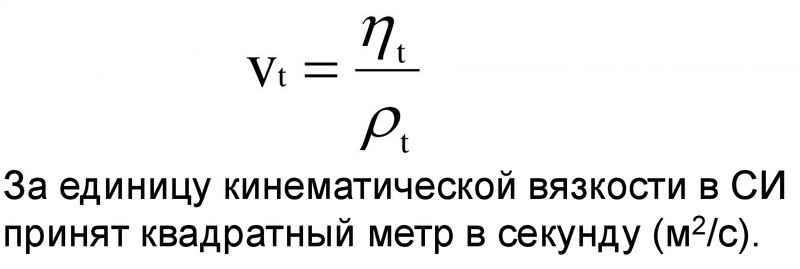Физические свойства воздуха
Воздух — это смесь различных газов (% по объему): азот — 78,03; кислород — 20,95; озон и другие инертные газы: аргон, гелий, неон, криптон, ксенон, радон — 0,94; углекислый газ — 0,03; водяной пар — 0,05. Содержание углекислого газа в атмосферном воздухе принимается равным (% по объему): в сельской местности — 0,03, в городах — 0,04—0,07. Содержание водяных паров в воздухе зависит от его температуры. Озон присутствует в лесном, горном и морском воздухе. Наружный воздух загрязняется отходящими от промышленных предприятий вредными для здоровья человека газами и пылью.

Плотность воздуха при нормальном атмосферном давлении 101,325 кПа (1 атм) и различной температуре
| Температура воздуха | Плотность воздуха, ρ |
| оС | кг/м3 |
| -20 | 1,395 |
| 0 | 1,293 |
| 5 | 1,269 |
| 10 | 1,247 |
| 15 | 1,225 |
| 20 | 1,204 |
| 25 | 1,184 |
| 30 | 1,165 |
| 40 | 1,127 |
| 50 | 1,109 |
| 60 | 1,060 |
| 70 | 1,029 |
| 80 | 0,9996 |
| 90 | 0,9721 |
| 100 | 0,9461 |
Динамическая и кинематическая вязкость воздуха при нормальном атмосферном давлении и различной температуре
| Температура воздуха | Динамическая вязкость воздуха, μ | Кинематическая вязкость воздуха, ν |
| оС | (Н • c / м2) x 10-5 | (м2 / с) x 10-5 |
| -20 | 1,63 | 1,17 |
| 0 | 1,71 | 1,32 |
| 5 | 1,73 | 1,36 |
| 10 | 1,76 | 1,41 |
| 15 | 1,80 | 1,47 |
| 20 | 1,82 | 1,51 |
| 25 | 1,85 | 1,56 |
| 30 | 1,86 | 1,60 |
| 40 | 1,87 | 1,66 |
| 50 | 1,95 | 1,76 |
| 60 | 1,97 | 1,86 |
| 70 | 2,03 | 1,97 |
| 80 | 2,07 | 2,07 |
| 90 | 2,14 | 2,20 |
| 100 | 2,17 | 2,29 |
Основные физические свойства воздуха при различной температуре
| Температура | Плотность, ρ | Удельная теплоёмкость, Cp | Теплопроводность, λ | Кинематическая вязкость, ν | Коэффициент температурного линейного расширения, α | Число Прандтля, Pr |
| оС | кг/м3 | кДж / (кг • К) | Вт / (м • К) | (м2 / с) x 10-6 | (1 / K) x 10-3 | — |
| 0 | 1,293 | 1,005 | 0,0243 | 13,30 | 3,67 | 0,715 |
| 20 | 1,205 | 1,005 | 0,0257 | 15,11 | 3,43 | 0,713 |
| 40 | 1,127 | 1,005 | 0,0271 | 16,97 | 3,20 | 0,711 |
| 60 | 1,067 | 1,009 | 0,0285 | 18,90 | 3,00 | 0,709 |
| 80 | 1,000 | 1,009 | 0,0299 | 20,94 | 2,83 | 0,708 |
| 100 | 0,946 | 1,009 | 0,0314 | 23,06 | 2,68 | 0,703 |
Формулы физических свойств воздуха
При проведении инженерных расчетов удобнее использовать приближённые формулы для определения физических свойств воздуха⋆:
Плотность воздуха
[ кг/м3 ]

Теплоёмкость воздуха
⋆ [ Дж/(кг • К) ]

Теплопроводность воздуха
⋆ [ Вт/(м • K) ]

Динамическая вязкость воздуха
⋆ [ Па • c ]

Кинематическая вязкость воздуха
[ м2/с ]

Температуропроводность воздуха
⋆ [ м2/с ]

Число Прандтля воздуха
[ — ]

⋆ Приближённые формулы физических свойств воздуха получены авторами настоящего сайта.
Размерность величин: температура — К (Кельвин).
Приближённые формулы действительны в диапазоне температур воздуха от 273 К до 473 К.
Плотность воздуха в зависимости от температуры
Представлена подробная таблица значений плотности воздуха в сухом состоянии при различных температурах и нормальном атмосферном давлении. Чему равна плотность воздуха? Аналитически определить плотность воздуха можно, если разделить его массу на объем, который он занимает при заданных условиях (давление, температура и влажность). Также можно вычислить его плотность по формуле уравнения состояния идеального газа. Для этого необходимо знать абсолютное давление и температуру воздуха, а также его газовую постоянную и молярный объем. Это уравнение позволяет вычислить плотность воздуха в сухом состоянии.
На практике, чтобы узнать какова плотность воздуха при различных температурах, удобно воспользоваться готовыми таблицами. Например, приведенной таблицей значений плотности атмосферного воздуха в зависимости от его температуры. Плотность воздуха в таблице выражена в килограммах на кубический метр и дана в интервале температуры от минус 50 до 1200 градусов Цельсия при нормальном атмосферном давлении (101325 Па).
| t, °С | ρ, кг/м3 | t, °С | ρ, кг/м3 | t, °С | ρ, кг/м3 | t, °С | ρ, кг/м3 |
|---|---|---|---|---|---|---|---|
| -50 | 1,584 | 20 | 1,205 | 150 | 0,835 | 600 | 0,404 |
| -45 | 1,549 | 30 | 1,165 | 160 | 0,815 | 650 | 0,383 |
| -40 | 1,515 | 40 | 1,128 | 170 | 0,797 | 700 | 0,362 |
| -35 | 1,484 | 50 | 1,093 | 180 | 0,779 | 750 | 0,346 |
| -30 | 1,453 | 60 | 1,06 | 190 | 0,763 | 800 | 0,329 |
| -25 | 1,424 | 70 | 1,029 | 200 | 0,746 | 850 | 0,315 |
| -20 | 1,395 | 80 | 1 | 250 | 0,674 | 900 | 0,301 |
| -15 | 1,369 | 90 | 0,972 | 300 | 0,615 | 950 | 0,289 |
| -10 | 1,342 | 100 | 0,946 | 350 | 0,566 | 1000 | 0,277 |
| -5 | 1,318 | 110 | 0,922 | 400 | 0,524 | 1050 | 0,267 |
| 0 | 1,293 | 120 | 0,898 | 450 | 0,49 | 1100 | 0,257 |
| 10 | 1,247 | 130 | 0,876 | 500 | 0,456 | 1150 | 0,248 |
| 15 | 1,226 | 140 | 0,854 | 550 | 0,43 | 1200 | 0,239 |
При 25°С воздух имеет плотность 1,185 кг/м3. При нагревании плотность воздуха снижается — воздух расширяется (его удельный объем увеличивается). С ростом температуры, например до 1200°С, достигается очень низкая плотность воздуха, равная 0,239 кг/м3, что в 5 раз меньше ее значения при комнатной температуре. В общем случае, снижение плотности газов при нагреве позволяет проходить такому процессу, как естественная конвекция и применяется, например, в воздухоплавании.
Если сравнить плотность воздуха относительно плотности воды, то воздух легче на три порядка — при температуре 4°С плотность воды равна 1000 кг/м3, а плотность воздуха составляет 1,27 кг/м3. Необходимо также отметить значение плотности воздуха при нормальных условиях. Нормальными условиями для газов являются такие, при которых их температура равна 0°С, а давление равно нормальному атмосферному. Таким образом, согласно таблице, плотность воздуха при нормальных условиях (при НУ) равна 1,293 кг/м3.
Динамическая и кинематическая вязкость воздуха при различных температурах
При выполнении тепловых расчетов необходимо знать значение вязкости воздуха (коэффициента вязкости) при различной температуре. Эта величина требуется для вычисления числа Рейнольдса, Грасгофа, Релея, значения которых определяют режим течения этого газа. В таблице даны значения коэффициентов динамической μ и кинематической ν вязкости воздуха в диапазоне температуры от -50 до 1200°С при атмосферном давлении.
Коэффициент вязкости воздуха с ростом его температуры значительно увеличивается. Например, кинематическая вязкость воздуха равна 15,06·10-6 м2/с при температуре 20°С, а с ростом температуры до 1200°С вязкость воздуха становиться равной 233,7·10-6 м2/с, то есть увеличивается в 15,5 раз! Динамическая вязкость воздуха при температуре 20°С равна 18,1·10-6 Па·с.
При нагревании воздуха увеличиваются значения как кинематической, так и динамической вязкости. Эти две величины связаны между собой через величину плотности воздуха, значение которой уменьшается при нагревании этого газа. Увеличение кинематической и динамической вязкости воздуха (как и других газов) при нагреве связано с более интенсивным колебанием молекул воздуха вокруг их равновесного состояния (согласно МКТ).
| t, °С | μ·106, Па·с | ν·106, м2/с | t, °С | μ·106, Па·с | ν·106, м2/с | t, °С | μ·106, Па·с | ν·106, м2/с |
|---|---|---|---|---|---|---|---|---|
| -50 | 14,6 | 9,23 | 70 | 20,6 | 20,02 | 350 | 31,4 | 55,46 |
| -45 | 14,9 | 9,64 | 80 | 21,1 | 21,09 | 400 | 33 | 63,09 |
| -40 | 15,2 | 10,04 | 90 | 21,5 | 22,1 | 450 | 34,6 | 69,28 |
| -35 | 15,5 | 10,42 | 100 | 21,9 | 23,13 | 500 | 36,2 | 79,38 |
| -30 | 15,7 | 10,8 | 110 | 22,4 | 24,3 | 550 | 37,7 | 88,14 |
| -25 | 16 | 11,21 | 120 | 22,8 | 25,45 | 600 | 39,1 | 96,89 |
| -20 | 16,2 | 11,61 | 130 | 23,3 | 26,63 | 650 | 40,5 | 106,15 |
| -15 | 16,5 | 12,02 | 140 | 23,7 | 27,8 | 700 | 41,8 | 115,4 |
| -10 | 16,7 | 12,43 | 150 | 24,1 | 28,95 | 750 | 43,1 | 125,1 |
| -5 | 17 | 12,86 | 160 | 24,5 | 30,09 | 800 | 44,3 | 134,8 |
| 0 | 17,2 | 13,28 | 170 | 24,9 | 31,29 | 850 | 45,5 | 145 |
| 10 | 17,6 | 14,16 | 180 | 25,3 | 32,49 | 900 | 46,7 | 155,1 |
| 15 | 17,9 | 14,61 | 190 | 25,7 | 33,67 | 950 | 47,9 | 166,1 |
| 20 | 18,1 | 15,06 | 200 | 26 | 34,85 | 1000 | 49 | 177,1 |
| 30 | 18,6 | 16 | 225 | 26,7 | 37,73 | 1050 | 50,1 | 188,2 |
| 40 | 19,1 | 16,96 | 250 | 27,4 | 40,61 | 1100 | 51,2 | 199,3 |
| 50 | 19,6 | 17,95 | 300 | 29,7 | 48,33 | 1150 | 52,4 | 216,5 |
| 60 | 20,1 | 18,97 | 325 | 30,6 | 51,9 | 1200 | 53,5 | 233,7 |
Удельная теплоемкость воздуха при температуре от -50 до 1200°С
Представлена таблица удельной теплоемкости воздуха при различных температурах. Теплоемкость в таблице дана при постоянном давлении (изобарная теплоемкость воздуха) в интервале температуры от минус 50 до 1200°С для воздуха в сухом состоянии. Чему равна удельная теплоемкость воздуха? Величина удельной теплоемкости определяет количество тепла, которое необходимо подвести к одному килограмму воздуха при постоянном давлении для увеличения его температуры на 1 градус. Например, при 20°С для нагревания 1 кг этого газа на 1°С в изобарном процессе, требуется подвести 1005 Дж тепла.
Удельная теплоемкость воздуха увеличивается с ростом его температуры. Однако, зависимость массовой теплоемкости воздуха от температуры не линейная. В интервале от -50 до 120°С ее величина практически не меняется — в этих условиях средняя теплоемкость воздуха равна 1010 Дж/(кг·град). По данным таблицы видно, что значительное влияние температура начинает оказывать со значения 130°С. Однако, температура воздуха влияет на его удельную теплоемкость намного слабее, чем на вязкость. Так, при нагреве с 0 до 1200°С теплоемкость воздуха увеличивается лишь в 1,2 раза – с 1005 до 1210 Дж/(кг·град).
Следует отметить, что теплоемкость влажного воздуха выше, чем сухого. Если сравнить теплоемкость воды и воздуха, то очевидно, что вода обладает более высоким ее значением и содержание воды в воздухе приводит к увеличению удельной теплоемкости.
| t, °С | Cp, Дж/(кг·град) | t, °С | Cp, Дж/(кг·град) | t, °С | Cp, Дж/(кг·град) | t, °С | Cp, Дж/(кг·град) |
|---|---|---|---|---|---|---|---|
| -50 | 1013 | 20 | 1005 | 150 | 1015 | 600 | 1114 |
| -45 | 1013 | 30 | 1005 | 160 | 1017 | 650 | 1125 |
| -40 | 1013 | 40 | 1005 | 170 | 1020 | 700 | 1135 |
| -35 | 1013 | 50 | 1005 | 180 | 1022 | 750 | 1146 |
| -30 | 1013 | 60 | 1005 | 190 | 1024 | 800 | 1156 |
| -25 | 1011 | 70 | 1009 | 200 | 1026 | 850 | 1164 |
| -20 | 1009 | 80 | 1009 | 250 | 1037 | 900 | 1172 |
| -15 | 1009 | 90 | 1009 | 300 | 1047 | 950 | 1179 |
| -10 | 1009 | 100 | 1009 | 350 | 1058 | 1000 | 1185 |
| -5 | 1007 | 110 | 1009 | 400 | 1068 | 1050 | 1191 |
| 0 | 1005 | 120 | 1009 | 450 | 1081 | 1100 | 1197 |
| 10 | 1005 | 130 | 1011 | 500 | 1093 | 1150 | 1204 |
| 15 | 1005 | 140 | 1013 | 550 | 1104 | 1200 | 1210 |
Теплопроводность, температуропроводность, число Прандтля воздуха
В таблице представлены такие физические свойства атмосферного воздуха, как теплопроводность, температуропроводность и его число Прандтля в зависимости от температуры. Теплофизические свойства воздуха даны в интервале от -50 до 1200°С для сухого воздуха. По данным таблицы видно, что указанные свойства воздуха существенно зависят от температуры и температурная зависимость рассмотренных свойств этого газа различна.
Теплопроводность воздуха λ при повышении температуры увеличивается во всем диапазоне, достигая при 1200°С величины 0,0915 Вт/(м·град). Другие теплофизические свойства воздуха такие, как его температуропроводность a и число Прандтля Pr, по-разному реагируют на изменение температуры. Температуропроводность, как и вязкость воздуха сильно зависит от температуры и при нагревании, например с 0 до 1200°С, ее значение увеличивается почти в 17 раз.
Число Прандтля воздуха слабо зависит от температуры и при нагревании этого газа его величина сначала снижается до величины 0,674, а затем начинает расти, и при температуре 1200°С достигает значения 0,724.
| t, °С | λ·102, Вт/(м·град) | а·106, м2/с | Pr | t, °С | λ·102, Вт/(м·град) | а·106, м2/с | Pr |
|---|---|---|---|---|---|---|---|
| -50 | 2,04 | 12,7 | 0,728 | 170 | 3,71 | 45,7 | 0,682 |
| -40 | 2,12 | 13,8 | 0,728 | 180 | 3,78 | 47,5 | 0,681 |
| -30 | 2,2 | 14,9 | 0,723 | 190 | 3,86 | 49,5 | 0,681 |
| -20 | 2,28 | 16,2 | 0,716 | 200 | 3,93 | 51,4 | 0,68 |
| -10 | 2,36 | 17,4 | 0,712 | 250 | 4,27 | 61 | 0,677 |
| 0 | 2,44 | 18,8 | 0,707 | 300 | 4,6 | 71,6 | 0,674 |
| 10 | 2,51 | 20 | 0,705 | 350 | 4,91 | 81,9 | 0,676 |
| 20 | 2,59 | 21,4 | 0,703 | 400 | 5,21 | 93,1 | 0,678 |
| 30 | 2,67 | 22,9 | 0,701 | 450 | 5,48 | 104,2 | 0,683 |
| 40 | 2,76 | 24,3 | 0,699 | 500 | 5,74 | 115,3 | 0,687 |
| 50 | 2,83 | 25,7 | 0,698 | 550 | 5,98 | 126,8 | 0,693 |
| 60 | 2,9 | 27,2 | 0,696 | 600 | 6,22 | 138,3 | 0,699 |
| 70 | 2,96 | 28,6 | 0,694 | 650 | 6,47 | 150,9 | 0,703 |
| 80 | 3,05 | 30,2 | 0,692 | 700 | 6,71 | 163,4 | 0,706 |
| 90 | 3,13 | 31,9 | 0,69 | 750 | 6,95 | 176,1 | 0,71 |
| 100 | 3,21 | 33,6 | 0,688 | 800 | 7,18 | 188,8 | 0,713 |
| 110 | 3,28 | 35,2 | 0,687 | 850 | 7,41 | 202,5 | 0,715 |
| 120 | 3,34 | 36,8 | 0,686 | 900 | 7,63 | 216,2 | 0,717 |
| 130 | 3,42 | 38,6 | 0,685 | 950 | 7,85 | 231,1 | 0,718 |
| 140 | 3,49 | 40,3 | 0,684 | 1000 | 8,07 | 245,9 | 0,719 |
| 150 | 3,57 | 42,1 | 0,683 | 1100 | 8,5 | 276,2 | 0,722 |
| 160 | 3,64 | 43,9 | 0,682 | 1200 | 9,15 | 316,5 | 0,724 |
Будьте внимательны! Теплопроводность воздуха в таблице указана в степени 102. Не забудьте разделить на 100! Температуропроводность воздуха указана в степени 106. Допускается интерполяция значений физических свойств воздуха в приведенных таблицах.
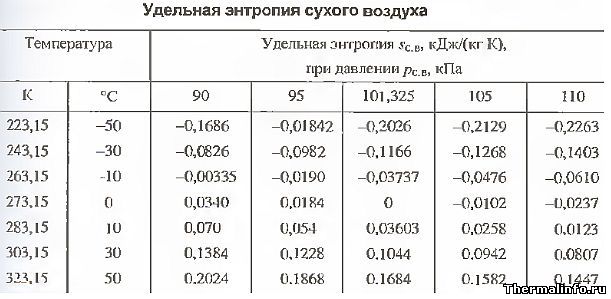
Энтропия сухого воздуха
В таблице представлены значения такого теплофизического свойства воздуха, как удельная энтропия. Значения энтропии даны для сухого воздуха в размерности кДж/(кг·град) в зависимости от температуры и давления. Удельная энтропия указана в таблице в интервале температуры от -50 до 50°С при давлении воздуха от 90 до 110 кПа. Следует отметить, что при нормальном атмосферном давлении (101,325 кПа) и температуре, например 30°С, удельная энтропия воздуха равна 0,1044 кДж/(кг·град).
- Михеев М.А., Михеева И.М. Основы теплопередачи.
- Богданов С.Н., Бурцев С.И., Иванов О.П., Куприянова А.В. Холодильная теника. Кондиционирование воздуха. Свойства веществ: Справ./ Под ред. С.Н. Богданова. 4-е изд., перераб. и доп. — СПб.: СПбГАХПТ, 1999.- 320 с.
4. ОПРЕДЕЛЕНИЕ
КОЭФФИЦИЕНТА ВЯЗКОСТИ ВОЗДУХА
Приборы и
принадлежности:
емкость 1, емкость 2, манометр и капилляр.
Цель работы:
изучение
явления внутреннего трения в газах;
экспериментальное определение
коэффициента вязкости воздуха; определение
средней длины свободного пробега молекул
воздуха.
4.1. Теоретическая
часть
Внутреннее трение
— это свойство жидкостей и газов оказывать
сопротивление перемещению одного слоя
относительно другого, отличающегося
по скорости.
Рассмотрим
ламинарное течение воздуха в капилляре.
Ламинарным
называется
течение, если вдоль потока каждый
выделенный слой скользит относительно
соседних, не перемешиваясь.
Такое течение в
капилляре можно разбить на отдельные
слои, отличающиеся друг от друга
скоростями, направленными вдоль слоев.
У стенок капилляра скорости молекул
близки к нулю, чем ближе к центру, тем
скорость упорядоченного движения больше
(см. рис. 4.2). Кроме упорядоченного движения
молекулы газа участвуют в хаотическом
движении.
Причиной внутреннего
трения в газах является перенос частицами
газа импульсов между соприкасающимися
слоями.
На рис. 4.1 условно
изображены соприкасающиеся слои газа
1 и 2, движущиеся с разными скоростями
υ1
и υ2
в направлении X.
Один слой скользит по другому, причем
υ1
> υ2
. Молекула из нижнего слоя, движущегося
медленно, попадает в верхний слой,
движущийся быстрее, и сталкивается с
молекулами этого слоя. Импульс молекулы
увеличивается за счет молекул верхнего
слоя.
Если частица из
верхнего слоя перейдет в нижний и
передаст ему импульс, совпадающий со
скоростью υ2,
скорость нижнего слоя увеличится. При
этом на верхний слой будет действовать
сила F21,
направленная влево, а на нижний слой —
сила внутреннего трения F12,
совпадающая по направлению со скоростью
υ2.
Cила внутреннего
трения зависит от площади поверхности
слоя и от того, насколько быстро меняется
скорость течения газа при переходе от
слоя к слою.
Градиент скорости
—
величина, которая показывает изменение
скорости на единицу длины. Градиент
скорости направлен перпендикулярно к
слоям в сторону слоя с наибольшей
скоростью.
∆Z
— расстояние между слоями, а ∆υ
= υ1
–
υ2.
Модуль силы
внутреннего трения по закону Ньютона
равен
, (4.1)
где S
— площадь
слоев, η
— коэффициент вязкости.
Коэффициент
вязкости η
равен силе внутреннего трения, действующей
на 1 м2
поверхности слоя при градиенте скорости,
равном 1 с-1.
Единица измерения коэффициента вязкости
— Паскаль·секунда (Па ·с).
Коэффициент
вязкости зависит от природы газа и от
температуры [см. формулы (4.10) и (4.11)].
Коэффициент внутреннего трения не
зависит от давления (плотности) газа.
Объясняется это тем, что при изотермическом
увеличении плотности газа, например, в
два раза, вдвое увеличивается число
переносчиков импульса, но каждая молекула
проходит без столкновения вдвое меньшее
расстояние и переносит вдвое меньший
импульс. Поэтому в целом перенос импульса
не меняется.
4.2. Методика
выполнения работы
Для определения
коэффициента вязкости η
воздуха воспользуемся методом капилляра.
Предположим, что
воздух течет по трубке радиуса R
(рис. 4.2) и длиной L
под действием
разности давлений Р1
— Р2
на ее
основаниях (Р1
>
Р2).
Скорость слоя жидкости, непосредственно
прилегающего к поверхности трубки,
равна нулю. По мере удаления от стенок
к оси капилляра скорость будет возрастать
и, наконец, на оси будет максимальна.
Вырежем мысленно
в газе цилиндр длиной L
и радиусом r.
На этот цилиндр действуют две силы —
сила, обусловленная разностью давлений
F = (Р1
— Р2)
πr2,
(4.2)
направленная вдоль
скорости газа, и сила трения на границе
данного цилиндра с остальной жидкостью,
направленная против скорости:
, (4.3)
где 2π
rL
— площадь
боковой поверхности цилиндра. Знак »
— » указывает, что с ростом r
скорость υ(r)
убывает и dυ/dr
< 0. Таким
образом, при ламинарном течении газа
имеем
.
(4.4)
Преобразуем
выражение (4.4) к виду
.
(4.5)
Возьмем интеграл
от выражения (4.5)
,
(4.6)
где const
определим из условия υ(R)
= 0, что дает
.
Подставив значение
const
в уравнение (4.6), получаем
.
(4.7)
Объем газа,
вытесненный за единицу времени, получаем
следующим образом
.
(4.8)
Это выражение
называется формулой
Пуазейля.
Отсюда мы получаем
расчетную формулу для коэффициента
внутреннего трения
,
(4.9)
где V
— объем перетекаемой жидкости, τ — время
перетекания.
Коэффициент
внутреннего трения η
связан со
средней длиной свободного пробега
молекул λ
соотношением
, (4.10)
где ρ
— плотность газа при данной температуре,
U
— средняя арифметическая скорость
молекул.
Известно, что
,
(4.11)
,
(4.12)
где M
— масса одного моля воздуха, Р
— атмосферное давление воздуха, T
— его абсолютная температура, R
— универсальная газовая постоянная.
Из формул (4.10) —
(4.12) можно определить λ:

(4.13)
4.3. Описание
установки
Основным элементом
установки является капилляр 3. Одним
концом капилляр соединен с емкостью 1,
другим — с атмосферой. Емкость 1 соединена
резиновой трубкой с емкостью 2. Для
проведения опыта емкость 2 должна быть
заполнена водой, ее заполнение производится
включением компрессора и нажатием
нижнего клапана 6. При этом воздух
вытесняет воду из емкости 1 в емкость
2. Уровень воды в стеклянной трубке,
сообщающейся с емкостью 1, в исходном
состоянии должен быть на отметке 170 мм.
При нажатии клапана 2 вода перетекает
из емкости 2 в емкость 1, вытесняя из
последней воздух через капилляр.
Вследствие внутреннего трения на концах
капилляра 1 возникает разность давлений,
которую измеряют манометром 2. Объем
вытесненного воздуха из мерной емкости
1 определяют по формуле V
= Sосн.
· ∆h,
где Sосн.
— площадь основания емкости, ∆h
— разность уровней воды в ней, определяемая
в опыте по стеклянной трубке.
Рис. 4.3. Схема
установки
4.4 Порядок
выполнения работы
-
Включить в сеть
стенд, секундомер. -
Включить компрессор
и нажать нижний клапан. -
Следить за
вытеснением воды из мерной емкости.
После достижения уровня воды отметки
150 мм, выключить компрессор и отпустить
нижний клапан. -
Нажать верхний
клапан и в момент прохождения уровня
воды нижней отметки включить секундомер. -
Через равные
промежутки времени τ
= 10 с
производить измерения разности уровней
воды в манометре. Результаты измерений
записать в табл. 4.1. -
Выписать данные
установки.
Длина капилляра
L
= 70 мм, ∆L
= 1 мм,
Радиус капилляра
r = 0,14 мм, ∆r
= 10-3
мм.
Объем воды в мерной
емкости между двумя метками,
если площадь
основания ее Sосн.
= 0,8·10-2
м2,
V
= S осн.
·h
= м3,
где h
— высота уровня воды в мерной емкости.
Атмосферное
давление Р
= Па , ∆Р
= Па.
Температура воздуха
Т = К , ∆Т
= К.
-
Атмосферное
давление воздуха в лаборатории определить
по барометру, и его температуру по
термометру.
Таблица
4.1
|
Номер опыта |
τ, |
(H1-H2),мм |
(P1-P2),Па |
η, Па ·с |
ηср., |
λ, |
4.5. Обработка
результатов измерений
-
Коэффициент
динамической вязкости рассчитать по
формуле (4.9) для трех опытов. -
Найти среднее
значение ηср. -
Провести расчет
погрешности ηср.
а) оценить абсолютную
погрешность ∆η.
∆η = tδ,n·S(ηср);
где tδ,n
— коэффициент Стьюдента при доверительной
вероятности δ=
0.95 и числе
измерений n
(найти по табл.),

средняя квадратичная погрешность.
б) оценить
относительную погрешность
.
-
Окончательный
результат записать в виде
η=( ηср.±∆η),
Па·с;
=
%.
-
Определить среднюю
длину свободного пробега по формуле
(4.13). -
Провести оценку
погрешности
λ.
а) рассчитать
относительную погрешность по формуле
.
б) вычислить
максимальную абсолютную погрешность
по формуле
.
-
Окончательный
результат записать в виде:
-
Сравнить
экспериментальные результаты с
табличными значениями. -
Сделать выводы.
Контрольные
вопросы
-
Что такое внутреннее
трение? Какое явление изучается в
работе? -
Каков механизм
внутреннего трения? -
От чего зависит
сила внутреннего трения? -
Что такое градиент
скорости? Направление и единица
измерения. -
Что такое коэффициент
вязкости? Единица измерения. -
От чего зависит
коэффициент вязкости. -
Какое течение
газа называется ламинарным? -
Выведите расчетную
формулу коэффициента вязкости. -
Опишите схему
установки. -
Как оценить
результат измерений?
Примечание:
1 мм.вод.столба = 9,8 Па.
Литература:
[1]…..[5]
Соседние файлы в папке Молекулярная
- #
- #
- #
- #
Вязкость воздуха
Коэффициент динамической вязкости воздуха можно определить по формуле Милликена:
$$mu=9.80665cdot(1.745cdot10^{-6}+5.03cdot10^{-9}cdot t)$$
Перевод динамической вязкости $mu$ в кинематическую $nu$ при помощи плотности $rho$:
$$nu=frac{mu}{rho}$$
| $mu$ | коэффициент динамической вязкости (Па/с) |
| $nu$ | коэффициент кинематической вязкости (м²/с) |
| $t$ | температура воздуха (°C) |
| $rho$ | плотность воздуха, (кг/м³) |
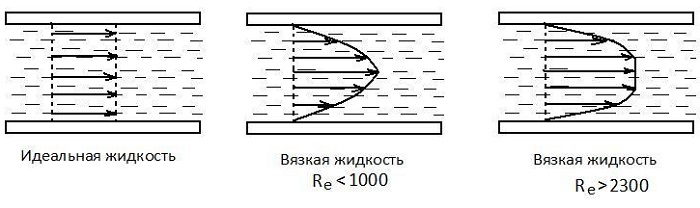
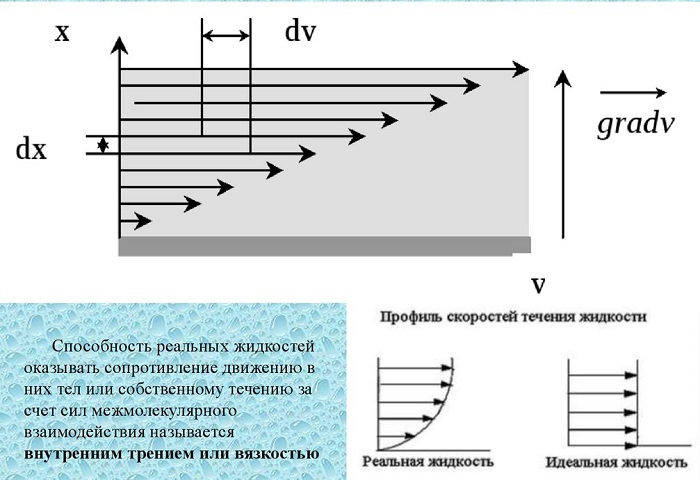
Коэффициент вязкости – это величина, используемая для обозначения силы внутреннего трения текучих веществ. Вязкость – разновидность явлений переноса. Жидкости и газы оказывают сопротивление перемещению двух слоев относительно друг друга. Эта особенность характерна для текучих веществ, связана с движением частиц, из которых и состоят вещества.
Вязкость называют внутренним трением. В его основе находится хаотическое движение молекул, передающих импульс между слоями. Такие импульсные обмены выравнивают скорости перемещения слоев.
Коэффициент динамической вязкости
Численное обозначение абсолютной вязкости является индексом сопротивляемости испытуемых веществ взаимному перемещению или скольжению их слоев.
Единицей измерения коэффициента в системе СИ приняты паскаль-секунды:
Физическая основа динамического показателя заключается в его соответствии касательному напряжению, которое происходит между слоями вещества, перемещающимися относительно друг друга, при условии расстояния между ними, равного единице длины, и на скорости, равной единице.
Вязкость жидкости
Вязкость жидкости определяется формулой, в которой динамический коэффициент определяет пропорциональность скорости движения слоев и расстояния между ними:
-
τ – касательное напряжение;
-
µ — показатель пропорциональности, который является динамическим индексом вещества.
Закон вязкости жидкости был установлен Ньютоном в конце 17 века. Абсолютный показатель зависит от типа газа или жидкости, температуры веществ.
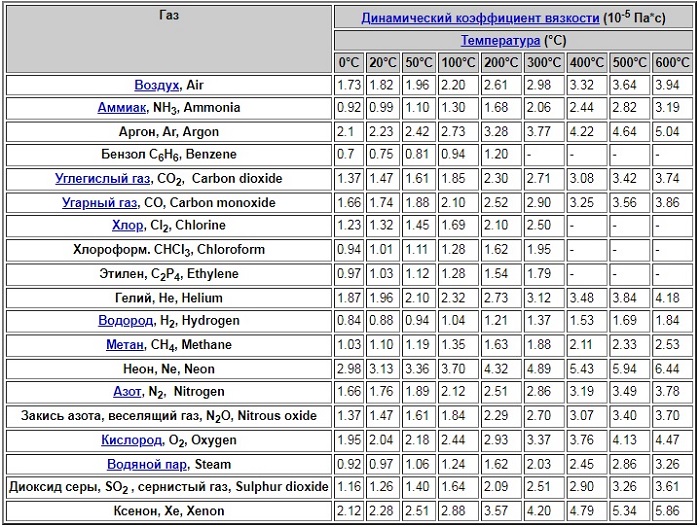
Коэффициент динамической вязкости газа
Для основных газов величины коэффициента при температуре 0 — 600 градусов Цельсия представлены в таблице:
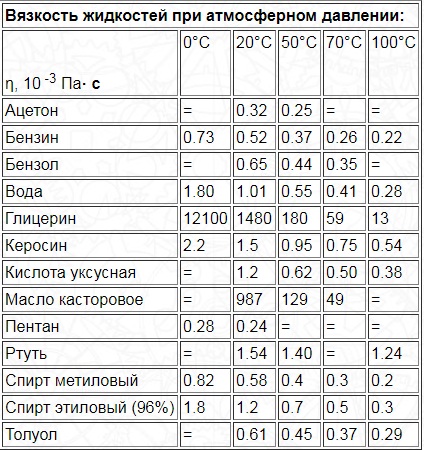
Коэффициент вязкости жидкостей
Для органических жидкостей показания напрямую зависят от температуры. Ниже приведена таблица со значениями абсолютного индекса для веществ при температурах от 0 до 100 градусов Цельсия.
Единица измерения – миллипаскаль-секунды, что соответствует сантипуазам.
Коэффициент динамической вязкости жидкостей уменьшается при условии нагревания вещества. Другими словами, чем выше температура жидкости, тем менее вязкой она становится.
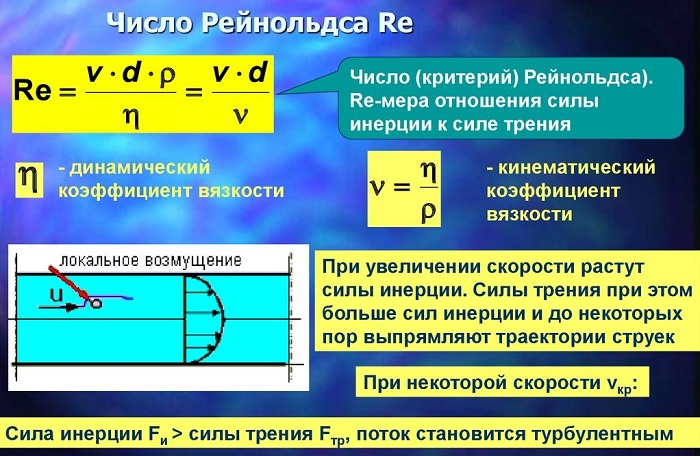
Связь коэффициента вязкости с числами Рейнольдса и силой трения
Английский механик, физик и инженер Оскар Рейнольдс установил (1876 — 1883 гг.), что характер течения зависит от величины, не имеющей размерностью, и называемой числом Re.
Число Рейнольдса используют для отображения соотношения кинематической энергии вещества к энергопотерям на установленной длине в условиях внутреннего трения.
Примеры решения задач
Попробуем решить следующую задачу.
Установить тип движения жидкого вещества по трубам теплообменника, имеющего структуру «труба в трубе». Параметры внутренней трубы – 25*2 мм, внешней – 50*2,5 мм. Массовый расход воды составляет 4000 кг/ч (обозначение G). Плотность жидкости – 1000 кг/м3. Абсолютный индекс составляет 1•10-3 Па*с.
Действие 1.
Следует узнать эквивалентный диаметр сечения межтрубного пространства:
Действие 2.
Определение скорости воды на основе уравнения расхода:
Действие 3.
По формуле Рейнольдса найти число Re:
Подставляя значения, получаем:
Ответ: режим перемещения воды в межтрубном пространстве является турбулентным.
Коэффициент кинематической вязкости
Кинематическая вязкость – это индекс, который отображает отношение абсолютного показателя вещества к его плотности при установленной температуре.
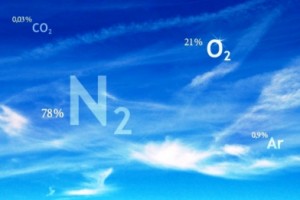
Физическая формула соотношения выглядит и единицы измерения можно увидеть на картинке:
Действие 4. Вычисление кинематического показателя, исходя из формулы:
Подставив в уравнение полученные и имеющиеся расчетные данные, получим кинематический индекс вещества.
Заключение
Физический смысл коэффициента вязкости заключается в том, что он демонстрирует, чему равна величина F внутреннего трения, действующая на 1 ед. площади поверхности соприкасающихся слоев при единичном градиенте скорости.
Размерность данной величины и перевод из одних единиц измерения в другие показаны на картинке: