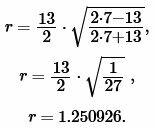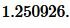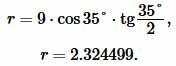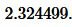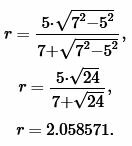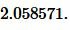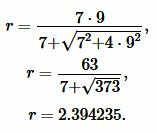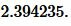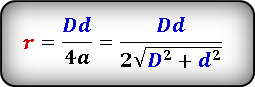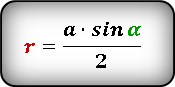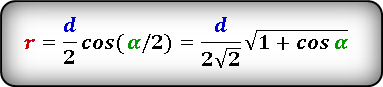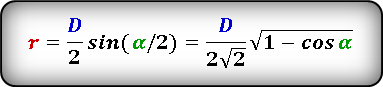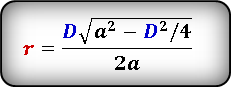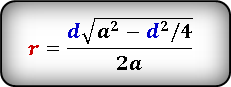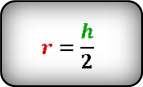Как найти диаметр вписанной окружности равнобедренного треугольника

Все формулы для радиуса вписанной окружности

Радиус вписанной окружности в треугольник

a , b , c — стороны треугольника

p — полупериметр, p=( a + b + c )/2

Формула радиуса вписанной окружности в треугольник ( r ):

Радиус вписанной окружности в равносторонний треугольник

a — сторона треугольника

r — радиус вписанной окружности

Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):

Радиус вписанной окружности равнобедренный треугольник

1. Формулы радиуса вписанной окружности если известны: стороны и угол

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

α — угол при основании

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :

2. Формулы радиуса вписанной окружности если известны: сторона и высота

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :

Радиус вписанной окружности в треугольник

Радиус вписанной в треугольник окружности
рассчитать и выразить через периметр, площадь,
высоту, основание, стороны, диаметр. Формулы
радиуса окружности вписанной в треугольник.

Центр вписанной в треугольник окружности — это одна
из замечательных точек треугольника, она расположена
в точке пересечения биссектрис треугольника, её
иногда называют инцентром.

Центр вписанной окружности правильного треугольника — это
точка, где пересекаются высоты, медианы и биссектрисы.

В любой треугольник можно вписать только одну
окружность, которая находится внутри треугольника.
Центр вписанной окружности равноудален от всех
сторон треугольника. Точка, где окружность пересекается
со стороной треугольника, называется точкой касания.

Все отрезки, которые проведены от точки касания к центру
вписанной окружности имеют одинаковую длину.

Чтобы найти радиус окружности вписанной в треугольник
надо площадь разделить на полупериметр.

Диаметр вписанной окружности в треугольник численно
равен двум радиусам вписанной окружности. Радиус
вписанной окружности можно найти по разным
формулам, все зависит от того, какой треугольник.

Всего различают четыре вида треугольников:

Разносторонний / любой
Правильный / равносторонний
Равнобедренный / равнобочный
Прямоугольный / прямой

Радиус вписанной окружности в любой треугольник

Радиус вписанной окружности в любой треугольник через площадь и полупериметр

S — площадь; p — полупериметр;
Радиус вписанной окружности в любой треугольник через все стороны и полупериметр

a, b, c — стороны; p — полупериметр;
Радиус вписанной окружности в любой треугольник через основание, высоту и полупериметр

a — основание, сторона на которую падает высота; h — высота; p — полупериметр;
Радиус вписанной окружности в любой треугольник через диаметр вписанной окружности

D — диаметр вписанной окружности;

Радиус вписанной окружности в правильный треугольник

Радиус вписанной окружности в правильный треугольник через сторону

a — сторона;
Радиус вписанной окружности в правильный треугольник через радиус описанной окружности

R — радиус описанной окружности;
Радиус вписанной окружности в правильный треугольник через диаметр вписанной окружности

D — диаметр вписанной окружности;

Радиус вписанной окружности в равнобедренный треугольник

Радиус вписанной окружности в равнобедренный треугольник через боковые стороны и основание

a — боковая сторона; b — основание;
Радиус вписанной окружности в равнобедренный треугольник через высоту и основание

b — основание; h — высота;
Радиус вписанной окружности в равнобедренный треугольник через диаметр вписанной окружности

D — диаметр вписанной окружности;

Радиус вписанной окружности в прямоугольный треугольник

Радиус вписанной окружности в прямоугольный треугольник через два катета и гипотенузу

a, b — катеты; с — гипотенуза.
Радиус вписанной окружности в прямоугольный треугольник через гипотенузу и два катета

c — гипотенуза; a, b — катеты;
Радиус вписанной окружности в прямоугольный треугольник через диаметр вписанной окружности

D — диаметр вписанной окружности;

Вписанная окружность в треугольник — это окружность,
которая вписана в треугольник и касается всех его сторон.

Радиус вписанной окружности в треугольник — это отрезок,
проведенный от центра вписанной окружности до любой стороны.

Длина радиуса вписанной окружности, диаметра
вписанной окружности а также других величин
измеряется в мм, см, м, км и так далее.

В любом треугольнике все радиусы и диаметры
равны, имеют одинаковую длину.

Радиус вписанной окружности в равнобедренный треугольник онлайн

С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности, в том числе радиус вписанной в равнобедренный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Открыть онлайн калькулятор

1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона

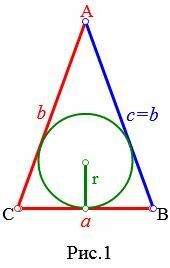
Пусть известны известны основание a и боковая сторона b равнобедренного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной окружности через основание и боковую сторону.

Радиус вписанной в треугольник окружности через три стороны a, b, c вычисляется из следующей формулы:

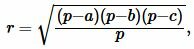(1)

где полупериметр p вычисляется из формулы:

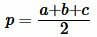(2)

Учитывая, что у равнобедренного треугольника боковые стороны равны (( small b=c )), имеем:

( small p=frac ) ( small =frac , )

(3)

( small p-a=frac -a ) ( small =frac , )

(4)

( small p-b=p-c=frac -b ) ( small =frac . )

(5)

Подставляя (3)-(5) в (1), получим формулу вычисления радиуса вписанной в равнобедренный треугольник окружности:

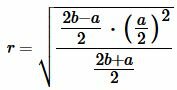
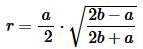(6)

Пример 1. Известны основание a=13 и боковая сторона b=7 равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значения ( small a,; b ) в (6):

Ответ:

2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании

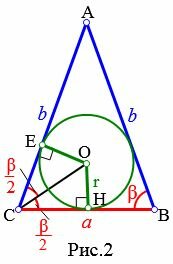
Пусть известны основание a и прилежащий к ней угол β равнобедренного треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.

Из центра вписанной окружности проведем перпендикуляры OH и OE к сторонам a=BC и b=AC, соответственно (r=OH=OE). Соединим точки C и O. Полученные прямоугольные треугольники OCE и OCH равны по гипотенузе и катету (см. статью Прямоугольный треугольник. Тогда ( small angle OCE=angle OCH=frac . ) Для прямоугольного треугольника OCH можно записать:

( small frac =frac >=mathrm frac .)

Откуда получим формулу радиуса вписанной в треугольник окружности:

( small r=frac cdot mathrm frac .)

(8)

( small r=frac cdot frac .)

(9)

Пример 2. Известны основание ( small a=15 ) и ( small beta=30° ) равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанный в треугольник воспользуемся формулой (8) (или (9)). Подставим значения ( small a=15, ; beta=30° ) в (8):

Ответ:

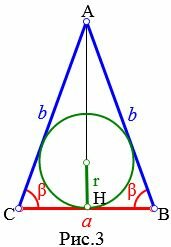
3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании

Пусть известны боковая сторона b и угол при основании β равнобедренного треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.

Высота равнобедренного треугольника AH делит равнобедренный треугольник ABC на две равные части. Тогда для треугольника AHC справедливо равенство:

( small frac =frac > = cos beta .)

( small a=2b cdot cos beta .)

(10)

Подставляя (10) в (8), получим формулу вписанной в равнобедренный треугольник окружности:

( small r=frac cdot mathrm frac =frac cdot mathrm frac ) ( small =b cos beta cdot mathrm frac )

( small r=b cdot cos beta cdot mathrm frac )

(11)

Учитывая формулы половинного угла тригонометрических функций, формулу (11) можно записать и так:

( small r=b cdot frac )

(12)

Пример 3. Известны боковая сторона равнобедренного треугольника: ( small b=9 ) и угол при основании β=35°. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11) (или (12)).

Подставим значения ( small b=9 ,; beta=35° ) в (11):

Ответ:

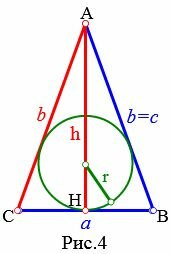
4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота

Пусть известны боковая сторона b и высота h равнобедренного треугольника (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.

Формула радиуса вписанной окружности через площадь и полупериметр имеет следующий вид (см. статью на странице Радиус вписанной в треугольник окружности онлайн) :

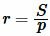(13)

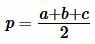(14)

Так как треугольник AHC прямоугольный, то из Теоремы Пифагора имеем:

( small left( frac right)^2=b^2-h^2 )

( small a=2 cdot sqrt )

(15)

Площадь равнобедренного треугольника по основанию и высоте вычисляется из формулы:

( small S=frac cdot a cdot h. )

(16)

Подставим (15) в (16):

( small S=h cdot sqrt )

(17)

Учитывая, что для равнобедренного треугольника b=c, а также равенство (15), получим:

( small p=frac ) ( small =frac ) ( small =frac +b )( small =b+ sqrt )

(18)

Подставляя, наконец, (17) и (18) в (13), получим формулу радиуса вписанной в равнобедренный треугольник окружности:

( small r=frac ) ( small =frac > > )

(19)

Пример 4. Боковая сторона и высота равнобедренного треугольника равны ( small b=7 ,) ( small h=5, ) соответственно. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (19). Подставим значения ( small b=7 ,) ( small h=5 ) в (19):

Ответ:

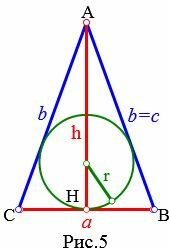
5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота

Пусть известны основание a и высота h равнобедренного треугольника (Рис.5). Найдем формулу радиуса вписанной в равнобедренный треугольник окружности.

Из формулы (15) найдем b:

( small b^2-h^2=left( frac right)^2 )

( small b^2= frac +h^2 )

( small b= frac cdot sqrt )

(20)

Подставляя (20) в (19), получим формулу радиуса вписанной окружности в равнобедренный треугольник:

( small r=frac > >) ( small =frac +h^2-h^2>> cdot sqrt + sqrt +h^2-h^2>>) ( small = large frac > cdot sqrt +frac >)

( small r=large frac >)

(21)

Пример 5. Основание и высота равнобедренного треугольника равны ( small a=7 ,) ( small h=9, ) соответственно. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (21). Подставим значения ( small a=7 ,) ( small h=9 ) в (21):

Ответ:

Все формулы для радиуса вписанной окружности

Радиус вписанной окружности в треугольник

a , b , c — стороны треугольника

p — полупериметр, p=( a + b + c )/2

Формула радиуса вписанной окружности в треугольник ( r ):

Радиус вписанной окружности в равносторонний треугольник

a — сторона треугольника

r — радиус вписанной окружности

Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):

Радиус вписанной окружности равнобедренный треугольник

1. Формулы радиуса вписанной окружности если известны: стороны и угол

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

α — угол при основании

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :

2. Формулы радиуса вписанной окружности если известны: сторона и высота

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :

Радиус вписанной окружности в треугольник

Центр вписанной в треугольник окружности — это одна
из замечательных точек треугольника, она расположена
в точке пересечения биссектрис треугольника, её
иногда называют инцентром.

Все отрезки, которые проведены от точки касания к центру
вписанной окружности имеют одинаковую длину.

Чтобы найти радиус окружности вписанной в треугольник
надо площадь разделить на полупериметр.

Всего различают четыре вида треугольников:

Разносторонний / любой
Правильный / равносторонний
Равнобедренный / равнобочный
Прямоугольный / прямой

Радиус вписанной окружности в любой треугольник

Радиус вписанной окружности в любой треугольник через площадь и полупериметр

D — диаметр вписанной окружности;

Радиус вписанной окружности в правильный треугольник

Радиус вписанной окружности в правильный треугольник через сторону

a — сторона;
Радиус вписанной окружности в правильный треугольник через радиус описанной окружности

D — диаметр вписанной окружности;

Радиус вписанной окружности в равнобедренный треугольник

Радиус вписанной окружности в равнобедренный треугольник через боковые стороны и основание

D — диаметр вписанной окружности;

Радиус вписанной окружности в прямоугольный треугольник

Радиус вписанной окружности в прямоугольный треугольник через два катета и гипотенузу

D — диаметр вписанной окружности;

Вписанная окружность в треугольник — это окружность,
которая вписана в треугольник и касается всех его сторон.

В любом треугольнике все радиусы и диаметры
равны, имеют одинаковую длину.

источники:

http://colibrus.ru/radius-vpisannoy-okruzhnosti-v-treugolnik/

http://b4.cooksy.ru/articles/kak-nayti-diametr-vpisannoy-okruzhnosti-ravnobedrennogo-treugolnika

Источник

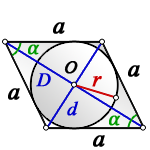
1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

a — сторона ромба

D — большая диагональ

d — меньшая диагональ

α — острый угол

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в ромб через диагонали ( r ) :

Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :

Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :

Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :

2. Радиус вписанной окружности ромба, равен половине его высоты

a — сторона ромба

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в ромб ( r ) :

Источник

Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов

Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.

Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.

Вокруг любого треугольника можно описать окружность, причем только одну.

Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.

В любой треугольник можно вписать окружность, причем только одну.

Рассмотрим важные теоремы, которые помогут нам при решении задач.

Теорема 1. Вокруг любого треугольника можно описать окружность, причем только одну. Ее центр – это точка пересечения серединных перпендикуляров к сторонам треугольника.

Иногда говорят, что окружность описана около треугольника. Это означает то же самое – все вершины треугольника лежат на окружности.

Доказательство этой теоремы здесь: Свойство серединных перпендикуляров.

Теорема 2. В любой треугольник можно вписать окружность, причем только одну. Ее центром является точка пересечения биссектрис треугольника.

Доказательство теоремы здесь: Свойства биссектрис треугольника.

Теорема 3. Центр окружности, описанной вокруг прямоугольного треугольника, лежит на середине гипотенузы, а радиус этой окружности равен половине гипотенузы.

Доказательство:

Медиана, проведенная к гипотенузе, равна ее половине, по свойству медианы прямоугольного треугольника.
Его доказательство можно найти здесь: Свойство медианы прямоугольного треугольника.

Поэтому середина гипотенузы – это точка, равноудаленная от вершины прямого угла и от концов гипотенузы, то есть от всех вершин прямоугольного треугольника.

Теорема 4.

Центр окружности, описанной вокруг остроугольного треугольника, лежит внутри этого треугольника.

Центр окружности, описанной вокруг прямоугольного треугольника, лежит на середине гипотенузы.

Центр окружности, описанной вокруг тупоугольного треугольника, лежит вне этого треугольника.

Теорема 5. Радиус окружности , вписанной в прямоугольный треугольник с катетами и и гипотенузой , вычисляется по формуле: $displaystyle r=frac{a+b-c}{2}.$

Доказательство теоремы здесь: Радиус окружности, вписанной в прямоугольный треугольник.

В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.

Напомним определение правильного многоугольника:

Правильным называется многоугольник, все стороны и все углы которого равны. Центры вписанной и описанной окружностей правильного многоугольника находятся в одной точке.

Из этого определения, понятно, что правильный треугольник – равносторонний. Для решения такого треугольника полезно уметь выводить формулы радиусов вписанной и описанной окружностей.

Теорема 6.

Для правильного треугольника со стороной а радиус описанной окружности равен $displaystyle R=frac{asqrt{3}}{3}.$

А радиус окружности, вписанной в правильный треугольник, равен $displaystyle r=frac{asqrt{3}}{6}.$

Докажем эту теорему.

У равностороннего треугольника медианы, биссектрисы, высоты и серединные перпендикуляры совпадают, и точка их пересечения является центром как вписанной, так и описанной окружностей.

Пусть в правильном треугольнике ABC стороны , точка О – центр вписанной и описанной окружностей, — медианы и высоты. По свойству медиан треугольника, отрезки в точке О делятся в отношении 2 : 1, считая от вершин. Тогда

Получаем, что $displaystyle R=OB=frac{2}{3}BH, r=OH=frac{1}{3}BH.$

Из треугольника АВН получаем, что длина стороны $displaystyle BH=frac{asqrt{3}}{2}.$

Тогда $displaystyle R=frac{2}{3}cdot frac{asqrt{3}}{2}=frac{asqrt{3}}{3}, r=frac{1}{3}cdot frac{asqrt{3}}{2}=afrac{sqrt{3}}{6}.$

Значит, формула радиуса окружности, описанной около правильного треугольника — $displaystyle r=frac{asqrt{3}}{3}.$

Формула радиуса окружности, вписанной в правильный треугольник $displaystyle r=frac{asqrt{3}}{6}.$

Как видим, часто геометрическая задача решается с помощью несложных формул, и помогает в этом алгебра.

Разберем задачи ОГЭ и ЕГЭ по теме: Вписанные и описанные треугольники.

Задача 1, тренировочная. Периметр правильного треугольника АВС равен 15. Найдите радиус вписанной и описанной окружностей.

Решение:

Длина стороны равностороннего треугольника ABC равна

Радиусы – вписанной и – описанной окружностей можно найти по формулам:

$displaystyle r=frac{asqrt{3}}{6}, R=frac{asqrt{3}}{3},$ где — сторона треугольника.

Значит, $displaystyle r=frac{5sqrt{3}}{6}, R=frac{5sqrt{3}}{3}.$

Ответ: $displaystyle r=frac{5sqrt{3}}{6}, R=frac{5sqrt{3}}{3}.$

Решая задачи по теме «Вписанные и описанные треугольники», мы часто пользуемся формулами площади треугольника, а также теоремой синусов.

Вот две полезные формулы для площади треугольника.

Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.

где $p=genfrac{}{}{}{0}{displaystyle 1}{displaystyle 2} left( a+b+c right)$ — полупериметр,

— радиус окружности, вписанной в треугольник.

Есть и еще одна формула, применяемая в основном в задачах части :

$S=genfrac{}{}{}{0}{abc}{4R},$

где a, b, c — стороны треугольника, — радиус описанной окружности.

Для любого треугольника верна теорема синусов:

Теорема синусов:

$displaystylefrac{a}{sinangle A}=frac{b}{sinangle B}=frac{c}{sinangle C}=2R,$

R — радиус описанной окружности

Задача 2, ЕГЭ. Найдите диаметр окружности, вписанной в треугольник со сторонами 13, 14 и 15.

Решение:

Выразим площадь треугольника двумя разными способами:

где $displaystyle p=frac{a+b+c}{2}$ – полупериметр треугольника, a a, b, c – его стороны.

$displaystyle p=frac{13+14+15}{2}=21,$

Тогда $displaystyle r=frac{S}{p}=frac{84}{21}=4$ , а диаметр окружности равен

Ответ: 8.

Задача 3, ЕГЭ. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .

Решение:

Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .

Запишем площадь треугольника АВС двумя способами:

$S=genfrac{}{}{}{0}{displaystyle 1}{displaystyle 2} a^2.$

$S=genfrac{}{}{}{0}{displaystyle 1}{displaystyle 2}left( 2a + asqrt{2}right)r.$

Приравняв эти выражения, получим, что . Поскольку r=2 , получаем, что .

Тогда .

В ответ запишем .

Ответ: 4.

Задача 4, ЕГЭ. В треугольнике ABC сторона равна , а угол равен $120^{circ}$ . Найдите радиус описанной около этого треугольника окружности.

Решение:

По теореме синусов $displaystyle frac{AC}{sin B}=2R.$

Тогда $displaystyle R=frac{7sqrt{3}}{2}:frac{sqrt{3}}{2}=7.$

Ответ: 7.

Задача 5, ЕГЭ. В треугольнике ABC угол А равен $57^{circ}$ , а угол В – $93^{circ}$ . Найдите радиус окружности, описанной около треугольника ABC , если сторона равна 10.

Решение:

Зная, что сумма углов треугольника равна $180^{circ}$ , найдем угол С.

$displaystyle angle C = 180^{circ }-(angle A+angle B)=180^{circ }-(53^{circ }+97^{circ })=30^{circ }.$

По теореме синусов $displaystyle frac{AB}{sinC}=frac{BC}{sinA}=frac{AC}{sinB}=2R.$

Значит, $displaystyle R=frac{AB}{2sinC}=10.$

Ответ: 10.

Задача 6, ЕГЭ. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.

По теореме синусов,

$genfrac{}{}{}{0}{AC}{sin B}=2R.$

Получаем, что $sin B=genfrac{}{}{}{0}{displaystyle 1}{displaystyle 2}$ . Угол — тупой. Значит, он равен $150^{circ}$ .

Ответ: 150.

Задача 7, ЕГЭ. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.

Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.

$S=genfrac{}{}{}{0}{abc}{4R}.$

$S=genfrac{}{}{}{0}{displaystyle 1}{displaystyle 2} ah$ , где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем h=32 .

Тогда R=25 .

Ответ: 25.

Задача 8, ОГЭ. В равнобедренном треугольнике ABC основание равно 10 см, а высота, проведенная к основанию, 12 см. Найдите периметр треугольника и радиус вписанной окружности.

Решение:

Высота , проведенная к основанию , является медианой. Значит, .

находится по теореме Пифагора из треугольника ABH :

$displaystyle AB=sqrt{AH^{2}+BH^{2}}=sqrt{5^{2}+12^{2}}=13.$

Периметр треугольника ABC – это сумма длин сторон, т.е.

Площадь треугольника $displaystyle S=frac{1}{2}ACcdot BH=frac{1}{2}cdot 10cdot 12=60.$

Радиус вписанной окружности r найдем по формуле

$displaystyle r=frac{S}{p}=frac{60}{18}=frac{10}{3}.$

Ответ: $displaystyle 30; frac{10}{3}.$

Задача 9, ОГЭ. Стороны и треугольника ABC равны 6 и соответственно, угол $B- 45^{circ }$ . Найдите диаметр окружности, описанной около треугольника ABC .

Решение:

Найдем длину стороны по теореме косинусов, используя длины сторон , и косинус угла В, противолежащего стороне :

$displaystyle AC^{2}=AB^{2}+BC^{2}-2cdot ABcdot BCcdot cosB=6^{2}+(3sqrt{2})^{2}-2cdot 6cdot 3sqrt{2}cdot frac{sqrt{2}}{2}=18,AC=3sqrt{2}.$

Теперь воспользуемся теоремой синусов:

$displaystyle frac{AC}{sin45^{circ }}=2R,$

$displaystyle 2R=3sqrt{2}:frac{sqrt{2}}{2}=6.$

Значит, диаметр окружности, описанной около треугольника ABC , равен 6.

Ответ: 6.

Задача 10. Найдите площадь прямоугольного треугольника, если радиус описанной окружности равен 5, а вписанной 1.

Решение:

Пусть длина радиуса описанной окружности R = 5 , а длина радиуса вписанной окружности r = 1.

Мы знаем, что $displaystyle r=frac{a+b-c}{2}, R=frac{c}{2}, S=pcdot r$ , где $displaystyle p=frac{a+b+c}{2}$ – полупериметр, a, b, c – стороны треугольника.

Значит, $displaystyle r=frac{a+b-c}{2}=frac{a+b+c-2c}{2}=frac{a+b+c}{2}-frac{2c}{2}=$

Отсюда

Тогда

Ответ: 11.

Задача 11. Найдите площадь прямоугольного треугольника, если радиус вписанной окружности равен 2, а гипотенуза 10.

Решение:

Пусть радиус вписанной окружности r = 2 , а гипотенуза c = 10.

Мы знаем, что в прямоугольном треугольнике $displaystyle r=frac{a+b-c}{2}.$

Значит, $displaystyle r=frac{a+b-c}{2}=frac{a+b+c-2c}{2}=frac{a+b+c}{2}-frac{2c}{2}=p-c,$ отсюда p =r+c.

Площадь находится по формуле S =pr, где $displaystyle p=frac{a+b+c}{2}$ – полупериметр, a, b, c – стороны треугольника.

Ответ: 24.

Рассмотрим также задачу из 2 части ЕГЭ по математике.

Задача 12. Точка О – центр вписанной в треугольник ABC окружности. Прямая вторично пересекает описанную около треугольника ABC окружность в точке Р.

а) Докажите, что

б) Найдите площадь треугольника APO , если радиус окружности, описанной около треугольника ABC равен 10, $displaystyle angle BAC=75^{circ }, angle ABC=60^{circ }.$

Решение:

а) Пусть О – центр вписанной окружности, значит, и – биссектрисы углов ABC и BAC соответственно, и

как вписанные углы, опирающиеся на одну и ту же дугу PC.
Тогда

– внешний угол треугольника AOB , поэтому он равен сумме двух внутренних углов, не смежных с ним, т.е.

Значит, Что и требовалось доказать.

б) , следовательно, треугольник POA – равнобедренный, – основание,

Угол ABC равен $60^{circ }$ , значит, $displaystyle angle ABO=angle OBC=30^{circ }.$

По теореме синусов для треугольника ABP :

$displaystyle frac{AP}{sinB}=2R, AP=2cdot 10cdot sin30^{circ }=10.$

Тогда отрезок равен отрезку , т.е. OP = 10 .

Найдем угол С из треугольника ABC : $displaystyle angle C= 180^{circ }-60^{circ }-75^{circ }=45^{circ }.$

$displaystyle angle APO=angle ACB=45^{circ }$ как вписанные углы, опирающиеся на дугу .

Площадь треугольника AOP находится по формуле: $displaystyle S=frac{1}{2}abcdot sinalpha.$

$displaystyle S_{APO}=frac{1}{2}cdot APcdot POcdot sinAPO=frac{1}{2}cdot 10cdot 10cdot sin45^{circ }=frac{1}{2}cdot 10cdot 10cdot frac{sqrt{2}}{2}=$

Ответ:

Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .

Если вам понравился наш материал — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Центр вписанной в треугольник окружности — это одна
из замечательных точек треугольника, она расположена
в точке пересечения биссектрис треугольника, её
иногда называют инцентром.

Центр вписанной окружности правильного треугольника — это
точка, где пересекаются высоты, медианы и биссектрисы.

Все отрезки, которые проведены от точки касания к центру
вписанной окружности имеют одинаковую длину.

Чтобы найти радиус окружности вписанной в треугольник
надо площадь разделить на полупериметр.

Всего различают четыре вида треугольников:

Разносторонний / любой
Правильный / равносторонний
Равнобедренный / равнобочный
Прямоугольный / прямой

Содержание

Радиус вписанной окружности в любой треугольник
Радиус вписанной окружности в правильный треугольник
Радиус вписанной окружности в равнобедренный треугольник
Радиус вписанной окружности в прямоугольный треугольник

Радиус вписанной окружности в любой треугольник

Радиус вписанной окружности в любой треугольник через площадь и полупериметр
[ r = frac{S}{p} ]

S — площадь; p — полупериметр;
Радиус вписанной окружности в любой треугольник через все стороны и полупериметр
[ r = sqrtfrac{{(p-a)(p-b)(p-c)}}{p} ]

a, b, c — стороны; p — полупериметр;
Радиус вписанной окружности в любой треугольник через основание, высоту и полупериметр
[ r = frac{frac{1}{2}a cdot h}{p} ]

a — основание, сторона на которую падает высота; h — высота; p — полупериметр;
Радиус вписанной окружности в любой треугольник через диаметр вписанной окружности
[ r = frac{D}{2} ]

D — диаметр вписанной окружности;

Радиус вписанной окружности в правильный треугольник

Радиус вписанной окружности в правильный треугольник через сторону
[ r = frac{a}{2sqrt 3} ]

a — сторона;
Радиус вписанной окружности в правильный треугольник через радиус описанной окружности
[ r = frac{R}{2} ]

R — радиус описанной окружности;
Радиус вписанной окружности в правильный треугольник через диаметр вписанной окружности
[ r = frac{D}{2} ]

D — диаметр вписанной окружности;

Радиус вписанной окружности в равнобедренный треугольник

Радиус вписанной окружности в равнобедренный треугольник через боковые стороны и основание
[ r = frac{b}{2} cdot sqrt{frac{2a-b}{2a+b}} ]

a — боковая сторона; b — основание;
Радиус вписанной окружности в равнобедренный треугольник через высоту и основание
[ r = frac{bh}{b + sqrt{4h^2+b^2}} ]

b — основание; h — высота;
Радиус вписанной окружности в равнобедренный треугольник через диаметр вписанной окружности
[ r = frac{D}{2} ]

D — диаметр вписанной окружности;

Радиус вписанной окружности в прямоугольный треугольник

Радиус вписанной окружности в прямоугольный треугольник через два катета и гипотенузу
[ r = frac{a+b-c}{2} ]

a, b — катеты; с — гипотенуза.
Радиус вписанной окружности в прямоугольный треугольник через гипотенузу и два катета
[ r = frac{ab}{a+b+c} ]

c — гипотенуза; a, b — катеты;
Радиус вписанной окружности в прямоугольный треугольник через диаметр вписанной окружности
[ r = frac{D}{2} ]

D — диаметр вписанной окружности;

Вписанная окружность в треугольник — это окружность,
которая вписана в треугольник и касается всех его сторон.

Радиус вписанной окружности в треугольник — это отрезок,
проведенный от центра вписанной окружности до любой стороны.

В любом треугольнике все радиусы и диаметры
равны, имеют одинаковую длину.

Источник

ВИДЕОУРОК

Описанная окружность
равнобедренного треугольника.

Для того, чтобы найти
радиус описанной окружности равнобедренного треугольника можно воспользоваться
следующей формулой:

ЗАДАЧА:

Основание равнобедренного тупоугольного треугольника
равно 18
см, а радиус описанной вокруг него окружности – 15
см. Найдите боковую сторону треугольника.

РЕШЕНИЕ:

В четырёхугольнике
АОВС

АО = ВО = СО = 15 см

как радиусы описанной окружности.

В равнобедренном треугольнике АВС

АС = ВС,

основание

АВ = 18 см.

Высота СD лежит на
серединном перпендикуляре основания АВ, поэтому

АD = ВD = 0,5АВ
= 0,5 × 18 = 9 см.

В треугольнике ОВD согласно теореме Пифагора:

СD = СО – DО =
= 15 – 12 = 3 (см).

В треугольнике СDВ согласно теореме Пифагора:

ОТВЕТ: 3√͞͞͞͞͞10
см

ЗАДАЧА:

Высота равнобедренного тупоугольного треугольника,
опущенная на его основание, равна 8 см, а радиус описанной вокруг неё окружности – 13 см. Найдите боковую сторону треугольника.

РЕШЕНИЕ:

Начертим чертёж.

ОА = ОВ = ОС = R = 13 см.

ОН = 13 – 8 = 5
(см).

Вписанная окружность
равнобедренного треугольника.

Для того, чтобы найти
радиус вписанной окружности равнобедренного треугольника можно воспользоваться
следующей формулой:

Радиус вписанной в равнобедренный треугольник
окружности, выраженный через боковую сторону и высоту, опущенную на основание, выражается
следующей формулой:

ЗАДАЧА:

Высота равнобедренного треугольника равна 18
см, а радиус вписанной в него окружности – 8 см. Найдите периметр данного треугольника.

РЕШЕНИЕ:

В треугольнику АВС

АВ = ВС,

отрезок ВD – высота,

ВD =
18 см, точка О – центр вписанной окружности.

Так как ∆ АВС – равнобедренный, то точка О принадлежит его высоте и биссектрисе ВD,
а отрезок ОD – радиус вписанной окружности,

ОD = 8 см. Тогда

ВО = ВD – ОD = 10 см.

Центром окружности, вписанной
в треугольник, будет точка пересечения биссектрис треугольника. Тогда отрезок АО – биссектриса
треугольника АDВ. Воспользуемся свойством биссектрисы треугольника

Пусть АВ = 5х
см, х
˃ 0,

тогда АD
=
4х см.

Из ∆ АDВ (∠ АDВ = 90°):

АВ² – АD² = ВD²_,

25х² – 16х² = 18²,

9х² = 324, х = 6.

Поэтому,

АВ = 30 см,
АD = 24 см,

АС = 2АD = 48 см.

Тогда

Р = 2АВ + АС = 108 см.

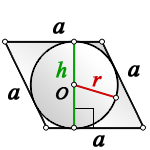
Радиус вписанной и описанной
окружности для равностороннего треугольника выражается следующими формулами:

У равностороннего треугольника центры вписанной
и описанной окружности, центр тяжести и ортоцентр совпадают, а сумма
радиусов описанной и вписанной окружности равна высоте.

ЗАДАЧА:

Найдите радиус окружности, вписанной в правильный
треугольник со стороною 12 см ?

РЕШЕНИЕ:

Так как треугольник
АВС –
равносторонний, в котором ВD является биссектрисой, высотой и медианой, то
угол DВС будет равен 30°.

Треугольник ВDС –
прямоугольный в котором против угла в 30° находится катет,
равный половине гипотенузы. Значит DС = 6 см.

По теореме Пифагора находим ВD.

Тогда

r = ¹/₃ВD = ¹/₃∙ 6√͞͞͞͞͞3 = 2√͞͞͞͞͞3 (см).

ЗАДАЧА:

Определить отношение радиуса вписанной в равносторонний
треугольник окружности к радиусу описанной окружности.

РЕШЕНИЕ:

В равностороннем АВС его три медианы,
биссектрисы и высоты совпадают и пересекаются в одной точке – центре
треугольника. Радиусом описанной окружности будет отрезок, соединяющий
центр О с одной из вершин треугольника.

А вписанной – апофема
ОD.
Но так как АО ещё и биссектриса,
то

∠ ОАD = 30°,

а ∆ АOD – прямоугольный, следовательно,

ЗАДАЧА:

Окружность касается одного из катетов равнобедренного
прямоугольного треугольника и проходит через вершину противоположного острого угла.
Найдите радиус окружности, если её центр находится на гипотенузе треугольника,
а катет треугольника равен 10 см.

РЕШЕНИЕ:

Пусть АВС – заданный прямоугольный треугольник (∠ А
= 90°),

АВ = АС = 10 см.

О ∈ ВС –
центр окружности, которая проходит через
точку С.

Е
– точка касания
окружности
до катета АВ.

В
треугольнику АВС

∠ В = ∠ С = 45°
і

АВ = АС = 10 (см).

Пусть ОС = ОЕ = х (см).

Из
треугольника

ОЕВ (∠ Е = 90°, ∠ В = 45°)

ОВ = √͞͞͞͞͞2 ∙ ОЕ = √͞͞͞͞͞2
х
(см).

Так как
ВС = ОВ + ОС,

то имеем:

10√͞͞͞͞͞2 = √͞͞͞͞͞2 х + х,

откуда

ОТВЕТ: 10(2 – √͞͞͞͞͞2) см

Задания к уроку 16

Задание 1
Задание 2
Задание 3

Другие уроки:

Урок 1. Точка и прямая
Урок 2. Угол
Урок 3. Параллельные и перпендикулярные прямые
Урок 4. Окружность
Урок 5. Угол и окружность
Урок 6. Треугольник (1)
Урок 7. Треугольник (2)
Урок 8. Прямоугольный треугольник (1)
Урок 9. Прямоугольный треугольник (2)
Урок 10. Равнобедренный треугольник (1)
Урок 11. Равнобедренный треугольник (2)
Урок 12. Периметр треугольника
Урок 13. Периметр равнобедренного (равностороннего) треугольника
Урок 14. Треугольник и окружность
Урок 15. Прямоугольный треугольник и окружность
Урок 17. Четырёхугольники
Урок 18. Параллелограмм
Урок 19. Периметр параллелограмма
Урок 20. Прямоугольник
Урок 21. Периметр прямоугольника
Урок 22. Квадрат
Урок 23. Ромб
Урок 24. Периметр ромба
Урок 25. Трапеция
Урок 26. Равнобедренная трапеция
Урок 27. Периметр трапеции
Урок 28. Четырёхугольник и окружность (1)
Урок 29. Четырёхугольник и окружность (2)
Урок 30. Многоугольник
Урок 31. Правильный многоугольник
Урок 32. Осевая и центральная симметрии

Источник

Все формулы для радиуса вписанной окружности

Радиус вписанной окружности в треугольник

Радиус вписанной окружности в равносторонний треугольник

Радиус вписанной окружности равнобедренный треугольник

Радиус вписанной окружности в треугольник

Радиус вписанной окружности в любой треугольник

Радиус вписанной окружности в правильный треугольник

Радиус вписанной окружности в равнобедренный треугольник

Радиус вписанной окружности в прямоугольный треугольник