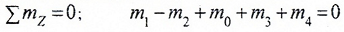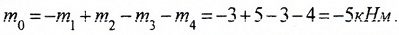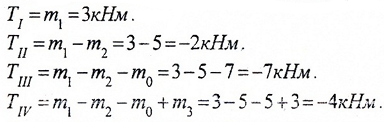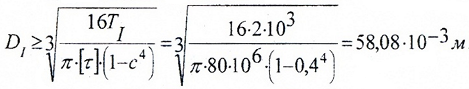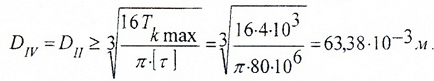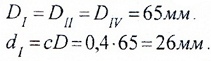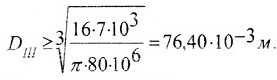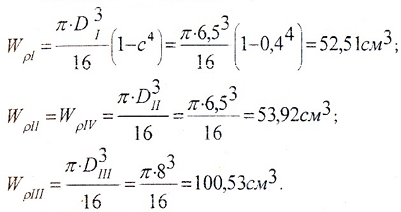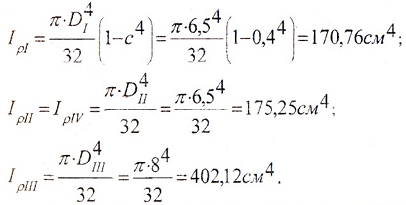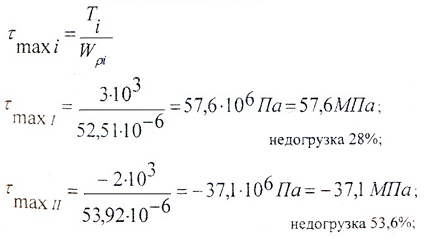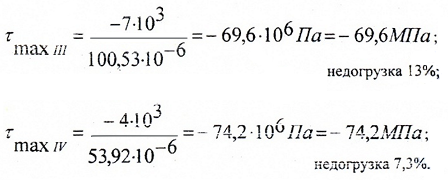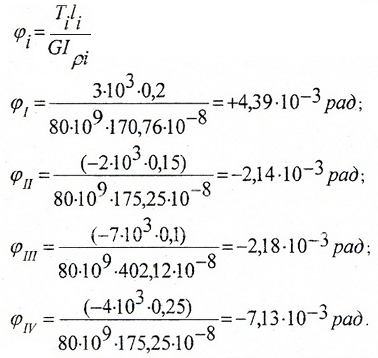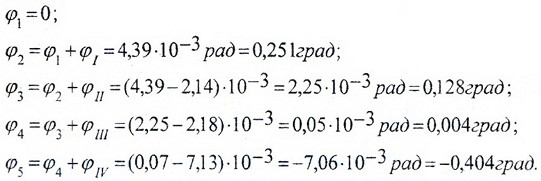Диаметры
валов могут быть определены по условному
расчёту на кручение. Минимальные диаметры
валов рассчитываем по формуле:
где
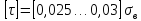
кручении, МПа.
Материал
валов — Сталь 40Х:

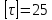
Результаты
расчётов сводим в таблицу 6.
Таблица 6
|
Вал (рис. 3) |
Материал |
Т. О. |
МПа |
МПа |
Т, Нм |
Расчётный |
Принятый |
|
|
|
||||||
|
0 |
Сталь 40Х |
У |
900 |
25 |
38,6 |
19,76 |
25 |
|
I |
Сталь 40Х |
У |
900 |
25 |
39,3 |
19,88 |
25 |
|
II |
Сталь 40Х |
У |
900 |
25 |
59,6 |
22,84 |
28 |
|
III |
Сталь 40Х |
У |
900 |
25 |
114,5 |
28,4 |
32 |
По
расчётному диаметру находим диаметры
участков под колесом и подшипником:
|
Валы |
0 |
I |
II |
III |
|
Принятый диаметр |
25 |
25 |
28 |
32 |
|
Диаметр под |
||||
|
Диаметр под |
7 Проверочный расчёт
7.1 Проверочный расчёт вала II
Проверка
вала IIна изгиб и кручение.
Силы,
действующие на вал II:
—
окружная сила:
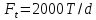
—
радиальная сила:
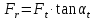
где
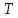
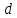
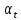
Осевая
сила отсутствует т.к. используется
прямозубая передача.
Расчёт
проводим по максимальному моменту
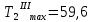
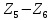
Расчёт
сил сведён в таблицу 7.
Таблица 7
|
Параметры |
Усилия |
||||
|
Наименование |
Обозн. |
|
|
|
|
|
Вращающий |
|
59,6 |
59,6 |
59,6 |
59,6 |
|
Делительный на на |
|
— 110 |
112,5 — |
150 — |
75 — |
|
Силы, |
|
— 1084 |
1060 — |
795 — |
1589 — |
|
|
|
395 |
386 |
289 |
578 |
Назначаем
в качестве опор вала IIподшипники шариковые однорядные ГОСТ
8338-75
Таблица 8
|
Параметры, наименование |
Обозначение |
Формула |
Результаты при зацеплении колёс |
||
|
Длина, мм |
|
С чертежа |
|||
|
Реакции опор, — в плоскости — — |
|
(R1x2+ R1y2)1/2 (R1x2+ R1y2)1/2 |
|||
|
Изгиб. моменты: — в плоскости — в плоскости — |
|
(M1x2+ M1y2)1/2 (M2x2+ |
|||
|
Вращ. момент , Нм |
Т |
(табл. 6) |
|||
|
Эквивалентный момент, Нм |
|
|
|||
|
|
|
||||
|
Диаметр вала в расчетном |
|
Внутренний диаметр |
|||
|
Эквивалентное — при перегрузках |
|
|
|||
|
Материал — предел текучести, МПа |
сталь |
— [4, с. |
|||
|
Допускаемое напряжение, |
|
|
|||
|
Условие статической прочности |
Примечание:
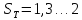
прочности по пределу,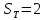
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пример решения задачи по расчёту диаметров стального ступенчатого вала сплошного и кольцевого сечения по условию прочности с построением эпюры крутящих моментов.
Задача
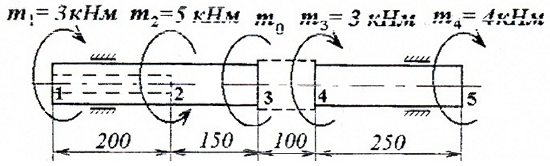
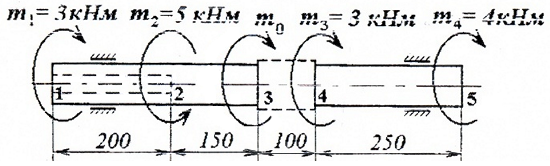
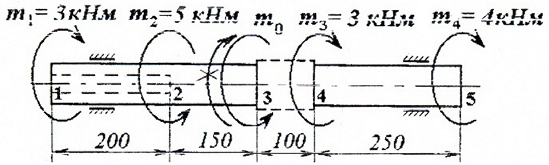
Стальной вал круглого сплошного и кольцевого сечения нагружен скручивающими моментами m0, m1=3кНм, m2=5кНм, m3=3кНм, m4=4кНм.
Расчетная схема вала:
Другие примеры решений >
Помощь с решением задач >
Требуется спроектировать ступенчатый вал заданной формы (по конструктивным соображениям, диаметр вала на участках 1-3 и 4-5 должен быть одинаков, причем на участке 1-2 вал имеет кольцевое сечение с соотношением внутреннего и наружного диаметров: c=d/D=0,4) и построить эпюры крутящих моментов и углов закручивания сечений.
Показать напряженное состояние по участкам вала.
Принять:
- допустимые касательные напряжения [τ]=80МПа;
- модуль сдвига G=80ГПа.
Решение
Посмотреть теорию по теме «Кручение»
Определение неизвестного момента
Определим величину и направление момента m0.
Направим m0 произвольно, например, по ходу часовой стрелки.
Тогда из условия равновесия вала:
находим
Здесь, знак “-” показывает, что направление m0 нужно изменить на противоположное.
Расчет крутящих моментов
Величину крутящих моментов на участках вала определяем методом сечений.
С учетом правила знаков, получаем:
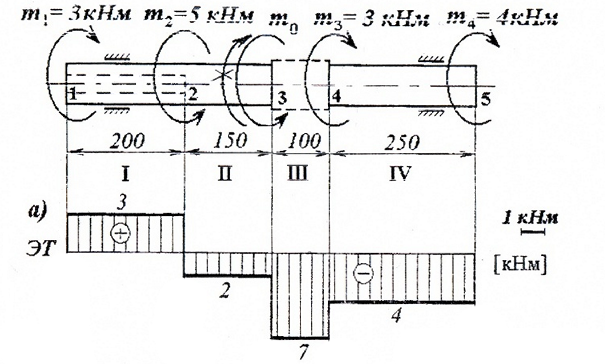
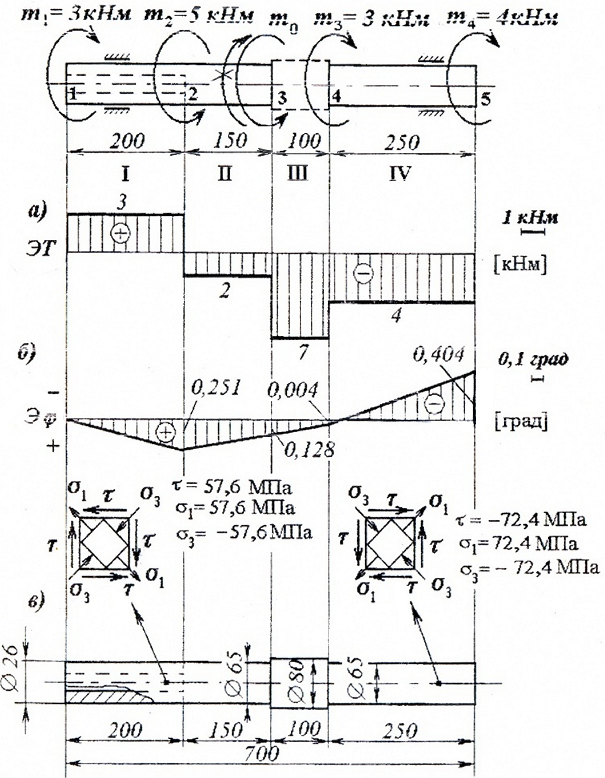
По этим значениям строим эпюру крутящих моментов T:
Расчет диаметров вала
Диаметры вала будем определять из условия прочности.
На участках I, II и IV диаметр вала одинаков.
Наружный диаметр кольцевого (полого) участка:
Сравнивая TII и TIV видим, что TII>TIV, поэтому:
Так как 63,38>58,08 мм, выбираем большее значение.
Окончательно, согласно ГОСТ 6636, принимаем стандартное значение диаметра:
Диаметр вала на III участке (TIII=7кНм)
По ГОСТ, принимаем DIII=80мм.
Расчет геометрических характеристик
Вычислим геометрические характеристики сечений на участках вала.
Моменты сопротивления:
Моменты инерции
Расчет касательных напряжений
Вычисляем максимальные касательные напряжения на участках по формуле:
Расчет деформаций
Определяем углы закручивания участков:
Построение эпюры перемещений
Рассчитаем углы закручивания характерных сечений.
Примем крайнее левое сечение вала за условно неподвижное.
По этим значениям строим эпюру углов закручивания сечений и вычерчиваем эскиз спроектированного вала.
Другие примеры решения задач >
Лекции по сопромату >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Примеры решения задач по сопротивлению материалов
На этой странице приведен еще один пример решения задачи по Сопромату, в которой необходимо произвести расчет вала переменного сечения (ступенчатого), нагруженного крутящими моментами. По результатам расчетов необходимо подобрать размеры вала, а также определить максимальную деформацию вала на скручивание (угол закручивания).
Результаты расчетов оформлены эпюрами крутящих моментов, касательных напряжений и углов закручивания бруса.
Студентам технических специальностей ВУЗов в качестве методической помощи предлагаются к скачиванию готовые варианты контрольных работ по сопромату (прикладной механике). Представленные задания и примеры их решения предназначены, в частности, для учащихся Алтайского Государственного технического университета.
Варианты контрольных работ можно скачать в формате Word для ознакомления с порядком решения заданий, или для распечатывания и защиты (при совпадении вариантов).
***
Расчет вала
Условие задачи:
К стальному валу, состоящему из 4-х участков длиной l1…l4 приложено четыре сосредоточенных момента М1…М4 (см. рис. 1 ).
Требуется:
Построить эпюру крутящих моментов Мкр, подобрать диаметр вала из расчета на прочность, построить эпюру максимальных касательных напряжений τmax, построить эпюру углов закручивания φ вала и определить наибольший относительный угол закручивания вала.
Исходные данные:
Нагрузки, кН×м:
- М1 = -4,5;
- М2 = -2,6;
- М3 = -3,1;
- М4 = -2,0;
Длина участков, м:
- l1 = 0,9;
- l2 = 0,6;
- l3 = 0,9;
- l4 = 0,4;
Указания:
Вычертить схему вала в соответствии с исходными данными.
Знаки моментов в исходных данных означают: плюс – момент действует против часовой стрелки относительно оси Z, минус – по часовой стрелке (см. навстречу оси Z). В дальнейшем значения моментов принимать по абсолютной величине.
Участки нумеровать от опоры.
Допускаемое касательное напряжение [τ] для стали принимать равным 100 МПа.
Решение:
1. Определим методом сечений значения крутящих моментов на каждом силовом участке от свободного конца вала.
Крутящий момент равен алгебраической сумме внешних моментов, действующих на вал по одну сторону сечения.
- МIV = -М1 = -4,5 (кН×м);
- МIII = -М1 — М2 = -4,5 — 2,6 = -7,1 (кН×м);
- МII = -М1 — М2 – М3 = -4,5 – 2,6 – 3,1 = -10,2 (кН×м);
- МI = -М1 — М2 – М3 – М4 = -4,5 – 2,6 – 3,1 – 2,0 = -12,2 (кН×м).
2. Подберем сечение вала из расчета на прочность при кручении по полярному моменту сопротивления для участка, где величина крутящего момента максимальная (без учета знака):
WP ≥ Мкр/[τ] .
Так как для круглого сечения полярный момент равен: Wр = πD3/16, то можно записать:
D ≥ 3√(16Мкр/π[τ]) ≥ 3√(16×12,2×103/3,14×[100×106]) = 0,0855 м или D ≥ 85,5 мм.
(Здесь и далее знак «√» означает квадратный корень из выражения)
В соответствии со стандартным рядом, предусмотренным ГОСТ 12080-66, принимаем диаметр вала D = 90 мм.
3. Определим угол закручивания для каждого участка вала по формуле:
φ = Мкр×l/G×Iр,
где
G – модуль упругости 2-го рода; для стали G = 8×1010 Па;
Ip – полярный момент инерции (для круглого сечения Iр = πD4/32 ≈ 0,1D4, м4).
Произведение G×Iр = 8×1010×0,1×0,094 ≈ 524880 Н×м2 – жесткость сечения данного вала при кручении.
Расчитываем углы закручивания на каждом участке:
- φI = -12,2×103×0,9/524880 = -0,0209 рад;
- φII = -10,2×103×0,6/524880 = -0,0116 рад;
- φIII = -7,1×103×0,9/524880 = -0,0122 рад;
- φIV = -4,5×103×0,4/524880 = -0,0034 рад.
4. Определяем углы закручивания сечений вала, начиная от жесткой заделки (опоры):
- φ0-0 = 0 рад;
- φ1-1 = φI = -0,0209 рад;
- φ2-2 = φI + φII = -0,0209 — 0,0116 = -0,0325 рад;
- φ3-3 = φI + φII + φIII = -0,0209 — 0,0116 — 0,0122 = -0,0447 рад;
- φ4-4 = φI + φII + φIII + φIV = -0,0209 — 0,0116 — 0,0122 -0,0034 = -0,0481 рад.
5. Определяем максимальное касательное напряжение на каждом силовом участке по формуле:
τmax = Мкр/Wp = 16Мкр/πD3 ≈ 5Мкр/D3.
Тогда:
- τmaxIV = 5×-4,5×103/0,093 = -30864197 Па ≈ -30,086 МПа;
- τmaxIII = 5×-7,1×103/0,093 = -48696844 Па ≈ -48,700 МПа;
- τmaxII = 5×-10,2×103/0,093 = -69958847 Па ≈ -69,959 МПа;
- τmaxI = 5×-12,2×103/0,093 = -83676268 Па ≈ -83,676 МПа.
6. Наибольший относительный угол закручивания Θmax определим по формуле:
Θmax = МКРmax/G×Iр = -12,2×103/524880 = 0,0232 рад/м.
7. По результатам расчетов строим эпюры крутящих моментов Мкр, касательных напряжений τmax и углов закручивания φ (см. рис. 2).
***
Расчет двутавровой балки на изгибную прочность
Сопротивление материалов
Выберите подписку для получения дополнительных возможностей Kalk.Pro
Любая активная подписка отключает
рекламу на сайте
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Более 10 000 пользователей уже воспользовались расширенным доступом для успешного создания своего проекта. Подробные чертежи и смета проекта экономят до 70% времени на подготовку элементов конструкции, а также предотвращают лишний расход материалов.
Подробнее с подписками можно ознакомиться здесь.
Крутящий момент на валу Mкр = кНм
Допускаемые касательные напряжения [τ] = МПа
Необходимый минимальный полярный момент сопротивления равен $$W_{rho} = frac{M_{кр}}{[tau]} = frac{ 40000}{ 100} = 400см^3$$
Поскольку полярный момент сопротивления круга $$W_{rho}=frac{pi cdot d^3}{16}$$ диаметр вала равен $$d = sqrt[3]{frac{16cdot W_{rho}}{pi}} = sqrt[3]{frac{16cdot 400}{pi}} = 12.7 см$$ Площадь сечения вала $$A = frac{pi cdot d^2}{4} = frac{pi cdot 12.7^2}{4} = 127см^2$$

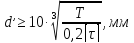
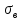 ,
,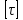 ,
, ,
, ,
, ,
, ,
, ,
,
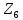

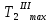
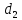
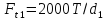

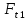
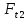
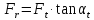
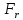
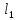
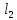


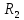
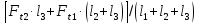
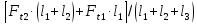
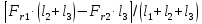
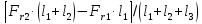
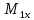
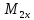
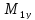
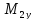
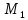
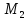
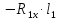
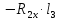
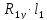
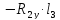
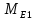
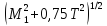
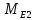
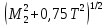
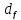
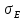
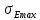
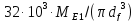
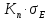
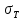
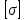
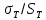
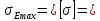 МПа
МПа