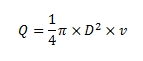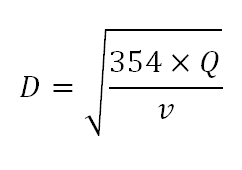Как найти диаметр от потока

Наиболее экономичной
скоростью воды в трубопроводе является
скорость от 1-3 м/с. На крупных системах
большая скорость, на малых системах
меньшая. Принимаем среднюю скорость
движения воды равной 1 м/с. Задаваясь
скоростью равной 1 м/с, определяем диаметр
трубопровода по формуле. В данном случае
диаметр трубопровода по участкам
расчетный.

,
(2)

где d_р
– расчетный
диаметр по участкам (м,
мм);

Q_p
–
расчетный
расход по участкам (м³/с);

–число ПИ,
соответствующее 3,14;

V
– средняя
скорость движения воды равная 1 м/с.

Единицу измерения
расчетного диаметра переводим из м
в мм.
Используя таблицу 2, округляем полученные
результаты диаметров до стандартных
предпочтительно в большую сторону.

Таблица 2

Удельные сопротивления
А_кв
(с²/м⁶)
труб из различных материалов в зависимости
от условного прохода d

5.4 Определение скорости движения воды в трубопроводе

По известным
значениям расхода Q_i
и
диаметра d_i
определяется средняя скорость потока
на каждом участке по формуле

,
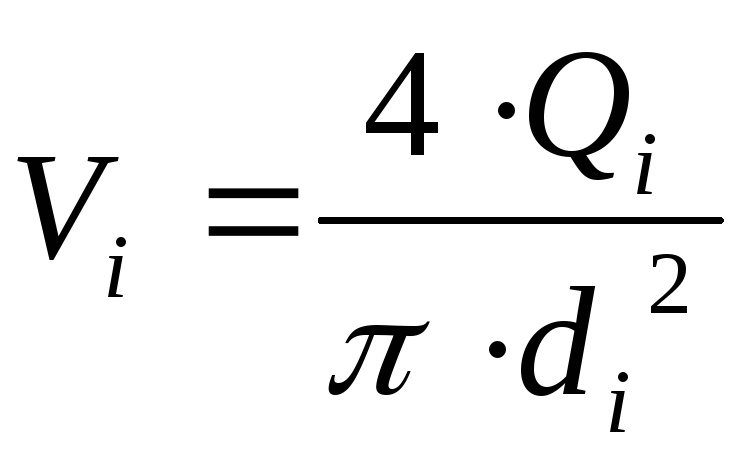
(3)

где V_i
– скорость потока на каждом участке
(м/c);

Q_i
– расчетный расход по участкам (м³/с);

–число Пи (отношение
длины окружности к радиусу), соответствующее
3,14;

d_i
– расчетный
диаметр по участкам (м).

Максимально
допустимые скорости в магистральных
трубопроводах не должны превышать 6
м/с, в распределительной сети 2-3 м/с.

5.5 Расчет потерь напора по участкам сети по преобразованной формуле д. Бернулли

Для водопроводных
систем характерен сравнительно узкий
интервал применяемых средних скоростей
потоков (0,6…3,0 м/с). Поэтому в уравнении
Д. Бернулли можно пренебречь удельной
кинетической энергией в сечении потока
(она не превышает 0,46 м), а для ускорения
расчета потерь напора на участках
трубопровода использовать упрощенную
зависимость, полученную путем
преобразования формулы Дарси–Вейсбаха:

,
(4)

где h
– потери напора (м);

k_м
– коэффициент, учитывающий влияние
местных сопротивлений, которые составляют
от 5 – 10% от сопротивления по длине
[k_м=1,05–1,1];

А_кв
– удельное
сопротивление трубы в квадратичной
области, с²/м⁶;

—
поправочный коэффициент, учитывающий
неквадратичность области сопротивления;

L
– расчетная длина участка трубопровода,
м;

Q_р
– расчетный расход на участке трубопровода,
м³/с.

Соответствующие
величины А_кв
и
,
которые представляются в уравнении (4)
для вычисления потерь напора находятся
по таблицам 2 и 3.

Таблица 3

Поправочный
коэффициентна степень турбулентности потока в
зависимости от скоростиV
движения воды

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Потеря давления в трубопроводе, кроме прочего, зависит от расхода скорости потока и вязкости среды протекания. Чем больше количество пара, проходящего через трубопровод определённого номинального диаметра, тем выше трение о стенки трубопровода. Иными словами, чем выше скорость пара, тем выше сопротивление или потери давления в трубопроводе.

На сколько высоки могут быть потери давления определяется назначением пара. Если перегретый пар подается через трубопровод к паровой турбине, то потери давления должны быть по возможности минимальными. Такие трубопроводы значительно дороже обычных, причём больший диаметр, в свою очередь, приводит к значительно большим затратам. Инвестиционный расчёт основывается на времени возврата (срок окупаемости) инвестиционного капитала в сравнении с прибылью от работы турбины.

Этот расчёт должен основываться не на средней нагрузке турбины, а исключительно на ее пиковой нагрузке. Если, например, в течении 15 минут набрасывается пиковая нагрузка в 1000 кг пара, то трубопровод должен иметь пропускную способность 60/15x 1000 = 4000 кг/ч.

Расчёт

В главе далее — Работа с конденсатом, поясняется методика расчёт диаметра конденсатопроводов. В расчётах паро- воздухо- и водопроводов действуют примерно те же исходные принципы. В завершении этой темы в этом разделе будут приведены расчеты для определения диаметра паро- воздухо- и водопроводов.

В расчётах диаметров в качестве основной применяется формула:

, где:

Q = расход пара, воздуха и воды в м³/с.

D = диаметр трубопровода в м.

v = допустимая скорость потока в м/с.

В практике рекомендуется вести расчет по расходу в м³/ч и по диаметру трубопровода в мм. в этом случае выше приведённая формула расчёта диаметра трубопровода изменяется следующим образом:

, где:

D = диаметр конденсатопровода в мм.

Q = расход в м³/ч.

V = допустимая скорость потока в м/с.

Расчет трубопроводов всегда ведется по объёмному расходу (м³/ч), а не по массовому (кг/ч). Если известен только массовый расход, то для пересчёта кг/ч в м³/ч необходимо учитывать удельный объём по таблице пара.

Пример:

Удельный объем насыщенного пара при давлении 11 бар составляет 0,1747 м³/кг. Таким образом, объемный расход от 1000 кг/ч насыщенного пара при 11 бар будет составлять 1000 * 0,1747 = 174,7 м³/ч. Если речь будет идти о таком же количестве перегретого пара при давлении 11 бар и 300 °С, то удельный объём составит 0,2337 м³/кг, а объемный расход 233,7 м³/ч. Таким образом это означает, что один и тот же паропровод не может одинаково подходить для транспорта одного количества насыщенного и перегретого пара.

Также для случая воздуха и других газов расчет необходимо повторить с учетом давления. Производители компрессорного оборудования указывают производительность компрессоров в м³/ч, под которым понимается объем в м³ при температуре 0 °С.

Если производительность компрессора 600 мп³/ч и давление воздуха 6 бар, то объемный расход составляет 600/6 = 100 м³/ч. в этом также заключается основа расчета трубопроводов.

Допустимая скорость потока

Допустимая скорость потока в системе трубопроводов зависит от многих факторов.

• стоимость установки: низкая скорость потока приводит к выбору большего диаметра.
• потеря давления: высокая скорость потока позволяет выбрать меньший диаметр, однако вызывает большую потерю давления.
• износ: особенно в случае конденсата высокая скорость потока приводит к повышенной эрозии.
• шум: высокая скорость потока увеличивает шумовую нагрузку, напр. Паровой редукционный клапан.

В ниже приведенной таблице представлены данные норм относительно скорости потока для некоторых сред протекания.

Нормы для определения скорости потока

Примеры:

a) Вода

Расчет диаметра трубопровода для воды при 100 м³/ч и скорости потока v = 2 м/с.

D = √ 354*100/2 = 133 мм. Выбранный номинальный диаметр DN 125 или DN 150.

b) Воздух под давлением

расчет диаметра трубопровода для воздуха при 600 м³/ч, давление 5 бар и скорости потока 8 м/с.

Перерасчет с нормального расхода 600 м³/ч на рабочий м³/ч 600/5 = 120 м³/ч.

D = √ 354*120/8 = 72 мм. Выбранный номинальный диаметр DN 65 или DN 80.

В зависимости от назначения воды или воздуха выбирается трубопровод DN 65 или DN 80. Необходимо иметь ввиду, что расчет диаметра трубопровода усреднен и не предусматривает случая наступления пиковой нагрузки.

c) Насыщенный пар

Расчет диаметра трубопровода для насыщенного пара при 1500 кг/ч, давлении 16 бар и скорости потока 15 м/с.

В соответствии с таблицей пара удельный объем насыщенного пара при давлении 16 бар составляет v = 0,1237 м³/кг.

D = √ 354*1500*0,1237/15 = 66 мм.

И здесь должен быть решен вопрос DN 65 или DN 80 в зависимости от возможной пиковой нагрузки. В случае необходимости предусматривается также возможность расширения установки в будущем.

d) Перегретый пар

Если в нашем примере пар перегреет до температуры 300 °С, то его удельный объем изменяется на v = 0,1585 м³/кг.

D = √ 354*1500*0,1585/15 = 75 мм, выбирается DN 80.

Изображение 4.9 в форме номограммы показывает, как можно произвести выбор трубопровода без проведения расчета. На изображении 4-10 этот процесс представлен для случая насыщенного и перегретого пара.

е) Конденсат

Если речь идёт о расчёте трубопровода для конденсата без примеси пара (от разгрузки), тогда расчёт ведётся как для воды.

Горячий конденсат после конденсатоотводчика, попадая в конденсатопровод, разгружается в нём. В главе 6.0 Работа с конденсатом поясняется, как определить долю пара от разгрузки.

Правило к проведению расчёта:

Доля пара от разгрузки = (температура перед конденсатоотводчиком минус температура пара после конденсатоотводчика) х 0,2. При расчёте конденсатопровода необходимо учитывать объём пара от разгрузки.

Объём оставшейся воды в сравнении с объёмом пара от разгрузки настолько мал, что им можно пренебречь.

Расчёт диаметра конденсатопровода на расход 1000 кг/ч сконденсированного пара 11 бар (h1 = 781 кДж/кг) и разгруженного до давления 4 бар (h’ = 604 кДж/кг,v = 0,4622 м³/кг и r — 2133 кДж/кг).

Доля разгруженного пара составляет: 781 – 604/ 100 % = 8,3%

Количество разгруженного пара: 1000 х 0,083 = 83 кг/ч или 83 х 0,4622 -38 м³/ч. Объёмная доля разгруженного пара составляет около 97 %.

Диаметр трубопровода для смеси при скорости потока 8 м/с:

D = √ 354*1000*0,083*0,4622/8 = 40 мм.

Для сети атмосферного конденсата (v“ = 1,694 м³/кг) доля разгруженного пара составляет:

781 – 418/2258*100 % = 16 % или 160 кг/ч.

В этом случае диаметр трубопровода:

D = √ 354*1000*0,16*1,694/8 = 110 мм.

Источник: «Рекомендации по применению оборудования ARI. Практическое руководство по пару и конденсату. Требования и условия безопасной эксплуатации. Изд. ARI-Armaturen GmbH & Co. KG 2010»

Для более верного выбора оборудования можно обратиться на эл. почту: info@nomitech.ru

Постановка задачи

Гидравлический расчёт при разработке проекта трубопровода направлен на определение диаметра трубы и падения напора потока носителя. Данный вид расчёта проводится с учетом характеристик конструкционного материала, используемого при изготовлении магистрали, вида и количества элементов, составляющих систему трубопроводов(прямые участки, соединения, переходы, отводы и т. д.), производительности,физических и химических свойств рабочей среды.

Многолетний практический опыт эксплуатации систем трубопроводов показал, что трубы, имеющие круглое сечение, обладают определенными преимуществами перед трубопроводами, имеющими поперечное сечение любой другой геометрической формы:

• минимальное соотношением периметра к площади сечения, т.е. при равной способности, обеспечивать расход носителя, затраты на изолирующие и защитные материалы при изготовлении труб с сечением в виде круга, будут минимальными;
• круглое поперечное сечение наиболее выгодно для перемещения жидкой или газовой среды сточки зрения гидродинамики, достигается минимальное трение носителя о стенки трубы;
• форма сечения в виде круга максимально устойчива к воздействию внешних и внутренних напряжений;
• процесс изготовления труб круглой формы относительно простой и доступный.

Подбор труб по диаметру и материалу проводится на основании заданных конструктивных требований к конкретному технологическому процессу. В настоящее время элементы трубопровода стандартизированы и унифицированы по диаметру. Определяющим параметром при выборе диаметра трубы является допустимое рабочее давление, при котором будет эксплуатироваться данный трубопровод.

Основными параметрами, характеризующими трубопровод являются:

• условный (номинальный) диаметр – D_N;
• давление номинальное – P_N;
• рабочее допустимое (избыточное) давление;
• материал трубопровода, линейное расширение, тепловое линейное расширение;
• физико-химические свойства рабочей среды;
• комплектация трубопроводной системы (отводы, соединения, элементы компенсации расширения и т.д.);
• изоляционные материалы трубопровода.

Условный диаметр (проход) трубопровода (D_N) – это условная  безразмерная величина, характеризующая проходную способность трубы, приблизительно равная ее внутреннему диаметру. Данный параметр учитывается при осуществлении подгонки сопутствующих изделий трубопровода (трубы, отводы, фитинги и др.).

Условный диаметр может иметь значения от 3 до 4000 и обозначается: DN 80.

Условный проход по числовому определению примерно соответствует реальному диаметру определенных отрезков трубопровода. Численно он выбран таким образом, что пропускная способность трубы повышается на 60-100% при переходе от предыдущего условного прохода к последующему.Номинальный диаметр выбирается по значению внутреннего диаметра трубопровода. Это то значение, которое наиболее близко к реальному диаметру непосредственно трубы.

Давление номинальное (PN) – это безразмерная величина, характеризующая максимальное давление рабочего носителя в трубе заданного диаметра, при котором осуществима длительная эксплуатация трубопровода при температуре 20°C.

Значения номинального давления были установлены на основании продолжительной практики и опыта эксплуатации: от 1 до 6300.

Номинальное давление для трубопровода с заданными характеристиками определяется по ближайшему к реально создаваемому в нем давлению. При этом,вся трубопроводная арматура для данной магистрали должна соответствовать тому же давлению. Расчет толщины стенок трубы проводится с учетом значения номинального давления.

Основные положения гидравлического расчета

Рабочий носитель (жидкость, газ, пар), переносимый проектируемым трубопроводом, в силу своих особых физико-химических свойств определяет характер течения среды в данном трубопроводе. Одним из основных показателей характеризующих рабочий носитель, является динамическая вязкость, характеризуемая коэффициентом динамической вязкости – μ.

Инженер-физик Осборн Рейнольдс (Ирландия), занимавшийся изучением течения различных сред, в 1880 году провел серию испытаний,  по результату которых было выведено понятие критерия Рейнолдса (Re) – безразмерной величины, описывающей характер потока жидкости в трубе. Расчет данного критерия проводится по формуле:

Критерий Рейнольдса (Re) дает понятие о соотношении сил инерции к силам вязкого трения в потоке жидкости. Значение критерия характеризует изменение соотношения указанных сил, что, в свою очередь, влияет на характер потока носителя в трубопроводе. Принято выделять следующие режимы потока жидкого носителя в трубе в зависимости от значения данного критерия:

• ламинарный поток (Re<2300), при котором носитель-жидкость движется тонкими слоями, практически не смешивающимися друг с другом;
• переходный режим (2300<Re<4000), который характеризуется нестабильной структурой потока, когда отдельные слои жидкости перемешиваются;
• турбулентный поток (Re>4000) – устойчивый режим, при котором в каждой отдельной точке потока происходит изменение его направления и скорости, что в итоге приводит к выравниванию скорости движения потока по объему трубы.

Критерий Рейнольдса зависит от напора, с которым насос перекачивает жидкость, вязкости носителя при рабочей температуре и геометрических размеров используемой трубы (d, длина). Данный критерий является параметром подобия для течения жидкости,поэтому, используя его, можно осуществлять моделирование реального технологического процесса в уменьшенном масштабе, что удобно при проведении испытаний и экспериментов.

Проводя расчеты и вычисления по уравнениям, часть заданных неизвестных величин можно взять из специальных справочных источников. Профессор, доктор технических наук Ф. А. Шевелев разработал ряд таблиц для проведения точного расчета пропускной способности трубы. Таблицы включают значения параметров, характеризующих как сам трубопровод (размеры, материалы), так и  их взаимосвязь с физико-химическими свойствами носителя. Кроме того, в литературе приводится таблица приближенных значений скоростей движения потока жидкости, пара,газа в трубе различного сечения.

Подбор оптимального диаметра трубопровода

Определение оптимального диаметра трубопровода – это сложная производственная задача, решение которой зависит от совокупности различных взаимосвязанных условий (технико-экономические, характеристики рабочей среды и материала трубопровода, технологические параметры и т.д.). Например, повышение скорости перекачиваемого потока приводит к уменьшению диаметра трубы, обеспечивающей заданный условиями процесса расход носителя, что влечет за собой снижение затрат на материалы, удешевлению монтажа и ремонта магистрали и т.д. С другой стороны, повышение скорости потока  приводит к потере напора, что требует дополнительных энергетических и финансовых затрат на перекачку заданного объема носителя.

Значение оптимального диаметра трубопровода рассчитывается по преобразованному уравнению неразрывности потока с учетом заданного расхода носителя:

 При гидравлическом расчете расход перекачиваемой жидкости чаще всего задан условиями задачи. Значение скорости потока перекачиваемого носителя определяется, исходя из свойств заданной среды и соответствующих справочных данных (см. таблицу).

Преобразованное уравнение неразрывности потока для расчета рабочего диаметра трубы имеет вид:

Расчет падения напора и гидравлического сопротивления

Полные потери напора жидкости включают в себя потери на преодоление потоком всех препятствий: наличие насосов, дюкеров, вентилей, колен, отводов, перепадов уровня при течении потока по трубопроводу, расположенному под углом и т.д. Учитываются потери на местные сопротивления, обусловленные свойствами используемых материалов.

Другим важным фактором, влияющим на потери напора, является трение движущегося потока о стенки трубопровода, которое характеризуется коэффициентом гидравлического сопротивления.

Значение коэффициента гидравлического сопротивления λзависит от режима движения потока и шероховатости материала стенок трубопровода. Под шероховатостью понимают дефекты и неровности внутренней поверхности трубы. Она может быть абсолютной и относительной. Шероховатость различна по форме и неравномерна по площади поверхности трубы. Поэтому в расчетах используется понятие усредненной шероховатости с поправочным коэффициентом (k1). Данная характеристика для конкретного трубопровода зависит от материала, продолжительности его эксплуатации, наличия различных коррозионных дефектов и других причин. Рассмотренные выше величины являются справочными.

Количественная связь между коэффициентом трения, числом Рейнольдса и шероховатостью определяется диаграммой Муди.

Для вычисления коэффициента трения турбулентного движения потока также используется уравнение Коулбрука-Уайта, с использованием которого возможно наглядное построение графических зависимостей, по которым определяется коэффициент трения:

В расчётах используются и другие уравнения приблизительного расчета потерь напора на трение. Одним из наиболее удобных и часто используемых в этом случае считается формула Дарси-Вейсбаха. Потери напора на трение рассматриваются как функция скорости жидкости от сопротивления трубы движению жидкости, выражаемой через значение шероховатости поверхности стенок трубы: 

Потери давления по причине трения для воды рассчитывают по формуле Хазена — Вильямса:

Расчет потерь давления

Рабочее давление в трубопроводе – это на большее избыточное давление, при котором обеспечивается заданный режим технологического процесса. Минимальное и максимальное значения давления, а также физико-химические свойства рабочей среды, являются определяющими параметрами при расчёте расстояния между насосами, перекачивающими носитель, и производственной мощности.

Расчет потерь на падение давления в трубопроводе осуществляют по уравнению:

Примеры задач гидравлического расчета трубопровода с решениями

Задача 1

В аппарат с давлением 2,2 бар по горизонтальному трубопроводу с эффективным диаметром 24 мм из открытого хранилища насосом перекачивается вода. Расстояние до аппарата составляет 32 м. Расход жидкости задан – 80 м³/час. Суммарный напор составляет 20 м. Принятый коэффициент трения равен 0,028.

Рассчитайте потери напора жидкости на местные сопротивления в данном трубопроводе.

Исходные данные:

Расход Q = 80 м³/час = 80·1/3600 = 0,022 м³/с;

эффективный диаметр d = 24 мм;

длина трубы l = 32 м;

коэффициент трения λ = 0,028;

давление в аппарате Р = 2,2 бар = 2,2·10⁵ Па;

общий напор Н = 20 м.

Решение задачи:

Скорость потока движения воды в трубопроводе рассчитывается по видоизмененному уравнению:

w=(4·Q) / (π·d²) = ((4·0,022) / (3,14·[0,024]²)) = 48,66 м/с

Потери напора жидкости в трубопроводе на трение определяются по уравнению:

H_Т = (λ·l) / (d·[w²/(2·g)]) = (0,028·32) / (0,024·[48,66]²) / (2·9,81) = 0,31 м

Общие потери напора носителя рассчитываются по уравнению и составляют:

h_п = H — [(p₂-p₁)/(ρ·g)] — H_г = 20 — [(2,2-1)·10⁵)/(1000·9,81)] — 0 = 7,76 м

Потери напора на местные сопротивления определяется как разность:

7,76 — 0,31=7,45 м

Ответ: потери напора воды на местные сопротивления составляют 7,45 м.

Задача 2

По горизонтальному трубопроводу центробежным насосом транспортируется вода. Поток в трубе движется со скоростью 2,0 м/с. Общий напор составляет 8 м.

Найти минимальную длину прямого трубопровода, в центре которого установлен один вентиль. Забор воды осуществляется из открытого хранилища. Из трубы вода самотеком изливается в другую емкость. Рабочий диаметр трубопровода равен 0,1 м. Относительная шероховатость принимается равной 4·10^-5.

Исходные данные:

Скорость потока жидкости W = 2,0 м/с;

диаметр трубы d = 100 мм;

общий напор Н = 8 м;

относительная шероховатость 4·10^-5.

Решение задачи:

Согласно справочным данным в трубе диаметром 0,1 м коэффициенты местных сопротивлений для вентиля и выхода из трубы составляют соответственно 4,1 и 1.

Значение скоростного напора определяется по соотношению:

w²/(2·g) = 2,0²/(2·9,81) = 0,204 м

Потери напора воды на местные сопротивления составят:

∑ζ_МС·[w²/(2·g)] = (4,1+1)·0,204 = 1,04 м

Суммарные потери напора носителя на сопротивление трению и местные сопротивления рассчитываются по уравнению общего напора для насоса (геометрическая высота Hг по условиям задачи равна 0):

h_п = H — (p₂-p₁)/(ρ·g) — = 8 — ((1-1)·10⁵)/(1000·9,81) — 0 = 8 м

Полученное значение потери напора носителя на трение составят:

8-1,04 = 6,96 м

Рассчитаем значение числа Рейнольдса для заданных условий течения потока (динамическая вязкость воды принимается равной 1·10^-3 Па·с,  плотность воды – 1000 кг/м³):

Re = (w·d·ρ)/μ = (2,0·0,1·1000)/(1·10^-3) = 200000

Согласно рассчитанному значению Re, причем 2320 <Re< 10/e, по справочной таблице рассчитаем коэффициент трения (для режима гладкого течения):

λ = 0,316/Re^0,25 = 0,316/200000^0,25 = 0,015

Преобразуем уравнение и найдем требуемую длину трубопровода из расчетной формулы потерь напора на трение:

l = (H_об·d) / (λ·[w²/(2g)]) = (6,96·0,1) / (0,016·0,204) = 213,235 м

Ответ:требуемая длина трубопровода составит 213,235 м.

Задача 3

В производстве транспортируют воду при рабочей температуре 40°С с производственным расходом Q = 18 м³/час. Длина прямого трубопровода l = 26 м, материал — сталь. Абсолютная шероховатость (ε) принимается для стали по справочным источникам и составляет 50 мкм. Какой будет диаметр стальной трубы, если перепад давления на данном участке не превысит Δp = 0,01 мПа (ΔH = 1,2 м по воде)? Коэффициент трения принимается равным 0,026.

Исходные данные:

Расход Q = 18 м³/час = 0,005 м³/с;

длина трубопровода l=26 м;

для воды ρ = 1000 кг/м³, μ = 653,3·10^-6 Па·с (при Т = 40°С);

шероховатость стальной трубыε = 50 мкм;

коэффициент трения λ = 0,026;

Δp=0,01 МПа;

ΔH=1,2 м.

Решение задачи:

Используя форму уравнения неразрывности W=Q/F и уравнение площади потока F=(π·d²)/4 преобразуем выражение Дарси – Вейсбаха:

∆H = λ·l/d·W²/(2·g) = λ·l/d·Q²/(2·g·F²) = λ·[(l·Q²)/(2·d·g·[(π·d²)/4]²)] = =(8·l·Q²)/(g·π²)·λ/d⁵ = (8·26·0.005²)/(9,81·3,14²)· λ/d⁵ = 5,376·10^-5·λ/d⁵

Выразим диаметр:

d⁵ = (5,376·10^-5·λ)/∆H = (5,376·10^-5·0,026)/1,2 = 1,16·10^-6

d = ⁵√1,16·10^-6 = 0,065 м.

Ответ: оптимальный диаметр трубопровода составляет 0,065 м.

Задача 4

Проектируются два трубопровода для транспортировки невязкой жидкости с предполагаемой производительностью Q₁ = 18 м³/час и Q₂ = 34 м³/час. Трубы для обоих трубопроводов должны быть одного диаметра.

Определите эффективный диаметр труб d, подходящих под условия данной задачи.

Исходные данные:

Q₁ = 18 м³/час;

Q₂ = 34 м³/час.

Решение задачи:

Определим возможный интервал оптимальных диаметров для проектируемых трубопроводов, воспользовавшись преобразованным видом уравнения расхода:

d = √(4·Q)/(π·W)

Значения оптимальной скорости потока найдем из справочных табличных данных. Для невязкой жидкости скорости потока составят 1,5 – 3,0 м/с.

Для первого трубопровода с расходом Q₁ = 18 м³/час возможные диаметры составят:

d_1min = √(4·18)/(3600·3,14·1,5) = 0,065 м

d_1max = √(4·18)/(3600·3,14·3.0) = 0,046 м

Для трубопровода с расходом 18 м³/час подходят трубы с диаметром поперечного сечения от 0,046 до 0,065 м.

Аналогично определим возможные значения оптимального диаметра для второго трубопровода с расходом Q₂ = 34 м³/час:

d_2min = √(4·34)/(3600·3,14·1,5) = 0,090 м

d_2max = √(4·34)/(3600·3,14·3) = 0,063 м

Для трубопровода с расходом 34 м³/час возможные оптимальные диаметром могут быть от 0,063 до 0,090 м.

Пересечение двух диапазонов оптимальных диаметров находится в интервале от 0,063 м до 0,065 м.

Ответ: для двух трубопроводов подходят трубы диаметром 0,063–0,065 м.

Задача 5

В трубопроводе диаметром 0,15 м при температуре Т = 40°C движется поток воды производительностью 100 м³/час. Определите режим течения потока воды в трубе.

Дано:

диаметр трубы d = 0,25 м;

расход Q = 100 м³/час;

μ = 653,3·10^-6 Па·с (по таблице при Т = 40°С);

ρ = 992,2 кг/м³ (по таблице при Т = 40°С).

Решение задачи: 

Режим течения потока носителя определяется по значению числа Рейнольдса (Re). Для расчета Re определим скорость движения потока жидкости в трубе (W), используя уравнение расхода:

W = Q·4/(π·d²) = [100/3600] · [4/(3,14·0,25²)] = 0,57 м/c

Значение числа Рейнольдса определим по формуле:

Re = (ρ·W·d)/μ = (992,2·0,57·0,25) / (653,3·10^-6) = 216422

Критическое значение критерия Re_кр по справочным данным равно 4000. Полученное значение Re больше указанного критического, что говорит о турбулентном характере течения жидкости при заданных условиях.

Ответ: режим потока воды – турбулентный.