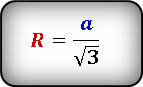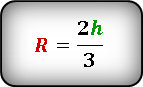Как найти диаметр описанной окружности равностороннего треугольника

Окружность, описанная около правильного треугольника

Окружность, описанная около правильного треугольника, обладает всеми свойствами описанной около произвольного треугольника окружности и, кроме того, имеет свои собственные свойства.

1) Центр описанной около треугольника окружности — точка пересечения серединных перпендикуляров к его сторонам.

Поскольку в равностороннем треугольнике медианы, высоты и биссектрисы совпадают, центр описанной около правильного треугольника окружности лежит в точке пересечения его медиан, высот и биссектрис.

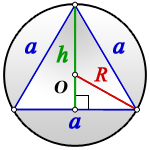
Например, в правильном треугольнике ABC AB=BC=AC=a

точка O — центр описанной окружности.

AK, BF и CD — медианы, высоты и биссектрисы треугольника ABC.

2) Расстояние от центра описанной окружности до вершин треугольника равно радиусу. Так как центр описанной около равностороннего треугольника окружности лежит на пересечении его медиан, а медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то радиус описанной окружности составляет две трети от длины медианы:

Таким образом, формула радиуса описанной около правильного треугольника окружности —

И обратно, сторона равностороннего треугольника через радиус описанной окружности —

3) Формула для нахождения площади правильного треугольника по его стороне —

Отсюда можем найти площадь через радиус описанной окружности:

Таким образом, формула площади площади правильного треугольника через радиус описанной окружности —

4) Центр описанной около правильного треугольника окружности совпадает с центром вписанной в него окружности.

5) Радиус описанной около равностороннего треугольника окружности в два раза больше радиуса вписанной окружности:

Радиус описанной окружности равностороннего треугольника

Свойства

Зная радиус описанной окружности, можно найти сразу не только сторону равностороннего треугольника, но и радиус вписанной в него окружности, так как они напрямую связаны друг с другом. Сторона треугольника будет равна произведению радиуса описанной окружности на корень из трех, а радиус вписанной окружности – его половине. (рис.100) a=√3 R r=R/2

Чтобы вычислить периметр и площадь равностороннего треугольника через радиус описанной вокруг него окружности, необходимо подставить полученное выражение для стороны в соответствующие формулы. P=3a=3√3 R S=(√3 a^2)/4=(3√3 R^2)/4

Высоты, медианы и биссектрисы являются одними и теми же отрезками в равностороннем треугольнике, и вычислить их можно по единой формуле, где искомая величина равна корню из трех, умноженному на сторону и деленному на два. Подставив вместо стороны произведение радиуса и корня из трех, получаем, что высота равна трем радиусам, деленным на два. (рис.99) h=m=l=(√3 a)/2=(√3 √3 R)/2=3R/2

Чтобы найти среднюю линию равностороннего треугольника через радиус описанной вокруг него окружности, необходимо разделить произведение радиуса и корня из трех на два. (рис.97.3) M=(√3 R)/2

Радиус описанной окружности равностороннего треугольника

— сторона треугольника

— высота

— радиус описанной окружности

Формула радиуса описанной окружности равностороннего треугольника через его сторону:

Калькулятор — вычислить, найти радиус описанной окружности равностороннего треугольника по стороне

Формула радиуса описанной окружности равностороннего треугольника через высоту:

Калькулятор — вычислить, найти радиус описанной окружности равностороннего треугольника по стороне

Радиус описанной окружности равностороннего треугольника

Свойства равностороннего треугольника

Свойство 1. В равностороннем треугольнике все углы равны между собой и равны ({{60}^{o }})

Естественно, не правда ли? Три одинаковых угла, в сумме ({{180}^{o }}), значит, каждый по ({{60}^{o }})

Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и серединных перпендикуляров совпадают – оказываются одной и той же точкой. И эта точка называется центром треугольника (равностороннего!).

Почему так? А посмотрим-ка на равносторонний треугольник.

Он является равнобедренным, какую бы его сторону ни принять за основание – так сказать, со всех сторон равнобедренный.

Значит, любая высота в равностороннем треугольнике является также и биссектрисой, и медианой, и серединным перпендикуляром!

В равностороннем треугольнике оказалось не (12) особенных линий, как во всяком обычном треугольнике, а всего три!

Итак, ещё раз:

Центр равностороннего треугольника является центром вписанной и описанной окружности, а также точкой пересечения высот и медиан.

Свойство 3. В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной. (R=2cdot r)

Уже должно быть очевидно, отчего так.

Посмотри на рисунок: точка( O) – центр треугольника.

Значит, (OB) – радиус описанной окружности (обозначили его (R)), а (OK) – радиус вписанной окружности (обозначим (r)).

Но ведь точка (O) – ещё и точка пересечения медиан! Вспоминаем, что медианы точкой пересечения делятся в отношении (2:1), считая от вершины.

Поэтому (OB=2cdot OK), то есть (R=2cdot r).

Свойство 4. В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны.

Давай удостоверимся в этом.

Вокруг любого треугольника можно описать окружность. Центр описанной вокруг треугольника окружности может лежать как во внутреннем пространстве, так и на стороне треугольника или даже вне его. Для того чтобы найти радиус окружности, описанной вокруг произвольного треугольника, необходимо произведение его сторон разделить на четыре квадратных корня из полупериметра, умноженного на его разность с каждой стороной.

Равнобедренный треугольник имеет стороны a, a, b, подставив которые в вышеприведенную формулу, можно значительно ее упростить и привести к следующему виду:

В прямоугольном треугольнике центр описанной окружности лежит в середине гипотенузы, разделяя ее на две части, каждая из которых соединяется с вершинами треугольника, следовательно, является радиусом. Таким образом, чтобы найти радиус окружности, описанной вокруг прямоугольного треугольника, необходимо гипотенузу разделить на два:

Или этот же радиус можно найти, подставив вместо гипотенузы катеты по теореме Пифагора:

Окружность, описанная около правильного треугольника, обладает всеми свойствами описанной около произвольного треугольника окружности и, кроме того, имеет свои собственные свойства.

1) Центр описанной около треугольника окружности — точка пересечения серединных перпендикуляров к его сторонам.

Поскольку в равностороннем треугольнике медианы, высоты и биссектрисы совпадают, центр описанной около правильного треугольника окружности лежит в точке пересечения его медиан, высот и биссектрис.

Например, в правильном треугольнике ABC AB=BC=AC=a

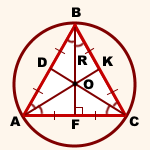
точка O — центр описанной окружности.

AK, BF и CD — медианы, высоты и биссектрисы треугольника ABC.

2) Расстояние от центра описанной окружности до вершин треугольника равно радиусу. Так как центр описанной около равностороннего треугольника окружности лежит на пересечении его медиан, а медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то радиус описанной окружности составляет две трети от длины медианы:

Таким образом, формула радиуса описанной около правильного треугольника окружности —

И обратно, сторона равностороннего треугольника через радиус описанной окружности —

3) Формула для нахождения площади правильного треугольника по его стороне —

Отсюда можем найти площадь через радиус описанной окружности:

Таким образом, формула площади площади правильного треугольника через радиус описанной окружности —

4) Центр описанной около правильного треугольника окружности совпадает с центром вписанной в него окружности.

5) Радиус описанной около равностороннего треугольника окружности в два раза больше радиуса вписанной окружности: