Курсовая работа
по дисциплине «Комбинаторные алгоритмы»
Диаметр множества
Содержание
1.
Введение 1
1.1. Постановка
задачи 1
1.2. Основные
понятия 1
2.
Теоретические материалы 1
2.1. Описание задачи
и методов ее решения 1
2.2. Описание
алгоритма 2
2.3. Оценка сложности
алгоритма 2
3.
Примеры работы алгоритма 2
4.
Описание программы 3
4.1. Функции
программы 3
4.2. Структура
программы 4
4.3. Исходные тексты 4
1. Введение
1.1. Постановка задачи
Необходимо составить демонстрационную
программу, показывающую работу алгоритма
нахождения диаметра множества. Для
нахождения диаметра использовать
алгоритм, основанный на разнице углов
между противолежащими сторонами выпуклой
оболочки множества.
1.2. Основные понятия
Для описания работы системы необходимо
ввести некоторые понятия.
Множество точек – множество точек
на плоскости М = {р1, р2,…,рn},
где рi – точка на плоскости с
координатами (xi,yi),
где i –индекс точки
множества,
n – количество точек в
множестве;
Диаметр множества – максимальное
расстояние между двумя точками множества
D = maxМ[d(pi,pj)],
где точки pi,
pjM,
а d(pi,pj)
– расстояние между двумя точками на
плоскости, d(pi,pj)
= ((xj
— xi)2
+ (yj
— yi)2);
Выпуклая оболочка – такое подмножество,
которое включает в себя все точки
множества, являясь при этом минимальным.
Для всех точек множества при этом должно
выполняться условие: если 2 точки лежат
в выпуклой оболочке, то и отрезок, их
соединяющий, лежит в выпуклой оболочке.
2. Теоретические материалы
2.1. Описание задачи и методов ее решения
Задача нахождения диаметра множества
может решаться несколькими способами.
Тривиально можно решить задачу при
помощи перебора всех пар точек, при этом
время решения составляет O(n2).
Однако имеются способы, позволяющие
решить задачу нахождения диаметра
множества за время O(n
log2n).
Заметим тот факт, что диаметр множества
равен диаметру его выпуклой оболочки
(очевидно). Для построения диаметра
множества нужно:
-
построить для множества выпуклую
оболочку (известны методы, позволяющие
сделать это за время O(n log2n)
– например, метод Киркпатрика-Сайделя); -
нужно рассматривать противолежащие
пары выпуклой оболочки (то есть такие
пары точек, через которые можно провести
опорные прямые – прямые, которые не
пересекают выпуклую оболочку); -
среди противолежащих пар выбрать
максимальную.
2.2. Описание алгоритма
Алгоритм нахождения диаметра множества:
-
Диаметр множества равен диаметру его
выпуклой оболочки, поэтому сначала для
множества находится выпуклая оболочка
(может использоваться метод
Киркпатрика-Сайделя). -
Сначала находятся две крайние по оси
абсцисс точки выпуклой оболочки. Если
есть несколько «левых» точек, то среди
них берется точка с максимальной
ординатой. Если есть несколько «правых»
точек, то среди них берется точка с
минимальной ординатой. Эти точки
выбираются в качестве текущих (P и Q). -
Повторяется последовательность
действий, приведенная ниже, пока точка
Q не окажется самой левой, а точка P –
самой правой.
-
в качестве «претендента» на роль
диаметра рассматривается пара [P,Q]; -
рассматриваются углы наклона прямых:
<P,next(P)> и
<next(Q),Q>
next(A) — следующая после A по часовой стрелке
вершина выпуклой оболочки
-
если угол1<угла2, то P=next(P)
-
если угол1>угла2, то Q=next(Q)
-
если угол1=углу2, то:
-
в качестве «претендентов» на роль
диаметра рассматриваются пары [next(P),Q]
и [P,next(Q)] -
P=next(P) и
Q=next(Q)
Соседние файлы в папке doc
- #
- #
- #
- #
Есть множество точек на плоскости. Нужно найти две самые удалённые из них.
Найдём выпуклую оболочку исходного множества и получим более простую задачу: найти две наиболее удалённые вершины в выпуклом многоугольнике. Сделать это можно за линейное время с помощью метода, который называется вращающиеся калиперы (англ. rotating calipers).
Обоснование: Пусть диаметр с одной стороны содержит точку, которая не принадлежит выпуклой оболочке. Тогда продлим диаметр в эту сторону до пересечения с выпуклой оболочкой. Очевидно, он станет длиннее. А потом заметим, что диаметр станет еще больше, если сдвинуть его к одному из концов ребра, в которое мы уперлись. Конец.
Содержание
- 1 Постановка задачи
- 2 Вращающиеся калиперы
- 2.1 Опорные прямые
- 2.2 Алгоритм
- 2.3 Асимптотика
- 3 Ссылки
Постановка задачи
Пусть — выпуклый многоугольник, в котором порядок обхода вершин направлен против часовой стрелки, и никакие три последовательные точки не лежат на одной прямой. Найти пару чисел , такие, что максимально.
Вращающиеся калиперы
Опорные прямые
| Определение: |
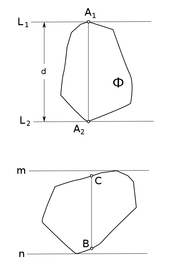
| Прямая называется опорной прямой (англ. line of support) для многоугольника , если его внутренность лежит по одну сторону от , при этом проходит хотя бы через одну из вершин . |
|
|
Так как и — какие угодно граничные точки фигуры , принадлежащие соответственно прямым и , то из перпендикулярности отрезка к прямым и следует, что ни одна из прямых , не может иметь с фигурой целый общий отрезок. Другими словами, каждая из этих прямых содержит единственную граничную точку фигуры .
|
|
Алгоритм
Заметим, что параллельные опорные прямые можно провести не через любую пару точек.
| Определение: |
| Точки, через которые можно провести параллельные опорные прямые, будем называть противолежащими (англ. antipodal). |
Благодаря предыдущей теореме нам нужно рассмотреть только противолежащие точки. Задача в том, чтобы рассмотреть их, не перебирая все пары точек.
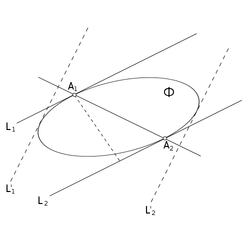
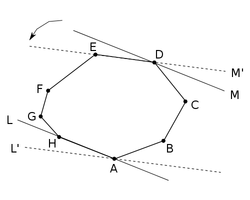
| Рассмотрим рисунок справа. и — опорные прямые, проходящие через вершины и соответственно. Значит, — противолежащая пара точек. Если начать вращать прямые против часовой стрелки вокруг данных точек, они будут оставаться опорными прямыми, пока одна из прямых не станет накладываться на сторону многоугольника. В нашем примере, при вращении к позиции , коснётся точки раньше, чем коснётся , поэтому становится новой парой противолежащих точек.
Теперь будет вращаться вокруг , а продолжит вращаться вокруг , и следующей парой противолежащих точек станет . Продолжая таким образом, мы сгенерируем все пары противолежащих точек, так как параллельные линии пройдут под всеми возможными углами. Определение новой пары противолежащих точек требует только одного сравнения углов, которое можно выполнить с помощью предиката поворота. |
|
Асимптотика
| Теорема: |
|
Представленный выше алгоритм генерирует все пары противолежащих точек в многоугольнике , состоящем из вершин, за время . |
| Доказательство: |
| Данный алгоритм можно реализовать следующим образом: хранить указатели на противолежащие вершины, и на каждой итерации алгоритма увеличивать либо один из данных указателей, либо сразу оба (когда обе прямые проходят через сторону многоугольника), и заканчивать работу, когда опорные прямые сделают полный круг. Таким образом, каждая из вершин будет посещена каждой из прямых не более двух раз. |
Ссылки
- M.I. Shamos Computational geometry, 1978 — С. 76.
- Яглом И.М., Болтянский В.Г. Выпуклые фигуры, 1951 — С. 20, 144.
- Реализация — Github.com
← →
Pat
(2003-04-06 21:39)
[0]
Дано евклидово пространство размерностью n, в котором находится k точек. Составить программу нахождения диаметра данного множества (максимального расстояния между точками множества). Вывести координаты диаметра.
Собственно, объясните мне, что такое диаметр множества. Как его найти…и как считаются координаты диаметра.
P.S. Просьба к книгам не отправлять. Просто ответьте, кто знает.
← →
kaif
(2003-04-06 21:44)
[1]
Ты же сам говоришь, что диаметром называется
«максимальное расстояние между точками множества».
Так в чем проблема?
Другое дело, что простой перебор всех расстояний при большом числе точек может оказаться слишком плохим алгоритмом…
Расстоянием между двумя точками, я так думаю, называется корень квадратный из суммы квадратов расстояний по всем осям системы координат.
← →
Pat
(2003-04-06 21:50)
[2]
>kaif © (06.04.03 21:44)
ОК…с расстоянием, вообще-то больших проблем не было. Да и там все точки вручную вводятся. Так что, обычный перебор подошел..
А как быть с
координатами диаметра? :-(( Вот тут совсем глухо. Хотя есть мысль, что это середина вектора, соединяющего крайние точки диаметра…
← →
uw
(2003-04-06 21:53)
[3]
Ну, пусть это будут координаты начала и конца.
← →
NetBreaker666
(2003-04-06 23:32)
[4]
Если метрич. пространство — евклидово, то метрика (т.е. расстояние) задается как sum((x[i]-y[i])^2) ^(1/2).
Диаметр — максимальное расстояние мажду двумя точками множества.
Его координаты — есть координаты точек.
Условие задачи не корректно: тебе дано множество из пространства. (А не само пространство).
Можно тупым перебором, но алгоритмы и побыстрее. Ща на метро опаздываю — если интересно — завтра расскажу.
← →
Pat
(2003-04-07 00:58)
[5]
Естественно интересно… :-))
Вот только не понятна формула sum((x[i]-y[i])^2) ^(1/2).
Всю жазнь расстояние считал как sqr((x1-x2)^2+(y1-y2)^2) — это для двухмерного пространства..аналогично и для n-мерного, только корень n-ой степени и сумма квадратов по всем координатам…
>Диаметр — максимальное расстояние мажду двумя точками множества.
Теперь для тех, кто в Таньке…т.е. для меня :-)) Это значит, что нужно найти всевозможные расстояние между всеми точками и выбрать среди них наибольшее. Это и будет диаметр. Так или я что-то не правильно понял?
← →
panov
(2003-04-07 01:36)
[6]
Координаты диаметра… Ну-ну…
← →
MBo
(2003-04-07 06:27)
[7]
>Вот только не понятна формула
Корень из суммы разностей координат двух точек по всем измерениям
k,l — номера точек
Sqrt(Sum по i до N, где N-размерность пространства Sqr(X[i,k]-X[i,l]))
X-общее обозначение координат, т.е., например, для трехмерного случая X[1]=x, X[2]=y, X[3]=z
← →
Думкин
(2003-04-07 07:15)
[8]
Диаметр множества скаляр. О каких координатах может идти речь?
Другое дело найти координаты точек, где сей «диаметр» реализуется.
← →
kaif
(2003-04-07 10:17)
[9]
Я думаю, что центром лучше всего называть точку, делящую «диаметр» пополам. То есть. если ты нашел две максимально удаленные точки, то это будет точка с координатами:
x2-x1/2,y2-y1/2….,
где x1 и x2 — координаты двух «крайних» точек по оси x и так далее.
← →
Pat
(2003-04-07 15:56)
[10]
>Координаты диаметра… Ну-ну…
Почему диаметр не может быть вектором?
← →
MBo
(2003-04-07 16:06)
[11]
потому что диаметр — скалярная величина, геометрическая характеристика.
← →
Mystic
(2003-04-07 16:09)
[12]
По определению
diam M = sup_{x,y in M} ||x-y||
diam M = sup ||x-y||
x,y in M
Из этого определения видно, что диаметр множества скаляр.
Кстати, ты не думал над способом задания множества? В общем случае задачка неразрешимая 
← →
NetBreaker666
(2003-04-07 16:29)
[13]
> Естественно интересно… :-))
> Вот только не понятна формула sum((x[i]-y[i])^2) ^(1/2).
> Всю жазнь расстояние считал как sqr((x1-x2)^2+(y1-y2)^2)
> — это для двухмерного пространства..аналогично и для n-мерного,
> только корень n-ой степени и сумма квадратов по всем координатам…
Для n-мерного пространства в евклидовом метр. пр-ве метрика задается как SQRT(SUMM((x[i]-y[i])^2, i=1..n)) (если в терминах Maple 
← →
kaif
(2003-04-07 22:49)
[14]
По-моему все и так понятно. Диаметр — максимальный корень квадратный из суммы квадратов разниц координат по каждой оси между каждыми двумя точками. Центр — видимо, просто центр отрезка, соединяющего две точки, расстояние между которыми максимально.
Единственное противоречие, которое мне бросается в глаза, так это то, что непонятно, что считать центром, если нашлись 2 пары точек, расстояния между которыми (в каждой паре) в точности равны диаметру множества.
Я думаю именно это противоречие сводит на нет понятие центра.
← →
Думкин
(2003-04-08 06:01)
[15]
> MBo © (07.04.03 16:06)
геометрические характерстики — это и многое иное. В данном случае речь, действительно, — просто о скаляре.
> kaif © (07.04.03 22:49)
Зачем мучить себя определениями, которые в угоду кому-то высасывать из пальца?
Если так, то что есть: «Прибыльно-убыточная экономика в свете планово-неубыточного факториала псевдодурости?»
|
Liori 4 / 4 / 5 Регистрация: 30.08.2012 Сообщений: 155 |
||||
|
1 |
||||
Найти диаметр множества29.03.2015, 00:45. Показов 5246. Ответов 5 Метки нет (Все метки)
Найти диаметр множества – максимальное расстояние между любыми двумя точками с помощью структуры
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
29.03.2015, 00:45 |
|
Ответы с готовыми решениями: Найти диаметр графа
Для множества точек на плоскости найти диаметр и центр минимальной описанной окружности Вычислить диаметр множества в метрическом пространстве 5 |
|
Gr1f0nn 244 / 164 / 133 Регистрация: 30.09.2012 Сообщений: 690 |
||||
|
29.03.2015, 00:54 |
2 |
|||
|
Скорее всего D должно было так считаться:
0 |
|
4 / 4 / 5 Регистрация: 30.08.2012 Сообщений: 155 |
|
|
29.03.2015, 00:58 [ТС] |
3 |
|
Gr1f0nn, к сожалению, так не работает, постоянно получается 0.0000
0 |
|
Gr1f0nn 244 / 164 / 133 Регистрация: 30.09.2012 Сообщений: 690 |
||||||||||||
|
29.03.2015, 01:09 |
4 |
|||||||||||
|
РешениеВ конце
Замените на
Добавлено через 52 секунды
0 |
|
4 / 4 / 5 Регистрация: 30.08.2012 Сообщений: 155 |
|
|
29.03.2015, 01:14 [ТС] |
5 |
|
Gr1f0nn, все равно не получается(
0 |
|
Gr1f0nn 244 / 164 / 133 Регистрация: 30.09.2012 Сообщений: 690 |
||||
|
29.03.2015, 01:20 |
6 |
|||
Про корень в формуле мы забыли ^_^
1 |
Автоматика, телемеханика и связь на железных дорогах
127
УДК 513.8
ОБ ОПРЕДЕЛЕНИИ ДИАМЕТРА КОНЕЧНОГО МНОЖЕСТВА ТОЧЕК В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
Е.Ю. Морозова
Аннотация
В работе предложен эффективный алгоритм определения диаметра конечного множества точек в евклидовом пространстве. При этом рассматривается задача нахождения глобального максимума выпуклой функции на выпуклом многогранном множестве. В основе подхода лежит комбинированный метод, позволяющий традиционными методами находить точки локального минимума и метод статистических испытаний, позволяющий улучшать найденные точки.
Введение
Задача определения диаметра конечного множества точек возникает во многих областях: астрономии, микробиологии, популяционной генетике и др. В случае больших значений числа точек множества непосредственное вычисление диаметра требует значительных затрат машинного времени. Настоящая статья посвящена описанию алгоритма определения диаметра множества точек, который при больших является значительно более эффективным.
1. Постановка задачи
В предлагаемом алгоритме задача определения диаметра конечного множества точек в евклидовом пространстве сводится к задаче нахождения глобального максимума выпуклой функции на выпуклом многогранном множестве.
Рассматривается задача выпуклого программирования вида:
Р(х,у) ~^ max,
(х,у) е conv(V) х conv(V),
где р(х, у) — евклидово расстояние между точками х и у, V — множество вершин выпуклого многогранника.
Известия Петербургского университета путей сообщения
2004/1
128
Автоматика, телемеханика и связь на железных дорогах
2. Основные замечания
Пусть X = {х\х2,…,х”} — конечное множество точек в евклидовом пространстве Rd.
Диаметром множества X называется число
Dx = max<р(л-\л-&) /, / = I..ч\, где
Р (x‘,xJ) = JZ(4-*Jty
евклидово
расстояние между точками х1 и х]. Предварительно заметим, что Dx=Dconv(X), где conv(X) — выпуклая оболочка множества X,
геометрически представляющая собой выпуклый многогранник с множеством вершин Extr(conv(X)) = {v&,…,vvJ = V. Поэтому
Dx =max{p(v&,vJ)| i,j = \,…,N}. Однако число N также может оказаться
большим, в этом случае эффективным оказывается алгоритм, приводимый в этой статье.
В настоящее время известны различные алгоритмы построения выпуклой оболочки множества, в частности, в пакете MATLAB имеется встроенная функция CONVHULLN, входным аргументом которой является матрица, образованная столбцами координат элементов множества X, а выходным аргументом является матрица, образованная столбцами координат элементов множества V. Незначительная модификация стандартного алгоритма позволяет параллельно с построением множества V строить также матрицу Z = z , где
1, если вершины V ,vJ смежны (соединены
ребром) в многограннике conv(V)
О, иначе
Таким образом, в дальнейшем будем считать, что имеется эффективная программа, выдающая по множеству X множество V и матрицу Z.
3. Описание алгоритма
Нетрудно видеть, что диаметр множества X является значением задачи (1), для решения которой может быть использован метод нахождения глобального минимума квазивогнутой функции на выпуклом многогранном множестве (Баушев А.Н., Морозова Е.Ю. и др., 2003). Для задачи нахождения глобального максимума выпуклой функции на выпуклом многогранном множестве основная теорема может быть переформулирована следующим образом.
Теорема 1. Квазивыпуклая функция /*’: С R, заданная на замкнутом ограниченном выпуклом множестве С с R», достигает
2004/1
Известия Петербургского университета путей сообщения
Автоматика, телемеханика и связь на железных дорогах
129
наибольшего значения, по крайней мере, в одной из крайних точек множества C.
Доказательство. Функция называется квазивыпуклой, если для каждого вещественного числа с множество {х :F(x)< с} выпукло.
Если х = а1х1 + … + akxk — выпуклая комбинация точек {х1,.—,-^}, то для квазивыпуклой функции F выполняется неравенство
F(x) < шах {EX*1F(xk)}.
Поскольку каждая точка выпуклого многогранника представима в виде выпуклой комбинации его вершин, то из этого неравенства следует, что в любой точке хеС значение функции F(x) не больше чем ее значение в крайней точке с наибольшим значением функции.
Следовательно, точка глобального максимума функции р на множестве С = conv(V) х conv(V) находится среди крайних точек этого множества.
Крайняя точка, в которой значение целевой функции не меньше ее значений в соседних точках, называется точкой локального максимума функции F (х). Основной проблемой при решении задачи (1) является то обстоятельство, что для квазивыпуклой функции, заданной на выпуклом множестве, точка локального максимума не обязательно является и точкой глобального максимума функции на этом множестве.
Приводимый ниже алгоритм включает следующие основные элементы:
1. Нахождение точки локального максимума.
2. Статистическое моделирование направлений поиска области в допустимом множестве с большим значением целевой функции.
3. Усечение исходного множества опорными гиперплоскостями к поверхности текущего уровня целевой функции.
Точка локального максимума функции может быть найдена просто, поскольку предполагается заданной матрица Z, по которой для каждой крайней точки легко находится множество соседних крайних точек. Если среди соседних точек находится точка с большим значением функции, то осуществляется переход к этой точке и т.д. до тех пор, пока не будет найдена точка локального максимума.
Пусть и0 — найденная точка локального максимума и р(и°) = т°. Обозначим соседние с и0 вершины (крайние точки) выпуклого множества С через uJ;j = \,…J . Пусть ис — случайная точка на
выпуклой оболочке conv{U,…, и1}.
Известия Петербургского университета путей сообщения
2004/1
130
Автоматика, телемеханика и связь на железных дорогах
Находим точку wc пересечения луча h = {u‘=и°+t(uc-u°),t >0} с выпуклым множеством С. Искомой точке wc будет соответствовать значение tc — max{/ Положим wc = utmsx, p(wc) = m.
Если m < in , то попытка моделирования uc считается неудачной, при этом следует повторить процесс моделирования. В противном случае, когда т > т , строим опорную гиперплоскость к поверхности уровня р (и) = т в точке wc. Из полупространств, определяемых этой
гиперплоскостью выберем то, которое не содержит и0. При этом допустимое множество сужается, и к полученной задаче снова применяется описанный алгоритм.
Процесс останавливается тогда, когда все попытки моделирования точки иc оказываются неудачными. Общее число попыток предполагается ограниченным числом м, которое является входным параметром алгоритма.
Опишем наиболее простой способ моделирования случайной точки ис. Используя стандартные датчики случайных чисел, смоделируем / -1 точку Xx,…,Xj_x с равномерным распределением на отрезке [0,1]. Образуем из этих точек вариационный ряд Х(х) < Х(2) <… < Х(М).
ПустьХ(0) =0, Х(1) =1, А,. =Х(.) -Х(._х), i = 1,…,/. Положим ис = ^Аг •и1.
2=1
Корректность работы алгоритма основывается на следующем утверждении.
Теорема 2. Обозначим через им крайнюю точку локального максимума, найденную после завершения работы алгоритма, а через С* множество точек глобального максимума функции р на множестве С.
Вероятность события {г/4 еС*} стремится к единице при неограниченном возрастании M.
Доказательство теоремы проводится аналогично доказательству теоремы 2 (Баушев А.Н., Морозова Е.Ю., 2004).
Для реализации описанного алгоритма была разработана программа на базе пакета MATLAB.
4. Пример
Для иллюстрации работы алгоритма был рассмотрен следующий пример. Было сгенерировано сто точек из двумерного нормального распределения и по описанному алгоритму найден диаметр этого множества. В процессе алгоритма были найдены две точки локального максимума функции р, которым соответствуют диагонали на рисунке 1. Вторая из этих точек оказалась точкой глобального максимума.
2004/1
Известия Петербургского университета путей сообщения
Автоматика, телемеханика и связь на железных дорогах
131
5. Заключение
Предложенный алгоритм позволяет находить диаметр конечного множества точек в евклидовом пространстве. Алгоритм является эффективным с точки зрения затрат машинного времени в случае большого числа точек .
Рис.1. Иллюстрация работы алгоритма на случайном плоском
множестве точек
6. Литература
Баушев А.Н., Морозова Е.Ю., Осьминин А.Т., Елисеев С.Ю., Рящиков А.С. О задаче квазивогнутого программирования и её применении к проблеме оптимизации железнодорожных перевозок. — Обозрение прикладной и промышленной математики. Т. 10. В. 3, 2003, с. 603-604
Баушев А.Н., Морозова Е.Ю. Метод статистических испытаний в задаче квазивогнутого программирования. // Обозрение прикладной и промышленной математики. Т.11. В.1, 2004, с.34-40
Известия Петербургского университета путей сообщения
2004/1
ДИАМЕТР МНОЖЕСТВА ВЫПУКЛАЯ ОБОЛОЧКА МНОЖЕСТВА ЗАДАЧА ВЫПУКЛОГО ПРОГРАММИРОВАНИЯ МЕТОД СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ


 дан радиус окружности найти её диаметр с++
дан радиус окружности найти её диаметр с++