Вычисление диаметра трубы по хорде
Бывают ситуации, когда необходимо измерить диаметр чего-либо, например, трубопровода, но нет возможности измерить длину окружности (из-за изоляции или температуры).
В этом случае можно применить метод вычисления диаметра по хорде. Для этого метода необходим только штангенциркуль.
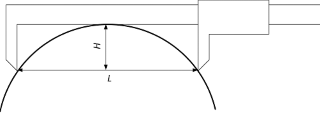
- Прикладываем его, как показано на рис. 1;
- измеряем длину L;
- измеряем высоту губок штангенциркуля Н;
- вычисляем диаметр по формуле D = (L 2 ⁄ 4H) + H или
- вычисляем радиус по формуле r = (L 2 + 4H 2 ) ⁄ 8H
Рисунок 1
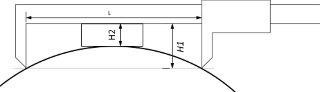
Если под рукой только «штангель» с длинными губками или не хватает его измеряемого диапазона можно применить какую-нибудь «проставку». В идеале подойдёт плоскопараллельная концевая мера… 
Её надо вставить, как показано на рисунке 2, и при вычислении, от длины губок отнять высоту этой «проставки». Н = Н1 — Н2
Рисунок 2
Точность этого метода зависит, только от инструмента, который Вы будете применять.
Как найти диаметр окружности
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.
Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.
Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.
Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Как узнать диаметр. Формулы
В данной теме нам предстоит узнать три формулы:
1. Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
2. Если перед нами стоит задача найти диаметр по длине окружности
D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.
Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
3. Если есть чертеж окружности
- Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.
- Отметить точки пересечения прямой и окружности.
- Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.
- Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
- Теперь осталось измерить диаметр круга при помощи линейки. Получилось!
Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.
Как найти диаметр окружности, зная хорду и расстояния от центра окружности до хорды?
Геометрия | 5 — 9 классы
Как найти диаметр окружности, зная хорду и расстояния от центра окружности до хорды?
Пол хорды и расстояние от хорды до центра окружности — это два катета.
По теореме Пифагора находите гипотенузу.
Гипотенуза — это радиус.
Соответственно, чтобы получить диаметр, умножьте его на два.
10 номер?
Длина хорды окружности 72, расстояние от центра окружности до этой хорды 27.
Длина хорды окружности равна 64, а расстояние от центра окружности до этой хорды равно 60?
Длина хорды окружности равна 64, а расстояние от центра окружности до этой хорды равно 60.
Найдите диаметр окружности.
Длинна хорды окружности равна 88, а расстояние от центра окружности до этой хорды равно 33?
Длинна хорды окружности равна 88, а расстояние от центра окружности до этой хорды равно 33.
Найдите диаметр окружности.
Длина хорды окружности равна 120 а расстояние от центра окружности до этой хорды 45 найдите диаметр окружности?
Длина хорды окружности равна 120 а расстояние от центра окружности до этой хорды 45 найдите диаметр окружности.
Длина хорды = 30 Диаметр окружности = 34 Найти : ОО’ от центра окружности до хорды?
Длина хорды = 30 Диаметр окружности = 34 Найти : ОО’ от центра окружности до хорды.
Длина хорды 48, а расстояние от центра окружности до этой хорды 70, найти диаметр окружности?
Длина хорды 48, а расстояние от центра окружности до этой хорды 70, найти диаметр окружности.
Длина хорды окружности равна88, а расстояние от центра окружности до этой хорды равно 33?
Длина хорды окружности равна88, а расстояние от центра окружности до этой хорды равно 33.
Найдите диаметр окружности.
Длина хорды окружности равна 26, а расстояние от центра окружности до этой хорды равно 10?
Длина хорды окружности равна 26, а расстояние от центра окружности до этой хорды равно 10.
Найдите диаметр окружности.
Длина хорды окружности равна 48 , а расстояние от центра окружности до этой хорды равно 7 ?
Длина хорды окружности равна 48 , а расстояние от центра окружности до этой хорды равно 7 .
Найдите диаметр окружности.
Длина хорды окружности равна 30, а расстояние от центра окружности до этой хорды равно 36?
Длина хорды окружности равна 30, а расстояние от центра окружности до этой хорды равно 36.
Найдите диаметр окружности.
Вы открыли страницу вопроса Как найти диаметр окружности, зная хорду и расстояния от центра окружности до хорды?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 5 — 9 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.
http://skysmart.ru/articles/mathematic/diametr-okruzhnosti
http://geometria.my-dict.ru/q/1311607_kak-najti-diametr-okruznosti-znaa-hordu/
|
Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.
Радиус окружности с длиной хорды окружности связан формулой:
Здесь R — радиус L — длина хорды, a — центральный угол. Далее я покажу построения для расчёта радиуса:
Найдём радиус из прямоугольного треугольника OKB. Здесь KB=L/2=72/2=36. Далее по теореме Пифагора получается: OB=sqrt(OK^2+KB^2)=sqrt(27^2+36^2)=45.Радиус окружности: R=OB=45 единиц. Диаметр окружности: D=2*R=2*45-90 единиц. Ответ: диаметр окружности D=90 единиц. автор вопроса выбрал этот ответ лучшим
Радиус окружности можно высчитать, как гипотенузу прямоугольного треугольника, где один катет, это половина длины хорды, а другой катет — это расстояние от центра окружности до хорды: sqr((72/2)² + 27²) = 45 единиц, а если радиус составляет 45 единиц, диаметр тогда будет равен 90 единиц. Знаете ответ? |
HOUSEHAND.ru —
Сегмент — плоская фигура, заключённая между дугой и её хордой. Как частный случай, круговой сегмент: часть круга, ограниченная дугой окружности и её хордой или секущей.
Для начала расчёта выберите известные параметры, по которым будут произведены расчёты, за тем введите их и нажмите кнопку «Рассчитать».
Если Вам необходим узнать по каким формулам ведется расчет для фигуры, а так же задать единицы измерения или сохранить расчет в PDF, то воспользуйтесь сайтом calc-online24.ru
Вычисление диаметра трубы по хорде
Бывают ситуации, когда необходимо измерить диаметр чего-либо, например, трубопровода, но нет возможности измерить длину окружности (из-за изоляции или температуры).
В этом случае можно применить метод вычисления диаметра по хорде. Для этого метода необходим только штангенциркуль.
- Прикладываем его, как показано на рис. 1;
- измеряем длину L;
- измеряем высоту губок штангенциркуля Н;
- вычисляем диаметр по формуле D = (L 2 ⁄ 4H) + H или
- вычисляем радиус по формуле r = (L 2 + 4H 2 ) ⁄ 8H
Рисунок 1
Если под рукой только «штангель» с длинными губками или не хватает его измеряемого диапазона можно применить какую-нибудь «проставку». В идеале подойдёт плоскопараллельная концевая мера… 😉 Её надо вставить, как показано на рисунке 2, и при вычислении, от длины губок отнять высоту этой «проставки». Н = Н1 — Н2
Рисунок 2
Точность этого метода зависит, только от инструмента, который Вы будете применять.
Длина хорды и высота сегмента круга
Зная длину хорды и высоту сегмента круга, необходимо для вычисления всех остальных параметров воспользоваться одновременно обеими формулами, выразив через них радиус круга. c=2r sin〖α/2〗 h=r(1-cos〖α/2〗 ) r=h/2+c^2/8h
Угол сегмента круга можно выразить через любую из вышеприведенных формул для хорды и высоты сегмента. В случае с хордой синус половинного угла будет равен ее длине, деленной на два радиуса. sin〖α/2〗=c/2r
Длина дуги и площадь сегмента круга вычисляются по стандартным формулам, в которые необходимо подставить полученное для радиуса выражение. P=αr=α(h/2+c^2/8h) S=r^2 (α/2-sinα )=1/2 (h/2+c^2/8h)^2 (α-sinα )
По какой формуле можно найти диаметр окружности? Если известна длина хорды и расстояние от цента окружности до этой хорды .
Светило науки — 88 ответов — 482 помощи
1. Проведите радиусы от центра окружности к концам хорды
2. Вам дано расстояние от центра окружности до хорды — это один катет получившегося прямоугольного треугольника, а половина длины хорды — второй. (т.к весь большой треугольник — равнобедренный, разбитый на два равных прямогугольных)
3. По теореме Пифагора найдите гипотенузу — радиус
4. Умножьте радиус на два и получите диаметр.
Обращайтесь 
Геометрия круга
Круг, его части, их размеры и соотношения — вещи, с которыми ювелир постоянно сталкивается. Кольца, браслеты, касты, трубки, шары, спирали — много всего круглого приходится делать. Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии?..
Давайте сначала рассмотрим, какие у круга бывают части и как они называются.
- Окружность — линия, ограничивающая круг.
- Дуга — часть окружности.
- Радиус — отрезок, соединяющий центр круга с какой-либо точкой окружности.
- Хорда — отрезок, соединяющий две точки окружности.
- Сегмент — часть круга, ограниченная хордой и дугой.
- Сектор — часть круга, ограниченная двумя радиусами и дугой.
Интересующие нас величины и их обозначения:
Теперь посмотрим, какие задачи, связанные с частями круга, приходится решать.
- Найти длину развертки какой-либо части кольца (браслета). Задан диаметр и хорда (вариант: диаметр и центральный угол), найти длину дуги.
- Есть рисунок на плоскости, надо узнать его размер в проекции после сгибания в дугу. Заданы длина дуги и диаметр, найти длину хорды.
- Узнать высоту детали, полученной сгибанием плоской заготовки в дугу. Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.
Жизнь подскажет и другие примеры, а эти я привел только для того, чтобы показать необходимость задания каких-нибудь двух параметров для нахождения всех остальных. Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.
Чтобы зря не грузить читателя, подробных решений я приводить не буду, а приведу лишь результаты в виде формул (те случаи, где нет формального решения, я оговорю по ходу дела).
И еще одно замечание: о единицах измерения. Все величины, кроме центрального угла, измеряются в одних и тех же абстрактных единицах. Это значит, что если, к примеру, вы задаёте одну величину в миллиметрах, то другую не надо задавать в сантиметрах, а результирующие значения будут измеряться в тех же миллиметрах (а площади — в квадратных миллиметрах). То же самое можно сказать и про дюймы, футы и морские мили.
И только центральный угол во всех случаях измеряется в градусах и ни в чём другом. Потому что, как показывает практика, люди, проектирующие что-нибудь круглое, не склонны измерять углы в радианах. Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.
1. Даны диаметр D и длина дуги L
; длина хорды 
;
высота сегмента 
; центральный угол 
.
2. Даны диаметр D и длина хорды X
; длина дуги 
;
высота сегмента ; центральный угол 
.
Поскольку хорда делит круг на два сегмента, у этой задачи не одно, а два решения. Чтобы получить второе, нужно в приведенных выше формулах заменить угол α на угол 
.
3. Даны диаметр D и центральный угол φ
; длина дуги ;
длина хорды ; высота сегмента .
4. Даны диаметр D и высота сегмента H
; длина дуги ;
длина хорды ; центральный угол .
6. Даны длина дуги L и центральный угол φ
; диаметр 
;
длина хорды ; высота сегмента .
8. Даны длина хорды X и центральный угол φ
; длина дуги 
;
диаметр ; высота сегмента .
9. Даны длина хорды X и высота сегмента H
; длина дуги ;
диаметр ; центральный угол .
10. Даны центральный угол φ и высота сегмента H
; диаметр 
;
длина дуги ; длина хорды .
Внимательный читатель не мог не заметить, что я пропустил два варианта:
5. Даны длина дуги L и длина хорды X
7. Даны длина дуги L и высота сегмента H
Это как раз те два неприятных случая, когда у задачи нет решения, которое можно было бы записать в виде формулы. А задача-то не такая уж редкая. Например, у вас есть плоская заготовка длины L, и вы хотите согнуть ее так, чтобы ее длина стала X (или высота стала H). Какого диаметра взять оправку (ригель)?
Задача эта сводится к решению уравнений:
; — в варианте 5
; — в варианте 7
и хоть они и не решаются аналитически, зато легко решаются программным способом. И я даже знаю, где взять такую программу: на этом самом сайте, под именем Segment. Всё то, что я тут длинно рассказываю, она делает за микросекунды.
Для полноты картины добавим к результатам наших вычислений длину окружности и три значения площадей — круга, сектора и сегмента. (Площади нам очень помогут при вычислении массы всяких круглых и полукруглых деталей, но об этом — в отдельной статье.) Все эти величины вычисляются по одним и тем же формулам:
длина окружности 
;
площадь круга 
;
площадь сектора 
;
площадь сегмента 
;
И в заключение еще раз напомню о существовании абсолютно бесплатной программы, которая выполняет все перечисленные вычисления, освобождая вас от необходимости вспоминать, что такое арктангенс и где его искать.
Программа Segment