Диагональ стороны куба является диагональю квадрата, который представляет собой грань куба. Исходя из этого, ребро куба может быть вычислено по формуле отношения диагонали стороны куба к корню из двух.
a=d/√2
Тогда площадь стороны куба, равная квадрату его ребра, будет рассчитываться как квадрат диагонали, деленный на два. Чтобы вычислить площадь боковой и полной поверхности куба, необходимо умножить полученное выражение на 4 или 6 соответственно.
S=a^2=d^2/2
S_(б.п.)=4a^2=(4d^2)/2=2d^2
S_(п.п.)=6a^2=(6d^2)/2=3d^2
Чтобы вычислить объем куба, нужно возвести его ребро в третью – кубическую – степень, для этого все выражение, полученное для ребра куба через диагональ его стороны, возводится в степень.
V=a^3=(d/√2)^3=d^3/(2√2)
Периметр куба равен ребру куба, умноженному на двенадцать. Подставив вместо ребра куба выражение через диагональ и сократив коэффициенты, получим следующую формулу для периметра:
P=12a=12d/√2=6√2 d
Диагональ куба через диагональ его стороны можно найти, используя теорему Пифагора, согласно которой квадрат диагонали куба равен сумме квадратов диагонали стороны и бокового ребра, соединенных в прямоугольный треугольник. (рис.2.1.)
a^2+d^2=D^2
D^2=d^2/2+d^2
D^2=(3d^2)/2
D=√(3/2) d
Чтобы вычислить радиус сферы, вписанной в куб, необходимо разделить на два ребро куба, то есть разделить на два корня из двух диагональ его стороны. Радиус сферы, описанной вокруг куба, в свою очередь равен половине диагонали куба, вместо которой также можно использовать полученное через диагональ стороны выражение. (рис.2.2.,2.3)
r=a/2=d/(2√2)
R=D/2=(√(3/2) d)/2
Как найти диагональ куба, если известна, например, длина его ребра, площадь, объем? Если вам известно хотя бы одно какое-либо значение куба, то вы запросто сможете найти не только его диагональ, но и все остальные значения. В этом вам поможет простой калькулятор. Заполните любую ячейку и нажмите на кнопку “Рассчитать”. В результате также появятся формулы вычислений, что способствует лучшему пониманию темы и самостоятельному решению задач.
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Радиус вписанной сферы (r)
Радиус описывающей сферы (R)
Радиус сферы, прилегающей к ребрам (Re)
Площадь поверхности куба (S)
Округление:
* — обязательно заполнить
|
Ответ зависит от исходных данных, которые у вас есть по этому кубу. К примеру, если у вас есть длина ребра этого куба (назовем ее а, диагональ куба можно найти в двух последовательных операциях:
В результате мы получаем длину диагонали куба с = a?3 автор вопроса выбрал этот ответ лучшим Ракитин Сергей 9 лет назад Насколько я понимаю, диагональ будет больше стороны куба в корень из 3 раз. Поможет в её нахождении Вам теорема Пифагора: диагональ будет равна гипотенузе треугольника, одним катетом которого будет сторона куба, а другим — диагональ основания. Знаете ответ? |
Смотрите также: Объемный куб своими руками, как, из чего сделать? Схемы, развертки куба? В каких городах Кубы есть аэропорты? Куб компаньон своими руками из игры portal как сделать? Где приобрести, купить брелок и вещи и сам куб компаньон из игры portal? Как найти объём куба зная диагональ? Если шар, идеально гладкий куб и цилиндр будут (см. в описании)? Формула. Как найти объем куба, если диагональ равна корню из 48, 12 или 3? Как узнать размеры телевизора, если дана диагональ в дюймах? Какой телевизор лучше купить в спальню: ЖК, плазму, LED или LCD? Может ли пешеход переходить дорогу или перекресток по диагонали? |
A cube is defined as a 3D solid object which has six square faces and all sides equal to each other. It is one of the five platonic solids and is also known as a regular hexahedron. Six square faces, eight vertices, and twelve edges make up the cube. Its length, breadth and height all are same as it is a square with all sides of the same length. The common line between any two faces of a cube is called its edge. It acts as a boundary line between two faces.
Diagonal of a cube
A cube’s diagonal is the line segment connecting any two non-adjacent vertices of the cube. There are two types of cube diagonals, that is, face diagonal and body diagonal. A face diagonal joins two non-adjacent vertices via a single face while a body diagonal does the same by passing through the body of the cube. There are 12 face diagonals and 4 body diagonals possible inside a cube.
Face diagonal formula
Length of face diagonal of cube = √2a
where,
a is the side length of cube.
Body diagonal formula
Length of body diagonal of cube = √3a
where,
a is the side length of cube.
Derivation
Suppose we have a cube with side length a, face diagonal d and body diagonal D.
Now it is known that face diagonal is the hypotenuse of the right triangle it forms with two side lengths.
So, using Pythagoras theorem we get,
d2 = a2 + a2
d2 = 2a2
d = √2a …….. (1)
Also, the face diagonal and one side length form a right triangle with body diagonal as hypotenuse.
Again using Pythagoras theorem we get,
D2 = a2 + d2
Using (1) we get,
D2 = a2 + (√2a)2
D2 = a2 + 2a2
D2 = 3a2
D = √3a
This derives the formulas for face diagonals and body diagonals of a cube.
Sample Problems
Problem 1. Calculate the face diagonal of a cube of side length 2 m.
Solution:
We have,
a = 2
Using the formula we get,
d = √2a
= √2 (2)
= (1.414) (2)
= 2.83 m
Problem 2. Calculate the face diagonal of a cube of side length 5 m.
Solution:
We have,
a = 5
Using the formula we get,
d = √2a
= √2 (5)
= (1.414) (5)
= 7.07 m
Problem 3. Calculate the body diagonal of a cube of side length 3 m.
Solution:
We have,
a = 3
Using the formula we get,
D = √3a
= √3 (3)
= (1.732) (3)
= 5.196 m
Problem 4. Calculate the body diagonal of a cube of side length 7 m.
Solution:
We have,
a = 7
Using the formula we get,
D = √3a
= √3 (7)
= (1.732) (7)
= 12.12 m
Problem 5. Calculate the side length if the face diagonal of a cube is 6 m.
Solution:
We have,
d = 6
Using the formula we get,
d = √2a
=> a = d/√2
= 6/√2
= 4.24 m
Problem 6. Calculate the side length if the body diagonal of a cube is 13√3 m.
Solution:
We have,
D = 13√3
Using the formula we get,
D = √3a
=> a = D/√3
= 13√3/√3
= 13 m
Problem 7. Calculate the body diagonal of a cube if its face diagonal is 9√2 m.
Solution:
We have,
d = 9√2
Find the side length.
d = √2a
=> a = d/√2
= 9√2/√2
= 9 m
Now using the formula we get,
D = √3a
= √3 (9)
= 15.58 m
Last Updated :
15 May, 2022
Like Article
Save Article
Формула диагонали куба через сторону
Нам нужна формула диагонали куба! И я до сих пор не знал о её существовании — мы докажем формулу диагонали куба и начнём с того, что покажем формулу диагонали куба – вот она:
Картинку куба см.ниже…
с = a√3
Что собственно мы должная сделать!?
Мы должны вывести чему равна диагональ «с» и выразить её через строну куба.
Доаказетльство формулы диагонали куба
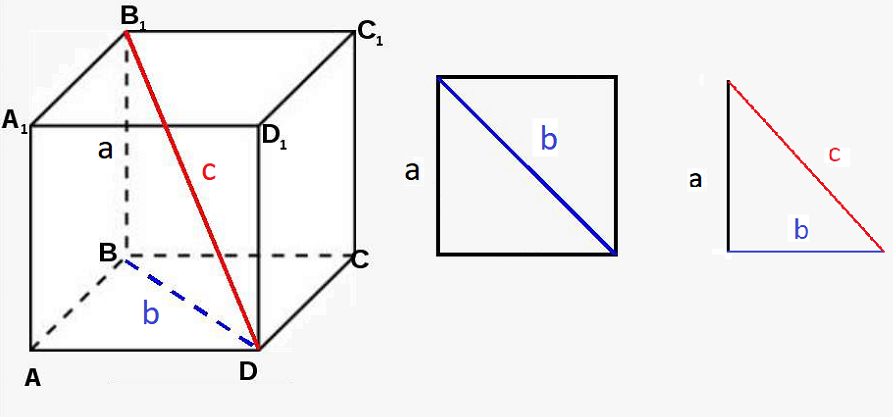
Начнем с того, что вот она картинка и по ней уже все становится ясно! Нам потребуется формула Пифагора, которая и позволит нам вывести и доказать формулу диагонали куба!
Как видим – нам нужна диагональ куба под буквой «c» из теоремы Пифагора мы знаем что:
Для трегольника справа:
c2 = a2 + b2
Получим корень от общего выражения — слева получим «с» — справа получим корень из суммы квадратов стронь…
c = √( a2 + b2)
Уже видите, что нужно сделать дальше!?
Далее нам нужен левый треугольник в котором нас интересует сторона «b»
Частный случай терема Пифагора ели две стороны треугольника равны:
b2 = 2a2
Теперь в верхней формуле заменяем нашу строну «b»
c = √(a2 + 2a2) => √(3а2) = а√3
Мы доказали формулу диагонали куба!
Написать что-нибудь…
куб диагональ формула ,
диагональ куба формула ,
куб диагональ куба формула ,
формула куба через диагональ ,
как найти диагональ куба формула ,
формула нахождения диагонали куба ,
формула диагонали куба через сторону ,
диагональ грани куба формула ,
чему равна диагональ куба формула ,
формула длины диагонали куба ,
диагональ куба равна сумме формула ,
главная диагональ куба формула ,