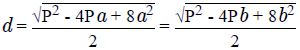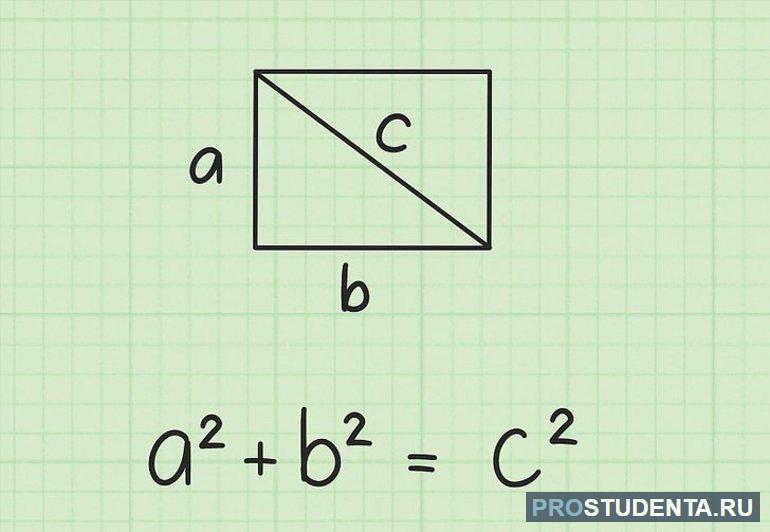Прямоугольник. Формулы и свойства прямоугольника
Определение.
Прямоугольник — это четырехугольник у которого две противоположные стороны равны и все четыре угла одинаковы.
Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.
Длинную сторону прямоугольника называют длиной прямоугольника, а короткую — шириной прямоугольника.
Стороны прямоугольника одновременно является его высотами.
Основные свойства прямоугольника
Прямоугольником могут быть параллелограмм, квадрат или ромб.
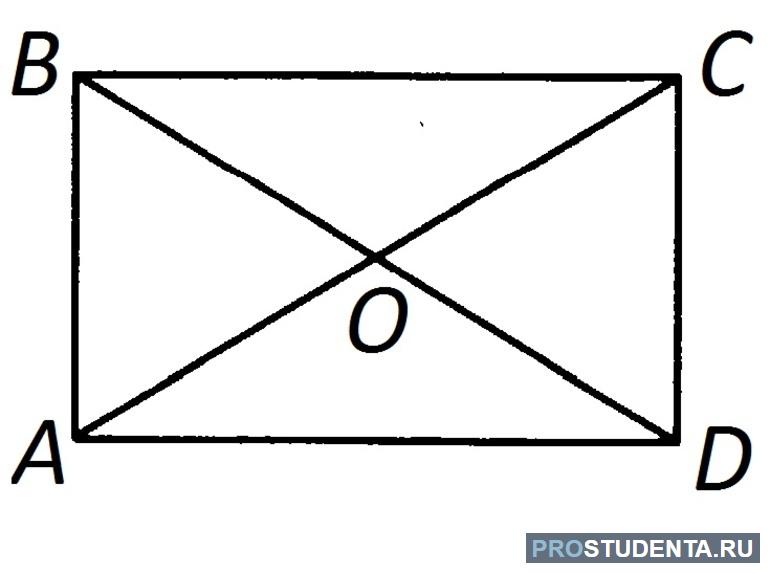
1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:
AB = CD, BC = AD
2. Противоположные стороны прямоугольника параллельны:
AB||CD, BC||AD
3. Прилегающие стороны прямоугольника всегда перпендикулярны:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
4. Все четыре угла прямоугольника прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
5. Сумма углов прямоугольника равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника имеют одинаковой длины:
AC = BD
7. Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
2d2 = 2a2 + 2b2
8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.
9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:
10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
11. Диагональ прямоугольника является диаметром описанной окружности
12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:
∠ABC + ∠CDA = 180° ∠BCD + ∠DAB = 180°
13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника — квадрат).
Стороны прямоугольника
Определение.
Длиной прямоугольника называют длину более длинной пары его сторон. Шириной прямоугольника называют длину более короткой пары его сторон.
Формулы определения длин сторон прямоугольника
1. Формула стороны прямоугольника (длины и ширины прямоугольника) через диагональ и другую сторону:
a = √d2 — b2
b = √d2 — a2
2. Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:
3. Формула стороны прямоугольника (длины и ширины прямоугольника) через периметр и другую сторону:
4. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол α:
a = d sinα
b = d cosα
5. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол β:
Диагональ прямоугольника
Определение.
Диагональю прямоугольника называется любой отрезок соединяющий две вершины противоположных углов прямоугольника.
Формулы определения длины диагонали прямоугольника
1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):
d = √a2 + b2
2. Формула диагонали прямоугольника через площадь и любую сторону:
| d = | √S2 + a4 | = | √S2 + b4 |
| a | b |
3. Формула диагонали прямоугольника через периметр и любую сторону:
| d = | √P2 — 4Pa + 8a2 | = | √P2 — 4Pb + 8b2 |
| 2 | 2 |
4. Формула диагонали прямоугольника через радиус описанной окружности:
d = 2R
5. Формула диагонали прямоугольника через диаметр описанной окружности:
d = Dо
6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
7. Формула диагонали прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника
d = √2S : sin β
Периметр прямоугольника
Определение.
Периметром прямоугольника называется сумма длин всех сторон прямоугольника.
Формулы определения длины периметру прямоугольника
1. Формула периметру прямоугольника через две стороны прямоугольника:
P = 2a + 2b
P = 2(a + b)
2. Формула периметру прямоугольника через площадь и любую сторону:
| P = | 2S + 2a2 | = | 2S + 2b2 |
| a | b |
3. Формула периметру прямоугольника через диагональ и любую сторону:
P = 2(a + √d2 — a2) = 2(b + √d2 — b2)
4. Формула периметру прямоугольника через радиус описанной окружности и любую сторону:
P = 2(a + √4R2 — a2) = 2(b + √4R2 — b2)
5. Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:
P = 2(a + √Do2 — a2) = 2(b + √Do2 — b2)
Площадь прямоугольника
Определение.
Площадью прямоугольника называется пространство ограниченный сторонами прямоугольника, то есть в пределах периметра прямоугольника.
Формулы определения площади прямоугольника
1. Формула площади прямоугольника через две стороны:
S = a · b
2. Формула площади прямоугольника через периметр и любую сторону:
| S = | Pa — 2a2 | = | Pb — 2b2 |
| 2 | 2 |
3. Формула площади прямоугольника через диагональ и любую сторону:
S = a√d2 — a2 = b√d2 — b2
4. Формула площади прямоугольника через диагональ и синус острого угла между диагоналями:
5. Формула площади прямоугольника через радиус описанной окружности и любую сторону:
S = a√4R2 — a2 = b√4R2 — b2
6. Формула площади прямоугольника через диаметр описанной окружности и любую сторону:
S = a√Do2 — a2 = b√Do2 — b2
Окружность описанная вокруг прямоугольника
Определение.
Окружностью описанной вокруг прямоугольника называется круг проходящий через четыре вершины прямоугольника, центр которого лежит на пересечении диагоналей прямоугольника.
Формулы определения радиуса окружности описанной вокруг прямоугольника
1. Формула радиуса окружности описанной вокруг прямоугольника через две стороны:
2. Формула радиуса окружности описанной вокруг прямоугольника через периметр квадрата и любую сторону:
| R = | √P2 — 4Pa + 8a2 | = | √P2 — 4Pb + 8b2 |
| 4 | 4 |
3. Формула радиуса окружности описанной вокруг прямоугольника через площадь квадрата:
| R = | √S2 + a4 | = | √S2 + b4 |
| 2a | 2b |
4. Формула радиуса окружности описанной вокруг прямоугольника через диагональ квадрата:
5. Формула радиуса окружности описанной вокруг прямоугольника через диаметр описанной окружности:
6. Формула радиуса окружности описанной вокруг прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
7. Формула радиуса окружности описанной вокруг прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
8. Формула радиуса окружности описанной вокруг прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:
Угол между стороной и диагональю прямоугольника
Формулы определения угла между стороной и диагональю
1. Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:
2. Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:
Угол между диагоналями прямоугольника
Формулы определения угла между диагоналями прямоугольника
1. Формула определения угла между диагоналями прямоугольника через угол между стороной и диагональю:
β = 2α
2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ:
Диагональю называется линия, соединяющая два угла выпуклого многоугольника во внутренней его части. У многих типовых плоских фигур диагональ образует внутри многоугольника прямоугольные треугольники, благодаря чему легко вычисляется через теорему Пифагора. В остальных случаях используется теорема косинусов и другие менее простые решения. Более того, диагональ часто становится осью симметрии фигуры, или пересечение двух диагоналей служит центром симметрии, разделяя фигуру на две зеркальные или конгруэнтные части.
Калькуляторы расчета диагонали фигур геометрических фигур
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Одна из основных фигур курса математики – прямоугольник.
Впервые о нем заговорили еще в Древнем Египте, а позже и в
Древней Греции. Именно свойства его диагоналей помогают
решить многие задания учебного курса. Подход, который
сейчас используется в геометрии разработал Евклид. Формулы,
представленные в данной статье, пригодятся как при решении
домашних упражнений, так и на ЕГЭ. Именно такие задачки
помогают набрать недостающие баллы, поэтому ими не стоит пренебрегать.
- Диагональ прямоугольника через его стороны
- Диагональ прямоугольника через площадь и известную сторону
- Диагональ прямоугольника через периметр и сторону
- Диагональ прямоугольника через диаметр описанной окружности
- Диагональ прямоугольника через радиус описанной окружности
- Диагональ прямоугольника через площадь и острый угол между диагоналями
- Диагональ прямоугольника через угол прилегающей диагонали и длину стороны прилегающей к этому углу
- Диагональ прямоугольника через угол прилегающей диагонали и длину стороны противоположной этому углу
- Что такое диагональ прямоугольника, когда требуется ее вычисление
Диагональ прямоугольника через его стороны
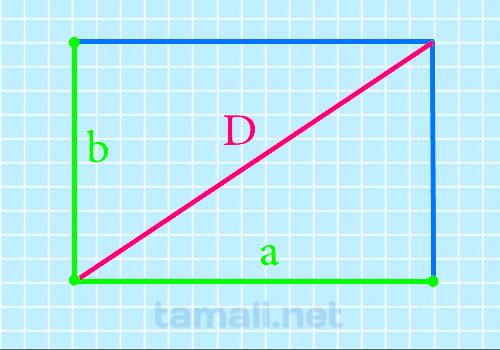
Если заданы хотя бы 2 стороны, то вычислить линию, соединяющую противоположные вершины, будет довольно просто. Применяется классическая теорема Пифагора. Достаточно подставить приведенные в дано числовые параметры в виде суммы квадратов под корнем:
Где a, b – это стороны, а d – прямая, которую мы ищем.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через площадь и известную сторону
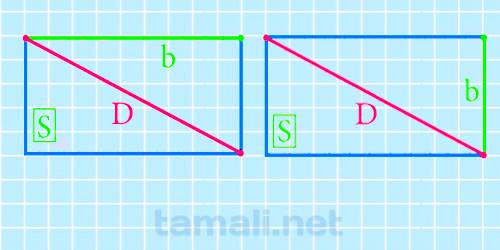
Когда в дано есть S и одна сторона, то узнать искомое значение можно используя следующее равенство:
Где D – это прямая, которую необходимо найти, a и b – любая заданная сторона, а S – площадь.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через периметр и сторону
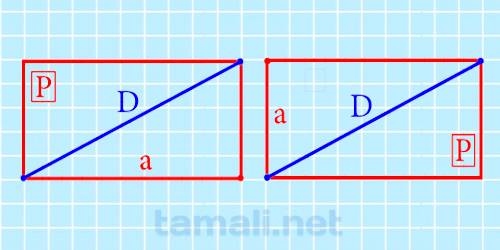
Когда задан периметр (сумма сторон) и, хотя бы одна сторона, отрезок, соединяющий несмежные точки высчитывают так:
Где P – сумма сторон, a и b – любая заданная сторона.
Рассчитать искомый отрезок можно и через соотношение сторон и площадь.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через диаметр описанной окружности
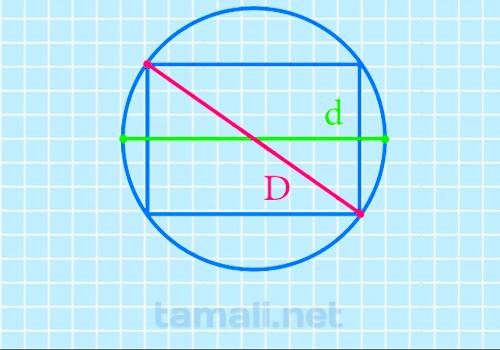
Поиск отрезка через описанную окружность еще более прост, здесь даже не придется проводить расчеты: D = d
Где d – это обозначенный диаметр.
Различить вписанную/описанную окружность легко. Когда геометрическое тело вписано куда-то, то оно всегда будет находиться в другой фигуре. Когда окружность описана, то она находится снаружи, она как бы описывает другое геометрическое тело. Описанные фигуры задевают собой точки, а вписанные – касаются сторон.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через радиус описанной окружности
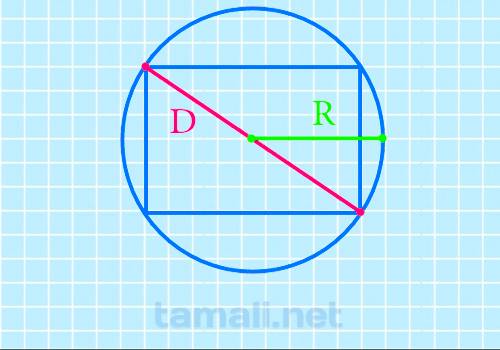
Для расчета искомого отрезка через описанную окружность нужно провести вычисления, где: D = 2R
Где R – это заданный радиус.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через площадь и острый угол между диагоналями
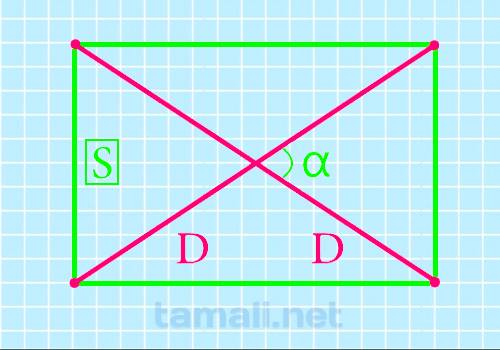
Если необходимо узнать прямую, соединяющую вершины 4-хугольника, это можно осуществить с помощью двух диагоналей. Для получения ответа к задаче понадобится sin β между ними и S (произведение длины и ширины).
Расчет проводится с равенством:
Где соответственно S – это площадь, а sin β – это острый угол, расположенный внутри фигуры (меж пересекающимися прямыми).
Если в 4-хугольнике расчертить 2 отрезка, объединяющие несмежные вершины, то они будут равны меж собой (все 4 отрезка), а точка пересечения разделит их пополам.
Пересечение всегда происходит в геометрическом центре самой фигурки. Этот же центр является центром описанной окружности.
Площадь (S):
Цифр после запятой:
Результат в:
Диагональ прямоугольника через угол прилегающей диагонали и длину стороны прилегающей к этому углу
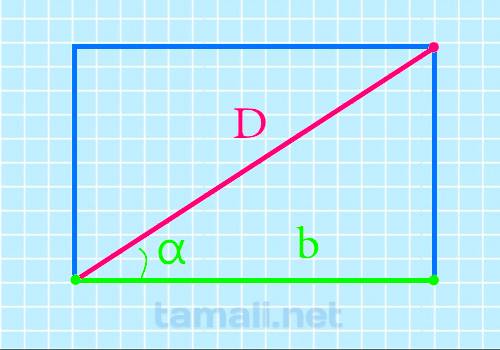
Когда одна из сторон 4-хугольника прилегает к углу, то просчитать отрезок, соединяющий вершины тоже возможно:
Где b – это сторона, прилегающая к углу, а cos a – это тот самый угол.
Косинус угла в треугольнике с прямым углом рассчитывается по формуле – длина соседней стороны, разделенная на гипотенузу. Синус – это противолежащий катет, разделенный на гипотенузу. Либо можно поступить еще проще, подсмотрев в таблицу Брадиса.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через угол прилегающей диагонали и длину стороны противоположной этому углу
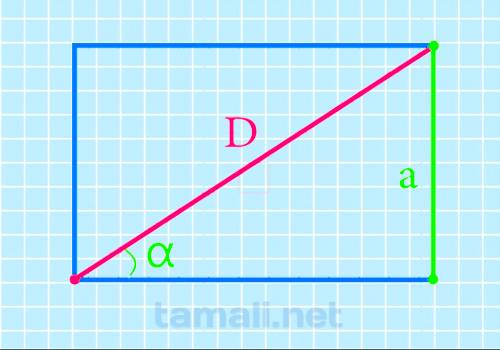
Чтобы найти нужный отрезок внутри четырехугольника, должен быть задан угол, прилегающий к искомому отрезку и сторона, противоположная углу:
Где a – это сторона четырехугольника, а sin a – это прилегающий угол.
Длинная сторона 4-хугольника– это длина, а короткая – его ширина. Помните, что каждая сторона одновременно является высотой.
Цифр после запятой:
Результат в:
Что такое диагональ прямоугольника, когда требуется ее вычисление
Прямоугольник – это частный случай параллелограмма. Иначе 4-хугольник с попарно равными сторонами, параллельными друг другу, а также равными прямыми углами по 90⁰. Сумма углов четырехугольника составляет 360⁰.
Диагональ разделяет фигуру на два новых элемента – треугольники с прямым углом. Это прямая, объединяющая противоположные вершины. Имея 2 прямоугольных треугольника, отрезок уже можно рассчитать по теореме Пифагора. По теореме гипотенуза – это квадрат из суммы катетов (обозначенных сторон треугольника), возведенных в квадрат.
Линии, соединяющие противоположные точки в четырехугольнике всегда пересекаются друг с другом.
Отрезок обозначают как d или D. Если названы все точки, то его можно называть в соответствии с ними – AC или BD.
Знания о линии, проходящей через несмежные точки 4-хугольника может понадобиться в легких геометрических упражнениях, так и в более сложных многоуровневых задачках, которые появляются на ЕГЭ. Свойства данного отрезка помогают находить важные параметры прямоугольника. Зная данные обеих линий, соединяющих противоположные углы, можно рассчитать S геометрического тела.
Перед решением любой геометрической задачки рекомендуется сделать чертеж и обозначить всю заданную информацию. Так будет значительно проще сосредоточиться на искомом значении.
Если регулярно решать тесты по геометрии, то формулы легче запомнятся, а их применение будет доведено до автоматизма.
Как вычислить длину диагонали
Диагональ – отрезок, соединяющий две вершины какой-либо фигуры, не лежащие на одной стороне. Для вычисления ее длины чаще всего используется теорема Пифагора или теорема косинусов.
Инструкция
диагонали/em/b» class=»colorbox imagefield imagefield-imagelink» rel=»gallery-step-images»> Прямоугольные четырехугольники (прямоугольник, квадрат) диагональ делит на два прямоугольных треугольника, в каждом из которых она будет гипотенузой. Следовательно, для ее вычисления возможно применение теоремы Пифагора. a²=b²+c², где a — гипотенуза, b и с — катеты. Пример 1: найдите диагональ AC , если известно, что длина BC=3 см, AB=5 см.Решение: вычислите гипотенузу AC в прямоугольном треугольнике ABC. AC²=AB²+BC²; AC²=5²+3²=34; из полученного значения извлеките квадратный корень: AC=√34=5,8 см.Ответ: диагональ прямоугольника равна 5,8 см.
Если перед вами квадрат, то вычислить диагональ можно, зная одну из его сторон или площадь. Т.к. все стороны квадрата равны, то теорема Пифагора для него будет иметь вид: a²=b²+b², a²=2b². Площадь — произведение двух сторон (S=b²). Значит, квадрат гипотенузы (в фигуре квадрат) равен его удвоенной площади (a²=2S).Пример 2: площадь квадрата 16 см². Найдите длину диагонали. Решение: вычислите длину диагонали а через площадь. a²=2S, a²=2*16 см²=32; извлеките корень квадратный: a=√32≈5,7 см.Ответ: длина диагонали квадрата – 5,7 см.
В некоторых случаях для вычисления диагонали необходимо делать дополнительные построения.Пример 3: равносторонний многоугольник со стороной, равной 6 см, угол BCD прямой. Найдите длину диагонали AB.Решение: соедините точки B и D. Получился прямоугольный треугольник BCD, в котором сторона BD является гипотенузой. Вычислите гипотенузу BD: BD²=BC+CD²; BD²=6²+6²=72; Гипотенуза BD из треугольника BCD является катетом в треугольнике ABD. А диагональ AB — гипотенуза в нем. Вычислите диагональ AB: AB²=BD²+AD²=72+36=108; AB=√108=10,4 см.Ответ: длина диагонали AB=10,4 см.
Диагональ куба можно найти через диагональ одной из его граней.Пример 4: куб со стороной 5 см. Найдите диагональ куба.Решение: достройте и вычислите диагональ грани куба. AC²=5²+5²=50. Диагональ AC перпендикулярна ребру CB, следовательно, угол ACB – прямой. Диагональ куба AB – гипотенуза в треугольнике ACB. Найдите длину диагонали куба: AB²=AC²+CB²=50+25=75; извлеките квадратный корень. AB=√75=8,7 см.Ответ: длина диагонали куба – 8,7 см.
Для вычисления диагоналей параллелограмма используют теорему косинусов: c²=a²+b²-2ab*cosγ.Пример 5: a = 2 см, b = 3 см, γ = 120°. Найдите диагональ с.Решение: подставьте значения в формулу. c²= 2²+3²-2*2*3*cos120°; cos120° найдите по таблице косинусов (-0,5). с² = 4+9-12*(-0,5)=13-(-6)=19. Из этого значения извлеките корень: с = √19 = 4,35 см.Ответ: длина диагонали с = 4,35 см.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
При решении задач по физико-математическим дисциплинам иногда необходимо найти диагонали прямоугольника. Формула в интернете не всегда является достоверной. Очень важно на начальных стадиях вычислений правильно идентифицировать фигуру, чтобы применить к ней нужные свойства и соотношения. Специалисты рекомендуют не приступать сразу к практике, а разобраться с теорией.
Оглавление:
- Общая информация
- Формулы и соотношения
- Пример расчета параметров
Общая информация
Прямоугольник — геометрическая плоская фигура, состоящая из четырех попарно параллельных сторон, между которыми образованы прямые углы. Ее можно перепутать с квадратом, имеющим похожие свойства и тождества. При решении задачи очень важно правильно найти фигуру, имеющую определенные признаки определения. Некоторые учащиеся путают последние со свойствами. Эти два термина отличаются между собой.
Методика идентификации
Признак — совокупность некоторых критериев, позволяющих правильно различать фигуры. Прямоугольник возможно идентифицировать по таким правилам:
- Неравенство сторон, являющихся смежными.
- Диагонали при пересечении не образуют угол в 90 градусов.
- Диагонали не являются биссектрисами углов больших треугольников, полученных при пересечении.
- Окружность можно только описать, а не вписать.
Если для искомой фигуры применим хотя бы один из признаков, то ее возможно классифицировать как прямоугольник.
После успешной идентификации необходимо перейти к рассмотрению свойств, которые рекомендовано специалистами использовать при расчетах параметров и доказательстве утверждений (тождеств и теорем).
Важные свойства
Свойства — набор или список утверждений и тождеств, используемых при вычислениях требуемых величин, а также для доказательства теорем, а именно:
- Все углы прямые, а их алгебраическая сумма равна 360.
- Несмежные стороны параллельны и равны.
- Точка пересечения диагоналей — центр симметрии и делит их на две части. Кроме того, средняя линия проходит через нее.
- Формула диагонали (m) прямоугольника через стороны p и t: m=(рp+tt]^1/2), т. е. квадратичное значение диагонали равно сумме сторон, каждая из которых умножена на эквивалентное значение.
- Подобность малого и большого треугольников, образованных диагоналями.
- Существует только описанная окружность, диаметр которой эквивалентен диагонали прямоугольника.
- При проведении диагонали образуются два равных треугольника, являющиеся прямоугольными.
Следует отметить, что вышеописанные свойства — это требуемый минимум, которого недостаточно для выполнения вычислений и доказательства других тождеств.
Формулы и соотношения
Чтобы ориентироваться в формулах, нужно ввести некоторые обозначения. К ним принадлежат следующие:
- Диагональ — m.
- Стороны — k и l.
- Периметр — P.
- Полупериметр — р.
- Площадь — S.
- Острый угол, который образуют две диагонали — Z, а тупой — Y.
- Диаметр — D.
После этого необходимо рассмотреть основные тождества. Их рекомендуется применять при вычислениях различных параметров фигуры.
К ним относятся такие выражения:
- Периметр: P=2S/к + (2/к)k 2 =2k+2(m 2 -k 2 )^(1/2))=2k+2(D 2 -k 2 )^(1/2)).
- Площадь: S=[Pк — 2к 2 ]/2=[Pl — 2l 2 ]/2=k[m 2 -k 2 ]=[sin(Z)/2]m^2 .
- Диагонали: m=[k 2 +l 2 ]^(1/2)=(1/k)(S 2 +k 4 )^(1/2).
Кроме того, найти диагональ прямоугольника возможно, используя формулу такого вида: m=((2k+2l) 2 -4(2k(k+l)+8k 2 )^(1/2) * 0,5. Величины «(2k+2l)» можно заменить периметром Р, когда он известен.
Следует отметить, что найти длину диагонали прямоугольника возможно при известном D. Соотношение имеет следующий вид: m=2R=D.
Пример расчета параметров
У прямоугольника известна диагональ (m=10) и периметр (Р=28). Необходимо узнать длину его сторон. Решать задачу нужно по такому алгоритму:
- Диагональ находится по следующему выражению: m^2=k^2+l^2.
- Формула для вычисления периметра: P=2(k+l).
- Составить систему уравнений для нахождения сторон: 100=k^2+l^2 и 28=2(k+l).
- Выразить из второго уравнения одну из сторон: k=14-l.
- Подставить в первое: (14-l)^2+l^2=100.
- Раскрыть скобки: 196-28l+l^2+l^2=2l^2-28l+196=100.
- Уравнение имеет такой вид: l^2-14l+48=0.
- Вычислить его корни: l1=6 и l2=8.
- Подставить в четвертый пункт и посчитать стороны: l=6 и к=8.
Следует отметить, что расчет корней производится подстановкой, при которой возникают дубли решений. Среди них требуется выбрать любых две пары. Исходя из девятого пункта, можно рассчитать значение площади, зная две стороны. Используя формулы, можно находить и другие параметры. Например, высчитать значение острого угла.
Таким образом, перед решением задач по геометрии математики рекомендуют правильно идентифицировать геометрическую фигуру при помощи признаков, а затем использовать какие-либо соотношения.