Онлайн калькулятор для расчета выборочной дисперсии (дисперсия выборки). Выборочная дисперсия - это показатель разброса, наблюдаемого в определенной выборке данных. С вычислительной точки зрения ее можно объяснить как — среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения.
Для того, чтобы оценить дисперсию по выборке необходимо:
— Вычислить математические ожидания данных (выборочное среднее — среднее арифметическое значений вариант в выборке).
— Вычитаем математическое ожидание из исходного значения для всех данных из выборки и возводим результат в квадрат.
— Складываем все полученные в предыдущем шаге значения и делим сумму на N-1.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Смотрите также
Выборочная дисперсия, описание
Выборочная дисперсия является сводной характеристикой для наблюдения рассеяния количественного признака выборки вокруг среднего значения.
Определение
Выборочная дисперсия – это среднее арифметическое значений вариантов части отобранных объектов генеральной совокупности (выборки).
Связь выборочной и генеральной дисперсии
Генеральная дисперсия представляет собой среднее арифметическое квадратов отступлений значений признаков генеральной совокупности от их среднего значения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Генеральная совокупность – это комплекс всех возможных объектов, относительно которых планируется вести наблюдение и формулировать выводы.
Выборочная совокупность или выборка является частью генеральной совокупности, выбранной для изучения и составления заключения касательной всей генеральной совокупности.
Как вычислить выборочную дисперсию
Выборочная дисперсия при различии всех значений варианта выборки находится по формуле:
({widehat D}_В=frac{displaystylesum_{i-1}^n{(x_i-{overline x}_В)}^2}n)
Для значений признаков выборочной совокупности с частотами n1, n2,…,nk формула выглядит следующим образом:
({widehat D}_В=frac{displaystylesum_{i-1}^kn_i{(x_i-{overline x}_В)}^2}n)
Квадратный корень из выборочной дисперсии характеризует рассеивание значений вариантов выборки вокруг своего среднего значения. Данная характеристика называется выборочным средним квадратическим отклонением и имеет вид:
({widehatsigma}_В=sqrt{{widehat D}_В})
Упрощенный способ вычисления выборочной или генеральной дисперсии производят по формуле:
(D=overline{x^2}-left[overline xright]^2)
Если вариационный ряд выборочной совокупности интервальный, то за xi принимается центр частичных интервалов.
Пример
Найти выборочную дисперсию выборки со значениями:
- xi: 1, 2, 3, 4;
- ni: 20, 15, 10, 5.
Решение
Для начала необходимо определить выборочную среднюю:
({overline x}_В=frac1{50}(1cdot20+2cdot15+3cdot10+4cdot5)=frac1{50}cdot100=2)
Затем найдем выборочную дисперсию:
(D_В=frac1{50}({(1-2)}^2cdot20+{(2-2)}^2cdot15+{(3-2)}^2cdot10+{(4-2)}^2cdot5)=1)
Исправленная дисперсия
Математически выборочная дисперсия не соответствует генеральной, поскольку выборочная используется для смещенного оценивания генеральной дисперсии. По этой причине математическое ожидание выборочной дисперсии вычисляется так:
(Mleft[D_Bright]=frac{n-1}nD_Г)
В данной формуле DГ – это истинное значение дисперсии генеральной совокупности.
Исправить выборочную дисперсию можно путем умножения ее на дробь:
(frac n{n-1})
Получим формулу следующего вида:
(S^2=frac n{n-1}cdot D_В=frac{displaystylesum_{i=1}^kn_i{(x_i-{overline x}_В)}^2}{n-1})
Исправленная дисперсия используется для несмещенной оценки генеральной дисперсии и обозначается S2.
Среднеквадратическая генеральная совокупность оценивается при помощи исправленного среднеквадратического отклонения, которое вычисляется по формуле:
(S=sqrt{S^2})
При нахождении выборочной и исправленной дисперсии разнятся лишь знаменатели в формулах. Различия в этих характеристиках при больших n незначительны. Применение исправленной дисперсии целесообразно при объеме выборки меньше 30.
Для чего применяют исправленную выборочную дисперсию
Исправленную выборочную используют для точечной оценки генеральной дисперсии.
Пример
Длину стержня измерили одним и тем же прибором пять раз. В результате получили следующие величины: 92 мм, 94 мм, 103 мм, 105 мм, 106 мм. Задача найти выборочную среднюю длину предмета и выборочную исправленную дисперсию ошибок измерительного прибора.
Решение
Сначала вычислим выборочную среднюю:
({overline x}_В=frac{92+94+103+105+106}5=100)
Затем найдем выборочную дисперсию:
(D_В=frac{displaystylesum_{i=1}^k{(x_i-{overline x}_В)}^2}n=frac{{(92-100)}^2+{(94-100)}^2+{(103-100)}^2+{(105-100)}^2+{(106-100)}^2}5=34)
Теперь рассчитаем исправленную дисперсию:
(S^2=frac5{5-1}cdot34=42,5)
Как найти дисперсию?
Лучшее спасибо — порекомендовать эту страницу
Дисперсия — это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая — значения сравнительно близки друг к другу, если большая — далеки друг от друга (см. примеры нахождения дисперсии ниже).
Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии — среднеквадратическое отклонение $sigma(X)=sqrt{D(X)}$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.
Еще одно формальное определение дисперсии звучит так: «Дисперсия — это второй центральный момент случайной величины» (напомним, что первый начальный момент — это как раз математическое ожидание).
Нужна помощь? Решаем теорию вероятностей на отлично
Формула дисперсии случайной величины
Дисперсия случайной величины Х вычисляется по следующей формуле:
$$
D(X)=M(X-M(X))^2,
$$
которую также часто записывают в более удобном для расчетов виде:
$$
D(X)=M(X^2)-(M(X))^2.
$$
Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.
Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx — left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Пример нахождения дисперсии
Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.
Пример 1. Вычислить и сравнить дисперсию двух законов распределения:
$$
x_i quad 1 quad 2 \
p_i quad 0.5 quad 0.5
$$
и
$$
y_i quad -10 quad 10 \
p_i quad 0.5 quad 0.5
$$
Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором — дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2 =\
= 1^2cdot 0.5 + 2^2 cdot 0.5 — (1cdot 0.5 + 2cdot 0.5)^2=2.5-1.5^2=0.25.
$$
$$
D(Y)=sum_{i=1}^{n}{y_i^2 cdot p_i}-left(sum_{i=1}^{n}{y_i cdot p_i} right)^2 =\
= (-10)^2cdot 0.5 + 10^2 cdot 0.5 — (-10cdot 0.5 + 10cdot 0.5)^2=100-0^2=100.
$$
Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $sigma(X)=0.5$, $sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором — на 10 единиц от среднего 0.
Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).
Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$
Снова используем формулу для дисперсии дискретной случайной величины:
$$
D(X)=M(X^2)-(M(X))^2.
$$
В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Потом математическое ожидание квадрата случайной величины:
$$
M(X^2)=sum_{i=1}^{n}{x_i^2 cdot p_i}
= (-1)^2cdot 0.1 + 2^2 cdot 0.2 +5^2cdot 0.3 +10^2cdot 0.3+20^2cdot 0.1=78.4.
$$
А потом подставим все в формулу для дисперсии:
$$
D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16.
$$
Дисперсия равна 32.16 квадратных единиц.
Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x in(0,6)$ и $f(x)=0$ в остальных точках.
Используем для расчета формулу дисперсии непрерывной случайной величины:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx — left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Вычислим сначала математическое ожидание:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{6} frac{x}{18} cdot x dx = int_{0}^{6} frac{x^2}{18} dx =
left.frac{x^3}{54} right|_0^6=frac{6^3}{54} = 4.
$$
Теперь вычислим
$$
M(X^2)=int_{-infty}^{+infty} f(x) cdot x^2 dx = int_{0}^{6} frac{x}{18} cdot x^2 dx = int_{0}^{6} frac{x^3}{18} dx = left.frac{x^4}{72} right|_0^6=frac{6^4}{72} = 18.
$$
Подставляем:
$$
D(X)=M(X^2)-(M(X))^2=18-4^2=2.
$$
Дисперсия равна 2.
Другие задачи с решениями по ТВ
Подробно решим ваши задачи на вычисление дисперсии
Вычисление дисперсии онлайн
Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку «Вычислить».
- Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.
Видео. Полезные ссылки
Видеоролики: что такое дисперсия и как найти дисперсию
Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Полезная страница? Сохрани или расскажи друзьям
Полезные ссылки
Не забывайте сначала прочитать том, как найти математическое ожидание. А тут можно вычислить также СКО: Калькулятор математического ожидания, дисперсии и среднего квадратического отклонения.
Что еще может пригодиться? Например, для изучения основ теории вероятностей — онлайн учебник по ТВ. Для закрепления материала — еще примеры решений задач по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Загрузить PDF
Загрузить PDF
Дисперсия случайной величины является мерой разброса значений этой величины. Малая дисперсия означает, что значения сгруппированы близко друг к другу. Большая дисперсия свидетельствует о сильном разбросе значений. Понятие дисперсии случайной величины применяется в статистике. Например, если сравнить дисперсию значений двух величин (таких как результаты наблюдений за пациентами мужского и женского пола), можно проверить значимость некоторой переменной.[1]
Также дисперсия используется при построении статистических моделей, так как малая дисперсия может быть признаком того, что вы чрезмерно подгоняете значения.[2]
-
1
Запишите значения выборки. В большинстве случаев статистикам доступны только выборки определенных генеральных совокупностей. Например, как правило, статистики не анализируют расходы на содержание совокупности всех автомобилей в России – они анализируют случайную выборку из нескольких тысяч автомобилей. Такая выборка поможет определить средние расходы на автомобиль, но, скорее всего, полученное значение будет далеко от реального.
- Например, проанализируем количество булочек, проданных в кафе за 6 дней, взятых в случайном порядке. Выборка имеет следующий вид: 17, 15, 23, 7, 9, 13. Это выборка, а не совокупность, потому что у нас нет данных о проданных булочках за каждый день работы кафе.
- Если вам дана совокупность, а не выборка значений, перейдите к следующему разделу.
-
2
Запишите формулу для вычисления дисперсии выборки. Дисперсия является мерой разброса значений некоторой величины. Чем ближе значение дисперсии к нулю, тем ближе значения сгруппированы друг к другу. Работая с выборкой значений, используйте следующую формулу для вычисления дисперсии:[3]
-
3
Вычислите среднее значение выборки. Оно обозначается как x̅.[4]
Среднее значение выборки вычисляется как обычное среднее арифметическое: сложите все значения в выборке, а затем полученный результат разделите на количество значений в выборке.- В нашем примере сложите значения в выборке: 15 + 17 + 23 + 7 + 9 + 13 = 84
Теперь результат разделите на количество значений в выборке (в нашем примере их 6): 84 ÷ 6 = 14.
Выборочное среднее x̅ = 14. - Выборочное среднее – это центральное значение, вокруг которого распределены значения в выборке. Если значения в выборке группируются вокруг выборочного среднего, то дисперсия мала; в противном случае дисперсия велика.
- В нашем примере сложите значения в выборке: 15 + 17 + 23 + 7 + 9 + 13 = 84
-
4
Вычтите выборочное среднее из каждого значения в выборке. Теперь вычислите разность
— x̅, где
– каждое значение в выборке. Каждый полученный результат свидетельствует о мере отклонения конкретного значения от выборочного среднего, то есть как далеко это значение находится от среднего значения выборки.[5]
-
5
Возведите в квадрат каждый полученный результат. Как отмечалось выше, сумма разностей
— x̅ должна быть равна нулю. Это означает, что средняя дисперсия всегда равна нулю, что не дает никакого представления о разбросе значений некоторой величины. Для решения этой проблемы возведите в квадрат каждую разность
— x̅. Это приведет к тому, что вы получите только положительные числа, которые при сложении никогда не дадут 0.[6]
-
6
-
7
Полученный результат разделите на n — 1, где n – количество значений в выборке. Некоторое время назад для вычисления дисперсии выборки статистики делили результат просто на n; в этом случае вы получите среднее значение квадрата дисперсии, которое идеально подходит для описания дисперсии данной выборки. Но помните, что любая выборка – это лишь небольшая часть генеральной совокупности значений. Если взять другую выборку и выполнить такие же вычисления, вы получите другой результат. Как выяснилось, деление на n — 1 (а не просто на n) дает более точную оценку дисперсии генеральной совокупности, в чем вы и заинтересованы. Деление на n – 1 стало общепринятым, поэтому оно включено в формулу для вычисления дисперсии выборки.[7]
- В нашем примере выборка включает 6 значений, то есть n = 6.
Дисперсия выборки =33,2
- В нашем примере выборка включает 6 значений, то есть n = 6.
-
8
Отличие дисперсии от стандартного отклонения. Заметьте, что в формуле присутствует показатель степени, поэтому дисперсия измеряется в квадратных единицах измерения анализируемой величины. Иногда такой величиной довольно сложно оперировать; в таких случаях пользуются стандартным отклонением, которое равно квадратному корню из дисперсии. Именно поэтому дисперсия выборки обозначается как
, а стандартное отклонение выборки – как
.
- В нашем примере стандартное отклонение выборки: s = √33,2 = 5,76.
Реклама
-
1
Проанализируйте некоторую совокупность значений. Совокупность включает в себя все значения рассматриваемой величины. Например, если вы изучаете возраст жителей Ленинградской области, то совокупность включает возраст всех жителей этой области. В случае работы с совокупностью рекомендуется создать таблицу и внести в нее значения совокупности. Рассмотрим следующий пример:
-
2
Запишите формулу для вычисления дисперсии генеральной совокупности. Так как в совокупность входят все значения некоторой величины, то приведенная ниже формула позволяет получить точное значение дисперсии совокупности. Для того чтобы отличить дисперсию совокупности от дисперсии выборки (значение которой является лишь оценочным), статистики используют различные переменные: [8]
-
3
Вычислите среднее значение совокупности. При работе с генеральной совокупностью ее среднее значение обозначается как μ (мю). Среднее значение совокупности вычисляется как обычное среднее арифметическое: сложите все значения в генеральной совокупности, а затем полученный результат разделите на количество значений в генеральной совокупности.
- Имейте в виду, что средние величины не всегда вычисляются как среднее арифметическое.
- В нашем примере среднее значение совокупности: μ =
= 10,5
-
4
Вычтите среднее значение совокупности из каждого значения в генеральной совокупности. Чем ближе значение разности к нулю, тем ближе конкретное значение к среднему значению совокупности. Найдите разность между каждым значением в совокупности и ее средним значением, и вы получите первое представление о распределении значений.
- В нашем примере:
— μ = 5 — 10,5 = -5,5
— μ = 5 — 10,5 = -5,5
— μ = 8 — 10,5 = -2,5
— μ = 12 — 10,5 = 1,5
— μ = 15 — 10,5 = 4,5
— μ = 18 — 10,5 = 7,5
- В нашем примере:
-
5
Возведите в квадрат каждый полученный результат. Значения разностей будут как положительными, так и отрицательными; если нанести эти значения на числовую прямую, то они будут лежать справа и слева от среднего значения совокупности. Это не годится для вычисления дисперсии, так как положительные и отрицательные числа компенсируют друг друга. Поэтому возведите в квадрат каждую разность, чтобы получить исключительно положительные числа.
- В нашем примере:
(— μ)
для каждого значения совокупности (от i = 1 до i = 6):
(-5,5)= 30,25
(-5,5)= 30,25
(-2,5)= 6,25
(1,5)= 2,25
(4,5)= 20,25
(7,5)= 56,25
- В нашем примере:
-
6
Найдите среднее значение полученных результатов. Вы нашли, как далеко каждое значение совокупности расположено от ее среднего значения. Найдите среднее значение суммы квадратов разностей, поделив ее на количество значений в генеральной совокупности.
- В нашем примере:
Дисперсия совокупности =24,25
- В нашем примере:
-
7
Соотнесите это решение с формулой. Если вы не поняли, как приведенное выше решение соотносится с формулой, ниже представлено объяснение решения:
Реклама
Советы
- Дисперсию довольно сложно интерпретировать, поэтому в большинстве случаев она вычисляется как промежуточная величина, которая необходима для нахождения стандартного отклонения.
- При вычислении дисперсии выборки деление на n-1, а не просто на n, называется коррекцией Бесселя. Дисперсия выборки представляет собой только оценочное значение дисперсии генеральной совокупности, при этом выборочное среднее смещено, чтобы соответствовать этому оценочному значению. Коррекция Бесселя устраняет такое смещение.[9]
Это связано с тем, что при анализе n – 1 значения использование n-го значения уже ограничено, так как только определенные значения приводят к выборочному среднему (x̅), которое используется в формуле для вычисления дисперсии.[10]
Реклама
Об этой статье
Эту страницу просматривали 122 353 раза.
Была ли эта статья полезной?
Генеральная и выборочная дисперсия
Для анализа полученных данных в математической статистике используют различные виды показателей вариации, среди которых:
- размах вариации;
- среднее абсолютное отклонение;
- дисперсия.
Разберем понятие дисперсии, ее виды и свойства.
Дисперсия — величина, являющаяся мерой разброса полученных в ходе наблюдений данных относительно истинного значения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Дисперсия является точечной оценкой параметра, так как имеет одно конкретное числовое значение.
Статистический анализ при исследовании некоторого объекта может быть сплошным или выборочным в зависимости от охватываемого объема данных.
В обоих вариантах результаты анализа распространяют на генеральную совокупность, однако при сплошном анализе наблюдению подвергают абсолютно все имеющиеся данные. Выборочный анализ, напротив, предполагает наблюдение только за некоторой выбранной частью данных. При этом выбранная совокупность должна сохранять структуру и закономерности генеральной.
Дисперсию также делят на два вида в зависимости от используемых данных:
- генеральная дисперсия;
- выборочная дисперсия.
Как видно из названия, дисперсии отличаются объемом выборки, на основе которой происходит расчет и анализ.
Выборочная дисперсия, определение, формулы для вычисления
Пусть имеется некоторая выборка Y из генеральной совокупности объемом n. Среднее значение выборки обозначим как ({overline y}_в).
Выборочная дисперсия (D_в) — величина, равная среднему арифметическому отклонению квадратов разности признаков выборки (y_1,;y_2,;…y_n) от ее среднего значения ({overline y}_в).
Данные в выборке могут располагаться хаотично, то есть быть несгруппированными, или же сформированы в вариационный ряд.
Выборочную дисперсию для несгруппированной выборки можно посчитать по формуле:
Формула 1
(D_в=frac{{displaystylesum_{i=1}^n}(y_i-{overline y}_в)}n)
В случае вариационного ряда используют кратные значения и частоты для дискретного представления; середины частичных интервалов и частоты для интервального представления.
Формула 2
(D_в=frac{{displaystylesum_{i=1}^k}(y’_i-{overline y}_в)cdot n_i}n)
где (y’_i )— кратное (одинаковое) значение в выборке или значение, соответствующее середине интервала;
(n_i )— частота.
Выборочная дисперсия, рассчитанная по приведенным выше формулам, дает недостоверное (заниженное) значение. Это значит, что при большом количестве экспериментов выборочная дисперсия будет давать смещенное относительно истинного значения генеральной совокупности значение.
Чтобы получить несмещенную выборочную дисперсию, используют следующую формулу:
Формула 3
(D_в=frac{{displaystylesum_{i=1}^n}{(y_i-{overline y}_в)}^2}{n-1})
Примечание 1
Как правило при использовании термина «выборочная дисперсия» имеют в виду именно несмещенную выборочную дисперсию.
Генеральная дисперсия, определение, что является оценкой, формулы для вычисления
Пусть имеется некоторая генеральная совокупность X объемом N и среднее значение признаков совокупности (X — {overline x}_г.)
Генеральная дисперсия (D_г) есть среднее арифметическое отклонение квадратов разности признаков (x_1,;x_2,;…x_n) генеральной совокупности X от их среднего значения ({overline x}_г).
Примечание 2
Иногда генеральную дисперсию называют теоретической.
Аналогично выборочной, генеральная дисперсия может быть рассчитана для несгруппированных данных генеральной совокупности:
Формула 4
(D_г=frac{{displaystylesum_{i=1}^N}{(x_i-{overline x}_г)}^2}N)
и для сформированного вариационного ряда:
Формула 5
(D_г=frac{{displaystylesum_{i=1}^K}{(x’_i-{overline x}_г)}^2cdot n_i}N)
Значение теоретической дисперсии бывает сложно вычислить из-за большого объема данных или их недостатка. Тогда для оценки используют выборочную дисперсию. Но если для оценки генеральной дисперсии применить выборочную, это приведет к возникновению ряда систематических ошибок. В результате оценка будет произведена неверно, а значение генеральной дисперсии занижено.
Чтобы устранить возникающую погрешность в качестве оценки генеральной дисперсии используют исправленную или несмещенную выборочную дисперсию, формула которой представлена выше.
Оценки параметров распределения
Оценкой параметра в статистике считают численное значение какого-либо параметра данной выборки.
Приведем оценки параметров распределения случайной величины, которые связаны с дисперсией.
Среднеквадратическое отклонение (δ) — характеристика рассеивания случайной величины относительно ее математического ожидания. Определяется как корень квадратный из дисперсии.
Формула 6
(delta=sqrt D)
Математическое ожидание случайной величины X — среднее (по весу вероятностей возможных значений) значение случайной величины. Обозначается как M(X).
Математическое ожидание и дисперсия для дискретной случайной величины связаны соотношением:
Формула 7
(D=Mleft[X-M(X)right]^2)
для непрерывной:
Формула 8
(D=int_{-infty}^infty(x-M{(x))}^2cdot f(x)dx)
где f(x) — функция распределения случайной величины.
Отметим, что указанные выше параметры могут быть определены как для генеральной совокупности, так и для некоторой выборки.
Примеры решения задач
Пример 1
Напряжение в цепи измеряют 6 раз с помощью одного и того же вольтметра. Получены следующие значения: 210 В, 200 В, 195 В, 205 В, 190 В, 200 В. Найти выборочную смещенную дисперсию и дать оценку генеральной дисперсии.
Решение.
Сначала вычислим выборочное среднее значение:
({overline x}_в=frac{210+200+195+205+190+200}6=200;B.)
Теперь найдем выборочную дисперсию:
(D_в=frac{{(210-200)}^2+{(200-200)}^2+{(195-200)}^2+{(205-200)}^2+{(190-200)}^2+{(200-200)}^2}6=frac{250}6approx42.)
Оценкой генеральной дисперсии является исправленная или выборочная несмещенная дисперсия. Чтобы вычислить исправленную дисперсию, умножим полученную ранее выборочную дисперсию на множитель (frac n{n-1} (n=6):)
(D_и=frac n{n-1}cdot D_в=frac65cdotfrac{250}6=50.)
Примечание 3
Данный пример показывает, что значение выборочной смещенной дисперсии занижено относительно генеральной.
Пример 2
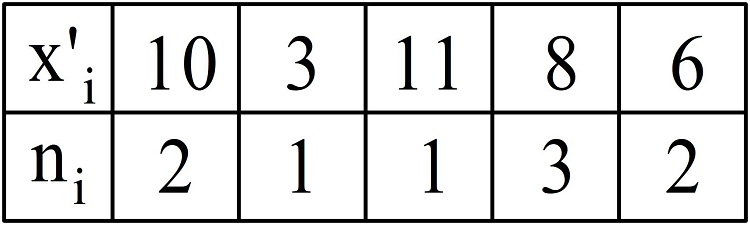
Случайная величина задана следующей таблицей распределения, среднее значение выборки равно 14. Найти выборочную несмещенную дисперсию и среднеквадратическое отклонение.
Решение.
Вычислим выборочную несмещенную дисперсию:
(D_в=frac{2{(10-14)}^2+1{(3-14)}^2+1{(11-14)}^2+3{(8-14)}^2+2{(6-14)}^2}9cdotfrac98=frac{398}8approx50.)
Теперь найдем среднеквадратическое отклонение:
(delta=sqrt{D_в}=sqrt{frac{398}8}=frac{sqrt{199}}2approx7.)