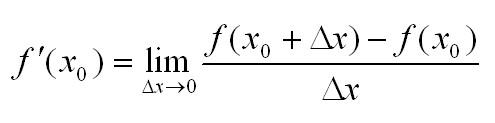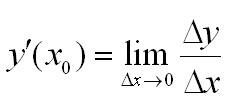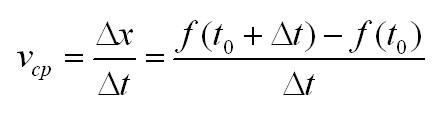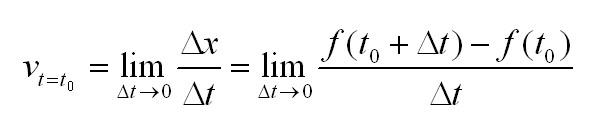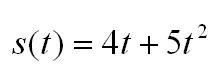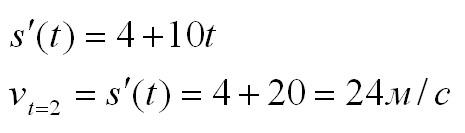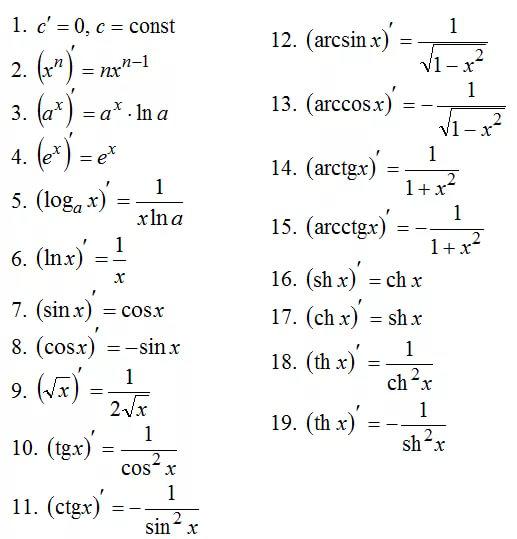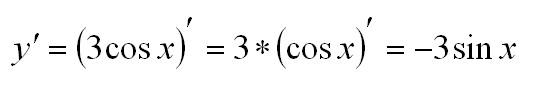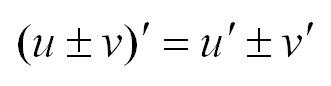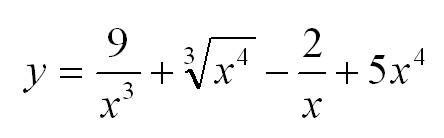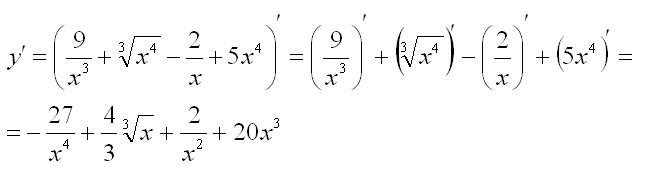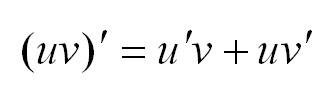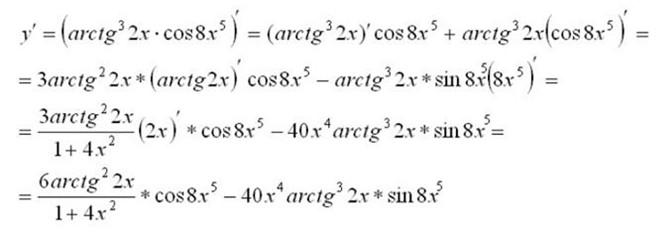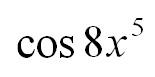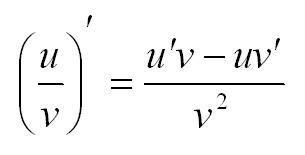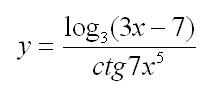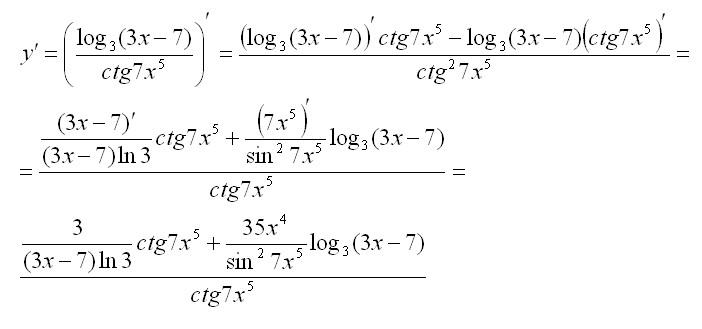На этой странице вы узнаете
- Почему функции похожи на американские горки?
- Как с помощью производной оценить рост популярности видео в соцсети?
- Какие фокусы творят тригонометрия и геометрия вместе?
Она спешит на помощь быстрее, чем Чип и Дейл. Она наш спасательный круг в океане математики. Давайте посмотрим, как производная способна на такие чудеса.
Производная
Функции достаточно часто встречаются при решении задач. Они могут быть как составными частями какого-то задания, так и отдельным номером. Разумеется, встречаются не только простые функции. Если открыть банк заданий, то мы удивимся, насколько сложными они бывают. Так что делать с такими сложными и непонятными функциями?
Производная — одно из самых важных понятий математического анализа. С ее помощью можно описать поведение любой функции.
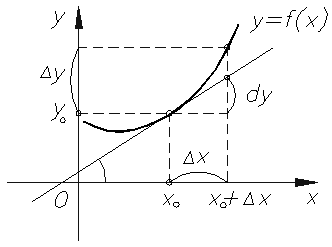
Предположим, мы хотим прокатиться на американских горках. Представим их вид сбоку: это череда подъемов и резких спусков. Мы можем с легкостью описать их: на каких участках будет подъем, а на каких спуск, насколько крутыми они будут, сколько раз вагончик преодолеет границу между подъемом и спуском или спуском или подъемом. Мы даже можем предположить, на каких участках вагончик разгоняется сильнее. Точно так же можно описать и любую функцию.
Представим наши американские горки в виде функции.
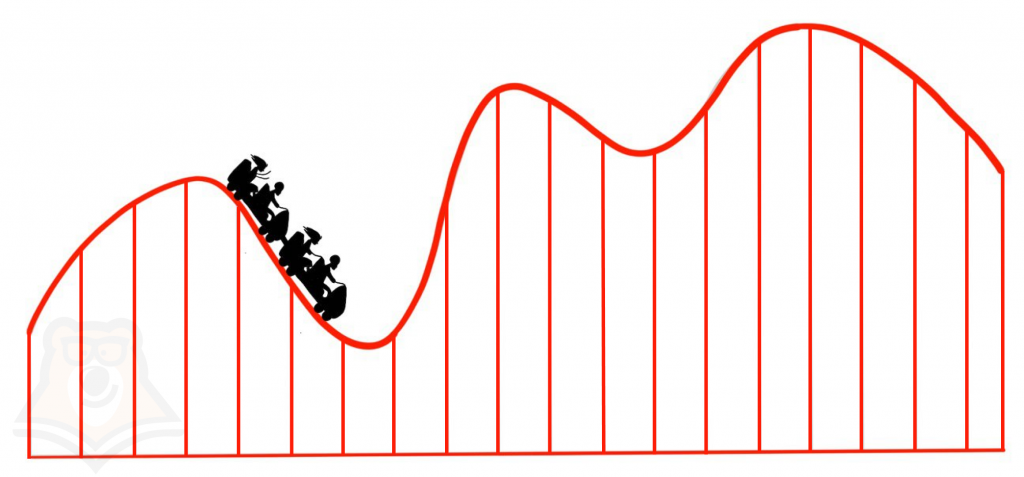
Функция будет на некоторых участках возрастать, а на некоторых убывать. Скорость ее изменения на разных участках будет разной.
Скорость изменения функции показывает, насколько сильно будет изменяться значение функции (то есть значение у) при небольшом изменении переменной функции (то есть значения х).
Отложим на нашем графике две точки: х и х1 и поднимем из них прямые, которые пересекут график в точках А и В. Тогда точка А будет иметь координаты (х;у), а точка В — (х1;у1).
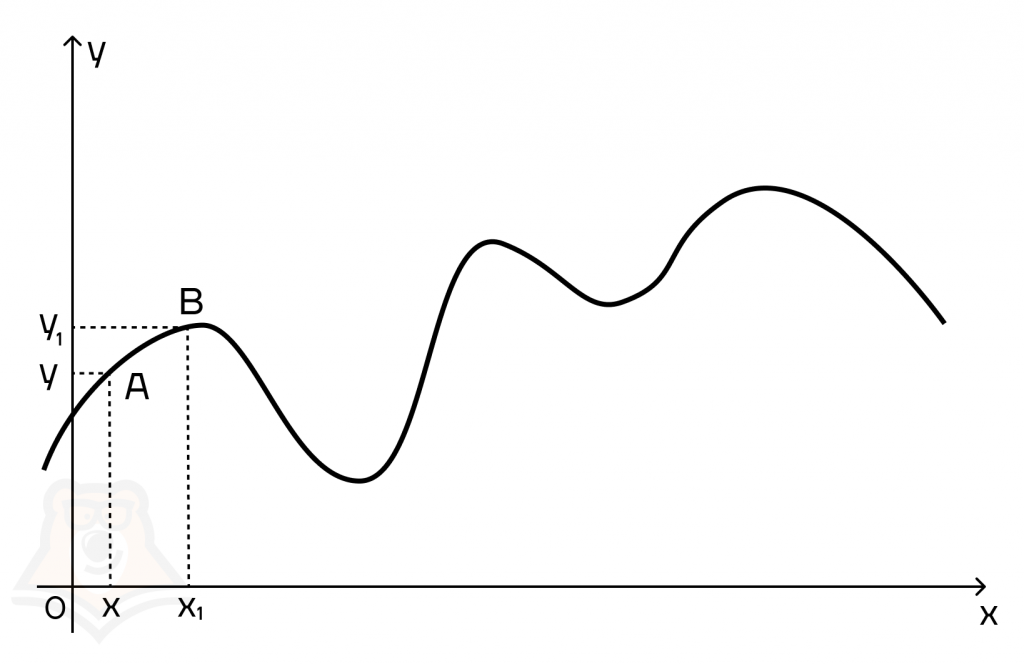
Представим, что наш вагончик проехал из точки А в точку В. Расстояние, которое он проехал по горизонтали, будет равно х1 — х, а поднялся он на высоту у1 — у. Для удобства дальнейших рассуждений примем эти расстояния за х и у.
Знак Δ “дельта” — означает изменение величины, то есть разность между тем, что было в точке А и стало в точке В.
Теперь мы можем ввести определение приращения.
Приращение функции — это разность между двумя значениями функции, то есть у.
Приращение аргумента — это разность между двумя значениями аргумента, то есть х.
Скорость изменения функции будет равна отношению приращения функции к приращению аргумента. При этом чем меньше будет приращение аргумента, тем точнее мы приблизимся к верному значению.
Отсюда мы получаем определение производной функции.
Производная функции — это понятие дифференциального исчисления, характеризующее скорость изменения функции.
Производную функции обозначают как f'(x).
(f'(x) = frac{Delta y}{Delta x}: при: Delta x rightarrow 0)
Если мы применим одинаковое приращение аргумента к разным участкам функции, то заметим, что приращение функции также будет разное. Где-то значение у изменится больше, где-то меньше. Именно так изменяется скорость функции на разных ее участках.
Нахождение производной называется дифференцированием.
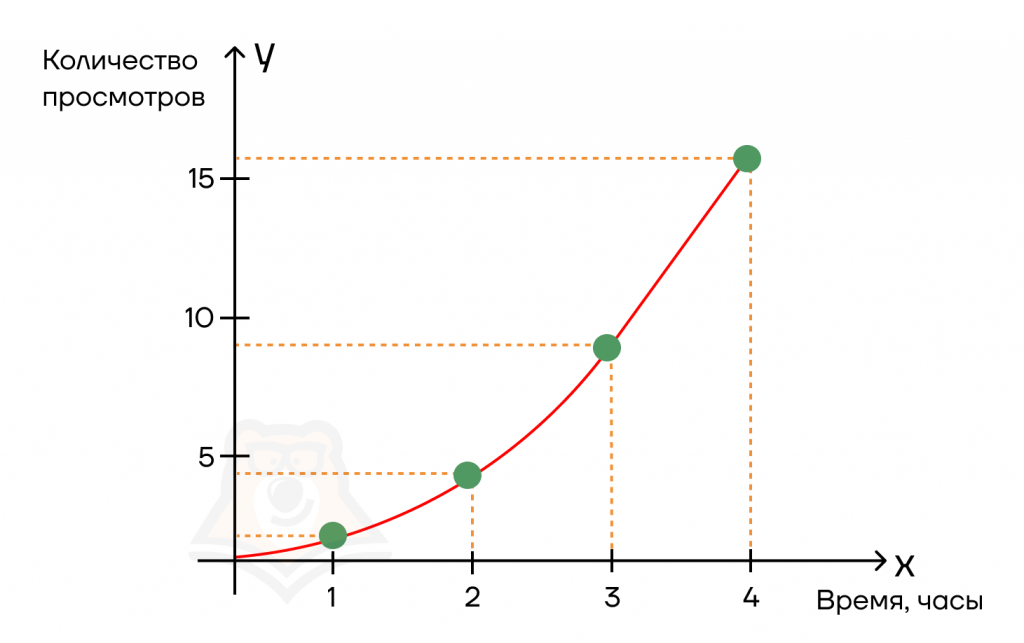
Допустим, мы выложили видео в соцсеть. Сначала было совсем невесело: за первый час всего один просмотр. За второй час ситуация сильно не изменилась — добавилось лишь 3 просмотра. Мы скинули ссылку на видео в чат друзей, и за третий час количество просмотров дошло до 9, а за четвертый час — до шестнадцати.
Возможно, ситуация не очень похожа на правду, и мы бы сразу попали в топ. Но пусть будет так для удобства цифр.
В результате мы имеем функцию, которая показывает, как количество просмотров менялось во времени.
Теперь зададимся вопросом: как быстро росла популярность у нашего ролика?
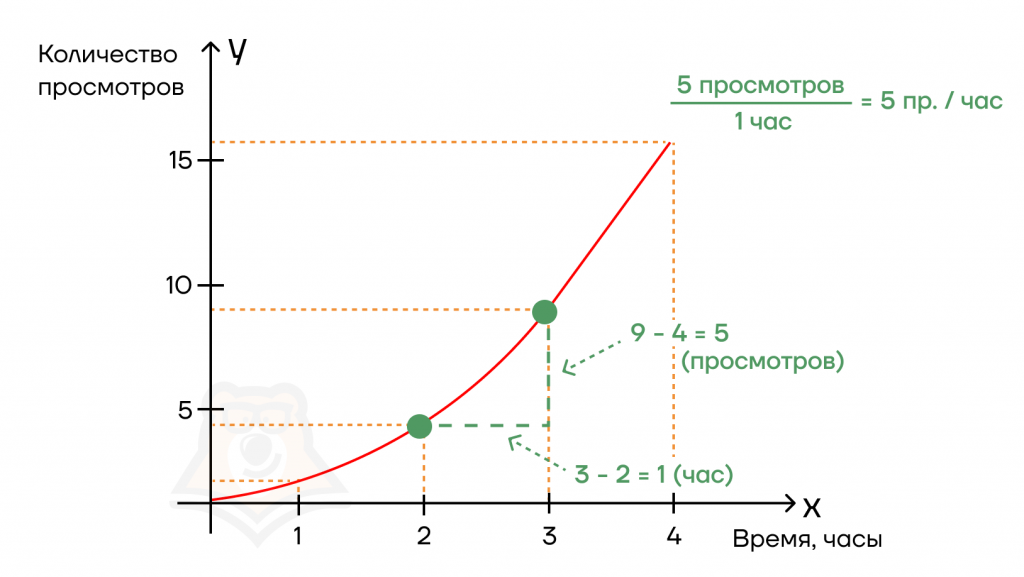
Чтобы это выяснить, мы возьмем две соседние точки на графике и посчитаем:
1) как изменилось количество просмотров между этими точкам (Δ количества просмотров);
2) как изменилось время между этими точками (Δ времени);
3) затем разделим Δ просмотров на Δ времени.
Получается, что “производительность” нашего видео была 5 просмотров в час.
Таким нехитрым образом, мы нашли производную от функции, показывающую рост популярности нашего ролика в сети за определенный промежуток времени:
(f'(x) = frac{Delta y}{Delta x} = frac{5}{1} = 5)(просмотров в час)
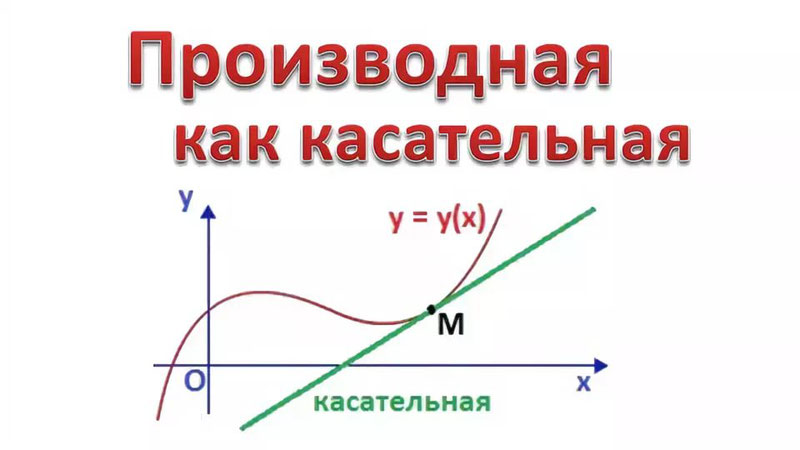
Геометрический смысл производной
Достроим прямоугольный треугольник АВС. Заметим, что отношение (frac{Delta x}{Delta y} = tg(BAC)), то есть равняется отношению противолежащего катета к прилежащему катету. Иначе это отношение можно записать как (tg(BAC) = frac{BC}{AC}).
Поскольку в этом примере мы взяли достаточно большое расстояние между значениями х, то АВ — секущая. Если мы будем сокращать расстояние между значениями аргумента, то две точки на графике будут ближе друг к другу, а секущая будет стремиться к касательной.

Следовательно, мы можем описать скорость изменения функции через тангенс угла наклона касательной, проведенной к графику функции в некоторой точке.
Из этих рассуждений мы можем вывести геометрический смысл производной:
Если провести касательную к функции в некоторой точке, то производная в этой точке будет равна тангенсу угла ее наклона.
Рассмотрим касательную отдельно. Это прямая, которая имеет уравнение y = kx+b, где к — коэффициент наклона.
Тогда мы получаем следующее уравнение:
f'(x) = k = tg(a)
Геометрический смысл производной — главный совместный номер. Производная равняется тангенсу угла наклона касательной, проведенной к функции в определенной точке.
Знак производной
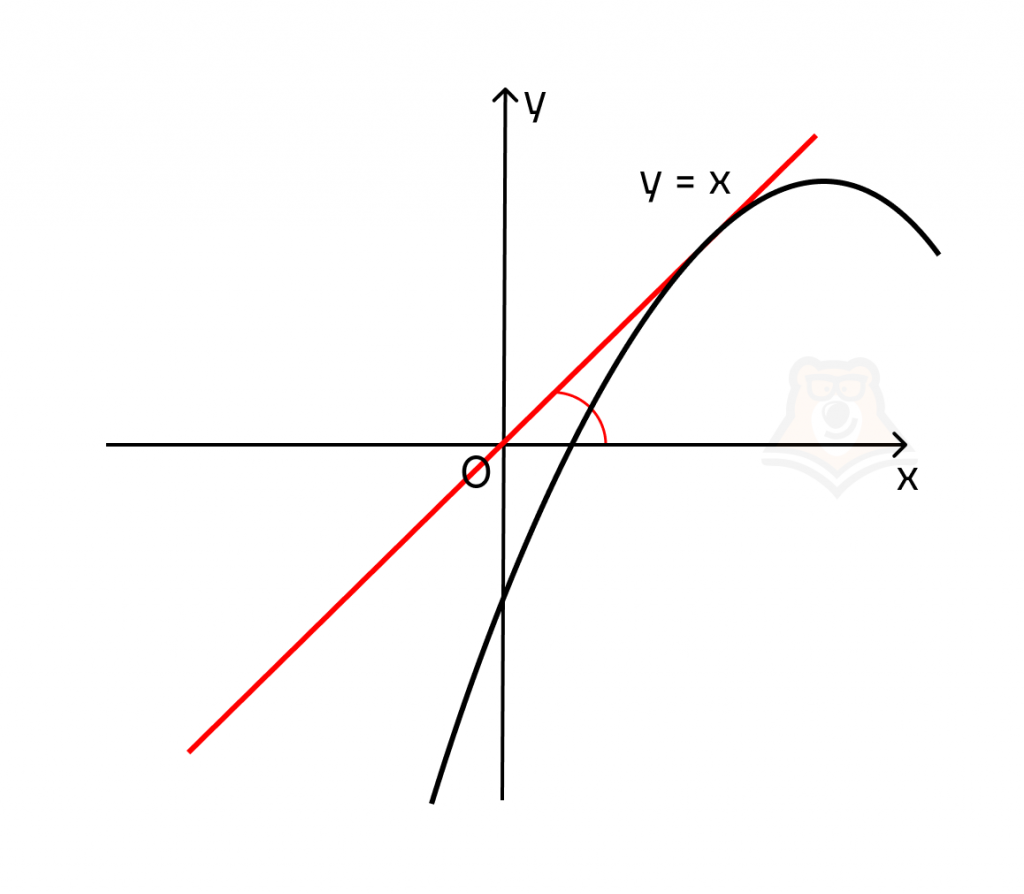
Построим графики двух прямых с разным углом наклона. Пусть в первом случае k = 1, а во втором k = -1. Тогда получаем графики функций у = х и у = -х.
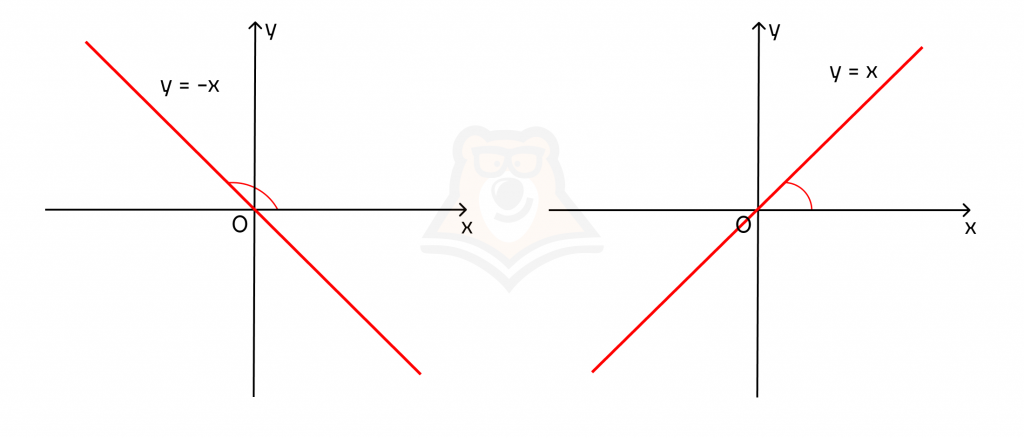
Заметим, что тангенс угла наклона имеет разные значения в этих случаях: tg(a) = -1 и tg(a) = 1.
Теперь достроим к касательным графики функций. В первом случае точка, к которой проведена касательная, будет лежать на участке функции, на котором она убывает. Во втором случае точка касания будет лежать на возрастающем участке функции.
Чтобы определить, убывает или возрастает функция, нужно посмотреть на ее наклон на участке.
Вспомним американские горки: пусть по функции будет слева направо ехать вагончик. В участках, где вагончик будет подниматься на гору, функция возрастает, а где вагончик съезжает с горки — функция убывает.
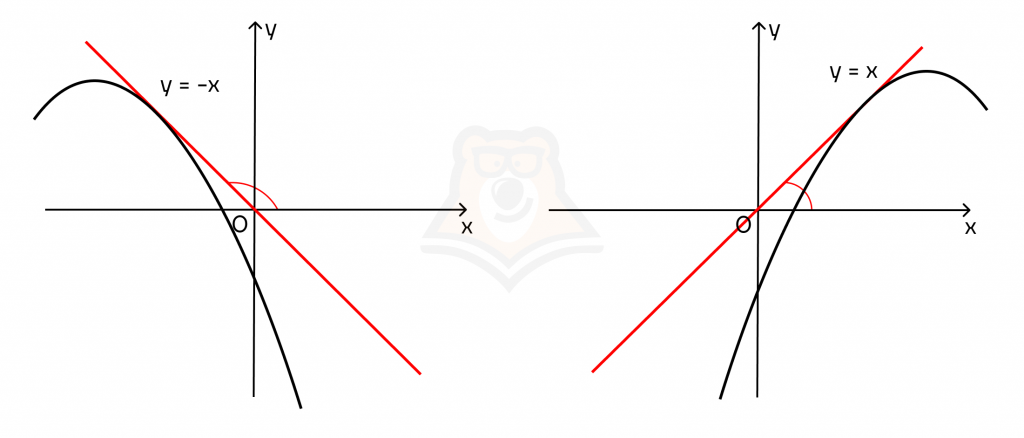
Из этих рассуждений мы можем вывести зависимость знака функции и знака производной.
1. Функция возрастает в точке тогда и только тогда, когда производная в данной точке положительна.
В этом случае касательная к функции также будет возрастать.
f'(x) = tg(a). Если tg(a) > 0, то и f'(x) > 0.
2. Функция убывает в точке тогда и только тогда, когда производная в данной точке отрицательна.
В этом случае касательная к функции будет убывать.
f'(x) = tg(a). Если tg(a) < 0, то и f'(x) < 0.

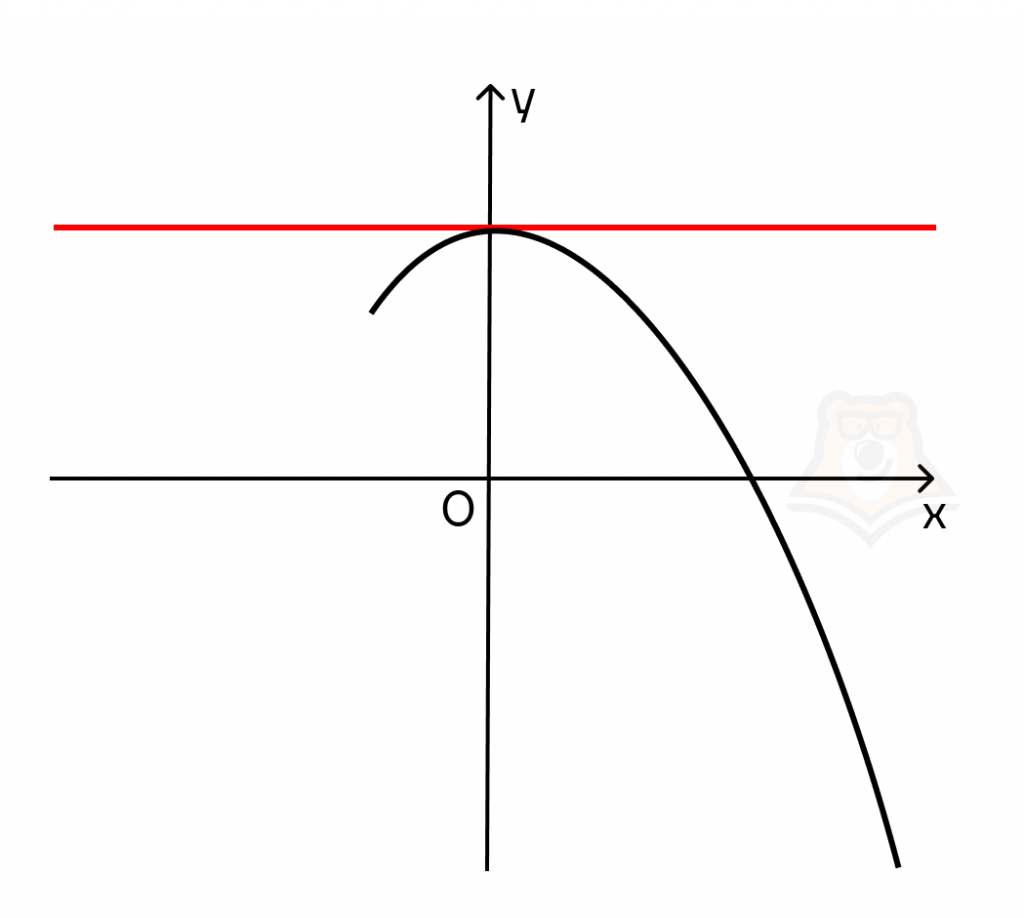
3. Если касательная к функции параллельна оси абсцисс, то производная в этой точке равна 0.
Поскольку прямая будет параллельна оси абсцисс, то у нее не будет угла наклона, а следовательно: k = tg(a) = 0 = f'(x).
Такие точки называются стационарными, это точки экстремума или седловые точки.
Подведем итог.
Знак производной определяется по изначальной функции:
- если функция возрастает, то производная положительна;
- если функция убывает, то производная отрицательна;
- в точках, где функция не возрастает и не убывает (стационарные точки), производная равна 0.
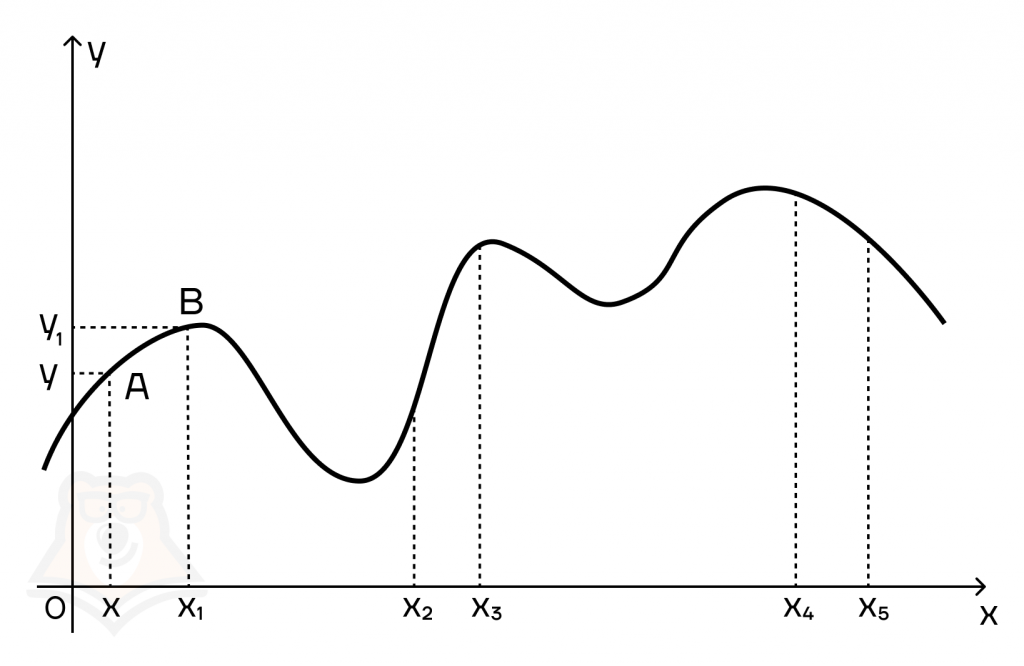
Точки экстремума
Как уже было сказано ранее, производная функции может равняться 0. Она принимает такое значение в точках экстремума.
Экстремум — это точка, в которой достигается максимальное или минимальное значение функции на заданном отрезке.
Точки экстремума — точки, в которых достигается экстремум.
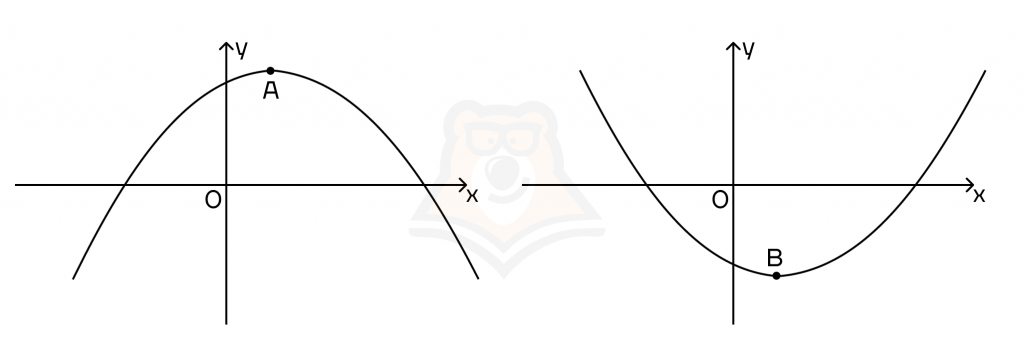
На рисунке видно, что точки А и В являются экстремумами. Например, до точки А функция будет возрастать, а после нее уже убывать, то есть наибольшее значение эта функция достигнет именно в точке экстремума.
Если вспомнить наш вагончик, то в точке А он достигнет наибольшую высоту над землей.
Во втором случае аналогичные рассуждения, но функция достигает уже наименьшее значение в точке В.
В теме производной есть такие термины, как “точка минимума” и “точка максимума”.
Точка минимума — это точка, в которой достигается минимальное значение функции.
В этой точке знак функции меняется с отрицательного на положительный (то есть сначала функция убывала, а потом начала возрастать). Это точка В.
Точка максимума — это точка, в которой достигается максимальное значение функции на отрезке.
В этой точке знак функции меняется с положительного на отрицательный (то есть сначала функция возрастала, а потом стала убывать). Это точка А.
Также с точками экстремума связаны наибольшее и наименьшее значение функции.
Важно!
Следует вспомнить, что когда мы говорим о значении функции, то имеем в виду значение ординаты, то есть у (или f(x)).
Наибольшее значение функции — точка на оси ординат, в которой достигается наибольшее значение функции на заданном отрезке.
Например, в точке А будет достигаться наибольшее значение функции.
Наименьшее значение функции — точка на оси ординат, в которой достигается наименьшее значение функции на заданном отрезке.
В точке В будет достигаться наименьшее значение функции.
Физический смысл производной
Предположим, что некоторая точка движется прямолинейно, и ее путь можно описать по закону х(t). То есть за определенное время t точка пройдет расстояние х.
А теперь вспомним формулу скорости: (v = frac{x}{t}).
Чтобы найти среднюю скорость на каком-то участке пути точки, нужно разделить весь путь на все время, или (v_{ср.} = frac{Delta x}{Delta t}). Таким образом, мы пришли к определению производной.
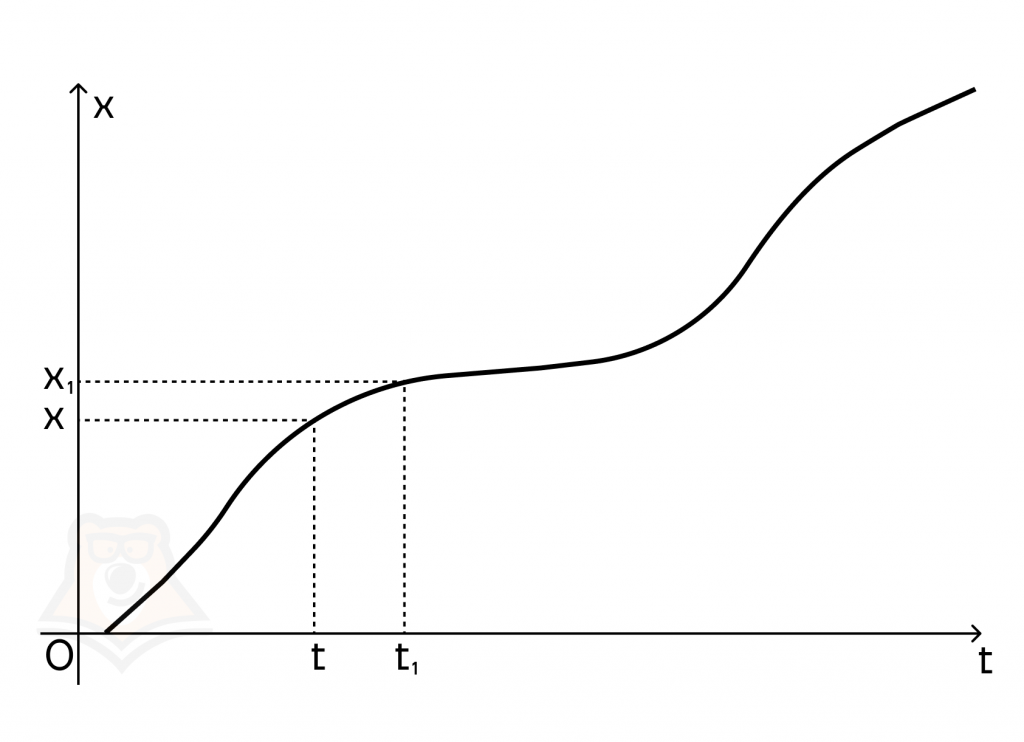
Физический (механический) смысл производной состоит в том, что производная от функции равняется скорости движения некоторого тела по траектории x(t) в момент времени t. x'(t) = v
Также вспомним, что скорость тела зависит от его ускорения. Тогда, применяя аналогичные рассуждения, получаем:
v'(t) = a
Производную можно брать несколько раз. Например, если мы дважды возьмем производную от x(t), то получим ускорение точки:
(x^{primeprime} (t) = v'(t) = a).
Как найти скорость и ускорение точки с помощью производной?
Для этого необходимо воспользоваться физическим смыслом производной: производная от функции равна скорости движения некоторого тела. Производная от скорости равна ускорению тела.
Фактчек
- Производная функции — это понятие дифференциального исчисления, характеризующее скорость изменения функции. Скорость изменения функции равняется отношению приращения функции к приращению аргумента. Нахождение производной называется дифференцированием.
- Если провести касательную к функции в некоторой функции, то производная в этой точке будет равна тангенсу угла ее наклона. Это геометрический смысл производной.
- Производная будет положительна на участках возрастания функции и отрицательна на участках убывания. В стационарных точках (точки экстремума и седловые точки) производная будет равна 0.
- Точка минимума — точка, в которой достигается минимальное значение на заданном отрезке, точка максимума — точка, в которой достигается максимальное значение.
- Физический (механический) смысл производной состоит в том, что производная от функции равняется скорости движения некоторого тела по траектории x(t) в момент времени t.
Термины
Абсцисса — координата определенной точки на оси Х.
Ордината — координата определенной точки на оси У.
Проверь себя
Задание 1.
Что такое приращение функции?
- Разность между значениями у;
- Разность между значениями х;
- Сумма значений у;
- Сумма значений х.
Задание 2.
Чему равна производная?
- Котангенсу угла наклона касательной;
- Тангенсу угла наклона касательной;
- Синусу угла наклона касательной;
- Косинусу угла наклона касательной.
Задание 3.
Как меняется знак производной в точке максимума?
- Знак производной не меняется;
- Производная всегда равна 0 и не имеет знака;
- Знак меняется с положительного на отрицательный;
- Знак меняется с отрицательного на положительный.
Задание 4.
В каком случае функция будет возрастать?
- Если производная положительна;
- Если производная отрицательна;
- Если производная равна 0;
- Ни один из вышеперечисленных случаев.
Задание 5.
Какая величина получится, если дважды взять производную у функции?
- Скорость;
- Ускорение;
- Путь;
- Время
Ответы: 1. — 1 2. — 2 3. — 3 4. — 1 5. — 1
здравствуй тема данного видеоурока определения производной давайте рассмотрим график некоторой функции y равна f от x здесь у нас ось x ось y возьмем значение этой функции в некоторой точке x соответствующее значение функции это f от x дадим аргументу x приращение получим точку x плюс дельта x а значение функции соответствующие будет f от x плюс дельта x теперь если мы будем постепенно уменьшать вот это приращение то есть . x + 2x у нас будет все время смещаться сюда тогда соответствие зачем функция тоже будет стремиться к f от x рассмотрим приращение функции дельта y при вращении функция это разность значений функции в точке x плюс дельта x и f от x теперь рассмотрим вот такой предел будем устремлять дельта x к нулю то есть постепенно его уменьшать и найдем отношение приращения функции приращение аргумента так вот согласно определению приращение функции отношение приращения функции к приращению аргумента когда это приращение стремится к нулю называется производной функции и обозначается как y штрих давайте рассмотрим пример пусть у нас есть функция y от x равна и x графики как мы знаем это просто прямая дадим прижечь аргументу x некоторые превращение x плюс дельта x и найдем значение функции в точке x плюс дельта x то есть сюда вместо икса мы должны поставить x плюс дельта x это будет x плюс дельта x отсюда мы можем найти приращение приращение функции это разность вот этого значение и вот этого мы получим дельта x а теперь найдем предел дельта x стремится к нулю отношение приращения функции к приращению аргумента как мы сказали по определению это есть производная это будет равняться предел дельта x стремится к нулю дельта y мы вычислили равняется дельта x делим на дельта x dx деленное дельта x сокращается получаем 1 значит этот предел будет равняться одному значит производной этой функции равняется 1 так как у нас y это x то мы можем записать первая формула производная икса это единица рассмотрим теперь вот такую функций пусть у нас есть прямая y равна и к x плюс b это у нас y от x найдем y от x плюс дельта x то есть найдем значение функции точки в точке x плюс z и x мы получим к вместо икса ставим x плюс дельта x плюс b теперь найдем превращения превращение это разные соответствующего от этого значение и вот этого если мы распишем мы получим что kx уничтожится ска xd уйдет бы останется к дэльта икс тогда предел при дэльта икс стремящейся к нулю от отношения приращения функции к приращению аргумента дельта x будет равняться как а это означает что производная данной функции будет равняться как иначе говоря производной от kx + b будет равняться к хотя рассмотрим пример попробуем найти производные функции и рекламные x квадрат для этого y штрих у нас равняется предел дельта x стремится к нулю а вот отношение приращения функции к приращению аргумента приращение функции это будет значение функции в точке x плюс дельта x в квадрате минус значение функции в точке x x квадрате деленный на дельта x давайте преобразуем данное выражение раскроем квадрат мы получим что x квадрат минус x квадрат уйдет останется 2 x дельта x плюс дельта x квадрате деленное на дельта x мы можем сократить на дельта x тогда здесь у нас уйдет dtx здесь идет квадрат здесь будет дельта x останется 2 x плюс bx если дельта x стремится к нулю это останется 2 x таким образом мы получили что производная от x квадрат равняется 2 x давайте рассмотрим другой пример найдем производную функции y равен единице x также находим предел дельта x стремится к нулю y от x плюс дельта x значит вместо икса оставлю x плюс x минус 1 на x деленная на дельта x преобразуем это выражение здесь надел общий знаменатель и этот знаменатель отправим вниз общий знаменатель будет x на x плюс дельта x умноженное на дельта x этого то дельта x сверху получим икс минус икс минус дельта x теперь икс минус икс у нас взаимно уничтожается дельта x сокращается с дельта x тогда сверху мне останется просто -13 дельта x стремящемся к 0-лю у нас вот это будет 0 останется минус 1 деленное на x умноженное на x то есть -1 на x квадрат таким образом мы получили что единица деленное на x производная это -1 на x-квадрат производное имеет несколько важных приложений первая из них это следующая пусть у вас есть некоторое тело которое движется согласно закону y равна и с от их то есть это некоторая функция тогда скорость этого тела будет находиться как производная этой функции то есть скорость тела есть лишь штрих от x таким образом зная как движется тело мы можем найти с помощью производной его скорость второй смысл производной это геометрический пусть у нас есть некоторая функция y равна f от x и пусть к некоторой точке этой функции мы хотим провести касательную прямую это касательно прямая наклонена к оси x под некоторым углом альфа так вот производная этой функции в точке касания пусть это . скажем x 0 то есть производная функции f от x точке x0 и то есть тангенс угла наклона соответствующий касательной в этом заключается геометрический смысл производной на этом данный видео урок и хочет
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Геометрический и физический смысл производной
Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.
Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:
Нам нужно найти скорость в момент времени t=2c. Вычислим производную:
Правила нахождения производных
Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.
Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте.
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Решение:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Пример:
Решение:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Дельта-функция Дирака и ее свойства
Содержание
Обнаружили ошибку?
Выделите ее мышью
и нажмите

Вводные замечания
При рассмотрении преобразования Фурье мы говорили, что условием существования преобразования Фурье является абсолютная интегрируемость исходного сигнала 
(1)
Данное ограничение существенно сужает класс функций, для которых может быть вычислено преобразование Фурье.
Так например, постоянный сигнал 

К счастью, в первой половине XX века в теоретической физике произошли большие перемены. Появилась теории относительности и квантовой механики, которые потребовали переосмыслить понятие функции в целом. В результате была разработана теория обобщенных функций, которые расширили область применения методов математического анализа, устранили некоторые неопределенности в физике, а также расширили применимость методов спектрального анализа на функции, для которых условие абсолютной интегрируемости не выполняется.
Кроме того, использование аппарата обобщенных функций позволило сформулировать и обосновать переход от аналоговых непрерывных сигналов и систем к дискретным и цифровым.
Математическую теорию обобщенных функций можно найти в литературе [1, 2, 3, 4]. Нас будет особенно интересовать дельта-функция Дирака, свойства которой позволяют распространить преобразование Фурье на случай неинтегрируемых сигналов, а также находят широкое применение в теории обработки сигналов.
Дельта-функция Дирака
Рассмотрим прямоугольный импульс 

(2)
Тогда при нормировке амплитуды импульса к длительности 


(3)
Семейство сигналов 

Если мы устремим длительность импульса 

(4)
которая также показана на рисунке 1. При этом свойство единичной площади
(5)
будет сохраняться и для функции (4).

Рисунок 1. Прямоугольный импульс единичной площади
Обратим внимание, что в (4) и на рисунке 1 использовалось обозначение 



Впервые функция одновременно обладающая свойствами (4) и (5) была использована Полем Дираком [1, стр. 84–88], поэтому мы будем называть данную функцию дельта-функция Дирака.
Очевидно, что выражения (4) и (5) противоречат классическим определениям функции и интеграла, поэтому дельта-функция Дирака 
Использование данной функции внутри линейного интегрального оператора: интеграла свертки, скалярного произведения, или интеграла Фурье, открывает определенные возможности для анализа.
Свойства дельта-функции Дирака
Чётность
Из выражения (2) и рисунка 1 можно заметить, что прямоугольный импульс 

Свойство скалярного произведения
Рассмотрим
скалярное произведение
некоторого непрерывного сигнала 

(6)
Подставим в (6) предел (4):
(7)
Представим интеграл (7) по определению Римана [5, стр. 301–302] в виде предела суммы площадей прямоугольных импульсов длительности 

Рисунок 2. Интегрирование по Риману
Тогда выражение (7) можно представить как:
(8)
Заметим, что 


(9)
Мы получили важнейшее свойство дельта-функции Дирака: скалярное произведение сигнала 



Фильтрующее свойство дельта-функции
Рассмотрим скалярное произведение 


(10)
Введем замену переменной 


(11)
Выражение (11) является следствием свойства скалярного произведения и называется фильтрующим свойством дельта-функции [6, стр. 29]. Благодаря именно фильтрующему свойству, дельта-функция получила широкое распространение при описании дискретных систем.
Заметим, что 



(12)
Свертка с дельта-функцией
Рассмотрим интеграл свертки некоторого сигнала 

(13)
В силу четности дельта-функции, а также используя фильтрующее свойство можно представить (13) в виде:
(14)
Таким образом, свертка с дельта-функцией не искажает и не задерживает сигнал. Выражение (14) называют динамическим представлением сигнала 
Если мы вспомним, что интеграл свертки описывает реакцию некоторого линейного фильтра на входной сигнал 




Размерность дельта-функцией
Рассматривая выражения (4) и (5) можно заметить, что размерность дельта функции обратна размерности ее аргумента. Так если аргумент 


![left[frac{1}{с} = Гцright]](https://ru.dsplib.org/content/fourier_transform_delta_func/img/eqlin-26.png)
(15)
Аналогично, если дельта-функция 

![left[frac{1}{с}right]](https://ru.dsplib.org/content/fourier_transform_delta_func/img/eqlin-29.png)
![[с]](https://ru.dsplib.org/content/fourier_transform_delta_func/img/eqlin-30.png)
Интегрирование дельта-функции
Подадим на вход интегратора дельта-функцию и рассмотрим выходной сигнал:
(16)
При 






(17)
Таким образом, окончательно можно записать 
(18)
Функция 


Рисунок 3. Интегрирование дельта-функции
Интегрирование сдвинутой во времени дельта-функции 
(19)
Тогда можно заметить, что 


(20)
Поменяем порядок интегрирования, и применим свойство свертки с дельта-функцией. Тогда:
(21)

Рисунок 4. Прямоугольный импульс как сумма функций Хевисайда
Таким образом мы показали, что 
С другой стороны, использование аппарата обобщенных функций позволяет задать производную функции 


Используя взаимосвязь функции Хевисайда и дельта-функции можно определить производные некоторых негладких функций в точке разрыва. Например производную прямоугольно импульса единичной площади 
Тогда производная прямоугольного импульса равна:
(22)
Дифференцирование дельта-функции Дирака
Аппарат обобщенных функций позволяет определить производную разрывных функций в точке разрыва. Но что еще более интересно, так это то, что мы можем использовать аппарат обобщенных функций для получения производной самой дельта-функции. Производную дельта-функции 

(23)
Поменяем местами оператор предела и дифференцирования, а также учтем (22):
(24)
Из (24) следует, что производная дельта-функции является нечетной функцией, т.е. 
Скалярное произведение сигнала 
(25)
Интегрирование ведется по переменной 

(26)
Можно заметить, что предел в выражении (26) ничто иное, как значение производной 



(27)
Соответственно скалярное произведение сдвинутой на 

(28)
а свертка исходного сигнала 

(29)
Таким образом, производная дельта-функции описывает импульсную характеристику идеального дифференциатора.
По аналогии можно определить производную дельта-функции произвольного порядка 



(30)
Выражение (30) легко доказывается, применяя правило интегрирования по частям.
Преобразование Фурье дельта-функции Дирака
Рассмотрим преобразование Фурье дельта-функции Дирака:
(31)
Используем фильтрующее свойство дельта-функции и получим:
(32)
Таким образом, спектральная плотность 

Рисунок 5. Представление дельта-функции:
а — во временно́й области; б — спектральная плотность
Вспомним, что преобразование Фурье возвращает спектральную плотность, чья размерность равна размерности входного сигнала, деленную на единицу полосы. В случае преобразования Фурье дельта-функции получаем, что 
![left[frac{1}{с} / Гцright]](https://ru.dsplib.org/content/fourier_transform_delta_func/img/eqlin-46.png)
Также заметим, что спектральная плотность дельта-функции Дирака не убывает с ростом частоты 
Чтобы понять этот эффект, необходимо снова обратиться к предельному переходу (4), и рассмотрим преобразование Фурье от левой и правой частей (4):
(33)
Вынесем оператор предела из под оператора преобразования Фурье (мы можем это делать ввиду свойства линейности преобразования Фурье), а также вспомним выражение для преобразования Фурье прямоугольного импульса рассмотренное в
предыдущем разделе.
Тогда (33) принимает вид:
(34)
Таким образом, спектральная плотность дельта-функции получается как предел функции 




Рисунок 6. Функции 

Из рисунка 6 видно, что при уменьшении параметра 


Выводы
В данном разделе мы ввели понятие обобщенной дельта-функции Дирака, и рассмотрели ее некоторые свойтсва.
Также была показана связь дельта-функции Дирака и функции Хевисайда, а также показана возможность применения дельта-функции для задач дифференцирования негладких функций.
Мы рассмотрели понятие производной дельта-функции и некторые ее свойства.
Также было рассмотрено преобразование Фурье 

Смотри также
Представление периодических сигналов рядом Фурье
Некоторые свойства разложения периодических сигналов в ряд Фурье
Свойства преобразования Фурье
Спектральные плотности некоторых сигналов
Список литературы
[1]
Принципы квантовой механики
Москва, Наука, 1979, 480 c.
[2]
Гельфанд, И.М. and Шилов, Г.Е.
Обобщенные функции и действия над ними.
Москва, Государственное издательство физико-математической литературы, 1959, 472 c.
[3]
Владимиров С.В.
Обобщенные функции в математической физике.
Москва
[4]
Колмогоров А.Н., Фомин С.В.
Элементы теории функций и функционального анализа.
Москва, Наука, 1968, 496 с.
[5]
Ильин, В.А., Позняк Э.Г.
Основы математического анализа.
Москва, Наука, 1965, 572 c.
[6]
Баскаков, С.И.
Радиотехнические цепи и сигналы.
Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4
[7]
Гоноровский И.С.
Радиотехнические цепи и сигналы
Москва, Советское радио, 1977, 608 c.
[8]
Bracewell R.
The Fourier Transform and Its Applications
McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6
Последнее изменение страницы: 12.05.2022 (19:42:46)
Страница создана Latex to HTML translator ver. 5.20.11.14
Содержание:
- Приращение аргумента и функции
- Определение производной
- Дифференцирование функции
Пусть задана некоторая функция $y=f(x)$. Возьмем какое-нибудь
значение $x_{0}$ из области определения этой функции:
$x_{0} in D[f]$ . Соответствующее значение функции в этой точке
будет равно $y_{0}=fleft(x_{0}right)$ .
Приращение аргумента и функции
Определение
Приращением аргумента называется разность между двумя значениями аргумента: «новым» и «старым».
Обычно обозначается как $Delta x=x_{1}-x_{0}$ .
Пример
Задание. Найти приращение аргумента $x$, если он переходит от значения 3 к значению 3,2.
Решение. Искомое приращение: $Delta x=3,2-3=0,2$ .
Ответ. $Delta x=0,2$
Зададим аргументу $x_{0}$ приращение
$Delta x$. А тогда значение функции в новой точке
$fleft(x_{0}+Delta xright)$.
Определение
Приращением функции $y=f(x)$ в точке
$x_{0}$, соответствующее приращению аргумента
$Delta x=x-x_{0}$, называется величина:
$Delta y=fleft(x_{0}+Delta xright)-fleft(x_{0}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти приращение функции $y=2 x^{2}$
при $x_{0}=3$ и
$Delta x=0,1$
Решение. Подставляя в формулу, получаем, что приращение функции:
$Delta y=y(3+0,1)-y(3)=2 cdot(3+0,1)^{2}-2 cdot 3^{2}=1,22$
Ответ. $Delta y=1,22$
Определение производной
Определение
Производной $y^{prime}(x)$ от функции
$y=f(x)$ в точке
$x_{0}$ называется предел отношения
приращения функции $Delta y$ к приращению аргумента
$Delta x$ :
$frac{Delta y}{Delta x}$ при
$Delta x rightarrow 0$, если он существует, то есть:
$y^{prime}left(x_{0}right)=f^{prime}left(x_{0}right)=lim _{Delta x rightarrow 0} frac{Delta y}{Delta x}=lim _{Delta x rightarrow 0} frac{fleft(x_{0}+Delta xright)-fleft(x_{0}right)}{Delta x}$
или
$y^{prime}left(x_{0}right)=lim _{x rightarrow x_{0}} frac{f(x)-fleft(x_{0}right)}{x-x_{0}}$
Пример
Задание. Найти производную функции $y=x^{2}+3 x$
в точке $x_{0}=0$.
Решение. Найдем приращение заданной функции в точке $x_{0}$ :
$Delta y=y(0+Delta x)-y(0)=y(Delta x)-y(0)=$
$=(Delta x)^{2}+3 Delta x-0=Delta x(Delta x+3)$
Тогда
$y^{prime}(0)=lim _{Delta x rightarrow 0} frac{Delta x(Delta x+3)}{Delta x}=lim _{Delta x rightarrow 0}(Delta x+3)=0+3=3$
Ответ. $y^{prime}(0)=3$
Дифференцирование функции
Определение
Операция нахождения производной функции называется дифференцированием этой функции.
Функция $y=f(x)$ имеет производную на интервале
$(a ; b)$ или называется дифференцируемой в этом
интервале, если производная $f^{prime}(x)$ существует в каждой точке этого интервала.
Функция $y=f(x)$ имеет в точке
$x$ бесконечную производную, если в этой точке
$f^{prime}(x)=lim _{Delta x rightarrow 0} frac{Delta y}{Delta x}=infty$ .
Теорема
(О непрерывности функции в точке)
Если функция $y=f(x)$ имеет конечную производную в
точке $x_{0}$ , то она непрерывна в этой точке.
Замечание. Обратное заключение не всегда верно: если функция $y=f(x)$
непрерывна в некоторой точке $x_{0}$ , то она может
и не иметь производной в этой точке.
Определение
Функция $y=f(x)$ называется дифференцируемой
в точке $x$, если приращение функции,
соответствующее приращению аргумента, можно представить в виде:
$Delta y=A cdot Delta x+alpha(Delta x) cdot Delta x$
где $A$ — число, не зависящее от
$Delta x$,
$alpha(Delta x)$ — б.м. функция при
$Delta x rightarrow 0$.
Теорема
(О необходимом и достаточном условии дифференцируемости)
Для того чтобы функция $y=f(x)$ была дифференцируемой
в точке $x$, необходимо и достаточно,
чтобы $y=f(x)$ имела в этой точке конечную производную.
Теорема устанавливает, что для функции $y=f(x)$
дифференцируемость в данной точке $x$ и существование конечной производной в этой точке — понятия равносильные.
Читать дальше: односторонние производные.