Ускорение свободного падения характеризует то, как быстро будет увеличиваться скорость тела при свободном падении. Свободным падением называется ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести. Из физики известно, что ускорение свободного падения на Земле составляет (9,8)
мс2
.
Вопрос, почему эта величина именно такая, мы рассмотрим в этой теме.
Ускорение свободного падения в упрощённом виде можно рассчитать по формуле
g=Fm
, которая получается из формулы
F=m⋅g
, где (F) — сила тяжести либо вес тела в состоянии покоя или равномерного прямолинейного движения, (m) — масса тела, которое притягивает планета, (g) — ускорение свободного падения.
Сила тяжести, действующая на тело, зависит от массы тела, массы планеты, притягивающей тело, и от расстояния, на котором находится тело от центра массы планеты.
(F) — сила тяжести, Н;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
(R) — расстояние между центрами планеты и объекта в метрах. Если притягиваемое тело находится на поверхности планеты, тогда (R) равен радиусу планеты (если планета имеет сферическую форму);
m1 и
m2
— масса планеты и притягиваемого тела, выраженные в кг.
Обрати внимание!
Если мы объединим обе формулы, тогда получим формулу
g=G⋅mR2
, с помощью которой можно вычислить ускорение свободного падения на любом космическом объекте — на планете или звезде.
Пример:
ускорение свободного падения у поверхности Земли вычисляют таким образом:
, где
(g) — ускорение свободного падения;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
Практически на Земле ускорение свободного падения на полюсах немного больше ((9,832)
мс2
), чем на экваторе ((9,78)
мс2
), так как Земля не имеет форму идеального шара, а на экваторе скорость вращения больше, чем на полюсах. Среднее значение ускорения свободного падения у поверхности Земли равно (9,8)
мс2
.
Ускорение свободного падения у поверхности любого космического тела — на планете или звезде — зависит от массы этого тела и квадрата его радиуса. Таким образом, чем больше масса звезды и чем меньше её размеры, тем больше значение ускорения свободного падения у её поверхности.
При помощи формулы расчёта ускорения свободного падения и измерений, проведённых для удалённых объектов, учёные-физики могут определить величину ускорения свободного падения на любой планете или звезде.
Рис. (1). Планеты Солнечной системы: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун; и карликовые планеты: Церера, Плутон, Эрида ((2003) UB (313))
Таблица (1). Ускорение свободного падения и другие характеристики планет Солнечной системы и карликовых планет
|
Небесное тело |
Ускорение свободного падения, мс2 |
Диаметр, км |
Расстояние до Солнца, миллионы км |
Масса, кг |
Соотношение с массой Земли |
|
Меркурий |
(3,7) |
(4878) |
(58) |
(3,3*) 1023 |
(0,055) |
|
Венера |
(8,87) |
(12103) |
(108) |
(4,9*) 1024 |
(0,82) |
|
Земля |
(9,8) |
(12756,28) |
(150) |
(6,0*) 1024 |
(1) |
|
Марс |
(3,7) |
(6794) |
(228) |
(6,4*) 1023 |
(0,11) |
|
Юпитер |
(24,8) |
(142984) |
(778) |
(1,9*) 1027 |
(317,8) |
|
Сатурн |
(10,4) |
(120536) |
(1427) |
(5,7*) 1026 |
(95,0) |
|
Уран |
(8,87) |
(51118) |
(2871) |
(8,7*) 1025 |
(14,4) |
|
Нептун |
(10,15) |
(49532) |
(4498) |
(1,02*) 1026 |
(17,1) |
|
Плутон |
(0,66) |
(2390) |
(5906) |
(1,3*) 1022 |
(0,0022) |
|
Луна |
(1,62) |
(3473,8) |
(0,3844 ) (до Земли) |
(7,35*) 1022 |
(0,0123) |
|
Солнце |
(274,0) |
(1391000) |
— |
(2,0*) 1030 |
(332900) |
Нейтронные звёзды имеют малый диаметр — порядка десятков километров, — а масса их сопоставима с массой Солнца. Поэтому гравитационное поле у них очень сильное.
Пример:
если диаметр нейтронной звезды равен (20) км, а масса её в (1,4) раза больше массы Солнца, тогда ускорение свободного падения будет в (200000000000) раз больше, чем у поверхности Земли.
Его величина приблизительно равна
2⋅1012 мс2
. Значение ускорения свободного падения для нейтронной звезды может достигать значения
7⋅1012 мс2
.
Формула ускорения свободного падения в физике
Формула ускорения свободного падения
Гравитационное поле и ускорение свободного падения
Гравитационные взаимодействия тел можно описывать, применяя понятие гравитационного поля. Считают, что передача любых взаимодействий между телами реализуется при помощи полей, которые создают рассматриваемые тела. Одно из тел не оказывает непосредственного действия на другое тело, но оно создает в окружающем его пространстве гравитационное поле, особый вид материи, которая и оказывает воздействие на второе тело. Наглядной картины поля дать нельзя, понятие физического поля относят к основным понятиям, которые невозможно определить, используя другие более простые понятия. Можно только определить свойства поля.
Гравитационное поле может создавать силу. Поле зависит только от тела, которое его создает и не зависит от тела, на которое оно действует. Силовой характеристикой гравитационного поля является его напряжённость, которую обозначают $overline{g}$. Напряженность гравитационного поля измеряется силой, которая действует на материальную точку единичной массы:
[overline{g}=frac{overline{F}}{m}left(1right).]
Если гравитационное поле создается материальной точкой массы $M$, то оно имеет сферическую симметрию. Это значит, что вектор $overline{g}$ в каждой точке поля направлен к точечной массе $M$, которое создает данное поле. Из закона всемирного тяготения следует, что модуль вектора напряженности гравитационного поля:
[gleft(rright)=gamma frac{M}{r^2}left(2right).]
Из формулы (2) следует, что $g$ зависит от расстояния ($r$) от источника поля до точки, в которой поле рассматривается. В таком поле движение происходит по законам Кеплера.
Гравитационные поля удовлетворяют принципу суперпозиции. Напряженность поля, которая создается несколькими телами, равна векторной сумме напряженностей полей, которые порождаются каждым телом отдельно. Принцип суперпозиции выполняется, поскольку гравитационное поле, создаваемое какой-либо массой, не зависит от присутствия других масс. Принцип суперпозиции дает возможность рассчитывать гравитационные поля, которые созданы телами, отличающимися от точечных (размеры которых следует учитывать).
Ускорение при свободном падении
Если тело около поверхности Земли движется только под воздействием силы тяжести ($overline{F}$), говорят, что оно свободно падает. Ускорение свободного падения обозначают буквой $g$. В соответствии со вторым законом Ньютона это ускорение равно:
[overline{g}=frac{overline{F}}{m}left(3right),]
где $m$ — масса свободно падающего тела.
В соответствии с законом гравитации величина силы $overline{F}$ на расстоянии $h$ от поверхности Земли равна:
[left|overline{F}right|=gamma frac{mM}{{(R+h)}^2}left(4right),]
где $gamma $- гравитационная постоянная; $M$ — масса Земли; $R$ — радиус Земли.
Получается, что модуль ускорения свободного падения у поверхности Земли ($hll R$) равен:
[g=gamma frac{M}{R^2}left(5right).]
Направлено ускорение свободного падения к центру Земли.
Правая часть выражения (5) дает величину напряженности гравитационного поля Земли вблизи к ее поверхности.
Получаем, что напряжённость гравитационного поля и ускорение свободного падения в поле гравитации — это одно и то же. Поэтому эти величины были сразу обозначены одной буквой.
Величина ускорения свободного падения на расстоянии $h$ от поверхности Земли вычисляется при помощи формулы:
[g=gamma frac{M}{({R+h)}^2}left(6right).]
В задачах о движении тел около поверхности Земли ускорение свободного падения считают постоянной величиной, которую вычисляют с помощью формулы (5), так как в сравнении с радиусом Земли рассматриваемые расстояния много меньше, чем $R$. Обычно, ускорение свободного падения на Земле считают равным $g=9,8 frac{м}{с^2}$.
Примеры задач с решением
Пример 1
Задание. Каково ускорение свободного падения на Меркурии, если его масса меньше массы Земли в 18,18 раза, отношение радиусов Земли ($R_z$) и радиуса Меркурия ($R_m$) составляет $frac{R_z }{R_m}=2,63$?
Решение. Модуль ускорения свободного падения у поверхности Земли определен формулой:
[g=gamma frac{M}{{R_z}^2}left(1.1right).]
Величина вектора напряженности гравитационного поля любого тела равна:
[gleft(rright)=gamma frac{M}{r^2} left(1.2right),]
если в формулу (1.2) вместо массы $M$ подставить массу Меркурия, а вместо $r$ его радиус, то мы получим ускорение свободного падения около поверхности Меркурия:
[g_m=gamma frac{M_m}{{R_m}^2}left(1.3right).]
Найдем отношение выражений (1.1) и (1.3):
[frac{g}{g_m}=frac{gamma frac{M}{{R_z}^2}}{gamma frac{M_m}{{R_m}^2}}=frac{M}{M_m}frac{{R_m}^2}{{R_z}^2}left(1.4right).]
Считая, что нам известно ускорение свободного падения на Земле ($g=9,8 frac{м}{с^2}$), выразим ускорение свободного падения на Меркурии:
[g_m=gfrac{M_m}{M}cdot frac{{R_z}^2}{{R_m}^2}.]
Вычислим искомое ускорение:
[g_m=9,8cdot frac{1}{18,18}cdot {left(2,63right)}^2=3,73 left(frac{м}{с^2}right).]
Ответ. $g_m=3,73frac{м}{с^2}$
Пример 2
Задание. Ускорение свободного падения на поверхности Земли считают равным $g_0$. Тело опускают в глубокую шахту под Землю. На какой глубине ($h$) от поверхности ускорение свободного падения данного тела будет составлять $g=$0,3 $g_0. $Радиус Земли равен $R. $Землю считайте однородным шаром.
Решение. Если тело находится на некоторой глубине, то считаем, что находящиеся выше слои Земли действуют на тело с силами гравитации, которые взаимно компенсируют друг друга. Поэтому тело притягивается только той массой Земли, которая находится ниже рассматриваемого тела.
В качестве основы для решения задачи используем закон всемирного тяготения в виде:
[F=gamma frac{mM}{r^2}left(2.1right),]
где $m$ — масса тела; $M$ — масса Земли; $r$ — расстояние от центра Земли до рассматриваемого тела, то есть:
[r=R-h left(2.2right),]
где $R$ — радиус Земли. Мы можем использовать закон гравитации в виде (2.1), так как по условию задачи Землю считаем однородным шаром (ее масса распределена сферически симметрично), а тело материальной точкой. С другой стороны на тело действует сила, которая равна:
[F=mg left(2.3right).]
Приравняем правые части выражений (2.1) и (2.3), учтем (2.2):
[mg=gamma frac{mM’}{{(R-h )}^2}to g=gamma frac{M’}{{left(R-h right)}^2}left(2.4right),]
где $M’=frac{4pi }{3}{rho left(R-h right)}^3$ — масса слоев Земли ниже рассматриваемого тела; $rho $ — плотность Земли.
У поверхности Земли мы знаем, что:
[g_0=gamma frac{M}{R^2}=gamma frac{frac{4pi }{3}rho R^3}{R^2}=frac{4pi }{3}gamma rho Rleft(2.5right).]
Выразим из (2.5) плотность Земли:
[rho =frac{3}{4pi }frac{g_0}{gamma R}left(2.6right).]
Подставим результат (2.6) в формулу (2.4) выразим высоту:
[g=gamma frac{frac{4pi }{3}{left(R-h right)}^3}{{left(R-h right)}^2}frac{3}{4pi }frac{g_0}{gamma R}=g_0frac{R-h}{R}to h=Rleft(1-frac{g}{g_0}right)=0,7R.]
Ответ. $h=Rleft(1-frac{g}{g_0}right)=0,7R$
Читать дальше: формула центростремительного ускорения.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
You should upgrade or use an alternative browser.
-
Forums
-
Other Sciences
-
Chemistry
How do you calculate delta G
-
Thread starter
afcwestwarrior -
Start date
Apr 12, 2007 -
-
Tags -
Delta
-
- Apr 12, 2007
- #1
or could i calculate it like i calculate delta h, products — reactants
Answers and Replies
- Apr 14, 2007
- #2
- Apr 14, 2007
- #3
ΔG = ΔH – T * ΔS
Is a more general way to do it since this will be true for any specified temperature, T.
You could calculate it as,
ΔG = G_products – G_reactants
But this will only be valid for the temperature which your table has its G values calculated in. You might have access to a table of standard G of formation, but this would only be true under standard conditions.
What if you had a non-spontaneous reaction (under standard conditions) and you wanted to find out the temperature you needed to raise it to in order to make it spontaneous? To do this, you would have to calculate it the old fashion way without the Free Energy table.
- Nov 28, 2020
- #4
Suggested for: How do you calculate delta G
- Apr 28, 2023
- Nov 1, 2020
- Nov 17, 2022
- Mar 14, 2021
- Feb 18, 2021
- Sep 30, 2019
- Nov 12, 2019
- May 17, 2022
- Jan 29, 2023
- Oct 31, 2018
-
Forums
-
Other Sciences
-
Chemistry
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
Ускоре́ние свобо́дного паде́ния g (обычно произносится как «Жэ» или «Жи»), — ускорение, сообщаемое телу под действием притяжения планеты или другого астрономического тела в безвоздушном пространстве — вакууме. Его значение для Земли обычно принимают равным 9,8 или 10 м/с². Стандартное («нормальное») значение, принятое при построении систем единиц, g = 9,80665 м/с², а в технических расчетах обычно принимают g = 9,81 м/с².
| Луна | 1,62 | Сатурн | 10,44 |
| Меркурий | 3,68 — 3,74 | Земля | 9,81 |
| Марс | 3,86 | Нептун | 11,09 |
| Уран | 8,86 | Юпитер | 23,95 |
| Венера | 8,88 | Солнце | 273,1 |
Значение g было определено как «среднее» в каком-то смысле ускорение свободного падения на Земле, примерно равно ускорению свободного падения на широте 45,5° на уровне моря.
Реальное ускорение свободного падения на поверхности Земли зависит от широты и варьируется от 9,780 м/с² на экваторе до 9,832 м/с² на полюсах[1]. Оно может быть вычислено по эмпирической формуле:
,
где φ — широта рассматриваемого места, h — высота над уровнем моря.[2]
[править] Вычисление ускорения свободного падения
| h, км | g, м/с2 | h, км | g, м/с2 |
|---|---|---|---|
| 0 | 9.8066 | 20 | 9.7452 |
| 1 | 9.8036 | 50 | 9.6542 |
| 2 | 9.8005 | 80 | 9.5644 |
| 3 | 9.7974 | 100 | 9.505 |
| 4 | 9.7943 | 120 | 9.447 |
| 5 | 9.7912 | 500 | 8.45 |
| 6 | 9.7882 | 1000 | 7.36 |
| 8 | 9.7820 | 10 000 | 1.50 |
| 10 | 9.7759 | 50 000 | 0.125 |
| 15 | 9.7605 | 400 000 | 0.0025 |
Ускорение свободного падения состоит из двух слагаемых: гравитационного ускорения и центростремительного ускорения.
Значение гравитационного ускорения на поверхности планеты можно приблизительно подсчитать, представив планету точечной массой M, и вычислив гравитационное ускорение на расстоянии её радиуса R:
,
где G — гравитационная постоянная (6,6742×10-11 м3с-2кг-1).
Если применить эту формулу для вычисления гравитационного ускорения на поверхности Земли, мы получим
м/с²
Полученное значение приблизительно совпадает с ускорением свободного падения. Отличия обусловлены:
- центростремительным ускорением в системе отсчёта, связанной с вращающейся Землёй;
- неточностью формулы из-за того, что масса планеты распределена по объёму, который имеет нешарообразную форму(см. геоид);
- неоднородностью Земли, что используется для поиска полезных ископаемых по гравитационным аномалиям;
| Город | Географические координаты (по Гринвичу) | Высота над уровнем моря, м | Ускорение свободного падения, м/с2 | |
|---|---|---|---|---|
| Долгота | Широта | |||
| Берлин | 13,40 в.д. | 52,50 с.ш. | 40 | 9,81280 |
| Будапешт | 19,06 в.д. | 47,48 с.ш. | 108 | 9,80852 |
| Вашингтон | 77,01 з.д. | 38,89 с.ш. | 14 | 9,80112 |
| Вена | 16,36 в.д. | 48,21 с.ш. | 183 | 9,80860 |
| Гринвич | 0,0 в.д. | 51,48 с.ш. | 48 | 9,81188 |
| Каир | 31,28 в.д. | 30,07 с.ш. | 30 | 9,79317 |
| Киев | 30,30 в.д. | 50,27 с.ш. | 179 | 9,81054 |
| Мадрид | 3,69 в.д. | 40,41 с.ш. | 655 | 9,79981 |
| Москва | 37,61 в.д. | 55,75 с.ш. | 151 | 9,8154 |
| Нью-Йорк | 73,96 з.д. | 40,81 с.ш. | 38 | 9,80247 |
| Одесса | 30,73 в.д. | 46,47 с.ш. | 54 | 9.80735 |
| Осло | 10,72 в.д. | 59,91 с.ш. | 28 | 9,81927 |
| Париж | 2,34 в.д. | 48,84 с.ш. | 61 | 9,80943 |
| Прага | 14,39 в.д. | 50,09 с.ш. | 297 | 9,81014 |
| Рим | 12,99 в.д. | 41,54 с.ш. | 37 | 9,80312 |
| Стокгольм | 18,06 в.д. | 59,34 с.ш. | 45 | 9,81843 |
| Токио | 139,80 в.д. | 35,71 с.ш. | 18 | 9,79801 |
Исторически масса Земли была впервые определена Генри Кавендишем, исходя из известного ускорения свободного падения и радиуса Земли, и впервые измеренной им гравитационной постоянной.
[править] Перегрузки
Термин «жэ» используется в космонавтике и авиации для обозначения перегрузок — увеличения веса тела, вызванного его ускоренным движением. Допустимое значение перегрузок для гражданских самолетов составляет 4,33 g. Обычный человек может выдерживать перегрузки до 5 g. Тренированные пилоты в антиперегрузочных костюмах могут переносить перегрузки до 9 g. Сопротивляемость к отрицательным, направленным вверх перегрузкам, значительно ниже. Обычно при 2-3 g в глазах «краснеет» и человек теряет сознание из-за прилива крови к голове.
В этом вопросе существует небольшая терминологическая путаница: к примеру, определение перегрузки выше даёт для стоящего неподвижно человека перегрузку в 0g, но в таблице ниже этот же случай рассматривается как перегрузка в 1g. Похожий казус происходит при измерении давления: мы говорим — давление 0, подразумевая давление в одну атмосферу вокруг нас, учёный скажет — давление 0, подразумевая полное отсутствие молекул в данном объёме.
| Человек, стоящий неподвижно | 1 g |
| Пассажир в самолете при взлете | 1,5 g |
| Парашютист при приземлении со скоростью 6 м/с | 1,8 g |
| Парашютист при раскрытии парашюта (при изменении скорости от 60 до 5 м/с) | 5,0 g |
| Космонавты при спуске в космическом корабле «Союз» | до 3,0—4,0 g |
| Летчик при выполнении фигур высшего пилотажа | до 5 g |
| Летчик при выведении самолета из пикирования | 8,0—9 g |
| Перегрузка (длительная), соответствующая пределу физиологических возможностей человека | 8,0—10,0 g |
| Наибольшая (кратковременная) перегрузка автомобиля, при которой человеку удалось выжить[3] | 179,8 g |
[править] Примечания
- ↑ «Свободное падение тел. Ускорение свободного падения»
- ↑ g-Extractor на сайте Physikalisch-Technische Bundesanstalt (PTB).
- ↑ Авария в предквалификации Гран-при Великобритании
[править] Литература
- А. С. Енохович Краткий справочник по физике. — М.: «Высшая школа», 1976. — 288 с.
Ускорение свободного падения
Ускорение свободного падения — движение объекта, который получает ускорение из-за действующей на него силы тяжести; обозначается буквой g и измеряется в м/с². На поверхности Земли ускорение свободного падения примерно равно 9,81 м/с².
На полюсах (Южном и Северном) ускорение свободного падения будет больше, а на экваторе — меньше. Это происходит из-за двух фактов:
- Земля — не идеальный круг, а приплюснутый шар и её радиус на полюсах меньше, чем на экваторе (ускорение зависит от радиуса),
- центробежные силы (при вращении Земли) минимально компенсируют гравитацию больше на экваторе, чем на полюсах.
В вакууме тела падают с одинаковой скоростью потому, что ускорение свободного падения не зависит от массы.
Таблица ускорения свободного падения небесных тел
| Небесное тело | g (в м/с²) |
|---|---|
| Луна | 1,62 |
| Солнце | 274 |
| Меркурий | 3,72 |
| Венера | 8,87 |
| Земля | 9,81 |
| Марс | 3,711 |
| Юпитер | 24,79 |
| Сатурн | 10,44 |
| Уран | 8,87 |
| Нептун | 11,15 |
От чего зависит ускорение свободного падения?
Ускорение свободного падения зависит от массы планеты и радиуса планеты — чем она тяжелее, тем сильнее притягивает тела (т.е. масса тела не влияет на ускорение).
Возможно для будущих вычислений нужны будут эти данные:
- Масса Земли = 5,98 × (10^24) кг (или 5,972E24 кг)
- Радиус Земли = 6 371 км = 6,37×(10^6) м.
Как найти ускорение свободного падения?
Формула ускорения свободного падения

g — ускорение свободного падения
G — гравитационная постоянная
M — масса планеты
R — радиус планеты
Гравитационная постоянная («G», не путайте с «g») — это фундаментальная физическая константа, которая примерно равна
и связывает силы гравитационного притяжения между двумя телами (G) с их массами (m1 и m2) и расстоянием между ними (R) в формуле:
Пример расчёта ускорения свободного падения (для Земли):
Вспомним формулу:

G — гравитационная постоянная
M — масса планеты
R — радиус планеты
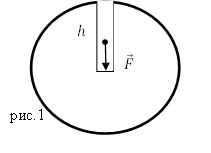
Как узнать время падения тела?
Формула времени свободного падения (когда тело падает вертикально):
t = V / g = √(2h/g)
Где:
- t — время
- V — скорость тела
- g — ускорение ≈ 9,8 м/с²
- h — расстояние
Пример:
Высота (h) = 20 м
Нужно найти скорость и время падения.
Решение:
Формула скорости:
V0 = 0
g ≈ 9,8 м/с²
h = 20 м
V² = 0² + 2 × 9,8 м/с² × 20 м ⇔ V = √392 м/с ≈ 19,8 м/с
Зная скорость, применяем эту формулу:
t = V / g = (19,8 м/с) / (9,8 м/с²) ≈ 2,02 с
Либо используя только высоту и ускорение:
t = √(2h/g) = √(2 × 20 м / 9,8 м/с²) ≈ 2,02 с
Где нужны знания о свободном падении?
Они могут понадобиться:
- в авиации,
- в космонавтике,
- при поиске полезных ископаемых (там, где есть залежи тяжёлых ископаемых, g меняется),
- при разработке новых лыжных трамплинов и полос приземления,
- при разработке новых автомобилей (рассчитываются наилучшие показатели для экономии топлива).
Узнайте также про Закон сохранения энергии, Силу Архимеда, Законы Ньютона и Космологию.


![g=9{,}780327left[1+0{,}0053024,sin^2(phi) - 0{,}0000058,sin^2(2phi)right] - 3,086cdot 10^{-6},h](https://web.archive.org/web/20100405053211im_/http://upload.wikimedia.org/math/6/5/8/658a780a8a3581d0f61972536d368ba5.png) ,
, ,
, м/с²
м/с²


