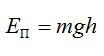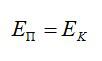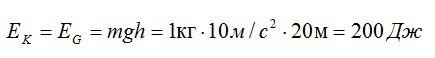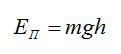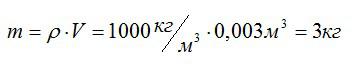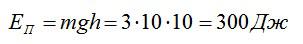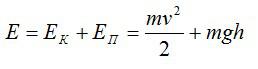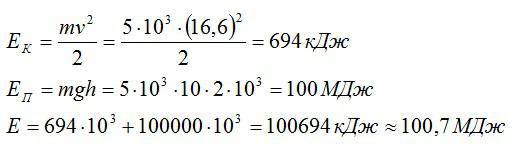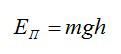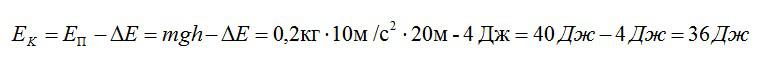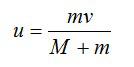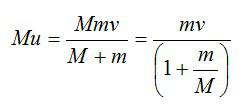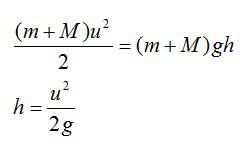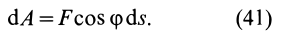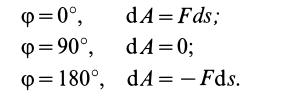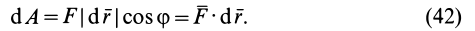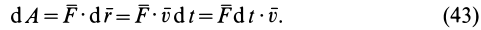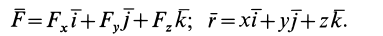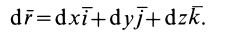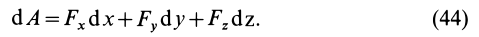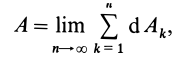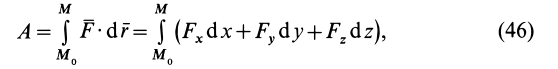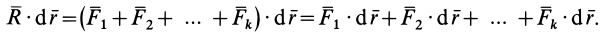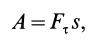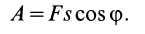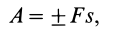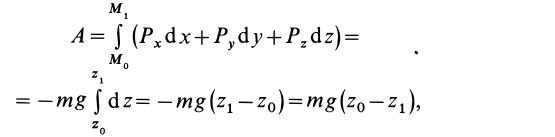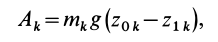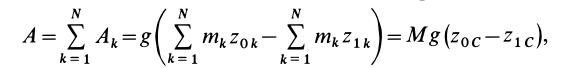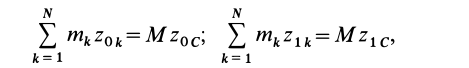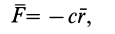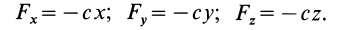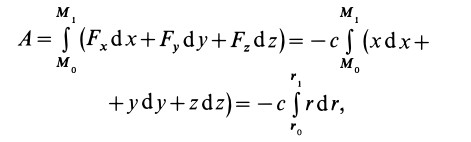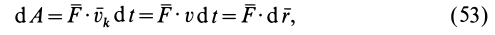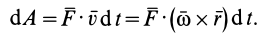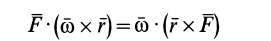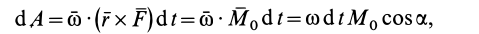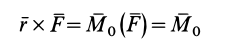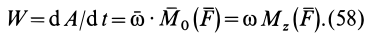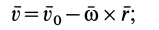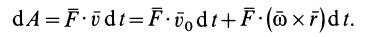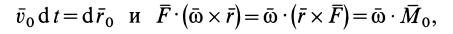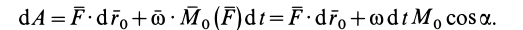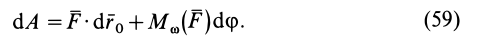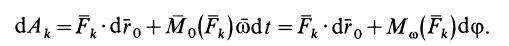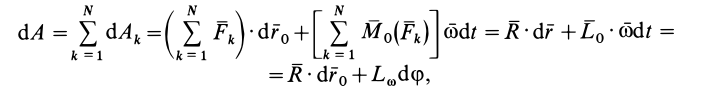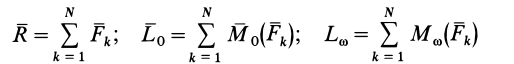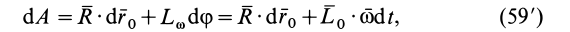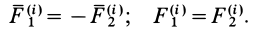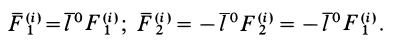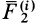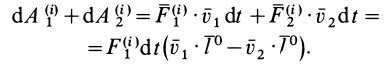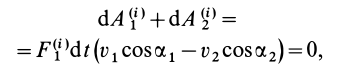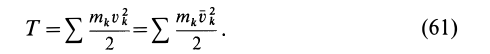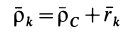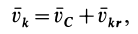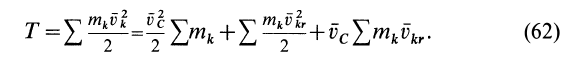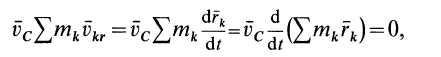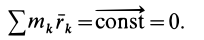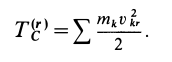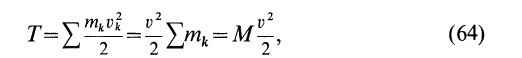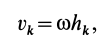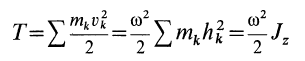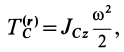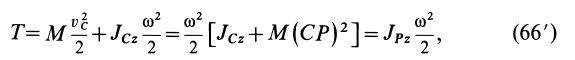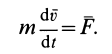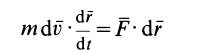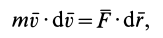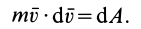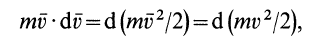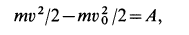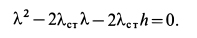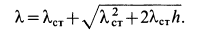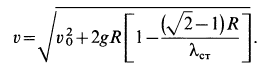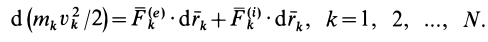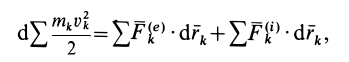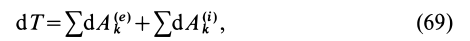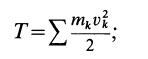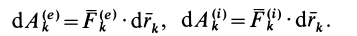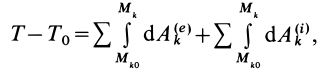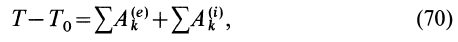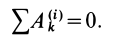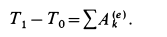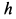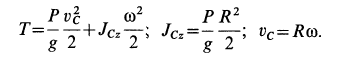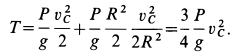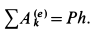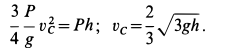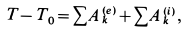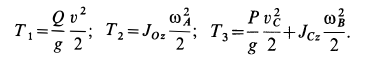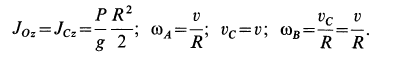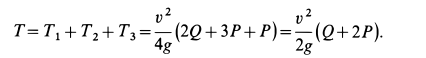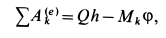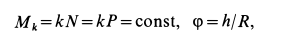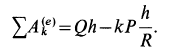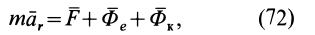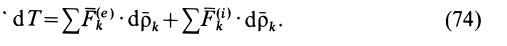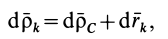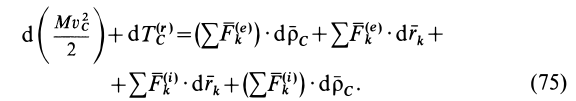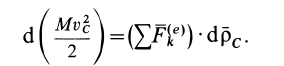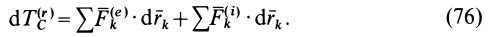А почему-бы и нет? У нас уже были задачи на свободное падение, законы Ньютона, силу трения и проч. и проч. Сегодня решаем задачи на кинетическую и потенциальную энергию.
А вообще, помните, что мы занимаемся далеко не только решением задач. Наш телеграм – это полезная информация для студентов всех специальностей, новости, лайфхаки, акции и скидки.
Задачи на кинетическую и потенциальную энергию
Приведем примеры задач на нахождение кинетической и потенциальной энергии с решением. Прежде чем приступать к практике, почитайте теорию по теме, повторите общую памятку по решению задач по физике и на всякий случай держите под рукой полезные формулы.
Задача №1 на кинетическую энергию
Условие
Максимальная высота, на которую поднимается тело массой 1 кг, подброшенное вертикально вверх, составляет 20 м. Найдите, чему была равна кинетическая энергия сразу же после броска.
Решение
Потенциальная энергия тела над поверхностью Земли составляет:
Здесь m – масса тела, g – ускорение свободного падения, h – высота. Согласно закону сохранения энергии, потенциальная энергия тела в наивысшей точке должна равняться кинетической энергии тела в начальный момент, то есть:
Принимая ускорение свободного падения равным 10 м/с2, находим кинетическую энергию тела сразу же после броска:
Ответ: 200 Дж.
Задача №2 на потенциальную энергию
Условие
Чему равна потенциальная энергия трех кубических дециметров воды на высоте 10 м?
Решение
По определению, потенциальная энергия равна в поле силы тяжести равна:
Масса трех кубических дециметров воды (трех литров) легко находится из формулы для плотности воды:
Осталось вычислить потенциальную энергию:
Ответ: 300 Дж.
При решении задач не забывайте переводить все размерности величин в систему СИ.
Задача №3 на полную механическую энергию
Условие
Какова полная механическая энергия дирижабля массой 5 тонн, если он летит на высоте 2 км со скоростью 60 км/ч?
Решение
Полная механическая энергия состоит из кинетической и потенциальной энергий:
Вычислим:
Ответ: 100,7 МДж.
Задача №4 на кинетическую и потенциальную энергию
Условие
Шарик массой 200 г падает с высоты 20 м с начальной скоростью, равной нулю. Какова его кинетическая энергия в момент перед ударом о землю, если потеря энергии за счет сопротивления воздуха составила 4 Дж? (Ответ дайте в джоулях.) Ускорение свободного падения принять равным 10 м/с2.
Решение
Перед началом падения потенциальная энергия шарика составляет:
По закону сохранения энергии, эта энергия должна перейти в кинетическую энергию Ек за вычетом потери за счет сопротивления воздуха дельта Е. Таким образом, можем найти кинетическую энергию:
Ответ: 36 Дж.
Задача №5 кинетическую и потенциальную энергию
Условие
Шарик висит на нити. В нем застревает пуля, летящая горизонтально, в результате чего нить отклоняется на некоторый угол. Как изменятся при увеличении массы шарика следующие величины: импульс, полученный шариком в результате попадания в него пули; скорость, которая будет у шарика тотчас после удара; угол отклонения нити?
Решение
Согласно закону сохранения импульса, скорость шарика с застрявшей в нем пулей равна
Здесь M и m – массы шарика и пули соответственно, v – скорость пули перед ударом. Таким образом, при увеличении массы шарика его скорость после удара уменьшится.
Найдем импульс, переданный шарику при попадании пули:
Следовательно, с увеличением массы шарика переданный ему импульс увеличивается.
Согласно закону сохранения энергии, кинетическая энергия пули перейдет в потенциальную энергию шарика с пулей:
Таким образом, при увеличении массы шарика угол отклонения нити уменьшится, поскольку уменьшится скорость u.
Ответ: см решение выше.
Вопросы на потенциальную и кинетическую энергию
Вопрос 1. Что такое энергия? Что такое механическая энергия?
Ответ. Для энергии существует множество определений. В наиболее общем смысле:
Энергия – мера способности тела совершать работу.
Механическая энергия – это энергия, связанная с движением тела или его положением в пространстве. Механическая энергия в механике описывается суммой кинетической и потенциальной энергии.
Вопрос 2. Сформулируйте закон сохранения энергии
Ответ. Закон сохранения энергии является фундаментальным физическим принципом. Для каждого вида энергии он имеет свою формулировку. Для механической энергии:
Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается неизменной.
Вопрос 3. Какие силы называются консервативными?
Ответ. Консервативные, или потенциальные силы – это силы, работа которых не зависит от формы траектории. В качестве примера такой силы можно привести силу тяжести.
Вопрос 4. Какую энергию называют кинетической?
Ответ. Кинетическая энергия является энергией движения. Ею обладают только движущиеся тела, она зависит от массы тела и его скорости.
Вопрос 5. Какую энергию называют потенциальной?
Ответ. Потенциальная энергия является энергией взаимодействия в поле консервативных сил. Она зависит от положения тела и выбора системы отсчета. Например, потенциальная энергия тела в поле силы тяжести зависит от массы тела, ускорения свободного падения и высоты над нулевым уровнем.
Не знаете, как решать задачи на кинетическую или потенциальную энергию? Проблемы с выполнением любых других студенческих работ? Обращайтесь в профессиональный сервис для учащихся за помощью и консультациями.
Содержание:
- Определение и формула кинетической энергии
- Кинетическая энергия материальной точки и тела
- Единицы измерения кинетической энергии
- Теорема Кенига
- Примеры решения задач
Определение и формула кинетической энергии
Определение
Кинетическую энергию тела определяют при помощи работы, которая совершается телом при его торможении от начальной скорости, до скорости, равной нулю.
Кинетическая энергия тела – мера механического движения тела. Она зависит от относительной скорости тел.
Встречаются следующие обозначения кинетической энергии: Ek,Wk,T.
Работу, которую производят над телом (A’) можно связать с изменением его кинетической энергии:
$$A^{prime}=E_{k 2}-E_{k 1}(1)$$
Кинетическая энергия материальной точки и тела
Кинетическая энергия материальной точки равна:
$$E_{k}=frac{m v^{2}}{2}=frac{p^{2}}{2 m}=frac{p v}{2}(2)$$
где m – масса материальной точки, p – импульс материальной точки, v – скорость ее движения. Кинетическая энергия является скалярной физической величиной.
Если тело нельзя принять за материальную точку, то его кинетическая энергия рассчитывается как сумма кинетических энергий всех материальных точек, которые составляют исследуемое тело:
$$E_{k}=frac{1}{2} int_{m} v^{2} d m=frac{1}{2} int_{m} rho v^{2} d V(3)$$
где dm – элементарный участок тела, который можно считать материальной точкой, dV – объем выделенного элементарного участка тела,
v – скорость перемещения рассматриваемого элемента, $rho$ — плотность участка, m–масса всего рассматриваемого тела, V – объем тела.
В том случае, если тело (отличное от материальной точки) движется поступательно, то его кинетическую энергию можно рассчитать, применяя формулу (2), в которой все параметры отнесены к телу в целом.
При вращении тело вокруг неподвижной оси его кинетическую энергию можно вычислить, применяя формулу:
$$E_{k}=frac{J omega^{2}}{2}=frac{omega^{2}}{2} int_{m} r^{2} d m=frac{L^{2}}{2 J}=frac{L omega}{2}(4)$$
где J – момент инерции тела по отношению к оси вращения, ?–модуль угловой скорости вращения тела,
r – расстояние от элементарного участка тела до оси вращения,
L – проекция момента импульса вращающегося тела на ось во круг которой идет вращение.
Если твердое тело совершает вращение относительно неподвижной точки (например, точки O), то его кинетическую энергию находят как:
$$E_{k}=frac{bar{L} bar{omega}}{2}(5)$$
$bar{L}$ – момент импульса рассматриваемого тела относительно точки О.
Единицы измерения кинетической энергии
Основной единицей измерения кинетической энергии (как и любого другого вида энергии) в системе СИ служит:
[Ek]=Дж (джоуль),
в системе СГС –[Ek]= эрг.
При этом: 1 дж= 107 эрг.
Теорема Кенига
Для самого общего случая при расчете кинетической энергии применяют теорему Кенига. В соответствии с которой,
кинетическая энергия совокупности материальных точек есть сумма кинетической энергии поступательного перемещения
системы со скоростью центра масс (vc) и кинетической энергии
(E’k) системы при ее относительном движении к поступательному перемещению системы отсчета.
При этом начало системы отсчета связывают с центром масс системы. Математически данную теорему можно записать как:
$$E_{k}=sum_{i=1}^{n} frac{m_{i} v_{i}^{2}}{2}=frac{m v_{c}^{2}}{2}+E_{k}^{prime}$$
где $mathrm{E}_{k}^{prime}=sum_{i=1}^{n} frac{m_{i} v_{i}^{prime 2}}{2}, v_{i}^{prime}=v_{i}-v_{c}, m=sum_{i=1}^{n} m_{i}$ –суммарная масса системы материальных точек.
Так, если рассматривать твердое тело, то его кинетическую энергию можно представить как:
$$E_{k}=frac{m v_{c}^{2}}{2}+frac{J_{c} omega^{2}}{2}(7)$$
где Jc — момент инерции тела по отношению к оси вращения, проходящей через центр масс. В частности, при плоском движении
Jc=const.В общем случае, ось (она называется мгновенной) перемещается в теле, тогда момент инерции является переменным во времени.
Примеры решения задач
Пример
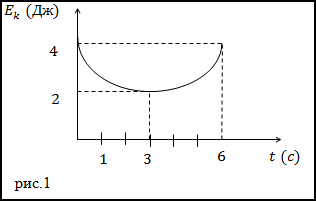
Задание. Какова работа, которая производится над телом за t=3 c (с начала отсчета времени),
при силовом взаимодействии, если изменение кинетической энергии исследуемого тела задано графиком (рис.1)?
Решение. По определению изменение кинетической энергии равно работе (A’),
которая производится над телом при силовом взаимодействии, то есть можно записать, что:
$$A^{prime}=Delta E_{k}(1.1)$$
Исследуя график, приведенный на рис.1 мы видим, что за время t=3 c кинетическая энергия тела изменяется от 4 Дж до 2 Дж, следовательно:
$A^{prime}=2-4=-2$ (Дж)
Ответ. A’=-2 Дж.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Материальная точка движется по окружности, радиус которой равен R. Кинетическая
энергия частицы связана c величиной пути (s), пройденного ей в соответствии с формулой:
$E_{k}=alpha s^{2}(alpha=$const$)$. Какое уравнение связывает силу (F), действующую на точку и путь s?
Решение. В качестве основы для решения задачи используем формулу, определяющую кинетическую энергию материальной точки:
$$E_{k}=frac{m v^{2}}{2}(2.1)$$
Но по условию задачи:
$$E_{k}=alpha s^{2}(2.2)$$
Следовательно, можно приравнять правые части выражений (2.1) и (2.2), и получить:
$$frac{m v^{2}}{2}=alpha s^{2} rightarrow v^{2}=frac{2 alpha s^{2}}{m} rightarrow v=s sqrt{frac{2 alpha}{m}}(2.3)$$
Из второго закона Ньютона нам известно, что сила, действующая на частицу, будет равна:
$$bar{F}=m bar{a}(2.4)$$
где
$$a=sqrt{a_{n}^{2}+a_{tau}^{2}}(2.5)$$
При этом нормальное ускорение частицы (an), перемещающейся по окружности найдем как:
$$a_{n}=frac{v^{2}}{R}=frac{2 alpha s^{2}}{R m}(2.6)$$
Тангенциальную составляющую ускорения (aт)используя определение тангенциального ускорения, определение скорости
($v=frac{d s}{d t}$) и выражение v(s) (2.3) вычислим как:
$$a_{tau}=frac{d v}{d t}=frac{d v}{d s} cdot frac{d s}{d t}=sqrt{frac{2 a}{m}} cdot v=s frac{2 a}{m}(2.7)$$
Используем выражения: (2.5), (2.6), (2.7), окончательно получаем для модуля силы:
$$F=m a=m sqrt{frac{4 alpha^{2} s^{4}}{R^{2} m^{2}}+s^{2} frac{4 alpha^{2}}{m^{2}}}=2 alpha s sqrt{frac{s^{2}}{R^{2}}+1}$$
Ответ. $F=2 alpha s sqrt{frac{s^{2}}{R^{2}}+1}$
Читать дальше: Формула массы тела.
Екатерина Владимировна Мосина
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Механической энергией называют энергию, которая связана с движением тел, их возможностью совершать механическую работу, взаимодействовать.
Подчеркнем, что наличие энергии у тела объясняют две причины:
- Перемещение тела с некоторой скоростью.
- Пребывание тела в потенциальном поле сил.
Энергия, связанная с движением тела называется кинетической энергией.
Потенциальную энергию называют энергией положения, она связывается с нахождением тела в поле сил.
Находят механическую энергию как сумму:
- кинетической энергии тела (системы тел) ($E_k$) и
- потенциальной энергии тела (системы) $E_p$.
Кинетическая энергия
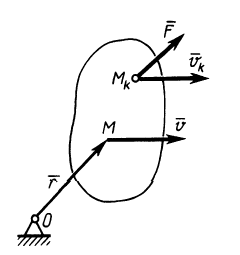
Допустим, что материальная точка, имеющая массу $m$, перемещается. Ее скорость равна $vec v$. Это тело воздействует на второе тело (рис.1), которое соприкасается с первым, с силой $vec F$.
Рисунок 1. Кинетическая энергия. Автор24 — интернет-биржа студенческих работ
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
За промежуток времени $dt$ точка, к которой приложена сила (точка $A$ рис.1) совершит перемещение, равное:
$dvec s=vec v dt (1)$.
Это означает, что сила (материальная точка 1) совершает над телом 2 работу, равную:
$dA=vec F dvec s =vec F vec v dt(2).$
Материальная точка 1 выполняет работу, поскольку имеет запас энергии, мы знаем, что она перемещается, и, значит, у нее есть кинетическая энергия. При отсутствии движения мы имели бы $ds=0$, следовательно, была бы равна нулю работа $dA=0$.
На этом основании работу, которую совершает тело 1, будем считать равной уменьшению его кинетической энергии:
$dA=-dE_{k1}(3).$
Учитывая формулу (2) получим:
$ dE_{k1}=-vec F vec v dt (4)$.
Из третьего закона Ньютона имеем (рис.1):
$vec F’ =- vec F (5),$
в результате скорость материальной точки 1 изменяется на величину $dvec v$ за отрезок времени $dt$:
$ dvec v = frac {1}{m}vec F’ dt=-frac {1}{m}vec F dt (6).$
Запишем скалярное произведение обеих частей уравнения (6) на величину $mvec v$:
$mvec v dvec v=-vec F cdot vec v dt (7).$
«Закон изменения механической энергии с формулами» 👇
Выполним сравнение выражений (2) и (7), имеем:
$d E_k=d(frac{m v^2}{2}) (8).$
Формула (8) показывает, что кинетическая энергия материальной точки определяется как:
$E_k=frac{m v^2}{2} = frac {p^2}{2m}(9),$
где $p$ — модуль импульса тела.
Закон изменения кинетической энергии
Работа, которую совершают над телом ($A’$), равна увеличению его кинетической энергии:
$Delta E_k=E_{k2}-E_{k1}=A’(10).$
Для доказательства данного утверждения следует воспользоваться выражением для элемента работы, которое мы запишем в виде:
$dA’=vec F’vec v dt (11),$
где $vec F’$ — сила, которая совершает работу над телом; $vec v$ — скорость тела. Используем второй закон Ньютона в виде:
$frac {dvec p}{dt}=vec F’ (12),$
следовательно, $m dvec v=vec F’ dt (13).$
Учитывая полученное в (13), имеем:
$dA’=mvec v dvec v=mvdv=d(frac {mv^2}{2})=d E_k (14)$.
Интегрирования выражения (14) приводит к результату:
$A’=Delta E_k (15).$
Потенциальная энергия
Определение 1
Потенциальным полем называют силовое поле, которое выражается при помощи скалярной потенциальной функции ($U(x,y,z,t)$), зависящей от пространственных координат и времени. Данную функцию называют потенциальной. При этом сила, оказывающая воздействие на частицу, и потенциальная функция связаны соотношением:
$vec F(x,y,z,t)=-(frac{partial U(x,y,z,t)}{partial x}vec i+frac{partial U(x,y,z,t)}{partial y}vec j+frac{partial U(x,y,z,t)}{partial y}vec k)=-grad U (16)$.
Градиент скалярной функции – это вектор, который направлен в сторону наиболее быстрого увеличения данной функции, равный по величине скорости ее увеличения в этом направлении. Знак минус в формуле (16) показывает то, что сила имеет направление в сторону наиболее быстрого уменьшения функции $U$.
Частным случаем потенциальных полей являются поля, которые не зависят в явном виде от времени. Такие поля именуют консервативными. Для консервативных полей $U=U(x,y,z)$.
Иначе говорят, что тело (частица) находится состоянии стационарных внешних условий, например, в постоянном поле гравитации. В этом случае потенциальную функцию $U$ называют потенциальной энергией частицы во внешнем консервативном поле.
Обозначим потенциальную энергию как $E_p$, в таком случае выполняется равенство:
$vec F=- grad E_p (x,y,z)(17).$
Конкретный вид потенциальной энергии зависит от характера силового поля, в котором находится тело.
Потенциальную энергию имеют:
- система тел, находящихся во взаимодействии;
- тело в состоянии упругой деформации.
Закон изменения потенциальной энергии
Работа в потенциальном поле сил не зависит от пути.
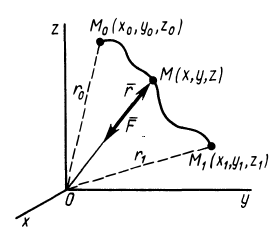
Рассмотрим материальную точку, находящуюся в потенциальном поле сил. Каждую точку поля будем характеризовать значением $E_p(vec r)$, где $vec r$ — радиус – вектор точки поля.
Допустим, что величина функции $E_p(vec r)$ в начальной точке равна:
$E_p(0)=E_{p0}.$
Для получения величины $ E_{p1} (vec r_1)$ в некоторой точке 1 выполним следующее действие:
$E_{p1}(vec r_1)= E_{p0}+A_{10}(18),$
где $ A_{10}$ — работа, которую совершают над материальной точкой силы поля, когда перемещают ее из начальной точки в точку 1.
Так как работа в поле потенциальных сил не зависима от пути, то величина E_{p1} является однозначной. Для второй точки по аналогии запишем:
$E_{p2}(vec r_2)= E_{p0}+A_{20}(19).$
Найдем разность $ E_{p1}- E_{p2}$, используя формулы (18) и (19), принимая во внимание, что $A_{20}=-A_{02}$
$ E_{p1}- E_{p2}= A_{10}- A_{20}= A_{10}+A_{02}(20), $
где $ A_{10}+A_{02}$ — работа, которую выполняют силы поля, если совершают перемещения тела из точки 1 в точку 2 через начальную точку. Но мы помним, что работа консервативных сил не будет зависеть от траектории движения тела, то есть работа при непосредственном перемещении из 1 в 2 будет такой же как из1 в 0, а потом в 2. Поэтому:
$ A_{10}+A_{02}=A_{21} (21)$.
В результате мы имеем:
$ E_{p1}- E_{p2}=A_{12} (22)$.
Выражение (22) показывает нам, что при помощи потенциальной энергии имеется возможность найти работу, которую силы потенциального поля совершают над телом при любом пути из точки 1 в точку 2. Данная работа будет равна уменьшению потенциальной энергии.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Механическая энергия и ее виды
- Два вида механической энергии
- Единицы измерения энергии
- Теорема о кинетической энергии
- Понятие консервативных сил
- Потенциальная энергия и работа в поле силы тяжести
- Потенциальная энергия упруго деформированного тела и работа силы упругости
- Задачи
п.1. Два вида механической энергии
Способность тела или системы тел совершить работу за счет изменения скорости тела или взаимного расположения тел при взаимодействии называют механической энергией.
Механическое состояние тела характеризуется его координатой в некоторой системе отсчета и скоростью.
Соответственно, энергия, связанная с изменением координаты – падением мяча, подъемом груза, сжатием газа – называется потенциальной энергией. А энергия, связанная с изменением скорости – ускорением, торможением, изменение направления движения – называется кинетической энергией тела.
Потенциальная энергия – физическая величина, характеризующая способность системы взаимодействующих тел совершить работу вследствие изменения взаимного положения тел (или частей одного тела).
Потенциальной энергией обладает груз, поднятый над поверхностью Земли. При падении, действующая на груз сила тяжести совершит работу.
Потенциальной энергией также обладает растянутая или сжатая пружина. При возвращении в недеформированное состояние, действующая на пружину сила упругости совершит работу.
Примеры тел, обладающих потенциальной энергией
Кинетическая энергия – физическая величина, равная работе, которую совершает движущееся тело при уменьшении его скорости до полной остановки.
Кинетической энергией обладает любое движущееся тело.
Чем больше скорость тела, тем больше его кинетическая энергия.
Примеры движения тел, обладающих кинетической энергией
п.2. Единицы измерения энергии
Когда тело совершает работу, его энергия уменьшается на величину, численно равную совершенной работе. Поэтому единица измерения энергии в СИ совпадает с единицей измерения работы.
Единицей энергии в системе СИ является джоуль (1 Дж)
Существует также множество внесистемных единиц для измерения энергии, например: эрг (1 эрг=10-7 Дж), калория (1 кал=4,1868 Дж), киловатт-час (1 кВт·ч=3,6·105 Дж), электрон-вольт (1 эВ=1,6·10-19 Дж) и др.
п.3. Теорема о кинетической энергии
Как известно, при равноускоренном движении перемещение s можно выразить формулой $$ s=frac{v^2_2-v^2_1}{2a} $$ (см. Задача 3 §11 данного справочника).
Тогда работа силы, направление которой совпадает с направлением перемещения, равна $$ A=Fs=macdot frac{v^2_2-v^2_1}{2a}=frac{mv^2_2}{2}-frac{mv^2_1}{2} $$
Введем величину $$ E_k=frac{mv^2}{2} $$ как выражение для кинетической энергии.
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела: $$ E_k=frac{mv^2}{2} $$
Тогда $$ A=frac{mv^2_2}{2}-frac{mv^2_1}{2}=E_{k2}-E_{k1}=Delta E_k $$
Теорема о кинетической энергии
Работа приложенной к телу силы равна изменению его кинетической энергии: $$ A=E_{k2}-E_{k1}=Delta E_k $$
Теорема о кинетической энергии носит общий характер в механике и справедлива:
1) при действии нескольких сил на тело (тогда рассматривается работа равнодействующей всех сил);
2) при действии переменной силы;
3) при действии силы, не совпадающей по направлению с перемещением;
4) для любых по своей природе сил – упругости, трения, тяжести и т.п.
п.4. Понятие консервативных сил
Потенциальная энергия определяется взаимных положением тел (например, высотой над поверхностью Земли). Понятие потенциальной энергии можно ввести только для так называемых консервативных сил.
Сила называется консервативной, если её работа не зависит от траектории движения и определяется только начальным и конечным положением тела.
Работа консервативной силы по замкнутой траектории равна нулю.
Свойством консервативности обладает сила тяжести и сила упругости. Для них можно ввести понятие потенциальной энергии.
Сила трения не обладает свойством консервативности – она является диссипативной силой (см. дальше §38 данного справочника). Работа силы трения зависит от пройденного пути. Поэтому для силы трения нельзя ввести понятие потенциальной энергии.
п.5. Потенциальная энергия и работа в поле силы тяжести
Физическая величина, равная произведению силы тяжести на высоту над поверхностью Земли $$ E_p=mgh $$ называется потенциальной энергией тела в поле силы тяжести.
 |
Потенциальная энергия зависит от выбора системы отсчета и точки отсчета (для определения высоты (h)). Физический смысл имеет не сама потенциальная энергия, а её изменение. Если тело падает с высоты (h_1) на высоту (h_2 (h_1gt h_2)), сила тяжести совершает работу: $$ A=mgDelta h=mg(h_1-h_2)=-mg(h_2-h_1)=-(E_{p2}-E_{p1}) $$ Работа силы тяжести при падении тела с высоты (h) на нулевой уровень ((h_1=h, h_2=0): A=mgh). Работа положительна, т.к. направление силы тяжести (вниз) и перемещения (вниз) совпадают. Работа силы тяжести при подъеме тела с нулевого уровня на высоту (h (h_1=0, h_2=h): A=-mgh). Работа отрицательна, т.к. направление силы тяжести (вниз) и перемещения (вверх) противоположны. |
Работа силы тяжести равна изменению потенциальной энергии в поле силы тяжести, взятой с противоположным знаком: $$ A=-(E_{p2}-E_{p1})=-Delta E_p $$
п.6. Потенциальная энергия упруго деформированного тела и работа силы упругости
Физическая величина, равная половине произведения жесткости пружины на квадрат деформации $$ E_p=frac{kx^2}{2} $$ называется потенциальной энергией упруго деформированного тела.
 |
Потенциальная энергия зависит от выбора системы отсчета и точки отсчета (для определения деформации (x)). Физический смысл имеет не сама потенциальная энергия, а её изменение. Если из начального состояния с деформацией (x_1), пружина переходит в состояние с деформацией (x_2), работа силы упругости по изменению деформации: $$ A_text{упр}=-(E_{p2}-E_{p1})=-left(frac{kx^2_2}{2}-frac{kx^2_1}{2}right) $$ Работа по возвращению пружины в недеформированное состояние: $$ A_text{упр}=-frac{kx^2}{2} $$ |
Работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятой с противоположным знаком: $$ A=-(E_{p2}-E_{p1})=-Delta E_p $$
п.7. Задачи
Задача 1. Как изменится кинетическая энергия автомобиля при увеличении его скорости в три раза?
Дано:
(v_2=3v_1)
__________________
(frac{E_{k2}}{E_{k_1}}-?)
Кинетическая энергия begin{gather*} E_k=frac{mv^2}{2} end{gather*} Отношение кинетических энергий begin{gather*} frac{E_{k2}}{E_{k_1}}=frac{mv^2_2}{2}:frac{mv^2_1}{2}=frac{mv^2_2}{2}cdot frac{2}{mv^2_1}=frac{v^2_2}{v^2_1}=left(frac{v_2}{v_1}right)^2 end{gather*} Получаем begin{gather*} frac{E_{k2}}{E_{k_1}}=3^2=9 end{gather*} Ответ: увеличится в 9 раз
Задача 2. Как изменится потенциальная энергия человека массой 80 кг при подъеме на воздушном шаре на высоту 300 м? Чему равна работа силы тяжести при подъеме?
Дано:
(h=300 text{м})
(m=80 text{кг})
(gapprox 10 text{м/с}^2)
__________________
(Delta E_p-?, A-?)
Потенциальная энергия на поверхности Земли: begin{gather*} E_{p1}=0 end{gather*} Потенциальная энергия на высоте (h): $$ E_{p2}=mgh $$ Изменение потенциальной энергии: begin{gather*} Delta E_p=E_{p2}-E_{p1}=mgh-0=mgh end{gather*} Работа силы тяжести: begin{gather*} A=-Delta E_p=-mgh end{gather*} Получаем: begin{gather*} Delta E_p=80cdot 10cdot 300=240000 (text{Дж})=240 (text{кДж})\[7pt] A=-Delta E_p=-240 (text{кДж}) end{gather*} Ответ: 240 кДж; -240 кДж
Задача 3. Автомобиль массой 1700 кг разгоняется из состояния покоя до скорости 108 км/ч за 6 с. Чему равна полезная мощность двигателя автомобиля, которая затрачивается на увеличение кинетической энергии? Ответ выразите в ваттах, киловаттах и лошадиных силах.
Дано:
(m=1700 text{кг})
(v_0=0 text{м/с})
(v=108frac{text{км}}{text{ч}}=frac{108cdot 1000}{3600}frac{text{м}}{text{с}}=30 text{м/с})
(t=6 text{с})
(1 text{л.с.}=735,5 text{Вт})
__________________
(N-?)
Работа силы тяги равна разности кинетических энергий автомобиля: begin{gather*} A=E_k-E_{k0}=frac{mv^2}{2}-frac{mv^2_0}{2}=frac{mv^2}{2}-0=frac{mv^2}{2} end{gather*} Мощность двигателя begin{gather*} N=frac At=frac{mv^2}{2t} end{gather*} Получаем begin{gather*} N=frac{1700cdot 30^2}{2cdot 6}=127500 (text{Вт})=127,5 (text{кВт})\[6pt] 127500 text{Вт} =frac{127500}{735,5} text{л.с.} approx 173 text{л.с.} end{gather*} Ответ: 127500 Вт = 127,5 кВт ≈ 173 л.с.
Задача 4. Пуля массой 10 г, движущаяся со скоростью 500 м/с, пробила деревянный щит толщиной 2 см и вылетела со скоростью 300 м/с. Чему равна работа силы сопротивления движению пули в щите и модуль среднего значения силы сопротивления?
Дано:
(m=10 text{г}=0,01 text{кг} )
(v_1=500 text{м/с})
(v_2=300 text{м/с})
(s=2=0,02)
(t=1 text{см}=60 text{м})
__________________
(A-?, F_text{ср})
Работа силы сопротивления равна разности кинетических энергий пули: begin{gather*} A=frac{mv^2_2}{2}-frac{mv^2_1}{2}=frac m2(v^2_2-v^2_1)=frac m2(v_2-v_1)(v_2+v_1) end{gather*} С другой стороны, работа равна произведению силы на перемещение: begin{gather*} A=F_text{ср}sRightarrow F_text{ср}=frac As end{gather*} Получаем begin{gather*} A=frac{0,01}{2}(300-500)(300+500)=-800 (text{Дж}) end{gather*} Работа отрицательна, т.к. тормозящая сила сопротивления направлена противоположно перемещению. В результате кинетическая энергия уменьшается. begin{gather*} F_text{ср}=frac{-800}{0,02}=-40000 (text{Н})=-40 (text{кН})\[6pt] |F_text{ср}|=40 text{кН} end{gather*} Ответ: -800 Дж; 40 кН
Задача 5. Медный и алюминиевый шары одинакового объема подняли на одинаковую высоту. Для какого шара изменение потенциальной энергии больше и во сколько раз?
Дано:
(rho_1=8930 text{кг/м}^3)
(rho_2=2700 text{кг/м}^3)
(V_1=V_2=V)
(h_1=h_2=h)
__________________
(frac{Delta E_{p1}}{Delta E_{p2}}-?)
Потенциальная энергия тела на высоте (h): begin{gather*} E_p=mgh=rho Vgh end{gather*} Потенциальная энергия на нулевом уровне: begin{gather*} E_{p0}=0 end{gather*} Изменение потенциальной энергии при подъеме: begin{gather*} Delta E_p=E_p-E_{p0}=rho Vgh-0=rho Vgh end{gather*} Отношение изменений потенциальных энергий для шаров: $$ frac{Delta E_{p1}}{Delta E_{p2}}=frac{rho_1 Vgh}{rho_2 Vgh}=frac{rho_1}{rho_2} $$ Изменение потенциальной энергии больше для более плотного медного шара. begin{gather*} frac{Delta E_{p1}}{Delta E_{p2}}=frac{8930}{2700}approx 3,3 (text{раз}) end{gather*} Ответ: больше для медного шара в 3,3 раза
Задача 6. Чему равна потенциальная энергия растянутой пружины, если она растянута на 4 см и для удержания её в этом состоянии необходимо прикладывать силу 60 Н?
Дано:
(x=4 text{см}=0,04 text{м})
(F=60 text{Н})
__________________
(E_p-?)
По закону Гука (см. §21 данного справочника) сила упругости, возникающая в растянутой пружине, равна: (F_text{упр}=kx), где (k) — жесткость пружины, (x) — величина деформации.
Сила, удерживающая пружину в растянутом состоянии, должна уравновешивать силу упругости, т.е. быть равной ей по величине (F=F_text{упр}=kx). По направлению эти силы противоположны: удерживающая сила растягивает пружину, сила упругости стремится вернуть её в исходное состояние.
Следовательно, жесткость пружины: begin{gather*} k=frac Fx. end{gather*} Потенциальная энергия растянутой пружины: begin{gather*} E_p=frac{kx^2}{2}=frac Fxcdot frac{x^2}{2}\[6pt] E_p=frac{Fx}{2} end{gather*} Получаем: begin{gather*} E_p=frac{60cdot 0,04}{2}=1,2 (text{Дж}) end{gather*} Ответ: 1,2 Дж
Задача 7*. Какую работу необходимо совершить, чтобы поднять на цепи из колодца глубиной 30 м ведро с водой? Масса цепи 8 кг, масса ведра с водой 10 кг. Размерами ведра можно пренебречь.
Дано:
(h=30 text{м})
(m=8 text{кг})
(M=10 text{кг})
(gapprox 10 text{м/с}^2)
__________________
(A-?)
Установим нулевой уровень (h=0) на дне колодца.
При подъеме на высоту (h) ведро массу не меняет и приобретает потенциальную энергию begin{gather*} E_{p1}=Mgh end{gather*} Работа силы тяжести при подъеме ведра (A’_text{в}=-Delta E_p=-Mgh). Работа силы тяжести отрицательна, т.к. направление силы тяжести (вниз) противоположно перемещению (вверх).
Работа сторонних сил (силы тяги) по преодолению силы тяжести (A_text{в}=-A’_text{в}=Mgh). Работа положительна, т.к. сила тяги направлена вверх.
С цепью немного сложней, т.к. масса цепи меняется при подъеме: в начале подъема она максимальна и равна (m=8 text{кг}), в конце подъема – минимальна и равна (m_0=0 text{кг}).
При равномерном подъеме средняя масса begin{gather*} m_text{ср}=frac{m+m_0}{2}=frac m2=4 text{кг}. end{gather*} Тогда работа силы тяги по подъему цепи $$ A_text{ц}=m_text{ср}gh=frac m2 gh. $$ Получаем: begin{gather*} A=A_text{в}+A_text{ц}=Mgh+frac m2 gh\[6pt] A=left(M+frac m2right)gh end{gather*} Подставляем begin{gather*} A=left(10+frac 82right)cdot 10cdot 30=4200 (text{Дж})=4,2 (text{кДж}) end{gather*} Ответ: 4,2 кДж
Содержание:
Теорема об изменении кинетической энергии:
Для рассмотрения теоремы об изменении кинетической энергии необходимо ввести новое понятие «работа силы» и рассмотреть некоторые простейшие способы ее вычисления.
Работа силы
Работа силы на каком-либо перемещении является одной из основных характеристик, оценивающих действие силы на этом перемещении. Рассмотрим элементарную работу, полную работу и мощность.
Элементарная работа силы
Элементарная работа
где 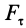
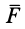
Элементарная работа является скалярной величиной. Ее знак определяется знаком проекции силы 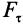
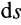
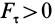
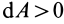
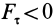
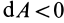
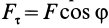
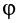
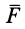
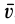
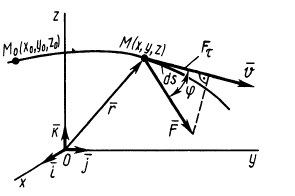
В этой формуле величины 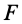
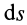
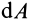
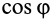
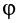
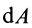
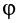
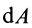
Рис. 60
Итак, элементарная работа силы равна произведению элементарного перемещения на проекцию силы на это перемещение. Отметим частные случаи, которые можно получить из (41):
Таким образом, если сила перпендикулярна элементарному перемещению, то ее элементарная работа равна нулю. В частности, работа нормальной составляющей к скорости силы 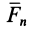
Приведем другие формулы для вычисления элементарной работы силы. Из кинематики точки известно, что 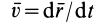
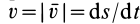
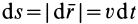
После этого, согласно (41), элементарная работа
Элементарная работа силы равна скалярному произведению силы на дифференциал радиуса-вектора точки приложения силы.
Так как 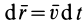
Элементарная работа равна скалярному произведению элементарного импульса силы на скорость точки.
Если силу 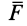
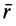
Из последней формулы имеем
Подставляя в (42) значения 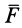
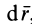
Формулу (44) называют обычно аналитическим выражением элементарной работы. Хотя выражение для элементарной работы (44) по форме и напоминает полный дифференциал функции координат точки, в действительности в общем случае элементарная работа не является полным дифференциалом. Элементарная работа является полным дифференциалом функции координат точки только для специального класса сил — так называемых стационарных потенциальных сил, которые рассмотрены ниже.
Полная работа силы
Для определения полной работы силы 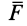
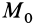
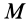
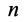
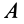
где 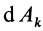
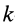
Так как сумма в определении работы является интегральной суммой определения криволинейного интеграла на участке кривой 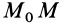
Используя другие выражения для элементарной работы, полную работу силы можно представить также в виде
где момент времени 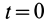
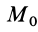
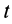
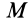
Формула (47) особенно удобная для вычисления работы силы, когда сила известна как функция времени. Отметим, что из определения элементарной и полной работы следует:
- работа равнодействующей силы на каком-либо перемещении равна алгебраической сумме работ составляющих сил на том же перемещении;
- работа силы на полном перемещении равна сумме работ этой же силы на составляющих перемещениях, на которые любым образом разбито все перемещение.
Первое свойство, очевидно, достаточно доказать только для элементарной работы равнодействующей силы.
Если сила 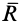
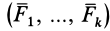
Первое свойство доказано.
Второе из отмеченных свойств непосредственно следует из возможности разбиения любым образом полного промежутка интегрирования на составляющие, причем определенный интеграл по полному промежутку интегрирования равен сумме интегралов по составляющим. Единицей полной работы, так же как и элементарной, в СИ является джоуль: 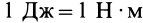
Если проекция силы на направление скорости 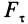
где 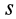
Так как 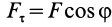
Следует отметить, что в этой формуле как 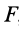
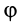
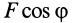
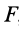
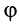
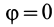
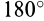
причем эта формула применима как для прямолинейного, так и для криволинейного движения. Для этого необходимо, чтобы сила 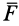
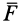
Мощность
Мощность силы или работоспособность какого-либо источника силы часто оценивают той работой, которую он может совершить за единицу времени.
Итак, по определению, мощность
Учитывая (43) для элементарной работы, мощность 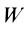
Таким образом, мощность равна скалярному произведению силы на скорость точки. Из формулы (48) получаем, что чем больше скорость, тем меньше сила при одной и той же мощности. Следовательно, если от источника силы с заданной мощностью нужно получить большую силу, то ее можно получить только при малой скорости. Так, например, когда железнодорожному локомотиву надо увеличить силу тяги, то для этого надо уменьшить скорость поезда.
В СИ единицей мощности является ватт: 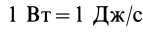
Примеры вычисления работы силы
Работа силы в общем случае зависит от характера движения точки приложения силы. Следовательно, для вычисления работы надо знать движение этой точки. Но в природе имеются силы и примеры движения, для которых работу можно вычислить сравнительно просто, зная начальное и конечное положение точки.
Рассмотрим работу силы тяжести и линейной силы упругости, изменяющейся по закону Гука, и вычисление работы силы, приложенной к какой-либо точке твердого тела в различных случаях его движения. В качестве простейших примеров движения укажем случаи, когда работа равна нулю. Так, работа любой силы равна нулю, если она приложена все время в неподвижной точке или в точках, скорость которых равна нулю, как, например, в случае, когда сила все время приложена в мгновенном центре скоростей при плоском движении тела или все время в точках, лежащих на мгновенной оси вращения, в случае вращения тела вокруг неподвижной точки. Эти случаи возможны в задачах, когда рассматривают работу силы трения в точке соприкосновения двух тел при отсутствии скольжения одного тела по другому. При этом работа силы трения равна нулю.
Рис. 61
Работа силы тяжести
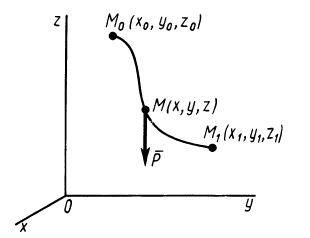
Силу тяжести 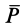
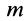
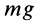
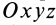
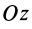
Вычисляя работу 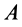
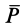
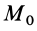
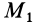
или
где 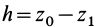
При подъеме точки высота 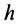
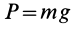
Работа силы тяжести равна произведению этой силы на высоту опускания (работа положительна) или высоту подъема (работа отрицательна). Из формулы (50) следует, что работа силы тяжести не зависит от формы траектории между точками 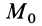
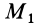
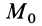
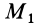
Рис. 62
Если имеем систему 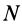
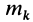
где 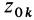
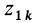
Работа всех сил тяжести системы материальных точек
так как
где 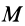
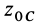
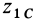
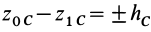
Из (50′) следует, что для перемещений точек системы, при которых 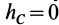
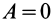
Работа линейной силы упругости
Линейной силой упругости (или линейной восстанавливающей силой) называют силу, действующую по закону Гука (рис. 62):
где 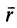
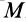
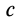
Выберем начало координат в точке равновесия 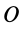
После этого работу на перемещении от точки 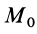
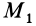
так как
где 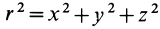
Выполняя интегрирование, получаем
По этой формуле вычисляют работу линейной силы упругости пружины при перемещении по любому пути из точки 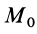
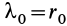
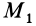
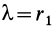
При перемещении из положения равновесия (пружина не деформирована), где 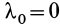
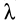
Работа линейной силы упругости на перемещении из состояния равновесия всегда отрицательна и равна половине произведения коэффициента жесткости на квадрат деформации. Из формулы (51) или (52) следует, что работа линейной силы упругости не зависит от формы перемещения и работа по любому замкнутому перемещению равна нулю. Она также равна нулю, если точки 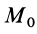
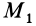
Работа силы, приложенной к твердому телу
Получим формулы для вычисления элементарной и полной работы силы, приложенной в какой-либо точке твердого тела, которое совершает то или иное движение. Сначала рассмотрим поступательное и вращательное движения тела, а затем общий случай движения твердого тела.
При поступательном движении твердого тела все точки тела имеют одинаковые по модулю и направлению скорости (рис. 63). Следовательно, если сила 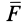
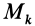
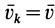
где 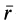
На каком-либо перемещении полная работа
При вращении твердого тела вокруг неподвижной оси скорость точки 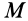
Рис. 63
Рис. 64
тогда элементарную работу силы 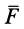
В смешанном векторном произведении, которое выражается в виде определителя, можно переставлять сомножители в круговом порядке:
и
так как
является моментом силы относительно точки 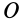
Учитывая, что 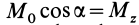
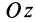
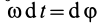
Таким образом, элементарная работа силы, приложенной к какой-либо точке тела, вращающегося вокруг неподвижной оси, равна произведению момента силы относительно оси вращения на дифференциал угла поворота тела.
Полная работа
В частном случае, если момент силы относительно оси вращения является постоянным, т. е. 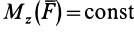
где 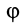
Так как 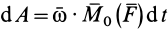
Мощность силы, приложенной к вращающемуся вокруг неподвижной оси твердому телу, равна произведению угловой скорости тела на момент силы относительно оси вращения . тела.
Рис. 65
Для свободного тела в общем случае движения скорость точки 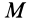
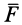
следовательно,
Учитывая, что
имеем
Но так как 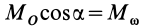
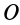
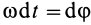
Таким образом, элементарная работа силы, приложенной в какой-либо точке твердого тела, в общем случае движения складывается из элементарной работы на элементарном поступательном перемещении вместе с какой-либо точкой тела и на элементарном вращательном перемещении вокруг этой точки.
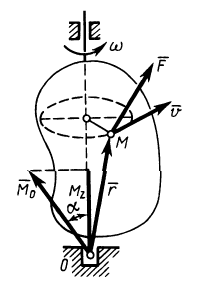
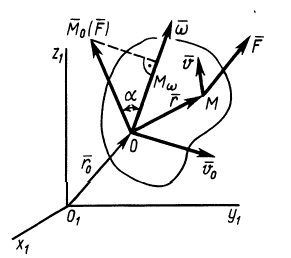
В случае вращения твердого тела вокруг неподвижной точки, выбрав эту точку за полюс 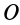
Поворот на угол 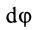
Формулу (59) применяют и для плоского движения твердого тела, только в этом случае мгновенная ось относительного вращения перпендикулярна плоскости движения и проходит через произвольную точку тела.
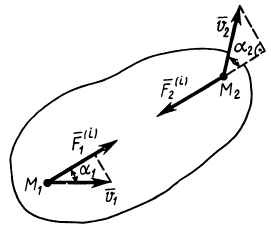
При действии на твердое тело системы сил 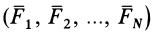
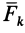
Элементарная работа системы сил
где
соответственно являются главным вектором и главными моментами системы сил относительно точки 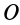
т. е. элементарная работа системы сил, приложенных к свободному твердому телу в общем случае его движения, складывается из элементарной работы главного вектора системы сил на элементарном поступательном перемещении вместе с какой-либо точкой тела и элементарной работы главного момента этих сил относительно выбранной точки на элементарном вращательном перемещении вокруг этой точки.
Работа внутренних сил твердого тела
Докажем, что для твердого тела сумма работ внутренних сил равна нулю при любом его перемещении. Очевидно, достаточно доказать, что сумма элементарных работ всех внутренних сил равна нулю. Рассмотрим две любые точки твердого тела: 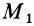
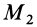
Введем единичный вектор 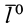
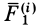
Сумма элементарных работ сил 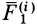
Рис. 66
Раскрывая скалярные произведения векторов в скобках, получаем
так как в кинематике твердого тела доказано, что проекции скоростей любых двух точек твердого тела на направление прямой линии, соединяющей эти точки, равны друг другу при любом движении твердого тела. В полученном выражении в скобках стоит разность этих проекций скоростей двух точек, т. е. величина, равная нулю.
Твердое тело можно считать состоящим из пар взаимодействующих точек, для каждой из которых сумма элементарных работ внутренних сил равна нулю.
Суммируя элементарные работы для всех пар точек, получаем 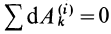
Как уже известно, главный вектор и главный момент всех внутренних сил для любой механической системы равны нулю. Сумма работ внутренних сил равна нулю только в случае твердого тела, а для любой механической системы в общем случае она не равна нулю.
В задачах в качестве механической системы часто рассматривают систему сочлененных твердых тел. При вычислении работы всех сил, приложенных к такой системе тел, очевидно, достаточно учесть работу внутренних сил в местах сочленения твердых тел. Если твердые тела сочленяются с помощью шарниров без трения, сумма работ таких двух внутренних сил равна нулю, так как внутренние силы в точке сочленения, как действие и противодействие, равны по модулю, но противоположны по направлению, а перемещение у точек приложения сил общее.
Таким образом, сочленение твердых тел с помощью шарниров без трения при вычислении работы внутренних сил не нарушает жесткости системы тел, так как сумма работ внутренних сил в этих шарнирах равна нулю при любых перемещениях системы сочлененных твердых тел. Систему сочлененных с помощью таких шарниров твердых тел при вычислении работы всех внутренних сил можно считать одним твердым телом. Это характерно и для случая сочленения системы твердых тел с помощью нерастяжимых нитей, канатов и т. п. В этом случае работа внутренних сил натяжений также равна нулю.
Кинетическая энергия
Кинетическая энергия точки и системы: Кинетической энергией материальной точки называют половину произведения массы точки на квадрат ее скорости, т.е. 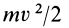
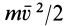
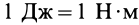
Кинетической энергией системы 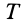
Кинетическая энергия как точки, так и системы не зависит от направления скоростей точек. Кинетическая энергия может быть равна нулю для системы только при условии, если все точки системы находятся в покое.
Вычисление кинетической энергии системы (теорема Кёнига)
Разложим движение механической системы на переносное поступательное вместе с центром масс системы и относительное по отношению к системе координат, движущейся поступательно вместе с центром масс. Аналогично тому, как это производилось при выводе формулы для кинетического момента при таком разложении абсолютного движения, для каждой точки системы 
и соответственно
где 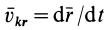
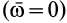
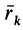
Подставляя значение скорости 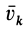
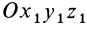
Но
так как
Учитывая, что 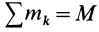
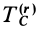
где
Величина 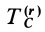
Формула (63) выражает так называемую теорему Кёнига: кинетическая энергия системы в абсолютном движении складывается из кинетической энергии центра масс, если в нем сосредоточить всю массу системы, и кинетической энергии системы относительно центра масс.
Кинетическая энергия твердого тела
При поступательном движении твердого тела кинетическая энергия
так как при поступательном движении твердого тела скорости всех точек тела одинаковы, т. е. 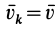
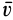
Таким образом, кинетическая энергия твердого тела при поступательном движении вычисляется так же, как и для одной точки, у которой масса равна массе всего тела.
При вращении тела вокруг неподвижной оси кинетическую энергию можно вычислить, если учесть, что скорость какой-либо точки тела 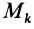
где 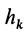
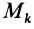
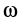
Тогда
или
где 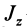
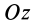
Следовательно, кинетическая энергия тела при вращательном движении вокруг неподвижной оси равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела.
Из сравнения (64) и (65) следует, что эти формулы подобны, только при вращательном движении аналогом массы является момент инерции тела относительно оси вращения, а скорости— угловая скорость тела. Такая аналогия между поступательным и вращательным движениями твердого тела может наблюдаться во многих формулах, относящихся к этим двум движениям.
При плоском движении твердого тела кинетическую энергию можно вычислить по теореме Кёнига. Так как в этом случае относительное движение относительно центра масс (точнее, относительно системы координат, движущейся поступательно вместе с центром масс) является вращением вокруг центра масс с угловой скоростью 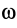
где 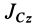
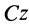
Таким образом, при плоском движении тела кинетическая энергия складывается из кинетической энергии поступательного движения тела вместе с центром масс и кинетической энергии от вращения вокруг оси, проходящей через центр масс и перпендикулярной плоскости движения.
Учитывая, что 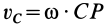
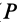
где 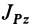
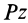
Если механическая система состоит из нескольких твердых тел, то следует вычислить кинетическую энергию каждого тела, а затем полученные кинетические энергии сложить. Так определяется кинетическая энергия системы тел.
Теорема об изменении кинетической энергии точки
Для материальной точки массой 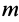
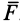
Умножая обе части этого соотношения скалярно на дифференциал радиуса-вектора точки 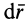
или
где 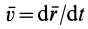
Учитывая, что 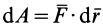
Так как
то окончательно
Формула (67) выражает теорему об изменении кинетической энергии для точки в дифференциальной форме: дифференциал кинетической энергии точки равен элементарной работе силы, действующей на точку.
Если обе части (67) разделить на 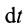
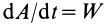
Производная по времени от кинетической энергии точки равна мощности, подводимой к этой точке.
Интегрируя обе части (67) от точки 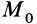
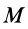
т. е. изменение кинетической энергии точки на каком-либо перемещении равно работе силы, действующей на точку на том же перемещении.
- Заказать решение задач по теоретической механике
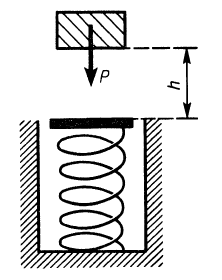
Пример 1. Тело, имеющее силу тяжести 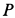
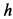
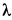
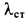
Решение. Применим к движению тела теорему об изменении кинетической энергии точки
приняв за начальное положение тела начало его падения с высоты 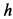
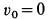
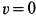
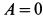
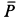
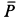
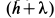
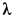
Рис. 67
Но так как в положении статического равновесия 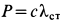
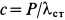
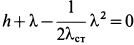
Решая это квадратное уравнение, имеем
Знак плюс перед корнем выбран потому, что 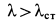
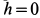
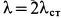
Рис. 68
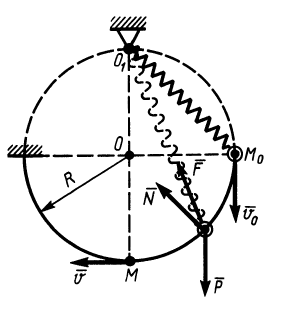
Пример 2. Грузу с силой тяжести 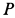
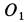
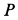
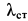
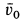
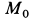
Определить скорость груза в положении 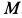
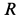
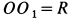
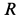
Решение. Применим к движению груза теорему об изменении кинетической энергии, приняв за начальное положение груза 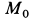
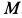
Работу совершают сила тяжести груза и сила упругости пружины. Нормальная реакция кольца 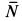
В рассматриваемом случае
поэтому
По теореме об изменении кинетической энергии имеем
и
Теорема об изменении кинетической энергии системы
Приложив к точкам системы все внешние и внутренние силы, для каждой точки системы можно выразить теорему об изменении кинетической энергии (67) в форме
Суммируя правые и левые части этих соотношений по всем точкам системы и вынося знак дифференциала за знак суммы, получаем
или
где кинетическая энергия системы
элементарная работа внешних и внутренних сил соответственно будет
Формула (69) и выражает теорему об изменении кинетической энергии системы в дифференциальной форме: дифференциал от кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему.
Если обе части (69) проинтегрировать между двумя положениями системы — начальным и конечным, в которых соответственно кинетическая энергия 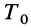
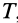
или
где 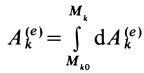
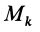
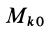
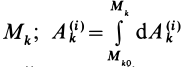
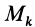
Формула (70) выражает теорему об изменении кинетической энергии системы в конечной или интегральной форме: изменение кинетической энергии системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних сил, действующих на систему, на соответствующих перемещениях точек системы при том же перемещении системы.
Частный случай: Для абсолютно твердого тела сумма работ всех внутренних сил системы равна нулю:
Следовательно, теорему об изменении кинетической энергии, например, в конечной форме можно представить в виде
Изменение кинетической энергии твердого тела при каком-либо перемещении равно сумме работ всех внешних сил, действующих на тело, на соответствующих перемещениях точек тела при том же перемещении твердого тела.
Рис. 69
Таким образом, в отличие от рассмотренных других общих теорем динамики системы в теорему об изменении кинетической энергии могут входить внутренние силы. Они не входят в эту теорему в случае абсолютно твердого тела.
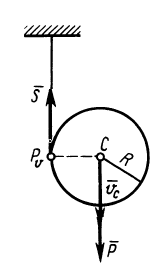
Пример 1. В маятнике Максвелла однородный цилиндр силой тяжести 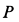
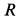
Определить скорость оси цилиндра в зависимости от высоты ее опускания 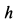
Решение. По теореме об изменении кинетической энергии цилиндра как твердого тела имеем
Так как в начальный момент времени цилиндр покоится, то 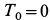
Поэтому
Внешними силами являются сила тяжести 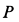
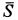
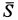
Подставляя вычисленные величины в теорему об изменении кинетической энергии, получаем
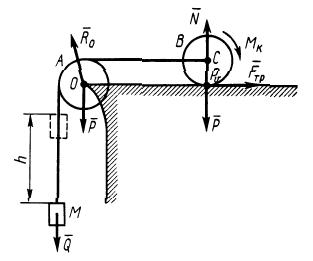
Пример 2. Груз 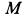
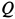
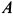
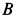
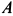
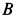
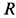
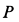
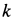
Определить скорость груза 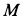
В начальный момент система покоится.
Рис. 70
Решение. По теореме об изменении кинетической энергии системы, состоящей из груза, нити, блока и катка, имеем
где 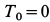
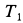
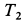
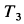
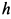
Но
Следовательно,
Так как работа внутренних сил натяжений нити равна нулю, то вообще 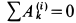
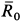
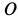
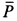
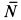
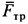
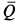
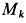
где 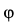
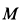
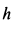
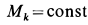
Так как
то
Подставляя значения полученных величин в теорему об изменении кинетической энергии, получаем
Заметим, что груз имеет не только силу тяжести 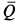
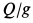
Теорема об изменении кинетической энергии в относительном движении
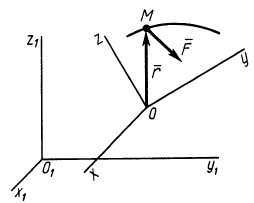
Теорема об изменении кинетической энергии материальной точки. Пусть точка 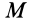
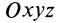
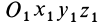
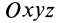
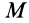
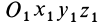
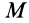
где 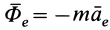
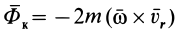
Рис. 71
Вывод теоремы об изменении кинетической энергии для точки в относительном движении произведем так же, как и вывод аналогичной теоремы в абсолютном движении, умножив обе части (72) скалярно на вектор элементарного относительного перемещения 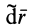
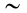
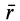
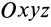
В правую часть входят элементарные работы сил 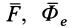
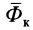
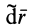
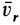
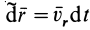
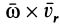
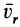
Итак, теорема об изменении кинетической энергии точки в дифференциальной форме имеет вид
Теорема об изменении кинетической энергии в относительном движении точки выражается так же, как и в абсолютном движении, только к элементарной работе приложенной силы добавляют элементарную работу силы инерции переносного движения на относительном перемещении.
Теорема об изменении кинетической энергии системы
Для системы рассмотрим наиболее важный случай, когда в качестве переносного движения берется поступательное движение системы вместе с центром масс и, следовательно, кинетическую энергию системы в абсолютном движении можно вычислить на основании теоремы Кёнига (63): 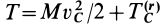
Теорему об изменении кинетической энергии системы для абсолютного движения (см. рис. 56) можно представить в виде
Так как
и, следовательно,
то, заменяя в (74) 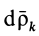
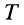
По свойству внутренних сил, 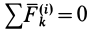
Если теорему об изменении кинетической энергии для центра масс выразить так же, как и для точки, у которой масса равна массе всей системы, и эта точка находится под действием всех внешних сил, действующих на систему, то
Отбросив в (75) эти члены, получим следующую теорему об изменении кинетической энергии системы в относительном движении по отношению к системе координат, движущейся поступательно вместе с центром масс:
Сравнивая (76) с (74), видим, что теорема об изменении кинетической энергии в относительном движении системы по отношению к системе координат, движущейся поступательно вместе с центром масс системы, формулируется так же, как и для абсолютного движения системы.
- Потенциальное силовое поле
- Закон сохранения механической энергии
- Принцип Даламбера
- Динамические реакции при вращении твердого тела вокруг неподвижной оси
- Свойства внутренних сил системы
- Дифференциальное уравнение движения системы
- Теоремы об изменении количества движения и о движении центра масс
- Теорема об изменении кинетического момента