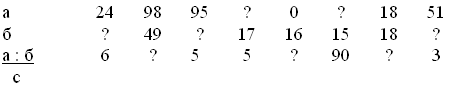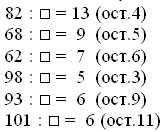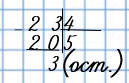Перед тем как найти делитель, нужно понимать, что такое делитель, что такое делимое и частное.
Делитель — это число, на которое можно разделить другое число без остатка.
Давайте рассмотрим пример: число 12. Если мы разделим 12 на 2, то получим 6, а если разделим на 3, то получим 4 без остатка. Это значит, что 2 и 3 являются делителями числа 12. Чтобы найти все делители числа, нужно просто проверять все числа, начиная с 1 и заканчивая самим числом.
Если число делится на какое-то из этих чисел без остатка, то это число является делителем. Например, чтобы найти все делители числа 12, мы можем проверить, делится ли 12 на 1, 2, 3, 4, 6 и 12 без остатка.
Также можно заметить, что делители всегда идут парами: например, 2 и 6, 3 и 4 являются парами делителей числа 12, так как 2 * 6 = 12 и 3 * 4 = 12.
Существует определенное правило для нахождения делителя. Вспомним, что такое делимое, делитель и частное.
Чтобы найти делитель, нужно делимое разделить на частное. В примере выше делитель у нас 4, поэтому мы разделим делимое 12 на частное 3. Легко, не так ли ? Теперь попробуем найти делитель в более сложных примерах.
Пример 1. Найдите делитель: (1080 : 24x = 15)
Решение:
(1080 : 24x = 15)
Алгоритм решения тот же: делимое делим на частное:
(1080:15 =72)
(24x=72)
(72:24=3)
Данное правило мы можем применять везде, где есть деление чисел.
Ответ: делитель равен (72) ((x=3)).
Если вы сомневаетесь, что на что надо делить, то придумайте такой же пример, только с простыми числами. Рассмотрим это на примере ниже.
Пример 2. Найдите делитель: (784:x=14)
Решение:
(784:x=14)
Аналогичный пример с простыми числами:
(6:x=2) — здесь понятно, чтобы найти (x) надо (6) разделить на (2), то есть делитель равен (3)
(784:14 = 56) — искомый делитель
Главная цель урока: познакомить с правилом
нахождения неизвестного делителя при делении с
остатком.
Образовательные цели:
- повторить способы записи частного;
- повторить названия компонентов действия
деления; - повторить правило нахождения неизвестного
делителя при делении нацело; - составить формулу нахождения неизвестного
делителя при делении с остатком; - формировать умение сравнивать, выделять
главное; - учить устанавливать причинно-следственные
связи, обобщать, делать выводы; - закреплять вычислительные навыки;
- закреплять решение текстовых задач на деление с
остатком; - формировать умение целенаправленно работать в
парах.
Воспитательные цели:
- воспитывать умение слушать одноклассников,
высказывать свою точку зрения и обосновывать её; - воспитывать интерес к математике.
Развивающие цели:
- развивать рефлексию.
Оздоровительные цели:
- профилактика утомления, нарушения осанки.
Оборудование:
- карточки с числами;
- схематическое изображение темы урока;
- формула нахождения неизвестного делителя при
делении с остатком; - распечатки для самостоятельной работы;
- карточки с условными знаками для проведения
рефлексии; - индивидуальные текстовые карточки для
проведения рефлексии.
Ход урока
1. Организационный момент.
Эмоциональный настрой на урок
— Сегодня у нас много гостей на уроке.
Повернитесь, поздоровайтесь и улыбнитесь им. Вот
видите, и они вам улыбнулись. В классе стало уютно
от ваших улыбок.
2. Чистописание.
На доске написана цифра 9.
— Сегодня на уроке мы с вами будем повторять
написание цифры 9.
— Напишите три цифры.
— Оцените свою работу. Если вы считаете, что все
три цифры написали каллиграфически верно,
поставьте на полях тетради знак плюс, если нет —
знак минус.
3. Актуализация знаний.
“Разминка для головы и рук”
— Что движется быстрее скорости света?
— Мне интересно будет сегодня на уроке
наблюдать, как движутся ваши мысли. Не прячьте их.
18 : 9 2 27 : 9 3
— Что записано на доске?
— Прочитайте выражения разными способами.
— Найдите закономерность записи чисел и
выражений.
— Какое деление выполнили?
— Продолжите закономерность до конца строчки.
— Что общего во всех выражениях?
— Как найти неизвестный делитель?
— Найдите компоненты действия деления.
— Какой компонент неизвестен в первом примере?
На доске представлена таблица. У каждого
учащегося на парте карточка с числом, которое
является значением одного из выражений. Всем
учащимся необходимо выполнить устные вычисления
и прикрепить свою карточку в нужное место
таблицы. Примеры решаются по порядку, карточки
прикрепляются по мере решения примеров.
Разминка закончилась.
4. Сообщение темы и задач урока.
— Теперь нам надо узнать тему нашего урока.
На доске открывается схематическое
изображение темы урока.
— Какое деление сегодня мы будем выполнять на
уроке?
— Какие компоненты при делении с остатком умеем
находить?
— Какой компонент будем сегодня учиться
находить?
— Задача нашего урока составить формулу
нахождения неизвестного делителя при делении с
остатком.
5. Этап “открытия” нового знания.
На доске открывается запись.
— Подумайте, как мы будем находить неизвестный
делитель?
— Можем ли мы использовать формулу нам уже
известную?
— Почему?
— Давайте уберём остаток. Как это сделать?
86 – 5 = 81
— Теперь можем воспользоваться уже известной
нам формулой?
— Воспользуйтесь.
81 : 9 = 9
— Проверьте себя.
9 · 9 + 5 = 86
— Можем ли мы теперь ответить на главный вопрос
урока?
— Как найти неизвестный делитель при делении с
остатком?
На доске открывается формула нахождения
неизвестного делителя при делении с остатком.
в = (а – ч ) : с
— Откройте учебники на стр. 61, найдите №122.
— Используя данную формулу, вставьте числа в
“окошки”.
— Считайте устно и комментируйте свой ответ.
6. Физкультурная минутка.
1) И.п.- сидя за партой, руки за голову. 1-2-руки
вверх, потянуться; 3-4-И.п.
2) И.п.- сидя за партой, ноги на ширину плеч, руки
на пояс. 1-2- наклон вправо; 3-4 – И.п. То же влево.
3) И.п. – сидя за партой. 1-2- встать, выпрямиться;
3-4 – И.п.
7. Закрепление пройденного материала.
— Что мы будем делать дальше на уроке, ведь на
главный вопрос урока мы дали ответ?
— Зачем нам тренироваться в решении примеров на
нахождение неизвестного делителя?
Учащиеся получают карточки для
самостоятельной работы.
— Найдите неизвестный делитель. Закройте
окошки.
— Выполненную работу передайте члену своей
пары. Оцените работы.
— При выполнениеиработы без ошибок, передайте
члену пары карточку со знаком плюс. При ошибках в
вычислениях передайте карточку со знаком минус.
— Покажите карточки.
На доске открываются значения выражений,
представленные на карточках.
6 7 8 15 19 14
— А теперь сравните свои результаты с
результатами на доске.
— Если результаты совпали, оставьте карточку со
знаком плюс, если нет, верните ее обратно члену
пары, который проверял вашу работу.
— Покажите карточки.
8. Повторение.
— Откройте учебник на стр.64.
— Прочитайте задачу № 28.
— Как вы думаете, почему именно данная задача
включена в урок?
— Что в задаче известно?
— Что значит “по 6 банок тушёнки”?
— Что надо узнать?
— Можем сразу ответить на вопрос задачи?
— Почему?
— Как узнать?
— Теперь можем ответить на поставленный вопрос?
— Что для этого нужно сделать?
— А как письменно оформить нашу мысль?
— Что мы записали?
— Прочитайте, как рассуждали при решении данной
задачи Миша и Маша.
— С чьим рассуждением совпадает наше?
— Кто прав: Маша и мы или Миша?
9. Подведение итогов урока. Домашнее задание.
Инструктаж его выполнения.
— Оцените себя и покажите, кто может
самостоятельно в домашнем задании найти
делитель при делении с остатком?
Учащиеся показывают карточки с условными
знаками: +,-, ?.
— Кому необходимо пользоваться формулой при
решении примеров на нахождение неизвестного
делителя при делении с остатком?
Учащиеся показывают карточки с условными
знаками: +,-, ?.
— В домашнем задании я предлагаю вам составить
примеры на деление с остатком с неизвестным
делителем. Напечатайте примеры, используя
компьютер. У вас получатся карточки для
самостоятельной работы. Мы будем использовать их
на следующих уроках.
-Урок окончен. Ваши мысли двигались
действительно быстрее скорости света. Мне было
интересно и комфортно на уроке.
— А как вы ощущали себя на уроке?
Каждый учащийся работает с индивидуальными
текстовыми карточками
— Выберите утверждение. Отметьте галочкой.
Ощущал себя на уроке:
- хорошо;
- уверенно;
- смело;
- гордо;
- комфортно;
- глупо;
- неуверенно;
- испуганно;
- сердито;
- грустно.
Спасибо.
На этом уроке продолжим разговор о делении натуральных чисел.
Вспомним название компонентов арифметической операции деления и установим, по каким правилам находится каждое из них.
Эта информация доступна зарегистрированным пользователям
Познакомимся с делением натуральных чисел с остатком, выясним алгоритм выполнения такой математической операции.
Определим компоненты арифметической операции деления с остатком.
Подробно рассмотрим взаимосвязь между компонентами деления с остатком и закрепим полученные знания, решая текстовые задачи по теме.
О математической операции деления вы уже имеете общее представление.
Уроком ранее выяснили, что деление- это арифметическая операция, с помощью которой по произведению и одному из множителей находят другой множитель.
Другими словами, деление- это математическая операция, противоположная умножению.
Разделить число а на число b— это значит найти такое число с, при умножении которого на число b, получается число а.
а ÷ b = с
а = с ∙ b
Рассмотрим данное утверждение на примере.
Умножение:
На детский праздник приготовили пирожные.
Всего на празднике присутствовало 6 детей, каждому ребенку досталось по 2 пирожных.
Определим сколько пирожных для детей приготовили на праздник.
Эта информация доступна зарегистрированным пользователям
Ответ: 12 пирожных.
Деление:
На детский праздник приготовили 12 пирожных.
Всего на празднике присутствовало 6 детей, каждого ребенка угостили одинаковым количеством пирожных.
Выясним сколько пирожных досталось каждому ребенку.
Эта информация доступна зарегистрированным пользователям
Ответ: каждому ребенку досталось по 2 пирожных.
Делимое- это число, которое делят.
Делитель- это число, на которое делят делимое.
Частное (от слова «часть»)- результат арифметической операции деления (число, которое получается в результате деления одного числа на другое).
Для записи деления используют математический знак в виде двух точек, как двоеточие «:».
Эта информация доступна зарегистрированным пользователям
Знак деления располагается между делимым и делителем.
Делимое всегда находится слева от знака делить, а делитель- справа.
В общем виде операция деления выглядит так:
Эта информация доступна зарегистрированным пользователям
Часто, решая различного рода задачи, приходится сталкиваться с ситуацией, когда один из компонентов операции деления неизвестен и его необходимо найти.
Определим, по каким правилам можно найти каждый компонент операции деления.
1. Так как частное- это результат, полученный при выполнении деления, то очевидно, что частное находят с помощью данной арифметической операции.
Зная делимое и делитель, можно найти частное.
Эта информация доступна зарегистрированным пользователям
Рассмотрим пример.
Дима купил 12 разноцветных воздушных шариков.
Каждому своему другу он подарил по 2 шарика.
Сколько друзей получили шарики?
Эта информация доступна зарегистрированным пользователям
Решение:
12 шариков (общее количество шариков)- делимое.
2 шарика (число шариков, которое достанется каждому другу)- делитель.
Частное- число друзей (это число, которое показывает на сколько частей придется разделить все шарики)- ?
Эта информация доступна зарегистрированным пользователям
Ответ: 6 друзей получили воздушные шарики.
2. Делимое- это общее количество чего-либо, число, которое делят на части.
Если неизвестно делимое число, то необходимо перемножить два известных компонента деления: делимое и частное.
Правило: чтобы найти неизвестное делимое, нужно частное умножить на делитель или делитель умножить на частное.
Эта информация доступна зарегистрированным пользователям
Рассмотрим пример.
Вова должен решить некоторое количество задач по математике за 3 дня.
Он собирался решать по 5 задач в день.
Сколько всего задач ему необходимо решить за три дня?
Эта информация доступна зарегистрированным пользователям
Решение:
5 задач (число задач, которые необходимо решать каждый день)- делитель.
3 дня (число промежутков времени, за которое необходимо решить все задачи)- частное
Делимое (общее количество задач)- ?
Эта информация доступна зарегистрированным пользователям
Ответ: 15 задач нужно решить Вове.
3. Делитель- это число, на которое делят делимое.
Если исходное делимое число разделить на равные части, то в итоге получится некоторое количество таких частей.
Правило: чтобы найти делитель, нужно делимое разделить на частное.
Эта информация доступна зарегистрированным пользователям
Рассмотрим пример.
Эта информация доступна зарегистрированным пользователям
Восемь кусочков пиццы разделили на четверых человек.
Каждому досталось одинаковое количество кусочков пиццы.
По сколько кусочков пиццы получил каждый?
Решение:
8 кусков пиццы (общее количество кусочков, которые необходимо разделить)- делимое.
4 человека (число человек, на которых делят пиццу)- частное.
Делитель (число кусочков пиццы, которые получит каждый)- ?
Эта информация доступна зарегистрированным пользователям
Ответ: по 2 кусочка пиццы получит каждый человек.
Эта информация доступна зарегистрированным пользователям
Математическая операция деление связано с разделением чего-либо на части.
Делить натуральное число на равные части вы уже умеете, данная математическая операция не вызовет у вас большого затруднения.
Однако, не всегда удается разделить натуральное число на равные части.
Рассмотрим пример.
Разложим поровну на 4 тарелки 13 абрикосов.
Сначала в каждую тарелку положим по одному абрикосу, далее по второму, затем по третьему.
В результате у нас останется 1 абрикос, но тарелок 4.
Таким образом, в каждую тарелку удалось положить по 3 абрикоса и еще 1 остался.
Эта информация доступна зарегистрированным пользователям
Так мы разделили число 13 на равные части, и у нас остался остаток.
Продемонстрируем рассмотренный пример на координатном луче.
Изобразим координатный луч, направленный вправо, с началом отсчета в точке О и единичным отрезком 1 деление = 1 единица.
Эта информация доступна зарегистрированным пользователям
На координатном луче отметим точку А(13)- эта точка показывает общее количество абрикосов, которые нужно поделить.
Отрезок ОА разобьем на 4 отрезка по 3 деления (так как абрикосы раскладывали на четыре тарелки по три абрикоса).
Заметим следующее: по три деления мы отложили четыре раза и одно деление еще осталось (это деление нам указывает на остаток абрикосов- 1 шт).
При делении с остатком результат деления записывают двумя числами: первое число называют неполным частным, так как число делится не полностью, второе число называют остатком.
Запись деления с остатком соответствует следующей схеме:
Эта информация доступна зарегистрированным пользователям
Неполное частное- это наибольшее число, которое может быть получено при умножении его на делитель, и не превосходящее делимое.
В буквенном виде деление с остатком можно записать так:
Эта информация доступна зарегистрированным пользователям
Для разобранного выше примера про абрикосы получаем следующее:
13 ÷ 3 = 4 (ост. 1)
Число 13— это делимое
Число 3— это делитель
Число 4— это неполное частное
Число 1— это остаток от деления
Важно знать и помнить, что остаток всегда должен быть меньше делителя.
Если при делении одного натурального числа на другое остаток равен нулю, то говорят: «Число делится нацело», т.е. первое число делится на второе без остатка.
Рассмотрим алгоритм деления с остатком.
1. Найти наибольшее число, которое будет удовлетворять одновременно следующим требованиям:
-
- найденное число будет меньше делимого
- это число делится на делитель без остатка.
2. Подобранное число разделить на делитель.
Таким образом находится значение неполного частного.
3. Вычесть из делимого наибольшее число (найденное в пункте 1 нашего алгоритма), полученный результат- это остаток.
4. Проверяем остаток сравнением, он должен быть меньше делителя.
Записывать деление с остатком можно в строчку а ÷ b = с (ост. r) или в столбик- «деление уголком».
Приведем пример.
Найдем значение выражения 19 ÷ 6.
Наибольшее число, которое меньше 19 и делится на 6— это 18.
18 разделим на делитель 6, получим 3-это неполное частное.
Вычтем из делимого числа 19 найденное наибольшее число 18, получим число 1— это остаток от деления.
Соберем все известные и полученные данные в равенство: 19 ÷ 6 = 3 (ост 1).
19— делимое.
6— делитель.
3— неполное частное.
1-остаток от деления.
Эта информация доступна зарегистрированным пользователям
Деление с остатком «уголком» выполняется по той же схеме, как и без остатка.
Разберем пример.
Разделим 45 на 13.
1. Выделим в делимом наибольшее неполное делимое, которое делится на 13.
В нашем случае это само число 45, следовательно, в неполном частном будет только одна цифра.
Эта информация доступна зарегистрированным пользователям
2. Разделим неполное делимое на делитель.
Предположим, что результатом такого деления будет число 4, тогда, умножив 13 на 4, получим число 52, но это число противоречит действительности, так как делимое 45 меньше числа 52, полученного при умножении 13 и 4.
Число 4 в качестве неполного частного нам не подходит.
Тогда возьмем число, которое предшествует 4, это число 3.
Делитель 13 умножим на 3.
3. Умножим делитель на найденное число.
13 ∙ 3 = 39 (полученное число 39 показывает, сколько единиц разделили из 45)
Число 39 меньше делимого 45, значит подобранная пробная цифра 3 подходит, записываем ее в частное
Эта информация доступна зарегистрированным пользователям
Произведение 13 и 3 запишем под делимым 45.
Эта информация доступна зарегистрированным пользователям
Важно помнить, что деление чисел в столбик происходит и записывается по разрядам, а начинается с высшего разряда.
4. Найдем остаток от деления вычитанием.
Из 45 вычтем 39, получаем остаток, он равен 45 – 39 = 6.
5. Сравним остаток от деления с делителем.
По правилу остаток всегда меньше делителя, иначе можно было бы продолжать деление.
Сравним: 13 > 6 (остаток 6 меньше делителя 13)
Эта информация доступна зарегистрированным пользователям
В делимом разрядов больше нет, выделить следующее неполное делимое не удается, следовательно, на этом деление можно считать законченным.
6. Однако, если есть следующее неполное делимое, то необходимо далее следовать данному алгоритму, начиная с пункта 2.
Эта информация доступна зарегистрированным пользователям
Запишем математическую операцию деления с остатком следующим образом:
Эта информация доступна зарегистрированным пользователям
Где а— это делимое, b— это делитель, с— это неполное частное, r— это остаток от деления.
1. Нахождение делимого, если известны делитель, неполное частное и остаток от деления.
Правило: чтобы найти неизвестное делимое, нужно неполное частное умножить на делитель (или наоборот делитель умножить на неполное частное) и к полученному произведению прибавить остаток.
Эта информация доступна зарегистрированным пользователям
Данное равенство используют для проверки операции деления с остатком.
В предыдущем разделе данного урока искали значение выражения 45 ÷ 13.
Нами был получен результат: 45 ÷ 13 = 3 (ост 6).
Проверим полученный результат деления с остатком.
Умножим делитель 13 на неполное частное 3 и прибавим остаток 6, если в итоге получится число, равное делимому 45, то деление с остатком выполнено верно.
Проверяем: 13 ∙ 3 + 6 = 39 + 6 = 45.
Деление было выполнено верно, неполное частное и остаток найдены правильно.
2. Нахождение делителя, если известны делимое, неполное частное и остаток от деления.
Правило: чтобы определить неизвестный делитель, нужно из делимого вычесть остаток, полученную разность разделить на неполное частное.
Данное правило в буквенной форме запишем так:
Эта информация доступна зарегистрированным пользователям
Рассмотрим пример, иллюстрирующий данное правило.
Мальчик заплатил за несколько альбомов 50 рублей.
Цена каждого альбома 15 рублей.
Ему сдали сдачу 5 рублей.
Сколько альбомов купил мальчик на 50 рублей?
Обозначим условно:
а— делимое (общее количество денег, которое было у мальчика).
с— неполное частное (часть денег, потраченных на каждый альбом).
r— остаток (сдача).
b— делитель (число альбомов, которое нужно купить на 50 руб.).
Запишем решение данной задачи.
Эта информация доступна зарегистрированным пользователям
3. Нахождение неполного частного, если известны все остальные компоненты деления с остатком.
Правило: чтобы найти неизвестное неполное частное, нужно из делимого вычесть остаток, полученную разность разделить на делитель.
Правило в буквенной форме запишем так:
Эта информация доступна зарегистрированным пользователям
Рассмотрим пример, демонстрирующий данное правило.
У бабушки было 30 конфет.
Она решила угостить ими своих внуков.
Каждому внуку дала по 7 конфет, и у нее осталось 2 конфеты.
Сколько внуков получило конфеты?
Введем условные обозначения для данной задачи.
а— делимое (общее количество конфет, которое было у бабушки).
b— делитель (число конфет, которые получил каждый внук).
r— остаток (оставшиеся конфеты).
с— неполное частное (число внуков).
Запишем решение данной задачи.
Эта информация доступна зарегистрированным пользователям
4. Нахождение остатка, если известно делимое, делитель, неполное частное.
Правило: остаток от деления равен разности делимого и произведения делителя на неполное частное.
Для данного случая справедливо равенство:
Эта информация доступна зарегистрированным пользователям
Рассмотрим данное правило на примере.
У учителя было 25 тетрадей.
Он раздал 12 ученикам по 2 тетради.
Сколько тетрадей осталось у учителя?
Введем условные обозначения для данной задачи.
а— делимое (общее количество тетрадей, которое были у учителя).
b— делитель (число тетрадей, которые получил каждый ученик).
с— неполное частное (число учеников, которым раздали тетради).
r— остаток (оставшиеся тетради).
Запишем решение данной задачи.
Эта информация доступна зарегистрированным пользователям
Читайте также
- Главная
- Справочники
- Справочник по математике для начальной школы
- Деление
- Деление с остатком
Начнём рассмотрение новой темы с решения задачи.
Мама принесла 8 конфет и разделила их поровну между двумя детьми. Сколько конфет получил каждый?
8 : 2 = 4 (к.)
Каждый ребёнок получил по 4 конфеты.
На следующий день мама опять принесла 8 конфет, но в гостях у её детей была ещё одна подружка. Мама опять разделила конфеты поровну, но уже между тремя детьми. Сколько конфет получил каждый ребёнок?
Каждый получил по 2 конфеты и 2 конфеты остались лишними.
Как это записать?
8 : 3 = 2 (ост. 2)
Как сделать проверку?
2 • 3 + 2 = 8
Правило 1
Деление с остатком — это деление одного числа на другое, при котором остаток не равен нулю.
16 : 7 = 2 (ост. 2)
23 : 8 = 2 (ост. 7)
Правило 2
При делении с остатком остаток всегда должен быть меньше делителя.
43 : 8 = 5 (ост. 3)
остаток 3 < делимого 5
34 : 4 = 8 (ост. 2)
остаток 2 < делимого 4
Правило 3
Если делимое меньше делителя, в частном получается ноль, а остаток равен делимому.
7 : 10 = 0 (ост. 7)
6 : 9 = 0 (ост. 6)
Порядок решения
14 : 5 = 2 (ост. 4)
1. Нахожу наибольшее число до 14, которое делится на 5 без остатка. Это число 10.
10 : 5 = 2
2. Вычитаю из делимого найденное число: 14 − 10 = 4
3. Сравниваю остаток с делителем
4 < 5
Решение верно.
Проверка деления с остатком
1. Умножаю неполное частное на делитель.
2. Прибавляю остаток к полученному результату.
3. Сравниваю полученный результат с делимым, он должен быть МЕНЬШЕ.
Деление в столбик
В 23 содержится 5 раз по 4, и ещё остаётся 3.
Решение записывают так:
23 : 4 = 5 (ост. 3) или так:
, где 23 — делимое, 4 — делитель, 5 — неполное частное, а 3 — остаток.
Советуем посмотреть:
Табличное деление
Внетабличное деление
Деление суммы на число
Деление на однозначное число
Деление чисел, оканчивающихся нулями
Свойства деления
Деление
Правило встречается в следующих упражнениях:
2 класс
Страница 76. Урок 29,
Петерсон, Учебник, часть 3
Страница 77. Урок 29,
Петерсон, Учебник, часть 3
Страница 79. Урок 30,
Петерсон, Учебник, часть 3
Страница 80. Урок 30,
Петерсон, Учебник, часть 3
Страница 81. Урок 31,
Петерсон, Учебник, часть 3
Страница 82. Урок 31,
Петерсон, Учебник, часть 3
Страница 84. Урок 32,
Петерсон, Учебник, часть 3
Страница 87. Урок 33,
Петерсон, Учебник, часть 3
Страница 108. Повторение,
Петерсон, Учебник, часть 3
3 класс
Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 51,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 75,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 34,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 58,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 63,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 68. Урок 28,
Петерсон, Учебник, часть 2
Страница 93. Урок 41,
Петерсон, Учебник, часть 2
Страница 15. Урок 7,
Петерсон, Учебник, часть 3
Страница 71. Повторение,
Петерсон, Учебник, часть 3
4 класс
Страница 61,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 12,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 39,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 50. Тест 1. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 62. ПР 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 29,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 30,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 34,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 28,
Моро, Волкова, Рабочая тетрадь, часть 2
5 класс
Задание 534,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 553,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 766,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1086,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1160,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1724,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 141,
Мерзляк, Полонский, Якир, Учебник
Номер 756,
Мерзляк, Полонский, Якир, Учебник
Номер 767,
Мерзляк, Полонский, Якир, Учебник
Номер 1091,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 184,
Мерзляк, Полонский, Якир, Учебник
Номер 356,
Мерзляк, Полонский, Якир, Учебник
Номер 363,
Мерзляк, Полонский, Якир, Учебник
Номер 372,
Мерзляк, Полонский, Якир, Учебник
Номер 1091,
Мерзляк, Полонский, Якир, Учебник
Номер 1333,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Задание 604,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 999,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1144,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 47,
Мерзляк, Полонский, Якир, Учебник
Номер 330,
Мерзляк, Полонский, Якир, Учебник
Номер 351,
Мерзляк, Полонский, Якир, Учебник
Номер 422,
Мерзляк, Полонский, Якир, Учебник
Номер 530,
Мерзляк, Полонский, Якир, Учебник
Номер 580,
Мерзляк, Полонский, Якир, Учебник
Номер 607,
Мерзляк, Полонский, Якир, Учебник
Номер 608,
Мерзляк, Полонский, Якир, Учебник
Номер 856,
Мерзляк, Полонский, Якир, Учебник
Номер 871,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 46,
Мерзляк, Полонский, Якир, Учебник
Номер 47,
Мерзляк, Полонский, Якир, Учебник
Номер 138,
Мерзляк, Полонский, Якир, Учебник
Номер 139,
Мерзляк, Полонский, Якир, Учебник
Номер 212,
Мерзляк, Полонский, Якир, Учебник
Номер 254,
Мерзляк, Полонский, Якир, Учебник
Номер 302,
Мерзляк, Полонский, Якир, Учебник
Номер 304,
Мерзляк, Полонский, Якир, Учебник
Номер 305,
Мерзляк, Полонский, Якир, Учебник
Номер 306,
Мерзляк, Полонский, Якир, Учебник
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.