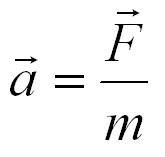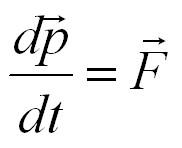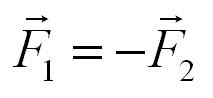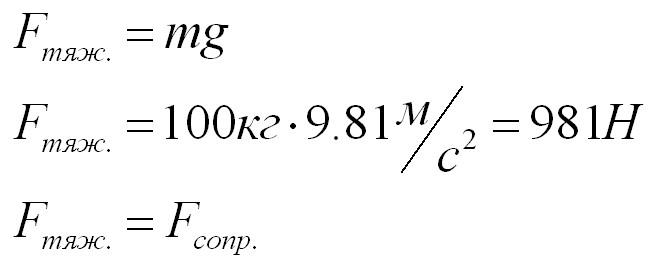В
этом случае дифференциальное уравнение
движения имеет вид:
.
(12)
Так
как
,
то получаем дифференциальное уравнение
первого порядка:
,
или
.
Интегрируя
это уравнение в соответствующих пределах,
имеем:
,
откуда:
.
(13)
Интегрируя
это уравнение первого порядка, получим
x
как функцию от t,
т.е. найдем искомый закон движения точки.
2.3.3. Сила зависит от положения точки
Задачи,
в которых равнодействующая всех сил,
приложенных к данной материальной
точке, есть функция координаты этой
точки. В этом случае дифференциальное
уравнение движения точки имеет вид:
,
(14)
или:
.
Используя
преобразование (10), получим:
,
или:
.
(15)
Интегрируя
это уравнение в соответствующих пределах,
имеем:

(16)
Из
этого равенства определяется скорость
V
как функция от расстояния х, т.е.
,
или, разделяя переменныеи проинтегрировав это уравнение первого
порядка, найдем зависимость междуx
и t.
Если
является линейной функцией отх,
то уравнение (3) будет линейным
дифференциальным уравнением второго
порядка с постоянными коэффициентами.
Поэтому для решения этого уравнения
можно воспользоваться теорией
интегрирования таких дифференциальных
уравнений, т.е. составить соответствующее
характеристическое уравнение, найти
его корни и затем – общее решение данного
дифференциального уравнения. Две
произвольные постоянные в общем решении
находятся по начальным условиям движения
точки.
2.3.4. Сила зависит от скорости точки
Такой
вид задач будет иметь место при движении
точки в сопротивляющейся среде.
В
этом случае дифференциальное уравнение
движения имеет вид:
,
(17)
или,
разделяя переменные:
.
Отсюда:

(18)
Выполняя
здесь интегрирование и разрешая
полученное уравнение относительно V,
находим скорость точки как функцию
времени, т.е.
.
Следовательно,
,
и:
.
(19)
Это
уравнение выражает искомый закон
движения точки. Если в задаче требуется
найти скорость V
как функцию расстояния х,
то левую часть уравнения (1) преобразуем:
.
Тогда
уравнение (17) принимает вид:
,
или,
разделяя переменные:
,
откуда:

(20)
3. Примеры решения задач
3.1. Примеры решения первой задачи динамики точки
Задача
1. Материальная
точка массой m
= 0,4 кг
совершает гармонические колебания по
горизонтальной оси Ох
по закону x
= 0,2 Sin
(/2t)
(x
выражено в метрах, t
– в секундах). Найти силу, действующую
на точку в функции оси x.
Решение.
Находим проекцию ускорения точки на
ось Ох:
(м/с2).
Далее
находим проекцию на ось действующей
силы:
(Н).
Но
по условию задачи
,
следовательно:(Н).
Рис.
1.
Так как проекция силы на
осьОх и
координата х движущейся точки
противоположны по знаку, то искомая
сила направлена вдоль оси Ох
к началу координат О
и пропорциональна расстоянию от
движущейся точки до начала координат.
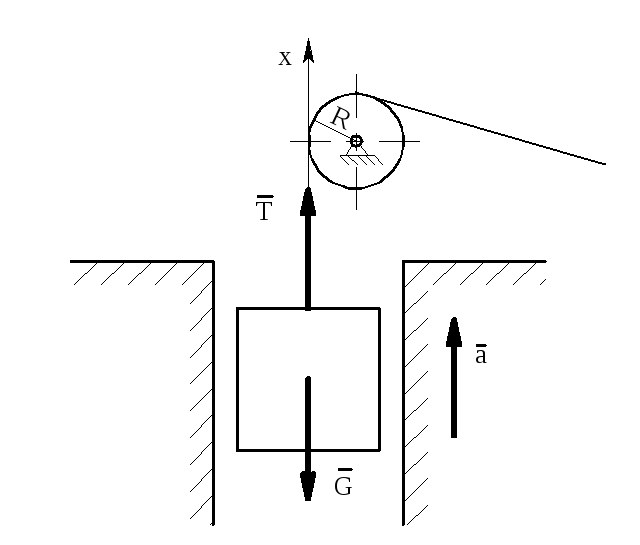
Задача
2. Лифт
весом G
поднимается с помощью каната. Канат
навернут на барабан радиуса R,
вращающийся вокруг неподвижной
горизонтальной оси по закону
.
Определить натяжение каната как функцию
высоты подъемаh.
Решение.
Так как лифт совершает поступательное
движение, при решении задачи будем
рассматривать его как материальную
точку. При повороте барабана на угол
лифт поднимается на высоту h
= R.
На него действует две силы: натяжение
каната Т
и вес лифта G.
Причем T
> G,
т.к. ускорение лифта направленно вверх.
Составим
дифференциальное уравнение движения
лифта в проекции на ось х:
,
или:
,
откуда:
Рис.
2.
.
Ускорение
лифта найдем из соотношения:
,
или:
.
Следовательно:
.
Задача
3. Материальная
точка массой m
= 0,5 кг
совершает движение согласно уравнениям:

Координаты
точки выражены в метрах, время – в
секундах. Определить величину и
направление силы, действующей на точку,
в момент времени t
= 1c.
Решение.
Находим
проекции ускорения точки на оси координат:

На
основании системы (2)
находим проекции равнодействующей на
оси координат:

По
системе уравнений (6) находим модуль и
направляющие косинусы равнодействующей
сил:

Задача
4. Материальная
точка массой m
= 2 кг описывает
криволинейную траекторию по закону
(S
выражено в метрах, время – в секундах).
В данный момент она занимает положение
М
и имеет скорость V
= 3 м/с,
радиус кривизны траектории в точке М
равен 6
м. Найти в
этот момент времени силу, действующую
на материальную точку.
Решение.
Находим скорость точки и проекции ее
ускорения на касательную и главную
нормаль траектории:

Согласно
условию задачи в данный момент времени
V
= 3 м/с.
Определяем время t:
.
Следовательно,
в этот момент:

Определяем
проекции равнодействующей на касательную
и главную нормали:
.
Модуль
равнодействующей:
Рис.
3.
.
Соседние файлы в папке Методички
- #
- #
- #
- #
Алгебра и начала математического анализа, 11 класс
Урок №19. Решение задач с помощью производной.
Перечень вопросов, рассматриваемых в теме
- механический смысл первой производной;
- механический смысл второй производных;
- скорость и ускорение.
Глоссарий по теме
Производная y’(x) функции y=f(x) – это мгновенная скорость изменения этой функции. В частности, если зависимость между пройденным путём S и временем t при прямолинейном неравномерном движении выражается уравнением S=f(t), то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени t нужно найти производную S’=f’(x) и подставить в неё соответствующее значение t, то есть v(t)=S’(t).
Производная от данной функции называется первой производной или производной первого порядка. Но производная функции также является функцией, и если она дифференцируема, то от неё, в свою очередь, можно найти производную.
Производная от производной называется второй производной или производной второго порядка и обозначается f
Производная от второй производной называется производной третьего порядка и обозначается 
Если первая производная функции – это мгновенная скорость изменения любого процесса, заданного функцией, то вторая производная – это скорость изменения скорости, то есть ускорение, то есть
Первая производная – это скорость изменения процесса, вторая производная – ускорение. (v= S’; a=v’)
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Давайте вспомним механический смысл производной:
Производная y’(x) функции y=f(x) – это мгновенная скорость изменения этой функции. В частности, если зависимость между пройденным путём S и временем t при прямолинейном неравномерном движении выражается уравнением S=f(t), то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени t нужно найти производную S’=f’(x) и подставить в неё соответствующее значение t, то есть v(t)=S'(t).
Пример 1. Точка движется прямолинейно по закону 
Решение:
скорость прямолинейного движения равна производной пути по времени, то есть 
Подставив в уравнение скорости t=3 с, получим v(3)=32+4∙3-1= 20 (м/с).
Ответ: 20 м/c.
Пример 2. Маховик, задерживаемый тормозом, поворачивается за t с на угол

а) угловую скорость вращения маховика в момент t = 6 с;
б) в какой момент времени маховик остановится?
Решение: а) Угловая скорость вращения маховика определяется по формуле ω=φ’. Тогда ω=(4t-0,2t2)=4-0,4t.
Подставляя t = 6 с, получим ω=4-0,4∙6=1,6 (рад/с).
б) В тот момент, когда маховик остановится, его скорость будет равна нулю (ω=0) . Поэтому 4-0,4t=0.. Отсюда t=10 c.
Ответ: угловая скорость маховика равна (рад/с); t=10 c.
Пример 3. Тело массой 6 кг движется прямолинейно по закону S=3t2+2t-5. Найти кинетическую энергию тела 
Решение: найдём скорость движения тела в любой момент времени t.
v= S’=(3t2+2t-5)’=6t+2
Вычислим скорость тела в момент времени t=3. v(3)=6∙3+2=20 (м/с)..
Определим кинетическую энергию тела в момент времени t=3.

Ответ: Е=1200 Дж
Производная второго порядка. Производная n-го порядка.
Производная от данной функции называется первой производной или производной первого порядка. Но производная функции также является функцией, и если она дифференцируема, то от неё, в свою очередь, можно найти производную.
Производная от производной называется второй производной или производной второго порядка и обозначается 
Производная от второй производной называется производной третьего порядка и обозначается y»’ или f»'(x) Производную n-го порядка обозначают f(n) (x) или y(n).
Примеры. Найдем производные четвёртого порядка для заданных функций:
1) f(x)= sin 2x
f'(x)=cos 2x∙(2x)’= 2cos 2x
f
f»'(x)= -4 cos 2x∙(2x)= -8 cos 2x
f(4)(x)= 8 sin2x∙(2x)’= 16 sin 2x
2) f(x)=23x
f’(x)=3∙ 23x ∙ln2
f
f»'(x)= 27∙ 23x ∙ln32
f(4)(x)= 81∙ 23x ∙ln42
Механический смысл второй производной.
Если первая производная функции – это мгновенная скорость изменения любого процесса, заданного функцией, то вторая производная – это скорость изменения скорости, то есть ускорение, то есть
Итак, первая производная – это скорость изменения процесса, вторая производная – ускорение. (v= S’; a=v’)
Пример 4. Точка движется прямолинейно по закону S(t)= 3t2-3t+8. Найти скорость и ускорение точки в момент t=4 c.
Решение:
найдём скорость точки в любой момент времени t.
v=S’=(3t2-3t+8)’=6t-3.
Вычислим скорость в момент времени t=4 c.
v(4)=6∙4-3=21(м/с)
Найдём ускорение точки в любой момент времени t.
a= v’= (6t-3)’=6 и a(4)= 6 (м/с2) , то есть ускорение в этом случае является величиной постоянной.
Ответ: v=21(м/с); a= v’= 6 (м/с2).
Пример 5. Тело массой 3 кг движется прямолинейно по закону S(t)=t3-3t2+5. Найти силу, действующую на тело в момент времени t=4 c.
Решение: сила, действующая на тело, находится по формуле F=ma.
Найдём скорость движения точки в любой момент времени t.
v=S’=(t3-3t2+5)’=3t2-6t.
Тогда v(4)=3∙42-6∙4=24 (м/с).
Найдём ускорение: a(t)=v’=(3t2-6t)’=6t-6.
Тогда a(4)= 6∙4-6= 18 (м/с2).
F=ma=3∙18= 54 Н
Ответ: F= 54 Н
Разбор решения заданий тренировочного модуля
№ 1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Напишите производную третьего порядка для функции:
f(x)= 3cos4x-5x3+3x2-8
_____________________
Решим данную задачу:
f’’’(x)=( 3cos4x-5x3+3x2-8)’’’=(((3cos4x-5x3+3x2-8)’)’)’=((-12sin4x-15x2+6x)’)’=(-48cos4x-30x)’=192sin4x-30.
Ответ: 192sin4x-30
№ 2. Тип задания: выделение цветом
Точка движется прямолинейно по закону S(t)= 3t2+2t-7. Найти скорость и ускорение точки в момент t=6 c.
- v=38 м/с; a=6 м/с2
- v=38 м/с; a=5 м/с2
- v=32 м/с; a=6 м/с2
- v=32 м/с; a=5 м/с2
Решим данную задачу:
Воспользуемся механическим смыслом второй производной:
v= S’(t)=( 3t2+2t-7)’=6t+2.
Вычислим скорость в момент времени t=6 c.
v(6)=6∙6+2=38 (м/с)
Найдём ускорение точки в любой момент времени t.
a= v’= (6t+2)’=6 и a(6)= 6 (м/с2) , то есть ускорение в этом случае является величиной постоянной.
Ответ: v=38(м/с); a= v’= 6 (м/с2).
Верный ответ:
- v=38 м/с; a=6 м/с2
- v=38 м/с; a=5 м/с2
- v=32 м/с; a=6 м/с2
- v=32 м/с; a=5 м/с2
Мы уже говорили об основах классической механики. Настала пора поговорить о них подробнее и затронуть в обсуждении чуть больше, чем просто основу. В этой статье мы подробно разберем основные законы классической механики. Как вы уже догадались, речь пойдет о законах Ньютона.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Основные законы классической механики Исаак Ньютон (1642-1727) собрал и опубликовал в 1687 году. Три знаменитых закона были включены в труд, который назывался «Математические начала натуральной философии».
Был долго этот мир глубокой тьмой окутан
Да будет свет, и тут явился Ньютон.
(Эпиграмма 18-го века)
Но сатана недолго ждал реванша —
Пришел Эйнштейн, и стало все как раньше.
(Эпиграмма 20-го века)
Что стало, когда пришел Эйнштейн, читайте в отдельном материале про релятивистскую динамику. А мы пока приведем формулировки и примеры решения задач на каждый закон Ньютона.
Первый закон Ньютона
Первый закон Ньютона гласит:
Существуют такие системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно, если на них не действуют никакие силы или действие других сил скомпенсировано.
Проще говоря, суть первого закона Ньютона можно сформулировать так: если мы на абсолютно ровной дороге толкнем тележку и представим, что можно пренебречь силами трения колес и сопротивления воздуха, то она будет катиться с одинаковой скоростью бесконечно долго.
Инерция – это способность тела сохранять скорость как по направлению, так и по величине, при отсутствии воздействий на тело. Первый закон Ньютона еще называют законом инерции.
До Ньютона закон инерции был сформулирован в менее четкой форме Галилео Галилеем. Инерцию ученый называл «неистребимо запечатленным движением». Закон инерции Галилея гласит: при отсутствии внешних сил тело либо покоится, либо движется равномерно. Огромная заслуга Ньютона в том, что он сумел объединить принцип относительности Галилея, собственные труды и работы других ученых в своих «Математических началах натуральной философии».
Понятно, что таких систем, где тележку толкнули, а она покатилась без действия внешних сил, на самом деле не бывает. На тела всегда действуют силы, причем скомпенсировать действие этих сил полностью практически невозможно.
Например, все на Земле находится в постоянном поле силы тяжести. Когда мы передвигаемся (не важно, ходим пешком, ездим на машине или велосипеде), нам нужно преодолевать множество сил: силу трения качения и силу трения скольжения, силу тяжести, силу Кориолиса.
Второй закон Ньютона
Помните пример про тележку? В этот момент мы приложили к ней силу! Интуитивно понятно, что тележка покатится и вскоре остановится. Это значит, ее скорость изменится.
В реальном мире скорость тела чаще всего изменяется, а не остается постоянной. Другими словами, тело движется с ускорением. Если скорость нарастает или убывает равномерно, то говорят, что движение равноускоренное.
Если рояль падает с крыши дома вниз, то он движется равноускоренно под действием постоянного ускорения свободного падения g. Причем любой дугой предмет, выброшенный из окна на нашей планете, будет двигаться с тем же ускорением свободного падения.
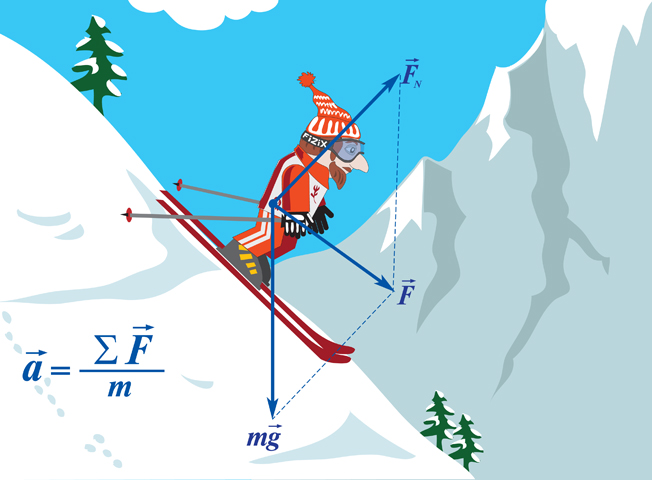
Второй закон Ньютона устанавливает связь между массой, ускорением и силой, действующей на тело. Приведем формулировку второго закона Ньютона:
Ускорение тела (материальной точки) в инерциальной системе отсчета прямо пропорционально приложенной к нему силе и обратно пропорционально массе.
Если на тело действует сразу несколько сил, то в данную формулу подставляется равнодействующая всех сил, то есть их векторная сумма.
В такой формулировке второй закон Ньютона применим только для движения со скоростью, много меньшей, чем скорость света.
Существует более универсальная формулировка данного закона, так называемый дифференциальный вид.
В любой бесконечно малый промежуток времени dt сила, действующая на тело, равна производной импульса тела по времени.
Третий закон Ньютона
В чем состоит третий закон Ньютона? Этот закон описывает взаимодействие тел.
3 закон Ньютона говорит нам о том, что на любое действие найдется противодействие. Причем, в прямом смысле:
Два тела воздействуют друг на друга с силами, противоположными по направлению, но равными по модулю.
Формула, выражающая третий закон Ньютона:
Другими словами, третий закон Ньютона — это закон действия и противодействия.
Пример задачи на законы Ньютона
Вот типичная задачка на применение законов Ньютона. В ее решении используются первый и второй законы Ньютона.
Десантник раскрыл парашют и опускается вниз с постоянной скоростью. Какова сила сопротивления воздуха? Масса десантника – 100 килограмм.
Решение:
Движение парашютиста – равномерное и прямолинейное, поэтому, по первому закону Ньютона, действие сил на него скомпенсировано.
На десантника действуют сила тяжести и сила сопротивления воздуха. Силы направлены в противоположные стороны.
По второму закону Ньютона, сила тяжести равна ускорению свободного падения, умноженному на массу десантника.
Ответ: Сила сопротивления воздуха равна силе тяжести по модулю и противоположна направлена.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
А вот еще одна физическая задачка на понимание действия третьего закона Ньютона.
Комар ударяется о лобовое стекло автомобиля. Сравните силы, действующие на автомобиль и комара.
Решение:
По третьему закону Ньютона, силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению. Сила, с которой комар действует на автомобиль, равна силе, с которой автомобиль действует на комара.
Другое дело, что действие этих сил на тела сильно отличаются вследствие различия масс и ускорений.
Исаак Ньютон: мифы и факты из жизни
На момент публикации своего основного труда Ньютону было 45 лет. За свою долгую жизнь ученый внес огромный вклад в науку, заложив фундамент современной физики и определив ее развитие на годы вперед.
Он занимался не только механикой, но и оптикой, химией и другими науками, неплохо рисовал и писал стихи. Неудивительно, что личность Ньютона окружена множеством легенд.
Ниже приведены некоторые факты и мифы из жизни И. Ньютона. Сразу уточним, что миф – это не достоверная информация. Однако мы допускаем, что мифы и легенды не появляются сами по себе и что-то из перечисленного вполне может оказаться правдой.
- Факт. Исаак Ньютон был очень скромным и застенчивым человеком. Он увековечил себя благодаря своим открытиям, однако сам никогда не стремился к славе и даже пытался ее избежать.
- Миф. Существует легенда, согласно которой Ньютона осенило, когда на наго в саду упало яблоко. Это было время чумной эпидемии (1665-1667), и ученый был вынужден покинуть Кембридж, где постоянно трудился. Точно неизвестно, действительно ли падение яблока было таким роковым для науки событием, так как первые упоминания об этом появляются только в биографиях ученого уже после его смерти, а данные разных биографов расходятся.
- Факт. Ньютон учился, а потом много работал в Кембридже. По долгу службы ему нужно было несколько часов в неделю вести занятия у студентов. Несмотря на признанные заслуги ученого, занятия Ньютона посещались плохо. Бывало, что на его лекции вообще никто не приходил. Скорее всего, это связано с тем, что ученый был полностью поглощен своими собственными исследованиями.
- Миф. В 1689 году Ньютон был избран членом Кембриджского парламента. Согласно легенде, более чем за год заседания в парламенте вечно поглощенный своими мыслями ученый взял слово для выступления всего один раз. Он попросил закрыть окно, так как был сквозняк.
- Факт. Неизвестно, как бы сложилась судьба ученого и всей современной науки, если бы он послушался матери и начал заниматься хозяйством на семейной ферме. Только благодаря уговорам учителей и своего дяди юный Исаак отправился учиться дальше вместо того, чтобы сажать свеклу, разбрасывать по полям навоз и по вечерам выпивать в местных пабах.
Дорогие друзья, помните — любую задачу можно решить! Если у вас возникли проблемы с решением задачи по физике, посмотрите на основные физические формулы. Возможно, ответ перед глазами, и его нужно просто рассмотреть. Ну а если времени на самостоятельные занятия совершенно нет, специализированный студенческий сервис всегда к вашим услугам!
В самом конце предлагаем посмотреть видеоурок на тему «Законы Ньютона».
Определение
Момент силы — это крутящий или вращательный момент, который является векторной величиной.
Чтобы определить, чему равен момент силы, нужно получить произведение вектора силы и радиус-вектора, который проводится к точке приложения силы от оси вращения. Поэтому величину можно назвать характеристикой вращательного воздействия силы на твердое тело.
Термины “крутящий” и “вращающий” моменты в данном случае не являются тождественными. Разница между ними состоит в том, что “вращающий” момент воспринимается как внешнее усилие, которое прикладывают к объекту. Термин “крутящий” же рассматривается как внутреннее усилие, которое появляется при приложении конкретных нагрузок (что делает определение схожим с используемым при изучении сопротивления материалов).
Понятие «момент силы»
Физики воспринимают этот термин в качестве так называемой “вращающей силы”. В соответствии с системой СИ, измеряется данная величина в ньютон-метрах. Иногда в литературе можно также встретить понятие “момент пары сил” (такое определение, например, появляется в исследованиях Архимеда над рычагами).
При использовании простых примеров (например, при приложении силы к рычагу в перпендикулярном отношении к нему) величина рассчитывается как произведение расстояния до оси вращения рычага и непосредственно силы, которая на него воздействует.
Пример: На рычаг оказывает воздействие силы в 3 ньютона, которую прикладывают на расстоянии 2 м от оси вращения рычага. В результате момент силы будет равнозначен силе в 1 ньютон, прикладываемой на расстоянии 6 м по отношению к рычагу.
Как определить, чему равен момент силы
Формула
Точно определить момент действия силы частицы удастся, применив следующую векторную формулу:
[vec{mathrm{M}}=vec{mathrm{r}} vec{mathrm{F}}]
В данном случае [vec{mathrm{r}}] — это радиус вектора частицы, а
[vec{mathrm{F}}] — сила, воздействующая на эту частицу.
Важно помнить, что в физике энергия воспринимается как скалярная величина. В то же время момент силы считается (псевдо)векторной величиной. Поэтому совпадение размерностей указанных величин никогда не бывает случайным. Например, момент силы в 1 Н/м, приложенный через целый оборот, при выполнении механической работы сообщает энергию в 2 Дж. В математическом отображении эта формула момента силы будет выглядеть так:
[mathbf{E}=mathbf{M} boldsymbol{theta}], где:
- [mathbf{E}] — это энергия;
- [mathbf{M}] — это вращающийся момент;
- [boldsymbol{theta}] — это угол в радианах.
В современных условиях момент силы измеряется при помощи особых датчиков нагрузки, которые могут быть трех типов:
- оптического;
- тензометрического;
- индуктивного.
Применение специальной техники позволяет определить величину предельно точно и избавляет ученых от необходимости производить лишние расчеты.
Нет времени решать самому?
Наши эксперты помогут!
Момент силы: формулы
Наиболее интересным в физике считается определение момента силы в поле. Для этого используется следующая формула:
[vec{M}=vec{M_{1}} vec{F}]
Где:
[vec{M_{1}}]- это момент рычага;
[vec{F}]- это величина силы, действующей на тело.
У такой формулы момента силы в физике будет один недостаток. С ее помощью не удастся определить, в каком направлении направлен момент силы. Известной станет только его величина. Если сила окажется перпендикулярной вектору, тогда момент рычага окажется равен расстоянию от центра до точки, в которой была приложена сила. В таком случае момент силы достигнет максимального значения:
[vec{T}=vec{r} quad vec{F}]
Если сила совершает какое-либо действие на определенном расстоянии, она параллельно выполняет механическую работу относительно того же объекта. В таком случае в физической практике считается, что и момент силы выполняет работу (при совершении действия через угловое расстояние).
[mathrm{P}=mathrm{M} {omega}]
Международная система измерений предлагает определять мощность в Ваттах, при этом момент силы измеряется в радианах в секунду. Для определения величину угловой скорости используется единица “радианы в секунду”).
Как определяется момент действия нескольких сил
Если на тело действуют одновременно две равные по величине и противоположно направленные силы (не лежащие на одной и той же прямой), оно находится в состоянии равновесия. Такая ситуация связана с тем, что результирующий момент данных сил по отношению к любой из осей не обладает нулевым значением. Ведь обе силы направлены в одну сторону момента и являются парой сил.
Если тело закреплено на оси, оно будет вращаться под влиянием пары сил. Когда же пара сил прилагается по отношению к свободному телу, последнее начнет крутиться вокруг той оси, которая проходит через центр тяжести.
В соответствии с правилом моментов сил в физике, момент пары сил считается одинаковым по отношению к любой оси, перпендикулярной плоскости этой пары. При этом суммарный момент пары M всегда определяется как произведение плеча пары (то есть расстояния l между силами) и одной из этих сил F. Данный расчет производится независимо от типов отрезков, на которые разделяется положение оси.
[mathrm{M}=mathrm{FL}_{1}+mathrm{FL}-2=mathrm{FL}_{1}+mathrm{L}_{2}=mathrm{FL}]
В случае, если равнодействующая момент нескольких сил равняется нулю, он будет одинаковым по отношению ко всем параллельным друг другу осям. Именно поэтому воздействие всех сил на тело можно заменить действием только одной пары сил, имеющих точно такой же момент.
Формула равнодействующей всех сил в физике
Формула равнодействующей всех сил
Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($overline{F}$) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $overline{F}$ — это векторная величина, то есть она обладает модулем (величиной) и направлением.
Определение и формула равнодействующей всех сил
В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:
[overline{F}=moverline{a} left(1right),]
где $m$ — масса тела, на которое действует сила $overline{F}$; $overline{a}$ — ускорение, которое сила $overline{F}$ сообщает рассматриваемому телу. Смысл второго закона Ньютона заключается в том, что силы, которые действуют на тело, определяют изменение скорости тела, а не просто его скорость. Следует знать, что второй закон Ньютона выполняется для инерциальных систем отсчета.
На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Силы, которые оказывают действие на тело, следует суммировать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline{F}$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
[overline{F}={overline{F}}_1+{overline{F}}_2+dots +{overline{F}}_N=sumlimits^N_{i=1}{{overline{F}}_i} left(2right).]
Формула (2) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена как вектор ускорения тела.
Основной закон динамики поступательного движения при наличии нескольких сил
Если на тело действуют несколько сил, тогда второй закон Ньютона записывают как:
[sumlimits^N_{i=1}{{overline{F}}_i}=moverline{a}left(3right).]
$overline{F}=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета скорость движения тела постоянна.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач на равнодействующую сил
Пример 1
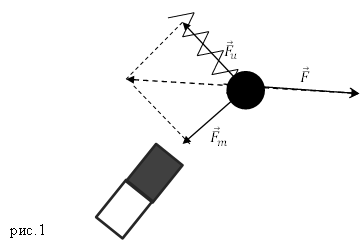
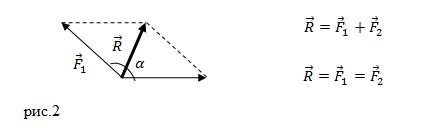
Задание. На материальную точку действуют две силы, направленные под углом $alpha =60{}^circ $ друг к другу. Чему равна равнодействующая этих сил, если $F_1=20 $Н; $F_2=10 $Н?
Решение. Сделаем рисунок.
Силы на рис. 1 складываем по правилу параллелограмма. Длину равнодействующей силы $overline{F}$ можно найти, используя теорему косинусов:
[F=sqrt{F^2_1+F^2_2+2F_1F_2{cos alpha }} left(1.1right).]
Вычислим модуль равнодействующей силы:
[F=sqrt{{20}^2+{10}^2+2cdot 20cdot 10{cos (60{}^circ ) }}approx 26,5 left(Нright).]
Ответ. $F=26,5$ Н
Пример 2
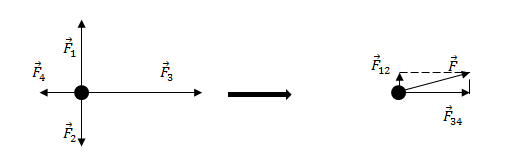
Задание. На материальную точку действуют силы (рис.2). Какова равнодействующая этих сил?
Решение. Равнодействующая сил, приложенных к точке (рис.2) равна:
[overline{F}={overline{F}}_1+{overline{F}}_2+{overline{F}}_3+{overline{F}}_4left(2.1right).]
Найдем равнодействующую сил ${overline{F}}_1$ и ${overline{F}}_2$. Эти силы направлены вдоль одной прямой, но в противоположные стороны, следовательно:
[F_{12}=F_1-F_2=17-11=6 left(Hright).]
Так как $F_1>F_2$, то сила ${overline{F}}_{12}$ направлена в туже сторону, что и сила ${overline{F}}_1$.
Найдем равнодействующую сил ${overline{F}}_3$ и ${overline{F}}_4$. Данные силы направлены вдоль одной вертикальной прямой (рис.1), значит:
[F_{34}=F_3-F_4=18-10=8 left(Нright).]
Направление силы ${overline{F}}_{34}$ совпадает с направлением вектора ${overline{F}}_3$, так как ${overline{F}}_3>{overline{F}}_4$.
Равнодействующую, которая действует на материальную точку, найдем как:
[overline{F}={overline{F}}_{12}+{overline{F}}_{34}left(2.2right).]
Силы ${overline{F}}_{12}$ и ${overline{F}}_{34}$ взаимно перпендикулярны. Найдем длину вектора $overline{F}$ по теореме Пифагора:
[F=sqrt{F^2_{12}+F^2_{34}}=sqrt{6^2+8^2}=10 left(Нright).]
Ответ. $F$=10 Н
Читать дальше: формула равнодействующей силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!