Давление столба жидкости
В каждой жидкости существует давление, обусловленное ее собственным весом. Так, например, давление на основание столба воды высотой 10м составляет около 105Па.
Давление столба жидкости
Если
| h | высота столба жидкости, | Метр |
|---|---|---|
| p | давление в жидкости на глубине h, | Паскаль |
| g | ускорение свободного падения, | 9.81 м/c2 |
| ρ | плотность жидкости, | кг/м3 |
то
давление в жидкости равно ее весу, деленному на площадь,
[
p = frac{G}{S} = frac{mg}{S}
]
используя формулу — масса через плотность и объем, имеем
[
p = frac{ρVg}{S}
]
Так как объем есть произведение высоты на площадь V = Sh, то
[
p = ρgh
]
Вычислить, найти давление столба жидкости
Давление столба жидкости |
стр. 501 |
|---|
Давление жидкостей и газов. Закон Паскаля
- Особенности давления жидкостей и газов
- Закон Паскаля
- Давление столба жидкости
- Давление столба газа
- Задачи
п.1. Особенности давления жидкостей и газов
Давление жидкостей и газов отличается от давления твердых тел. Причина – в особенностях поведения частиц вещества в разных агрегатных состояниях (см. §16 данного справочника).
В отличие от твердых тел, молекулы жидкостей и газов подвижны.
Жидкость принимает форму сосуда, который предохраняет её от растекания. Поэтому жидкость в сосуде оказывает давление не только на дно, но и на стенки. Верхние слои жидкости давят на нижние, и давление растет с глубиной (с увеличением столба жидкости).
Газ заполняет весь предоставленный ему объем. В закрытом сосуде хаотически движущиеся молекулы газа будут сталкиваться с дном, стенками и крышкой сосуда. Таким образом, газ будет оказывать давление во все стороны: вниз, по бокам и даже вверх.
Давление газа также растет с увеличением высоты столба. Однако за счет малой плотности газов этот рост менее заметен по сравнению с жидкостями. В небольшом сосуде давление газа можно считать постоянным во всем объеме сосуда.
п.2. Закон Паскаля
При давлении на жидкость или газ в определенной области происходит сжатие; расстояние между молекулами становится меньше, начинают сильнее действовать силы отталкивания. В результате молекулы перемещаются из области сжатия с большим давлением в области с меньшим давлением. Это происходит достаточно быстро; например, у кислорода при 0°С средняя скорость молекул 425 м/с, у паров воды — 570 м/с. Поэтому в течение небольшого времени давление в сосуде выравнивается.
Закон Паскаля
Жидкости и газы передают давление по всем направлениям одинаково.
Для подтверждения закона Паскаля можно провести следующие эксперименты.
п.3. Давление столба жидкости
Как было замечено выше, давление жидкостей заметно увеличивается с глубиной. Это объясняется тем, что верхние слои давят на нижние.
Найдем давление столба жидкости высотой (h)
Согласно закону Паскаля, давление в жидкости передается во всех направлениях одинаково. Поэтому на данной глубине (h) в каждой точке уровня давление будет постоянно.
 |
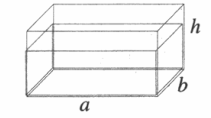
Рассмотрим сосуд в форме прямоугольного параллелепипеда. Пусть в его основании – прямоугольник с длиной (a) и шириной (b). Нальем в этот сосуд воду до отметки высотой (h). Нас интересует давление воды на дно сосуда. Сила давления на дно направлена вертикально вниз и равна силе тяжести: $$ F=mg=rho Vg $$ Объем воды в сосуде: $$ V=abh $$ |
Получаем: $$ F=rhocdot abhcdot g $$ Давление на дно сосуда равно отношению силы давления к площади дна: $$ p=frac FS=frac{rhocdot abh cdot g}{ab}=rho gh $$
Давление столба жидкости
На глубине (h) давление жидкости равно $$ p=rho gh $$
Давление не зависит от площади дна, и, следовательно, не зависит от его формы.
Полученное выражение будет справедливо для вертикального столба жидкости высотой (h) с любым сечением (квадратным, круглым, треугольным, совершенно фантазийным).
Это интересно
 |
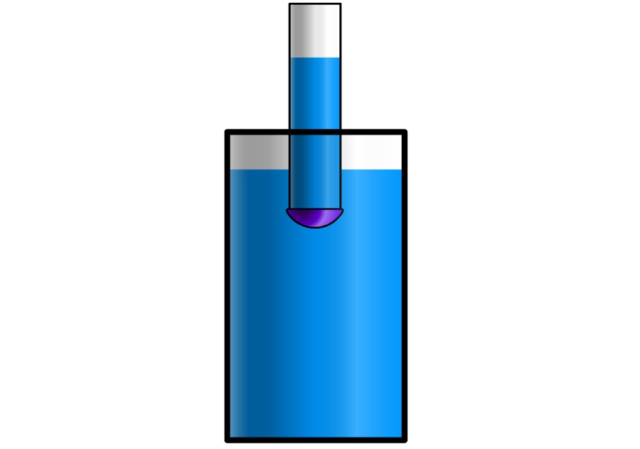
Давление не зависит ни от формы, ни от размеров сечения столба жидкости, зато резко увеличивается с высотой. Это свойство использовал Паскаль, продемонстрировав своим современникам забавный эксперимент. Он взял прочную дубовую бочку, наполнил ее доверху водой, плотно закрыл и вставил очень узкую, но очень длинную трубку (около 4 м). Затем он поднялся на второй этаж и вылил в трубку кружку воды. Бочка тут же …лопнула. Действительно, ведь давление в бочке увеличилось на (p=1000cdot 10cdot 4=40 text{кПа}): её будто «придавило» четырьмя тоннами воды, хотя понадобилась всего лишь кружка. Тем не менее, результат этого фокуса всегда кажется неожиданным. |
п.4. Давление столба газа
Газы, как и жидкости, также имеют некоторую плотность. Поэтому, рассматривая давление столба газа по аналогии с жидкостью, можно прийти к тем же результатам.
Давление столба газа
Давление столба газа высотой (h) равно $$ p=rho gh $$
Понимание того, что газ также оказывает разное давление в разных слоях, возникло не сразу. Это объясняется небольшой плотностью газов по сравнению с жидкостями.
 |
Для иллюстрации рассчитаем давление столба воды и столба воздуха высотой (h=1 text{м}). Плотность воды (rho_text{воды}=1000 text{кг/м}^3), плотность воздуха при 20°C (rho_text{возд}=1,2 text{кг/м}^3). Получаем: begin{gather*} p_text{вода}= rho_text{вода}ghapprox 1000cdot 10cdot 1=10000 (text{Па})\[7pt] p_text{возд}= rho_text{возд}ghapprox 1,2cdot 10cdot 1=12 (text{Па}) end{gather*} Из-за разности в плотности, давление отличается почти в 1000 раз, ведь масса кубометра воды – 1 тонна, а масса кубометра воздуха – всего 1,2 кг. |
Поэтому при изучении процессов в небольших сосудах разность в давлении газа в верхних и нижних слоях практически не заметна.
С другой стороны, если рассматривать значительные по высоте «столбы» газов, например, атмосферу планеты, давление становится существенной величиной. Так, на поверхности Земли атмосферное давление составляет около 100 000 (Па). Подробней этот вопрос будет рассмотрен в §31 данного справочника.
В итоге, для открытого сосуда с жидкостью, где на поверхность дополнительно оказывает давление атмосфера, давление жидкости на глубине h равно сумме: $$ p=p_text{атм}+rho gh $$
п.5. Задачи
Задача 1. Пятый этаж расположен выше первого на 15 м.
На каком этаже давление в трубах водопровода больше и на сколько?
Дано:
(h=15 text{м})
(p=1000 text{кг/м}^3)
(gapprox 10 text{м/с}^2)
__________________
(Delta p-?)
Давление в водопроводе на первом этаже $$ p_1=p_text{внеш}+rho gh, $$ где (p_text{внеш}) – давление, связанное с действием внешних сил (атмосфера, водонапорная башня, насос и т.п.), второе слагаемое – давление вертикального столба жидкости в трубе в доме.
Давление в водопроводе на пятом этаже (p_5=p_text{внеш}).
Давление больше на первом этаже.
Разность давлений $$ Delta p=p_1-p_5= p_text{внеш}+rho gh -p_text{внеш}=rho gh $$ Получаем: $$ Delta p=1000cdot 10cdot 15=150 000 (text{Па})=150 (text{кПа}) $$ Ответ: на первом; на 150 кПа
Задача 2. Давление в трубах водопровода (4cdot 10^5 text{Па}). На какую максимальную высоту можно достать струей воды в случае пожара, если подключить оборудование к пожарному гидранту на поверхности земли? Атмосферное давление примите равным (1cdot 10^5 text{Па})
Дано:
(p=4cdot 10^5 text{Па})
(p_text{атм}=1cdot 10^5 text{Па})
(p=1000 text{кг/м}^3)
(gapprox 10 text{м/с}^2)
__________________
(h-?)
При подключении на струю воды, направленную вертикально вверх, будет действовать снизу давление водопровода, сверху атмосферное давление.
Под действием разности этих давлений вода может подняться на высоту $$ h=frac{p-p_text{атм}}{rho g} $$ Получаем: $$ h=frac{(4-1)cdot 10^5}{1000cdot 10}=30 (text{м}) $$ Ответ: 30 м
Задача 3. Рассчитайте, какую силу давления воды должен выдерживать жесткий водолазный скафандр, предназначенный для глубоководных работ на глубине до 365 м, если общая поверхность скафандра составляет 2,5 м2?
(Плотность морской воды 1010 кг/м3, g=9,8 м/с2). Ответ округлите до меганьютонов.
Дано:
(rho=1010 text{кг/м}^3)
(g=9,8 text{м/с}^2)
(h=365 text{м})
(S=2,5 text{м}^2)
__________________
(F-?)
Давление воды на максимальной глубине $$ p=rho gh $$ Сила давления $$ F=pS=rho ghS $$ Получаем: $$ F=1010cdot 9,8cdot 365cdot 2,5approx 9,03cdot 10^6 (text{Н})=9 (text{МН}) $$ Ответ: ≈9 МН
Задача 4*. В цилиндрический сосуд налиты ртуть и вода. Общая высота столба жидкости 20 см. Чему равно давление, создаваемое жидкостями на дно сосуда, если:
а) объемы жидкостей одинаковы; б массы жидкостей одинаковы?
Дано:
(rho_1=1000 text{кг/м}^3)
(rho_2=13600 text{кг/м}^3)
(H=20 text{см}=0,2 text{м})
(gapprox 10 text{м/с}^2)
(text{а)} V_1=V_2; text{б)} m_1=m_2)
__________________
(p-?)
Ответ: а) 14,6 кПа; б) 3,7 кПа
Закон Паскаля: давление, производимое на жидкость или газ, передается жидкостью или газом во все стороны одинаково.
Такая особенность передача давления жидкостями и газами связана с подвижностью молекул в жидком и газообразном состояниях.
Давление столба жидкости определяется формулой:
p = ρжgh
p — давление столба жидкости (Па), ρж — плотность жидкости (кг/м3), g — ускорение свободного падения (≈10 м/с2), h — высота столба жидкости, или ее глубина (м).
Важно! Высоту h нужно определять от поверхности жидкости.
Сила давления жидкости
Сила давления жидкости на дно сосуда — это произведение давления, оказываемого жидкостью на дно сосуда, на площадь этого дна:
F = pS = ρжghab
Сила давления жидкости на боковую грань сосуда — это произведение половины давления, оказываемого жидкостью на дно сосуда, на площадь грани:
F=ρжgh2hb
Подсказки к задачам:
- Плотность пресной воды равна 1000 кг/м3.
- Плотность соленой воды равна 1030 кг/м3.
Пример №1. Чему равно давление, созданное водой, на глубине 2 м?
Давление в жидкостях определяется формулой:
p = ρжgh.
Давление, созданное пресной водой, равно:
p = 1000∙10∙2 = 20000 (Па) = 20 (кПа)
Давление, созданное соленой водой, равно:
p = 1030∙10∙2 = 20600 (Па) = 20,6 (кПа)
Гидростатический парадокс
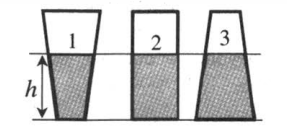
Из закона Паскаля следует, что давление на дно сосуда определяется только плотностью жидкости и высотой ее столба. Поэтому, если в разные сосуды налить одинаковую жидкость одинаковой высоты, давление, оказываемое ею на дно каждого из сосудов, будет одинаковым.
p1 = p2 = p3
Сила давления при этом будет разная, так как она прямо пропорционально зависит от площади дна. Так как площадь дна первого сосуда минимальна, а третьего максимальна, силы давления, оказываемые жидкостью на дно сосудов, будут такими:
F1 < F2 < F3
Пример №2. На рисунке изображены три сосуда с разными жидкостями. Площади дна сосудов равны. В первом сосуде находится вода (ρ1 = 1 г/см3), во втором — керосин (ρ2 = 0,8 г/см3), в третьем — спирт (ρ3 = 0,8 г/см3). В каком сосуде оказывается максимальное давление на дно?
Давление зависит только от плотности жидкости и от ее столба: площадь сосудов никакой роли не играет. Так как столбы жидкостей во всех сосудах одинаково, остается сравнивать плотности. Плотность воды больше плотности керосина и плотности спирта. Поэтому в сосуде 1 давление на дно сосуда будет максимальным.
Задание EF18645
В сосуд высотой 20 см налита вода, уровень которой ниже края сосуда на 2 см. Чему равна сила давления воды на дно сосуда, если площадь дна 0,01м2? Атмосферное давление не учитывать.
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Записать формулу для вычисления силы давления.
- Выполнить решение задачи в общем виде.
- Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
- Высота сосуда H = 20 см.
- Разница между высотой сосуда и уровнем налитой в него воды: b = 2 см.
- Площадь дна сосуда: S = 0,01 м2.
20 см = 0,2 м
2 см = 0,02 м
Сила давления равна произведению давления на площадь, на которую это давление оказывается:
F = pS
Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. А высота столба воды в данном случае равна разности высоту стакана и разнице между высотой сосуда и уровнем воды. Поэтому:
F = pS = ρжghS = ρжg(H – b)S = 1000∙10∙(0,2 – 0,02)∙0,01 = 18 (Н)
Ответ: 18
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22709
Какова сила давления керосина, заполняющего цистерну, на заплату в её стене, находящуюся на глубине 2 м? Площадь заплаты 10 см2. Атмосферное давление не учитывать.
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Записать формулу для вычисления силы давления.
- Выполнить решение задачи в общем виде.
- Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
- Глубина заплаты в цистерне h = 2 м.
- Площадь заплаты: S = 10 см2.
10 см2 = 0,001 м2
Сила давления равна произведению давления на площадь, на которую это давление оказывается:
F = pS
Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. Поэтому:
F = pS = ρкghS = 800∙10∙2∙0,001 = 16 (Н)
Ответ: 16
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18804
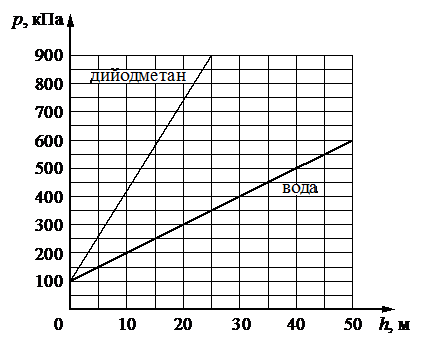
На рисунке представлены графики зависимости давления p от глубины погружения h для двух покоящихся жидкостей: воды и тяжёлой жидкости дийодметана, при постоянной температуре.
Выберите два верных утверждения, согласующихся с приведёнными графиками.
Ответ:
а) В воде на глубине 25 м давление p в 2,5 раза больше атмосферного.
б) С ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде.
в) Плотность керосина 0,82 г/см3, аналогичный график зависимости давления от глубины для керосина окажется между графиками для воды и дийодметана.
г) Если внутри пустотелого шарика давление равно атмосферному, то в воде на глубине 10 м давления на его поверхность извне и изнутри будут равны друг другу.
д) Плотность оливкового масла 0,92 г/см3, аналогичный график зависимости давления от глубины для масла окажется между графиком для воды и осью абсцисс (горизонтальной осью).
Алгоритм решения
1.Проверить все утверждения на истинность.
2.Записать буквы, соответствующие верным утверждениям, последовательно без пробелов.
Решение
Проверим истинность первого утверждения (а). Для этого определим по графику давление воды на глубине 25 м. Если пустить перпендикуляр к графику зависимости давления воды от глубины погружения через h = 25 м, то он пересечет график в точке, которой соответствует давление p = 350 кН. Атмосферное давление равно 100 кН. Следовательно, давление воды на этой глубине в 3,5 раза превышает атмосферное давление. Утверждение неверно.
Проверим второе утверждение (б). Согласно ему, с ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде. Это действительно так, потому что угол наклона графика зависимости давления дийодметана от глубины погружения к оси абсцисс больше того же графика для воды. Это можно подтвердить и математически: давление в более плотной жидкости с глубиной растет быстрее, так как давление имеет прямо пропорциональную зависимость с глубиной. Утверждение верно.
Проверим третье утверждение (в). Согласно ему, если на этом же рисунке построить график зависимости давления керосина от глубины погружения, то он окажется между двумя уже существующими графиками. Но этого не может быть, потому что давление в воде растет медленнее, чем давление в дийодметане, так как вода менее плотная. По этой же причине давление в керосине будет расти медленнее, чем в воде, так как керосин менее плотный по сравнению с водой. Третий график в этом случае займет положение между графиком зависимости давления воды от глубины погружения и осью абсцисс. Утверждение неверно.
Проверим четвертое утверждение (г). Согласно графику, давление воды на глубине 10 м равно 200 кПа. Поэтому давление на поверхность шарика снаружи, погруженного на такую глубину, будет вдвое больше, чем давление, оказываемое на его стенки изнутри (при условии, что давление внутри равно 1 атм.). Утверждение неверно.
Проверим последнее утверждение (д). Согласно ему, если на этом же рисунке построить график зависимости давления оливкового масла от глубины погружения, то он окажется между графиком для воды и осью абсцисс. Это действительно так, потому что плотность оливкового масла меньше плотности воды. Утверждение верно.
Верный ответ: бд.
Ответ: бд
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 8.5k
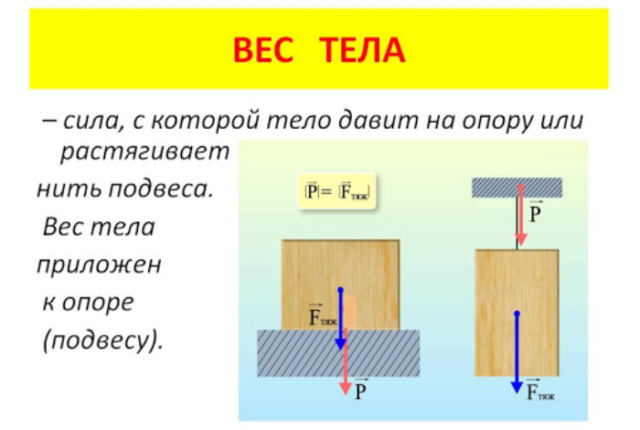
Конспект по физике для 7 класса «Расчёт давления жидкости на дно и стенки сосуда». ВЫ УЗНАЕТЕ: Что такое гидростатическое давление. Как рассчитать давление жидкости на дно сосуда. Как рассчитать давление жидкости на стенки сосуда. ВСПОМНИТЕ: Как формулируется закон Паскаля? Как определить давление твёрдого тела на опору? Как зависит масса тела от его плотности? Что такое вес тела? Как вес тела зависит от его массы?
Конспекты по физике Учебник физики Тесты по физике
Расчёт давления жидкости на дно и стенки сосуда
Жидкость, находящаяся в сосуде, оказывает давление как на дно сосуда, так и на его стенки. Поверхность жидкости, которая не соприкасается со стенками сосуда, называют свободной поверхностью жидкости. Давление, оказываемое покоящейся жидкостью, называют гидростатическим.
РАСЧЁТ ДАВЛЕНИЯ ЖИДКОСТИ НА ДНО СОСУДА
Вычислим давление жидкости на дно сосуда площадью S, если высота столба жидкости в этом сосуде равна h. Как известно, давление определяется по формуле p = F/S.
В нашем случае сила F, с которой жидкость действует на дно сосуда, равна её весу. Вес жидкости определяется по формуле Р = mg. (1)
Следовательно, для определения веса жидкости необходимо найти её массу. Для этого воспользуемся формулой m = pV, где р — плотность жидкости, а V — объём жидкости. Для определения объёма необходимо найти произведение площади дна сосуда и высоты столба жидкости: V = Sh.
Следовательно, масса жидкости в сосуде определяется по формуле m = рSh. (2)
Подставим это выражение в формулу (1) и получим Р = gpSh. (3)
Теперь для нахождения давления необходимо вес жидкости разделить на площадь сосуда: P = gpSh/S
Сократив в полученном выражении S в числителе и знаменателе, получим формулу для расчёта давления жидкости на дно сосуда: p = pgh. (4)
Давление жидкости на дно сосуда рассчитывают по формуле p = pgh.
РАСЧЁТ ДАВЛЕНИЯ ЖИДКОСТИ НА СТЕНКИ СОСУДА
Так как по закону Паскаля давление внутри жидкости на одном и том же уровне одинаково по всем направлениям, то по формуле (4) можно находить давление жидкости на стенки сосуда на любой глубине.
Из формулы (4) видно, что давление жидкости на дно и стенки сосуда прямо пропорционально высоте столба жидкости и зависит по только от высоты столба жидкости, но и от плотности жидкости р. Чем больше плотность жидкости, тем большее давление она оказывает при условии, что высота столба жидкости остаётся постоянной.
Даже при использовании дыхательных трубок, выступающих над водой, глубина погружения человека не может превышать 1,5 м, так как из-за давления воды у него не хватает сил увеличив объём грудной клетки и вдохнуть воздух. В 1943 г французами Ж. Кусто и Э. Ганьяном был изобретён акваланг специальный аппарат со сжатым воздухом, предназначенный для дыхания под водой и позволяющий находиться под водой от нескольких минут (на глубине около 40 м) до часа и более.
В соответствии с формулой (4) давление жидкости также зависит от ускорения свободного падения g. Значит, если представить себе один и тот же сосуд с жидкостью, помещенный на разные планеты, то давление на дно и стенки сосуда в нем будет различно в зависимости от значения g на планете.
ГИДРОСТАТИЧЕСКИЙ ПАРАДОКС
Из формулы (4) видно, что давление жидкости на дно и стенки сосуда зависит только от плотности и высоты столба жидкости и не зависит от формы сосуда.
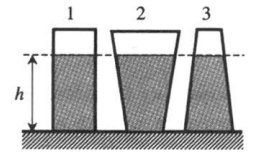
Приведённая схема опыта показывает, что сила, с которой жидкость оказывает давление на дно сосудов различной формы, но с одинаковой площадью дна и одинаковой высотой столба жидкости в них, будет одной и той же. Каждый из сосудов снабжён съемным дном, и динамометры показывают именно 3 силу воздействия воды на дно сосудов, но не вес жидкости. Очевидно, что вес жидкости в сосудах будет различным, так как объёмы жидкости в сосудах неодинаковы.
По закону Паскаля давление столба жидкости высотой h равномерно передаётся в любую точку дна каждого из сосудов. Именно поэтому сила, с которой жидкость оказывает давление на дно, больше веса жидкости в сосуде В, но меньше веса жидкости в сосуде С. Несмотря на кажущееся противоречие, ничего парадоксального в этих опытах нет.
ОПЫТ ПАСКАЛЯ
Даже небольшим количеством воды можно создать очень большое давление. В 1648 г. этот факт очень убедительно продемонстрировал В. Паскаль, поразив своих современников. В прочную, наполненную водой и закрытую со всех сторон бочку площадью поверхности 2 м2 была вставлена тоненькая трубочка площадью сечения 1 см2 и высотой 5 м. Затем Паскаль поднялся на балкон второго этажа и влил в эту трубочку всего кружку воды. Из-за малого диаметра трубки вода поднялась до большой высоты, и давление на стенки бочки так возросло, что планки (клёпки) бочки разошлись и вода стала вытекать из бочки.
Вы смотрели Конспект по физике для 7 класса «Расчёт давления жидкости на дно и стенки сосуда»: Что такое гидростатическое давление. Как рассчитать давление жидкости на дно сосуда. Как рассчитать давление жидкости на стенки сосуда.
Вернуться к Списку конспектов по физике (В оглавление).
Давление жидкости

4.7
Средняя оценка: 4.7
Всего получено оценок: 111.
Обновлено 28 Июля, 2021
4.7
Средняя оценка: 4.7
Всего получено оценок: 111.
Обновлено 28 Июля, 2021
Давление — это мера распределения силы на некоторой площади. Давление может создаваться не только твёрдыми телами, но и жидкими или газообразными. Использование этой физической величины для жидкостей имеет некоторые особенности, которые изучают на уроках физики в 7 классе. Рассмотрим их подробнее, выведем формулу давления жидкости.
Распределение давления в жидкости
Давление подразумевает действие некоторой силы. Для жидкостей такая сила может иметь два источника. И первый возможный источник — это внешняя сила.
Представим себе вертикальный цилиндр с поршнем в верхней части, полностью заполненный жидкостью. Теперь, если со стороны поршня на молекулы жидкости начнёт действовать сила, то ближайшие к поршню молекулы жидкости начнут смещаться вниз. При этом они встретят на пути противодействие молекул более глубоких слоёв и начнут передавать усилие им. Молекулы более глубоких слоёв в свою очередь будут передавать усилия ещё более глубоким слоям, и так далее, до самого дна поршня.
Напомним, что молекулы в жидкости связаны друг с другом слабо и совершают хаотичные тепловые движения. Если на молекулу действует сила со стороны вышележащего слоя, а вниз её «не пускает» нижележащий слой, то молекула начинает смещение вбок. Получается, что усилие поршня, направленное вниз, будет передаваться в жидкости не только вниз, но и в стороны. При этом за счёт хаотичного движения молекул «траектория передачи силы» может быть любой, сколь угодно извилистой — сила будет передаваться по этому пути через жидкость и создавать давление в любой точке.
Давление, производимое на жидкость, передаётся в любую точку жидкости без изменения во всех направлениях. Данный закон был открыт Б. Паскалем, и носит его имя. В честь этого физика также была названа единица измерения давления.
Давление в глубине жидкости
Вторым источником давления жидкости является её собственный вес.
Этот вес будет распределён по площади дна ёмкости, содержащей жидкость, и мера этого распределения характеризуется давлением.
Если сосуд имеет площадь дна $S$, и столб жидкости в нём будет иметь высоту $h$, то объём этой жидкости будет равен:
$$V=Sh$$
Если плотность жидкости равна $rho$, то масса жидкости равна:
$$m=rho V=rho Sh$$
Вес покоящегося тела равен силе тяжести. То есть:
$$P=mmathrm{g} =rho Sh mathrm{g}$$
Этот вес распределён по площади дна $S$. Следовательно, давление на дне сосуда будет равно:
$$p={Pover S}={ rho Sh mathrm{g}over S} $$
Сокращая значение площади, получаем формулу давления жидкости на глубине $h$:
$$p = rho mathrm{g} h$$
В данную формулу не входит площадь дна сосуда. Сосуд может иметь любую форму, давление жидкости на его дно будет определяться только высотой столба жидкости и её плотностью. По этой же формуле определяется давление в любой точке жидкости, не только на дне.
Что мы узнали?
Давление в жидкости распространяется во все стороны без изменений. Источником этого давления может являться внешняя сила или вес самой жидкости. В последнем случае давление жидкости зависит только от плотности этой жидкости и от глубины точки измерения.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Дамир Хамзин
5/5
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 111.
А какая ваша оценка?