Каталог заданий
Версия для печати и копирования в MS Word
1
Задания Д28 C1 № 3558
i
Какую силу давления оказывает нить на ось блока? Массы грузов одинаковы и равны
Трение не учитывать. Нить невесома и нерастяжима.
1. mg
2.
3.
4.
Решение
·
Критерии
·
3 комментария
·
Помощь
Lerank — 28 сентября, 2008 — 15:54

Задача из: «Механика. Молекулярная физика. Термодинамика». Домашние задания по курсу общей физики за первый семестр. Учебное пособие, под общей редакцией Б. А. Федорова.
- версия для печати
Сообщения без ответов | Активные темы | Избранное
|
|
Определить силу давления на ось блока
|
|
02/01/23 |
|
|
|
|
|
EUgeneUS |
Re: Определить силу давления на ось блока
|
|
11/12/16 |
WinterPrimat Сила натяжения нити у Вас неверно записана (если правильно понял, там форматирование ЛаТуХом сломалось).
|
|
|
|
|
Ende |
Re: Определить силу давления на ось блока
|
||
02/02/19 |
WinterPrimat Не забывайте, что в начале и конце формулы должен стоять знак доллара. Поправил.
|
||
|
|
|||
|
wrest |
Re: Определить силу давления на ось блока
|
|
05/09/16 |
Удивительно, как Вы получили ревное выражение для ускорения при неверном для силы натяжения нити. Так натяжение складывается с собой с обратным знаком, в итоге из уравнения для ускорения — пропадает.
|
|
|
|
|
EUgeneUS |
Re: Определить силу давления на ось блока
|
|
11/12/16 |
WinterPrimat Ваше выражение для силы натяжения нити не проходит проверку на крайние случаи: если масса хотя бы одного груза — ноль, то сила натяжени нити также должна обращаться в ноль. — 06.03.2023, 10:59 — Так натяжение складывается с собой с обратным знаком, в итоге из уравнеие для ускорения — пропадает. Ага. Можно и так систему решать.
|
|
|
|
|
wrest |
Re: Определить силу давления на ось блока
|
|
05/09/16 |
25Н, кстати, у меня тоже не получилось. Получится, если взять
|
|
|
|
|
WinterPrimat |
Re: Определить силу давления на ось блока
|
|
02/01/23 |
Изменение:
|
|
|
|
|
miflin |
Re: Определить силу давления на ось блока
|
|
27/02/12 |
|
|
|
|
|
wrest |
Re: Определить силу давления на ось блока
|
|
05/09/16 |
Изменение: Осталось применить теорему косинусов, и найдёте силу реакции опоры оси блока…
|
|
|
|
|
EUgeneUS |
Re: Определить силу давления на ось блока
|
|
11/12/16 |
Осталось применить теорему косинусов… Э… зачем? Сложения сил «параллелограммом» будет достаточно. Получится, если взять Чёй-та не дотягивает до 25Н. Минимально, что получилось «натянуть» вниз — (Оффтоп) Раз ТС написал верное выражение для силы натяжения нити, то напишите, пожалуйста, сколько у Вас оно получилось в ньютонах? WinterPrimat Теперь напишите выражение для силы действующей на ось блока.
|
|
|
|
|
wrest |
Re: Определить силу давления на ось блока
|
|
05/09/16 |
Чёй-та не дотягивает до 25Н. Минимально, что получилось «натянуть» вниз — Mу bad — у меня проблемы с арифметикой случились. Да, 30 правильно.
|
|
|
|
|
miflin |
Re: Определить силу давления на ось блока
|
|
27/02/12 |
(Оффтоп) Осталось применить теорему косинусов… Э… зачем? Сложения сил «параллелограммом» будет достаточно. Имелось в виду вычисление равнодействующей через проекции на вертикаль и горизонталь?
|
|
|
|
|
WinterPrimat |
Re: Определить силу давления на ось блока
|
|
02/01/23 |
Да, 30 правильно О, так, значит, я прав оказался. А то вообще 25Н не получалось. Именно 30 и есть.
|
|
|
|
|
miflin |
Re: Определить силу давления на ось блока
|
|
27/02/12 |
|
|
|
|
|
wrest |
Re: Определить силу давления на ось блока
|
|
05/09/16 |
Как-то так? Тут вам повезло что при
|
|
|
|
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: sergey zhukov |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
2017-05-21
Через блок, прикрепленный к потолку кабины лифта, перекинута нить, к концам которой привязаны грузы $m_{1} = 0,5 кг$ и $m_{2} = 0,6 кг$ (рис.). Найти силу давления блока на ось при движении грузов в двух случаях: лифт поднимается равномерно и с ускорением $a_{0} = 1,2 м/с^{2}$. Масса блока пренебрежимо мала. Трением в оси пренебречь.
Решение:
Сила давления блока на ось $vec{F}_{д} = — vec{N}$. где $vec{N}$ — сила реакции оси, действующая на блок и направленная вверх. Кроме этой силы на блок действуют силы натяжения нити $vec{T}_{1}$, и $vec{T}_{2}$, направленные вниз. Уравнение второго закона Ньютона для блока имеет вид
$m_{бл} vec{a}_{ц} = vec{N} + vec{T}_{1} + vec{T}_{2} + m_{бл} vec{g}$,
где $vec{a}_{ц}$ — ускорение центра масс блока относительно Земли, $m_{бл}$ — его масса. Если $m_{бл} rightarrow 0$, то независимо от ускорения центра масс
$vec{N} + vec{T}_{1} + vec{T}_{2} = 0, N = T_{1} + T_{2}$.
Таким образом, задача сводится к нахождению сил натяжения нити. Поскольку нить связывает заданные грузы, то силы натяжения могут быть найдены из рассмотрения движения грузов. При равномерном движении лифта можно выбрать систему отсчета, связанную как с Землей, так и с лифтом. При ускоренном движении лифта система отсчета, связанная с лифтом, неинерциальная, поэтому она должна быть связана с Землей. Задачу можно решить сразу для ускоренного движения лифта, а первый случай получится как частное решение при $a_{0} = 0$.
Грузы движутся относительно блока (относительно лифта) и участвуют в движении лифта с ускорением $vec{a}_{0}$. Если нить нерастяжима, то ускорения грузов относительно блока одинаковы по модулю, но противоположны по направлениям.
Для доказательства запишем условия нерастяжимости нити. Введем ось $O^{ prime} eta$, связанную с лифтом (рис.), координаты обоих тел $eta_{1}$, и $eta_{2}$. Тогда условие нерастяжимости нити
$eta_{1} + eta_{2} + l_{0} = const$,
где $l_{0}$ — длина части нити, соприкасающейся с блоком. При движении грузов относительно лифта координаты $eta_{1}$ и $eta_{2}$ изменяются, но
$dot{ eta}_{1} + dot{ eta}_{2} = 0, ddot{ eta}_{1} + ddot{ eta}_{2} = 0$ (1)
(точка над буквой обозначает производную по времени); $dot{ eta}_{r} = a^{ prime}_{1 eta}$ — проекция ускорения первого груза относительно лифта на вертикальную ось $O^{ prime} eta; ddot{ eta}_{2} = a_{2 eta}^{ prime}$ — проекция ускорения второго груза на ту же вертикальную ось. Из соотношения (1) найдем $a_{1 eta}^{ prime} = — a_{2 eta}^{ prime}$. Поскольку грузы движутся вдоль оси $O^{ prime} eta$, то
$vec{a}_{1}^{ prime} = — vec{a}_{2}^{ prime}$.
Относительно Земли ускорения грузов
$vec{a}_{1} = vec{a} + vec{a}_{1}^{ prime}, vec{a}_{2} = vec{a}_{0} + vec{a}_{2}^{ prime}$.
Каждый из грузов движется под действием силы тяжести и силы натяжения нити. Невесомость нити позволяет считать силу натяжения вдоль нити постоянной по модулю. Неизменяемость силы натяжения по модулю при переходе через блок может быть доказана при условии, что массой блока можно пренебречь. Таким образом, $T_{1} = T_{1}^{ prime} = T_{2} = T_{2}^{ prime}$. Уравнения второго закона Ньютона, записанные в скалярном виде для каждого из тел, составят систему, в которой неизвестными будут силы натяжения нити и относительные ускорения грузов.
Коллинеарность сил, действующих на каждый из грузов, позволяет записать уравнения движения сразу в скалярной форме для проекций на ось OY. Для первого груза
$a_{1y} = a_{0} + a^{ prime}, m_{1} (a_{0} + a^{ prime}) = T — m_{1}g$; (2)
для второго груза
$a_{2y} = a_{0} — a^{ prime}, m_{2} ( a_{0} — a^{ prime}) = T — m_{2}g$, (3)
где $T = T_{1}^{ prime} = T_{1}, i = 1, 2$.
Уравнения (2) и (3) образуют систему с двумя неизвестными $T$ и $a^{ prime}$. Умножая уравнение (2) на $m_{2}$, а уравнение (3) на $m_{1}$ и складывая их почленно, получаем
$T = 2m_{1}m_{2}(a_{0} + g)/(m_{1} + m_{2})$.
Искомая сила давления блока на ось
$F_{д} = N = 2T$.
При равномерном движении лифта ($a_{0} = 0$)
$F_{д} = 4 m_{1}m_{2}g/(m_{1} + m_{2}) = 10,7 Н$.
При подъеме с ускорением $a_{0} = 1,2 м/с^{2}$
$F_{д} = 4m_{1}m_{2} (g + a_{0})/(m_{1} + m_{2}) = 12,0 Н$.
Пример решения и оформления задачи Задача
Невесомая
нерастяжимая нить перекинута через
вращающийся около горизонтальной оси
неподвижный блок. К концам нити привязаны
грузы m1
и m2.
При движении грузов сила давления блока
на ось равна F,
ускорение грузов а.
Массой
блока и трением в оси можно пренебречь.
Определить неизвестную величину в
табл.2.
Таблица 2
|
m1, |
m2, |
F, |
а, |
|
650 |
350 |
? |
– |
Решение
Движение
грузов поступательное, поэтому их можно
считать материальными точками. На каждый
из рассматриваемых грузов действует
сила тяжести (
и
)
и сила натяжения нити (
и
),
как показано на рисунке 1.
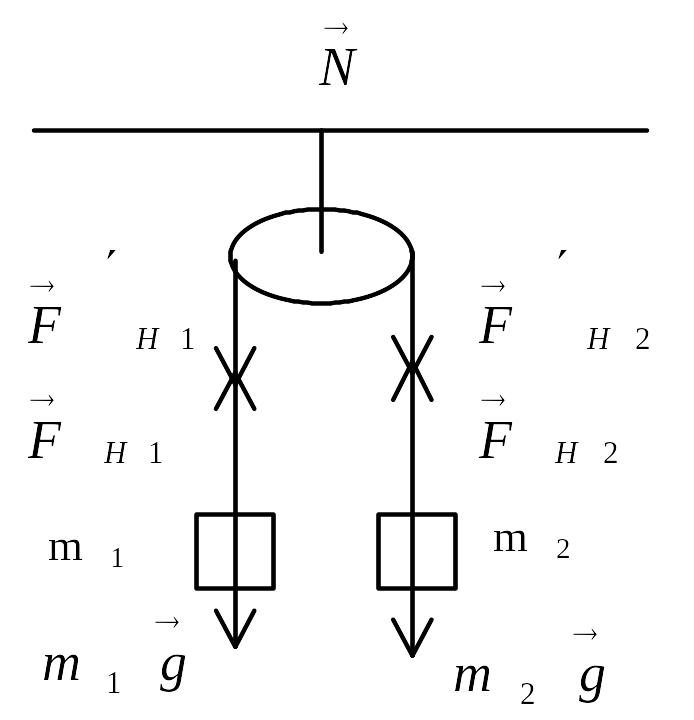
Схема приложения
сил.
Второй
закон Ньютона для каждого из грузов
может быть записан следующим образом:

Невесомость
нити (возможность пренебречь ее массой)
позволяет считать силу натяжения вдоль
всей нити постоянной. Неизменяемость
силы натяжения при переходе через блок
следует из того, что массой блока,
следовательно, его моментом инерции, и
трением в оси можно пренебречь, а потому
разность моментов сил натяжения,
действующих на блок с противоположных
сторон, должна равняться нулю. Отсюда
вытекает, что силы натяжения нити,
действующие как на оба груза, так и на
блок, можно считать равными между собой:
.
Не
растяжимость нити позволяет найти связь
между ускорениями грузов. Движение
грузов происходит только в одном
вертикальном направлении, поэтому
достаточно рассматривать только одну
координату у
– будем отсчитывать ее вниз от оси блока
(см. рисунок). Длина нити постоянна,
поэтому: у1+у2=const.
Дифференцируя,
получаем:
Здесь
.
Ускорения грузов равны по абсолютной
величине и противоположны по направлению.
Обозначив ускорение груза m1
через а,
имеем: а1у=–а2у=а.
В
уравнениях второго закона Ньютона
перейдем от векторных соотношений к
скалярным, взяв проекции всех векторов
на ось у.
Учитывая уже полученные соотношения
между величинами, входящими в уравнения,
имеем:
m1a=m1g–FH
,
–m2a=m2g–FH
.
Отсюда
можно найти а
и FH.
По
условию задачи требуется найти силу
давления блока на ось. На блок действуют
две силы натяжения нити F¢H1=F¢H2
и сила реакции оси
(см. рисунок). Центр масс блока неподвижен,
следовательно, сумма действующих на
блок сил равна нулю:
;
2FH–N=0
.
Отсюда
N=2FH.
Согласно третьему закону Ньютона сила
реакции оси равна по величине искомой
силе давления F
блока на ось. Решая уравнения, получаем:
;
.
Выразим данные
задачи в системе СИ и проведем вычисления.
|
СИ
m1=
m2=
g ____________
F |
|
В
соответствии с правилами приближенных
вычислений результат округляем до двух
значащих цифр. В ответ заносим значение
силы F
в ньютонах – число +8,900.
Проверка
размерностей:
.
Анализ
полученных результатов показывает, что
значение силы натяжения нити FH
лежит между m1g
и m2g.
Сила давления блока на ось F
при движении грузов меньше суммы сил
тяжести, действующих на грузы.
Равнодействующая сил, действующих на
груз большей массы, направлена вниз, а
сил, действующих на груз меньшей массы,
– вверх. Поэтому ускорение груза большей
массы направлено вниз, а ускорение груза
меньшей массы – вверх.
Если
массы грузов одинаковы (m1=m2),
то сила натяжения нити равна силе
тяжести, действующей на каждый груз, и
ускорения грузов равны нулю. В этом
случае грузы находятся в покое или
движется равномерно, и сила давления
блока на ось F
равна 2mg
– равномерное движение грузов не меняет
величину силы давления блока на ось.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #






 )
)
 выходит так что
выходит так что 
 не повезло бы.
не повезло бы.