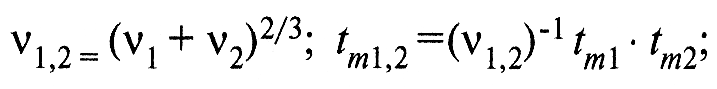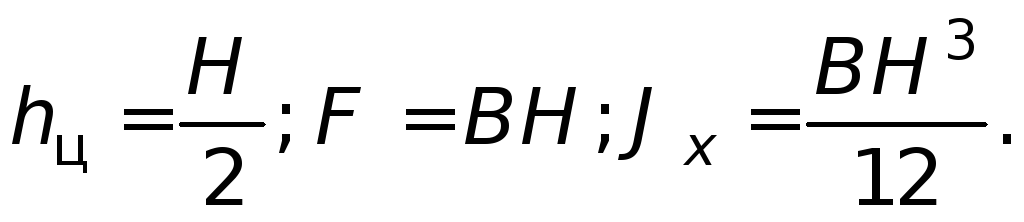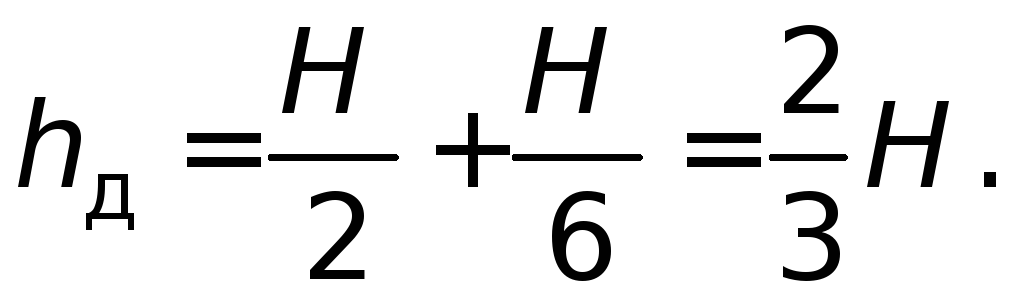Эпюры
распределения в поперечном сечении деталей соединения нормальных напряжений
окружного а, и нормальных напряжений радиального аг направлений
согласно решению Ляме имеют вид, показанный на рис. 5.8; вдоль оси соединения и
по центральному углу напряжения не меняются.
Наибольшие
напряжения возникают у внутренней поверхности охватывающей детали и согласно решению
Ляме при внутреннем давлении ρ они равны
При использовании
для изготовления деталей соединения одинаковых материалов обычно более слабым
элементом оказывается охватывающая деталь (ступица детали, насаженной на вал).
Расчет ее на прочность можно проводить в следующем порядке.

Рис. 5.8. Эпюры
распределения напряжений аг
и σ, в деталях соединения с натягом
Для стандартной посадки, подобранной по нагрузочной способности,
находят N,.Tmax или N¥miai, и, вводя
поправку U, по формуле
(5.4) находят максимальный расчетный натяг: ■^max = ^ст max — ^ или ^max ~ ^Р max ~~ ^ ■ Используя формулу (5.3) Ляме,
определяют максимальное давление на поверхности контакта при максимальном
натяге
Далее по формулам (5.5)
находят соответствующие максимальные напряжения
Наибольшие
эквивалентные напряжения по теории прочности максимальных касательных
напряжений
Напряжения
оЖВ|Т1ах и σίπ13χ не должны (по возможности) превышать предела текучести στ2 материала
охватывающей детали.
Появление пластических
деформаций не является во всех случаях недопустимым. Опыт свидетельствует, что
надежные соединения с натягом получаются и при наличии небольшой пластической
зоны вблизи внутренней поверхности ступицы. Давление на поверхности контакта,
соответствующее началу пластических деформаций на внутренней поверхности
ступицы, равно
где
στ2 — предел
текучести материала охватывающей детали (ступицы).
Увеличение
Ad2
наружного диаметра охватывающей детали (ступицы, втулки), вызванное растяжением
от давления р, можно определить по формуле
Приведенные
выше формулы основаны на предположении, что давление на поверхности контакта
деталей соединения равномерно распределено
по этой поверхности. Расчеты методом конечных элементов и эксперименты
показывают, что давление в направлении оси соединения распределяются
неравномерно.
электронное научно-техническое издание
НАУКА и ОБРАЗОВАНИЕ
Эя №ФС 77 — 30569. Государственная регистрация №0421100025.155Н 1994-040В_
Определение эпюры контактного давления для соединения деталей по цилиндрическим поверхностям с малым зазором (случай, когда охватывающая деталь безгранична в радиальном направлении). # 05, май 2011
авторы: Блинов Д. С., Алешин В. Ф.
УДК 621.813, 621.815
МГТУ им. Н.Э. Баумана victorfa@mail. т dmitriyblinov@mail.ru
Введение. В машинах многие детали соединены между собой. По признаку возможности разборки соединения делят на неразъемные, которые нельзя разобрать без разрушения или повреждения, и разъемные /1/.
Рассмотрим две соединяемые детали, одна из которых имеет наружную цилиндрическую сопрягаемую поверхность (охватываемая деталь), а другая -внутреннюю цилиндрическую сопрягаемую поверхность (охватывающая деталь). В соединении этих деталей сопрягаемые поверхности находятся во взаимодействии.
Неразъемное соединение рассматриваемых деталей называется цилиндрическим соединением с натягом. Такие соединения очень широко применяются. Нагрузка через цилиндрическое соединение с натягом чаще всего передается за счет сил трения, которые порождаются контактным давлением, осесимметрично распределенным по сопрягаемым поверхностям соединяемых деталей. При этом величина передаваемой через соединение нагрузки зависит от целого ряда параметров (см. /1/), но наиболее значимым или ключевым параметром является величина натяга. Для расчета цилиндрических соединений с натягом используют зависимости Ляме /1/.
Разъемные соединения рассматриваемых деталей также широко применяются в машиностроении. Например, в резьбовых соединениях (рис. 1, а), в различных опорах и шарнирах (рис. 1, б), при определенных допущениях в клеммовых соединениях (рис. 1, в) и в другие соединениях и узлах.
а
1—1
5
А'»»»»»/
Рис. 1. Примеры конструкций разъемных соединений деталей с цилиндрическими
Разъемные соединения деталей с цилиндрическими сопрягаемыми поверхностями можно условно разделить на две группы. В разъемных соединениях первой группы между отверстием охватывающей детали и цилиндрической поверхностью охватываемой детали имеется конструктивный зазор, который сопоставим с миллиметрами или десятками миллиметров. В этом случае в зависимости от назначения и требуемой точности расчета считают, что после приложения силы ¥ (см. рис. 1):
— детали взаимодействуют по начальной линии контакта, вдоль которой действует распределенная (погонная) нагрузка q = ¥ /Ь (Ь — протяженность контакта);
— используя задачу Герца /1/, детали взаимодействуют по плоской линейчатой контактной поверхности, на которой действует контактное давление. Эпюра контактного давления постоянна вдоль площадки контакта, а поперек — распределяется по уравнению эллипса. Формулы Герца позволяют определить размеры площадки контакта, максимальное значение контактного давления и напряженное состояние деталей.
Чаще всего в разъемных соединениях второй группы номинальные значения диаметра отверстия охватывающей детали и диаметра цилиндрической поверхности охватываемой детали одинаковы, а зазор мал и определяется полями допусков на указанные диаметры сопрягаемых поверхностей деталей. К этой группе также надо отнести соединение деталей с конструктивным зазором между их сопрягаемыми поверхностями, если по отношению к диаметру отверстия охватывающей детали этот зазор мал и задача Герца неприменима, см. /1 и 2/.
сопрягаемыми поверхностями.
В курсе «Детали машин» для расчета разъемных соединениях второй группы принято использовать, так называемые, напряжения смятия. При этом в расчет величина зазора, которая является ключевым параметром для указанных соединений, не входит. Причина заключается в том, что отсутствует достаточно достоверная и простая в применении инженерная методика расчета разъемных соединений по цилиндрическим поверхностям с малым зазором.
Целью данной статьи и ее продолжений является разработка инженерных методик расчета разъемных соединений по цилиндрическим поверхностям с малым зазором на базе теоретических исследований, выполненных методами теории упругости и строительной механики машин. Чтобы инженерные методики обладали общностью, теоретические исследования выполнялись в безразмерном виде.
Анализ конструкций разъемных соединений по цилиндрическим поверхностям с малым зазором. Рассмотрим упрощенную расчетную схему взаимодействия охватываемой детали 1 и охватывающей детали 2, выполнен-ной в виде кольца, см. рис. 2.
Рис. 2. Геометрические параметры.
На рисунке обозначены все радиусы этих деталей, а также радиальный зазор
е = г 2 — Г1 (1)
По разрабатываемым инженерным методикам расчета необходимо определять размеры площадки контакта, вид эпюры контактного давления после приложения нагрузки и напряженно-деформированное состояние соединяе-мых деталей. Для анализа влияния на указанные параметры соотношения размеров охватывающей детали 2 введем безразмерную толщину этой детали
И =(гз — г2) / г2 (2)
В общем случае напряжения, действующие в охватывающей детали, можно условно разделить на контактные оН и изгибные Ор. Если безразмерная толщина И близка к
нулю, то охватывающую деталь можно считать тонкостенной, в которой доминируют изгибные напряжения о, а контактные напряжения оН можно считать пренебрежимо малыми. Если безразмерная толщина к велика, то охватывающую деталь можно считать безграничной в радиальном направлении, и в этой детали действуют только контактные напряжения аН. При этом форма в плане охватывающей детали может быть любой. Если к имеет средние значения, то при расчетах надо учитывать изгибные и контактные напряжения. Таким образом, мы имеем три зоны, определяемые жесткостью охватывающей детали, см. табл. 1. В этой таблице по усредненным оценкам представлены ориентировочные границы этих зон.
Таблица 1.
Зона Диапазон значений Л ор Вид эпюры
I А ^ 0,3 Пренебрежимо малы • Доминируют д % А />(<р) 0О Л = СОПБ!
II 0,3 < А <0,8 Соизмеримы *
^—___ /
/<Ф)
III Л £0,8 Доминируют Пренебрежимо малы / / 7* \
\ ¿г
р ((¡>) изменяется по
уравнению эллипса
В таблице 1 для каждой зоны эпюра контактного давления р(ф) распределена на дуге, соответствующей углу контакта 2 ф0 (для расчетов удобен параметр ф0 — полуугол контакта). Инженерные методики расчета удалось разработать для I зоны и III зоны.
2. Разработка инженерной методики расчета для случая, когда охватываемое тело можно считать безграничным в радиальном направлении (для зоны III, см. табл. 1).
2.1. Определение размеров площадки контакта (полуугла контакта фо).
На рис. 3 показана расчетная схема, на которой охватываемая деталь 1 с радиусом r1 установлена в цилиндрическое отверстие с радиусом r2 в охватывающей детали 2, которую считаем безграничной в радиальном направлении.
Деталь 1 нагружена сосредоточенной силой р (погонной нагрузкой При этом на дуге 1-ой детали для произвольной угловой координаты ф (-ф<ф < ф0), возникает
контактного давления р (ф’), которое необходимо определить для неизвестного полуугла
контакта ф0. Форма (зависимость р от ф ) эпюры контактного давления также неизвестна.
Рис. 3. Расчетная схема задачи.
В основу разрабатываемой методики положена задача И.Я.Штаермана о контакте цилиндра с внутренней цилиндрической поверхностью в безграничном теле /2/.
В работе /2/ методами задачи плоской деформации теории упругости /3, 4 / с дополнительными допущениями для определения полуугла контакта ф0 и эпюры контактного давления р (ф’) выведены уравнения: — равновесия охватываемой детали 1
УО
* = Ь • Г | р (V)- СОБ (ф’)йф’
( 3 )
— совместности перемещений точек с координатой ф сопрягаемых деталей 1 и 2 под действием силы Г (погонной нагрузки д)
2-Г +^2 -Г2) | Р(ф’
СОБ (ф-ф’)^ 1п
С
ф-ф
— СОБ ф • СОБ ф’• 1п
(
-(хх • г + Х2 • Г) | Р(ф’)-[§1п|ф-ф’|-С0Бф-бш|ф’|]йф +
tg
йф —
( 4 )
+2 г •(! — СОБ ф) | р (ф’) йф =( г — Г )•(! — СОБф)
1 (1 + ^(1 — 2 и)
где: ц=-^; х = —
ж • Е
2 • Е
Е и и — модули упругости и коэффициенты Пуассона деталей 1 и 2;
, = * — распределенная вдоль оси (погонная) нагрузка;
Ь
Ь — протяженность контакта деталей 1 и 2 вдоль оси;
ф — угловая координата ( -ф0 < ф < ф0, ф0 — полуугол контакта);
Будем считать, что тела металлические. Если принять и=и=и = 0,3, то наибольшая ошибка при расчетах составит доли процента.
Радиусы г1 и г2 близки по величине, и можно считать, что г1 &т2, а радиальный зазор
е = г 2 — Г1.
В книге /2/ приведено совместное решение уравнений (3) и (4) для случая, когда сопрягаемые детали изготовлены из одного и того же материала, то есть их модули
упругости Ej = Е2 = Е. Такое допущение существенно упростило совместное решение указанных уравнений.
На практике сопрягаемые детали могут быть изготовлены из различных металлов, поэтому необходимо было совместное решение указанных уравнений выполнить в общей постановке (развить решение И.Я.Штаермана).
Для совместного решения исходных уравнений (3) и (4) целесообразно считать, что полуугол контакта ф0 известен, и надо определить соответствующую этому углу силу F. Для расчета использовался метод конечных разностей /5, 6/. Для этого эпюру контактного давления pв интервале полуугла контакта (р0 разобьем на М равных углов у = Ф0/М. В интервале каждого малого угла y считаем эпюру контактного давления постоянной, то есть
р(J) = const, для J = ,2,..M ( 5 )
После ряда преобразований получим систему М алгебраических уравнений
а
[ I,J ]• q [J ] = b[l I
I = 1,2,…M ; J = 1,2,..M
( 6 )
где: a[I, J] = 2■ S(J)■ cos(I -y)-S(I + J)■-S(K); K = (J -1) для J > I; K = (I — J + 1) для J < I;
S(J) = Q(J)-Q(J -) + щ
1 -P 1+ P
Q (J ) = -2 ■ sin (y-J )■ ln
g
щ J
2 ■ж
-cos
(¥-J);
ф]== ЮП^Ц ; ВД = -cos(Iy) ; P= ^ ;
r 2 ■ E ■ E2
Enp =- — приведенный модуль упругости.
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
E + E2
При J = 0 функция Q(J) имеет в первом слагаемом неопределенность типа 0 • да, после раскрытия которой по правилу Лопиталя / 7 / получается Q(0) = 2•ж /7. Уравнение равновесия детали 1 преобразуется к виду
M
F = 2 ■ L ■ r ^ p (J) ■ [ sin (J ■ y) — sin (J щ-щУ^
( 7 )
j =
Путем численного решения на ЭВМ системы алгебраических уравнений ( 6 ) и ( 7 ) определялись искомые значения контактных давлений р (J) и безразмерной величины
д / (Едр •£) в зависимости от полуугла контакта ф0, приведенного модуля упругости Епр и
отношения в модулей упругости. Результаты этих расчетов представлены в виде
семейства кривых, см. рис. 4. %
град
60
20 Ш
о
На рис. 4 кривая с коэффициентом в = 1 является повторением решения И.Я.Штаермана, опубликованного в работе /2/. С учетом графических ошибок полученная кривая и кривая, полученная И.Я.Штаерманом, совпадают.
В 80-ые годы прошлого века на кафедре «Детали машин» МВТУ им.Н.Э.Баумана велась дискуссия о том, является ли приведенный модуль упругости ЕПР физической величиной или он удобное для расчетов сокращение?
Рассмотрим две модели взаимодействующих тел. Пусть в первой модели деталь 1 изготовлена из стали, а деталь 2 — из чугуна. Для первой модели в ~ 1/2. Во второй модели наоборот деталь 1 изготовлена из чугуна, а деталь 2 — из стали. Для второй модели в ~ 2. Графики (см. рис. 4) для в = 1/2 и для в = 2 не совпадают, а приведенный модуль упругости для двух указанных моделей одинаковый. Следовательно, одного приведенного
Рис. 4. Графики для определения полуугла контакта ф0.
модуля упругости недостаточно для решения данной задачи (нужен еще коэффициент в), и ЕПР поэтому не является физической величиной.
2.2. Определение эпюры контактного давления.
Для определения функциональной зависимости контактного давления от угловой координаты были выполнены расчеты, в которых полуугол контакта <р0 разбивался на
достаточно большое число М равных углов щ = сра/М . В интервале каждого малого угла у эпюра контактного давления является постоянной.
Как показал анализ результатов расчетов /8/, в качестве эпюры контактного давления целесообразно принять эллипс. С этим согласны и другие исследователи этого вопроса /9/. Для практического применения эллиптическую эпюру контактного давления удобно представить в виде единичной окружности, см. рис. 5. На рис. 5 рМАх — максимальное значение контактного давления.
Рис. 5. Эпюра контактного давления
Величину максимального контактного давления рМАх можно определить по графику (см. рис. 6) или по следующей формуле
рмлх = 7 ТТ , ( 8 )
ж I • гх • (ро)
где ^ — функция Бесселя первого рода порядка 1 / 10 /.
Таким образом выполненные исследования по известным размерам деталей соединения, действующей силе Г и модулям упругости деталей Е} и Е2 позволяют определить размер контактной эпюры (полуугол контакта ф0) и максимальное значение рМАХ эллиптической эпюры контактного давления.
Я
л
¥> а б А г
о й 20 30 ^ 50 ^граа
Рис. 6. График для определения рмАх ВЫВОДЫ ПО РАБОТЕ
1. В настоящее время отсутствуют достаточно достоверные и удобные в применении инженерные методики расчета разъемных соединений по цилиндрическим поверхностям с учетом радиального зазора между сопрягаемыми поверхностями деталей соединения. При этом указанный зазор является ключевым параметром для расчета.
2. Разъемные соединения по цилиндрическим поверхностям в зависимости от отношения толщины охватывающей детали к радиусу ее отверстия можно условно разделить на три группы (три зоны), для каждой из которых требуется индивидуальный подход при разработке инженерной методики расчета.
3. Данная статья посвящена разработке инженерной методики расчета для случая, когда охватываемое тело можно считать безграничным в радиальном направлении. В основу инженерной методики расчета положена известная задача И.Я.Штаермана о контакте цилиндра с внутренней цилиндрической поверхностью в безграничном теле.
4. Выполнено развитие задачи И.Я.Штаермана о контакте цилиндра с внутренней цилиндрической поверхностью в безграничном теле. В результате этого для общего случая, когда контактирующие тела изготовлены из различных материалов, получены зависимости и графики для определения размеров и формы эпюры контактного давления
в зависимости от радиального зазора, других размеров деталей соединения, силы и модулей упругости материалов деталей.
5. Анализ полученных результатов позволил сделать вывод о том, что приведенный модуль упругости материалов контактирующих тел не является физической величиной, а является удобным для расчетов сокращением.
СПИСОК ЛИТЕРАТУРЫ
1. Решетов Д.Н. Детали машин: Учебник для студентов машиностроительных и механических специальностей вузов. — М.: Машиностроение, — 1989. — 496 с.
2. Штаерман И.Я. Контактная задача теории упругости. — М.: Гостехиздат, — 1949.
— 270 с
3. Демидов С.П. Теория упругости. — М.: Высшая школа, 1979. — 432 с.
4. Тимошенко С.П., Гудьер Дж. Теория упругости. — М.: Наука, 1979. — 560 с.
5. Бахвалов Н. С. Численные методы. — М.: Наука, 1975. — 632 с.
6. Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. — М.: Физматгиз, 1963. — 400 с.
7. Мышкис А. Д. Лекции по высшей математике. — М.: Наука, 1973. — 640 с.
8. Блинов Д.С., Шатилов А.А. Определение усилий закрепления заготовок в станочных приспособлениях методами контактной задачи теории упругости // Труды МВТУ. — 1978. — № 281. — С. 63-75.
9. Кузьменко А.Г., Фукс Ю.М. Аппроксимация решений контактной задачи о внутреннем касании цилиндров. // Вопросы исследования надежности и динамики элементов подвижного состава железных дорог: Сборник статей. — Брянск, — 1974.
— С. 118-130.
10. Янке Е., Эмде Ф., Леш Ф. Специальные функции. — М.: Наука, 1964. — 344 с.
КОНТАКТ ТВЁРДЫХ ТЕЛ
Поскольку реальный профиль поверхностей отличается от номинального, заданного чертежом, контакт твердых тел также отличается от номинального и осуществляется за счет сближения этих тел путем деформации отдельных микронеровностей на контактирующих поверхностях — волн и микровыступов. Поэтому реальный контакт трущихся тел всегда дискретен, так что механический контакт твердых тел представляет собой совокупность пятен контакта, через которые эти тела прижимаются друг к другу.
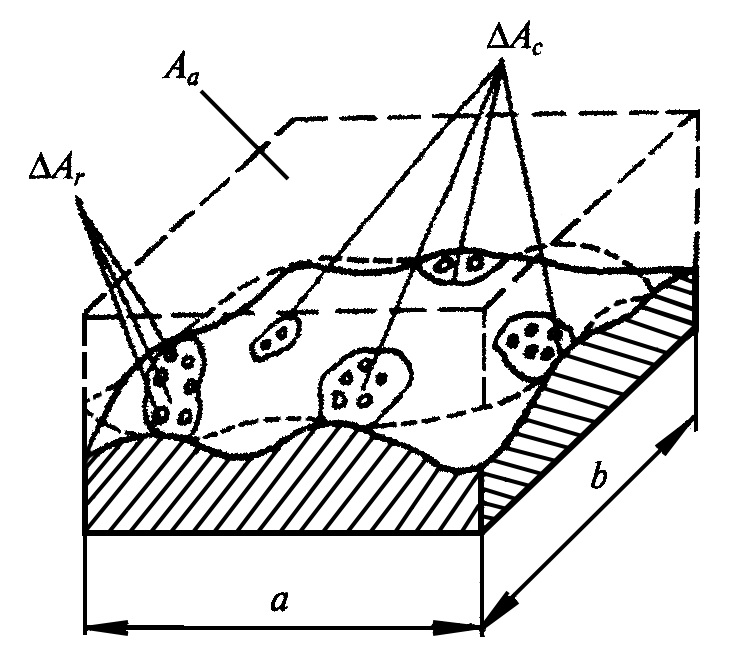
К тому же приходится учитывать три разновидности площади контакта: номинальная Аa (НПК), фактическая Ar (ФПК) и контурная Ac (КПК).
Номинальная площадь контакта Aa ограничена геометрическими очертаниями площади контакта и представляет собой геометрическую площадь соприкосновения контактирующих тел (рис.1), т.е. для прямоугольного очертания такой площадки длиной а и шириной b будем иметь Аa = ab.
Контурная площадь контакта Ас формируется в результате деформации (обычно, упругой) элементов волнистости поверхностей контактирующих тел в процессе смятия вершин этих элементов
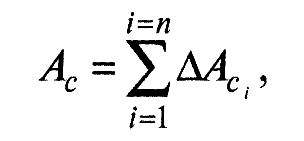
где ΔАсi – площадка, образованная деформацией отдельного элемента волнистости.
Фактическая площадь контакта Ar формируется в результате деформирования вершин микровыступов сопряженных поверхностей. Эти деформированные микровыступы (см. рис. 1) расположены на контурных площадках контакта, ограниченных ее площадью.
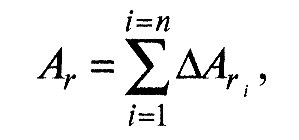
где ΔAri – площадка, образованная деформацией отдельного микровыступа.
Рис.1. Схема контакта шероховатых поверхностей: Аа – номинальная площадь контакта; ΔAc – единичная площадка контурного контакта; ΔAr – единичная площадка фактического контакта.
Следует учитывать, что фактическая площадь контакта составляет незначительную долю от номинальной площади контакта (от сотых и даже тысячных долей до 20-40%)
Соответственно трем видам площадей контакта различают три вида контактных давлений: номинальное ра, контурное рс и фактическое рr:
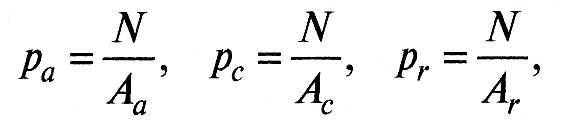
где N – сила, действующая на контактирующие тела.
Определение этих давлений необходимо для большинства расчетов в трибологии.
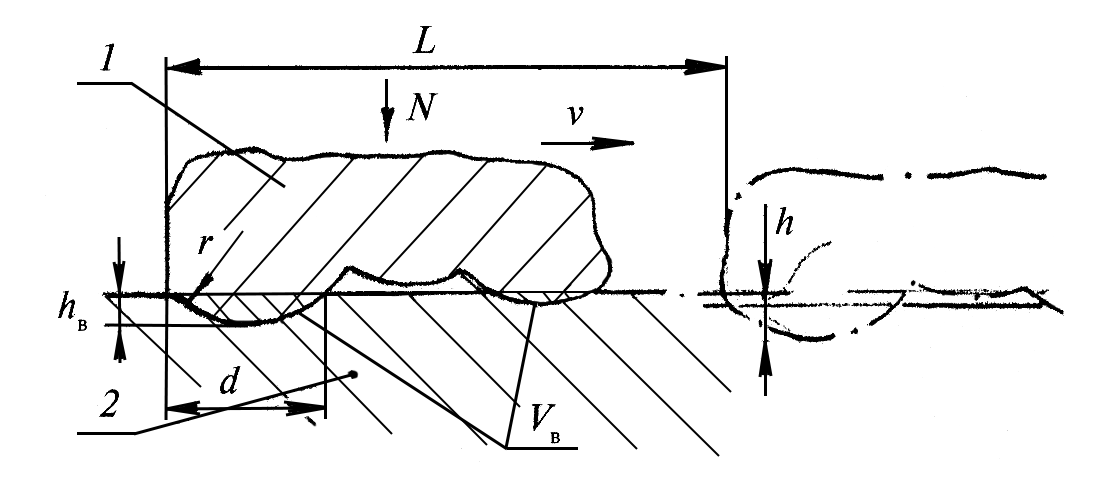
Поскольку реальный контакт осуществляется по ФПК, то его определению придается особое значение. Как уже показано, контакт шероховатых тел имеет дискретный характер. Опыт показывает, что отдельные микровыступы по форме близки к полусферическим сегментам и ФПК представляет собой сумму элементарных пятен контакта, образовавшихся в результате деформирования (упругого или пластического) этих сегментов. Поэтому модель шероховатого слоя представлена И.В. Крагельским и Н.Б. Демкиным в виде набора сегментов полусферической формы, имеющих одинаковый радиус, но расположенных по высоте на различном уровне так, чтобы распределение материала по высоте соответствовало распределению материала в реальном шероховатом слое, а площадь сечения выступов в горизонтальной плоскости при различных уровнях сближения (рис. 2) соответствовала экспериментально определяемой кривой опорной поверхности tp.
Рис. 2. Модель контакта жесткого шероховатого недеформируемого тела 1 с деформируемым идеально гладким телом 2: hB – глубина внедрения; d и r – диаметр полусферической неровности и радиус закругления ее вершины; h – деформация тела 2; VB – объем материала тела 2, выдавленный единичной неровностью тела 1; L – длина пути тела 1 по телу 2; N – сила, действующая на контактирующие тела.
Средний радиус кривизны вершин выступов r представляет собой среднее значение кривизны вершин выступов, определенное для пяти наиболее высоких выступов в пределах базовой длины. Радиусы кривизны выступов определяют из профилограммы, снятых в направлении, перпендикулярном следам механической обработки, и в направлении следов обработки. Средний радиус кривизны отдельной неровности ri определяется по длине сечения выступа d на расстоянии h от вершины неровности по приближенной формуле
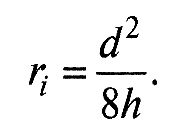
В трибологических расчетах используют значение приведенного радиуса кривизны вершин выступов
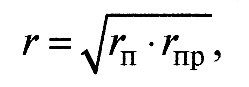
где rп и rпр – радиусы кривизны вершин выступов в поперечном и продольном направлениях, соответственно.
Значения r в зависимости от режима механической обработки меняются от 15-55 мкм при точении и от 5-18 мкм при внутреннем шлифовании, до 230-670 мкм при полировании и 300-3000 мкм при доводке плоских поверхностей.
По характеру деформации контакт может быть упругим, упруго-пластическим и пластическим. При упругом контакте при снятии нагрузки форма деформированных неровностей восстанавливается полностью; при упруго-пластическом контакте – лишь частично, и при пластическом контакте не восстанавливается совсем:
а) при упругом контакте рr < сдσт, где σт – предел текучести более мягкого материала трибосопряжения, сд – коэффициент, учитывающий форму деформируемых неровностей. Экспериментально-теоретические исследования показали, что для сферы сд ~ 3, но Зσт ~ НВ, где НВ — твердость по Бринеллю. Следовательно, при рr < НВ контакт упругий;
б) при пластическом контакте рr > сдσт или рr > НВ. Установлено, что при пластическом контакте обычно пластичны только микрошероховатости, тогда как волны деформируются упруго;
в) при упруго-пластическом контакте соотношение между напряженностью контакта и твердостью по Бринеллю занимает промежуточное положение.
По уровню насыщенности контакт может быть:
а) ненасыщенный – формируется, когда деформируемые неровности не оказывают друг на друга влияния, поскольку расположены далеко друг от друга. По мере роста нагрузки площадь контакта увеличивается, главным образом, путем увеличения числа вступающих в контакт вершин микронеровностей. В этом случае расчеты площадей контакта производят с учетом только начального участка кривой опорной поверхности;
б) насыщенным – имеет место, когда деформируемые неровности расположены столь близко друг от друга, что на их деформирование влияет присутствие соседних неровностей, и увеличение площади контакта происходит за счет роста элементарных участков контакта, т.е. величины d. Тогда кривую опорной поверхности рассчитывают по формуле:
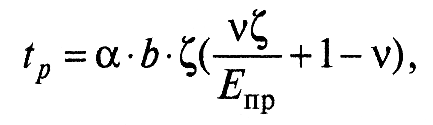
где α – коэффициент усадки; Епр – приведенный модуль упругости.
Контакт считается полностью насыщенным, когда Аr становится равным Ас.
Расчет давлений на фактическом пятне контакта. Критерий Гринвуда-Уильямсона. Прежде чем рассчитывать фактическое давление, необходимо оценить вид контакта, т.е. выяснить, следует его рассчитывать по формуле для упругого или пластического контакта. Предварительная оценка характера деформации производится по критерию Гринвуда-Уильямсона (индексу пластичности):
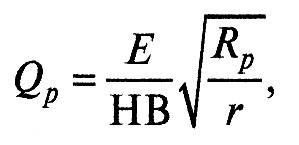
где Е – модуль упругости; НВ – твердость по Бринеллю; Rp – высота сглаживания; r – радиус единичной неровности.
Если Qp > 3, то контакт пластический; если меньше – то упругий. Руководствуясь этим, следует выбрать уравнение для расчета величины давления на фактической площади контакта.
Примечание. Здесь и во всех последующих расчетах следует:
а) учитывать параметры шероховатости и волнистости более твердого тела, а твердость – более мягкого. При упругом контакте принимать значение модуля упругости для того тела, для которого он меньше;
б) если шероховатость сопряженных тел одного порядка, то следует брать для расчета эквивалентные значения параметров: v1,2; Rp1,2; tm1,2 и т.д., учитывая микрогеометрию и первой, и второй поверхностей. Так,
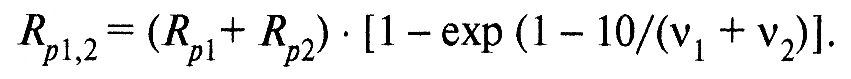
Расчет давлений на фактической площади контакта при упругой деформации. При упругом контакте единичной сферы с деформируемым полупространством величины деформаций, контактных давлений и площадей контакта рассчитываются по формуле Герца.
При упругом множественном контакте давления на ФПК рассчитывают по формуле:
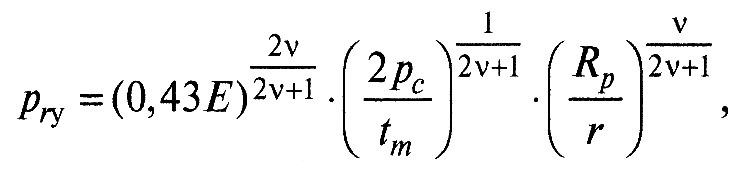
где Е – модуль упругости; r – приведенный радиус кривизны вершин неровностей; рс – контурное давление, определяемое по формуле.
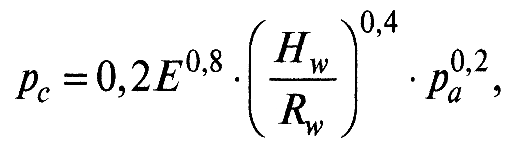
где Hw и Rw – соответственно высота и радиус волны, рa – номинальное давление.
При наиболее распространенных в машиностроении видах механической обработки поверхностей трения tm = 0,5, v = 2. Тогда
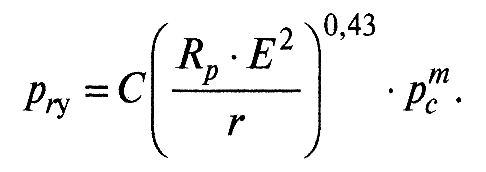
При контактировании двух шероховатых поверхностей С = 0,61; m = 0,14. При контактировании гладкой и шероховатой поверхности С = 0,86; m = 0,2.
Расчет давлений на фактической площади контакта при пластической деформации. При расчете контактных давлений в условиях пластического контакта рекомендуется формула:
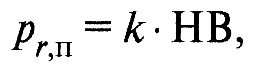
где для неупрочняемых материалов k = 1; для упрочняемых k =1,3.
Если силой N осуществляется повторное нагружение контакта, ранее пластически деформированного силой N0, то при N ≤ N0 деформация будет упругой и давление на ФПК рассчитывается по формуле:
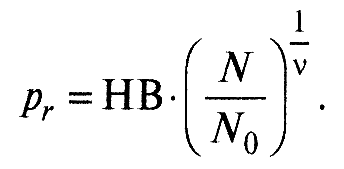
Расчет величины сближения. Взаимное сближение δ контактирующих тел при их совместном деформировании определяется следующим образом:
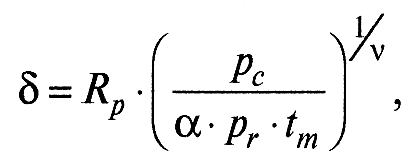
где α – коэффициент усадки выступов. Для абсолютно упругого тела α = 0,5; для абсолютно пластичного α = 1.
Другие характеристики контакта, которые рассчитываются из значения рr:
- фактическая площадь контакта
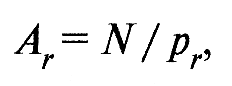
где N – нормальная нагрузка на узел трения.
- число пятен фактического контакта
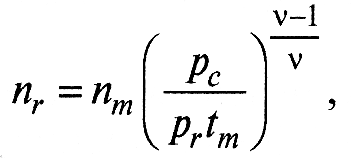
где nm – число выступов, вершины которых лежат выше средней линии.
В заключение необходимо отметить следующее:
- В значение усилия N, прижимающего друг к другу контактирующие тела, определенный вклад вносит адгезия этих тел. Это становится заметным при сближении их контактирующих поверхностей на расстояния действия межмолекулярных сил и при относительно низких нагрузках. Это следует учитывать при расчетах.
- Фактическая площадь контакта взаимодействующих тел и при неподвижном состоянии, и при относительном перемещении одного тела по другому практически одинакова. В то же время величина внедрения единичной неровности при ее перемещении по деформируемому полупространству приблизительно вдвое превышает внедрение в статическом состоянии, что и следует из геометрии трибоконтакта.
- В ряде случаев необходимо учитывать динамические характеристики контакта трущихся тел. Узлы трения не только подвергаются динамическим воздействиям извне, но и сами могут явиться источником этих воздействий.
Литература
- Доценко А.И., Буяновский И.А. / Основы триботехники. Учебник. — М.: Инфра-М, 2014.
-
Крагельский И.В., Михин Н.М. Узлы трения машин : справочник — Москва: Машиностроение, 1984.
-
Трение, изнашивание и смазка: Справочник. В 2-х кн. / Под ред. И.В. Крагельского, В.В. Алисина. — М.: Машиностроение, 1978, Кн.1
-
А.В. Чичинадзе, Э.Д. Браун, Н.А. Буше и др.; Под общ. ред. А.В. Чичинадзе. / Основы трибологии (трение, износ, смазка). 2-е изд. переработ, и доп. — М.: Машиностроение, 2001.
Формула давления на дно и стенки сосуда
Давление жидкости обусловлено ее весом и, соответственно сила этого давления F равна весу жидкости P. Вес жидкости можно определить, зная ее массу m. А массу можно вычислить по формуле: m=ρV. Объем жидкости в прямоугольном сосуде легко рассчитать. Обозначим высоту сосуда h, а площадь дна буквой S. Тогда объем будет равен: V=Sh. Формула массы в таком случае принимает вид: m=ρV=ρSh . Вес жидкости будет равен: P=gm=gρSh. чтобы рассчитать давление, нам нужна сила этого давления. А мы уже говорили, что сила давления в данном случае равна весу жидкости, поэтому формула давления принимает следующий вид:
Формула для этого давления в атмосфере. Кроме того, поскольку давление представляет собой силу на единицу измерения площади, то. Чтобы рассчитать давление через инструмент барометра, можно было бы заменить объем ртути в барометре в уравнение. Это дало бы уравнение. Вероятно, метеоролог даст атмосферное давление или барометрическое давление в 30 дюймов. Он состоит из длинной трубки, закрытой на одном конце, заполненной ртутью и перевернутой в сосуде с ртутью. На уровне моря сила атмосферного давления будет поддерживать колонку с содержанием ртути 760 мм в высоту.
p=P/S=gρSh/S или p=gρh
То есть в итоге мы пришли к очень интересному моменту — давление не зависит от объема и формы сосуда. Оно зависит только от плотности и высоты столба конкретной жидкости в данном случае. Из чего следует, что, увеличив высоту сосуда, мы можем при небольшом объеме создать довольно высокое давление.
Для давления газа на дно и стенки сосуда формула будет иметь точно такой же вид.
Простые приложения, связанные с давлением
Фактически вес столба ртути равен силе атмосферного давления. Подобным же образом атмосферное давление заставляет воду в подобной колонне высотой до 34 футов! После запуска атмосферное давление на поверхность верхнего контейнера заставляет воду за короткую трубу заменить воду, вытекающую из длинной трубки.
- Фактически это приводит к снижению давления воздуха внутри соломы.
- Сифон можно запустить, заполнив трубку водой.
Наблюдения Бойля можно суммировать в утверждении: при постоянной температуре объем газа изменяется обратно пропорционально давлению, оказываемому на него.
Применение давления на дно и стенки сосуда
Еще один интересный момент заключается в том, что согласно закону Паскаля давление распределяется равномерно не только на дно и стенки, но и в направлении вверх. То есть, если мы погрузим какое-либо тело на определенную глубину, то на него снизу будет действовать сила, равная силе давления на данной глубине, как бы выталкивая тело на поверхность. Именно благодаря этому явлению возможно плавание кораблей. Несмотря на довольно внушительный вес, вода выталкивает судно вследствие эффекта давления воды на стенки сосуда, которыми в данном случае являются борта корабля. С понижением глубины давление увеличивается. Люди научились использовать это явление
, делая борта кораблей в форме сужающихся вниз конусов. Именно поэтому нас доступно покорение морей и океанов.
Кинетическая молекулярная теория Пояснение
Наблюдения за давлением можно объяснить, используя следующие идеи. Быстрое движение и столкновения молекул со стенками контейнера вызывает давление. Давление пропорционально числу молекулярных столкновений и силе столкновений в определенной области. Чем больше столкновений молекул газа со стенками, тем выше давление.
В 17 веке Роберт Бойл впервые сформулировал связь между давлением, объемом и температурой, поскольку они связаны с газом по формуле. Эта формула была результатом его экспериментов с газом, и, как он заметил, газ имел тенденцию к изменению давления, когда он занимал контейнеры различного размера.
А что по поводу давления газов?
Что касается газов, то для них расчет будет абсолютно таким же. Соответственно, наибольший вес окружающего нас газа — воздуха, будет у поверхности Земли. А с увеличением высоты будет уменьшаться как среднее давление, так и плотность окружающего газа. Поэтому воздух на высоте очень разреженный. Там очень трудно как дышать, так и летать, потому что крыльям самолетов не на что опираться. Именно поэтому набирать очень большую высоту летательные аппараты могут только на очень высокой скорости, увеличивая таким образом количество воздуха под крылом в единицу времени.
Эта связь часто упоминается как Закон Бойля. Кроме того, Бойл отметил, что газы имеют тенденцию «возвращаться» к его первоначальному давлению после удаления из контейнера, в котором он либо был сжат, либо расширен. Общая разница в высоте напрямую коррелировала с давлением атмосферы.
Бойл проиллюстрировал это через формула. Рон Куртус. Давление — это сила на объекте, который распространяется по поверхности. Уравнение для давления — это сила, деленная на область, где применяется сила. Хотя это измерение является простым, когда твердое тело надавливает на твердое тело, корпус твердого тела, нажимая на жидкость или газ, требует, чтобы жидкость была ограничена в контейнере.
Нужна помощь в учебе?
Предыдущая тема: Давление в жидкости и газе
Следующая тема: Сообщающиеся сосуды
В соответствии с законом Паскаля
гидростатическое давление на уровне
горизонтального дна сосуда при высоте
жидкости в сосуде, равной Н
,
Сила также может быть создана весом объекта. Вопросы, которые могут возникнуть, включают.
- Какое давление, когда твердое тело подталкивает другое твердое тело?
- Что происходит, когда твердое тело нажимает на ограниченную жидкость?
- Что происходит, когда сила исходит из гравитации?
Этот урок ответит на эти вопросы.
Когда вы применяете силу к твердому объекту, давление определяется как прилагаемое усилие, деленное на область применения. Вы можете видеть, что при заданной силе, если площадь поверхности меньше, давление будет больше. Если вы используете большую область, вы распространяете силу, и давление становится меньше.
Отсюда следует, что абсолютное давление
р
на горизонтальное дно не зависит
от формы сосуда и объема жидкости в нем.
При данной плотности жидкости оно
определяется лишь высотой столба
жидкостиН
и внешним давлениемр
0 .
Сила давления жидкости Р
ж на
дно сосуда зависит от его площадиF
:
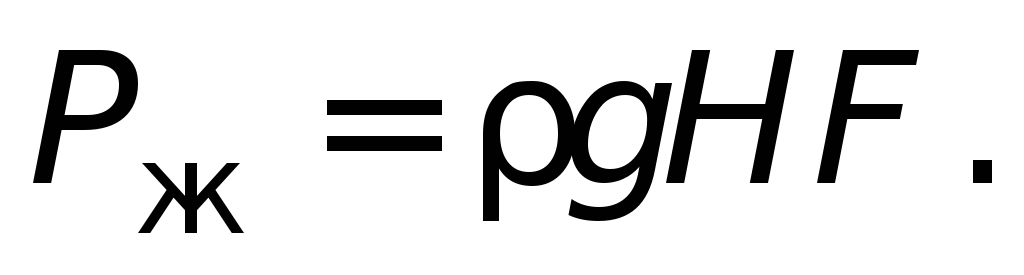
Твердое прессование на ограниченной жидкости
Когда жидкость или газ заключены в контейнер или цилиндр, вы можете создать давление, применяя усилие с помощью твердого поршня. В ограниченной жидкости — пренебрегая влиянием силы тяжести на жидкость — давление одинаково во всем контейнере, одинаково нажимая на все стенки. В случае велосипедного насоса давление, создаваемое внутри насоса, будет передаваться через шланг в велосипедную шину. Но воздух все еще ограничен.
Увеличение силы увеличит давление внутри цилиндра. Поскольку вес объекта является силой, вызванной гравитацией, мы можем заменить вес в уравнении давления. Таким образом, давление, вызванное весом объекта, — это вес, разделенный на область, где применяется вес.
Общая сила давления на дно сосуда
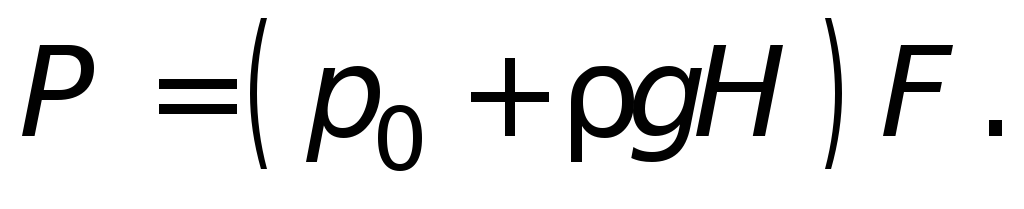
Внешнее давление р 0 передается
жидкостью каждому элементу поверхности
стенки одинаково, поэтому равнодействующая
внешнего давления приложена в точке
центра тяжести поверхности стенки.
Давление веса жидкости на стенку не
одинаково по высоте: чем глубже расположен
элемент стенки, тем большее давление
веса жидкости он испытывает. Поэтому
центр давления жидкости на вертикальную
стенку расположен всегда ниже центра
тяжести смоченной поверхности стенки.
Если вы помещаете твердый предмет на пол, давление на пол над областью контакта — это вес предмета, разделенного областью на полу. Хороший пример того, как сила на небольшой площади может привести к очень сильному давлению, наблюдается в обуви женщин с высокими шипами. Эти типы обуви могут нанести ущерб некоторым полам из-за очень высокого давления на пол на каблук.
Средний ботинок распределяет вес человека более 20 квадратных дюймов. В некоторых случаях этого достаточно, чтобы повредить пол. Если вы положите жидкость в контейнер, вес этой жидкости будет нажимать на дно контейнера, аналогичную весу твердого объекта. Давление на дно контейнера будет таким же, как если бы вес был из твердого вещества.
Сила полного гидростатического давления
на плоскую стенку равна произведению
гидростатического давления в центре
тяжести этой стенки и ее площади:
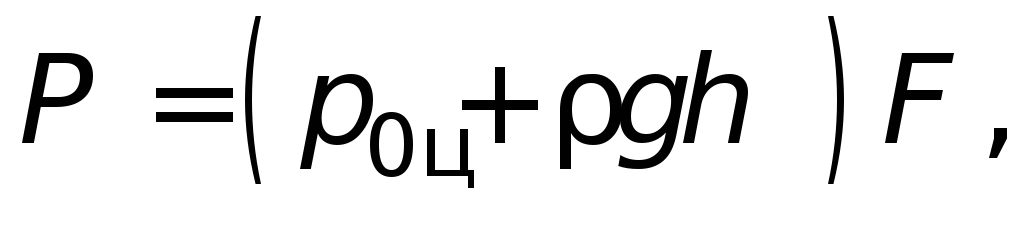
где
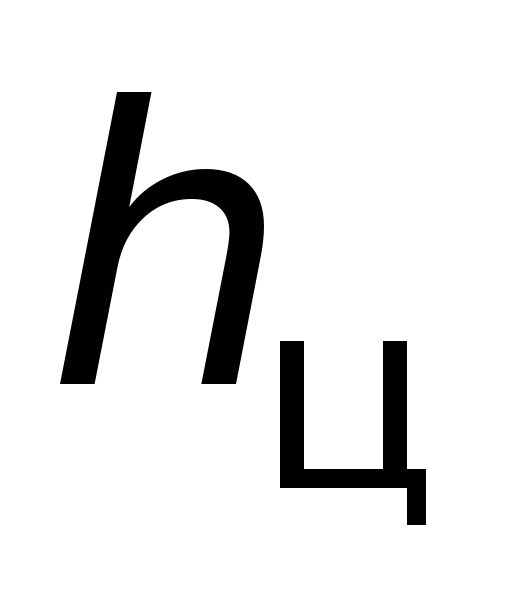
до центра тяжести смоченной поверхности
стенки; оно зависит от геометрической
формы стенки.
Единственное различие заключается в том, что давление в жидкости идет во все стороны. Таким образом, давление на сторонах внизу будет одинаковым. Газы и жидкости проявляют давление из-за их веса в каждой точке жидкости. Давление может быть измерено для твердого тела, нажимая на твердое тело, но в случае твердого тела, нажимающего на жидкость или газ, требуется, чтобы жидкость была ограничена в контейнере. Надавите на себя, чтобы преуспеть.
Самые популярные книги по физике силы. Если да, отправьте электронное письмо с отзывами. Пожалуйста, включите его в качестве ссылки на свой сайт или в качестве ссылки в своем отчете, документе или тезисе. Участники, подверженные воздействию осесимметричных нагрузок.
Точка приложения сил Р
иР
изб носит название центра давленияh
д и может быть определена в соответствии
с законами теоретической механики через
момент инерции смоченной поверхности
стенки
Тонкостенный цилиндр под давлением. Преамбула: сосуды высокого давления чрезвычайно важны в промышленности. Обычно в обычной практике используются два типа сосудов высокого давления, такие как цилиндрический сосуд высокого давления и сферический сосуд высокого давления.
При анализе этих стеновых цилиндров, подвергнутых внутренним давлениям, предполагается, что радиальные планы остаются радиальными, а доза толщины стенки не изменяется из-за внутреннего давления. Далее, при анализе их стеновых цилиндров, вес жидкости считается пренебрежимым.
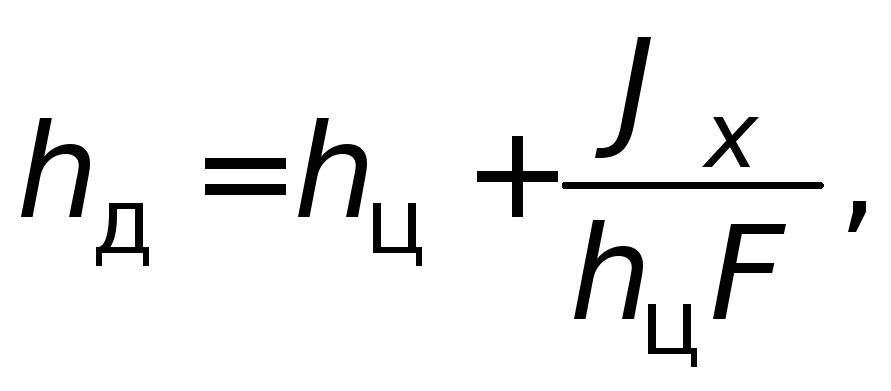
где J
x
– момент инерции
стенки относительно осиox
.
Для прямоугольной стенки при уровне
жидкости в сосуде, равном Н
, и ширине
стенкиВ
Следовательно,
Этот цилиндр подвергается разности гидростатического давления р между его внутренней и внешней поверхностями. Во многих случаях р между давлением избыточного давления внутри цилиндра, заставляя внешнее давление быть окружающим. Небольшой кусок стенки цилиндра показан изолированно, а напряжения в соответствующем направлении также показаны.
Такой компонент не срабатывает, поскольку при чрезмерно высоком внутреннем давлении. Хотя это может потерпеть неудачу, разрываясь по пути, следующему окружности цилиндра. При нормальных обстоятельствах он терпит неудачу по обстоятельствам, которые он терпит неудачу, разрываясь вдоль пути, параллельного оси. Это говорит о том, что напряжение пялец значительно выше, чем осевое напряжение.
-
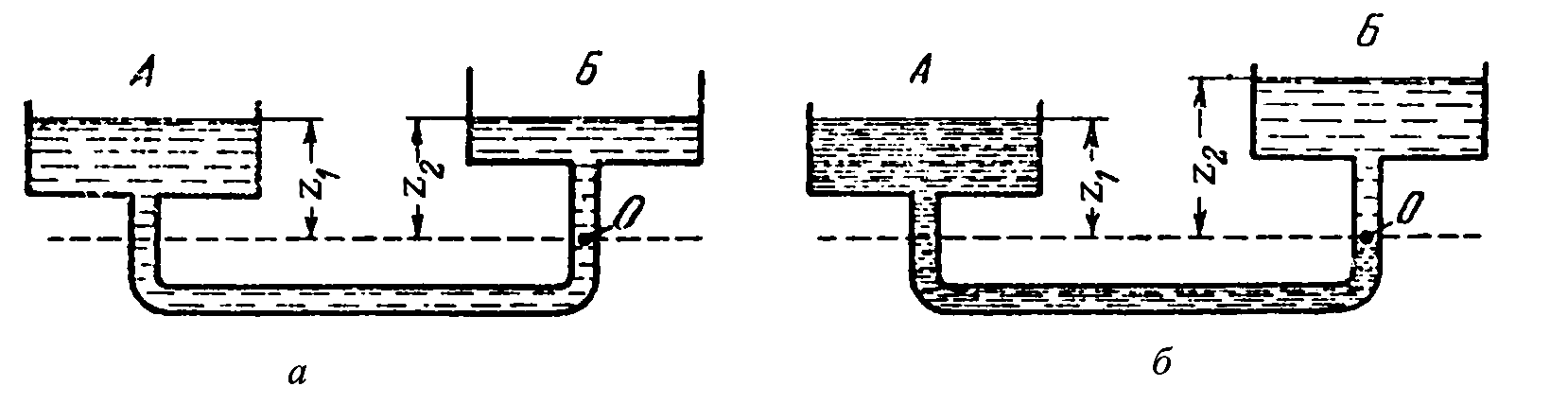
Практическое использование законов гидростатики
Применив закон Паскаля к сообщающимся
сосудам, можно прийти к следующим
выводам.
Если сосуды (рис. 1.4 а
) заполнены
однородной жидкостью (одинаковой
плотности), то при равновесии давление
в точке 0 может быть выражено:
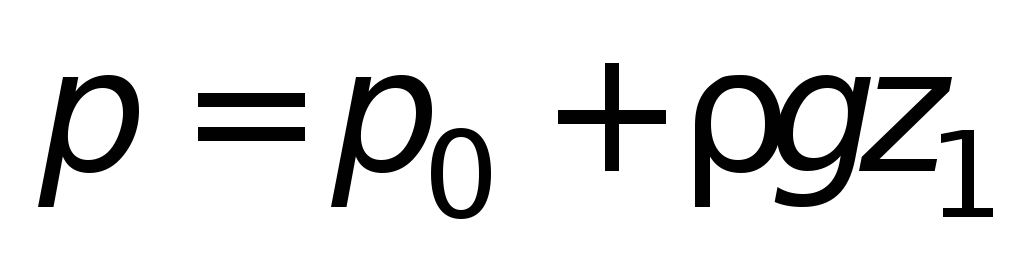
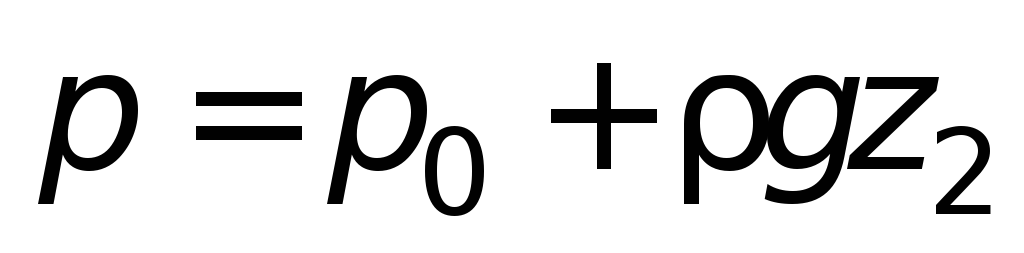
Чтобы получить выражения для различных напряжений, сделаем следующее. Жидкие резервуары и емкости для хранения, водопроводные трубы, котлы, корпуса подводных лодок и некоторые компоненты воздушной плоскости являются общими примерами тонкостенных цилиндров и сфер, куполов крыши.
В стенке нет напряжений сдвига. Продольные и пястные напряжения не меняются через стену. Состояние выноса для элемента тонкостенного сосуда высокого давления считается двухосным, хотя внутреннее давление, действующее нормали к стене, вызывает локальное напряжение сжатия, равное внутреннему давлению. На самом деле состояние трехосевого напряжения существует на внутри судна. Однако для тогдашнего стенного сосуда давления третье напряжение намного меньше, чем два других напряжения, и по этой причине в этом можно пренебречь.
т.е. в сообщающихся сосудах заполняющая
их однородная жидкость располагается
на одинаковом уровне.
При заполнении сосудов жидкостями с
различной плотностью (рис 1.4 б
) в
условиях равновесия давление в точке
О будет
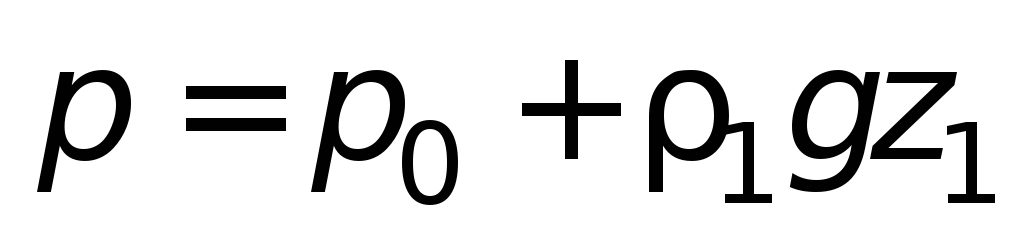
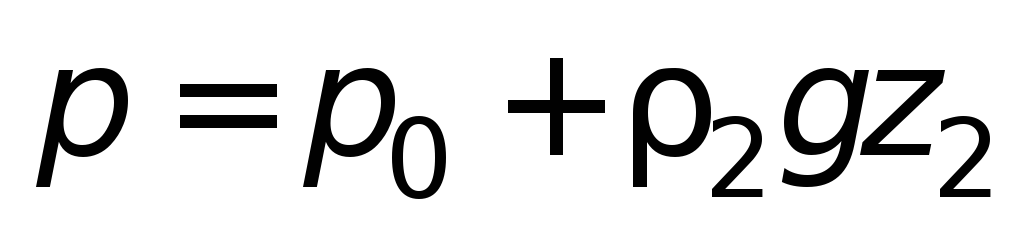
Тонкие цилиндры, подверженные внутреннему давлению. Когда тонкостенный цилиндр подвергается внутреннему давлению, в материалах цилиндра будут установлены три взаимно перпендикулярных главных напряжения, а именно. Окружность или шероховатость. Теперь определим эти напряжения и определим выражения для них.
Обруч или периферический стресс. Это напряжение, которое создается в противодействии разрушающему эффекту приложенного давления и может быть наиболее удобно обрабатываться с учетом равновесия цилиндра. На рисунке мы показали одну половину цилиндра. Общее усилие на одной половине цилиндра из-за внутреннего давления р.
Рисунок 1.4
– Сообщающиеся сосуды, заполненные
жидкостью:
а
– одной плотности;б
– разной плотности
Следовательно
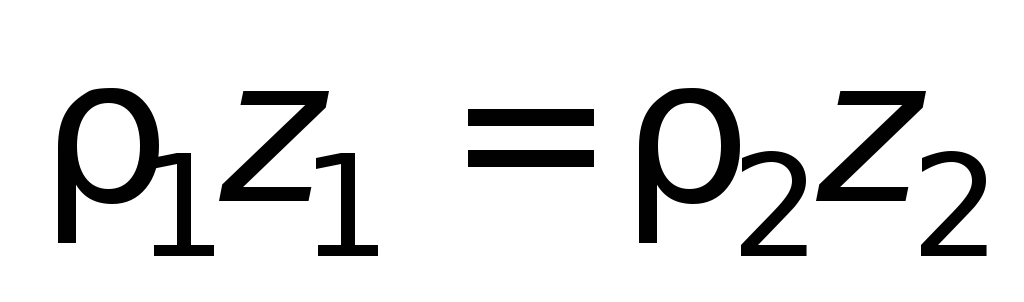
т.е.
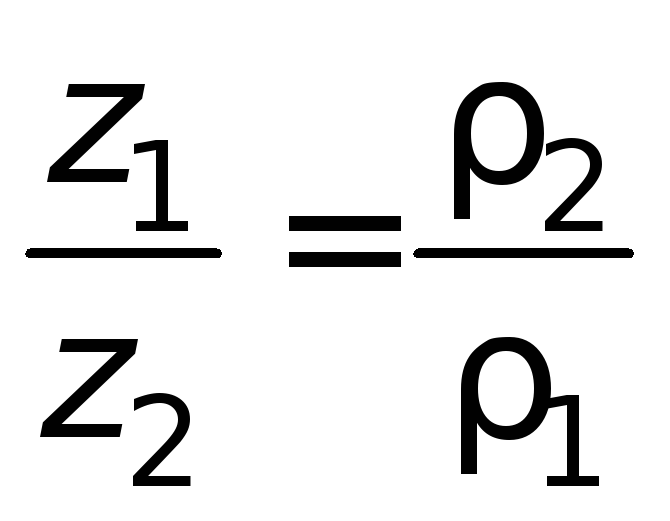
Т. — сила в одной стенке полуцилиндра. Требования к сложным системам автоматизированной обработки, потребность во все более жестком управлении технологическими процессами и все более строгая нормативная среда приводят к тому, что инженеры-разработчики стремятся получать более точные и надежные системы измерения уровня. Повышенная точность позволяет снизить изменчивость химического процесса, что приводит к повышению качества продукта, снижению затрат и меньшему количеству отходов. Правила, особенно касающиеся электронных документов, устанавливают жесткие требования к точности, надежности и электронной отчетности.
Соотношение (1.12) указывает на то, что
высоты уровней жидкости, отсчитываемые
от поверхности раздела, обратно
пропорциональны плотностям жидкостей.
Этот принцип используется для измерения
уровня жидкости в закрытых аппаратах
с помощью водомерных стёкол, в жидкостных
манометрах.
Если сообщающиеся сосуды заполнены
одной и той же жидкостью, но давление
над уровнем жидкости в них разное – р
1 ир
2 , то при равновесии
Технология измерения уровня в переходном периоде
Новые технологии измерения уровня помогают удовлетворить эти требования. Простейшим и самым старым промышленным устройством, конечно же, является смотровое стекло. Ручной подход к измерению, очки зрения всегда имели ряд ограничений. Уплотнения подвержены утечке, а наращивание, если оно присутствует, скрывает видимый уровень. Можно безоговорочно заявить, что обычные смотровые стекла являются самым слабым звеном любой установки. Поэтому их быстро заменяют более современные технологии.
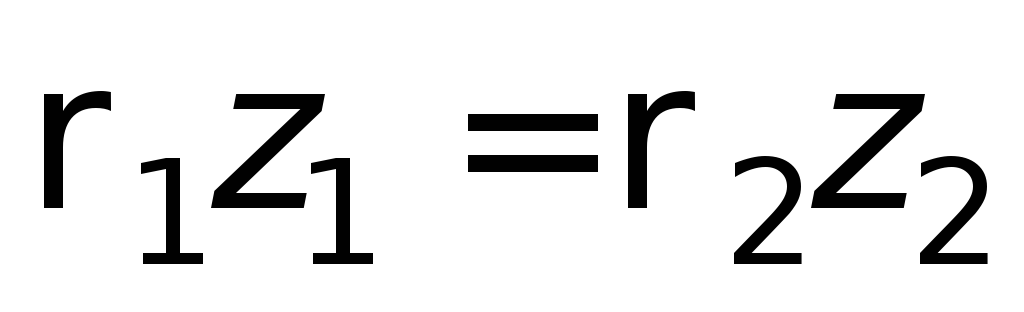
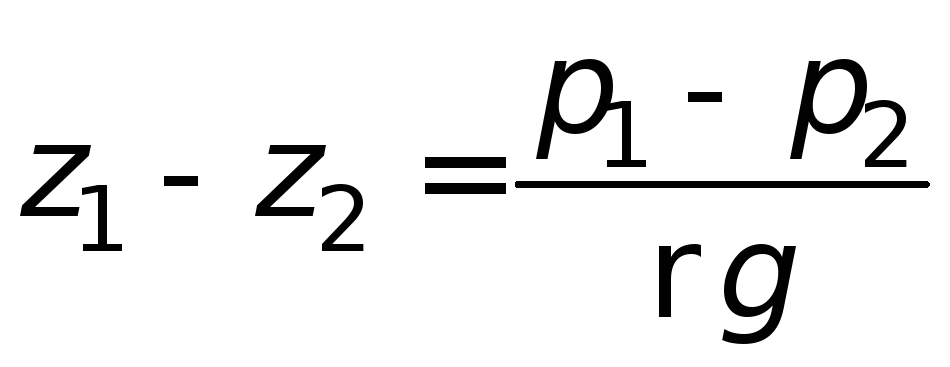
Последнее выражение используется при
измерении давления или разности давлений
между различными точками с помощью
дифференциальных U
-образных
манометров.
Другие устройства обнаружения уровня включают те, которые основаны на удельном весе, физическом свойстве, наиболее часто используемом для восприятия поверхности уровня. Простой поплавок, имеющий удельный вес между потоками технологической жидкости и паром свободного пространства, будет плавать на поверхности, точно после ее подъемов и падений. Измерения гидростатической головки также широко использовались для определения уровня.
Когда задействованы более сложные физические принципы, возникающие технологии часто используют компьютеры для выполнения вычислений. Это требует отправки данных в машиночитаемом формате от датчика к системе управления или мониторинга. Полезными форматами выходных сигналов преобразователя для компьютерной автоматизации являются токовые петли, аналоговые напряжения и цифровые сигналы. Аналоговые напряжения просты в настройке и работе, но могут иметь серьезные проблемы с помехами и помехами.
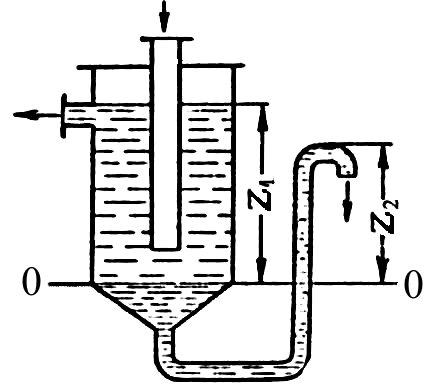
Рисунок 1.5.
– К определению высоты гидравлического
затвора
Этот же принцип используется для
определения высоты гидравлического
затвора в аппаратах, заполненных
жидкостью (рис. 1.5).
На рисунке представлен сосуд, заполненный
двумя жидкостями с плотностями 1 и 2 ; уровень
их раздела на глубинеz
1 необходимо поддерживать в процессе
работы постоянным с помощью гидрозатвора,
представляющего собойU
-образную
трубку, подсоединённую снизу (на выходе
жидкости из аппарата).
В соответствии с уравнением (1.12) высота
гидравлического затвора в случае
одинакового давления над жидкостью
внутри аппарата и на выходе из затвора
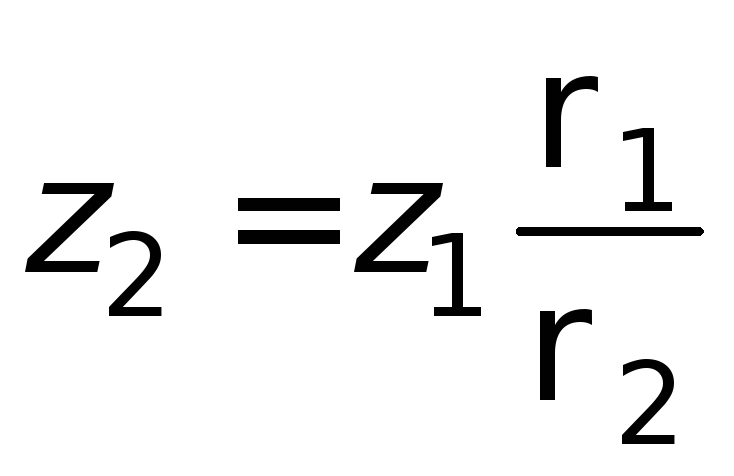
На использовании данного уравнения
гидростатики основана работа таких
простейших гидравлических машин, как
гидравлический пресс, мультипликатор
(для повышения давления), домкрат,
подъемник и др.
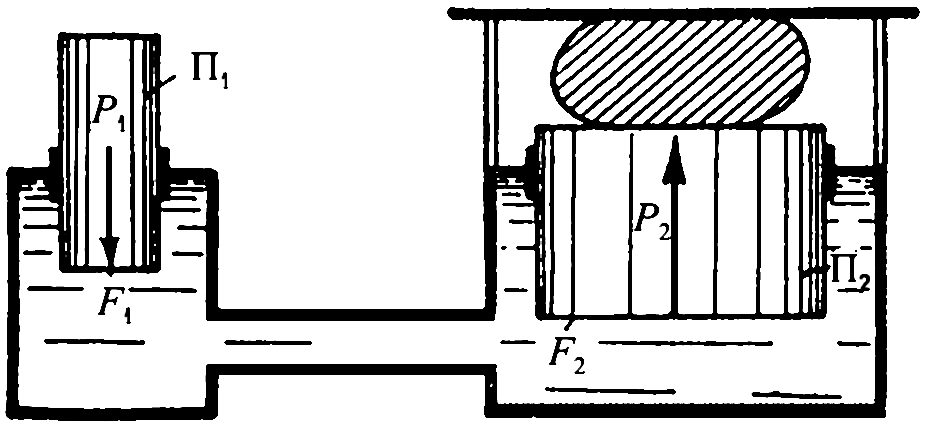
Рисунок 1.6
– Схема гидравлического пресса
На рис. 1.6 показана схема
гидравлического пресса. Если к поршню
П 1 , имеюшему площадьF
1 ,
приложена силаР
1 , то эта сила
будет передаваться на жидкость; жидкость
же будет давить на поршень П 2 ,
имеющий площадьF
2 , с силойР
2
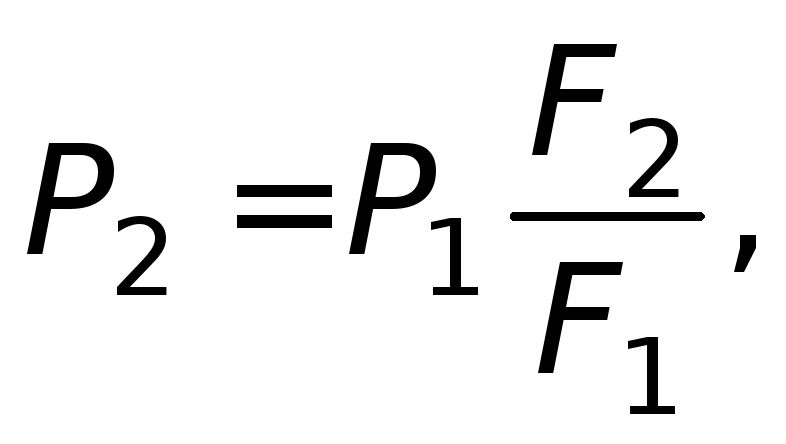
так как гидростатические давления в
точках площади F
1 и площадиF
2 практически равны между собой:
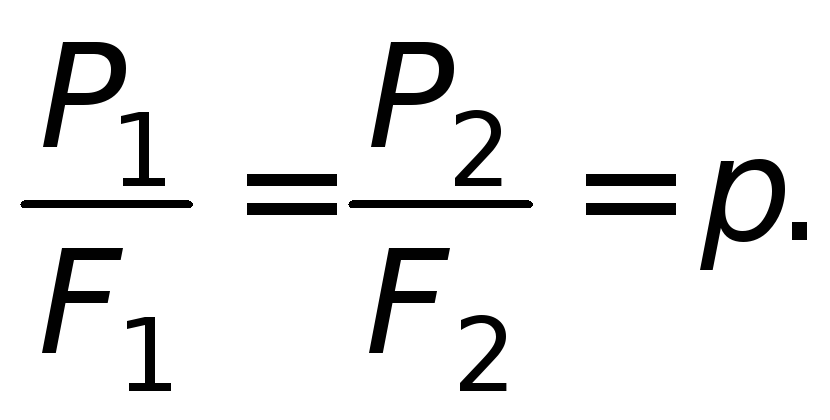
Из уравнения (1.16) следует, что при помощи
пресса сила Р
1 увеличивается
во столько раз, во сколько площадьF
2 больше площадиF
1 .
Давление
Известно, что человеку удобнее ходить по глубокому снегу на лыжах, так как при этом он меньше проваливается под снег. А разрезать предметы удобнее остро отточенным ножом. Причина этого – давление. В первом случае мы стремимся уменьшить давление на снег, а во втором случае, мы стараемся максимально увеличить давление.
Формула давления твердого тела
Рассмотрим твердое тело, например, кирпич. Пусть он лежит на горизонтальной поверхности и давит на нее своим весом (рис. 1).
Рис. 1. Твердое тело опирается на поверхность площадью S и давит на нее своим весом mg
На рисунке символом S обозначена нижнее основание тела – это площадь, на которую тело опирается (давит). Сила, с которой тело давит на поверхность – это сила тяжести mg.
Давление, которое твердое тело оказывает на поверхность, можно рассчитать так:
[ large boxed{ P = frac{F_{perp}}{S} }]
Примечание: Эта формула подходит для расчета давления твердых тел. Существует еще одна формула, с помощью которой рассчитывают давление жидкостей.
( P left( text{Па}right) ) – давление;
( F_{perp} left(H right) ) – сила, которая давит (сила давления). Эта сила располагается под прямым углом к поверхности;
( S left( text{м}^{2}right) ) – площадь, на которую давит сила.
Иногда в условии задачи указывают площадь в квадратных сантиметрах, или других единицах, отличающихся от основных единиц, принятых в СИ. Чтобы правильно рассчитать давление, нужно уметь переводить площадь в квадратные метры.
В системе СИ давление измеряется в Паскалях.
[ large 1 text{Па} = frac{1 H}{1 text{м}^{2}} ]
Поэтому, перед решением задач, нужно давление переводить в Паскали, если в условии встретятся другие единицы измерения давления.
В некоторых школьных задачах просят найти не давление, а силу давления. Нужно уметь их различать.
Сила давления, как и любая сила, измеряется в Ньютонах. Именно она давит на поверхность.
А давление — это дробь, в числителе расположена сила, которая давит, а в знаменателе — площадь поверхности, на которую давят. Давление измеряют в Паскалях.
Примечание: Давление – это сила, деленная на площадь. Сила должна располагаться перпендикулярно поверхности (рис. 2а).
Когда сила не перпендикулярна поверхности
Силу раскладываем на проекции, если она направлена к поверхности не под прямым углом (рис. 2б). Выберем часть силы, расположенную перпендикулярно поверхности. Именно эту часть силы и нужно подставлять в формулу для расчета давления.
Рис. 2. Если сила, которая давит на поверхность, направлена не под прямым углом к поверхности, раскладываем силу на проекции и выбираем часть, которая располагается к поверхности перпендикулярно
Оценка статьи:
Загрузка…